Next Article in Journal
Reliability of the Ginzburg–Landau Theory in the BCS-BEC Crossover by Including Gaussian Fluctuations for 3D Attractive Fermions
Next Article in Special Issue
The Strange-Metal Behavior of Cuprates
Previous Article in Journal
Silicon Drift Detectors’ Spectroscopic Response during the SIDDHARTA-2 Kaonic Helium Run at the DAΦNE Collider
Previous Article in Special Issue
Nanoscale Phase Separation of Incommensurate and Quasi-Commensurate Spin Stripes in Low Temperature Spin Glass of La2−xSrxNiO4
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Condensed Matter
Volume 6
Issue 4
10.3390/condmat6040048
condensedmatter-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Out-of-Plane Sulfur Distortions in the Bi4O4S3 Superconductor

by
Sharon S. Philip
1,
Anushika Athauda
1,†,‡,
Yosuke Goto
2,†,
Yoshikazu Mizuguchi
2,† and
Despina Louca
1,*
1
Department of Physics, University of Virginia, Charlottesville, VA 22904, USA
2
Department of Physics, Tokyo Metropolitan University, 1-1 Minami-Osawa, Tokyo 192-0397, Japan
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
‡
Current address: Department of Physics and Astronomy, Virginia Military Institute, Lexington, VA 24450, USA.
Condens. Matter 2021, 6(4), 48; https://doi.org/10.3390/condmat6040048
Submission received: 19 October 2021 / Revised: 16 November 2021 / Accepted: 22 November 2021 / Published: 26 November 2021
(This article belongs to the Special Issue Quantum Complex Matter from Charge Density Waves to Superstripes)
Browse Figures
Versions Notes

Abstract

:
The local atomic structure of the non-magnetic layered superconductor Bi 4 O 4 S 3 was investigated using neutron diffraction and pair density function (PDF) analysis. Although on average, the crystal structure is well ordered, evidence for local, out–of–plane sulfur distortions is provided, which may act as a conduit for charge transfer from the SO 4 blocks into the superconducting BiS 2 planes. In contrast with LaO 1 − x F x BiS 2 , no sulfur distortions were detected in the planes, which indicates that charge density wave fluctuations are not supported in Bi 4 O 4 S 3 .

1. Introduction

Superconductors with competing ground states have been extensively studied ever since the discovery of the cuprates [1]. Most of the recent interest has been in materials whose parent ground state is magnetic. The bismuth sulfide class of superconductors [2,3,4,5,6,7,8], although not magnetic, is a test bed for investigating the effects of charge density wave (CDW) instabilities [9,10], lattice modes leading to phonon softening [9], and spin–orbit (SO) interactions [11,12] on the superconducting mechanism. The BiS 2 superconductors exhibit strong electronic correlations [11]. Density functional theory calculations suggested that spin polarization is present even though the crystal lattice is centrosymmetric [10,11]. Given its quasi-two-dimensional nature, BiS 2 may exhibit SO coupling without breaking crystal inversion symmetry, but instead driven by atomic site asymmetry [11].
Two kinds of superconductors were discovered in the earlier stage, Bi 6 O 4 S 4 (SO 4 ) 1 − x [2] and LnO 1 − x F x BiS 2 with Ln = Pr, Ce, La, and Yb [3,13]. The former consists of a sulfate layer where vacancies and crystal defects are common. The structure is analogous to that of LaOFeAs, an Fe-based superconductor [14]. Superconductivity occurs in the BiS 2 layer that has vacancies, while in the latter, crystal defects induced under pressure have been linked to a higher T c . The LnO 1 − x F x BiS 2 system exhibits a peculiar relationship between its structural and superconducting properties where doping with F brings significant disorder to the crystal structure, as well as inducing superconductivity.
In the BiS 2 system, the dominant carriers arise from the Bi 6p orbitals that strongly hybridize with the S 3p orbitals near the Fermi surface. A CDW instability has been proposed in LnO 1 − x F x BiS 2 that arises from a ( π , π , 0 ) mode, which corresponds to in–plane displacements of S atoms around the M point [10]. This was verified experimentally in our previous work in [15] on LaO 1 − x F x BiS 2 . The xy–mode of S displacements breaks the long–range symmetry, indicating a long–range CDW state. Whether or not these kinds of distortions exist in the Bi 6 O 4 S 4 (SO 4 ) 1 − x class of materials has not been investigated. The (SO 4 ) –deficient compound Bi 4 O 4 S 3 corresponding to x = 0.5 is superconducting with T c = 4.5 K [2,16]. Using neutron scattering and pair density function (PDF) analysis, we verified the absence of in–plane S displacements in the BiS 2 superconducting plane of Bi 4 O 4 S 3 . This finding points to the absence of the CDW instability, as proposed in LaO 1 − x F x BiS 2 . Instead, an out–of–plane S displacement along the c–axis (0.29 Å in magnitude) is observed, which may lead to a possible charge transfer mechanism from the charge reservoir layers to the superconducting Bi planes. This motion is reminiscent of what was proposed in the cuprate–based superconductor, YBa 2 Cu 3 O 7 − δ , in which oxygen motion in the chains above the superconducting CuO2 layer was attributed to charge transfer [17,18,19]. The role of out–of–plane S displacement in the charge transfer mechanism for self-doping of the active BiS 2 –layer has been reported in other BiS 2 –based superconductors as well [20,21].

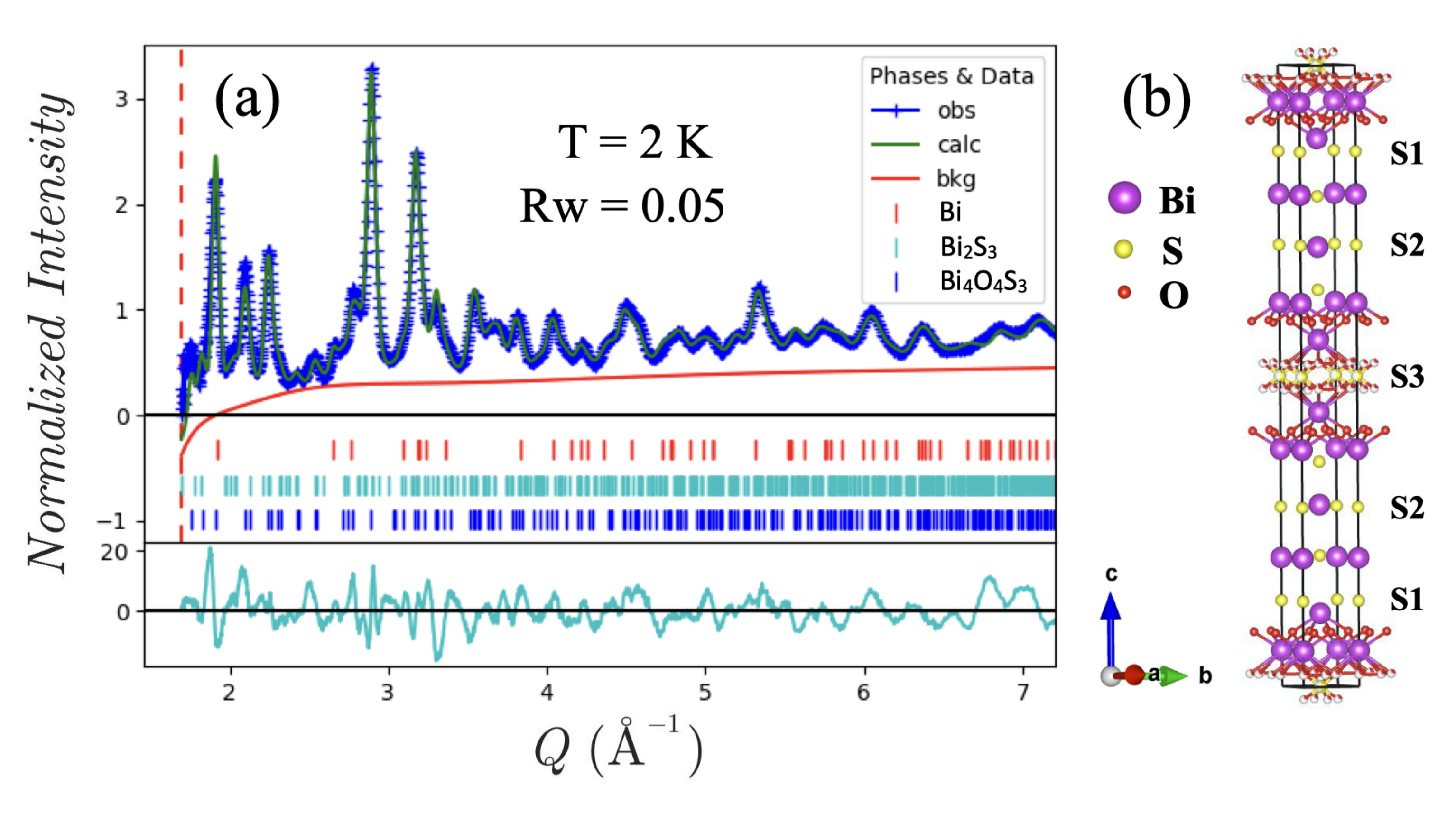
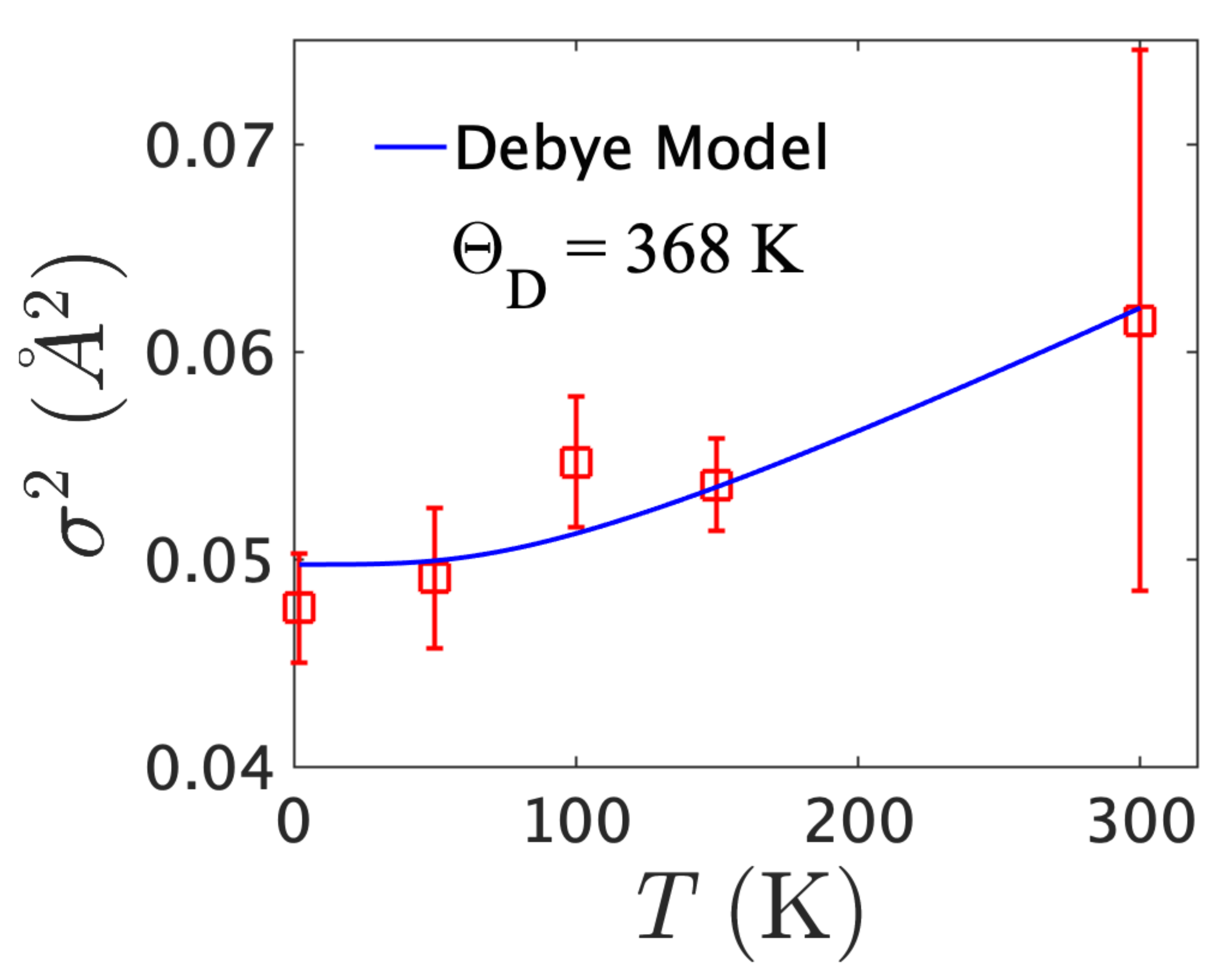
2. Results and Discussion

Bi 4 O 4 S 3 has a tetragonal crystal structure with the I 4 / m m m space group and lattice parameters a = b = 3.981 Å and c = 41.466 Å. The refinement results with the neutron powder diffraction data at 2 K fit well using the tetragonal structure. The results are shown in Figure 1a, with a goodness of fit parameter of R w = 0.05. The powder sample contained additional phases of Bi2S3 and unreacted bismuth. Shown in Figure 1b is the unit cell of Bi 4 O 4 S 3 with the BiS 2 planes. The three S atom positions along the c axis are labeled S1, S2, and S3, as shown in the diagram for the unit cell. The S2 atoms in the BiS 2 layers lie on the same plane as the Bi atoms, whereas the S1 atom is above the BiS 2 layer, at the apical site. The S3 atoms are part of the SO4 layer at z = 0.5 , which is sandwiched by the Bi2O2 layers. Defects of SO4 ions exist in Bi 4 O 4 S 3 , the chemical composition being Bi 6 O 4 S 4 (SO 4 ) 1 − x where x = 0.5 , and the site occupancies of S3 and O atoms in this layer are 0.5 and 0.25, respectively.
Shown in Figure 2a,b is the temperature dependence of the a and c lattice constants, respectively, obtained from the average structure refinement. Both the a and c lattice constants increase with temperature due to thermal expansion. Figure 2c shows the position z along the c axis within the unit cell for the S1 atom as a function of temperature. The z coordinate is plotted as obtained from both the average and local structure refinement results. The local structure was determined from the PDF by Fourier transforming the powder diffraction spectrum (Bragg peaks + diffuse scattering) into the real space (see the Methods Section). It can be seen that the z coordinate obtained from the local structure refinement is consistently higher than the one obtained from the average crystal structure refinement, which will be explored further. However, the larger uncertainty in z from PDF refinement suggests that we cannot make inferences on the temperature dependence of the S1 atom displacements from the PDF analysis.
Shown in Figure 2d is the magnetization (M) as a function of temperature in the presence of an applied magnetic field of 10 Oe below 6 K. A large increase in the diamagnetic response of the sample is seen below ∼4.5 K in the zero-field-cooled (ZFC) magnetization, indicating the onset of superconductivity, in agreement with previous reports [2].
Figure 3 shows the results of the PDF analysis, which provides information on the local arrangement of atoms in the real space and is very sensitive to short-range distortions [22,23]. Shown in Figure 3a is a comparison of the reduced pair distribution function G ( r ) obtained from the experimental data (for Bi 4 O 4 S 3 at 2 K) to G ( r ) calculated from the “average” model based on the structural parameters obtained from Rietveld refinement. The splitting of the peak at ∼3 Å, which corresponds to S atom correlations with other atoms, cannot be reproduced using this average model. Figure 3c shows the same experimental data as in Figure 3a, but comparing to a “local” model of G ( r ) where the S1 and S2 atoms are displaced along the c axis by 0.29 Å and 0.05 Å, respectively. (The calculated peaks below r = 2 Å arising from the atom correlations within the sulfate layer are comparable to the noise level of the experimental data.) Figure 3b shows the difference between the average and local models, with arrows marking the displacements of the apical sulfur atom towards the BiS 2 layers in the local model relative to the average model. There is good agreement between the data and the local model. In particular, the splitting of the second peak was reproduced after the apical S atom was displaced from the average-model position. In the local model, the Bi–S bond becomes shorter and the S1 atom moves further from the Bi 2 O 2 layer towards the superconducting BiS 2 planes as compared to the average model. This suggests the presence of a charge transfer mechanism, which is reminiscent of what is observed in other layered superconducting systems such as YBa2Cu3O7 − δ (YBCO), where the oxygen atom movement towards the CuO2 planes has been explored [17]. Charge fluctuations are known to exist in materials belonging to the family of BiS 2 superconductors. LaO 1 − x F x BiS 2 , for instance, shows in–plane short-range distortions of sulfur atoms [15,24]. In Bi 4 O 4 S 3 , however, the BiS 2 layer is robust, and no evidence for in–plane distortions or charge fluctuations were found in contrast to other BiS 2 –based superconductors.
The effects of the lattice vibrations on the PDF peak widths were modeled using the correlated Debye model [25,26] (see the Methods Section), and the Debye temperature for Bi4O4S3 was estimated by studying the mean-squared relative displacements of atomic pair motion as a function of temperature. The PDF peak width FWHM ( σ ) values from the experimental data were extracted by fitting Gaussian functions to the Bi–O atom pair nearest neighbor correlation peak. Shown in Figure 4 is the temperature dependence of σ 2 fit using the correlated Debye model. The Debye temperature, θ D , from the model was determined to be 368 K.

3. Materials and Methods

Polycrystalline samples of Bi 4 O 4 S 3 were prepared by the solid state reaction method using Bi, S, and Bi2O3. The details of the sample preparation were reported in [2]. The temperature dependence of the magnetic susceptibility from 2 K to 6 K was measured in the zero–field–cooled (ZFC) and field–cooled (FC) modes using a superconducting quantum interference device (SQUID) magnetometer with a 10 Oe applied magnetic field.
The time–of–flight (TOF) neutron diffraction experiment was carried out at the Nanoscale Ordered Materials Diffractometer (NOMAD) at the Spallation Neutron Source (SNS) of Oak Ridge National Laboratory (ORNL). The data were analyzed using Rietveld refinement to find parameters characterizing the crystal structure [27], resulting in what we label the “average model”. The PDF analysis [28,29], which provides information on the local arrangement of atoms in the real space without the assumption of periodicity, was performed on the same neutron diffraction data used for the Rietveld refinement. NOMAD is a diffractometer with a large bandwidth of momentum transfer Q, and it provides the total structure function S ( Q ) . S ( Q ) was Fourier transformed into the real space, as shown in Equation (1), to obtain G ( r ) [30,31].
G ( r ) e x p = 2 π ∫ 0 ∞ Q [ S ( Q ) − 1 ] s i n ( Q r ) d Q .
The instrument background and empty sample can were subtracted from S ( Q ) , and the data were normalized by vanadium. A maximum Q of 40 Å−1 was used. G ( r ) corresponds to the probability of finding a particular pair of atoms with an inter-atomic distance r [32].
The crystal structure models were generated using the VESTA software [33]. The correlated Debye model [25,26,34] was used to find the Debye temperature, θ D , from the temperature dependence of PDF peak widths. Using Equation (2), the full-width at half-maximum (FWHM), defined as σ i j , was extracted from the PDF peak corresponding to the Bi–O nearest neighbor correlations. Here, the Debye wavevector is given by k D = ( 6 π 2 N / V ) 1 / 3 , where N / V is the number density of the crystal; the Debye cutoff frequency is ω D = k B θ D / ℏ , where k B is the Boltzmann constant; Φ n = ∫ 0 θ D / T x n ( e x − 1 ) − 1 d x , where x is a dimensionless integration variable.
σ i j 2 = 6 ℏ M ω D [ 1 4 + T θ D 2 Φ 1 − 1 − c o s ( k D r i j ) 2 ( k D r i j ) 2 − T θ D 2 ∫ 0 θ D T s i n k D r i j T x θ D / k D r i j T θ D e x − 1 d x ]

4. Conclusions

The crystal structure and local atomic distortions in the layered superconductor Bi4O4S3 were investigated as a function of temperature. The lattice undergoes a thermal expansion in the temperature range from 2 K to 300 K in both the in–plane and out–of–plane directions. While the average crystal structure is consistent with the I 4 / m m m space group symmetry across the temperature range, the local structure analysis revealed that the apical S1 atoms move up by 0.29 Å toward the superconducting BiS2 planes, suggesting a charge transfer mechanism.

Author Contributions

Conceptualization, D.L.; data curation, S.S.P. and A.A.; formal analysis, S.S.P.; funding acquisition, D.L.; investigation, S.S.P.; methodology, S.S.P.; resources, Y.G., Y.M. and D.L.; supervision, D.L.; writing—original draft, S.S.P.; writing—review and editing, D.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the U.S. Department of Energy (DOE), Grant Number DE-FG02-01ER45927.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

A portion of this research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by Oak Ridge National Laboratory. We thank John Schneeloch (University of Virginia) for valuable inputs on the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Egami, T.; Louca, D.; McQueeney, R. Nonuniform metallic state in manganites and cuprates. J. Supercond. 1997, 10, 323–327. [Google Scholar] [CrossRef]
  2. Mizuguchi, Y.; Fujihisa, H.; Gotoh, Y.; Suzuki, K.; Usui, H.; Kuroki, K.; Demura, S.; Takano, Y.; Izawa, H.; Miura, O. BiS2-based layered superconductor Bi4O4S3. Phys. Rev. B 2012, 86, 220510. [Google Scholar] [CrossRef] [Green Version]
  3. Mizuguchi, Y.; Demura, S.; Deguchi, K.; Takano, Y.; Fujihisa, H.; Gotoh, Y.; Izawa, H.; Miura, O. Superconductivity in Novel BiS2-Based Layered Superconductor LaO1-xFxBiS2. J. Phys. Soc. Jpn. 2012, 81, 114725. [Google Scholar] [CrossRef] [Green Version]
  4. Demura, S.; Mizuguchi, Y.; Deguchi, K.; Okazaki, H.; Hara, H.; Watanabe, T.; James Denholme, S.; Fujioka, M.; Ozaki, T.; Fujihisa, H.; et al. New Member of BiS2-Based Superconductor NdO1-xFxBiS2. J. Phys. Soc. Jpn. 2013, 82, 033708. [Google Scholar] [CrossRef]
  5. Xing, J.; Li, S.; Ding, X.; Yang, H.; Wen, H.H. Superconductivity appears in the vicinity of semiconducting-like behavior in CeO1-xFxBiS2. Phys. Rev. B 2012, 86, 214518. [Google Scholar] [CrossRef] [Green Version]
  6. Usui, H.; Suzuki, K.; Kuroki, K. Minimal electronic models for superconducting BiS2 layers. Phys. Rev. B 2012, 86, 220501. [Google Scholar] [CrossRef] [Green Version]
  7. Kotegawa, H.; Tomita, Y.; Tou, H.; Izawa, H.; Mizuguchi, Y.; Miura, O.; Demura, S.; Deguchi, K.; Takano, Y. Pressure study of BiS2-based superconductors Bi4O4S3 and La(O, F)BiS2. J. Phys. Soc. Jpn. 2012, 81, 103702. [Google Scholar] [CrossRef] [Green Version]
  8. Deguchi, K.; Mizuguchi, Y.; Demura, S.; Hara, H.; Watanabe, T.; Denholme, S.; Fujioka, M.; Okazaki, H.; Ozaki, T.; Takeya, H.; et al. Evolution of superconductivity in LaO1-xFxBiS2 prepared by high-pressure technique. EPL (Europhys. Lett.) 2013, 101, 17004. [Google Scholar] [CrossRef] [Green Version]
  9. Yildirim, T. Ferroelectric soft phonons, charge density wave instability, and strong electron-phonon coupling in BiS2 layered superconductors: A first-principles study. Phys. Rev. B 2013, 87, 020506. [Google Scholar] [CrossRef] [Green Version]
  10. Wan, X.; Ding, H.C.; Savrasov, S.Y.; Duan, C.G. Electron-phonon superconductivity near charge-density-wave instability in LaO0.5F0.5BiS2: Density-functional calculations. Phys. Rev. B 2013, 87, 115124. [Google Scholar] [CrossRef] [Green Version]
  11. Zhang, X.; Liu, Q.; Luo, J.W.; Freeman, A.J.; Zunger, A. Hidden spin polarization in inversion-symmetric bulk crystals. Nat. Phys. 2014, 10, 387–393. [Google Scholar] [CrossRef] [Green Version]
  12. Mazziotti, M.V.; Valletta, A.; Raimondi, R.; Bianconi, A. Multigap superconductivity at an unconventional Lifshitz transition in a three-dimensional Rashba heterostructure at the atomic limit. Phys. Rev. B 2021, 103, 024523. [Google Scholar] [CrossRef]
  13. Yazici, D.; Huang, K.; White, B.; Chang, A.; Friedman, A.; Maple, M. Superconductivity of F-substituted LnOBiS2 (Ln = La, Ce, Pr, Nd, Yb) compounds. Philos. Mag. 2013, 93, 673–680. [Google Scholar] [CrossRef] [Green Version]
  14. Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-based layered superconductor La[O1-xFx] FeAs (x = 0.05 − 0.12) with Tc = 26 K. J. Am. Chem. Soc. 2008, 130, 3296–3297. [Google Scholar] [CrossRef]
  15. Athauda, A.; Yang, J.; Lee, S.; Mizuguchi, Y.; Deguchi, K.; Takano, Y.; Miura, O.; Louca, D. In-plane charge fluctuations in bismuth-sulfide superconductors. Phys. Rev. B 2015, 91, 144112. [Google Scholar] [CrossRef] [Green Version]
  16. Singh, S.K.; Kumar, A.; Gahtori, B.; Sharma, G.; Patnaik, S.; Awana, V.P. Bulk superconductivity in bismuth oxysulfide Bi4O4S3. J. Am. Chem. Soc. 2012, 134, 16504–16507. [Google Scholar] [CrossRef] [Green Version]
  17. Conradson, S.; Raistrick, I.D. The axial oxygen atom and superconductivity in YBa2Cu3O7. Science 1989, 243, 1340–1343. [Google Scholar] [CrossRef]
  18. Bianconi, A.; Saini, N.; Lanzara, A.; Missori, M.; Rossetti, T.; Oyanagi, H.; Yamaguchi, H.; Oka, K.; Ito, T. Determination of the Local Lattice Distortions in the CuO2 Plane of La1.85Sr0.15CuO4. Phys. Rev. Lett. 1996, 76, 3412. [Google Scholar] [CrossRef] [Green Version]
  19. Bianconi, A.; Lusignoli, M.; Saini, N.; Bordet, P.; Kvick, Å.; Radaelli, P. Stripe structure of the CuO2 plane in Bi2Sr2CaCu2O8+y by anomalous X-ray diffraction. Phys. Rev. B 1996, 54, 4310. [Google Scholar] [CrossRef]
  20. Pugliese, G.; Paris, E.; Capone, F.; Stramaglia, F.; Wakita, T.; Terashima, K.; Yokoya, T.; Mizokawa, T.; Mizuguchi, Y.; Saini, N. The local structure of self-doped BiS2-based layered systems as a function of temperature. Phys. Chem. Chem. Phys. 2020, 22, 22217–22225. [Google Scholar] [CrossRef]
  21. Paris, E.; Mizuguchi, Y.; Wakita, T.; Terashima, K.; Yokoya, T.; Mizokawa, T.; Saini, N. Suppression of structural instability in LaOBiS2-xSex by Se substitution. J. Phys. Condens. Matter 2018, 30, 455703. [Google Scholar] [CrossRef]
  22. Egami, T.; Petrov, Y.; Louca, D. Lattice effects on charge localization in cuprates. J. Supercond. 2000, 13, 709–712. [Google Scholar] [CrossRef]
  23. Louca, D.; Brosha, E.; Egami, T. Structure and lattice defects in LaMnO 3+ δ and La 0.96 Sr 0.04 MnO 3+ δ. Phys. Rev. B 2000, 61, 1351. [Google Scholar] [CrossRef]
  24. Athauda, A.; Yang, J.; Li, B.; Mizuguchi, Y.; Lee, S.; Louca, D. The Crystal Structure of Superconducting LaO1-xFxBiS2. J. Supercond. Nov. Magn. 2015, 28, 1255–1259. [Google Scholar] [CrossRef]
  25. Beni, G.; Platzman, P. Temperature and polarization dependence of extended x-ray absorption fine-structure spectra. Phys. Rev. B 1976, 14, 1514. [Google Scholar] [CrossRef]
  26. Jeong, I.K.; Heffner, R.; Graf, M.; Billinge, S. Lattice dynamics and correlated atomic motion from the atomic pair distribution function. Phys. Rev. B 2003, 67, 104301. [Google Scholar] [CrossRef] [Green Version]
  27. Toby, B.H. EXPGUI, a graphical user interface for GSAS. J. Appl. Crystallogr. 2001, 34, 210–213. [Google Scholar] [CrossRef] [Green Version]
  28. Proffen, T.; Billinge, S.; Egami, T.; Louca, D. Structural analysis of complex materials using the atomic pair distribution function—A practical guide. Z. Krist.-Cryst. Mater. 2003, 218, 132–143. [Google Scholar] [CrossRef]
  29. Proffen, T.; Page, K.L.; McLain, S.E.; Clausen, B.; Darling, T.W.; TenCate, J.A.; Lee, S.Y.; Ustundag, E. Atomic pair distribution function analysis of materials containing crystalline and amorphous phases. Z. Krist.-Cryst. Mater. 2005, 220, 1002–1008. [Google Scholar] [CrossRef]
  30. Warren, B.E. X-ray Diffraction; Courier Corporation: North Chelmsford, MA, USA, 1990. [Google Scholar]
  31. Peterson, P.; Gutmann, M.; Proffen, T.; Billinge, S. PDFgetN: A user-friendly program to extract the total scattering structure factor and the pair distribution function from neutron powder diffraction data. J. Appl. Crystallogr. 2000, 33, 1192. [Google Scholar] [CrossRef] [Green Version]
  32. Egami, T.; Billinge, S.J. Underneath the Bragg Peaks: Structural Analysis of Complex Materials; Elsevier: Oxford, UK, 2003. [Google Scholar]
  33. Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
  34. Philip, S.S.; Yang, J.; Louca, D.; Rosa, P.; Thompson, J.; Page, K. Bismuth kagome sublattice distortions by quenching and flux pinning in superconducting RbBi2. Phys. Rev. B 2021, 104, 104503. [Google Scholar] [CrossRef]
Condensedmatter 06 00048 g001 550
Figure 1. (a) The neutron powder diffraction pattern of Bi4O4S3 collected at 2 K. The data are fit well by a tetragonal model with I 4 / m m m symmetry. Shown on the right in (b) is the model of the crystal structure. The three sulfur atom positions are labeled S1, S2, and S3.
Figure 1. (a) The neutron powder diffraction pattern of Bi4O4S3 collected at 2 K. The data are fit well by a tetragonal model with I 4 / m m m symmetry. Shown on the right in (b) is the model of the crystal structure. The three sulfur atom positions are labeled S1, S2, and S3.
Condensedmatter 06 00048 g001
Condensedmatter 06 00048 g002 550
Figure 2. (a) The in–plane lattice constant a and (b) the out–of–plane lattice constant c, both showing the expected positive thermal expansion behavior. (c) A comparison of the z position of sulfur atom S1 obtained from average structure refinement and local structure refinement, plotted as a function of temperature. (d) Low-temperature magnetization for an applied field of 10 Oe. The zero–field–cooling (ZFC) curve shows the superconducting transition below T c .
Figure 2. (a) The in–plane lattice constant a and (b) the out–of–plane lattice constant c, both showing the expected positive thermal expansion behavior. (c) A comparison of the z position of sulfur atom S1 obtained from average structure refinement and local structure refinement, plotted as a function of temperature. (d) Low-temperature magnetization for an applied field of 10 Oe. The zero–field–cooling (ZFC) curve shows the superconducting transition below T c .
Condensedmatter 06 00048 g002
Condensedmatter 06 00048 g003 550
Figure 3. (a) The PDF fit by the average model. (b) The crystal model showing the S1 atom displacement. One half of a unit cell showing the comparison between the average model and local model is shown here. (c) The G ( r ) function determined for Bi 4 O 4 S 3 at 2 K compared to a local model G ( r ) indicated by the solid line. The peak splitting at ∼3 Å is reproduced by the model where the apical S1 atoms move out-of-plane towards the superconducting BiS 2 planes. Partial PDFs representing atom pair correlations between S and either Bi, S, or O atoms are shown.
Figure 3. (a) The PDF fit by the average model. (b) The crystal model showing the S1 atom displacement. One half of a unit cell showing the comparison between the average model and local model is shown here. (c) The G ( r ) function determined for Bi 4 O 4 S 3 at 2 K compared to a local model G ( r ) indicated by the solid line. The peak splitting at ∼3 Å is reproduced by the model where the apical S1 atoms move out-of-plane towards the superconducting BiS 2 planes. Partial PDFs representing atom pair correlations between S and either Bi, S, or O atoms are shown.
Condensedmatter 06 00048 g003
Condensedmatter 06 00048 g004 550
Figure 4. The temperature dependence of squared FWHM values of the PDF peak corresponding to Bi–O correlation in Bi 4 O 4 S 3 , extracted from Gaussian fitting. The fit of correlated Debye model is represented by the solid line.
Figure 4. The temperature dependence of squared FWHM values of the PDF peak corresponding to Bi–O correlation in Bi 4 O 4 S 3 , extracted from Gaussian fitting. The fit of correlated Debye model is represented by the solid line.
Condensedmatter 06 00048 g004
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Philip, S.S.; Athauda, A.; Goto, Y.; Mizuguchi, Y.; Louca, D. Out-of-Plane Sulfur Distortions in the Bi4O4S3 Superconductor. Condens. Matter 2021, 6, 48. https://doi.org/10.3390/condmat6040048

AMA Style

Philip SS, Athauda A, Goto Y, Mizuguchi Y, Louca D. Out-of-Plane Sulfur Distortions in the Bi4O4S3 Superconductor. Condensed Matter. 2021; 6(4):48. https://doi.org/10.3390/condmat6040048

Chicago/Turabian Style

Philip, Sharon S., Anushika Athauda, Yosuke Goto, Yoshikazu Mizuguchi, and Despina Louca. 2021. "Out-of-Plane Sulfur Distortions in the Bi4O4S3 Superconductor" Condensed Matter 6, no. 4: 48. https://doi.org/10.3390/condmat6040048

Article Metrics

Back to TopTop