Reliability of the Ginzburg–Landau Theory in the BCS-BEC Crossover by Including Gaussian Fluctuations for 3D Attractive Fermions
Abstract
:1. Introduction
2. Methods
2.1. Gap Equation and Number Equation
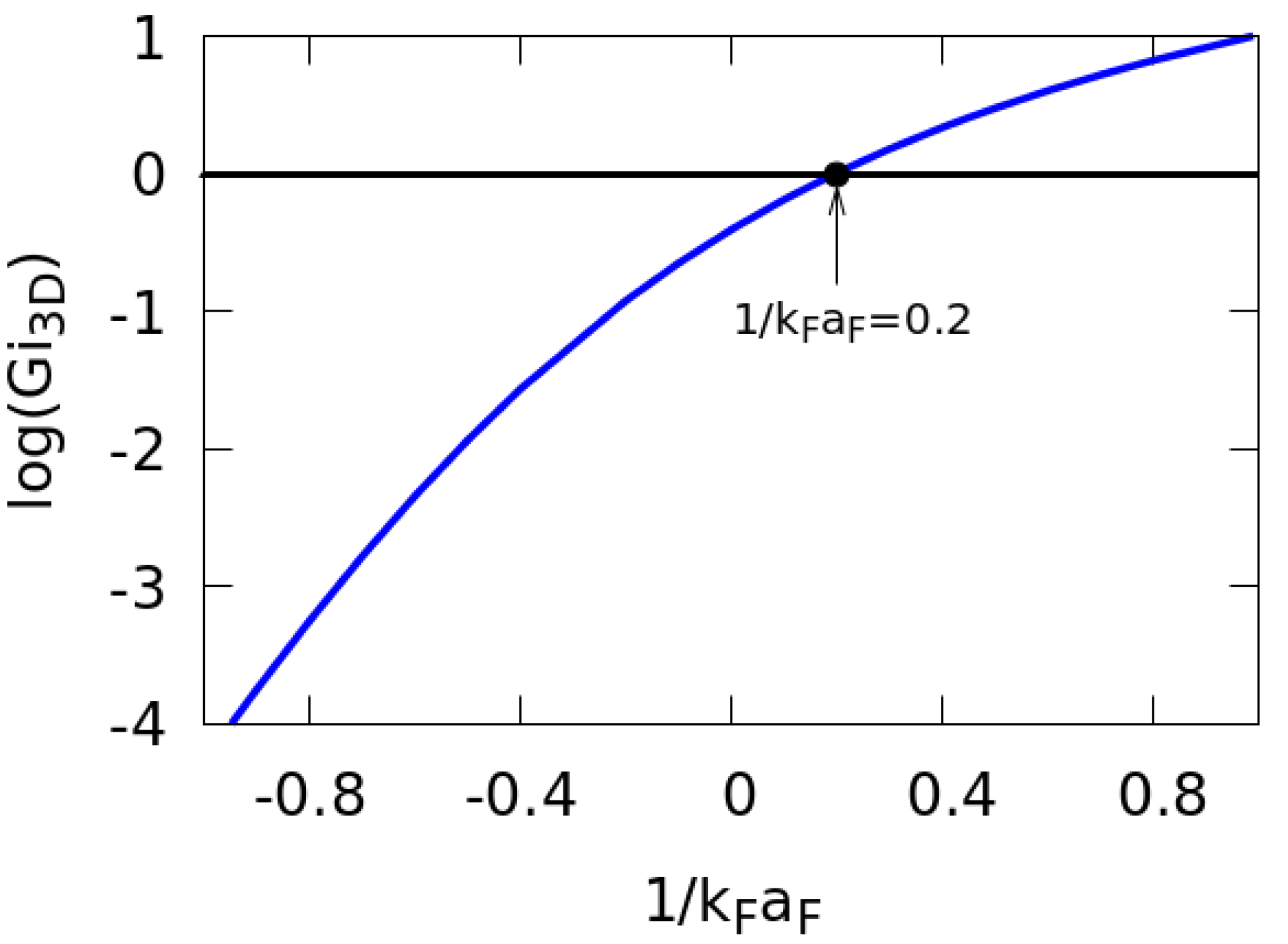
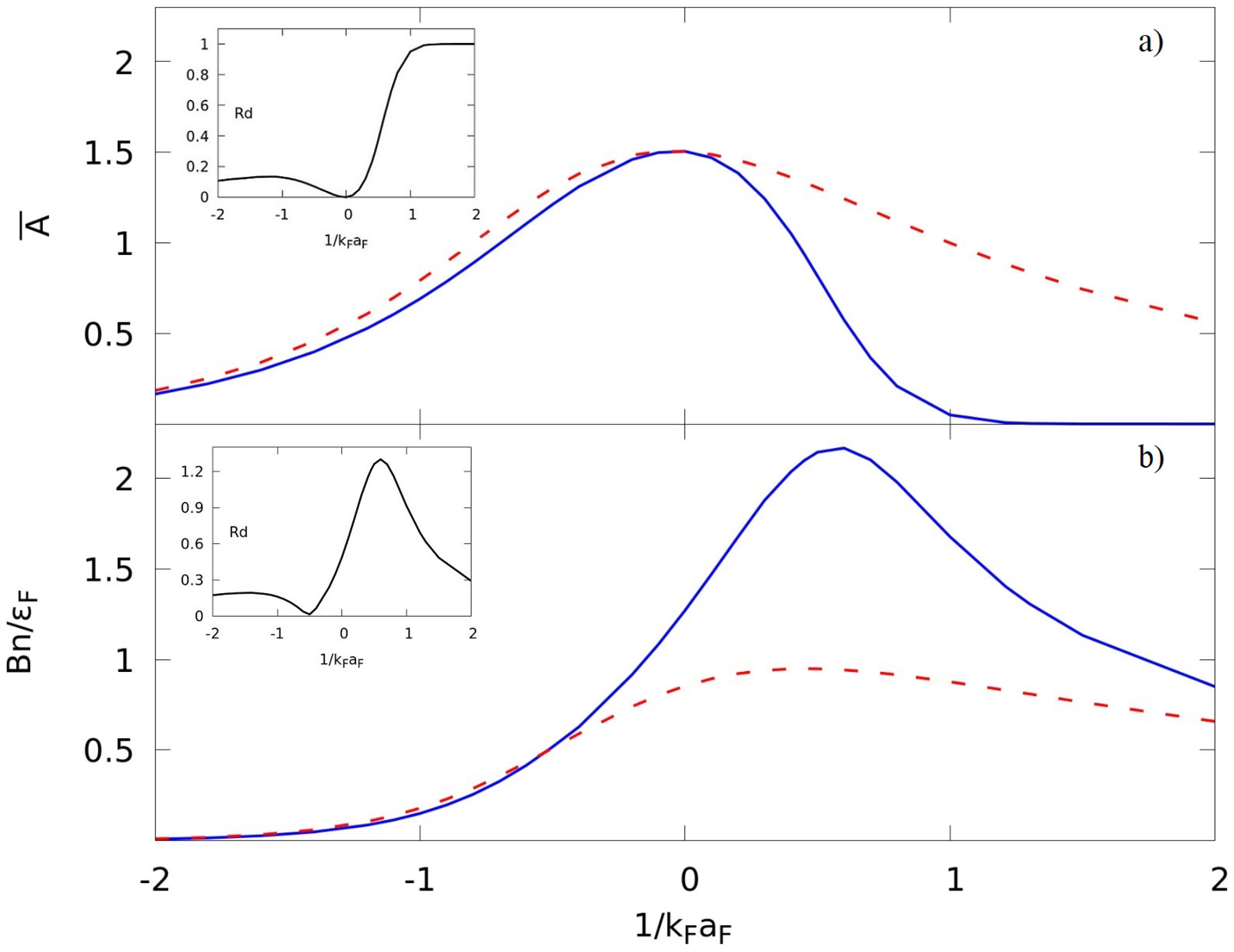
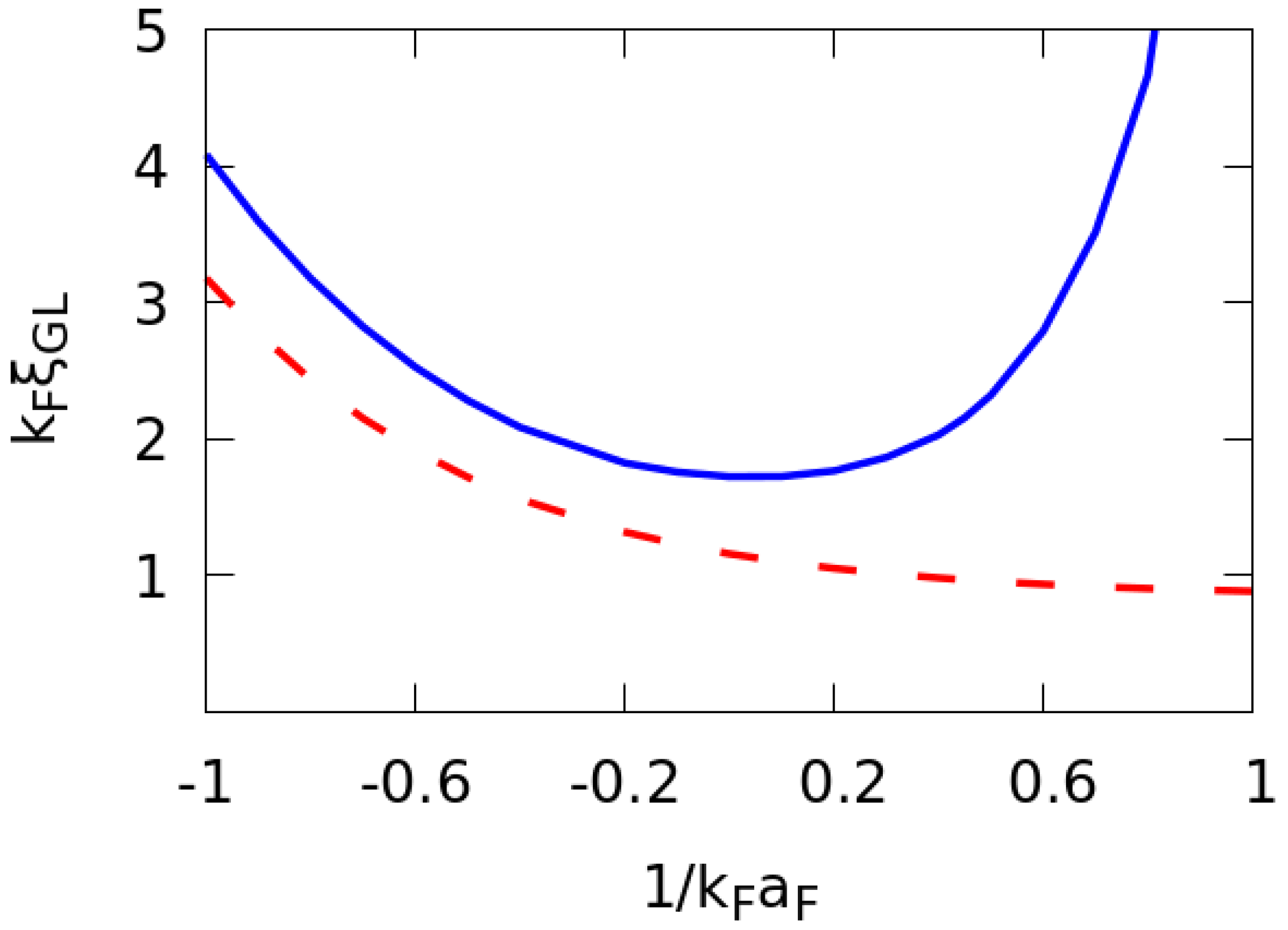
2.2. Ginzburg–Landau Parameters and Characteristic Quantities
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hu, H.; Liu, X.J.; Drummond, P.D. Equation of state of a superfluid Fermi gas in the BCS-BEC crossover. Europhys. Lett. 2006, 74, 574. [Google Scholar] [CrossRef]
- Diener, R.B.; Sensarma, R.; Randeria, M. Quantum fluctuations in the superfluid state of the BCS-BEC crossover. Phys. Rev. A. 2008, 77, 023626. [Google Scholar] [CrossRef] [Green Version]
- Regal, C.A.; Greiner, M.; Jin, D.S. Observation of Resonance Condensation of Fermionic Atom Pairs. Phys. Rev. Lett. 2004, 92, 040403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kinast, J.; Hemmer, S.L.; Gehm, M.E.; Turlapov, A.; Thomas, J.E. Evidence for Superfluidity in a Resonantly Interacting Fermi Gas. Phys. Rev. Lett. 2004, 92, 150402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Inouye, S.; Andrews, M.R.; Stenger, J.; Miesner, H.-J.; Stamper-Kurn, D.M.; Ketterle, W. Observation of Feshbach resonances in a Bose–Einstein condensate. Nature 1998, 392, 151. [Google Scholar] [CrossRef]
- Ginzburg, V.L.; Landau, L.D. On the theory of superconductivity. Zh. Eksp. Teor. Fiz 1950, 20, 1064. [Google Scholar]
- Banerjee, S.; Ramakrishnan, T.V.; Dasgupta, C. Phenomenological Ginzburg–Landau-like theory for superconductivity in the cuprates. Phys. Rev. B 2011, 83, 024510. [Google Scholar] [CrossRef] [Green Version]
- Salasnich, L.; Shanenko, A.A.; Vagov, A.; Aguiar, J.A.; Perali, A. Screening of pair fluctuations in superconductors with coupled shallow and deep bands: A route to higher-temperature superconductivity. Phys. Rev. B 2019, 100, 064510. [Google Scholar] [CrossRef] [Green Version]
- Saraiva, T.T.; Cavalcanti, P.J.F.; Vagov, A.; Vasenko, A.S.; Perali, A.; Dell’Anna, L.; Shanenko, A.A. Multiband Material with a Quasi-1D Band as a Robust High-Temperature Superconductor. Phys. Rev. Lett. 2020, 125, 217003. [Google Scholar] [CrossRef]
- Milošević, M.V.; Geurts, R. The Ginzburg—Landau theory in application. Phys. C 2010, 470, 19. [Google Scholar] [CrossRef] [Green Version]
- Combescot, R.; Kagan, M.Y.; Stringari, S. Collective mode of homogeneous superfluid Fermi gases in the BEC-BCS crossover. Phys Rev. A 2004, 74, 042717. [Google Scholar] [CrossRef] [Green Version]
- Pascucci, F.; Salasnich, L. Josephson effect with superfluid fermions in the two-dimensional BCS-BEC crossover. Phys Rev. A 2020, 102, 013325. [Google Scholar] [CrossRef]
- Gor’kov, L.P. Microscopic Derivation of the Ginzburg–Landau equation in the theoty of superconductivity. JETP 1959, 9, 6. [Google Scholar]
- Melo, C.S.D.; Randeria, M.; Engelbrecht, J.R. Crossover from BCS to Bose superconductivity: Transition temperature and time dependent Ginzburg–Landau theory. Phys. Rev. Lett. 1993, 71, 3202. [Google Scholar] [CrossRef] [PubMed]
- Drechsler, M.; Zwerger, W. Crossover from BCS-superconductivity to Bose-condensation. Ann. Physik 1992, 1, 15. [Google Scholar] [CrossRef]
- Micnas, R. On the crossover from BCS superconductivity to Bose condensation. Acta Phys. Polon. A 2001, 100, 177. [Google Scholar] [CrossRef]
- Palestini, F.; Strinati, G.C. Temperature dependence of the pair coherence and healing lengths for a fermionic superfluid throughout the BCS-BEC crossover. Phys. Rev. B 2014, 89, 224508. [Google Scholar] [CrossRef] [Green Version]
- Falk, G.; Stenschke, H. Note on rotating He in according to the theory of Ginzburg-Pitaevskii. Zeitschrift für Physik 1966, 197, 505. [Google Scholar] [CrossRef]
- Larkin, A.; Varlamov, A. Theory of Fluctuations and Superconductors; Clarendon Press: Oxford, UK, 2005; Volume 127. [Google Scholar]
- Nozieres, P.; Schmitt-Rink, S. Bose condensation in an attractive fermion gas: From weak to strong coupling superconductivity. J. Low Temp. Phys. 1985, 59, 195. [Google Scholar] [CrossRef]
- Pistolesi, F.; Strinati, G.C. Evolution from BCS superconductivity to Bose condensation: Role of the parameter kFξ. Phys. Rev. B 1994, 49, 6356. [Google Scholar] [CrossRef] [PubMed]
- Tinkham, M. Introduction to Superconductivity, 2nd ed.; Dover Publications: New York, NY, USA, 2004; ISBN 0486435032. [Google Scholar]
- Pieri, P.; Pisani, L.; Strinati, G.C. BCS-BEC crossover at finite temperature in the broken-symmetry phase. Phys Rev. B 2004, 70, 094508. [Google Scholar] [CrossRef] [Green Version]
- Landau, L.; Lišits, E.M. Fisica Statistica: Teoria Dello Stato Condensato, 1981 ed.; Editori Riuniti: Roma, Italy, 1981; pp. 146–147. ISBN 88-359-0042-5. [Google Scholar]
- Song, T.L.; Ma, C.R.; Ma, Y.L. Vortex lattices in a rotating Fermi superfluid in the BCS–BEC crossover with many Landau levels. Ann. Phys. 2012, 327, 8. [Google Scholar] [CrossRef]
- Ghosh, T.K.; Machida, K. Collective modes of a Fermi superfluid containing vortices along the BEC-BCS crossover. Phys. Rev. A 2006, 73, 025601. [Google Scholar] [CrossRef] [Green Version]
- Simonucci, S.; Pieri, P.; Strinati, G.C. Vortex arrays in neutral trapped Fermi gases through the BCS–BEC crossover. Nat. Phys. 2015, 11, 941. [Google Scholar] [CrossRef]
- Huang, K.; Yu, Z.Q.; Yin, L. Ginzburg–Landau theory of a trapped Fermi gas with a BEC-BEC crossover. Phys. Rev. A 2004, 79, 053602. [Google Scholar] [CrossRef] [Green Version]
- Petrov, D.S.; Salomon, C.; Shlyapnikov, G.V. Weakly Bound Dimers of Fermionic Atoms. Phys. Rev. Lett. 2004, 93, 090404. [Google Scholar] [CrossRef] [Green Version]
- Palestini, F.; Strinati, G.C. Systematic investigation of the effects of disorder at the lowest order throughout the BCS-BEC crossover. Phys. Rev. B 2013, 88, 174504. [Google Scholar] [CrossRef] [Green Version]
- Spuntarelli, A.; Pieri, P.; Strinati, G.C. Josephson Effect throughout the BCS-BEC Crossover. Phys. Rev. Lett. 2007, 99, 040401. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pascucci, F.; Perali, A.; Salasnich, L. Reliability of the Ginzburg–Landau Theory in the BCS-BEC Crossover by Including Gaussian Fluctuations for 3D Attractive Fermions. Condens. Matter 2021, 6, 49. https://doi.org/10.3390/condmat6040049
Pascucci F, Perali A, Salasnich L. Reliability of the Ginzburg–Landau Theory in the BCS-BEC Crossover by Including Gaussian Fluctuations for 3D Attractive Fermions. Condensed Matter. 2021; 6(4):49. https://doi.org/10.3390/condmat6040049
Chicago/Turabian StylePascucci, Filippo, Andrea Perali, and Luca Salasnich. 2021. "Reliability of the Ginzburg–Landau Theory in the BCS-BEC Crossover by Including Gaussian Fluctuations for 3D Attractive Fermions" Condensed Matter 6, no. 4: 49. https://doi.org/10.3390/condmat6040049
APA StylePascucci, F., Perali, A., & Salasnich, L. (2021). Reliability of the Ginzburg–Landau Theory in the BCS-BEC Crossover by Including Gaussian Fluctuations for 3D Attractive Fermions. Condensed Matter, 6(4), 49. https://doi.org/10.3390/condmat6040049







