Uniformly Frustrated XY Model: Strengthening of the Vortex Lattice by Intrinsic Disorder
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Clean Case
3.2. Disordered Case
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fisher, D.S.; Fisher, M.P.A.; Huse, D.A. Thermal fluctuations, quenched disorder, phase transitions, and transport in type-II superconductors. Phys. Rev. B 1991, 43, 130–159. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blatter, G.; Feigel’man, M.V.; Geshkenbein, V.B.; Larkin, A.I.; Vinokur, V.M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 1994, 66, 1125–1388. [Google Scholar] [CrossRef]
- Klein, T.; Joumard, I.; Blanchard, S.; Marcus, J.; Cubitt, R.; Giamarchi, T.; Le Doussal, P. A Bragg glass phase in the vortex lattice of a type II superconductor. Nature 2001, 413, 404–406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guillamón, I.; Suderow, H.; Fernández-Pacheco, A.; Sesé, J.; Córdoba, R.; De Teresa, J.M.; Ibarra, M.R.; Vieira, S. Direct observation of melting in a two-dimensional superconducting vortex lattice. Nat. Phys. 2009, 5, 651–655. [Google Scholar] [CrossRef] [Green Version]
- Roy, I.; Dutta, S.; Roy Choudhury, A.N.; Basistha, S.; Maccari, I.; Mandal, S.; Jesudasan, J.; Bagwe, V.; Castellani, C.; Benfatto, L.; et al. Melting of the Vortex Lattice through Intermediate Hexatic Fluid in an a-MoGe Thin Film. Phys. Rev. Lett. 2019, 122, 047001. [Google Scholar] [CrossRef] [Green Version]
- Berezinsky, V.L. Destruction of Long-range Order in One-dimensional and Two-dimensional Systems Possessing a Continuous Symmetry Group. II. Quantum Systems. Sov. Phys. JETP 1972, 34, 610. [Google Scholar]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C Solid State Phys. 1973, 6, 1181–1203. [Google Scholar] [CrossRef]
- Kosterlitz, J.M. The critical properties of the two-dimensional xy model. J. Phys. C Solid State Phys. 1974, 7, 1046. [Google Scholar] [CrossRef]
- Halperin, B.I.; Nelson, D.R. Theory of Two-Dimensional Melting. Phys. Rev. Lett. 1978, 41, 121–124. [Google Scholar] [CrossRef] [Green Version]
- Nelson, D.R.; Halperin, B.I. Dislocation-mediated melting in two dimensions. Phys. Rev. B 1979, 19, 2457–2484. [Google Scholar] [CrossRef]
- Young, A.P. Melting and the vector Coulomb gas in two dimensions. Phys. Rev. B 1979, 19, 1855–1866. [Google Scholar] [CrossRef]
- Giamarchi, T.; Le Doussal, P. Elastic theory of flux lattices in the presence of weak disorder. Phys. Rev. B 1995, 52, 1242–1270. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Le Doussal, P.; Giamarchi, T. Dislocations and Bragg glasses in two dimensions. Phys. C Supercond. 2000, 331, 233–240. [Google Scholar] [CrossRef] [Green Version]
- Ganguly, R.; Roy, I.; Banerjee, A.; Singh, H.; Ghosal, A.; Raychaudhuri, P. Magnetic field induced emergent inhomogeneity in a superconducting film with weak and homogeneous disorder. Phys. Rev. B 2017, 96, 054509. [Google Scholar] [CrossRef] [Green Version]
- Barabash, S.; Stroud, D.; Hwang, I.J. Conductivity due to classical phase fluctuations in a model for high-Tc superconductors. Phys. Rev. B 2000, 61, R14924–R14927. [Google Scholar] [CrossRef] [Green Version]
- Wysin, G.M.; Pereira, A.R.; Marques, I.A.; Leonel, S.A.; Coura, P.Z. Extinction of the Berezinskii-Kosterlitz-Thouless phase transition by nonmagnetic disorder in planar symmetry spin models. Phys. Rev. B 2005, 72, 094418. [Google Scholar] [CrossRef]
- Erez, A.; Meir, Y. Effect of amplitude fluctuations on the Berezinskii-Kosterlitz-Thouless transition. Phys. Rev. B 2013, 88, 184510. [Google Scholar] [CrossRef] [Green Version]
- Costa, B.V.; Lima, L.S.; Coura, P.Z.; Leonel, S.A.; Lima, A.B. Kosterlitz-Thouless Transition: The Diluted XY model. J. Phys. Conf. Ser. 2014, 487, 012008. [Google Scholar] [CrossRef]
- Maccari, I.; Maiorano, A.; Marinari, E.; Ruiz-Lorenzo, J.J. A numerical study of planar arrays of correlated spin islands. Eur. Phys. J. B 2016, 89, 127. [Google Scholar] [CrossRef] [Green Version]
- Kumar, M.; Chatterjee, S.; Paul, R.; Puri, S. Ordering kinetics in the random-bond $XY$ model. Phys. Rev. E 2017, 96, 042127. [Google Scholar] [CrossRef] [Green Version]
- Maccari, I.; Benfatto, L.; Castellani, C. Broadening of the Berezinskii-Kosterlitz-Thouless transition by correlated disorder. Phys. Rev. B 2017, 96, 060508. [Google Scholar] [CrossRef] [Green Version]
- Maccari, I.; Benfatto, L.; Castellani, C. The BKT Universality Class in the Presence of Correlated Disorder. Condens. Matter 2018, 3, 8. [Google Scholar] [CrossRef] [Green Version]
- Maccari, I.; Benfatto, L.; Castellani, C. Disordered XY model: Effective medium theory and beyond. Phys. Rev. B 2019, 99, 104509. [Google Scholar] [CrossRef] [Green Version]
- Maccari, I.; Defenu, N.; Benfatto, L.; Castellani, C.; Enss, T. Interplay of spin waves and vortices in the two-dimensional XY model at small vortex-core energy. Phys. Rev. B 2020, 102, 104505. [Google Scholar] [CrossRef]
- Teitel, S.; Jayaprakash, C. Phase transtions in frustrated two-dimensional $\mathrm{XY}$ models. Phys. Rev. B 1983, 27, 598–601. [Google Scholar] [CrossRef]
- Franz, M.; Teitel, S. Vortex lattice melting in 2D superconductors and Josephson arrays. Phys. Rev. Lett. 1994, 73, 480–483. [Google Scholar] [CrossRef] [Green Version]
- Franz, M.; Teitel, S. Vortex-lattice melting in two-dimensional superconducting networks and films. Phys. Rev. B 1995, 51, 6551–6574. [Google Scholar] [CrossRef] [Green Version]
- Hattel, S.A.; Wheatley, J.M. Flux-lattice melting and depinning in the weakly frustrated two-dimensional XY model. Phys. Rev. B 1995, 51, 11951–11954. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, A.; Hu, X. Numerical study of the flux lattice melting transition in 2D superconductors. Phys. C Supercond. 2001, 357-360, 438–441. [Google Scholar] [CrossRef]
- Hasenbusch, M.; Pelissetto, A.; Vicari, E. Multicritical behaviour in the fully frustrated XY Model Relat. Syst. J. Stat. Mech. Theory Exp. 2005, 2005, P12002. [Google Scholar] [CrossRef]
- Alba, V.; Pelissetto, A.; Vicari, E. The uniformly frustrated two-dimensionalXYmodel in the limit of weak frustration. J. Phys. A Math. Theor. 2008, 41, 175001. [Google Scholar] [CrossRef]
- Teitel, S. The Two-Dimensional Fully Frustrated XY Model. In 40 Years of Berezinskii–Kosterlitz–Thouless Theory; World Scientific: Singapore, 2013; pp. 201–235. [Google Scholar] [CrossRef] [Green Version]
- Alba, V.; Pelissetto, A.; Vicari, E. Quasi-long-range order in the 2D XY model with random phase shifts. J. Phys. A Math. Theor. 2009, 42, 295001. [Google Scholar] [CrossRef]
- Alba, V.; Pelissetto, A.; Vicari, E. Magnetic and glassy transitions in the square-latticeXYmodel with random phase shifts. J. Stat. Mech. Theory Exp. 2010, 2010, P03006. [Google Scholar] [CrossRef] [Green Version]
- Hadzibabic, Z.; Dalibard, J. BKT Physics with Two-Dimensional Atomic Gases. In 40 Years of Berezinskii–Kosterlitz–Thouless Theory; World Scientific: Singapore, 2013; pp. 297–323. [Google Scholar] [CrossRef] [Green Version]
- Yazdani, A.; White, W.R.; Hahn, M.R.; Gabay, M.; Beasley, M.R.; Kapitulnik, A. Observation of Kosterlitz-Thouless-type melting of the disordered vortex lattice in thin films of a-MoGe. Phys. Rev. Lett. 1993, 70, 505–508. [Google Scholar] [CrossRef]
- Chen, B.; Halperin, W.P.; Guptasarma, P.; Hinks, D.G.; Mitrović, V.F.; Reyes, A.P.; Kuhns, P.L. Two-dimensional vortices in superconductors. Nat. Phys. 2007, 3, 239–242. [Google Scholar] [CrossRef] [Green Version]
- Misra, S.; Urban, L.; Kim, M.; Sambandamurthy, G.; Yazdani, A. Measurements of the Magnetic-Field-Tuned Conductivity of Disordered Two-Dimensional Mo43Ge57 and InOx Superconducting Films: Evidence for a Universal Minimum Superfluid Response. Phys. Rev. Lett. 2013, 110, 037002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benyamini, A.; Telford, E.J.; Kennes, D.M.; Wang, D.; Williams, A.; Watanabe, K.; Taniguchi, T.; Shahar, D.; Hone, J.; Dean, C.R.; et al. Fragility of the dissipationless state in clean two-dimensional superconductors. Nat. Phys. 2019, 15, 947–953. [Google Scholar] [CrossRef]
- Ma, M.; Lee, P.A. Localized superconductors. Phys. Rev. B 1985, 32, 5658–5667. [Google Scholar] [CrossRef] [PubMed]
- Cea, T.; Bucheli, D.; Seibold, G.; Benfatto, L.; Lorenzana, J.; Castellani, C. Optical excitation of phase modes in strongly disordered superconductors. Phys. Rev. B 2014, 89, 174506. [Google Scholar] [CrossRef] [Green Version]
- Ioffe, L.B.; Mézard, M. Disorder-Driven Quantum Phase Transitions in Superconductors and Magnets. Phys. Rev. Lett. 2010, 105, 037001. [Google Scholar] [CrossRef] [Green Version]
- Lemarié, G.; Kamlapure, A.; Bucheli, D.; Benfatto, L.; Lorenzana, J.; Seibold, G.; Ganguli, S.C.; Raychaudhuri, P.; Castellani, C. Universal scaling of the order-parameter distribution in strongly disordered superconductors. Phys. Rev. B 2013, 87, 184509. [Google Scholar] [CrossRef] [Green Version]
- Nelson, D.R.; Kosterlitz, J.M. Universal Jump in the Superfluid Density of Two-Dimensional Superfluids. Phys. Rev. Lett. 1977, 39, 1201–1205. [Google Scholar] [CrossRef] [Green Version]
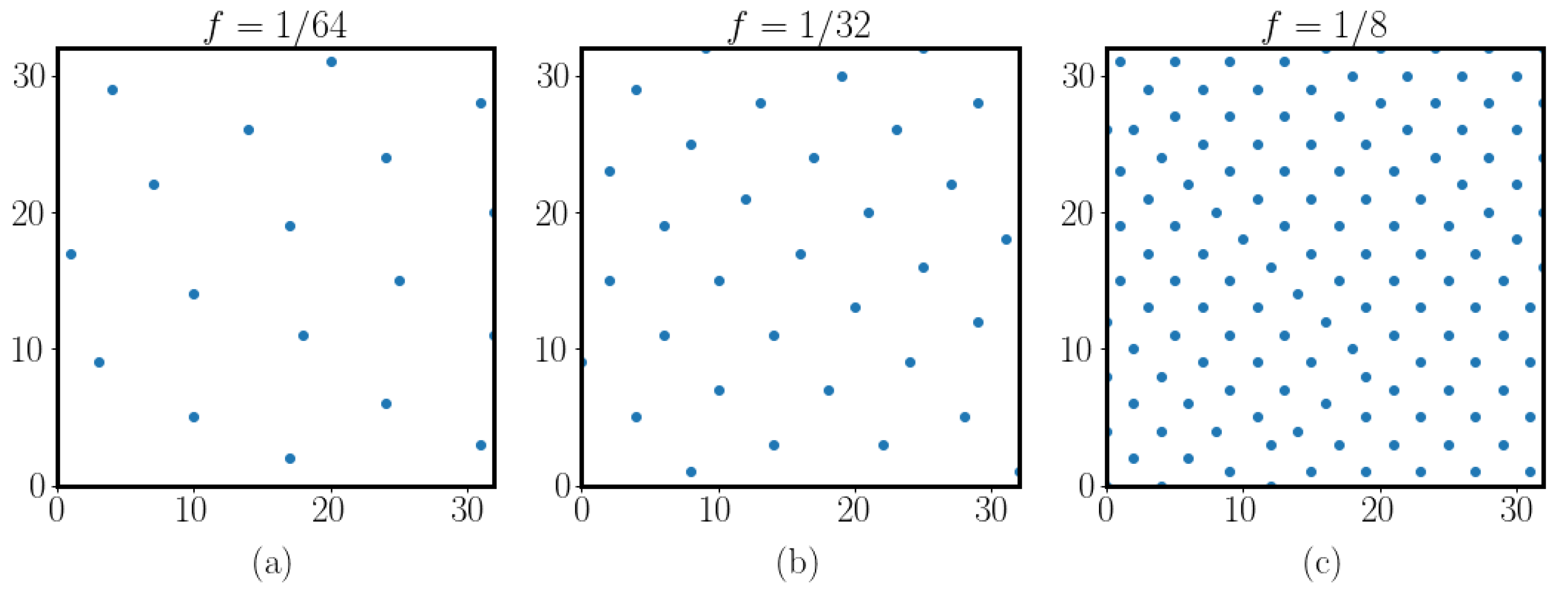
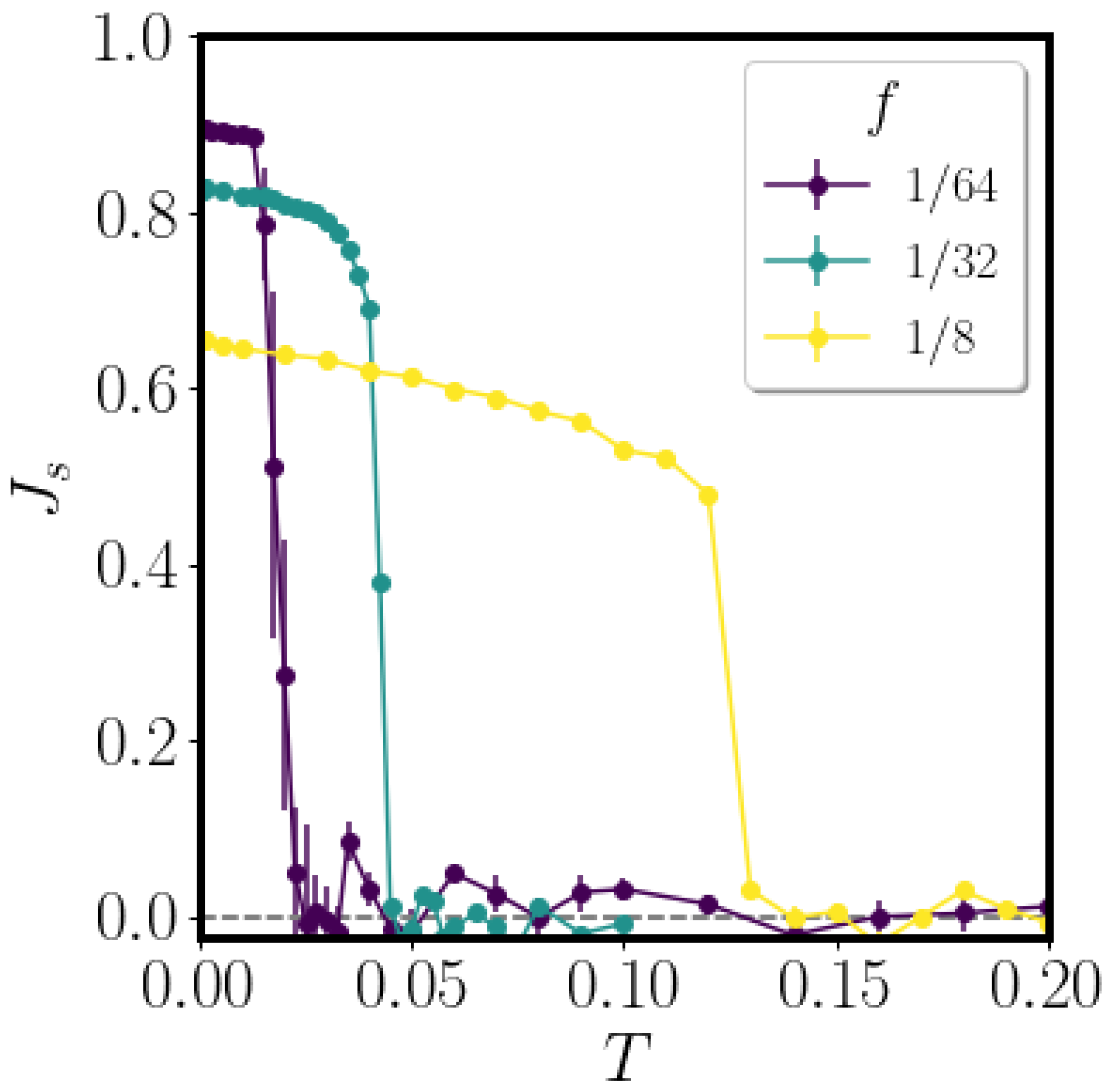
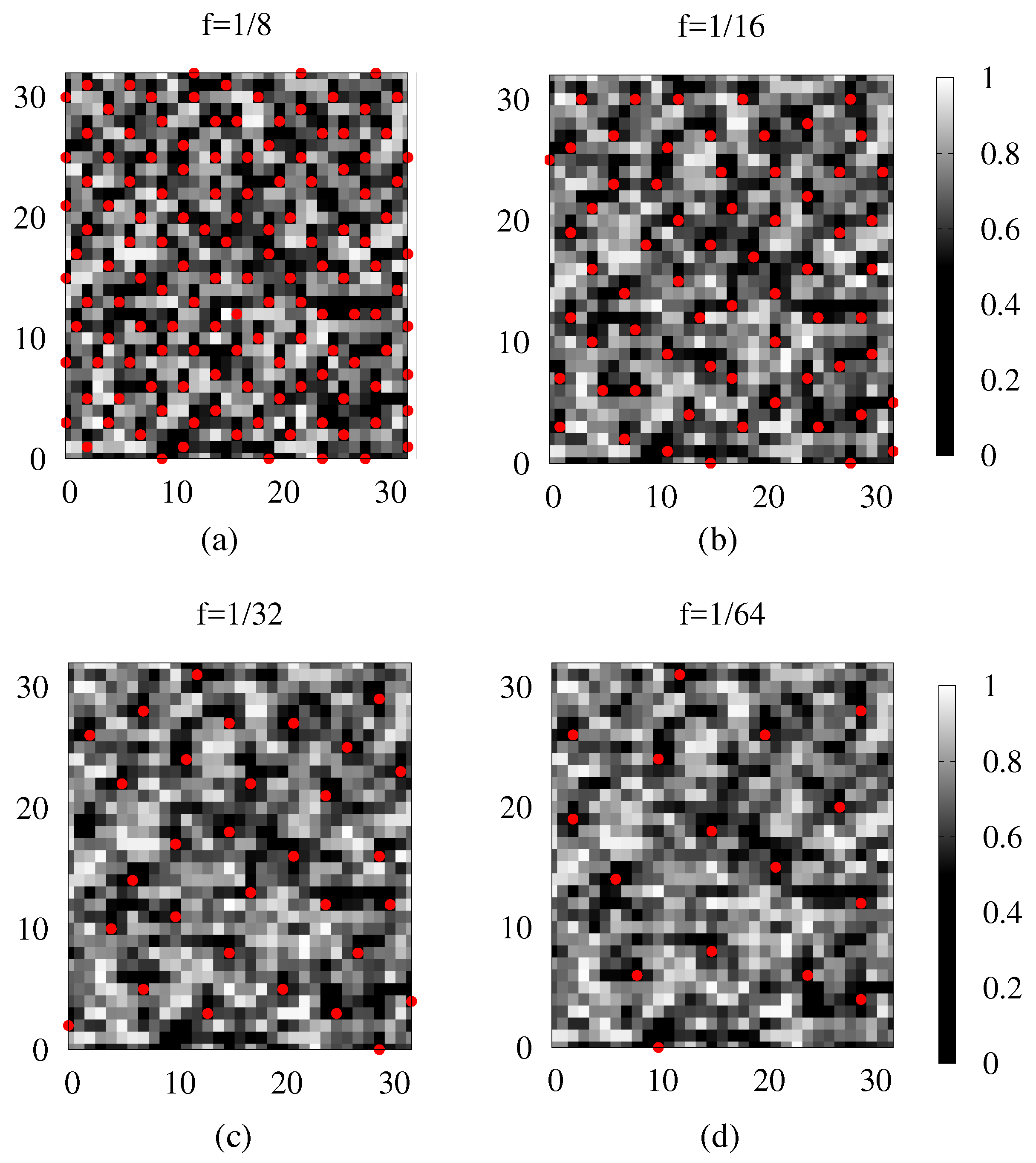

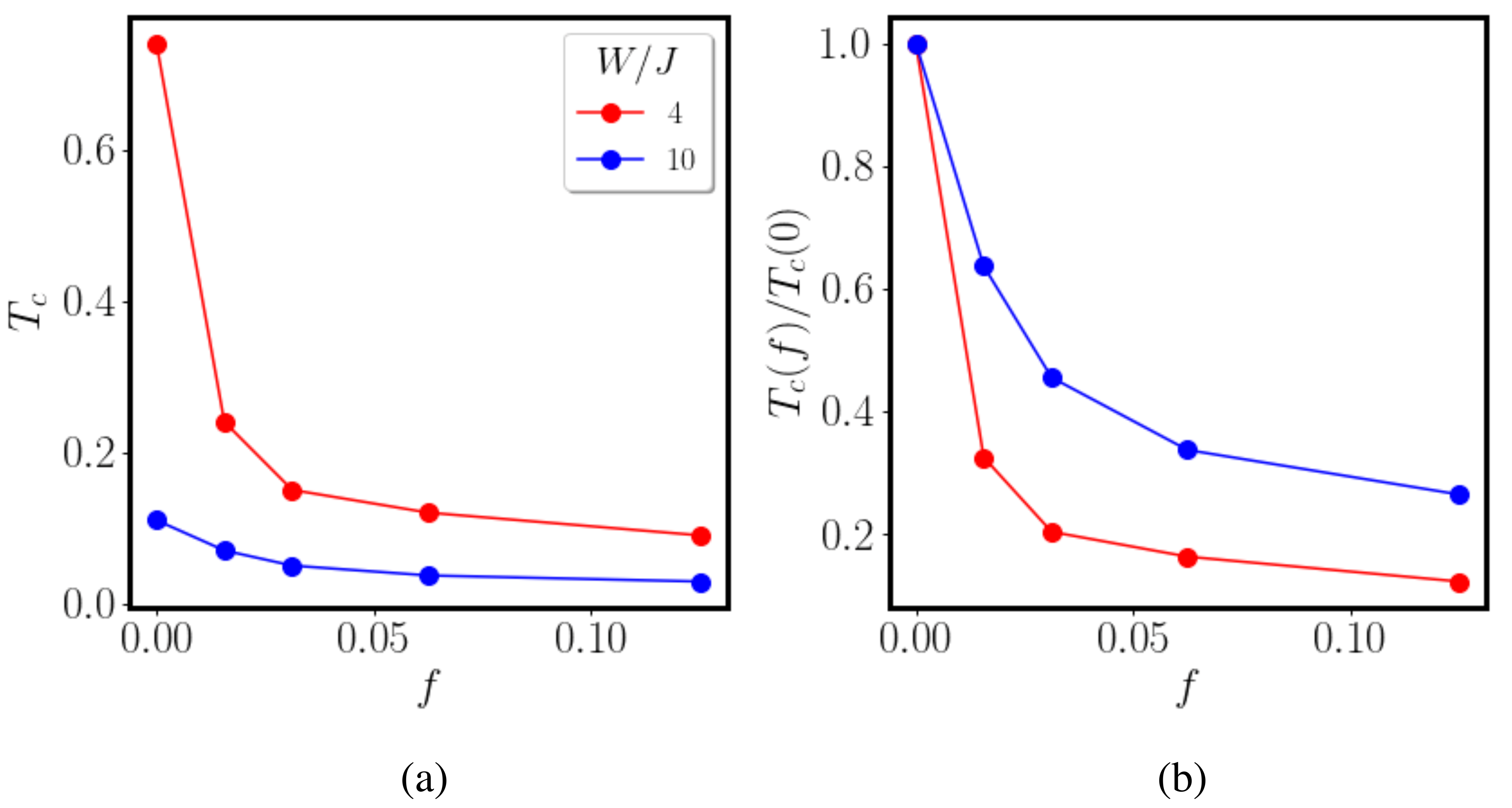
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maccari, I.; Benfatto, L.; Castellani, C. Uniformly Frustrated XY Model: Strengthening of the Vortex Lattice by Intrinsic Disorder. Condens. Matter 2021, 6, 42. https://doi.org/10.3390/condmat6040042
Maccari I, Benfatto L, Castellani C. Uniformly Frustrated XY Model: Strengthening of the Vortex Lattice by Intrinsic Disorder. Condensed Matter. 2021; 6(4):42. https://doi.org/10.3390/condmat6040042
Chicago/Turabian StyleMaccari, Ilaria, Lara Benfatto, and Claudio Castellani. 2021. "Uniformly Frustrated XY Model: Strengthening of the Vortex Lattice by Intrinsic Disorder" Condensed Matter 6, no. 4: 42. https://doi.org/10.3390/condmat6040042
APA StyleMaccari, I., Benfatto, L., & Castellani, C. (2021). Uniformly Frustrated XY Model: Strengthening of the Vortex Lattice by Intrinsic Disorder. Condensed Matter, 6(4), 42. https://doi.org/10.3390/condmat6040042





