Temperature Dependent Structural Evolution of WSe2: A Synchrotron X-ray Diffraction Study
Abstract
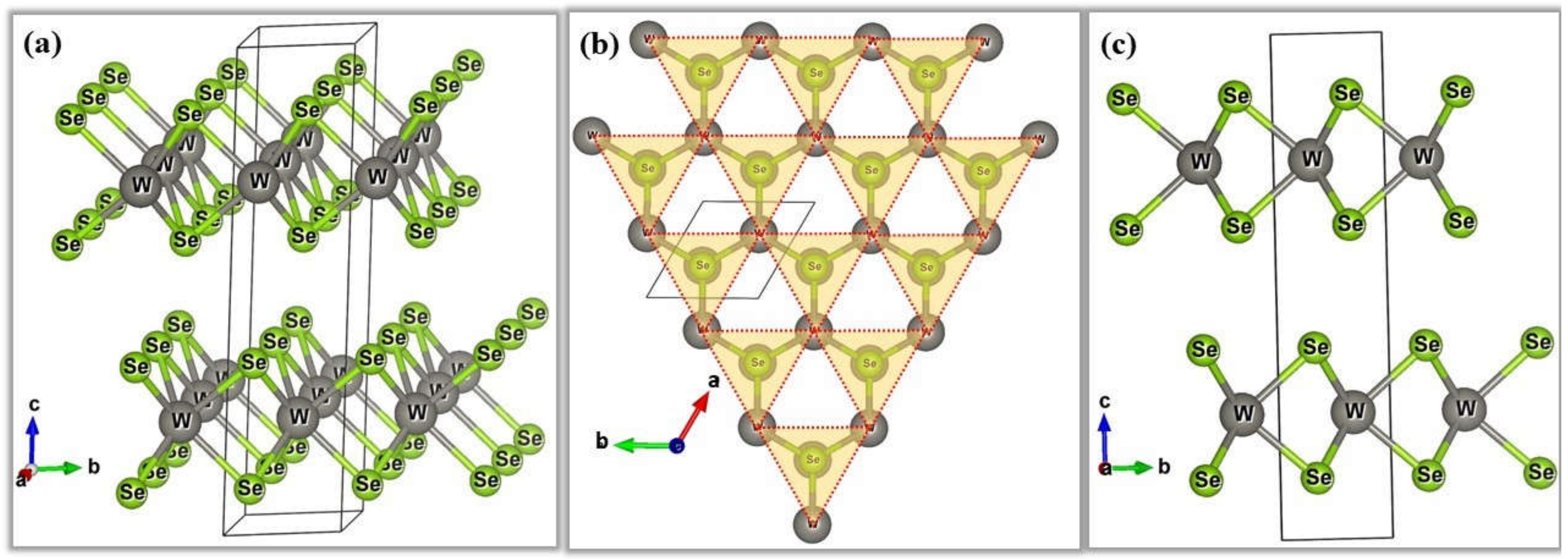
1. Introduction
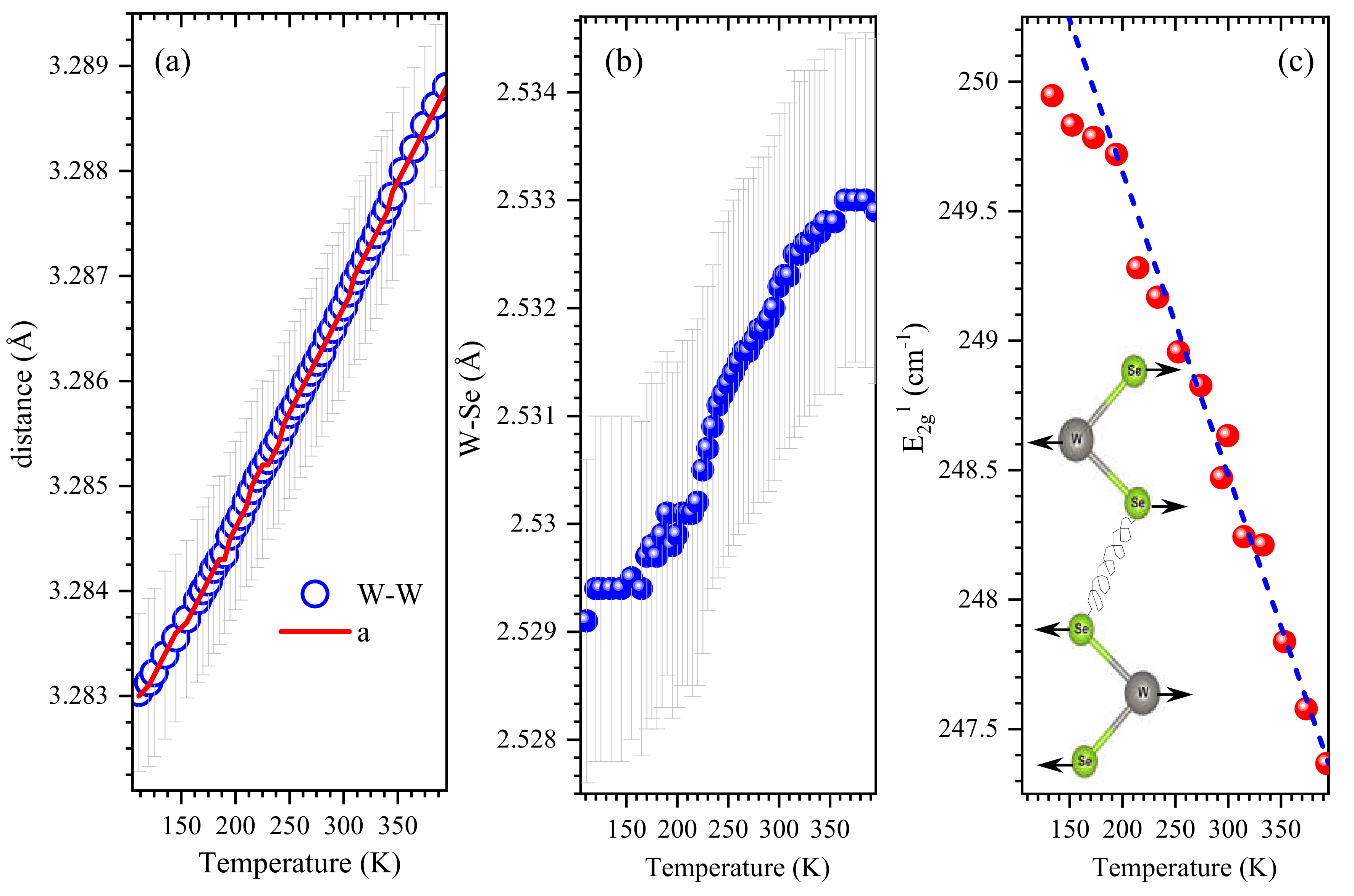
2. Results and Discussion
3. Materials and Methods
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wilson, J.A.; Yoffe, A.D. The transition metal dichalcogenides discussion and interpretation of the observed optical, electrical and structural properties. Adv. Phys. 1969, 18, 193–335. [Google Scholar] [CrossRef]
- Rao, C.N.R.; Waghmare, U.V. (Eds.) 2D Inorganic Materials beyond Graphene; World Scientific: Singapore, 2017. [Google Scholar]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.J.; Heinz, T.F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [PubMed]
- Mathew, S.K.; Gopinadhan, K.; Chan, T.K.; Yu, X.J.; Zhan, D.; Cao, L.; Rusydi, A.; Breese, M.B.H.; Dhar, S.; Shen, Z.X.; et al. Magnetism in MoS2 induced by proton irradiation. Appl. Phys. Lett. 2012, 101, 102103. [Google Scholar] [CrossRef]
- Sarkar, S.; Goswami, S.; Trushin, M.; Saha, S.; Panahandeh-Fard, M.; Prakash, S.; Tan, S.J.R.; Scott, M.; Loh, K.P.; Adam, S.; et al. Polaronic Trions at the MoS2/SrTiO3 Interface. Adv. Mater. 2019, 31, 1903569. [Google Scholar] [CrossRef]
- Trushin, M.; Sarkar, S.; Mathew, S.; Goswami, S.; Sahoo, P.; Wang, Y.; Yang, J.; Li, W.; MacManus-Driscoll, J.L.; Chhowalla, M.; et al. Evidence of rotational Fröhlich coupling in polaronic trions. Phy. Rev. Lett. 2020, 125, 86803. [Google Scholar] [CrossRef]
- Chellappan, V.; Pang, A.L.C.; Sarkar, S.; Ooi, Z.E.; Goh, K.E.J. Effect of Phonons on Valley Depolarization in Monolayer WSe2. Electron. Mater. Lett. 2018, 14, 766–773. [Google Scholar] [CrossRef]
- Kristen, K.; Thygesen, K.S.; Jacobsen, K.W. Phonon-limited mobility in n-type single-layer MoS2 from first principles. Phys. Rev. B 2012, 85, 115317. [Google Scholar] [CrossRef]
- Hu, X.; Yasaei, P.; Jokisaari, J.; Öğüt, S.; Salehi-Khojin, A.; Robert, K.F. Mapping Thermal Expansion Coefficients in Freestanding 2D Materials at the Nanometer Scale. Phys. Rev. Let. 2018, 120, 055902. [Google Scholar] [CrossRef]
- Murray, R.; Evans, B. The thermal expansion of 2H-MoS2 and 2H-WSe2 between 10 and 320 K. J. Appl. Cryst. 1979, 12, 312–315. [Google Scholar] [CrossRef]
- Late, D.J.; Shirodkar, S.N.; Waghmare, U.V.; Dravid, V.P.; Rao, C.N.R. Thermal expansion, anharmonicity and temperature-dependent Raman spectra of single- and few-layer MoSe2 and WSe2. Chem. Phys. Chem. 2014, 15, 1592–1598. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Commission on Powder Diffraction (IUCr). Newsletter 2001, 26, 12–19. [Google Scholar]
- Joseph, B.; Demitri, N.; Lotti, P.; Lausi, A.; Dore, P. Unraveling the Peculiarities in the Temperature-Dependent Structural Evolution of Black Phosphorus. Condens. Matter 2017, 2, 11. [Google Scholar] [CrossRef]
- Schutte, W.J.; de Boer, J.L.; Jellinek, F.J. Crystal structures of tungsten disulfide and diselenide. J. Solid State Chem. 1987, 70, 207–209. [Google Scholar] [CrossRef]
- Vočadlo, L.; Knight, K.S.; Price, G.D.; Wood, I.G. Thermal expansion and crystal structure of FeSi between 4 and 1173 K determined by time-of-flight neutron powder diffraction. Phys. Chem. Min. 2002, 29, 132–139. [Google Scholar] [CrossRef]
- Hu, S.Y.; Lee, Y.C.; Shen, J.J.; Chen, K.W.; Huang, Y.S. Urbach tail in the absorption spectra of 2H-WSe2 layered crystals. Phys. Status Solidi a 2007, 204, 2389–2395. [Google Scholar] [CrossRef]
- Selvi, E.; Aksoy, R.; Knudson, R.; Ma, Y. High-pressure X-ray diffraction study of tungsten diselenide. J. Phys. Chem. Solids 2008, 69, 2311–2314. [Google Scholar] [CrossRef]
- Bhatt, S.V.; Deshpande, M.P.; Sathe, V.; Rao, R.; Chakia, S.H. Raman spectroscopic investigations on transition-metal dichalcogenides MX2 (M = Mo, W; X = S, Se) at high pressures and low temperature. J. Raman Spectrosc. 2014, 45, 971–979. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q.; Yap, C.C.R.; Tay, B.K.; Edwin, T.H.T.; Olivier, A.; Baillargeat, D. From Bulk to Monolayer MoS2: Evolution of Raman Scattering. Adv. Funct. Mater. 2012, 22, 1385–1390. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Y.; Jiang, J.; Liang, Y.; Zhong, B.; Zhang, H.; Yu, K.; Kan, G.; Zou, M. Temperature-dependent Raman spectroscopy studies of 1–5-layer WSe2. Nano Res. 2020, 13, 591–595. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A.; Poccia, N.; Bianconi, G.; Barba, L.; Arrighetti, G.; Innocenti, D.; Karpinski, J.; Zhigadlo, N.D.; Kazakov, S.M.; et al. Inhomogeneity of Charge-Density-Wave Order and Quenched Disorder in a High-Tc Superconductor. Nature 2015, 525, 359–362. [Google Scholar] [CrossRef]
- Joseph, B.; Schiavo, B. Effects of ball-milling on the hydrogen sorption properties of LaNi5. J. Alloys Compd. 2009, 480, 912–916. [Google Scholar] [CrossRef]
- Joseph, B.; Marini, C.; Demitri, N.; Capitani, F.; Bernasconi, A.; Zhou, W.; Xing, X.; Shi, Z. Temperature dependent structural modulation in Ca0.82La0.18FeAs2 pnictide superconductors. Supercond. Sci. Technol. 2015, 28, 092001. [Google Scholar] [CrossRef]
- Grant, A.J.; Wilson, J.A.; Yoffe, A.D. Optical studies of transition metal dichalcogenide layer crystals at high pressures. Philos. Mag. A 1972, 25, 625–636. [Google Scholar] [CrossRef]
- EL-Mahalawy, S.H.; Evans, B.L. Temperature Dependence of the Electrical Conductivity and Hall Coefficient in 2H-MoS2, MoSe2, WSe2, and MoTe2. Phys. Status Solidi B 1977, 79, 713–722. [Google Scholar] [CrossRef]
- Lotti, P.; Milani, S.; Merlini, M.; Joseph, B.; Alabarse, F.; Lausi, A. Single-crystal diffraction at the high-pressure Indo-Italian beamline Xpress at Elettra, Trieste. J. Synchrotron. Rad. 2020, 25, 222–229. [Google Scholar] [CrossRef]
- Hammersley, A.P.; Svensson, S.O.; Hanfland, M.; Fitch, A.N.; Hausermann, D. Two-dimensional detector software: From real detector to idealized image or two-theta scan. High Press. Res. 1996, 14, 235–248. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mathew, S.; Abraham, A.R.; Chintalapati, S.; Sarkar, S.; Joseph, B.; Venkatesan, T. Temperature Dependent Structural Evolution of WSe2: A Synchrotron X-ray Diffraction Study. Condens. Matter 2020, 5, 76. https://doi.org/10.3390/condmat5040076
Mathew S, Abraham AR, Chintalapati S, Sarkar S, Joseph B, Venkatesan T. Temperature Dependent Structural Evolution of WSe2: A Synchrotron X-ray Diffraction Study. Condensed Matter. 2020; 5(4):76. https://doi.org/10.3390/condmat5040076
Chicago/Turabian StyleMathew, Sinu, Aben Regi Abraham, Sandhya Chintalapati, Soumya Sarkar, Boby Joseph, and Thirumalai Venkatesan. 2020. "Temperature Dependent Structural Evolution of WSe2: A Synchrotron X-ray Diffraction Study" Condensed Matter 5, no. 4: 76. https://doi.org/10.3390/condmat5040076
APA StyleMathew, S., Abraham, A. R., Chintalapati, S., Sarkar, S., Joseph, B., & Venkatesan, T. (2020). Temperature Dependent Structural Evolution of WSe2: A Synchrotron X-ray Diffraction Study. Condensed Matter, 5(4), 76. https://doi.org/10.3390/condmat5040076




