Abstract
Internal energies, enthalpies, phonon dispersion curves, and superconductivity of atomic metallic hydrogen are calculated. The standard use of pseudopotentials in density-functional theory are compared with full Coulomb-potential, all-electron linear muffin-tin orbital calculations. Quantitatively similar results are found as far as internal energies are concerned. Larger differences are found for phase-transition pressures; significant enough to affect the phase diagram. Electron–phonon spectral functions also show significant differences. Against expectation, the estimated superconducting critical-temperature T of the first atomic metallic phase I4/amd (Cs-IV) at 500 GPa is actually higher.
1. Introduction
Hydrogen is the simplest and most abundant element in the universe. Under pressure, it exhibits remarkable physics. First it solidifies and crystallizes, and then it evolves through a series of high-density solid phases. In 1935, Wigner and Huntington predicted [1] that sufficient pressure would even dissociate hydrogen molecules, and that any Bravais lattice of such atoms would be metallic. The problem of metallic hydrogen has received considerable attention, as reviewed in Ref. [2]. Herein, the structures and stabilities of atomic metallic hydrogen are considered. The background of what is known (from calculations; as motivated below) and relevant to this work will be discussed in context.
Initial interest in metallic hydrogen was primarily related to astrophysical problems [3]. Subsequently and more recently, there has been significant interest in it at relatively low temperatures. This can be attributed to the remarkable properties that are expected. This includes, for example, high-temperature superconductivity [4,5,6]. This will be considered herein. The possibility of a zero-temperature liquid ground-state has also been suggested [7]. In this case, hydrogen may have quantum-ordered states that represent novel types of quantum fluids [8]. Applications of the expected remarkable physics could revolutionize several fields. Possible scientific investigations and technological uses have been speculated on in Refs. [9,10].
Despite experimental advances (e.g., diamond anvil cell (DAC) [11] experiments, even coupled with single-crystal X-ray diffraction [12]), it is still extremely difficult to determine the crystal structure of hydrogen under extreme conditions. In addition, novel experimental approaches have been and continue to be necessary to extend higher the pressures possible to apply to hydrogen (in this context, under static conditions). Dias and Silvera [13] use reactive ion etching, vacuum annealing, as well as aluminum as a hydrogen embrittlement barrier. Another recent method has been the use of a small taurus on the cutlet [14]. Therefore, sophisticated calculations, often ab initio ones based on density-functional theory (DFT) [15] have become a powerful theoretical tool to understand high-pressure hydrogen and its physical properties.
Pseudopotentials, the focus of this work, are an essential ingredient of most of these calculations. These potentials, which are smooth and nodeless, are used to replace the Coulomb potential, to reach more rapidly convergent results. This same idea applies to the case of hydrogen, even though it only has one electron.
For many properties, it is reasonable to assume that the pseudopotential should be almost numerically identical to the Coulomb one, as long as the cut-off radius is chosen to be small. Under high pressure, the distance between nearest-neighbor protons in atomic metallic hydrogen is approximately two-fold of the Wigner–Seitz radius [, where V is the volume per electron and the Bohr radius]. According to the evolution of shortest (interatomic) H–H distance under pressure, changes from 3.12 to 1.23 when the pressure increases from ambient to 500 GPa [16]. The concern comes to be whether the pseudopotential with cut-off radius is suitable to ensure minimal core overlap.
The validity of the pseudopotential approximation in the above contexts has been discussed by McMahon and Ceperley [17]. The internal energies of two structures, with Hermann–Mauguin space-group notation I4/amd () (the family of structures to which this belongs will be considered further below) and Rm, with different cut-off radii ( and a.u.) of norm-conserving Troullier–Martins pseudopotentials [18], were compared. Their study indicated that this approximation has a very small impact on these calculations (subject to the above constraint). In another study [19], the energy difference between face- (Fmm; ) and body-centered cubic (Imm; ) phases were compared, by using a projector augmented wave (PAW) method pseudopotential [20,21] and an all-electron one. This work showed that the error introduced for these calculations is insignificant. The structures considered in these studies though have very high symmetry. Another important consideration is whether using a pseudopotential will influence the calculation of properties, such as the superconducting critical-temperature . This was made long ago by Gupta and Sinha [22], suggesting that the estimate of may be considerably reduced by screening effects. This is based on the idea [23] that in the vicinity of the proton the electron wavefunction is rigidly displaced together with the proton, and hence is not involved in the electron–phonon interaction, i.e., the screening of the bare Coulomb potential should result in a decrease of coupling constant . This will be discussed in more detail further below.
There are still several open comments and questions concerning the use of the pseudopotential method. Some specific ones are as follows: Compared with the and phases, which both belong to the cubic system of crystal structures, lower-symmetry ones may be more representative and convincing. How are the internal energies of these affected? Are transition pressures, being a function of both energy and its change to first order, affected? Finally, is the superconductivity-physics affected?
The purpose of this work is to make a thorough analysis of the error made using pseudopotentials, using modern calculation techniques. Calculations of internal energies, the first phase-transition pressure, and superconducting properties of atomic metallic hydrogen under high pressures are performed. Structures that come from different crystal systems (cubic, rhombohedral, tetragonal, and orthorhombic) are considered. These quantities will be compared as calculated within the pseudopotential method to the full-potential, all-electron linearized augmented plane-wave (LAPW) method [24,25] one.
2. Methods
Both the pseudopotential and all-electron calculations were performed from first principles. These were based on DFT [15]. Exchange–correlation effects were described using the generalized gradient approximation (GGA), according to the Perdew–Burke–Ernzerhof (PBE) [26] form. Other settings were chosen similarly between the two methods, for as direct comparisons as reasonably possible. These are described in the following.
The pseudopotential calculations were performed using Quantum ESPRESSO (QE) [27]. A PAW pseudopotential [20,21] with a cut-off radius of a.u. was used to describe the region near the nucleus of hydrogen. Convergence tests (energy to within 1 meV/proton) required and Ry for the plane-wave basis-set cutoffs (kinetic energy) for the wavefunction and charge density, respectively.
All-electron calculations were performed self-consistently using the full-potential LAPW method as implemented in the Elk code [28]. A plane-wave cut-off of ( is the average of the muffin-tin radii in the unit cell) was used for the expansion of the wavefunction in the interstitial region. The muffin-tin radius for hydrogen is a.u., which is comparable to that in the PAW pseudopotential. The cut-off for charge density, which is the maximum length of for expanding the interstitial density, was where .
It is important to briefly recognize the difference between the all-electron and PAW methods. Both consider a plane-wave basis set, but augmented in the region near the nucleus to describe the atomic-like wavefunction while retaining or increasing efficiency. For the PAW method, however, inside the augmentation region, the (pseudo) wavefunction will be much smoother than the all-electron one; i.e., the physics in this region, for this method, are similar to what happens in the (standard) pseudopotential approximation. The advantage of this is computational efficiency. The trade-off, however, is the nonphysical description of electrons in this region. Whether this affects results depends on the importance of this description. This is considered herein, for calculations of several properties.
Convergence (to the same criterion as above) with respect to the number of points needed to sample (integrate over) the irreducible Brillouin zone were tested individually between QE and Elk. Values obtained for the considered structures were as follows: I4/amd ( both), Cmcm ( and for QE and Elk, respectively), I3d ( and ), and Fmm (). Smearing was used to improve convergence (of the integrations): in QE, the scheme of Methfessel–Paxton [29] was used, with a value of Ry; in Elk, that of Fermi–Dirac [30], with a suggested value [31] of Ha.
For the phonon calculations, the GGA functional is implemented with the finite-displacement method (supercell method), but not with density-functional perturbation theory (DFPT) [32] in the version of Elk that was used (6.3.2). To make the comparison under the same conditions, phonon dispersions were calculated using the former approach with supercell in both QE and Elk, combined with the phonopy code [33]. Such a grid is sufficient for a quantitative determination of the phonons in this system [5,6]. For phonon dispersions, paths between high-symmetry points, covering all special points and lines necessarily and sufficiently, in the Brillouin zone were determined automatically, using the SeeK-path tool [34].
For the superconductivity calculations, again in order to use the GGA functional, electron–phonon coupling calculations were carried out using DFPT in QE and the supercell method in Elk. These two methods should give (numerically) the same results, as long as the sampling in reciprocal space (former method) is consistent with the supercell size (latter method); that is, the difference is one of computational efficiency [35]. Considering this, a q-point grid and supercell were used for all calculations. This should be sufficient to make a quantitative comparison between the two methods, even if only calculate approximate values of the superconducting parameters themselves [5,6].
T was estimated by numerically solving the nonlinear Eliashberg equations. Detailed derivation of the isotropic Eliashberg gap equations have been presented by Allen and Mitrovic [36]. The following corresponding numerical method has been explained in Refs. [37,38]. The expressions are for the superconducting order parameter ≡ (i) along the imaginary frequency axis (i = ), the maximum value of which corresponds to the wavefunction of the superconducting condensate, and wavefunction renormalization factor Z ≡ Z(i),
and
where = 1/kT where k denotes the Boltzmann constant and T the temperature, is the Coulomb pseudopotential, is the Heaviside function, is the phonon cut-off frequency, where is the maximum phonon frequency, is the n-th fermion Matsubara frequency with the pairing kernel for electron–phonon interaction has the form where is the phonon frequency, and is the Eliashberg spectral function where F() is the density of states of lattice vibrations (the phonon spectrum), and describes the coupling of phonons to electrons on the Fermi surface. Ashcroft demonstrated [39], via an ab initio calculation that in metallic hydrogen. This value is used herein. These two equations are iteratively solved self-consistently at a certain temperature T. T is defined as that at which the Matsubara gap becomes zero. Herein, 2201 Matsubara frequencies () were used.
The most stable structures of atomic metallic hydrogen from 500 to 3000 GPa, as predicted by calculations, were considered. These include I4/amd (Cs-IV) [17], Cmcm [40], and I3d [40]. Lower-symmetry, related structures, essentially the same up to a distortion(s) (such as Fddd [19] and C222 [41] for the first two structures, respectively), were not considered. Fmm was also considered, for reference. The considered pressures cover the range from approximately the expected molecular-to-atomic phase transition [42,43] to just above the first predicted atomic phase transition I4/amd → Cmcm [40].
3. Results and Discussion
The structures (themselves) of high-pressure hydrogen are extremely difficult to determine by experiment. Based on first-principles calculations [17], a body-centered tetragonal (BCT) is considered to be the most promising candidate, for the first atomic phase(s). Representations of structures from this family are shown in Figure 1.
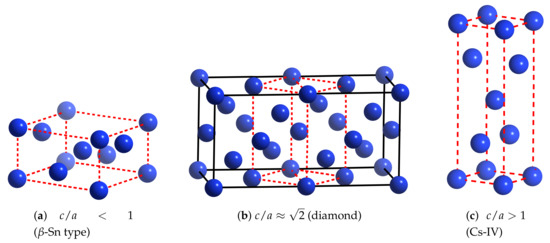
Figure 1.
(Color online) Body-centered tetragonal (BCT) representation of (some) structures of atomic metallic hydrogen. These are characterized in terms of their ratio. BCT lattices are depicted in dotted red.
These can be characterized in terms of their ratio, and they are often done so using an “elemental” naming scheme. Specific ones of importance are (-Sn type), ≈ (diamond), and >1 (Cs-IV).
3.1. Internal Energy
Internal energies as a function of ratio were calculated at six volumes. Zero-point energies were not directly included in these (or below) calculations. This ratio was varied from to 10, for each volume. Volumes were determined by geometry optimizations with QE over the considered pressure range (see above) in steps of 500 GPa. These volumes were then fixed, and used in both QE and Elk. The results are shown in Figure 2.
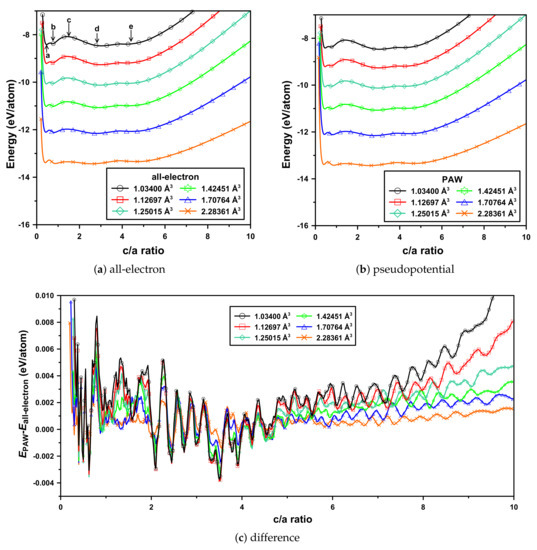
Figure 2.
(Color online) Calculated internal energies per atom of the BCT structures of atomic hydrogen, as a function of ratio at six volumes. BCT structures pointed by arrows in (a) are, from left to right: , (-Sn), , (Cs-IV), and , respectively. Pressures corresponding to these volumes are discussed in the text.
For both sets of calculations, there are four energy minima: a shallow one at , the deepest one at (Cs-IV), and two deep ones at (-Sn) and . Notice that (diamond) is always unstable. These ratios are indicated with arrows in Figure 2a. From the difference plot (Figure 2c), a few meV/proton difference (the PAW pseudopotential energies are, in general, higher) occur on both sides of . Although this difference does not change the relative stabilities of the (BCT) structures (see Figure 2a), it is still significant, considering the relative magnitudes of energies.
Consider also the changes as a function of volume. The global energy minimum is always for Cs-IV. As the volume decreases, increases. For the pseudopotential calculations, this ranges from to . For the all-electron ones, from to . These ranges are in very good agreement. For both sets of calculations, the energies of -Sn and diamond decrease with increasing volume.
The above results show that as far as (relative) energies, structures, and both qualitative and quantitative changes with volume are concerned, the replacement of Coulomb potential by a pseudopotential appears to be reasonable. This is consistent with previous results [19], which focused on structures with very high symmetries. In addition (in a way) to verifying the approach, the results here extend and altogether generalize these conclusions for structures with low(er) symmetries.
3.2. Phase Diagram
To quantify the aforementioned considerations with volume, the pressure–volume () phase diagram was constructed. This is a more sensitive measure [than internal energies (above)], as the free energy (enthalpy H, in this case) depends on both the energy and its first-order change via the hydrostatic pressure,
where E is the internal energy. Pressures were calculated according to Equation (1), by derivatives of the equation of state (EoS) with respect to volume (instead of directly calculating the trace of external stress tensor). Specifically, once the volume dependence is known, the energy as a function of volume can be constructed, then this data is fitted with the 3rd-order Birch–Murnaghan EoS [44], and derivatives are calculated.
Results for the first predicted phases of atomic hydrogen are shown in Figure 3.
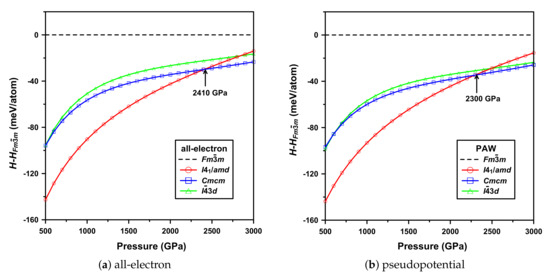
Figure 3.
(Color online) Calculated enthalpies H as a function of pressure of the predicted most stable structures of atomic hydrogen, relative to the Fmm phase. Values were calculated every 250 GPa.
Now using Hermann–Mauguin space-group notation (as common), these are, in order of increasing pressure, I4/amd (Cs-IV), Cmcm, and I3d. The pseudopotential results are in both qualitative and quantitative agreement with earlier work [40]. The all-electron ones show some important differences, however.
Consider first the trends in relative enthalpy differences though. These are consistent with earlier work. In particular, I4/amd becomes very unstable with increasing pressure, relative to a set of structures with much flatter enthalpy changes.
Consider now the phase-transition pressures. That of the (first) I4/amd → Cmcm transition is 2300 GPa, which is in agreement with the approximate value of >2100 GPa calculated in Ref. [40] (the latter based on a less-dense pressure grid). For the all-electron calculations, this transition occurs at 2410 GPa. Compared to the above results (for the two pseudopotential calculations—herein and in Ref. [40]), this difference (increase) is relatively small. However, this trend appears consistent with the next (potential) phase transition, discussed below.
Consider finally the latter structures. It appears that a phase-transition Cmcm → I3d will occur. (It does, but with consideration of zero-point energy. This is predicted [40] above TPa.) Considering this phase transition, a significant difference can be seen. Consistent with the first transition, it appears that this one will also be pushed to even higher pressures. In this case, however, it is enough such that this transition may not occur. This can be understood by calculating the difference in enthalpy between these two structures, . The maximum value with the pseudopotential approximation is meV/proton at 1700 GPa, and this decreases to meV/proton by 3000 GPa. This is even qualitatively much different in the all-electron calculations, where increases from to meV/proton at these pressures. Therefore, a phase transition, in this case, seems unlikely.
Considering the results together, all-electron calculations seem to (at least, in this region of the phase diagram considered) push phase-transition pressures higher. Relative stabilities may also change. These results may be significant enough to affect the phase diagram.
3.3. Phonon Dispersion
An important consideration for phase stabilities (by zero-point energy), properties (e.g., superconductivity), etc. is lattice vibrations. Throughout reciprocal space, these are illustrated most clearly by phonon dispersions.
The dispersion relation of I4/amd (Cs-IV) at 500 GPa is considered, as an example. These results are shown in Figure 4.
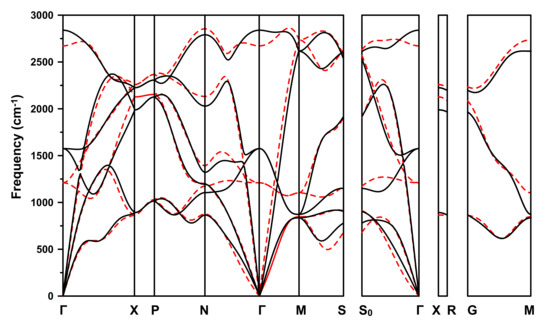
Figure 4.
(Color online) Phonon dispersion curves along high-symmetry directions of I4/amd (Cs-IV) at 500 GPa. Solid black curves are from the all-electron calculation, and dashed red ones from the PAW pseudopotential one.
Comparison shows that the results calculated by the two methods are similar. The most significant difference is near the point, where the frequencies of the optical modes as calculated with the pseudopotential approximation are much flatter. A possible explanation for this is that, with this approximation, the electrons near the proton are not (as) bound with its motion (unlike the all-electron method — see below). This would mean that the change in the electronic charge density become noticeable, and hence its phonon density of states is large and phonon dispersion flat.
3.4. Superconductivity
Superconductivity of atomic metallic hydrogen is considered, in this section.
Superconductivity of I4/amd at 500 GPa is again used, as an example. Figure 5 shows a detailed comparison of and .
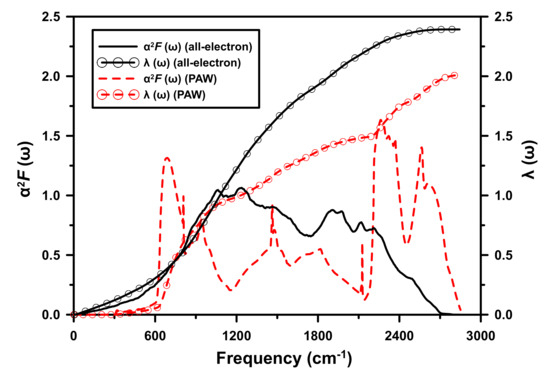
Figure 5.
(Color online) Eliashberg spectral function and the electron–phonon pairing parameter of I4/amd at 500 GPa. The results from the PAW calculation are consistent with those of Ref. [5], calculated using another pseudopotential method.
There are significant differences in the quantities as calculated by the two methods, both qualitatively and quantitatively. The pseudopotential calculations display significant and “peaked” electron–phonon interaction at both (relatively) low and high frequencies, but much less at intermediate ones. This can be compared to the broad spectral function, centered at intermediate frequencies, as calculated by the all-electron method.
At high frequencies, this result is consistent with the work of Gupta and Sinha [22]. This interaction is mainly due to that near the proton (in metallic hydrogen). (Consider the change in the bare Coulomb interaction with r — this scales as , and hence is largest for small r.) However, the electrons in this vicinity are not at all free-electron-like; their motion is bound with that of the proton. These electrons should therefore not significantly participate in the electron–phonon interaction.
Unlike the earlier expectation [22] of a decrease in though, it is actually found to increase by the all-electron calculation. Figure 5 shows, by integration of , that this can be attributed to the increased contribution at intermediate frequencies to .
The dependence of the maximum value of the order parameter on temperature is shown in Figure 6. The superconducting transition temperature is defined as that at which this parameter vanishes, . The obtained T is 352 K in the all-electron calculation, compared to 339 K with the pseudopotential approximation.
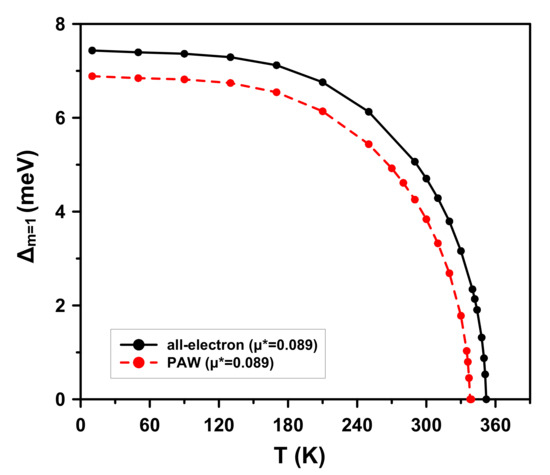
Figure 6.
(Color online) Dependence of the maximum value of the order parameter on temperature T of I4/amd at 500 GPa. Calculations are shown by both the all-electron method (solid black) and with the PAW pseudopotential approximation (dashed red).
4. Conclusions and Outlook
The reliability of the standard use of pseudopotentials to simulate atomic metallic hydrogen was studied. This was done for calculations of internal energy, enthalpy, the phonon dispersion spectrum, and superconductivity, by comparing pseudopotential to all-electron calculations. In the case of calculating internal energy, as has been considered to some extent before, the accuracy that can be obtained by pseudopotentials is sufficient. Differences occur for enthalpy and phonon dispersion relations, however. These may be significant enough to affect the phase diagram, by both pushing phase-transition pressures higher and changing relative stabilities. Significant differences also occur for the calculation of (at least, some) properties. For superconductivity, for example, the magnitude of the Eliashberg spectral function at both (relatively) low and high frequencies is considerably smaller as calculated by the all-electron method than with the pseudopotential approximation, while that at intermediate frequencies is increased. Together, these changes increase the value of , which causes the calculated superconducting critical temperature to be higher.
The presented results are important for understanding metallic hydrogen; and will be so for future studies, especially calculations, of this system. Discussed above were applications for which the use of pseudopotentials in such calculations are expected to give accurate results. A further consideration is whether (practical) improvements could be made, to extend their range of applicability. The results suggest this to be the case for properties that depend mostly on electronic effects in the “valence” region (internal energy, enthalpy, and phonon dispersions). Improvements could straightforwardly be made by decreasing the pseudopotential cut-off radius, such that these electrons are more fully accounted for. This is especially important at high pressures, where the distance between protons decreases. For properties that depend more strongly on effects in the “core” region (e.g., superconductivity), similar improvements are not as practical. Although the cut-off could be reduced even further (with a limit of zero), the advantage of computational efficiency would be simultaneously reduced. Both the pseudopotential and all-electron methods are therefore expected to remain useful for such future studies. These studies should carefully consider the effects expected to contribute to their results. Based on these, the results and discussion herein can then be considered in the choice of calculation approach.
Author Contributions
J.M.M. proposed and supervised the research. J.Z. and J.A. performed the calculations. J.Z., J.A., and J.M.M. analyzed the results. J.Z. and J.M.M. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by NASA, Award Number 80NSSC19K0250. J.M.M. also acknowledges startup support from Washington State University and the Department of Physics and Astronomy thereat.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this Article:
| DAC | diamond anvil cell |
| DFT | density-functional theory |
| fcc | face-centered cubic |
| bcc | body-centered cubic |
| PAW | projector augmented wave (method) |
| LAPW | linearized augmented plane-wave (method) |
| GGA | generalized gradient approximation |
| PBE | Perdew–Burke–Ernzerhof |
| QE | Quantum ESPRESSO |
| DFPT | density-functional perturbation theory |
| BCT | body-centered tetragonal |
| EoS | equation of state |
References
- Wigner, E.; Huntington, H.B. On the Possibility of a Metallic Modification of Hydrogen. J. Chem. Phys. 1935, 3, 764–770. [Google Scholar] [CrossRef]
- McMahon, J.M.; Morales, M.A.; Pierleoni, C.; Ceperley, D.M. The properties of hydrogen and helium under extreme conditions. Rev. Mod. Phys. 2012, 84, 1607–1653. [Google Scholar] [CrossRef]
- Baraffe, I.; Chabrier, G.; Barman, T. The physical properties of extra-solar planets. Rep. Prog. Phys. 2010, 73, 016901. [Google Scholar] [CrossRef]
- Ashcroft, N.W. Metallic Hydrogen: A High-Temperature Superconductor? Phys. Rev. Lett. 1968, 21, 1748–1749. [Google Scholar] [CrossRef]
- McMahon, J.M.; Ceperley, D.M. High-temperature superconductivity in atomic metallic hydrogen. Phys. Rev. B 2011, 84, 144515. [Google Scholar] [CrossRef]
- McMahon, J.M.; Ceperley, D.M. Erratum: High-temperature superconductivity in atomic metallic hydrogen [Phys. Rev. B 84, 144515 (2011)]. Phys. Rev. B 2012, 85, 219902. [Google Scholar] [CrossRef]
- Mon, K.K.; Chester, G.V.; Ashcroft, N.W. Simulation studies of a model of high-density metallic hydrogen. Phys. Rev. B 1980, 21, 2641–2646. [Google Scholar] [CrossRef]
- Babaev, E.; Sudbo, A.; Ashcroft, N.W. A superconductor to superfluid phase transition in liquid metallic hydrogen. Nature 2004, 431, 666–668. [Google Scholar] [CrossRef]
- Nellis, W.J. Metastable solid metallic hydrogen. Philos. Mag. Part B 1999, 79, 655–661. [Google Scholar] [CrossRef]
- Nellis, W.J. Metastable ultracondensed hydrogenous materials. J. Phys. Condens. Matter 2017, 29, 504001. [Google Scholar] [CrossRef]
- Eremets, M. High Pressure Experimental Methods; Oxford Science Publications; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Ji, C.; Li, B.; Liu, W.; Smith, J.S.; Majumdar, A.; Luo, W.; Ahuja, R.; Shu, J.; Wang, J.; Sinogeikin, S.; et al. Ultrahigh-pressure isostructural electronic transitions in hydrogen. Nature 2019, 573, 558–562. [Google Scholar] [CrossRef]
- Dias, R.P.; Silvera, I.F. Observation of the Wigner-Huntington transition to metallic hydrogen. Science 2017, 355, 715–718. [Google Scholar] [CrossRef]
- Dewaele, A.; Loubeyre, P.; Occelli, F.; Marie, O.; Mezouar, M. Toroidal diamond anvil cell for detailed measurements under extreme static pressures. Nat. Commun. 2018, 9, 2913. [Google Scholar] [CrossRef]
- Jones, R.O. Density functional theory: Its origins, rise to prominence, and future. Rev. Mod. Phys. 2015, 87, 897–923. [Google Scholar] [CrossRef]
- Labet, V.; Gonzalez-Morelos, P.; Hoffmann, R.; Ashcroft, N. A fresh look at dense hydrogen under pressure. I. An introduction to the problem, and an index probing equalization of H–H distances. J. Chem. Phys. 2012, 136, 581. [Google Scholar] [CrossRef]
- McMahon, J.M.; Ceperley, D.M. Ground-state structures of atomic metallic hydrogen. Phys. Rev. Lett. 2011, 106, 165302. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef]
- Geng, H.Y.; Song, H.X.; Li, J.; Wu, Q. High-pressure behavior of dense hydrogen up to 3.5 TPa from density functional theory calculations. J. Appl. Phys. 2012, 111, 063510. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Gupta, R.; Sinha, S. Superconductivity in metallic hydrogen. In Superconductivity in d-and f-Band Metals; Springer: Boston, MA, USA, 1976; pp. 583–592. [Google Scholar]
- Maksimov, E.G.; Shilov, Y.I. Hydrogen at high pressure. Phys. Uspekhi 1999, 42, 1121. [Google Scholar] [CrossRef]
- Andersen, O.K. Linear methods in band theory. Phys. Rev. B 1975, 12, 3060–3083. [Google Scholar] [CrossRef]
- Koelling, D.D.; Arbman, G.O. Use of energy derivative of the radial solution in an augmented plane wave method: Application to copper. J. Phys. F Met. Phys. 1975, 5, 2041–2054. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- The Elk Code is Open Source, Freely. Available online: http://elk.sourceforge.net/ (accessed on 12 November 2020).
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef]
- Mermin, N.D. Thermal Properties of the Inhomogeneous Electron Gas. Phys. Rev. 1965, 137, A1441–A1443. [Google Scholar] [CrossRef]
- The Elk Code Manual. Available online: http://elk.sourceforge.net/elk.pdf (accessed on 12 November 2020).
- Baroni, S.; De Gironcoli, S.; Dal Corso, A.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515. [Google Scholar] [CrossRef]
- Togo, A.; Oba, F.; Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl1-type SiO1 at high pressures. Phys. Rev. B 2008, 78, 134106. [Google Scholar] [CrossRef]
- Hinuma, Y.; Pizzi, G.; Kumagai, Y.; Oba, F.; Tanaka, I. Band structure diagram paths based on crystallography. Comput. Mater. Sci. 2017, 128, 140–184. [Google Scholar] [CrossRef]
- Giustino, F. Electron-phonon interactions from first principles. Rev. Mod. Phys. 2017, 89, 015003. [Google Scholar] [CrossRef]
- Allen, P.B.; Mitrović, B. Theory of superconducting Tc. In Solid State Physics; Elsevier: Amsterdam, The Netherlands, 1983; Volume 37, pp. 1–92. [Google Scholar]
- Szczesniak, R. The numerical solution of the imaginary-axis Eliashberg equations. Acta Phys. Pol. A 2006, 109, 179. [Google Scholar] [CrossRef]
- Szcze, R.; Szcze, D.; Drzazga, E. Superconducting state in the atomic metallic hydrogen just above the pressure of the molecular dissociation. Solid State Commun. 2012, 152, 2023–2026. [Google Scholar]
- Richardson, C.F.; Ashcroft, N.W. High Temperature Superconductivity in Metallic Hydrogen: Electron-Electron Enhancements. Phys. Rev. Lett. 1997, 78, 118–121. [Google Scholar] [CrossRef]
- Liu, H.; Wang, H.; Ma, Y. Quasi-Molecular and Atomic Phases of Dense Solid Hydrogen. J. Phys. Chem. C 2012, 116, 9221–9226. [Google Scholar] [CrossRef]
- Geng, H.Y.; Wu, Q. Predicted reentrant melting of dense hydrogen at ultra-high pressures. Sci. Rep. 2016, 6, 36745. [Google Scholar] [CrossRef]
- McMinis, J.; Clay, R.C.; Lee, D.; Morales, M.A. Molecular to Atomic Phase Transition in Hydrogen under High Pressure. Phys. Rev. Lett. 2015, 114, 105305. [Google Scholar] [CrossRef]
- Eremets, M.I.; Drozdov, A.P.; Kong, P.P.; Wang, H. Molecular semimetallic hydrogen. arXiv 2017, arXiv:1708.05217. [Google Scholar]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).