1. Introduction
Are superconductivity mechanisms a matter for chemists? Such a question was a hot topic half a century ago, when the excitonic origin of superconductivity was widely discussed by scientists such as Schafroth, Blatt and Butler [
1] or Little [
2], in terms of strong interactions in real space (r-space, familiar to chemists). However, the success of the Bardeen–Cooper–Schrieffer (BCS) theory [
3], based on a delayed coupling between electrons of opposite spin and momentum, by exchange of phonons in reciprocal space (k-space), was immediately validated by experiment and discouraged many chemists from pursuing the r-space approach. Actually, the BCS theory predicted an upper value of ca. 30 K for the superconducting transition temperature
TC.
At its early stage, solid state chemistry rather focused on metal-insulator transitions, more spectacular as for example in vanadium oxides in which electric conductivity varies by more than ten orders of magnitude across the transition [
4], and is correlated with small crystallographic changes (r-space). This is why many new families of solids, discovered by chemists, were only later found superconducting by physicists. In particular, this was the case of the so-called Chevrel phases discovered by Prigent, Sergent and Chevrel [
5], for which superconductivity (
TC = 15 K) was evidenced two years later by Matthias [
6].
A fourteen-year gap occurred between the synthesis of the first cuprates +III of lamellar perovskite type (Hagenmuller, Goodenough, Pouchard and Demazeau [
7]) and the discovery of their superconductivity (
TC = 32 K) by Bednorz and Müller [
8]; meanwhile, Raveau, Studer and Nguyen [
9] had evidenced the key mixed valency +III/+II of copper in these systems. From then on, chemists participated actively in the so-called “golden rush” for new superconducting families and higher
TC values.
Thirty years later, there is still no consensus on the origin of this unconventional, high-
TC superconductivity: (bi-)polaronic, electronic, magnetic, excitonic, etc. Solving this mystery has been mostly the playground of physicists. However, a few chemists’ concepts were proposed as early as 1987: copper +II disproportionation (similar to silver +II and gold +II) and oxygen to copper charge transfer [
10,
11,
12], which have remained disregarded.
In 1990, Micnas, Ranninger and Robaczkiewicz [
13] published a paper titled “superconductivity in narrow band systems with local non-retarded attractive interactions”, which grabbed the attention of Simon concerning the properties of his rare-earth halogeno-carbides [
14]. Actually, Micnas et al. provided an intermediate model, mixture of local pairs and itinerant electrons interacting via a charge-exchange mechanism, giving rise to a mutually induced superconductivity in these systems. Among popular topics in today’s physics are the relations between three types of order, namely magnetism (spins), ferroelectricity (charges) and superconductivity (Cooper pairs); an example is multi-ferroicity. Solid state chemistry and its conceptual framework (structure-bonding-properties) are intrinsically involved in these three types of ordering.
In this article, we present a chemist’s approach to the effect of doping in SrTiO
3, which progressively turns from a quantum ferroelectric insulator to a metal and to a superconductor, as recently presented by Rischau et al. [
15] and by Gabay and Triscone [
16]. Then, while developing further some of our previous work [
17], we describe the features underlying the transition from an antiferromagnetic Mott-type insulator such as La
2CuO
4 into a high-
TC superconductor. Finally, we tentatively apply these approaches to another family of high-
TC superconductors, the iron pnictides/chalcogenides [
18,
19].
3. Metallic and Superconducting Behavior of SrTiO3
From the crystallographic point of view, SrTiO
3 is a perfect perovskite; its Goldschmidt factor is strictly equal to unity. When stoichiometric, SrTiO
3 is a dielectric insulator with the relative permittivity rising to about 20,000 at low temperature, typical of a quantum ferroelectric. The substitution of Ca
2+ for Sr
2+ (a few %), with different ionic radii, induces a ferroelectric instability. On the other hand, a slight non-stoichiometry due to oxygen vacancies generates n-type charge carriers and a metallic state, and even a superconducting state below 1 K, despite a very small carrier density [
15,
24]. Soft phonon modes and oxygen non-linear polarizability were proven to play a key role in the ferroelectric and superconducting properties of SrTiO
3, among other systems [
25,
26,
27]. As mentioned earlier, there might exist a link between the charge ordering in an insulating ferroelectric phase and the spin/momentum ordering in a superconducting phase. Actually, materials both metallic and polar are scarce and poorly understood so far [
16]. In 2017, Rischau et al. proposed that these two kinds of order can coexist upon homogeneous doping, even reinforce each other [
15]; however, many works have evidenced inhomogeneous doping in SrTiO
3 as well, resulting in metallic regions coexisting with insulating ones [
28,
29,
30].
Is there a chemical explanation to those unconventional results? In the first part, we showed how the nonbonding electrons of pure oxygen character, at the top of the valence band, could become partly bonding following a tetragonal distortion of ferroelectric type in BaTiO
3. Conversely, the nonbonding states of pure Ti-character are destabilized; the band gap increases, but the stability of the compound is not affected since the conduction band is empty. The latter argument is no longer valid if electrons are introduced by doping: their destabilization competes with the stabilization of the top of the valence band, and thus with the ferroelectric instability itself. This is observed in tungsten bronzes such as Na
xWO
3 (0 < x < 1), known for more than a century, in which the ferroelectric instability of WO
3 disappears progressively for x up to ca. 0.2 [
31]. It is therefore understandable that superconductivity in SrTiO
3 remains limited by the extent of electron doping (<0.001). Two preliminary remarks must be made:
- (i)
The Mott-type insulator-metal transition limits the value of
close to 0.2, where
n is the carrier density and
is the Bohr radius corrected by the dielectric constant, as illustrated by Edwards and Sienko [
32]. When the dielectric constant is very high,
may reach values as high as a micrometer; this is precisely what occurs in SrTiO
3 at low temperature.
- (ii)
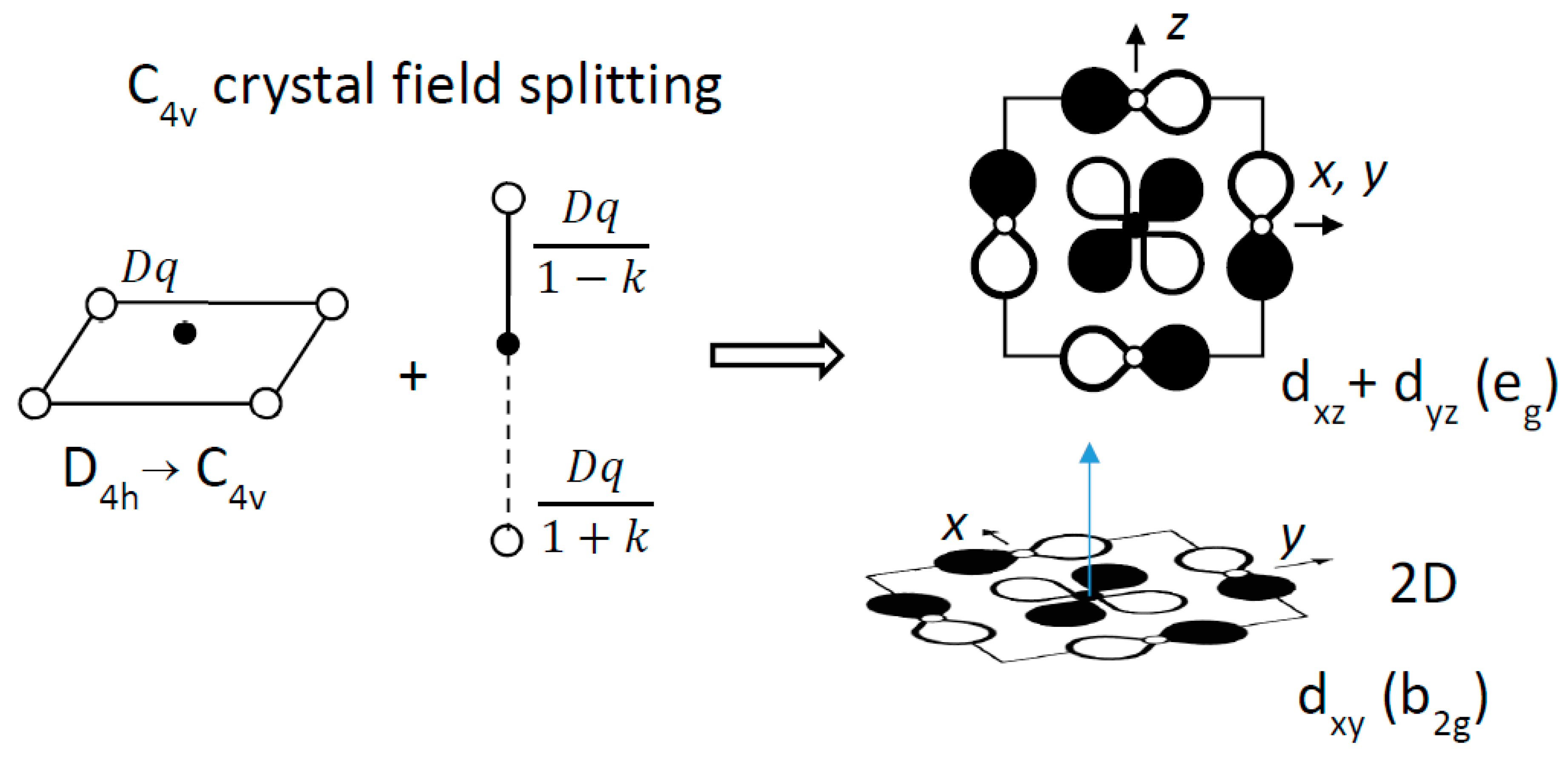
The ferroelectric distortion induces a splitting of the conduction band, namely, π*(e
g) and π*(b
2g), where e
g = (xz, yz) and b
2g = xy (
Figure 3).
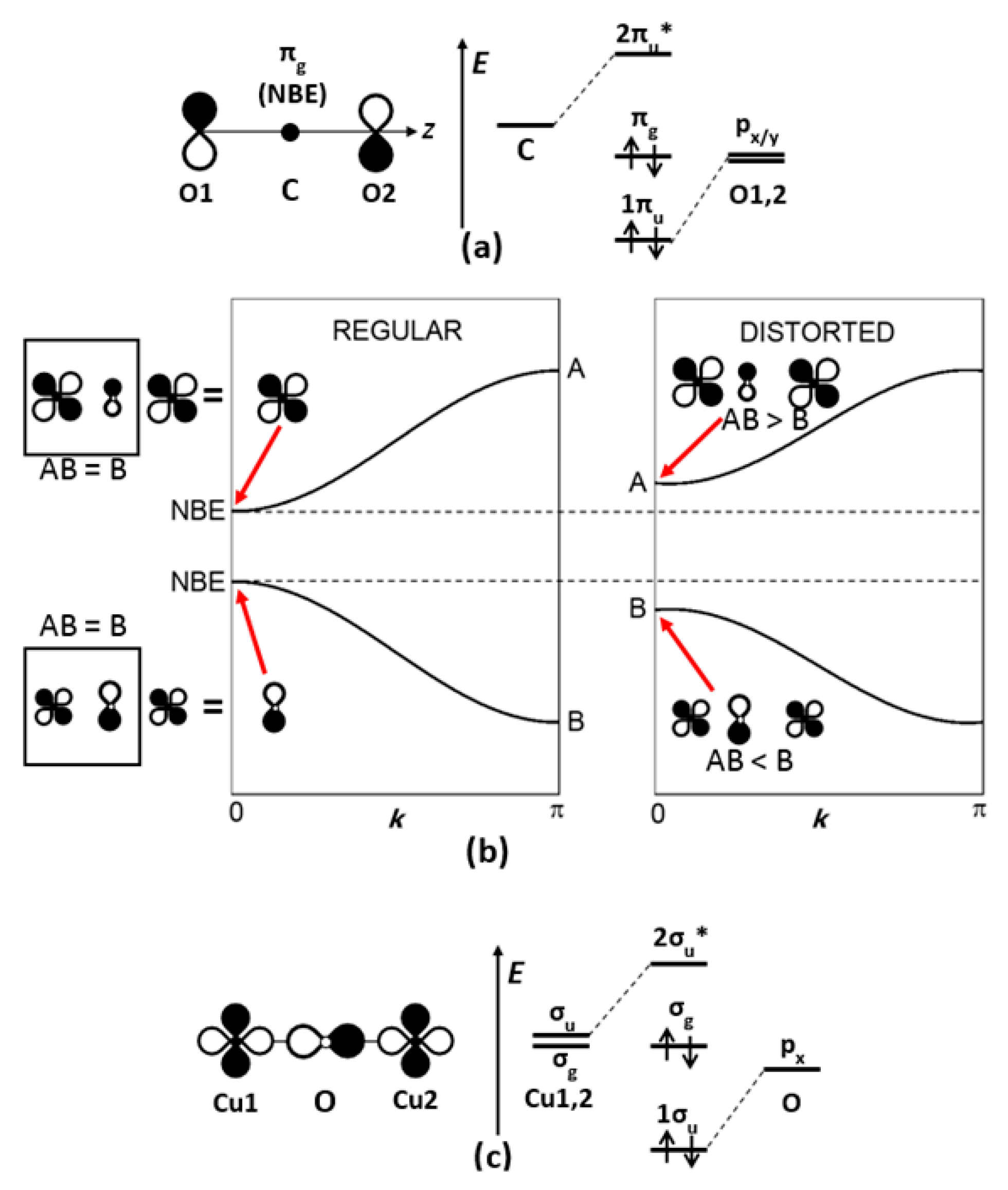
A simple crystal field consideration accounts qualitatively for this band splitting, by summing the potentials in units of Dq, the phenomenological parameter used by chemists. The short (axial), the long (axial), and the normal (equatorial) Ti–O interactions are described by the potentials Dq/(1-k), Dq/(1+k) and Dq, respectively (0 < k < 1). The band splitting leads to a stabilization of the b2g state (−6.28k2) with respect to the eg state (+1.14k2). From the point of view of chemical bonding, the Ti4+ displacement above (or below) the O4 plane (i) lifts the degeneracy of t2g states and (ii) decreases significantly the 3dxy/2p overlap, decreasing consequently the width of the b2g band (as well known for the VO2+ vanadyl ion).
The first carriers then occupy the narrow 2D π*(b
2g) band, of the fermion character, but also as electron pairs of the boson type, since their Coulomb repulsion on the same orbital almost vanishes (
U ≈ 0). Their coherence length should be close to the one in BCS-type superconductors such as Nb
3Sn (few hundreds nm). Under the phonon modes discussed above, those pseudo-local pairs, which are not yet proper Cooper pairs, mix, at each ¼ period, with empty t
2g states arising from t
2g = b
2g + e
g. Then, they can separate according to b
2g2 → b
2g1 + e
g1 (“t
2g2”) into a Fermi liquid, or mix with empty e
g or t
2g states according to b
2g2 (pseudo-local pairs) + t
2g0 (“t
2g⇵”) into Cooper pairs with opening of a superconducting gap.
In essence, the ferroelectric instability (provided by the small doping of Ca2+ and by the nonbonding character of electrons at the top of the valence band) induces a bistable electron system coupled to the oscillations of the axial oxygen atom. Here, we had all the ingredients for a two-band scenario, with a broad and a narrow band; the first band consists of empty states, the second contains electron pairs due to U ≈ 0 and a large dielectric constant. The two bands mix before the gap closure, into a superconducting state even with such low carrier densities as 1017 cm−3.
A simple electronic Hamiltonian H’ replaces here the (delayed) electron–phonon coupling Hamiltonian of the BCS model. This chemist’s view applies to SrTiO3-LaAlO3 heterostructures as well, justifying the intrinsic doping and the ferroelectric-type distortions expected in these structures. SrTiO3 can be viewed as a succession of neutral TiO2 and SrO layers; LaAlO3, a perovskite as well, has charged AlO2− and LaO+ layers. Thus, the interface of the heterostructures can be regarded as a charged layer La0.5Sr0.5O+0.5. The electric field gradient between LaO+ and neutral SrO layers should be screened, as in p–n junctions, by a charge transfer: TiO2 + AlO2− → (TiO2)-δ +(AlO2)−(1−δ), which is actually a charge transfer between O2− (AlO2) and Ti4+ (TiO2); the e−/h+ pair opposes then the electric field gradient.
Additionally, the Ti-O-Al entity is dissymmetrical in terms of chemical bonding and, in the same way as a ferroelectric distortion, induces both a band splitting from t
2g to b
2g+ e
g and a dynamical polarization of TiO
2 layers away from the interface. Therefore, the first nonbonding electrons in the conduction band (t
2g) will undergo a succession of quasi-local pair states (b
2g⇵, few hundreds nm) and delocalized Cooper-pair states, due to the mixing with empty e
g or t
2g states when the gap closes. Such a description is close to that of Gariglio et al. [
33] in their review on interface superconductivity.
4. High-TC Superconducting Cuprates
A significant difference between cuprates and titanates is the one-electron energy (Coulomb integral) for 3d orbitals. The Ti and Cu 3d states lie respectively above and below the O 2p state, which affects the electronic structure: in cuprates with optimum doping, the valence band should be of dominant Cu-character, the conduction band being mostly of oxygen character.
La2CuO4, the structural parent of superconducting cuprates, is a charge transfer insulator with a first excited state described by O2− + Cu2+ → O− + Cu+. It is also an antiferromagnet with a Néel temperature close to the ambient temperature. La2CuO4 is mostly p-doped by substitution of Ba2+ or Sr2+ for La3+, or by chemical or electrochemical intercalation of oxygen in La2O2 rock salt-type layers. Doping of 8–20% induces a metallic then superconducting state (TC ≈ 40 K), along with a significant decrease in the unit cell volume; shortened interatomic distances lead to larger tCu-O transfer integrals and thus to larger band widths, but also to stronger oxygen–oxygen interactions that turn out to be of major relevance here. Along with doping, the band widths increase and the value of the Hubbard parameter decreases due to covalency (U is related to Racah repulsion parameters B and C, familiar to chemists, and sensitive to covalency); this is consistent with an insulator-metal transition of the Mott–Hubbard type, for increasing the t/U ratio.
We start from this framework, with U ≈ 0, to describe the electronic structure of cuprates with optimum doping (i.e., formally Cu(2+x)+ with x close to 0.15). U ≈ 0 means a full O2− + Cu2+ → O− + Cu+ transfer, Cu+/O− being the ground state. This is justified by several arguments:
- (i)
Coulomb integrals,
Hdd (Cu) = −18.7 eV and
Hpp(O) = −17.1 eV [
34]. Tight-binding calculations for (CuO
4)
5− square planar clusters, as found in La
2Li
0.5Cu
0.5O
4 [
35], show clearly this charge transfer situation (
Figure 4 in Ref. [
36]).
- (ii)
Doped holes in cuprates are essentially located on oxygen atoms, as demonstrated by the pioneering work of Bianconi et al. [
37] by X-ray absorption spectroscopy (XANES), later on by electron-loss spectroscopy (EELS) [
38] and by spectacular atomic scale imaging from tunneling asymmetry, even on underdoped samples, by Hanaguri et al. [
39], Kohsaka et al. [
40] and Pasupathy et al. [
41], showing inhomogeneous charge distributions as nano-scale stripes or checkerboard patterns on oxygen atoms.
- (iii)
Recent studies by Jurkutat et al. [
42] using NMR on
63–65Cu and
17O doped samples, leading to a phase diagram for
TC as a function of the distribution of doped holes at Cu and O sites.
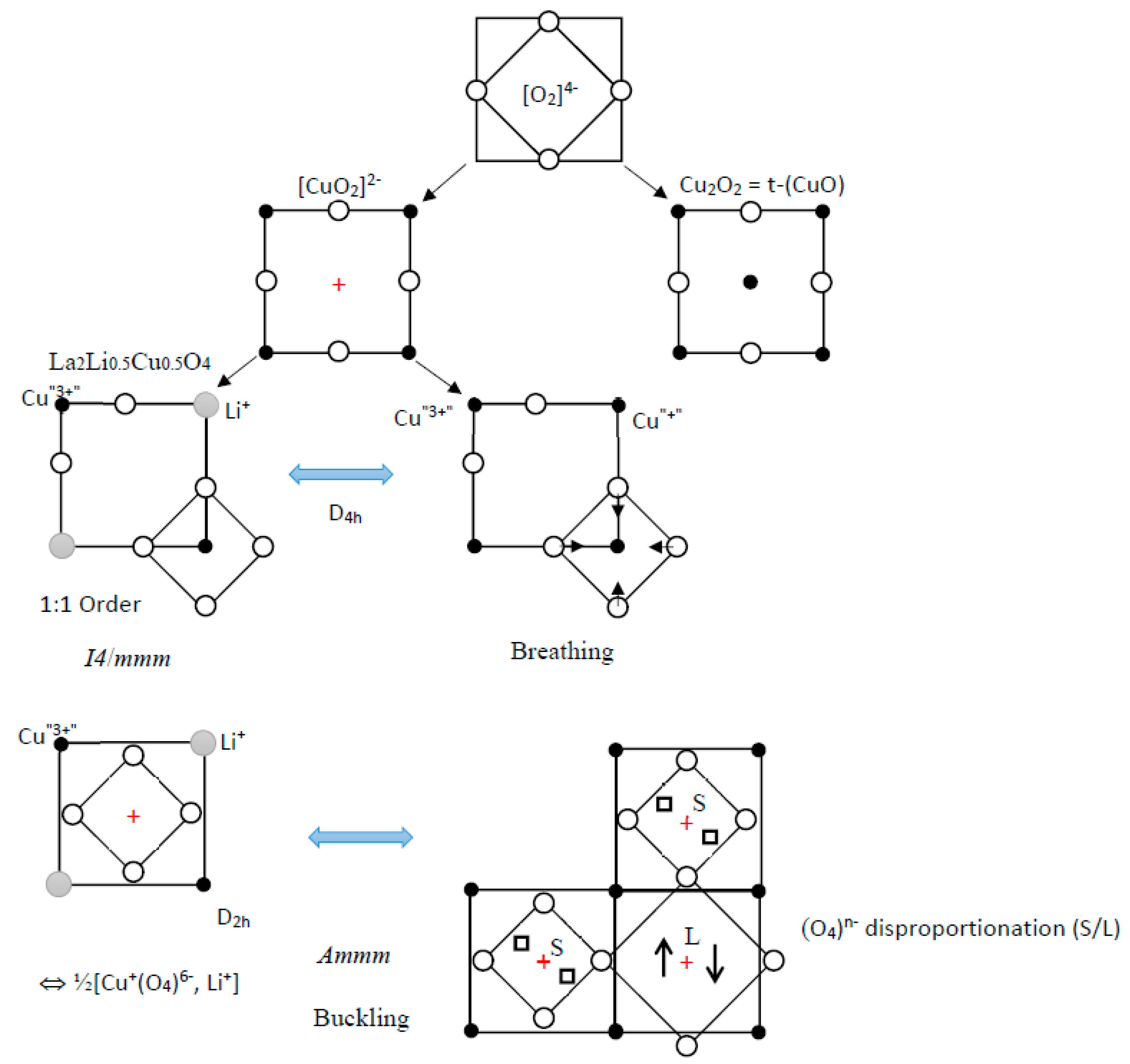
4.1. (CuO2)2− Unit Cell
The input data for our tight-binding calculations are reported in
Table 1.
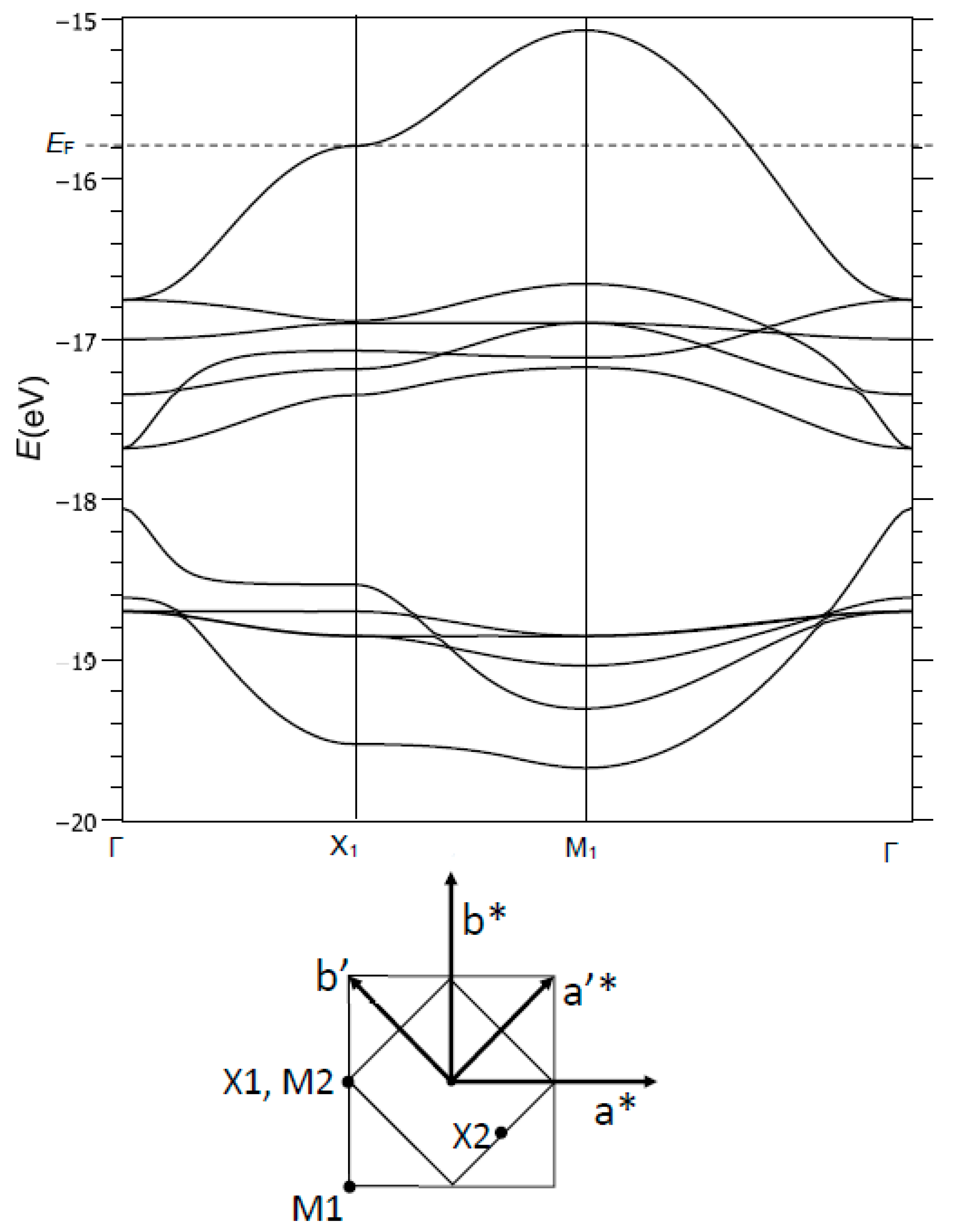
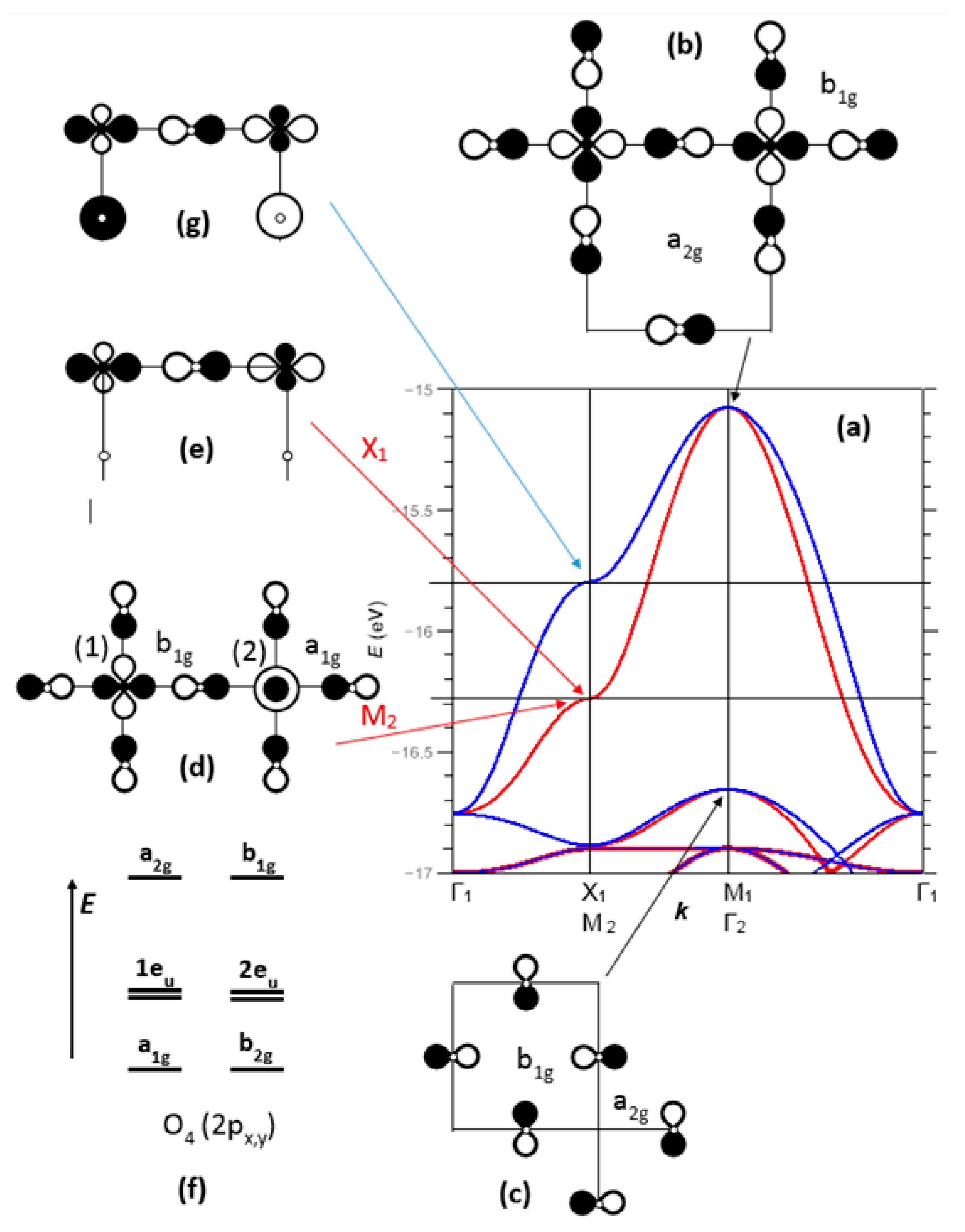
Figure 4 (top) shows the dispersion curves
E(
k) in the −19 to −15 eV range. Several bands are identified:
- (i)
Around −19 eV, a valence band of Cu character and Cu-O bonding interactions,
- (ii)
Between −18 and −15 eV, a broad conduction band of oxygen character, and Cu-O generally antibonding.
Figure 5 shows an enlarged view of the two top bands, between −17 and −15 eV, noted here σ*(b
1g) and π*(a
2g) (as referred to the point symmetry of the copper site, at the M1 point of BZ1). At Γ, these two bands are degenerate and of pure oxygen character (
Figure 5a). The top band, σ*(b
1g), is broad (
W ≈ 1.5 eV) due to strong Cu-O and O-O antibonding interactions; the π*(a
2g) band is narrow (
W ≈ 0.3 eV) because of its Cu-O nonbonding character (especially in Γ, M1) or by compensation of Cu-O and O-O antibonding/bonding interactions (in X1).
The
E(
k) vs.
k plot for σ*(b
1g) shows a saddle point in X1, associated with a van Hove-type peak in the density of states (this point will be discussed later). The corresponding crystal orbital has contributions from Cu 4s, z
2 and x
2 − y
2 with respective weights of 0.037, 0.088 and 0.252. The 4s/3z
2 hybridization is well known for the Jahn-Teller Cu
2+ ion. The other contribution is from the 2p
x orbital of one oxygen, with a weight of 0.650. Thus, the oxygen character is approximately twice the copper character in this crystal orbital, and the bonding is strongly anisotropic with large antibonding interactions along [100] and nonbonding interactions along [010] (
Figure 5e). This nonbonding character in X1 offers the possibility of opening a static or dynamical gap of nematic type (a ≠ b), with the creation of a double-well potential as in SrTiO
3. For the Fermi level to be located in X1 for the σ*(b
1g) band, a hole doping rate of 12–15% should be necessary. This approach, which agrees with experiment, does not discriminate electrons and doped holes; doping is used to shift the Fermi level toward a high-symmetry point of the Brillouin zone.
4.2. The Double Unit Cell (Cu2O4)4−
Figure 5a shows the same dispersion curves
E(
k) for a double unit cell (Cu
2O
4)
4− but with a different crystal orbital distribution in the two unit cells. The hybridization of z
2 and x
2 − y
2 reinforces the anisotropy of the (anti)bonding between copper and oxygen (
Figure 5e). Besides, we can consider the hypothesis of a distribution of those two orbitals over two distinct sites (orbital ordering).
The correspondence between the Brillouin zones and high symmetry k-points of the single (BZ1, M1, X1…) and double unit cell (BZ2, Γ2, M2…) is shown in
Figure 4 (bottom).
The M2 point, corresponding to X1 for the single unit cell, shows a degeneracy between an energy band arising from σ*(b
1g) (M1 corresponds to Γ2) and a lower energy band arising from
(Γ1) (
Figure 5a). Both bands show a full and opposite orbital ordering on copper sites labelled (1) and (2) (
Figure 5d), and appeared isotropic since the weights on oxygen atoms were identical. The symmetries on the two copper sites were different:
and
, which confirms the proposed 1:1 orbital ordering. Each oxygen atom, overall nonbonding, becomes a Janus entity, bonding on one side (with respect to a
1g O–O bonding) and Cu-O antibonding on both sides, but weakly in a
1g (c
i2 = 0.15), stronger in b
1g (c
i2 = 0.22), thus fully dissymmetric. Compared to X1 (spatially dissymmetric, antibonding/bonding along [100] and nonbonding along [010] (
Figure 5e), with the reverse situation at Y1), M2 does not show any tendency to nematicity, but rather a strong tendency to couple to an optical mode of breathing type, with a dynamical inversion of the copper sites (1) and (2) (Peierls-type 2D instability); a tight-binding calculation (EHTB) leads to a gap opening of 33 meV per pm of phonon amplitude.
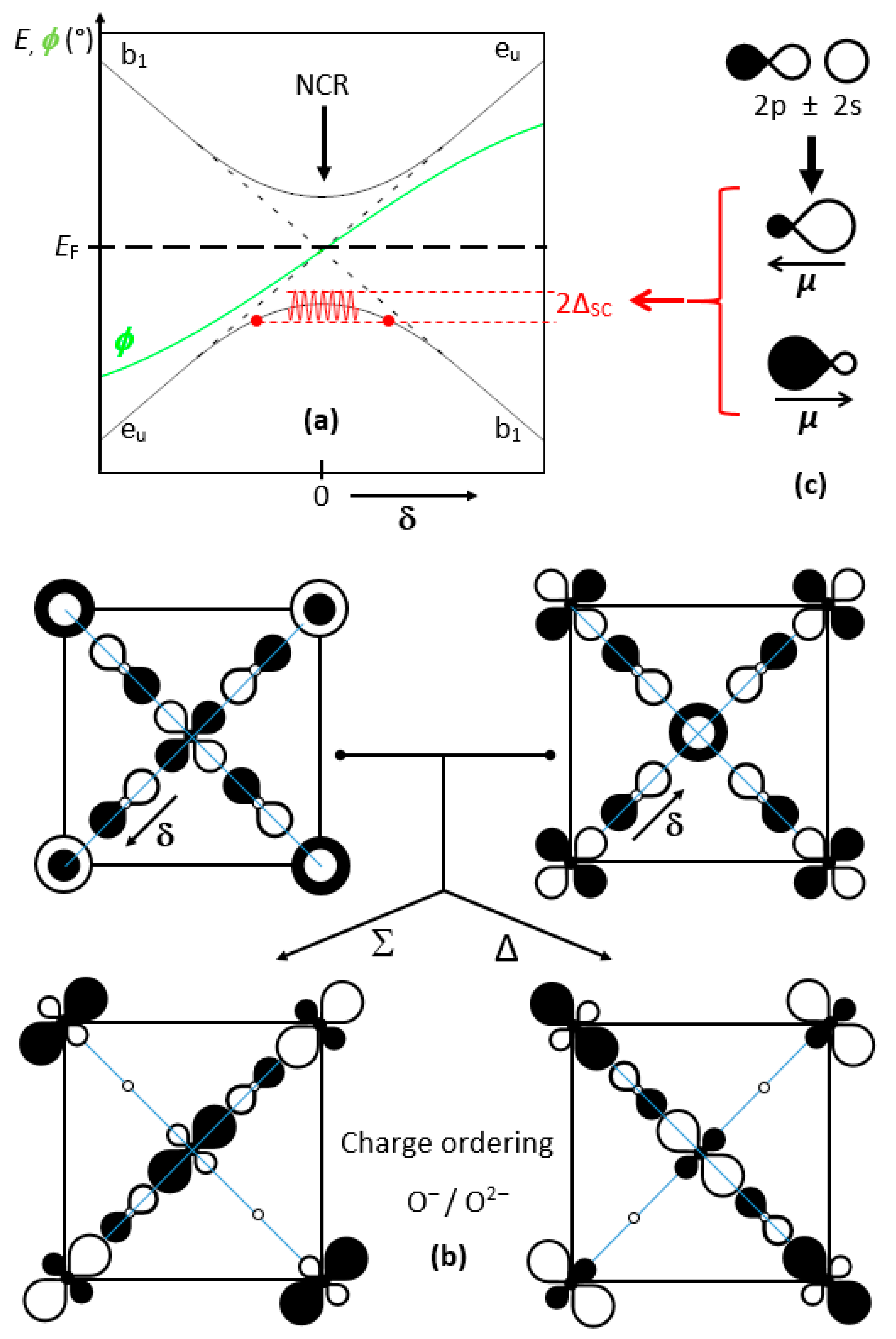
We too had here a critical hypothesis, with an oscillating band gap driven by a phonon mode. At each half-period, the two bands cross; at this very moment, the noncrossing rule suggests the opening of an electronic gap, followed by a superconducting gap 2Δ
SC by mixing the two bands according to:
Figure 6a shows the evolution of the ground state along a phonon half-period (−π/2 to +π/2), from a b
1g (a
1g) enlarged (compressed) site, as a function of the oxygen displacement δ. Two types of domains can be observed: (i) on both sides, a smooth evolution of the e
u and b
1 band edges with δ; (ii) in the middle, a progressive mixing of e
u and b
1, up to a full reversal.
Figure 6b represents the crystal orbitals before and after mixing for a 50:50 ratio.
The hybridization of x2 − y2 and z2 favors one direction out of [100] and [010], as observed above in X1, and evens the weights on both copper ions; conversely, it strongly discriminates the four oxygen atoms, two of them with vanishing crystal orbital coefficients. However, as we will discuss later, this charge ordering is likely to vanish partially by delocalization of the two holes among an (O4)6− cluster. From the above, it can be stated that such crystal orbital mixing leads to a charge transfer through electron (hole) pairs.
Another important feature is the high polarizability of O
2−, whose electronic dipole (due to its Janus character) may oscillate at high frequency, a few orders of magnitude faster than phonons (red curve in
Figure 6a). Such a behavior can be considered as the result of the O(2p)/O(2s) hybridization (
Figure 6c). This dipole oscillation may contribute, as in atomic spinodes, to induce a decomposition into various components of the e
u/b
1 mixtures in equilibrium, exchanging hole pairs, and consequently leading to the Whangbo Hamiltonian of pair-occupied and pair-unoccupied states [
23,
43].
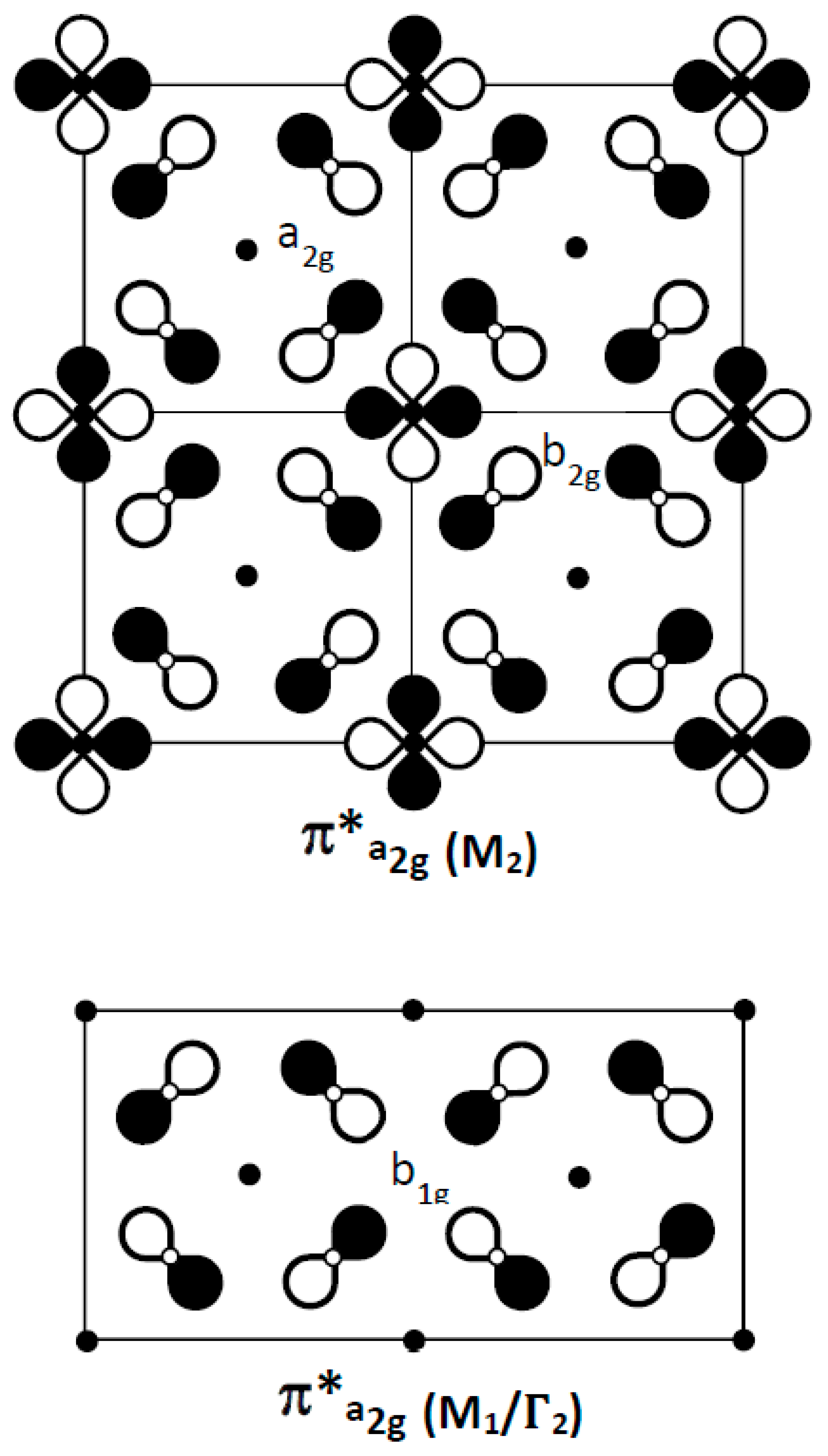
4.3. The π*(a2g) Band
As proposed in 1990 by Micnas et al. and later illustrated by Simon [
13,
14], the crossing of a broad and a narrow band close to the Fermi level would be a key factor for the coupling of quasi-local pairs (narrow band) and fermions (broad band), to form Cooper pairs. Could the narrow, 300 meV-wide π*(a
2g) band, which lies approximately 400 meV below the Fermi level, be raised to the Fermi level and generate local electron pairs? For this band,
Figure 7 illustrates: (i) in X1(M2): the
-
orbital ordering, with overall O–O nonbonding character and Cu-O antibonding character at the
b2g site; (ii) in M1: the
a2g symmetry of each copper site, for which oxygen atomic orbitals show
-type overlap on vacant cationic sites (½ ½ 0) with an antibonding O–O character identical to the σ*(b
1g) band for copper (see also
Figure 5c).
4.3.1. Positioning of the π*(a2g) Band
The (CuO2)2− layer is sandwiched between so-called reservoir layers, in which the doping adjusts the amount of charge carriers in the CuO2 layer. Additionally, being ionic, these reservoir layers generate an electrostatic (Madelung) potential that can be estimated by the Ewald summation method. One has to consider as well the screening of the Madelung potential by the charge carriers of the conducting layer; therefore, we restricted the calculation of Madelung potentials to the contribution of a few neighbor cells, and considered orders of magnitude only.
It is also straightforward to compare the importance of the Cu-O charge transfer in CuO2 layers, by considering three cases of the Madelung terms: Cu2+/O2−, Cu+/O1.5− and Cu0/O−. A few comments arise from these rough calculations: (i) as expected, the potential at the copper site is negative, whichever the Cu-O charge transfer case is; (ii) the potential at the oxygen site is positive, except for the insignificant Cu0/O− case, and iii) at the vacant cationic site (½ ½ 0), which will be labeled (+) in the following, the Madelung potential, VM(+), is negative to whichever the charge transfer case is, but is lower by ca. 1/3 than the potential at the occupied site, in absolute value. This justifies a specific treatment for the antibonding electrons in the π*(a2g) band; iv) the negative character of VM(+) increases when the apical Cu-O distance (i.e., the separation between the CuO2 and the reservoir layer) increases. Therefore, the negative Madelung potential reinforces the destabilization of electrons at the vacant cationic site, adding up to the antibonding character of the O–O interactions. These features should favor the stabilization of doped holes near the vacant (½ ½ 0) cationic sites of the CuO2 layer. How many holes? Can we envisage a hole pair on oxygen entities as well known for electrons and in b2g of electron doped SrTiO3, i.e., a dimerization (O4)5− + (O4)5− → (O4)4− + (O4)6− ? We would then obtain what chemists would call a hole lone pair, or an antiatom with a pseudo negative nucleus arising from VM(+) ≤ 0; the two holes would then have a wave function of x2 − y2 type of symmetry.
These distortions agreed perfectly with features revealed by Bianconi et al. [
44] from extended X-ray absorption fine structure (EXAFS) spectroscopy on La
1.85Sr
0.15CuO
4 crystals, showing a heterogeneous stripe system with an accumulation of hole carriers in a region with elongated apical and shortened equatorial Cu-O bonds (2.40 Å and 1.88 Å, respectively).
4.3.2. Mulliken–Jaffé Electronegativity for Oxygen
In M1, the π*(a
2g) band is of pure oxygen character. We can express the energy
E(
q) of the oxygen ion as a function of its charge
q, its electronic affinity
EA(
q) and its ionization energy
EI(
q):
where
is the Mulliken electronegativity,
β is Pearson’s hardness and
γ is an adjustable parameter; for oxygen, α = 6.925,
β = 6.190 and
γ = 0.505.
E(
q) is plotted on
Figure 8. The Mulliken–Jaffé electronegativity χ
MJ is defined as the derivative of
E(
q) with respect to
q. As seen in
Figure 8, χ
MJ vanishes for
q ≈ −0.6 and is negative below this
q value. Additionally, it shows that O
2− is not stable in the gaseous phase, and will likely lose an electron at the surface of an oxide—catalysts take advantage of this effect.
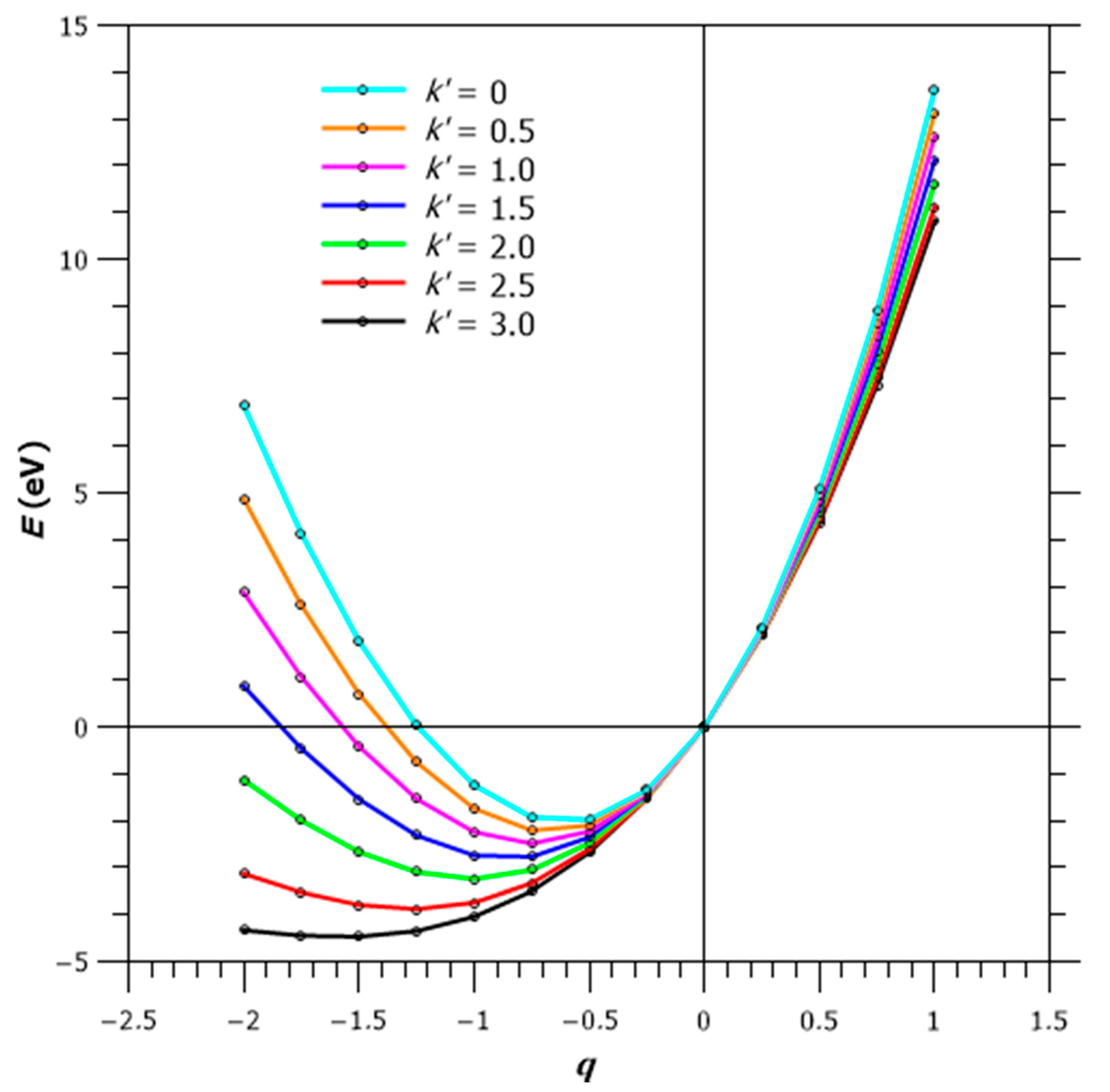
Therefore, to account for the electronegativity of oxygen in an ionocovalent lattice, it is necessary to add a Madelung-type term in Equation (6). The magnitude of this term is difficult to estimate, since outer electrons of oxygen lie away from the exact atom site. Since the Madelung energy is proportional to
q2, we will use the corrected expression
for the energy of the oxygen ion as a function of its charge
q.
Figure 8 illustrates the importance of this Madelung term: (i) the minima are displaced toward the most negative charges (most ionic configurations), (ii)
E(
q) vs.
q curves flatten, around their minima, until
k’ ≈ 3 and the appearance of an inflexion point. If we start from the (O
4)
8− cluster, oxidized into (O
4)
6− by charge transfer, at the X-point of the BZ, its progressive oxidation by doping into (O
4)
5− then (O
4)
4− corresponds to a maximum 0.5 electron per oxygen, for example between O
−1 and O
−1.5, whose formation energies
E(
q = −1.0) and
E(
q = −1.5) do not differ by more than 50 meV (
Figure 8). This energy difference is less than the O–O resonance energy, which can be estimated to be approximately a hundred meV (
Figure 4 of Ref. [
36]); this leads to
U < 0, as in the negative-
U model for superconductivity [
45].
According to the above discussion, we can describe the electronic structure of (CuO
2)
2− layers by a network of O
4 square planar entities (
Figure 9), which provide the four sets of molecular orbitals (b
1g, a
2g), (1e
u, 2e
u) and (a
1g, b
2g) as indicated in
Figure 5f (by neglecting the out of plane 2p
z orbitals), in order of decreasing energy. In this network, cationic sites are either (i) fully occupied by Cu
2+ ions, in the tetragonal epitaxial form of t-CuO, (ii) half-occupied by Cu
2+ in high-
TC cuprate layers, (iii) one-fourth occupied by Cu and one-fourth by Li
+, in an ordered manner, in insulating La
4LiCuO
8, which can be described in terms of (Li
+)(Cu
+)(O
4)
6− layers (
I4/
mmm), with two holes in the σ*(b
1g) molecular orbital centered on each Cu
+ ion. At low
T, this phase undergoes an orthorhombic distortion (
Ammm), from D
4h to D
2h for Cu
+ and Li
+ ions, with a buckling of distorted sites. Besides, the buckling of square-planar entities splits the unoccupied cationic sites (+) into two types of sites of the same D
4 symmetry but a different size (labeled hereafter L and S). This atomic distortion and the increase in antibonding at the S site are reinforced by a 2p–2s oxygen orbital hybridization towards the S site (see below). These two situations can be transposed to the distortions of the O
4 network of the (Cu
2O
4)
4− layer, with a breathing mode (arrows in
Figure 9) but also a “hole disproportionation” and octahedra buckling (2a
2g1→a
2g0 + a
2g2); this π*(a
2g) band, already narrow (ca. 300 meV) and further split by phonons, should serve as a seed for Cooper pairs delocalized in the broad σ*(2e
u) band of the superconducting phase. This hole-acceptor character of π*(a
2g) agreed with the statement of Hirsh et al. for locating the cuprate holes preferentially in the oxygen 2p
π* bands [
46,
47].
4.3.3. Role of Oxygen 2s Atomic Orbitals
So far in our discussion, the role of semi-core (or rather deep-valence) 2s orbitals of oxygen was not discussed; by introducing them in the tight-binding calculations, we noticed that the energy at X1 shifted upward by ca. 500 meV (blue line in
Figure 5a) due to z
2(Cu)-2s(O) antibonding interactions along [010] (
Figure 5g). Such a 2s ± 2p hybridization modified the electron density in the vicinity of the oxygen ion, increasing the Cu-O antibonding character of the band in an asymmetric way and contributing significantly to the Janus effect. In an axially distorted (a
1g) Cu
2O
4 cell, for example, the 2s ± 2p hybridization reinforced the strong antibonding interactions with x
2 − y
2, while it weakened the already weaker antibonding interactions with the equatorial lobe of d
z2 orbitals. Overall, this favored the charge transfer from oxygen to copper.
Similarly, for the
Ammm transverse distortion, the 2s ± 2p hybridization reinforced the strong antibonding O–O interactions in the small (S) square planar O
4 groups, while weakening them in the large (L) ones. This favors the introduction of doping holes in this region of cationic type (negative value of the Madelung potential
VM), even their pairing. Additionally, a much smaller hole density is necessary to reach the X1 point; it actually corresponds to a slight electron-doping (as in n-type cuprates). The contribution of 2s orbitals will be modulated by the competing oxygen-rare earth bonding. The important role of oxygen 2s orbitals had already been mentioned many years ago with respect to the gap value for the parent insulating phase [
48].
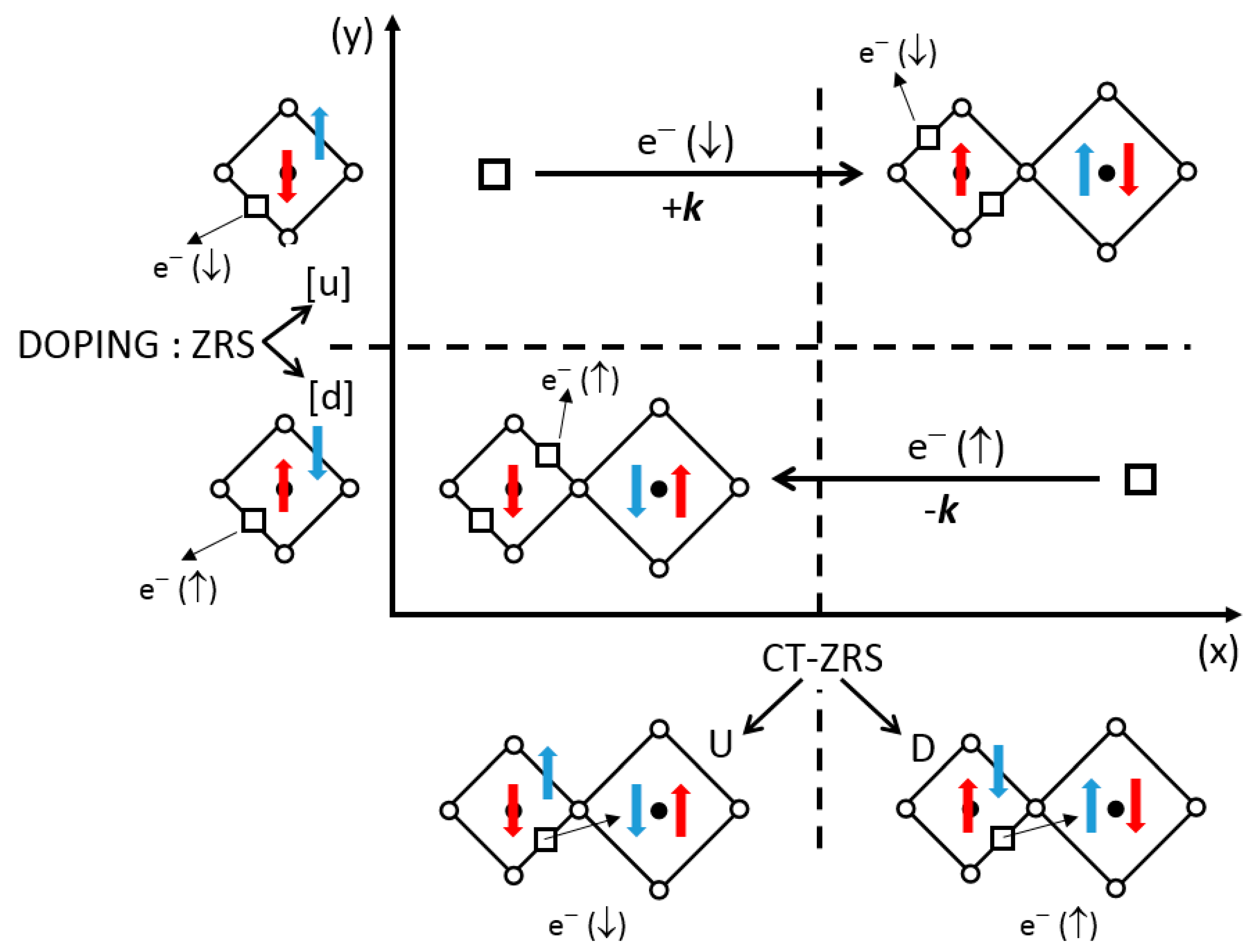
4.4. Underdoped Cuprates
The phase diagram is complex (pseudo-gap, charge density waves, stripes, checkerboard patterns, etc. [
49,
50]); however, those phases should be related to characteristics of the pristine La
2CuO
4 phase. La
2CuO
4 is an insulating antiferromagnet of Mott or rather charge-transfer type, in which the lowest excitation involves the gap between the oxygen-character band and the upper Hubbard band: O
2− + Cu
2+ → O
− + Cu
+. This charge transfer can be symmetric, leading to an antiferromagnetic coupling by superexchange. We will examine the non-symmetric transfer only, which involves two copper ions (labeled 1 and 2) according to:
where the arrows indicate the spin orientation. The remaining spin on oxygen couples with the spin ½ on Cu(2), in a bonding state in Equation (8), in the same way as the Zhang and Rice singlet (ZRS) description [
51] in the well-known
t–
J model. The charge transfer (CT) of this type will be noted CT-ZRS(U) or CT-ZRS(D), by reference to the remaining spin of the oxygen ion. This transfer breaks the C
2 symmetry of the Cu-O-Cu bridge, Cu
+ being larger than Cu
2+ associated to O
−. Thus, we can imagine a local two-dimensional 1:1 order of CT-ZRS(D) and CT-ZRS(U), which can be static or coupled to a phonon mode (see
Figure 10). Three remarks arise:
- (i)
The charge transfer rate is formally 50% (i.e., half the optimal doping value),
- (ii)
One magnetic network over two must disappear at each phonon half-period; this scheme is consistent with the sharp decrease of Néel temperature with doping,
- (iii)
Local ordering domains appear (U or D), separated by antiphase boundaries, and alternating at each half-period.
Figure 10 (bottom) illustrates these two situations. What is the role of doping? At each half-period, when the symmetry is not broken, doping holes can form as many ZRS-[u] as ZRS-[d] (
y-axis in
Figure 10). However, the formation of CT-ZRS (either D or U) at each quarter-period, on each side of the antiphase boundary, is only compatible with doping holes of the opposite norm (d/U or u/D), thereby rejecting doping holes of the same norm (d/D or u/U) toward the other domain.
In essence, this is a collective displacement of holes of opposite spins (u vs. d) in opposite directions (+
k vs. –
k), i.e., characteristic of Cooper pairs for a possible superconducting state. Note that this mechanism leads to a density of pairs, which is half the expected value, as seen experimentally [
52].
In conclusion, this model agrees with the description by Reznick [
53] titled “Electron-phonon coupling reflecting dynamic charge inhomogeneity in oxide superconductors”, invoking strong bond stretching phonon anomalies common to stripe-ordered and superconducting materials, between ordered magnetic and hole-free layers, and charge transferred Cu
+ and hole-rich oxygen ones.
5. Iron Arsenides and Selenides
As early as 1965, Bertaut reported the anomalous nonmagnetic behavior of FeS, a rare mineral of mackinawite type, first identified in 1962 [
54]. Due to its low thermal stability, FeS is difficult to obtain as a pure phase (i.e., without metallic iron as impurity). Besides, not long after the discovery of high-
TC superconductivity in the doped pnictide LaO
1−xF
xFeAs (
TC = 26 K) by Hosono et al. in 2008 [
55], the selenide β-FeSe showed superconductivity below c.a. 10 K. FeSe has the same mackinawite (
P4/
nmm) structure as does FeS, but is more stable. Furthermore,
TC in FeSe can reach 30 K either under pressure or upon S-Se substitution; both conditions correspond to a decrease in the unit cell volume, as often observed for the spin transition S = 2 → S = 0 in ferrous materials [
56].
We chose to apply our tight-binding approach to FeSe, to check if similar features arise in the case of chalcogenides, as found in our analysis of the titanates and cuprates. The tight-binding parameters for Fe and Se are listed in
Table 1. The values of Coulomb integrals for Fe 3d and Se 4p orbitals lie within 0.6 eV, indicating a strong covalency for Fe–Se bonds. This justifies the use of a vanishing (
U = 0) Hubbard parameter for electron–electron repulsion, although a nonzero
U value would have to be considered for crystal orbitals of pure Fe character, at certain points of the Brillouin zone.
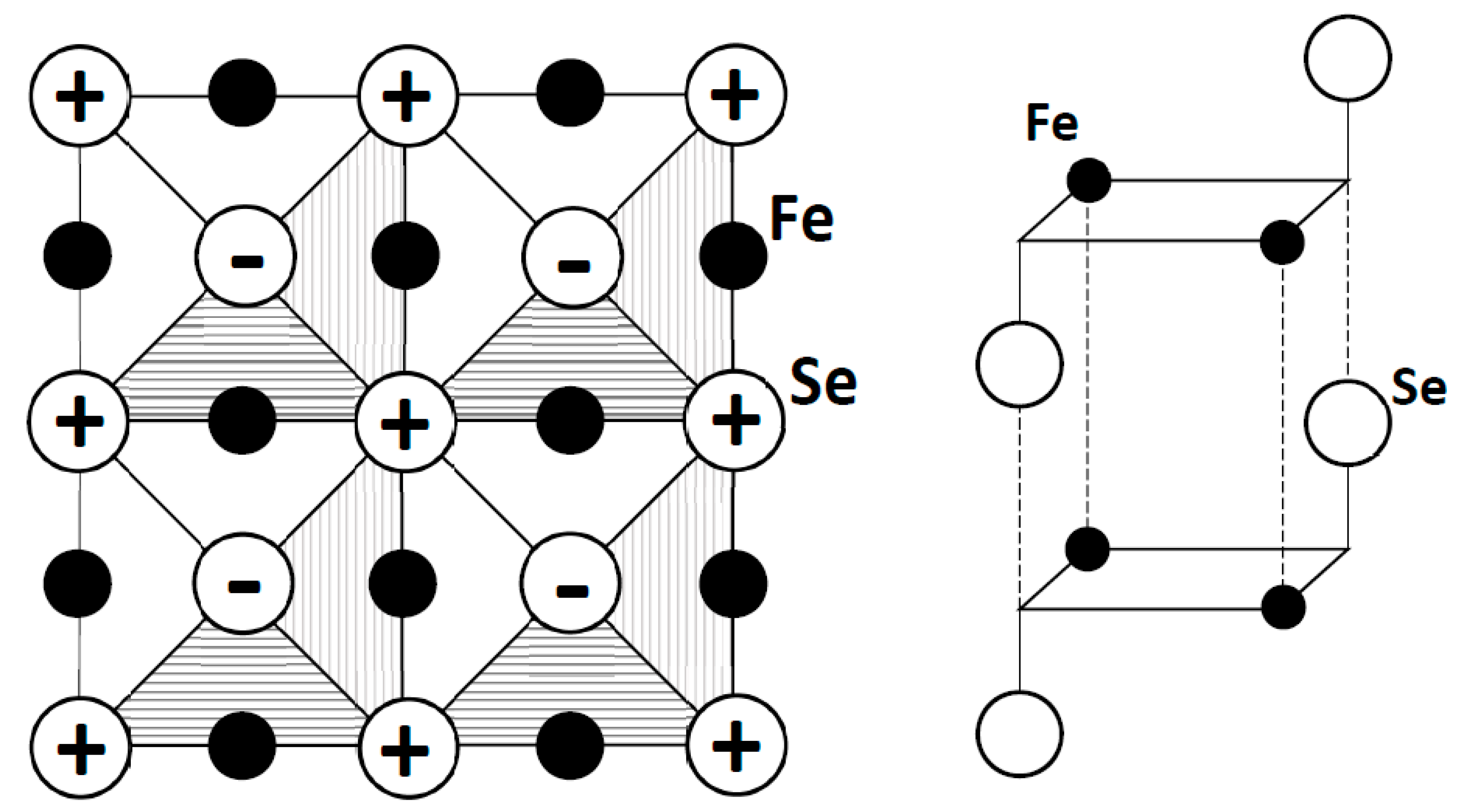
Figure 11 shows the crystal structure of β-FeSe. The iron atoms form a square plane network identical to the one found for the oxygen atoms in cuprates, an essential feature for our scenario of high-
TC superconductivity. However, the cationic vs. anionic character of Fe vs. O limits this analogy; in particular, the
E(
q) curve for iron cannot show a minimum near
q = 2 (see
Figure 8 for oxygen). Additionally, the cationic sites differ from an elongated octahedron (D
4h) or a pyramid (C
4v) in cuprates to a slightly elongated tetrahedron (T
d) in iron selenides or slightly compressed in iron pnictides. The distortion of the FeSe
4 tetrahedron lifts the degeneracy of the iron t
2 orbitals into an
e doublet (xz, yz) and a
b2 singlet (xy), only partly compensated by the crystal field (D
4h) of the four Fe
n+ next-neighbors (at the distance of 2.67 Å).
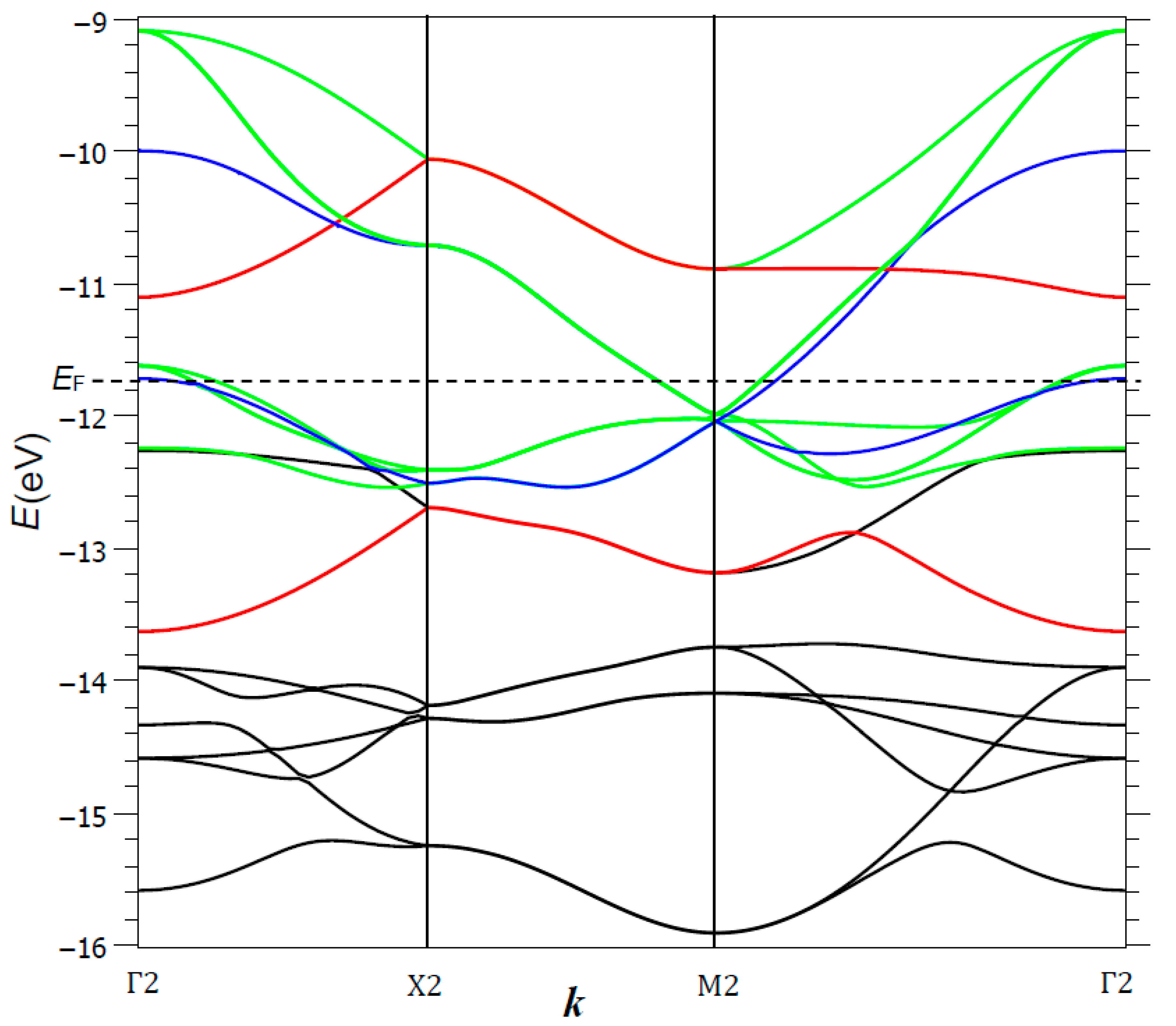
Figure 12 shows the dispersion curves obtained from the tight-binding calculations for a Fe
2Se
2 primitive cell; the Fermi level is situated at −11.74 eV. Several band stacks can be identified, in order of increasing energy: (i) around −21/−22 eV, two Se 4s-character bands (not represented in the figure); (ii) between ca. −15.5 and −14 eV, six rather narrow Se 4p-character valence bands, with a significant Fe contribution and iii) broad conduction bands, divided in two stacks (according to the bonding or antibonding Fe–Fe interactions) that overlap slightly at Γ2 and M2 points, close to the Fermi level. This creates two charge carrier pockets of p type around Γ2 and n type around M2, with main components x
2 − y
2 and (xz, yz). We observe that the Fe–Fe bonding and antibonding bands of xy-character were well separated, lying respectively below and above the Fermi level, and corresponding to configurations σ(b
2)
2 and σ*(b
2)
0.
The conduction band σ*(xz,yz) was broad (width > 3 eV); its top was strongly hybridized, with respective weights of 42% and 58% for Fe and Se, and its bottom was mostly of Fe character. It shows a progressive change into a broad domain (ca. 2 eV) with narrower bands built on Fe–Fe interactions. It is close to half-filling, leading to a (xz)
1(yz)
1 configuration of Pauli-type states. The two x
2 − y
2 bands, bonding and antibonding with respect to the Fe–Fe interactions, are noted as 1π
u and 1π
g, respectively.
Figure 13 represents a zoomed-in view of
Figure 12 around M2 and close to E
F, for the six bands arising from 1e
u, 2e
u and 3e
u, based on (x
2 − y
2/4p
x, 4p
y), (xz, yz) and (xz, yz/4p
z) respectively. This corresponds to a (x
2 − y
2)
1 configuration for Fe.
Two narrower d
z2 bands are full, for a (z
2)
2 configuration. Overall, this is consistent with divalent Fe, with xy and x
2 − y
2 electrons providing the strong cohesion of the network (d
Fe-Fe = 2.67 Å, close to the distance observed in γ-Fe). The hypothesis of a (1π
u)
2(1π
g)
0 configuration corresponds to a very low
U value. Otherwise, the spin polarization of these bands would induce a non-compensation magnetism, as observed in insulating phases of similar structure, with ordered Fe vacancies, such as K
0.8Fe
1.6Se
2 (a
× a
, S.G.
I4/
m) in which ferromagnetic Fe
4 clusters order in an antiferromagnetic way below ca. 500 K [
57].
The occurrence of Fe
4 clusters recalls the O
4 groups in the cuprates discussed above. Furthermore, the low temperature form of FeSe shows an orthorhombic distortion (S.G.
Cmma, a/b = 0.9957) whose nematicity arises from the anisotropy of global Fe–Fe nonbonding interactions (bonding along
a, antibonding along
b) with a
a superstructure [
19,
58]. This led us to extend our tight-binding calculations to a double unit cell. The correspondences between crystal orbital notations in the single and double unit cells are given in
Table 2. We compare in the following the crystal orbitals of such a double cell for the high temperature
P4/
nmm and the low temperature
Cmma forms, the latter presenting a nematic distortion; we suppose a phonon regime where the parameter ratio a/b oscillates around 1, (1
δ).
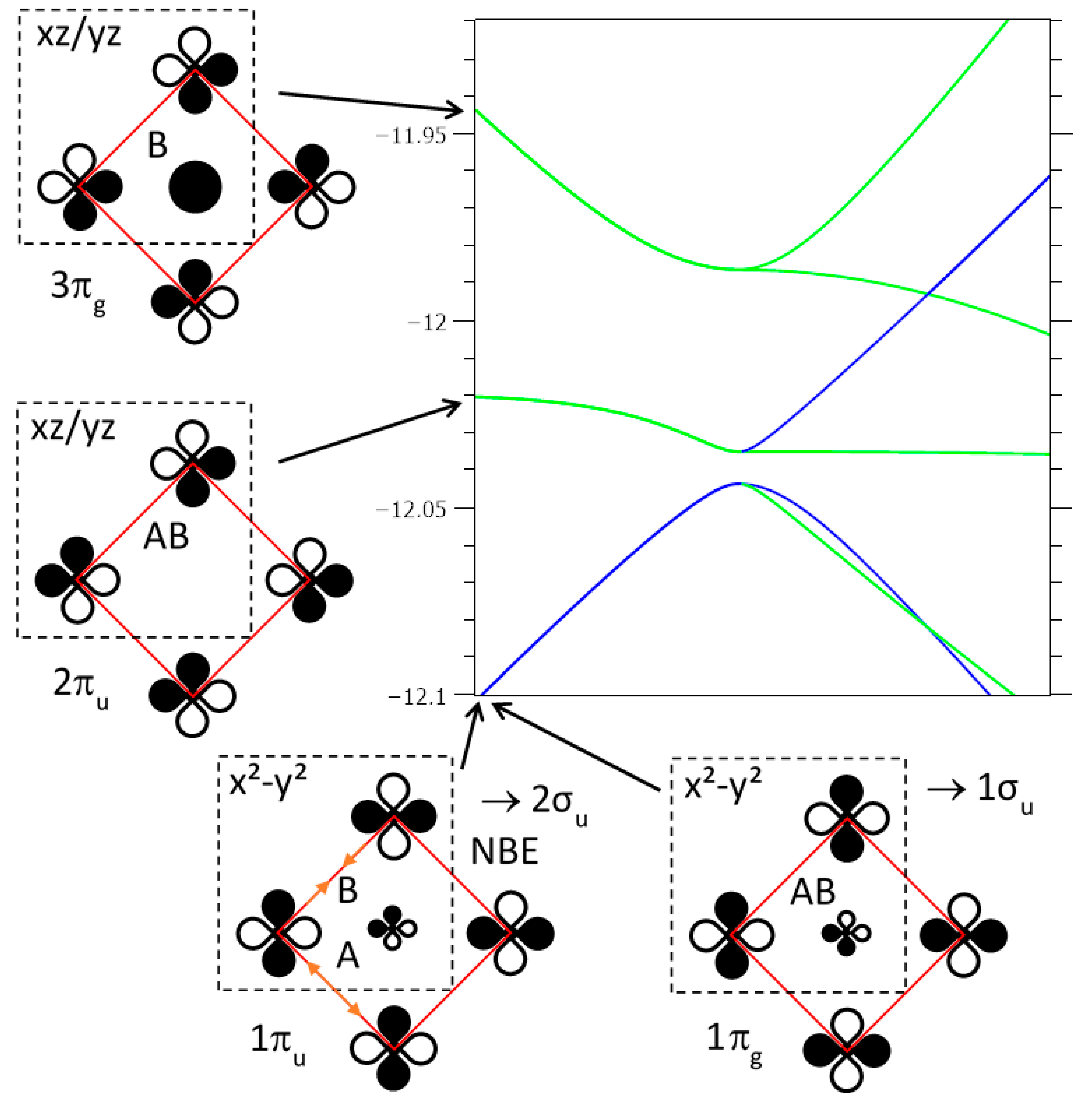
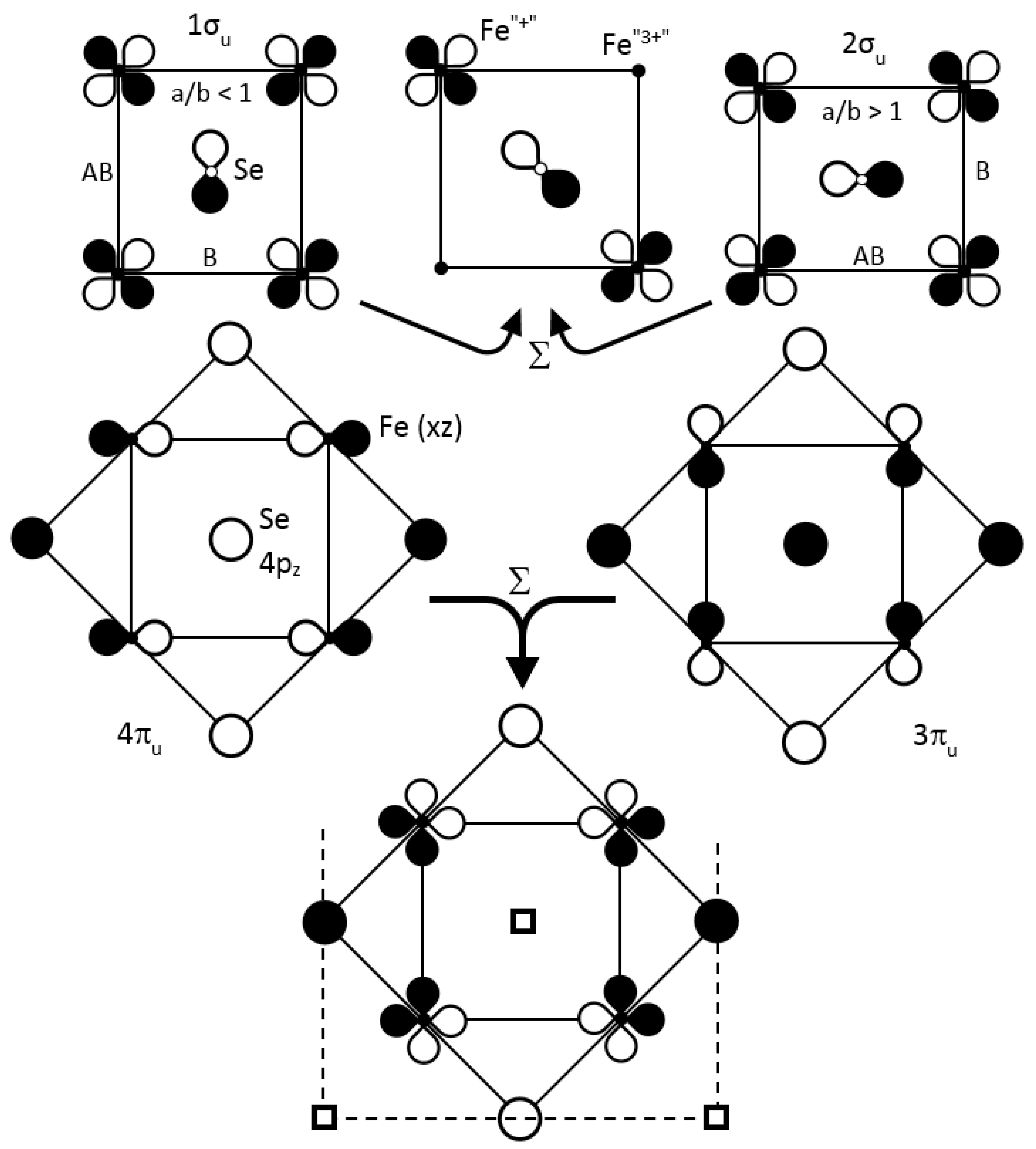
We focus our attention on the three degenerate crystal orbitals in M2, i.e., 1eu, 2eu and 3eu at respectively −12.044, −12.035 and −11.986 eV, respectively, and their six split bands towards Γ4 (note that, for the double cell, x2 − y2 is transformed into xy): (i) an antibonding-hybridized Fe xy with Se 4px and 4py AOs in an orbital ordering way, noted as 1eu (1πg, 1πu→1σu, 2σu). Globally, Fe–Fe interactions are NB, the sum of bonding in the a direction and antibonding in the b direction, thus justifying the nematic instability. (ii) A purely Fe, 2eu (2πg, 2πu→1πu, 2πu) band involving equally distributed weights of xz and yz on each Fe atom, arranged in an antibonding manner with the first neighbors and antibonding/bonding ways with the second neighbors. (iii) An antibonding-hybridized Fe–Se, 3eu (3πg, 3πu→3πu, 4πu) band, involving an orbital ordering, xz for the former and yz for the latter, mixed with Se 4pz AOs; each coefficient ci is close for each site. On the basis of degeneracies and regular weight distribution in the various sites, we cannot envisage any tendency of charge fluctuations, quoted here schematically “disproportionation”, cationic and anionic, in the tetragonal phase.
What about the orthorhombic Cmma distortion? For a small iron atom displacement of 0.40 pm, the three bands in are split by 15, 11 and 25 meV respectively, allowing us to envisage a possible disproportionation.
- (i)
For the pure iron 2πu/2πg (2eu) bands, we observed an orbital ordering for yz and xz in the two bands; their mixing should only suppressed such an order.
- (ii)
For the Fe–Se hybridized xy (x
2 − y
2), i.e., the 1σ
u/2σ
u bands, their coefficients c
i were equally distributed on each atom (
0.46 for Fe,
0.17 for Se) conserving an orbital ordering. Distortion and iron oscillation away from their symmetrical positions (phonons), which favored bonding along
a (shortest Fe–Fe bonds) in 1σ
u and along
b in 2σ
u, changed signs of some AO coefficients. As for the corresponding band of cuprates (
Figure 6a), at each half period, the ground state changed from 1σ
u to 2σ
u, violating the NCR of chemistry. To avoid that, the two bands did mix together, progressively up to a complete inversion, with three consequences:
- -
The creation of an electronic band gap,
- -
The different sign for the coefficients in the four iron sites between 1σu and 2σu bands inversed their sum (Σ) or their difference (Δ),
- -
Passage during this mixture by an appropriate number of pair-occupied states and pair-unoccupied states may induce superconductivity with a 2Δ
SC gap [
23,
43].
Using the previous values of c
i, we obtained for Σ: c
1 = c
2 = 0; c
3 = c
4 =
0.46 for the lower 50:50 mixture (
Figure 14), and for Δ: c
1 = c
2 =
0.46 and c
3 = c
4 = 0 for the upper one. Two iron atoms out of four carry charge densities on their xy (x
2 − y
2) AOs corresponding to 4(x
2 − y
2)
1 = 2(x
2 − y
2)
2 + 2(x
2 − y
2)
0, or 4 Fe
2+ = 2 Fe
+ + 2 Fe
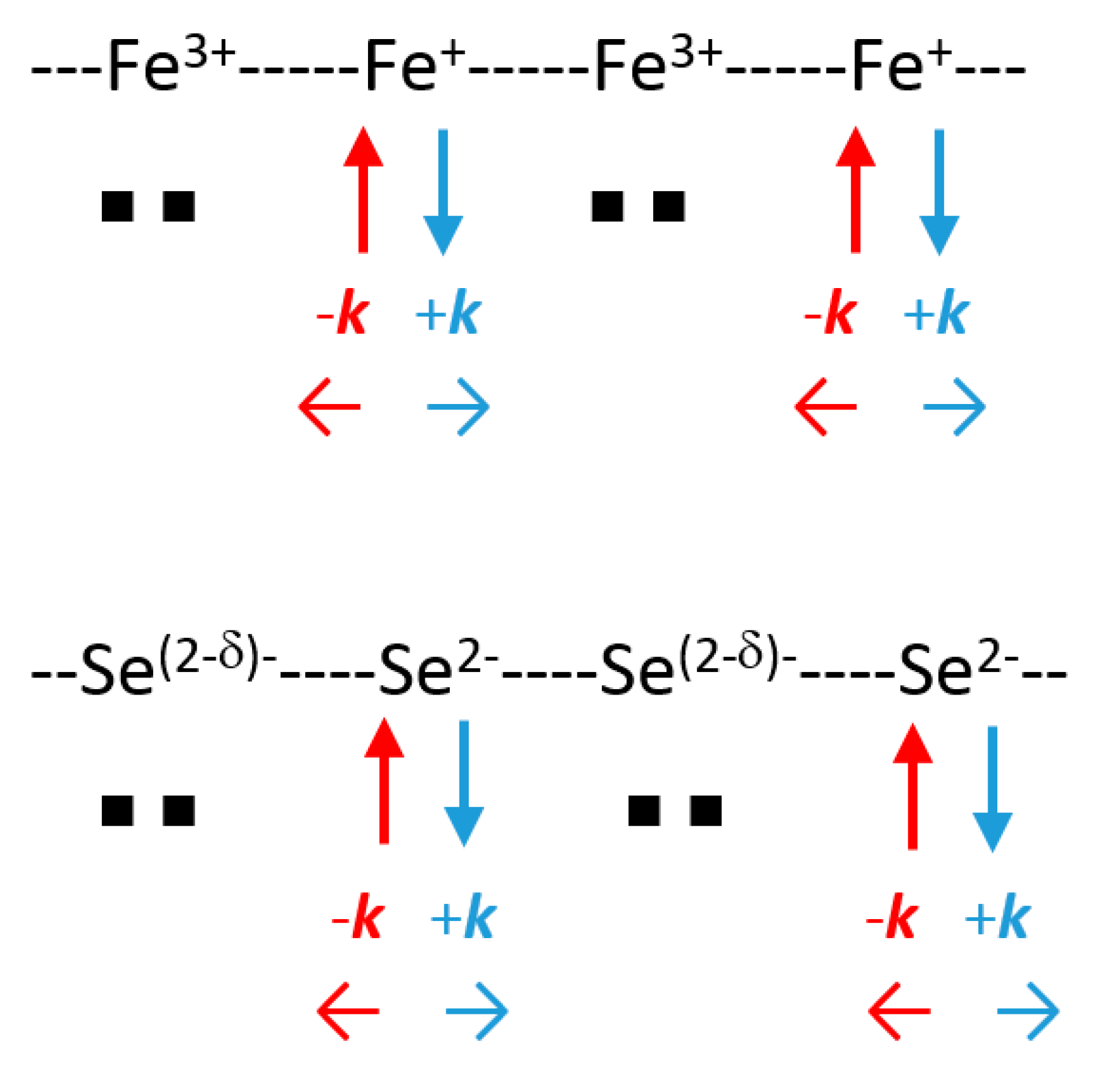
3+, qualitatively speaking. Such a succession along [100] and [010] of “Fe
+” and “Fe
3+” allows for the Cooper pair formation and condensation at
TC (
Figure 15). Such a “disproportionation” is related to the Hubbard parameter
U for Fe 3d orbitals and deals also with the difference between the third and the second ionization energies (
EI) of Fe, which is the lowest (
EI3 −
EI2 = 14.5 V) value for the M
2+ 3d transition metal series, as shown in
Table 3. However, a similar mixing between Se 4p
x and 4p
y AOs does not show any charge fluctuations in this 1σ
u/2σ
u band.
Besides, the highly split 3e
u (3π
u/4π
u) states at the bottom of the wide conduction band with xz/yz orbital ordering (
Figure 13) differentiate two out of four selenium positions, above and below the iron layer: c
1(Σ) = −c
2(Σ) = 0.20; c
3(Σ) = c
4(Σ) = 0 and c
1(Δ) = c
2(Δ) = 0; c
3(Δ) = −c
4(Δ) = 0.20). Note that these states, upon mixing, do not induce Fe disproportionation.
The Se atoms form a square lattice of a/
parameter (tetrahedron edge) above and below the iron layer with π-antibonding Se–Se interactions. At Γ point, these interactions add to those of the Fe–Se antibonding character for destabilizing the top of the occupied states, favoring charge transfer. As discussed previously for the cuprates (
Figure 8) for the
E(
q) curve of oxygen, strong similarities were observed for selenium; the created holes can be coupled into pairs and the mixing of the 3π
u/4π
u bands can also contribute to the superconducting gap 2Δ
SC (
Figure 15). Thus, the Fe–Se system disposed of two, cationic and anionic, phonon coupled carriers for coupling them into pairs and condensing them in Cooper pairs below
TC.
Similarly to the case of p-doped cuprates, we examined in which way the Fermi level could shift by a hundred meV to reach the M
2 (x
2 − y
2) point: this would be achieved through an electron transfer from (x
2 − y
2)* to (xz, yz)* bands, i.e., from σ to π, the latter being more stabilized by the intercalation of cations in the interlayer space, as demonstrated by Pickett and An for MgB
2 vs. graphite [
59]. The 30 K superconductors A
0.6Fe
2Se
2 (A = M
+) illustrated such a behavior, increasing the amount of Fe
+ and consequently the Fermi energy, but conversely stabilizing π*(xz, yz) versus σ*(x
2 − y
2) as discussed previously [
60].
7. Conclusions
The answer to the question in the title is clear: we believe that chemical bonding is at the heart of physical ordering phenomena and contributes to the understanding of the mechanisms of unconventional, high-TC superconductivity. It sheds light on the key role of nonbonding electrons, from which an electronic instability occurs through a double-well situation, inducing a static or dynamic (phonons) distortion of the atomic network. The coupling of nonbonding electrons with phonons was the core of our chemists’ approach.
At low temperature, the softening of phonons led to a succession of symmetry broken and non-broken states, i.e., the alternation of an insulating distorted phase and a metallic phase. Importantly, it was also at the origin, on a shorter timescale, of a superconducting phase in which the mixing of occupied and unoccupied electron-pair states (described by Whangbo in [
23,
43]) could be achieved through a purely electronic Hamiltonian. This situation avoids the noncrossing rule for band-edge states, which should swap at each phonon half-period.
Besides, the approach of Micnas et al., based on the mixing of local pairs and itinerant electrons (when wide and narrow bands cross at the Fermi level) giving rise to a mutually induced superconductivity, was also relevant for our model. As discussed recently ([
43] and references therein), such an interband electron pairing should also result from the breakdown of the Born–Oppenheimer approximation, favoring interband pair state excitations through nested Fermi surfaces.
The whole scheme applies to the three families of solids discussed here:
- (i)
Titanates, in which the top of the valence band was nonbonding and induced both a ferroelectric-type distortion, the splitting of the π*(t2g) band into a narrow 2D band of b2g symmetry (xy) and a broader 2D band of eg symmetry (xz, yz),
- (ii)
Cuprates (at optimal p doping) had a wide conduction band, of oxygen character and σ*(b1g) symmetry, with a 2D Peierls-type instability for nonbonding electrons at the band center. This instability is probably of dynamical nature, and occurred at the Fermi level in the vicinity of a narrow band of pure oxygen character and of π*(a2g) symmetry;
- (iii)
β-FeSe and iron pnictides of similar crystal structure had a broad conduction band (due to the strong Se (4p)-Fe (xz, yz) hybridization) and, close to the Fermi level, a much narrower band of Fe character, likely to split from a nonbonding situation into two bands of x2 − y2 in character, which are Fe–Fe bonding and antibonding, respectively.
In each family, the occurrence of bosonic local pairs was favored by specific features:
- (i)
A high dielectric constant that minimized the Coulomb repulsion between the two electrons of the b2g2 local pair (U→0),
- (ii)
The occurrence of a poly-oxide (even peroxide) cluster (O4)n−, favored both by the almost constant formation energy of the O−q ion for charges q between −1 and −1.5, a large transfer integral to-o for hole delocalization, and the local crystal field at the copper-free(+) site, leading to a negative U situation,
- (iii)
The existence of two (x2 − y2) sub-bands by splitting of 1eu in Cmma, of nonbonding Fe–Fe character with Fe +II large charge fluctuations, crossing a broad 3D band of (xz,yz) character and strongly hybridized with the chalcogen. As in the case of oxygen atoms in the cuprates, the anionic Se layer underwent also similar charge fluctuations, likely coupled together.
These situations agreed perfectly with the requirements of the negative
U pairing mechanism, i.e., quasi degenerate states, same coordination and hybridization with the conduction band, as recently reported by Geballe, Hammond and Wu in a general introduction of superconductivity mechanisms [
45].
The antagonism between several types of order can be discussed, magnetism vs. superconductivity, and magnetism vs. charge transfer: (i) as well known, magnetism destroys superconductivity above a critical field value, but the magnetic ordering is itself destroyed by charge transfer arising from p-doping in Cu +II cuprates, leading eventually to a collapse of
TC. However, both appear to be at the origin of superconductivity of under-doped cuprates, and their stripe-type insulating phases. (ii) Ferroelectricity and superconductivity seem to be incompatible, despite a few exceptions (see the discussion in Ref. [
16]), because a significant carrier density is required (Mott transition). However, studies suggest that ferroelectric-type distortions also induce electron pairing. For both apparent antagonisms, the chemist’ toolbox provides key arguments for possible interpretations.
Finally, the general model proposed here appeared as a coherent mixture of parts of physics and parts of chemistry: (i) the phonon role, alternating broken and unbroken symmetry, (ii) the broad and narrow band crossing of Micnas et al., (iii) the negative U Hubbard model, as ingredients of the BCS theory, for physics, (iv) the non-bonding electron instability, (v) the non-crossing rule of states and bands and (vi) the charge-transfer disproportionation (which is equivalent to negative U), for chemistry. In addition, chemistry also suggests that anionic hybridization like O2p O2s AOs, rejecting alternatively electron densities on both sides from the symmetry center, describes very well the atomic polarizability and could be a high frequency alternative to phonons. In addition, coupling cationic and anionic disproportionation could enhance superconductivity as observed in cuprates and selenides.