Statistical Mechanics of Discrete Multicomponent Fragmentation
Abstract
1. Introduction
2. Random Fragmentation
2.1. One-Component Random Fragmentation
2.1.1. Probability of Random Fragment Distribution
2.1.2. Mean Fragment Distribution
2.2. Two-Component Random Fragmentation
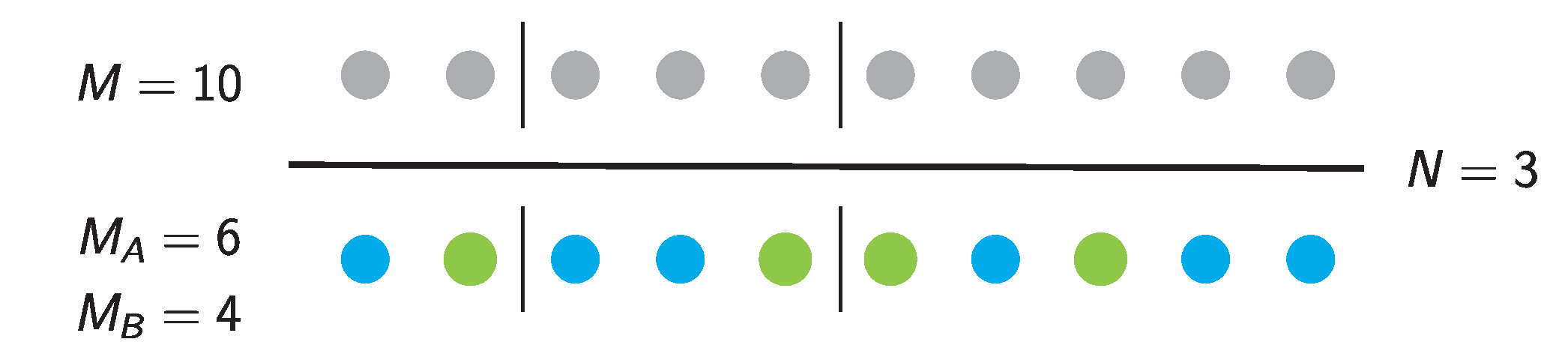
2.2.1. Representations of Bicomponent Populations
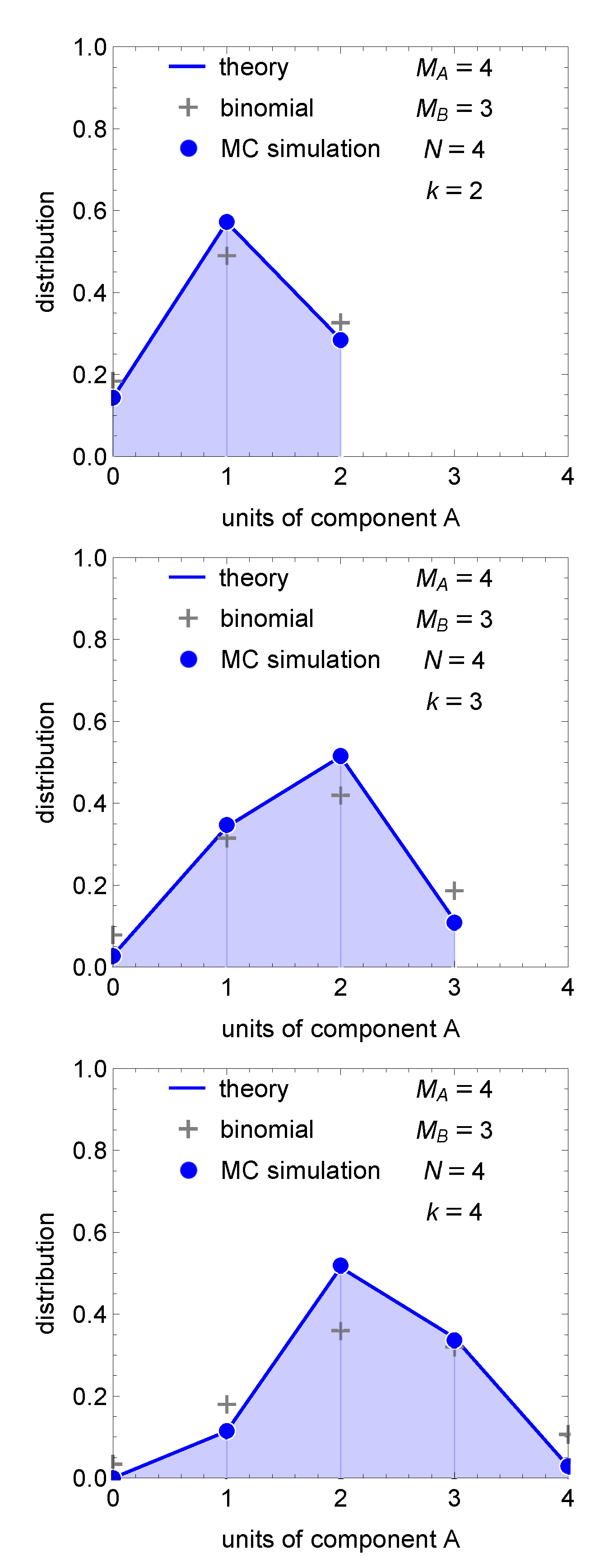
2.2.2. The Ensemble of Random Fragment Distributions
2.2.3. Mean Fragment Distribution
2.3. Any Number of Components
3. Nonrandom Bicomponent Fragmentation
3.1. Linear Ensemble
3.2. Composition-Independent Bias
4. Simulation of Biased Fragmentation
4.1. Monte Carlo Sampling by Exchange Reaction
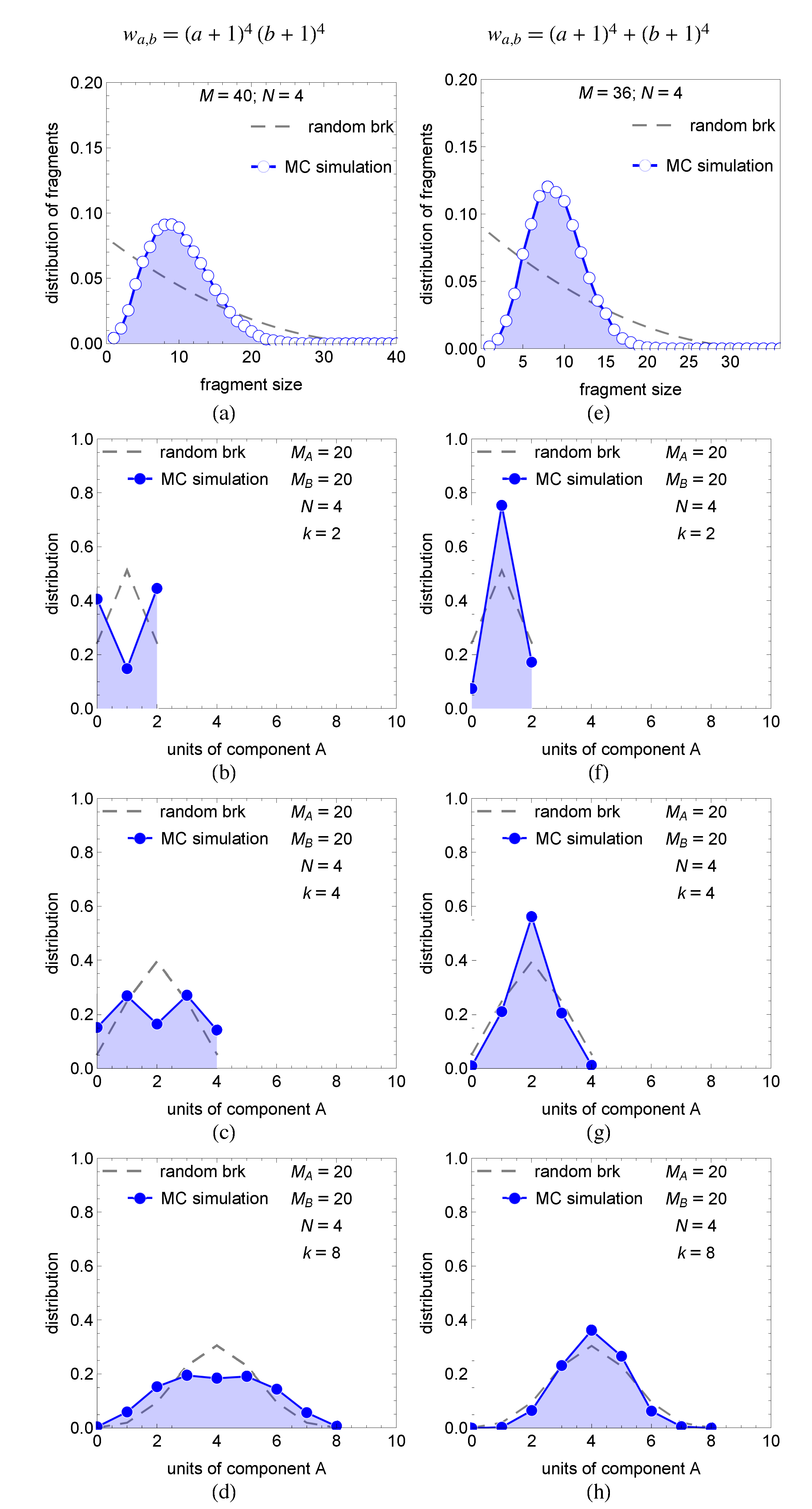
4.2. Two Examples
- Case I (positive deviations)
- Case II (negative deviations)
5. Concluding Remarks
Funding
Conflicts of Interest
References and Note
- Gross, D.H.E. Microcanonical thermodynamics and statistical fragmentation of dissipative systems. The topological structure of the N-body phase space. Phys. Rep. 1997, 279, 119–201. [Google Scholar] [CrossRef]
- Das, C.; Dasgupta, S.; Lynch, W.; Mekjian, A.; Tsang, M. The thermodynamic model for nuclear multifragmentation. Phys. Rep. 2005, 406, 1–47. [Google Scholar] [CrossRef][Green Version]
- Désesquelles, P.; Pasquiers, S.; Blin-Simiand, N.; Magne, L.; Van-Oanh, N.T.; Thomas, S.; Domin, D. The statistical molecular fragmentation model compared to experimental plasma induced hydrocarbon decays. Phys. Chem. Chem. Phys. 2020, 22, 7586–7596. [Google Scholar] [CrossRef] [PubMed]
- Martinet, G.; Díaz-Tendero, S.; Chabot, M.; Wohrer, K.; Negra, S.D.; Mezdari, F.; Hamrita, H.; Désesquelles, P.; Padellec, A.L.; Gardés, D.; et al. Fragmentation of Highly Excited Small Neutral Carbon Clusters. Phys. Rev. Lett. 2004, 93, 063401. [Google Scholar] [CrossRef] [PubMed]
- Hervieux, P.A.; Zarour, B.; Hanssen, J.; Politis, M.F.; Martín, F. Fragmentation in collisions of Na9+clusters with Cs atoms. J. Phys. B At. Mol. Opt. Phys. 2001, 34, 3331–3355. [Google Scholar] [CrossRef]
- Gueron, S.; Levin, S.A. The dynamics of group formation. Math. Biosci. 1995, 128, 243–264. [Google Scholar] [CrossRef]
- Chen, Y.; Paul, G.; Cohen, R.; Havlin, S.; Borgatti, S.P.; Liljeros, F.; Stanley, H.E. Percolation theory applied to measures of fragmentation in social networks. Phys. Rev. E 2007, 75, 046107. [Google Scholar] [CrossRef]
- Allard, A.; Hébert-Dufresne, L.; Noël, P.A.; Marceau, V.; Dubé, L.J. Exact solution of bond percolation on small arbitrary graphs. EPL Europhys. Lett. 2012, 98, 16001. [Google Scholar] [CrossRef]
- Brown, W.K.; Karpp, R.R.; Grady, D.E. Fragmentation of the universe. Astrophys. Space Sci. 1983, 94, 401–412. [Google Scholar] [CrossRef]
- Melzak, Z.A. A scalar transport equation. Trans. Am. Math. Soc. 1957, 85, 552–560. [Google Scholar] [CrossRef]
- Ziff, R.M.; McGrady, E.D. The kinetics of cluster fragmentation and depolymerisation. J. Phys. A Math. Gen. 1985, 18, 3027. [Google Scholar] [CrossRef]
- Montroll, E.W.; Simha, R. Theory of Depolymerization of Long Chain Molecules. J. Chem. Phys. 1940, 8, 721–726. [Google Scholar] [CrossRef]
- Simha, R. Kinetics of Degradation and Size Distribution of Long Chain Polymers. J. Appl. Phys. 1941, 12, 569–578. [Google Scholar] [CrossRef]
- Simha, R. On the Degradation of Branched Chain Molecules. J. Chem. Phys. 1956, 24, 796–802. [Google Scholar] [CrossRef]
- Ziff, R.M.; McGrady, E.D. Kinetics of polymer degradation. Macromolecules 1986, 19, 2513–2519. [Google Scholar] [CrossRef]
- McGrady, E.D.; Ziff, R.M. “Shattering” Transition in Fragmentation. Phys. Rev. Lett. 1987, 58, 892–895. [Google Scholar] [CrossRef]
- Ziff, R.M. New solutions to the fragmentation equation. J. Phys. A Math. Gen. 1991, 24, 2821. [Google Scholar] [CrossRef]
- Krapivsky, P.L.; Ben-Naim, E. Scaling and multiscaling in models of fragmentation. Phys. Rev. E 1994, 50, 3502–3507. [Google Scholar] [CrossRef]
- Connaughton, C.; Dutta, A.; Rajesh, R.; Siddharth, N.; Zaboronski, O. Stationary mass distribution and nonlocality in models of coalescence and shattering. Phys. Rev. E 2018, 97, 022137. [Google Scholar] [CrossRef]
- Krapivsky, P.L.; Ben-Naim, E. Shattering transitions in collision-induced fragmentation. Phys. Rev. E 2003, 68, 021102. [Google Scholar] [CrossRef]
- Ernst, M.H.; Szamel, G. Fragmentation kinetics. J. Phys. A Math. Gen. 1993, 26, 6085. [Google Scholar] [CrossRef]
- Ziff, R.M. An explicit solution to a discrete fragmentation model. J. Phys. A Math. Gen. 1992, 25, 2569. [Google Scholar] [CrossRef]
- Bauer, W.; Dean, D.; Mosel, U.; Post, U. New approach to fragmentation reactions: The nuclear lattice model. Phys. Lett. B 1985, 150, 53–56. [Google Scholar] [CrossRef]
- Hendriks, E.M.; Spouge, J.L.; Eibl, M.; Schreckenberg, M. Exact solutions for random coagulation processes. Z. Für Phys. B Condens. Matter 1985, 58, 219–227. [Google Scholar] [CrossRef]
- Durrett, R.; Granovsky, B.; Gueron, S. The Equilibrium Behavior of Reversible Coagulation-Fragmentation Processes. J. Theor. Probab. 1999, 12, 447–474. [Google Scholar] [CrossRef]
- Berestycki, J. Exchangeable Fragmentation-Coalescence Processes and their Equilibrium Measures. Electron. J. Probab. 2004, 9, 770–824. [Google Scholar] [CrossRef]
- Berestycki, N.; Pitman, J. Gibbs Distributions for Random Partitions Generated by a Fragmentation Process. J. Stat. Phys. 2007, 127, 381–418. [Google Scholar] [CrossRef]
- Austin, L.; Shoji, K.; Bhatia, V.; Jindal, V.; Savage, K.; Klimpel, R. Some Results on the Description of Size Reduction as a Rate Process in Various Mills. Ind. Eng. Chem. Process Des. Dev. 1976, 15, 187–196. [Google Scholar] [CrossRef]
- Rozenblat, Y.; Grant, E.; Levy, A.; Kalman, H.; Tomas, J. Selection and breakage functions of particles under impact loads. Chem. Eng. Sci. 2012, 71, 56–66. [Google Scholar] [CrossRef]
- Abberger, T. Chapter 24 Population balance modelling of granulation. In Handbook of Powder Technology; Granulation, A.D., Salman, M.H., Seville, J., Eds.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2007; Volume 11, pp. 1109–1186. [Google Scholar] [CrossRef]
- Bóna, M. A Walk Through Combinatorics—An Introduction to Enumeration and Graph Theory, 2nd ed.; World Scientific Publishing: Singapore, 2006. [Google Scholar]
- Evans, M.R.; Hanney, T. Nonequilibrium statistical mechanics of the zero-range process and related models. J. Phys. A Math. Gen. 2005, 38, R195–R240. [Google Scholar] [CrossRef]
- Feller, W. On the Time Distribution of So-Called Random Events. Phys. Rev. 1940, 57, 906–908. [Google Scholar] [CrossRef]
- Ruark, A. The Time Distribution of So-Called Random Events. Phys. Rev. 1939, 56, 1165–1167. [Google Scholar] [CrossRef]
- Matsoukas, T. Generalized Statistical Thermodynamics: Thermodynamics of Probability Distributions and Stochastic Processes; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Matsoukas, T. Statistical Thermodynamics of Irreversible Aggregation: The Sol-Gel Transition. Sci. Rep. 2015, 5, 8855. [Google Scholar] [CrossRef] [PubMed]
- Matsoukas, T. Fundamentals of Chemical Engineering Thermodynamics; Pearson Education, Inc.: London, UK, 2013. [Google Scholar]
- Kelly, F.P. Reversibility and Stochastic Networks; Wiley: Cambridge, UK, 2011. [Google Scholar]
- Schrödinger, E. Statistical Thermodynamics; Dover Publications: Mineola, NY, USA, 1989; Reprint of the 2nd edition originally published by Cambridge University Press, 1952, under the subtitle A Course Seminar Lectures Delivered in January-March 1944 at the School of Theoretical Physics, Dublin Institute for Advanced Studies. [Google Scholar]
- Matsoukas, T. Thermodynamics Beyond Molecules: Statistical Thermodynamics of Probability Distributions. Entropy 2019, 21, 890. [Google Scholar] [CrossRef]
| Case 1 | 1 | |
| Case 2 | ||
| Case 3 ‡ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsoukas, T. Statistical Mechanics of Discrete Multicomponent Fragmentation. Condens. Matter 2020, 5, 64. https://doi.org/10.3390/condmat5040064
Matsoukas T. Statistical Mechanics of Discrete Multicomponent Fragmentation. Condensed Matter. 2020; 5(4):64. https://doi.org/10.3390/condmat5040064
Chicago/Turabian StyleMatsoukas, Themis. 2020. "Statistical Mechanics of Discrete Multicomponent Fragmentation" Condensed Matter 5, no. 4: 64. https://doi.org/10.3390/condmat5040064
APA StyleMatsoukas, T. (2020). Statistical Mechanics of Discrete Multicomponent Fragmentation. Condensed Matter, 5(4), 64. https://doi.org/10.3390/condmat5040064





