Micromagnetic Simulation of Vortex Development in Magnetic Bi-Material Bow-Tie Structures
Abstract
:1. Introduction
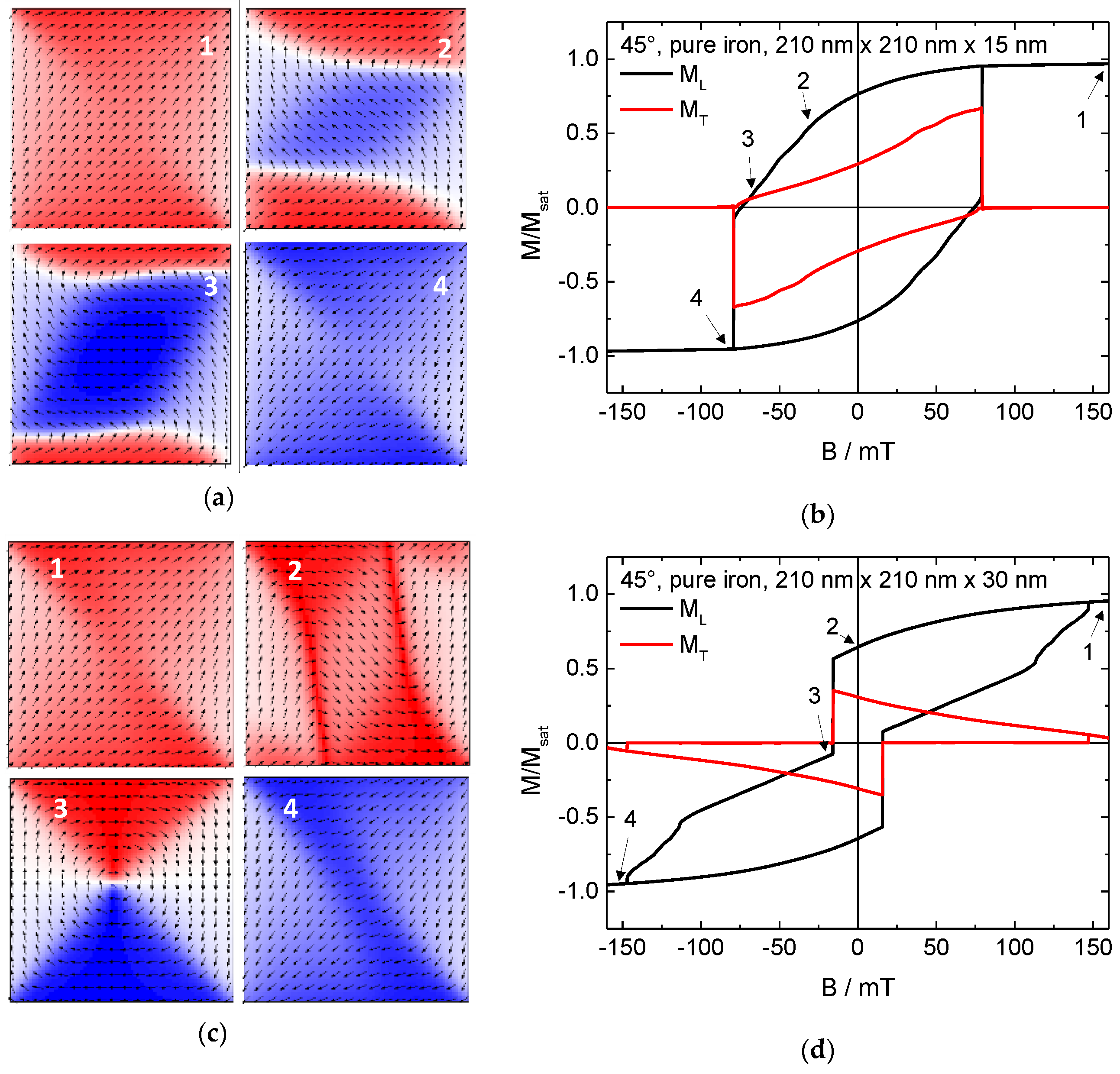
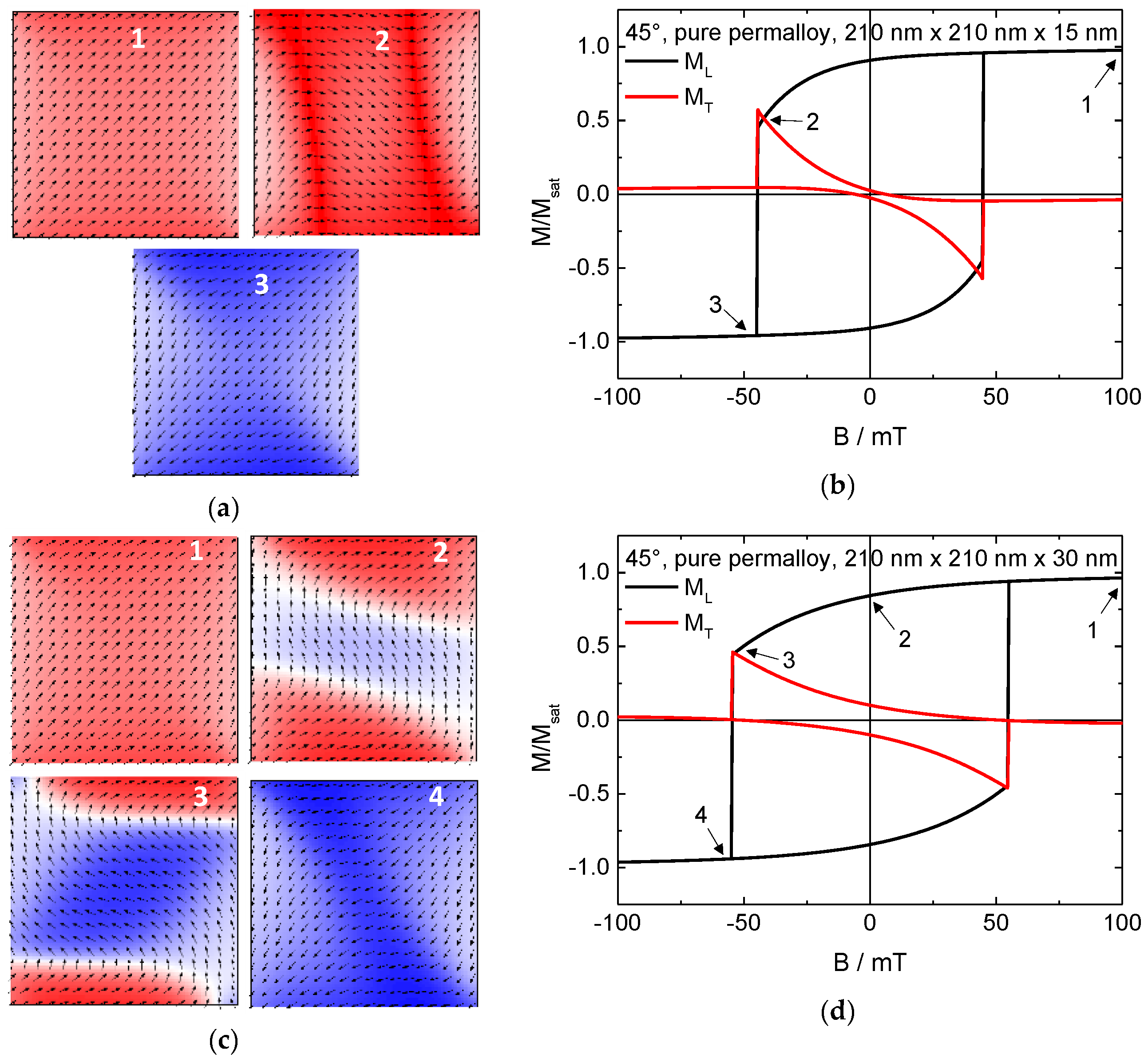
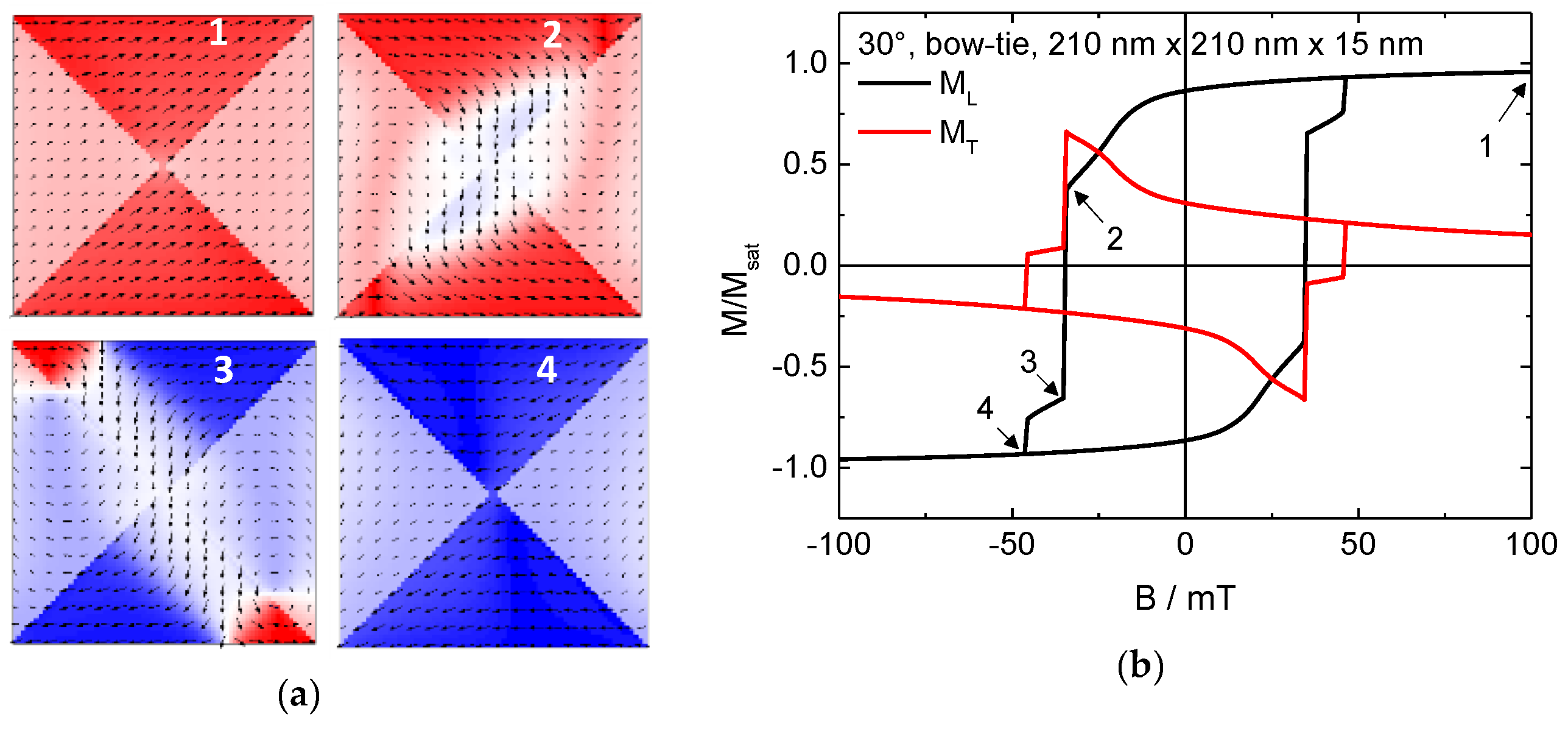
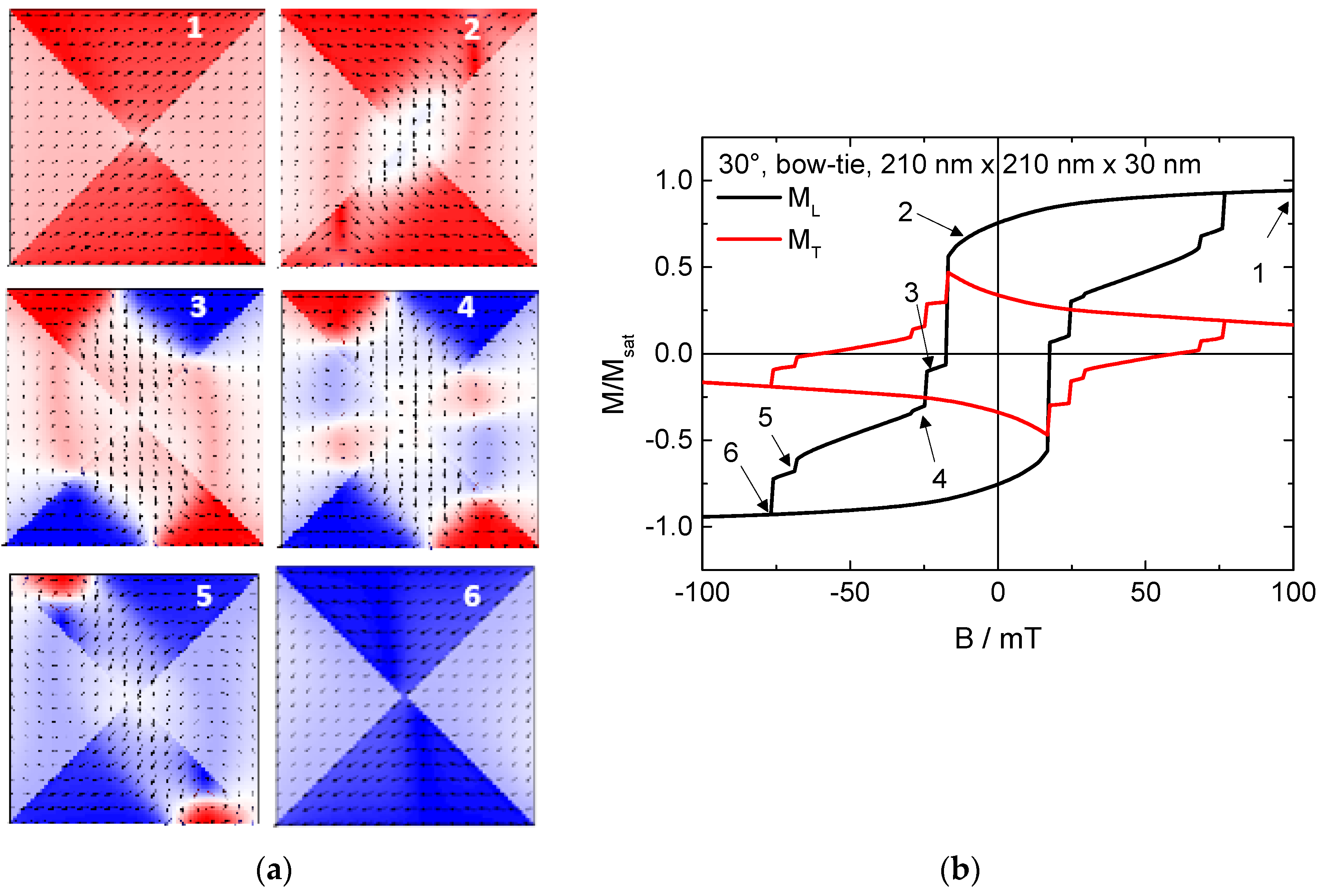
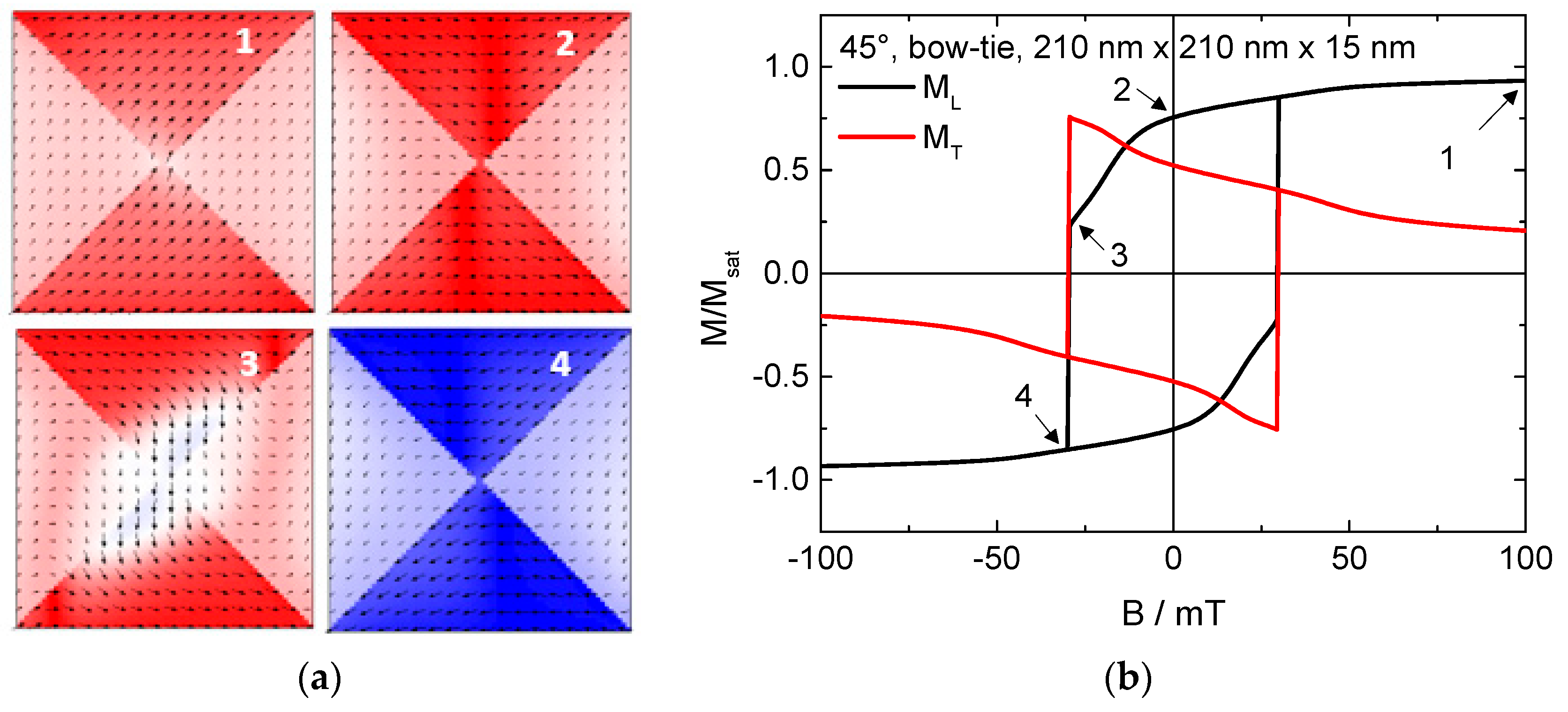
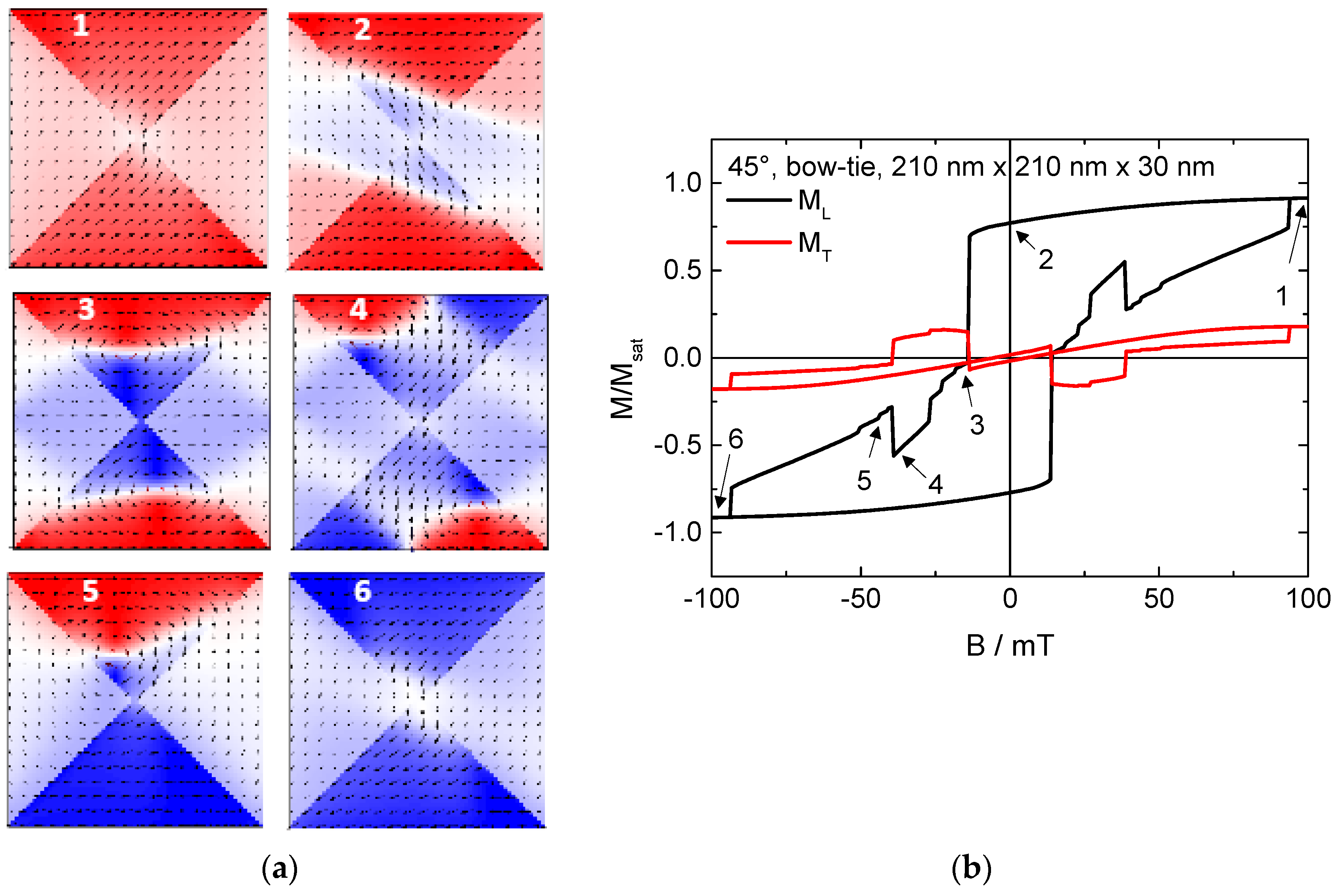
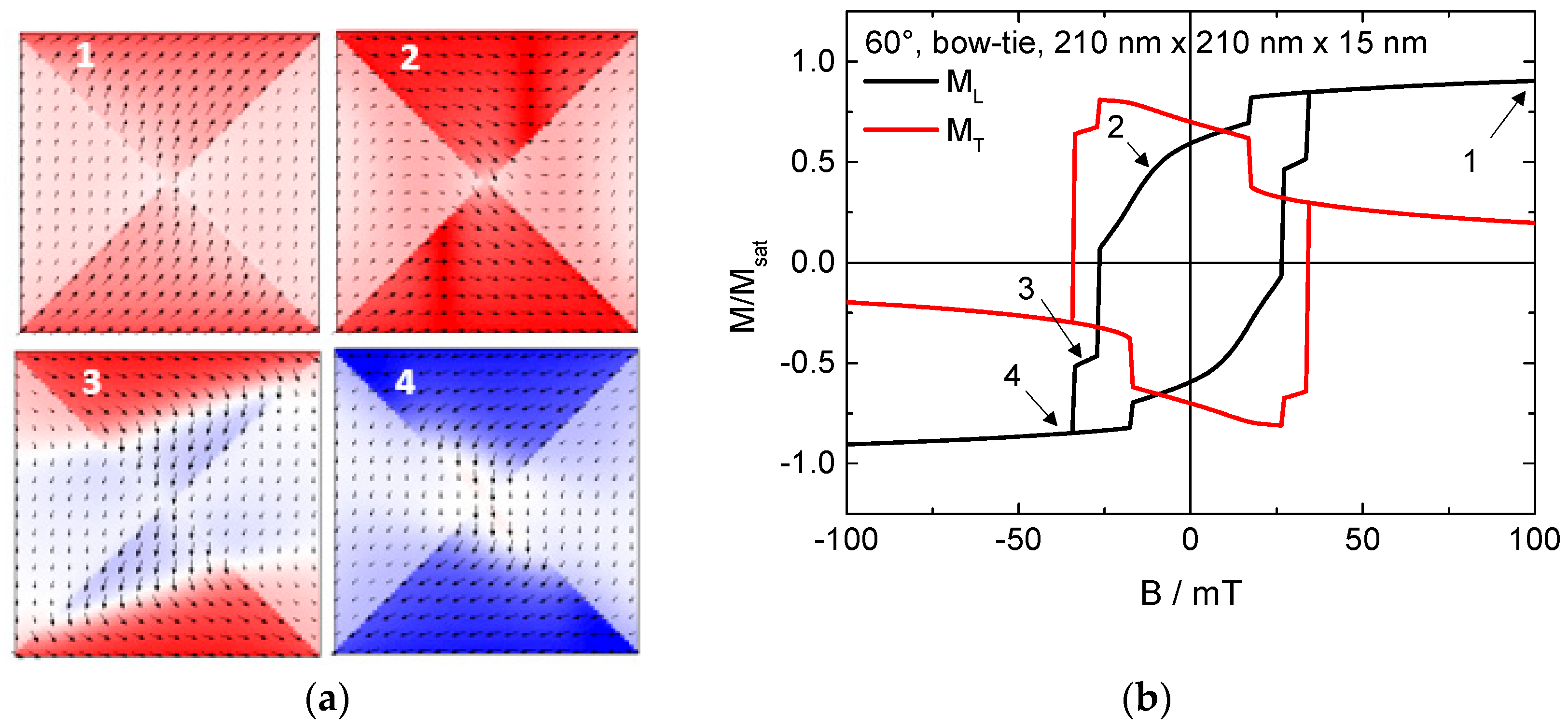
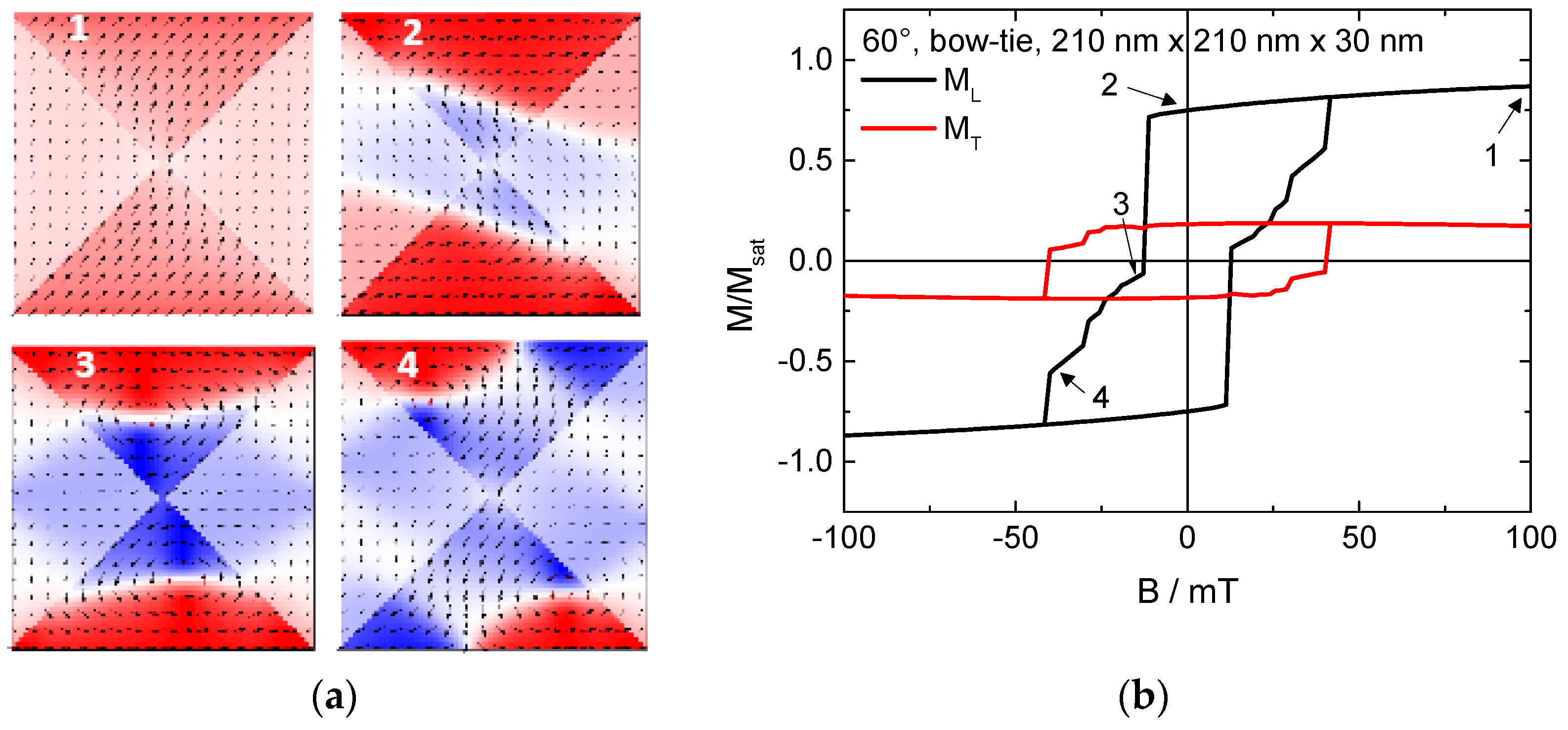
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Blachowicz, T.; Kosmalska, D.; Döpke, C.; Leiste, H.; Hahn, L.; Ehrmann, A. Varying steps in hysteresis loops of Co square nano-frames. J. Magn. Magn. Mater. 2019, 491, 165619. [Google Scholar] [CrossRef]
- Ehrmann, A.; Blachowicz, T.; Komraus, S.; Nees, M.-K.; Jakobs, P.-J.; Leiste, H.; Mathes, M.; Schaarschmidt, M. Magnetic properties of square Py nanowires: Irradiation dose and geometry dependence. J. Appl. Phys. 2015, 117, 173903. [Google Scholar] [CrossRef]
- Pagnanelli, F.; Altimari, P.; Bellagamba, M.; Granata, G.; Moscardini, E.; Schiavi, P.G.; Toro, L. Pulsed electrodeposition of cobalt nanoparticles on copper: Influence of the operating parameters on size distribution and morphology. Electrochim. Acta 2015, 155, 228–235. [Google Scholar] [CrossRef]
- Romero, M.; Pardo, H.; Faccio, R.; Suescun, L.; Vazquez, S.; Laborda, I.; Fernandez-Werner, L.; Acosta, A.; Castiglioni, J.; Mombru, A.W. A Study on the Polymer Precursor Formation and Microstructure Evolution of Square-Shaped (La0.5Ba0.5)(Mn0.5Fe0.5)O3Ceramic Nanoparticles. J. Ceram. Sci. Tech. 2015, 6, 221–230. [Google Scholar]
- Nogués, J.; Sort, J.; Langlais, V.; Skumryev, V.; Surinach, S.; Munoz, J.S.; Baro, M.D. Exchange bias in nanostructures. Phys. Rep. 2005, 422, 65. [Google Scholar] [CrossRef]
- Mahato, B.K.; Choudhury, S.; Mandal, R.; Barman, S.; Otani, Y.; Barman, A. Tunable configurational anisotropy in collective magnetization dynamics of Ni80Fe20 nanodot arrays with varying dot shapes. J. Appl. Phys. 2015, 117, 213909. [Google Scholar] [CrossRef] [Green Version]
- Thevenard, L.; Zeng, H.T.; Petit, D.; Cowburn, R.P. Macrospin limit and configurational anisotropy in nanoscale permalloy triangles. J. Magn. Magn. Mater. 2010, 322, 2152–2156. [Google Scholar] [CrossRef] [Green Version]
- Cowburn, R.P.; Adeyeye, A.O.; Welland, M.E. Configurational anisotropy in nanomagnets. Phys. Rev. Lett. 1998, 81, 5414. [Google Scholar] [CrossRef]
- Wachowiak, A.; Wiebe, J.; Bode, M.; Pietzsch, O.; Morgenstern, M.; Wiesendanger, R. Direct Observation of Internal Spin Structure of Magnetic Vortex Cores. Science 2002, 298, 577–580. [Google Scholar] [CrossRef] [PubMed]
- Guslienko, K.Y.; Aranda, G.R.; Gonzalez, J.M. Topological gauge field in nanomagnets: Spin-wave excitations over a slowly moving magnetization background. Phys. Rev. B 2010, 81, 014414. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Haas, S. Phase diagram of magnetization reversal processes in nanorings. Phys. Rev. B 2010, 81, 064433. [Google Scholar] [CrossRef] [Green Version]
- Zhu, F.Q.; Fan, D.L.; Zhu, X.C.; Zhu, J.G.; Cammarata, R.C.; Chien, C.L. Ultrahigh-Density Arrays of Ferromagnetic Nanorings on Macroscopic Areas. Adv. Mater. 2004, 16, 2155. [Google Scholar] [CrossRef]
- Mejia-López, J.; Altbir, D.; Romero, A.H.; Batlle, X.; Roshchin, I.V.; Li, C.-P.; Schuller, I.K. Vortex state and effect of anisotropy in sub-100-nm magnetic nanodots. J. Appl. Phys. 2006, 100, 104319. [Google Scholar] [CrossRef] [Green Version]
- Ehrmann, A.; Blachowicz, T. Influence of shape and dimension on magnetic anisotropies and magnetization reversal of Py, Fe, and Co nano-objects with four-fold symmetry. AIP Adv. 2015, 5, 097109. [Google Scholar] [CrossRef] [Green Version]
- Subramani, A.; Geerpuram, D.; Domanowski, A.; Baskaran, V.; Metlushko, V. Vortex state in magnetic rings. Phys. C 2004, 404, 241. [Google Scholar] [CrossRef]
- Wang, J.; Adeyeye, A.O.; Singh, N. Magnetostatic interactions in mesoscopic Ni80Fe20 ring arrays. Appl. Phys. Lett. 2005, 87, 262508. [Google Scholar] [CrossRef]
- Gao, X.S.; Adeyeye, A.O.; Goolaup, S.; Singh, N.; Jung, W.; Castano, F.J.; Ross, C.A. Inhomogeneities in spin states and magnetization reversal of geometrically identical elongated Co rings. J. Appl. Phys. 2007, 101, 09F505. [Google Scholar] [CrossRef]
- Vavassori, P.; Grimsditch, M.; Novosad, V.; Metlushko, V.; Ilic, B. Metastable states during magnetization reversal in square permalloy rings. Phys. Rev. B 2003, 67, 134429. [Google Scholar] [CrossRef]
- Vavassori, P.; Bovolenta, R.; Metlushko, V.; Ilic, B. Vortex rotation control in Permalloy disks with small circular voids. J. Appl. Phys. 2006, 99, 053902. [Google Scholar] [CrossRef] [Green Version]
- Leong, T.G.; Zarafshar, A.M.; Gracias, D.H. Three-dimensional fabrication at small size scales. Small 2010, 6, 792. [Google Scholar] [CrossRef]
- Amaladass, E.; Ludescher, B.; Schütz, G.; Tyliszczak, T.; Lee, M.-S.; Eimüller, T. Nanospheres generate out-of-plane magnetization. J. Appl. Phys. 2010, 107, 053911. [Google Scholar] [CrossRef]
- Blachowicz, T.; Ehrmann, A.; Steblinski, P.; Pawela, L. Magnetization reversal in magnetic half-balls influenced by shape perturbations. J. Appl. Phys. 2010, 108, 123906. [Google Scholar] [CrossRef] [Green Version]
- Ehrmann, A.; Blachowicz, T. Vortex and double-vortex nucleation during magnetization reversal in Fe nanodots of different dimensions. J. Magn. Magn. Mater. 2019, 475, 727–733. [Google Scholar] [CrossRef]
- Lyberatos, A.; Komineas, S.; Papanicolaou, N. Precessing vortices and antivortices in ferromagnetic elements. J. Appl. Phys. 2011, 109, 023911. [Google Scholar] [CrossRef] [Green Version]
- Ehrmann, A.; Blachowicz, T. Systematic study of magnetization reversal in square Fe nanodots of varying dimensions in different orientations. Hyperfine Interact. 2018, 239, 48. [Google Scholar] [CrossRef]
- Mohler, G.; Harter, A.W. Micromagnetic investigation of resonance frequencies in ferromagnetic particles. J. Appl. Phys. 2005, 97, 10E313. [Google Scholar] [CrossRef]
- Kanso, H.; Pate, R.; Baltz, V.; Ledue, D. Influence of finite-size and edge effects on the exchange-bias properties of ferromagnetic/antiferromagnetic nanodots: Granular Monte Carlo investigation. Phys. Rev. B 2019, 99, 054410. [Google Scholar] [CrossRef] [Green Version]
- Depondt, P.; Levy, J.-C.S.; Mamica, S. Vortex polarization dynamics in a square magnetic nanodot. J. Phys. Cond. Matter 2013, 25, 466001. [Google Scholar] [CrossRef]
- Ivanov, Y.P.; Nefedev, K.V.; Iljin, A.I.; Pustovalov, E.V.; Chebotkevich, L.A. Magnetization reversal of nanodots with different magnetic anisotropy and magnetostatic energy. J. Phys. Conf. Ser. 2011, 266, 012117. [Google Scholar] [CrossRef]
- Song, S.Y.; Zhang, G.F.; Song, W.B.; Guo, G.H. Dynamical reversal of rectangular nanodot studied by micromagnetics. Act. Phys. Sin. 2009, 58, 5757–5762. [Google Scholar]
- Tillmanns, A.; Blachowicz, T.; Fraune, M.; Güntherodt, G.; Schuller, I.K. Anomalous magnetization reveral mechanism in unbiased Fe/FeF2 investigated by means of the magneto-optic Kerr effect. J. Magn. Magn. Mater. 2009, 321, 2932–2935. [Google Scholar] [CrossRef]
- Nasirpouri, F.; Engbarth, M.A.; Bending, S.J.; Peter, L.M.; Knittel, A.; Fangohr, H.; Milosevic, M.V. Three-dimensional ferromagnetic architectures with multiple metastable states. Appl. Phys. Lett. 2011, 98, 222506. [Google Scholar] [CrossRef] [Green Version]
- Mulkers, J.; Milosevic, M.V.; van Waeyenberge, B. Cycloidal versus skyrmionic states in mesoscopic chiral magnets. Phys. Rev. B 2016, 93, 214405. [Google Scholar] [CrossRef] [Green Version]
- Mulkers, J.; van Waeyenberge, B.; Milosevic, M.V. Effects of spatially engineered Dzyaloshinskii-Moriya interaction in ferromagnetic films. Phys. Rev. B 2017, 95, 144401. [Google Scholar] [CrossRef] [Green Version]
- Mulkers, J.; van Waeyenberge, B.; Milosevic, M.V. Tunable Snell’s law for spin waves in heterochiral magnetic films. Phys. Rev. B 2018, 97, 104422. [Google Scholar] [CrossRef] [Green Version]
- Menezes, R.M.; Mulkers, J.; de Souza Silva, C.C.; Milosevic, M.V. Deflection of ferromagnetic and antiferromagnetic skymions at heterochiral interfaces. Phys. Rev. B 2019, 99, 104409. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.Y.; Zhan, Q.W. Modified bow-tie antenna with strong broadband field enhancement for RF photonic applications. Proc. SPIE 2013, 8806, 88061V. [Google Scholar]
- Ehrmann, A.; Blachowicz, T. Influence of the distance between nanoparticles in clusters on the magnetization reversal process. J. Nanomater. 2017, 2017, 5046076. [Google Scholar] [CrossRef] [Green Version]
- Ehrmann, A.; Blachowicz, T. Interaction between magnetic nanoparticles in clusters. AIMS Mater. Sci. 2017, 4, 383–390. [Google Scholar] [CrossRef]
- Donahue, M.J.; Porter, D.G. OOMMF User’s Guide, Version 1.0; Interagency Report NISTIR 6376; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1999.
- Gilbert, T.L. A phenomenological theory of damping in ferromagnetic materials. IEEE Trans. Magn. 2004, 40, 3443. [Google Scholar] [CrossRef]
- Leliart, J.; Dvornik, M.; Mulkers, J.; de Clercq, J.; Milosevic, M.V.; van Waeyenberge, B. Fast micromagnetic simulations on GPU—Recent advances made with mumax3. J. Phys. D Appl. Phys. 2018, 51, 123002. [Google Scholar] [CrossRef]
- Oezelt, H.; Kirk, E.; Wohlhüter, P.; Müller, E.; Heyerman, L.J.; Kowacs, A.; Schrefl, T. Vortex motion in amorphous ferrimagnetic thin film elements. AIP Adv. 2017, 7, 056001. [Google Scholar] [CrossRef] [Green Version]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sudsom, D.; Juhász Junger, I.; Döpke, C.; Blachowicz, T.; Hahn, L.; Ehrmann, A. Micromagnetic Simulation of Vortex Development in Magnetic Bi-Material Bow-Tie Structures. Condens. Matter 2020, 5, 5. https://doi.org/10.3390/condmat5010005
Sudsom D, Juhász Junger I, Döpke C, Blachowicz T, Hahn L, Ehrmann A. Micromagnetic Simulation of Vortex Development in Magnetic Bi-Material Bow-Tie Structures. Condensed Matter. 2020; 5(1):5. https://doi.org/10.3390/condmat5010005
Chicago/Turabian StyleSudsom, Devika, Irén Juhász Junger, Christoph Döpke, Tomasz Blachowicz, Lothar Hahn, and Andrea Ehrmann. 2020. "Micromagnetic Simulation of Vortex Development in Magnetic Bi-Material Bow-Tie Structures" Condensed Matter 5, no. 1: 5. https://doi.org/10.3390/condmat5010005
APA StyleSudsom, D., Juhász Junger, I., Döpke, C., Blachowicz, T., Hahn, L., & Ehrmann, A. (2020). Micromagnetic Simulation of Vortex Development in Magnetic Bi-Material Bow-Tie Structures. Condensed Matter, 5(1), 5. https://doi.org/10.3390/condmat5010005






