Transition Metal Dichalcogenides as Strategy for High Temperature Electron-Hole Superfluidity
Abstract
1. Introduction
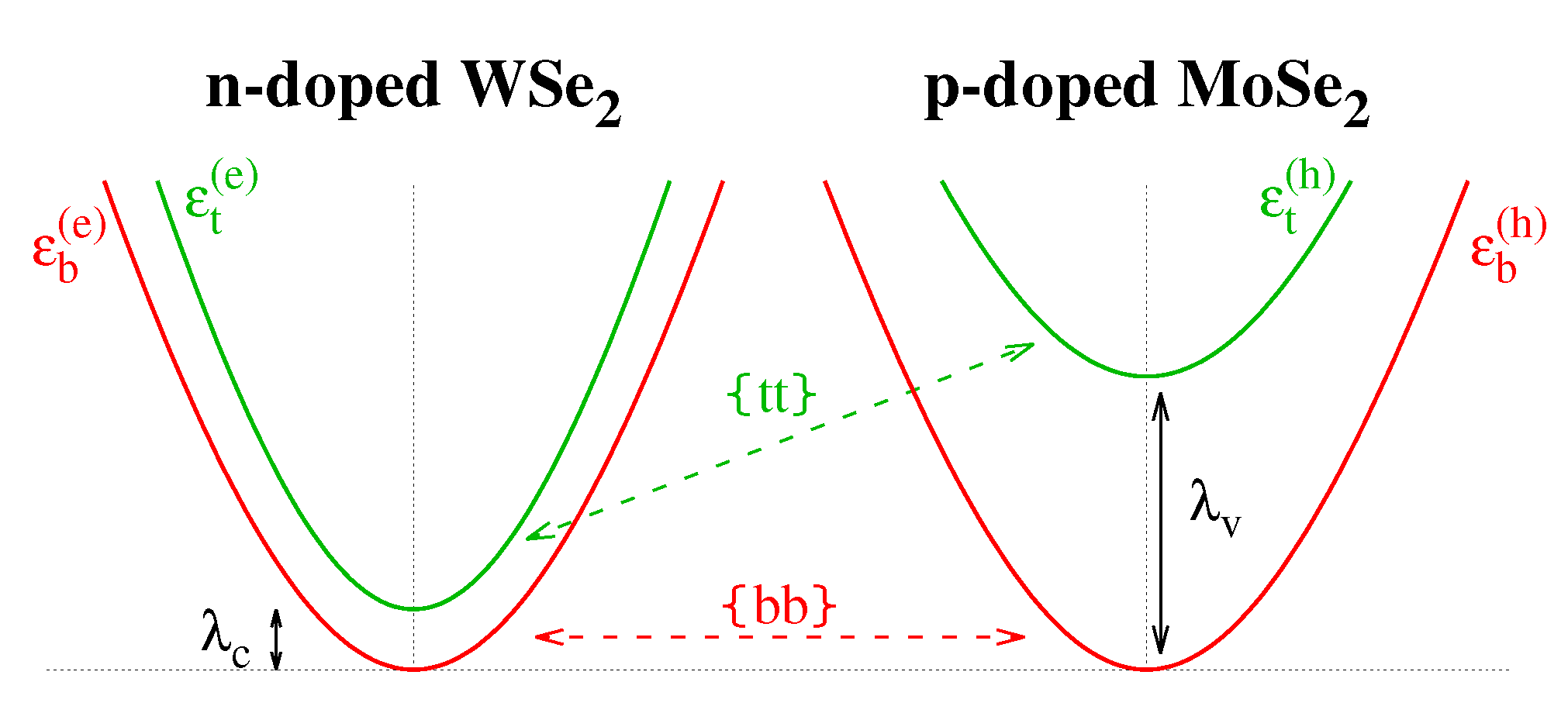
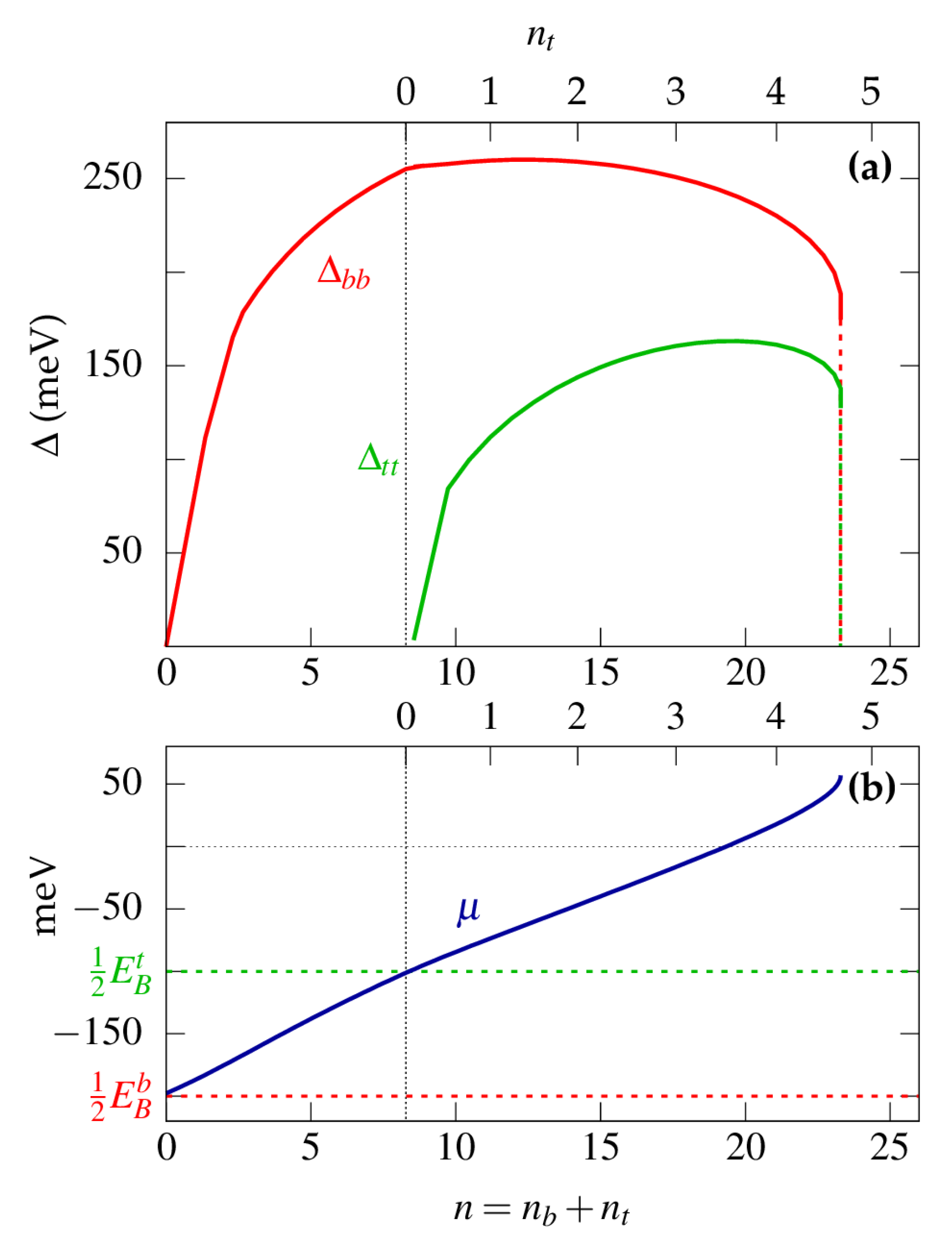
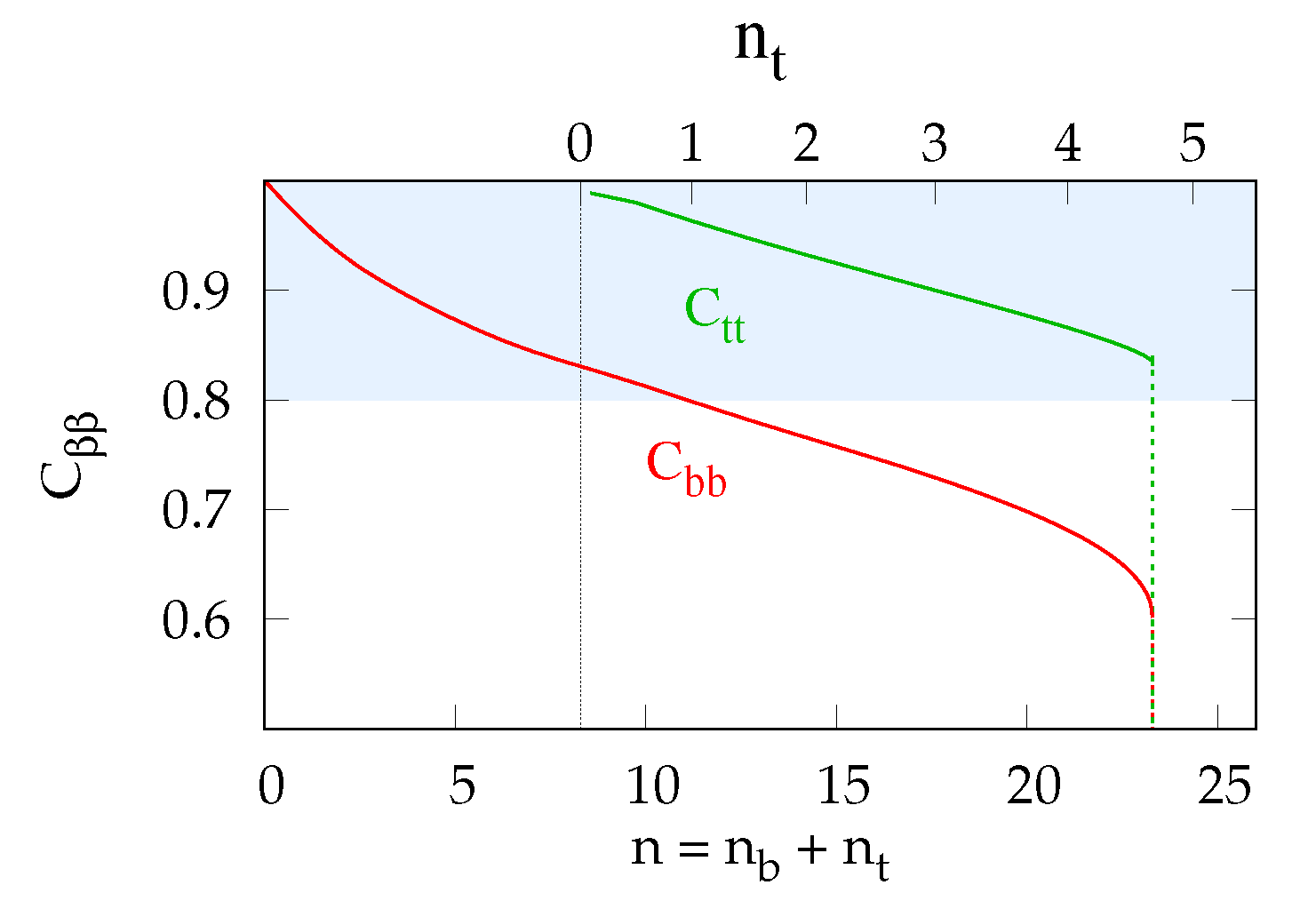
2. Results
3. Discussion
4. Materials and Methods
4.1. Materials
4.2. Method
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| 2D | Two-dimensional |
| DQW | Double Quantum-Wells |
| DMG | Double Monolayer Graphene |
| hBN | hexagonal Boron Nitride |
| DBG | Double Bilayer Graphene |
| TMD | Transition Metal Dichalcogenides |
| BEC | Bose-Einstein Condensation |
| BKT | Berezinskii-Kosterlitz-Thouless |
References
- Zhu, X.; Littlewood, P.B.; Hybertsen, M.S.; Rice, T.M. Exciton Condensate in Semiconductor Quantum Well Structures. Phys. Rev. Lett. 1995, 74, 1633. [Google Scholar] [CrossRef]
- Croxall, A.F.; Das Gupta, K.; Nicoll, C.A.; Thangaraj, M.; Beere, H.E.; Farrer, I.; Ritchie, D.A.; Pepper, M. Anomalous Coulomb Drag in Electron-Hole Bilayers. Phys. Rev. Lett. 2008, 101, 246801. [Google Scholar] [CrossRef] [PubMed]
- Seamons, J.A.; Morath, C.P.; Reno, J.L.; Lilly, M.P. Coulomb Drag in the Exciton Regime in Electron-Hole Bilayers. Phys. Rev. Lett. 2009, 102, 026804. [Google Scholar] [CrossRef] [PubMed]
- Lozovik, Y.E.; Yudson, V.I. Feasibility of superfluidity of paired spatially separated electrons and holes. JETP Lett. 1975, 22, 274, (Pis’ma Zh. Eksp. Teor. Fiz. 22, 556 (1975)). [Google Scholar]
- Saberi-Pouya, S.; Conti, S.; Perali, A.; Croxall, A.F.; Hamilton, A.R.; Peeters, F.M.; Neilson, D. Experimental conditions for observation of electron-hole superfluidity in GaAs heterostructures. arXiv 2019, arXiv:1910.06631. [Google Scholar]
- Neilson, D.; Perali, A.; Hamilton, A.R. Excitonic superfluidity and screening in electron-hole bilayer systems. Phys. Rev. B 2014, 89, 060502. [Google Scholar] [CrossRef]
- Pieri, P.; Neilson, D.; Strinati, G.C. Effects of density imbalance on the BCS-BEC crossover in semiconductor electron-hole bilayers. Phys. Rev. B 2007, 75, 113301. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666. [Google Scholar] [CrossRef]
- Britnell, L.; Gorbachev, R.V.; Jalil, R.; Belle, B.D.; Schedin, F.; Katsnelson, M.I.; Eaves, L.; Morozov, S.V.; Mayorov, A.S.; Peres, N.M.; et al. Electron tunneling through ultrathin Boron Nitride crystalline barriers. Nano Lett. 2012, 12, 1707. [Google Scholar] [CrossRef]
- Min, H.; Bistritzer, R.; Su, J.J.; MacDonald, A.H. Room-temperature superfluidity in graphene bilayers. Phys. Rev. B 2008, 78, 121401. [Google Scholar] [CrossRef]
- Lozovik, Y.E.; Sokolik, A.A. Coherent phases and collective electron phenomena in graphene. J. Phys. Conf. Ser. 2008, 129, 012003. [Google Scholar] [CrossRef]
- Gorbachev, R.V.; Geim, A.K.; Katsnelson, M.I.; Novoselov, K.S.; Tudorovskiy, T.; Grigorieva, I.V.; MacDonald, A.H.; Morozov, S.V.; Watanabe, K.; Taniguchi, T.; et al. Strong Coulomb drag and broken symmetry in double-layer graphene. Nat. Phys. 2012, 8, 896. [Google Scholar] [CrossRef]
- Lozovik, Y.E.; Ogarkov, S.L.; Sokolik, A.A. Condensation of electron-hole pairs in a two-layer graphene system: Correlation effects. Phys. Rev. B 2012, 86, 045429. [Google Scholar] [CrossRef]
- Perali, A.; Neilson, D.; Hamilton, A.R. High-Temperature Superfluidity in Double-Bilayer Graphene. Phys. Rev. Lett. 2013, 110, 146803. [Google Scholar] [CrossRef]
- Burg, G.W.; Prasad, N.; Kim, K.; Taniguchi, T.; Watanabe, K.; MacDonald, A.H.; Register, L.F.; Tutuc, E. Strongly Enhanced Tunneling at Total Charge Neutrality in Double-Bilayer Graphene-WSe2 Heterostructures. Phys. Rev. Lett. 2018, 120, 177702. [Google Scholar] [CrossRef] [PubMed]
- Conti, S.; Perali, A.; Peeters, F.M.; Neilson, D. Multicomponent screening and superfluidity in gapped electron-hole double bilayer graphene with realistic bands. Phys. Rev. B 2019, 99, 144517. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, T.T.; Girit, C.; Hao, Z.; Martin, M.C.; Zettl, A.; Crommie, M.F.; Shen, Y.R.; Wang, F. Direct observation of a widely tunable bandgap in bilayer graphene. Nature 2009, 459, 820. [Google Scholar] [CrossRef]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef]
- Jiang, H. Electronic band structures of molybdenum and tungsten dichalcogenides by the GW approach. J. Phys. Chem. C 2012, 116, 7664. [Google Scholar] [CrossRef]
- Fogler, M.M.; Butov, L.V.; Novoselov, K.S. High-temperature superfluidity with indirect excitons in van der Waals heterostructures. Nat. Commun. 2014, 5, 4555. [Google Scholar] [CrossRef]
- Conti, S.; der Donck, M.V.; Perali, A.; Peeters, F.M.; Neilson, D. A doping-dependent switch from one- to two-component superfluidity at temperature above 100K in coupled electron-hole van der Waals heterostructures. arXiv 2019, arXiv:1909.03411. [Google Scholar]
- Wang, Z.; Rhodes, D.A.; Watanabe, K.; Taniguchi, T.; Hone, J.C.; Shan, J.; Mak, K.F. Evidence of high-temperature exciton condensation in two-dimensional atomic double layers. Nature 2019, 574, 76. [Google Scholar] [CrossRef] [PubMed]
- Strinati, G. A Survey on the Crossover from BCS Superconductivity to Bose-Einstein Condensation. Phys. Essays 2000, 13, 427. [Google Scholar] [CrossRef]
- Randeria, M.; Duan, J.M.; Shieh, L.Y. Superconductivity in a two-dimensional Fermi gas: Evolution from Cooper pairing to Bose condensation. Phys. Rev. B 1990, 41, 327. [Google Scholar] [CrossRef] [PubMed]
- Pistolesi, F.; Strinati, G.C. Evolution from BCS superconductivity to Bose condensation: Role of the parameter kFξ. Phys. Rev. B 1994, 49, 6356. [Google Scholar] [CrossRef] [PubMed]
- Singh, G.; Jouan, A.; Herranz, G.; Scigaj, M.; Sánchez, F.; Benfatto, L.; Caprara, S.; Grilli, M.; Saiz, G.; Couëdo, F.; et al. Gap suppression at a Lifshitz transition in a multi-condensate superconductor. Nat. Mater. 2019, 18, 948. [Google Scholar] [CrossRef]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C: Solid State 1973, 6, 1181. [Google Scholar] [CrossRef]
- Saberi-Pouya, S.; Zarenia, M.; Perali, A.; Vazifehshenas, T.; Peeters, F.M. High-temperature electron-hole superfluidity with strong anisotropic gaps in double phosphorene monolayers. Phys. Rev. B 2018, 97, 174503. [Google Scholar] [CrossRef]
- Conti, S.; Perali, A.; Peeters, F.M.; Neilson, D. Multicomponent electron-hole superfluidity and the BCS-BEC crossover in double bilayer graphene. Phys. Rev. Lett. 2017, 119, 257002. [Google Scholar] [CrossRef]
- Xiao, D.; Liu, G.B.; Feng, W.; Xu, X.; Yao, W. Coupled Spin and Valley Physics in Monolayers of MoS2 and Other Group-VI Dichalcogenides. Phys. Rev. Lett. 2012, 108, 196802. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Cheng, Y.C.; Schwingenschlögl, U. Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors. Phys. Rev. B 2011, 84, 153402. [Google Scholar] [CrossRef]
- Kośmider, K.; González, J.W.; Fernández-Rossier, J. Large spin splitting in the conduction band of transition metal dichalcogenide monolayers. Phys. Rev. B 2013, 88, 245436. [Google Scholar] [CrossRef]
- Van der Donck, M.; Peeters, F.M. Interlayer excitons in transition metal dichalcogenide heterostructures. Phys. Rev. B 2018, 98, 115104. [Google Scholar] [CrossRef]
- Kumar, P.; Chauhan, Y.S.; Agarwal, A.; Bhowmick, S. Thickness and Stacking Dependent Polarizability and Dielectric Constant of Graphene–Hexagonal Boron Nitride Composite Stacks. J. Phys. Chem. C 2016, 120, 17620. [Google Scholar] [CrossRef]
- Yu, F.F.; Ke, S.S.; Guan, S.S.; Deng, H.X.; Guo, Y.; Lü, H.F. Effects of Se substitution and transition metal doping on the electronic and magnetic properties of a MoSxSe2-x/h-BN heterostructure. Phys. Chem. Chem. Phys. 2019, 21, 20073. [Google Scholar] [CrossRef] [PubMed]
- Gerber, I.C.; Marie, X. Dependence of band structure and exciton properties of encapsulated WSe2 monolayers on the hBN-layer thickness. Phys. Rev. B 2018, 98, 245126. [Google Scholar] [CrossRef]
- Shanenko, A.A.; Aguiar, J.A.; Vagov, A.; Croitoru, M.D.; Milošević, M.V. Atomically flat superconducting nanofilms: Multiband properties and mean-field theory. Supercond. Sci. Tech. 2015, 28, 054001. [Google Scholar] [CrossRef]
- Vargas-Paredes, A.A.; Shanenko, A.A.; Vagov, A.; Milošević, M.V.; Perali, A. Cross-band versus intra-band pairing in superconductors: Signatures and consequences of the interplay. arXiv 2019, arXiv:1906.06528. [Google Scholar]
- Lozovik, Y.E.; Sokolik, A.A. Multi-band pairing of ultrarelativistic electrons and holes in graphene bilayer. Phys. Rev. A 2009, 374, 326. [Google Scholar] [CrossRef]
- Kochorbe, F.G.; Palistrant, M.E. Superconductivity in a two-band system with low carrier density. J. Exp. Theor. Phys. 1993, 77, 442. [Google Scholar]
- Giorgini, S.; Pitaevskii, L.; Stringari, S. Condensate fraction and critical temperature of a trapped interacting Bose gas. Phys. Rev. A 1996, 54, 4633. [Google Scholar] [CrossRef] [PubMed]
- Salasnich, L.; Manini, N.; Parola, A. Condensate fraction of a Fermi gas in the BCS-BEC crossover. Phys. Rev. A 2005, 72, 023621. [Google Scholar] [CrossRef]
- Benfatto, L.; Capone, M.; Caprara, S.; Castellani, C.; Di Castro, C. Multiple gaps and superfluid density from interband pairing in a four-band model of the iron oxypnictides. Phys. Rev. B 2008, 78, 140502. [Google Scholar] [CrossRef]
- Botelho, S.S.; Sá de Melo, C.A.R. Vortex-Antivortex Lattice in Ultracold Fermionic Gases. Phys. Rev. Lett. 2006, 96, 040404. [Google Scholar] [CrossRef] [PubMed]
| () | () | (eV) | (nm) | (nm) | (K) | (K) | |||
|---|---|---|---|---|---|---|---|---|---|
| DQW | 0.067 | 0.3 | 1.5 | 15 [5] | 25 [2,3] | <0.7 [5] | − | ∼1 [5] | − |
| DMG | 0 | 0 | 0 | 1.0 [11] | 1.0 [12] | − | − | − | − |
| DBG | 0.04 | 0.04 | ≤0.25 | 1.4 [14,16] | 1.4 [15] | 7.0 [16] | 8.0 [15] | 17 [14] | 1.5 [15] |
| TMD | 0.3–0.5 | 0.4–0.6 | 1.5–2.0 | 1.0 [21] | 1.0 [22] | 150 [21] | 10 [22] | ≳100 [21] | 100 [22] |
| (a) | p-MoS | p-MoSe | p-WS | p-WSe | (b) | p-MoS | p-MoSe | p-WS | p-WSe |
|---|---|---|---|---|---|---|---|---|---|
| n-MoS | 249 | 228 | −37 | −69 | n-MoS | 396 | 405 | 390 | 388 |
| n-MoSe | 276 | 253 | −9 | −49 | n-MoSe | 405 | 412 | 400 | 390 |
| n-WS | 252 | 232 | −28 | −65 | n-WS | 375 | 385 | 375 | 368 |
| n-WSe | 260 | 233 | −24 | −57 | n-WSe | 372 | 375 | 368 | 365 |
| () | () | (eV) | (eV) | (eV) | |
|---|---|---|---|---|---|
| MoS | 0.40 | 0.48 | 1.66 | −0.003 | 0.15 |
| MoSe | 0.43 | 0.50 | 1.47 | −0.021 | 0.18 |
| WS | 0.33 | 0.30 | 1.79 | 0.027 | 0.43 |
| WSe | 0.36 | 0.30 | 1.60 | 0.038 | 0.46 |
| Masses Ratio | [0pt]Effective Masses | [0pt]Valence Band Screening | [0pt]Multicomponent Superfluidity | |
|---|---|---|---|---|
| DQW | 10 | 0.07 − 0.3 | no | no |
| DMG | 0 | yes | no superfluidity | |
| DBG | 0.04 | yes | no | |
| TMD | 1.3 | 0.4 − 0.5 | no | yes |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Conti, S.; Neilson, D.; Peeters, F.M.; Perali, A. Transition Metal Dichalcogenides as Strategy for High Temperature Electron-Hole Superfluidity. Condens. Matter 2020, 5, 22. https://doi.org/10.3390/condmat5010022
Conti S, Neilson D, Peeters FM, Perali A. Transition Metal Dichalcogenides as Strategy for High Temperature Electron-Hole Superfluidity. Condensed Matter. 2020; 5(1):22. https://doi.org/10.3390/condmat5010022
Chicago/Turabian StyleConti, Sara, David Neilson, François M. Peeters, and Andrea Perali. 2020. "Transition Metal Dichalcogenides as Strategy for High Temperature Electron-Hole Superfluidity" Condensed Matter 5, no. 1: 22. https://doi.org/10.3390/condmat5010022
APA StyleConti, S., Neilson, D., Peeters, F. M., & Perali, A. (2020). Transition Metal Dichalcogenides as Strategy for High Temperature Electron-Hole Superfluidity. Condensed Matter, 5(1), 22. https://doi.org/10.3390/condmat5010022






