Abstract
We have investigated the Pb-substitution effect upon the superconductivity of NaCl-type In1−xPbxTe. Polycrystalline samples with x = 0–0.8 were synthesized using high-pressure synthesis. The lattice parameter was systematically increased by Pb substitution. For x ≤ 0.6, bulk superconductivity was observed, and the superconducting transition temperature increased from 3 K (for InTe) to 5 K by Pb substitutions. From analyses of specific heat jumps at the superconducting transition, conventional (phonon-mediated) weak-coupling pairing mechanisms were suggested for In1−xPbxTe.
1. Introduction
Metal chalcogenides have drawn great attention in the research community of superconductivity, because of the observation of high transition temperature (Tc) and unconventional pairing mechanisms in those materials [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. Particularly, SnTe has been extensively studied, because it is a topological crystalline insulator [15], and shows superconductivity when the Sn site was substituted by In or Ag [8,9,10,11,12,13,14]. Although non-doped SnTe also shows superconductivity below 0.3 K [16], hole doping effectively increases Tc to 4.8 K in the In-substituted system [8,9,10,11,12], and to 2.4 K in the Ag-substituted system [13,14]. In addition, possible topological superconductivity has been proposed for the Sn1−xInxTe system [15,17]. Due to these findings, Sn1−xInxTe has been one of hot-topic materials in the superconductivity community. Recently, superconductivity in the In-rich phases of Sn1−xInxTe has been reported [18,19]. The solubility limit of In for the Sn site can be extended to x = 1.0 using high-pressure synthesis [18,19]. Interestingly, the sample with x = 1.0 (pure InTe) with a NaCl-type structure also shows superconductivity (Tc ~ 3 K). As shown in Figure 1a,b, InTe exhibits a pressure-induced structural transition from a TlSe-type to the NaCl-type structure. Although In+ and In3+ occupy different sites in the TlSe-type structure (low-pressure phase), this In occupies a single site in the NaCl-type structure (high-pressure phase). Namely, the valence states of In within the NaCl-type InTe can be regarded as the valence-skipping state of In+ and In3+ [19].
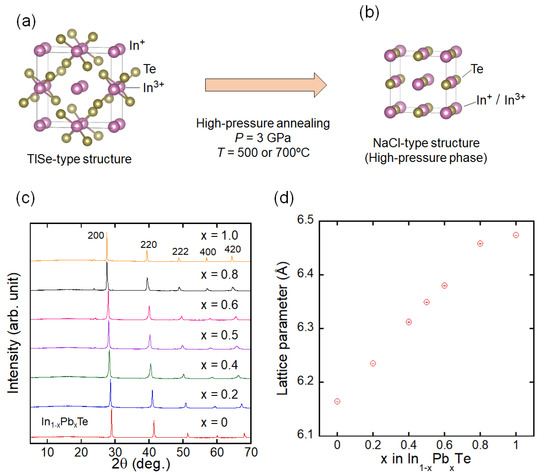
Figure 1.
(a,b) Schematic images of crystal structure of InTe: (a) ambient-pressure phase with a TlSe-type structure and (b) high-pressure phase with a NaCl-type structure. (c) Powder X-ray diffraction patterns for In1−xPbxTe. Numbers in this figure are Miller indices. (d) Pb concentration (x) dependence of lattice parameter of a for In1−xPbxTe.
The relationship between valence-skipping states and superconductivity has been typically investigated in Bi-based oxide BaBiO3 [20,21] and Tl-doped PbTe (Pb1−xTlxTe) [22] (See Table 1). In BaBiO3, Bi valence is considered as the valence-skipping state of Bi3+ and Bi5+, and the non-doped phase is an insulator with a perovskite-derived structure. Superconductivity is induced by K doping, and a high Tc ~ 30 K has been observed. In Pb1−xTlxTe, a small amount of Tl was doped for the Pb site in PbTe, which is an n-type semiconductor with an NaCl-type structure. Although the carrier doping amount in Pb1−xTlxTe is quite small, a superconducting transition with a Tc higher than 1 K has been observed, which cannot be explained with conventional electron-phonon pairing. Therefore, InTe and In-doped PbTe (In1−xPbxTe), which are the target phases of this study, are good systems for investigating the relationship between valence skipping and superconductivity.

Table 1.
Comparison of crystal structure, valence states, and physical properties of Ba1−xKxBiO3, Pb1−xTlxTe and In1−xPbxTe.
In this study, we have investigated the effect of Pb substitution on the superconductivity in In1−xPbxTe. In a previous study, the solubility limit of In for the Pb site was reported to be 24% when the materials were synthesized under ambient pressure [23]. This solubility limit can be expanded to the end (InTe, x = 1) by utilizing high-pressure synthesis. We observed an increase in Tc by Pb substitution, and established a superconductivity phase diagram. Possible mechanisms for the superconductivity of In1−xPbxTe have been discussed.
2. Results
Powder X-ray diffraction (XRD) patterns for In1−xPbxTe are shown in Figure 1c. The XRD peak position shifts toward lower angles by Pb substitution, which indicates a lattice expansion by Pb substitution. The XRD patterns were refined using a cubic NaCl-type model (Fm-3m, #225, Oh5) by Rietveld refinement with the RIETAN-FP software [24]. Lattice parameters obtained from refinements are plotted in Figure 1d as a function of Pb concentration x. The lattice parameter monotonically increases with increasing Pb concentration.
Figure 2a shows the temperature dependences of magnetic susceptibility for x = 0–0.8 measured after both zero-field cooling (ZFC) and field cooling (FC). Note that PbTe (x = 1.0) is a narrow-gap semiconductor for this sample, and does not show a superconducting transition. For all the samples, superconducting (diamagnetic) signals were observed, and a large shielding volume fraction was observed for x = 0–0.8. Although we cannot estimate the fraction with demagnetization correction due to the fragile nature of the high-pressure-synthesized sample, the largest shielding fraction is ~180% for x = 0, and the smallest shielding fraction exceeds 130% for x = 0.8. From the temperature dependences of magnetic susceptibility, a Tc (M: magnetic) was estimated as the temperature where a 1% shielding fraction (the dashed line in Figure 2b) is achieved. Tc increases with increasing x up to x = 0.6, while Tc is almost saturated for higher x. The highest Tc of 5.1 K is obtained for x = 0.6, but those for x = 0.4–0.8 are comparable to that for x = 0.6.
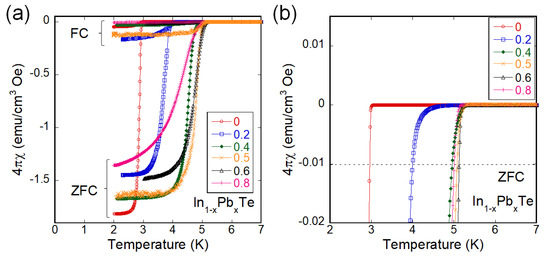
Figure 2.
(a) Temperature dependences of magnetic susceptibility 4πχ for In1−xPbxTe. (b) Zoomed plot of the temperature dependences of magnetic susceptibility. The dashed line indicates 1% shielding line in the zero-field cooling (ZFC) data, which was used for estimation of magnetic Tc (M).
Figure 3a shows the temperature dependences of electrical resistivity for x = 0–1.0. In addition, PbTe (x = 1.0) exhibits a semiconducting behavior. For x = 0.8, the insulating behavior of pure PbTe is suppressed, and the temperature dependence becomes almost temperature-independent. With an increasing In concentration (with decreasing x), electrical resistivity decreases, and metallic conductivity is induced. The trend of the temperature dependence of electrical resistivity for PbTe is consistent with a previous study [25]. A zoomed figure for low-temperature resistivity data is displayed in Figure 3b. Zero-resistivity states were observed for all the superconducting samples.
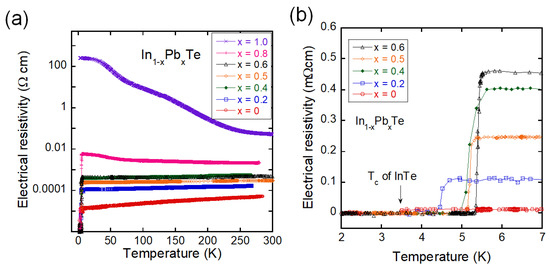
Figure 3.
(a) Temperature dependences of electrical resistivity for In1−xPbxTe. (b) Low-temperature data of the temperature dependences of electrical resistivity for In1−xPbxTe.
To investigate the superconducting properties of In1−xPbxTe under magnetic fields, electrical resistivity was measured under various magnetic fields. Figure 4a shows the temperature dependences of electrical resistivity for x = 0.4 under magnetic fields up to 3.0 T. To obtain an upper critical field (μ0Hc2) phase diagram, Tc was estimated as the temperature where the resistivity becomes 80% of normal state resistivity near Tconset. The Hc2-temperature data were analyzed by the Werthamer–Helfand–Hohemberg (WHH) model [26], as shown in Figure 4b, and the estimated μ0Hc2 (T = 0 K) was 3.1 T. This value is clearly lower than that expected from the Pauli limit: μ0HPauli = 1.85*Tc.
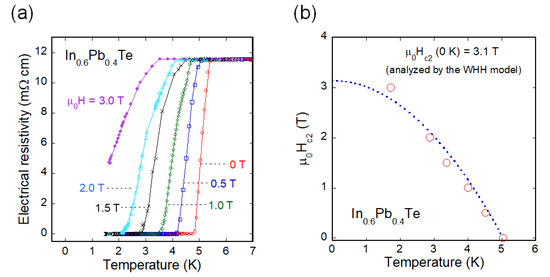
Figure 4.
(a) Temperature dependences of electrical resistivity for x = 0.4 under magnetic fields of 0–3 T. (b) Temperature dependence of μ0Hc2 for x = 0.4 where Tc was estimated as the temperature where the resistivity becomes 80% of normal state resistivity just above Tconset. The dashed line is the fitting result by the Werthamer–Helfand–Hohemberg (WHH) model.
In Figure 5, results of specific heat (C) experiments for x = 0.2, 0.4 and 0.6 are summarized. As shown in Figure 5a–c, which display the temperature dependences of C/T under 0 and 5 T, a clear specific-heat jump of a superconducting transition (ΔCSC) was observed at Tc. Figure 5d–f show the electronic contributions of specific heat (Cel), which was calculated by subtracting phonon contributions from the total specific heat. The phonon contributions were estimated using a formula of low-temperature specific heat: C (T) = γT + A1T3 + A2T5, where A1T3 + A2T5 describes the phonon contributions at low temperatures. From the temperature dependences of Cel/T, ΔCSC/γTc was estimated as 1.3, 1.4 and 1.3 for x = 0.2, 0.4 and 0.6. The ΔCSC/γTc values are consistent with ΔCSC/γTc = 1.43, which is expected from conventional (phonon-mediated) weak-coupling pairing [27]. Here, we regard a sample showing ΔCSC/γTc close to 1.43 as a bulk superconductor. Therefore, the superconductivity observed in x = 0.2, 0.4 and 0.6 is bulk in nature. We notice that the superconducting transition for x = 0.2 is relatively broad. Although the origin of this broad transition is unclear, compositional inhomogeneity may be locally present, while the XRD profile for x = 0.2 is comparably sharp as other samples. The γ values estimated in the analyses will be used for discussion later.
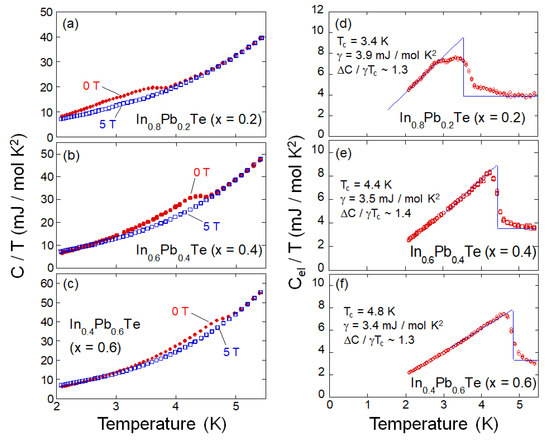
Figure 5.
(a–c) Temperature dependences of C/T measured at 0 and 5 T for x = 0.2, 0.4 and 0.6. (d–f) Temperature dependences of electronic specific heat Cel/T measured under 0 T for x = 0.2, 0.4 and 0.6.
For x = 0.8, no clear specific-heat jump was observed, as shown in Figure 6a. To investigate the nature of superconductivity for x = 0.8, the specific heat difference (ΔC) was calculated from ΔC = C (0 T) − C (5 T), and plotted as a function of temperature in Figure 6b. Although a clear superconducting jump was not observed in the temperature dependence of C/T, a superconducting transition was observed below 4.9 K. Due to small γ, ΔCSC is not clear, but the value of ΔCSC/γTc is roughly 0.8. Although the ΔCSC/γTc value is obviously lower than that expected from the conventional model, the characteristics of the superconductivity for x = 0.8 is different from so-called filamentary superconductivity, where no superconducting transitions can be detected in specific heat measurements.
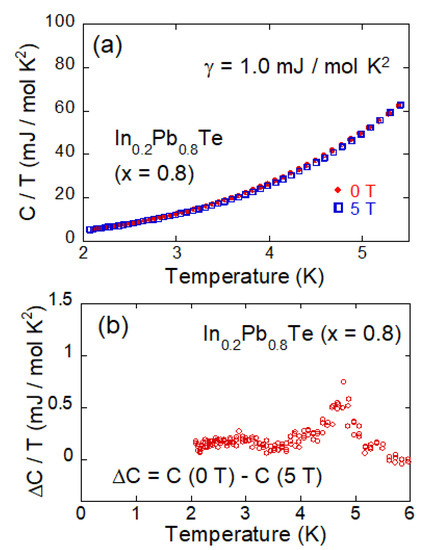
Figure 6.
(a) Temperature dependences of C/T measured at 0 and 5 T for x = 0.8. (b) Temperature dependences of specific heat jump ΔC/T for x = 0.8: ΔC was calculated by subtracting C (5 T) from C (0 T).
Thus, on the basis of the results of magnetic susceptibility, electrical resistivity and specific heat, we consider that the composition of x = 0.8 is located near the boundary between bulk and non-bulk superconductivity. This scenario is consistent with the previous report for x = 0.24 [23] (ambient-pressure sample), which showed the absence of superconductivity.
To obtain information about carrier type and carrier concentration, the x dependence of the Seebeck coefficient at room temperature was measured for In1−xPbxTe (Figure 7). The large negative Seebeck coefficient of −342 μV/K for x = 1 (PbTe) is originated from its nature as an n-type semiconductor. By In substitution, the absolute value of this Seebeck coefficient becomes very small and positive in sign, even for x = 0.8. This suggests that only 20% substitution of In for the Pb site can generate large amount of hole carriers, because of the relationship between the carrier concentration and Seebeck coefficient (S) in metal [28]:
where kB is the Boltzmann constant, m* is the effective mass of the carrier, e is the elementary charge, h is the Planck constant and n is the carrier concentration.
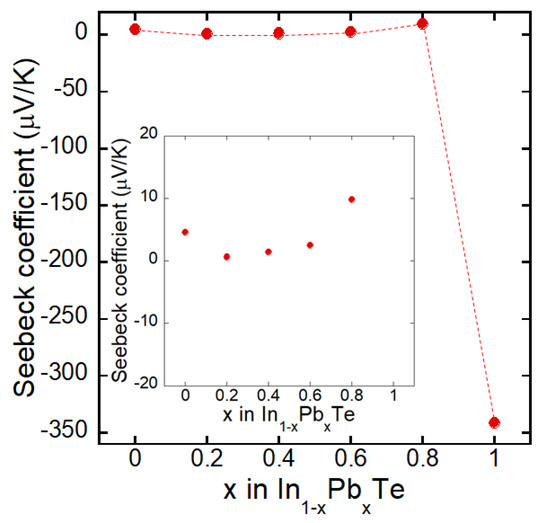
Figure 7.
Pb concentration (x) dependence of the Seebeck coefficient for In1−xPbxTe. The inset shows a zoomed plot for x = 0–0.8.
To further discuss about the evolution of carrier concentration by Pb substitution, γ estimated from specific heat analyses is plotted as a function of x in Figure 8. This γ is the highest for x = 0 (InTe) [18], and decreases with increasing Pb concentration. This suggests that the carrier concentration increases with increasing In concentration in In1−xPbxTe. The transition temperature, however, decreases with increasing In concentration. Since γ is represented as a function of the density of states, this trend is contrasted to what is expected from conventional pairing mechanisms [27], in which a larger γ achieves a higher Tc. Hence, the superconductivity pairing mechanisms of In1−xPbxTe may not be fully explained by the conventional model only.
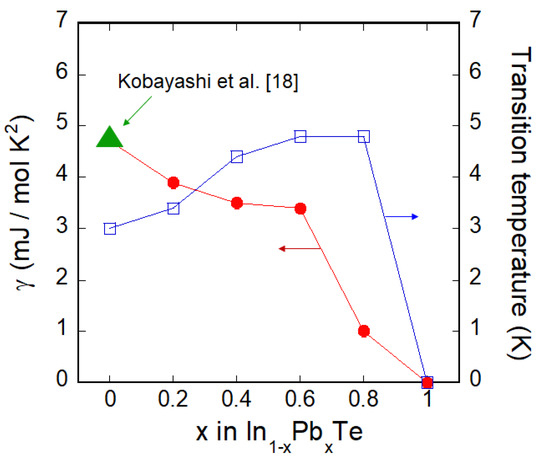
Figure 8.
Pb concentration dependence of γ (electronic-specific-heat parameter) and Tc estimated from specific heat analyses for In1−xPbxTe. γ = 0 was assumed for semiconducting PbTe (x = 0).
3. Discussion
In this article, we reported that Tc of NaCl-type InTe (Tc ~ 3 K) can be increased to 5 K by Pb substitution for the In site. We confirmed the bulk nature of superconductivity for 0 ≤ x ≤ 0.6. The Tcs estimated from magnetic susceptibility (Tc (M)), electrical resistivity (Tc (ρ)) and specific heat (Tc (C)) are plotted in a superconductivity phase diagram (Figure 9). For 0 ≤ x ≤ 0.6, Tc increases with increasing x, and reaches the highest at x = 0.6. However, the sample with x = 0.8 also shows a comparable Tc. As mentioned above, the sample (x = 0.8) may be located in the vicinity of bulk-superconducting (bulk SC) and non-bulk superconductivity phases. Therefore, Tc may contentiously increase with increasing Pb concentration up to the boundary where superconductivity is induced.
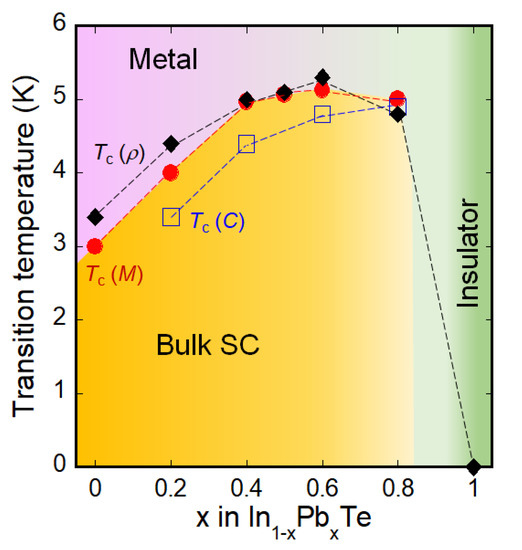
Figure 9.
Superconductivity phase diagram for In1−xPbxTe. Tc (M), Tc (ρ), and Tc (C) denote Tcs estimated from magnetic susceptibility, electrical resistivity, and specific heat, respectively.
Although we have not analyzed the pairing mechanisms of In1−xPbxTe so far, we briefly discuss about the possible mechanisms of superconductivity in this system. From specific heat analyses (specific heat jumps at Tc), the conventional phonon-mediated BCS model [27] seems reasonable. The conventional scenario is also consistent with the estimated upper critical field lower than the Pauli limit. However, the relationship between carrier concentration and Tc seems not consistent with the conventional scenario. The inconsistency may be caused by the presence of valence skipping states of In in NaCl-type InTe. As in Pb1−xTlxTe [29], the valence skipping states of In may affect the evolution of superconductivity in In1−xPbxTe. To further clarify that, further experiments sensitive to valence skipping states and local structures, like X-ray absorption spectroscopy and theoretical investigations, are needed.
In conclusion, we have investigated the Pb-substitution effects on crystal structure and normal-state, and the superconducting properties of NaCl-type In1−xPbxTe. Polycrystalline samples with x = 0–0.8 were synthesized using high-pressure synthesis. The lattice parameter systematically increased by Pb substitution. For x ≤ 0.6, bulk superconductivity was observed, and the superconducting Tc increased from 3 K (for InTe) to 5 K by Pb substitutions. From the resistivity measurements under magnetic fields, the upper critical field μ0Hc2 (0 K) was estimated as 3.1 T for x = 0.4. From analyses of the specific heat jump at Tc, conventional (phonon-mediated) weak-coupling pairing mechanisms were suggested for In1−xPbxTe. However, the relationship between γ and Tc estimated from specific heat analyses does not satisfy the prediction of conventional pairing mechanisms. To understand the mechanisms of superconductivity in In1−xPbxTe, investigation on the valence-skipping states would be needed.
4. Materials and Methods
Polycrystalline powders of In1−xPbxTe were prepared by melting a mixture of In (99.99%), Pb (99.9%), and Te (99.999%) grains with a nominal composition of In1−xPbxTe. The mixture was sealed in an evacuated quartz tube and heated at 800 ºC for 10 h. The obtained sample was ground and pelletized into a pellet with a diameter of 5 mm. The pellet was placed in a high-pressure cell, which is composed of a BN sample capsule, a carbon heater capsule, electrodes, and a pyrophyllite cubic cell. The high-pressure synthesis was performed using 180 ton cubic-anvil-type system (CT factory). The pressure used for the high-pressure synthesis was 3 GPa, and the heating temperature was 700 °C for x = 0 and 500 °C for x = 0.2–0.8. The PbTe (x = 1.0) sample was prepared by melting in an evacuated quartz tube without carrying out high-pressure synthesis.
Powder X-ray diffraction (XRD) was performed by the θ-2θ method using MiniFlex600-D/tex-Ultra (RIGAKU) with a CuKα radiation. The crystal structure parameters were refined using the Rietveld method with RIETAN-FP [24]. The crystal structure image was depicted using VESTA [30].
The temperature dependence of magnetic susceptibility was measured using a superconducting quantum interference device (SQUID) magnetometer (MPMS-3, Quantum Design, San Diego, CA, USA) with a typical applied field of 10 Oe after zero-field cooling (ZFC) and field cooling (FC). Electrical resistivity measurements were performed on cryostat (GM refrigerator) equipped with a superconducting magnet (designed by AXIS, Tsukuba, Japan). The temperature dependence of electrical resistivity was measured by a four-terminal method. Au wires with a diameter of 25 μm were attached on the polished surface of the samples by using Ag pastes. A typical current of 1 mA was used for the resistivity measurements. The temperature dependence of specific heat was measured by a relaxation method on the Physical Property Measurement System (PPMS, Quantum Design, San Diego, CA, USA) under 0 and 5 T. The Seebeck coefficient was obtained from the linear slope of the thermo-electromotive force (∆V) versus the temperature difference (∆T) plots.
Author Contributions
Conceptualization, Y.M.; methodology, M.K.; R.J.; K.H.; R.S.; Y.G. and Y.M.; validation, M.K. and Y.M.; formal analysis, Y.M.; investigation, M.K.; R.J.; K.H.; R.S.; Y.G. and Y.M.; resources, Y.G. and Y.M.; data curation, M.K. and Y.M.; writing—original draft preparation, Y.M.; writing—review and editing, Y.M.; visualization, M.K.; R.J. and Y.M.; supervision, Y.G. and Y.M.; project administration, Y.M.; funding acquisition, Y.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partly supported by Grants-in-Aid for Scientific Research by JSPS (Nos. 15H05886, 19K15291, and 18KK0076) and Advanced Research Program under the Human Resources Funds of Tokyo (H31-1).
Acknowledgments
The authors thank Hase, I. and Kobayashi, K. for fruitful discussion.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hsu, F.C.; Luo, J.Y.; Yeh, K.W.; Chen, T.K.; Huang, T.W.; Wu, P.M.; Lee, Y.C.; Huang, Y.L.; Chu, Y.Y.; Yan, D.C.; et al. Superconductivity in the PbO-type structure α-FeSe. Proc. Natl. Acad. Sci. USA 2008, 105, 14262. [Google Scholar] [CrossRef] [PubMed]
- Mizuguchi, Y.; Takano, Y. Review of Fe chalcogenides as the simplest Fe-based superconductor. J. Phys. Soc. Jpn. 2010, 79, 102001. [Google Scholar] [CrossRef]
- Hor, Y.S.; Williams, A.J.; Checkelsky, J.G.; Roushan, P.; Seo, J.; Xu, Q.; Zandbergen, H.W.; Yazdani, A.; Ong, N.P.; Cava, R.J. Superconductivity in CuxBi2Se3 and its implications for pairing in the undoped topological insulator. Phys. Rev. Lett. 2010, 104, 057001. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, S.; Kriener, M.; Segawa, K.; Yada, K.; Tanaka, Y.; Sato, M.; Ando, Y. Topological superconductivity in CuxBi2Se3. Phys. Rev. Lett. 2011, 107, 217001. [Google Scholar] [CrossRef] [PubMed]
- Mizuguchi, Y. Review of superconductivity in BiS2-based layered materials. J. Phys. Chem. Solids 2015, 84, 34. [Google Scholar] [CrossRef]
- Mizuguchi, Y. Material development and physical properties of BiS2-Based layered compounds. J. Phys. Soc. Jpn. 2019, 88, 041001. [Google Scholar] [CrossRef]
- Ren, Z.; Kriener, M.; Taskin, A.A.; Sasaki, S.; Segawa, K.; Ando, Y. Anomalous metallic state above the upper critical field of the conventional three-dimensional superconductor AgSnSe2 with strong intrinsic disorder. Phys. Rev. B 2013, 87, 064512. [Google Scholar] [CrossRef]
- Erickson, A.S.; Chu, J.H.; Toney, M.F.; Geballe, T.H.; Fisher, I.R. Enhanced superconducting pairing interaction in indium-doped tin telluride. Phys. Rev. B 2009, 79, 024520. [Google Scholar] [CrossRef]
- Balakrishnan, G.; Bawden, L.; Cavendish, S.; Lees, M.R. Superconducting properties of the In-substituted topological crystalline insulator SnTe. Phys. Rev. B 2013, 87, 140507. [Google Scholar] [CrossRef]
- Novak, M.; Sasaki, S.; Kriener, M.; Segawa, K.; Ando, Y. Unusual nature of fully gapped superconductivity in In-doped SnTe. Phys. Rev. B 2013, 88, 140502. [Google Scholar] [CrossRef]
- Zhong, R.D.; Schneeloch, J.A.; Shi, X.Y.; Xu, Z.J.; Zhang, C.; Tranquada, J.M.; Li, Q.; Gu, G.D. Optimizing the superconducting transition temperature and upper critical field of Sn1−xInxTe. Phys. Rev. B 2013, 88, 020505. [Google Scholar] [CrossRef]
- Haldolaarachchige, N.; Gibson, Q.; Xie, W.; Nielsen, M.B.; Kushwaha, S.; Cava, R.J. Anomalous composition dependence of the superconductivity in in-doped Snte. Phys. Rev. B 2016, 93, 024520. [Google Scholar] [CrossRef]
- Mizuguchi, Y.; Miura, O. High-pressure synthesis and superconductivity of ag-doped topological crystalline insulator Snte (Sn1−xAgxTe with x = 0–0.5). J. Phys. Soc. Jpn. 2016, 85, 053702. [Google Scholar] [CrossRef]
- Mizuguchi, Y.; Yamada, A.; Higashinaka, R.; Matsuda, T.D.; Aoki, Y.; Miura, O.; Nagao, M. Specific heat and electrical transport properties of Sn0.8Ag0.2Te superconductor. J. Phys. Soc. Jpn. 2016, 85, 103701. [Google Scholar] [CrossRef][Green Version]
- Ando, Y.; Fu, L. Topological crystalline insulators and topological superconductors: From concepts to materials. Annu. Rev. Condens. Matter Phys. 2015, 6, 361. [Google Scholar] [CrossRef]
- Mathur, M.P.; Deis, D.W.; Jones, C.K.; Carr, W.J., Jr. Superconductivity as a function of carrier density and magnetic spin concentration in the SnTe-MnTe system. J. Phys. Chem. Solids 1973, 34, 183. [Google Scholar] [CrossRef]
- Sato, T.; Tanaka, Y.; Nakayama, K.; Souma, S.; Takahashi, T.; Sasaki, S.; Ren, Z.; Taskin, A.A.; Segawa, K.; Ando, Y. Fermiology of the strongly spin-orbit coupled superconductor Sn1−xInxTe: Implications for topological superconductivity. Phys. Rev. Lett. 2013, 110, 206804. [Google Scholar] [CrossRef]
- Kobayashi, K.; Ai, Y.; Jeschke, H.O.; Akimitsu, J. Enhanced superconducting transition temperatures in the rocksalt-type superconductors In1−xSnxTe (x ≤ 0.5). Phys. Rev. B 2018, 97, 104511. [Google Scholar] [CrossRef]
- Kriener, M.; Kamitani, M.; Koretsune, T.; Arita, R.; Taguchi, Y.; Tokura, Y. Tailoring band structure and band filling in a simple cubic (IV, III)-VI superconductor. Phys. Rev. Mater. 2018, 2, 044802. [Google Scholar] [CrossRef]
- Sleight, A.W.; Gillson, J.L.; Bierstedt, P.E. High-temperature superconductivity in the BaPb1−xBixO3 systems. Solid State Commun. 1975, 17, 27. [Google Scholar] [CrossRef]
- Cava, R.J.; Batlogg, B.; Krajewski, J.J.; Farrow, R.; Rupp, L.W., Jr.; White, A.E.; Short, K.; Peck, W.F.; Kometani, T. Superconductivity near 30 K without copper: The Ba0.6K0.4BiO3 perovskite. Nature 1988, 332, 814. [Google Scholar] [CrossRef]
- Matsushita, Y.; Bluhm, H.; Geballe, T.H.; Fisher, I.R. Evidence for charge kondo effect in superconducting Tl-doped pbte. Phys. Rev. Lett. 2005, 94, 157002. [Google Scholar] [CrossRef] [PubMed]
- Rosenberg, A.I.; Woolley, J.C.; Nikolic, P.; Grierson, R. Solid solutions of CdTe and InTe in PbTe and SnTe. Trans. Metall. Soc. AIME 1964, 230, 342. [Google Scholar]
- Izumi, F.; Momma, K. Three-dimensional visualization in powder diffraction. Solid State Phenom. 2007, 130, 15. [Google Scholar] [CrossRef]
- Martin, J.; Nolas, G.S.; Zhang, W.; Chen, L. PbTe nanocomposites synthesized from PbTe nanocrystals. Appl. Phys. Lett. 2007, 90, 222112. [Google Scholar] [CrossRef]
- Werthamer, N.R.; Helfand, E.; Hohemberg, P.C. Temperature and purity dependence of the superconducting critical field, Hc2. III. Electron spin and spin-orbit effects. Phys. Rev. 1966, 147, 295. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105. [Google Scholar] [CrossRef]
- Hase, I.; Yanagisawa, T. Madelung energy of the valence-skipping compound BaBiO3. Phys. Rev. B 2007, 76, 174103. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).