Dispersion and Damping of Phononic Excitations in Fermi Superfluid Gases in 2D
Abstract
1. Introduction
2. Gaussian Pair Fluctuation Approximation
3. Results and Discussion
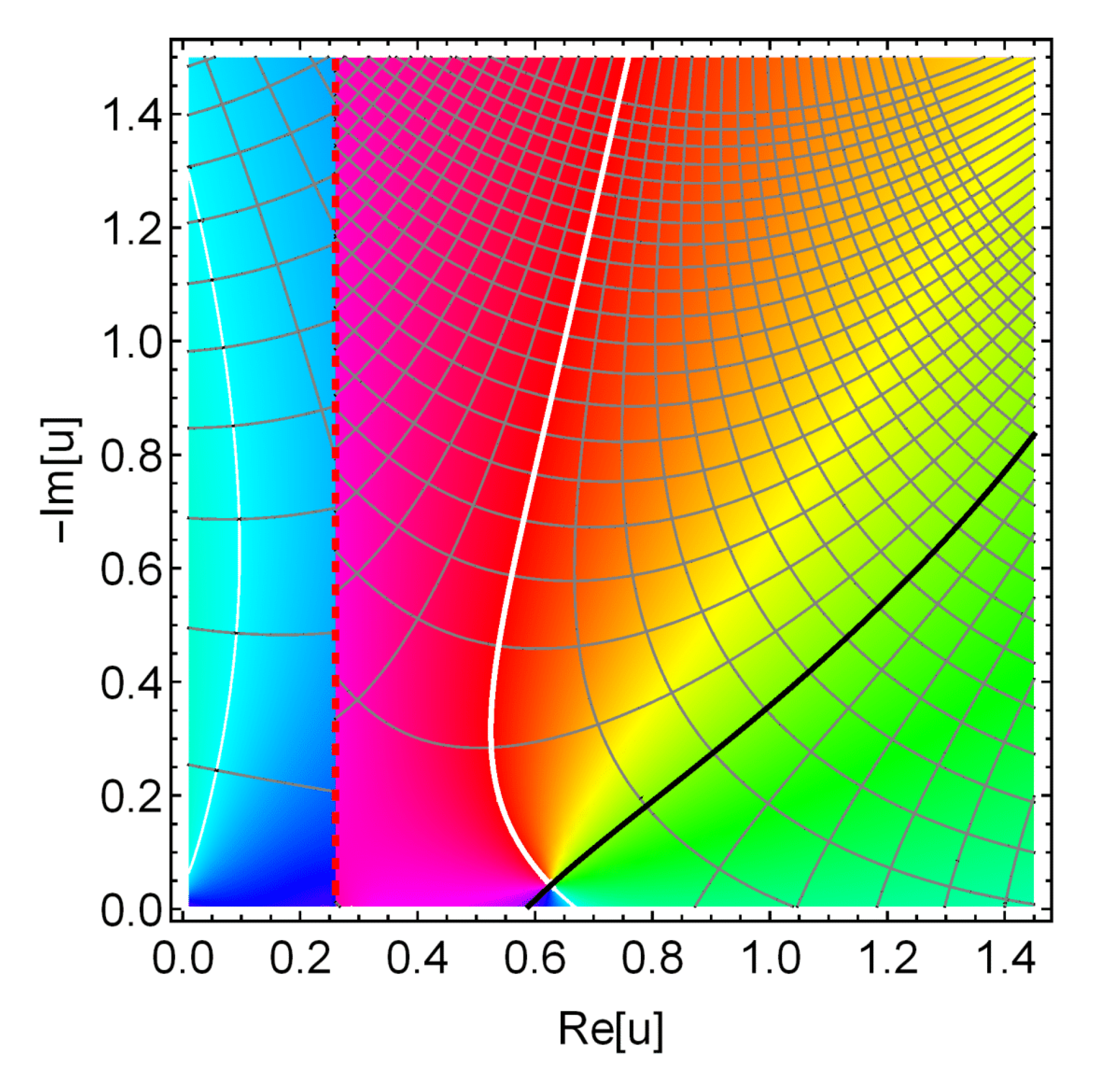
3.1. Sound Mode as Pole of the Propagator
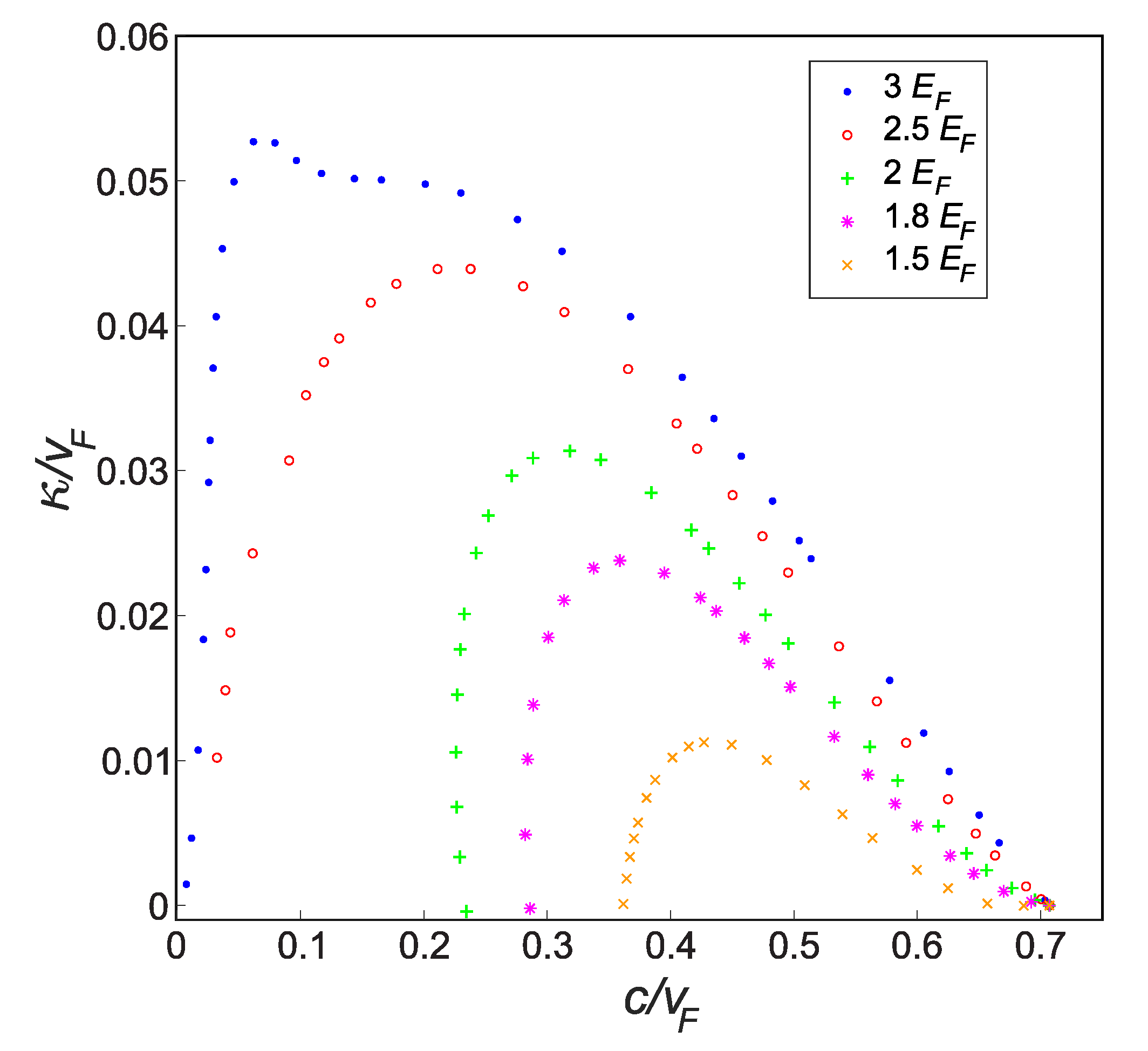
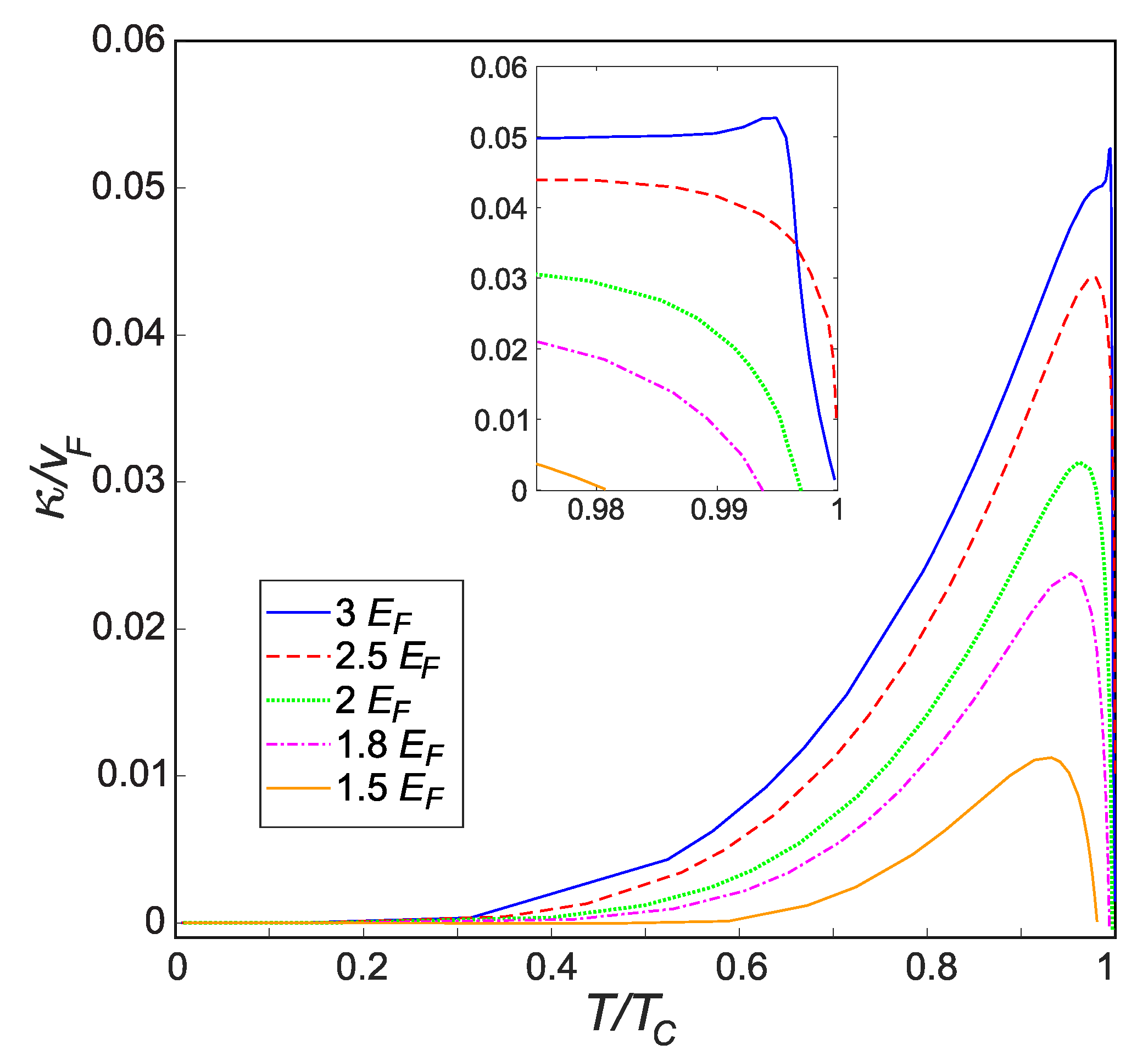
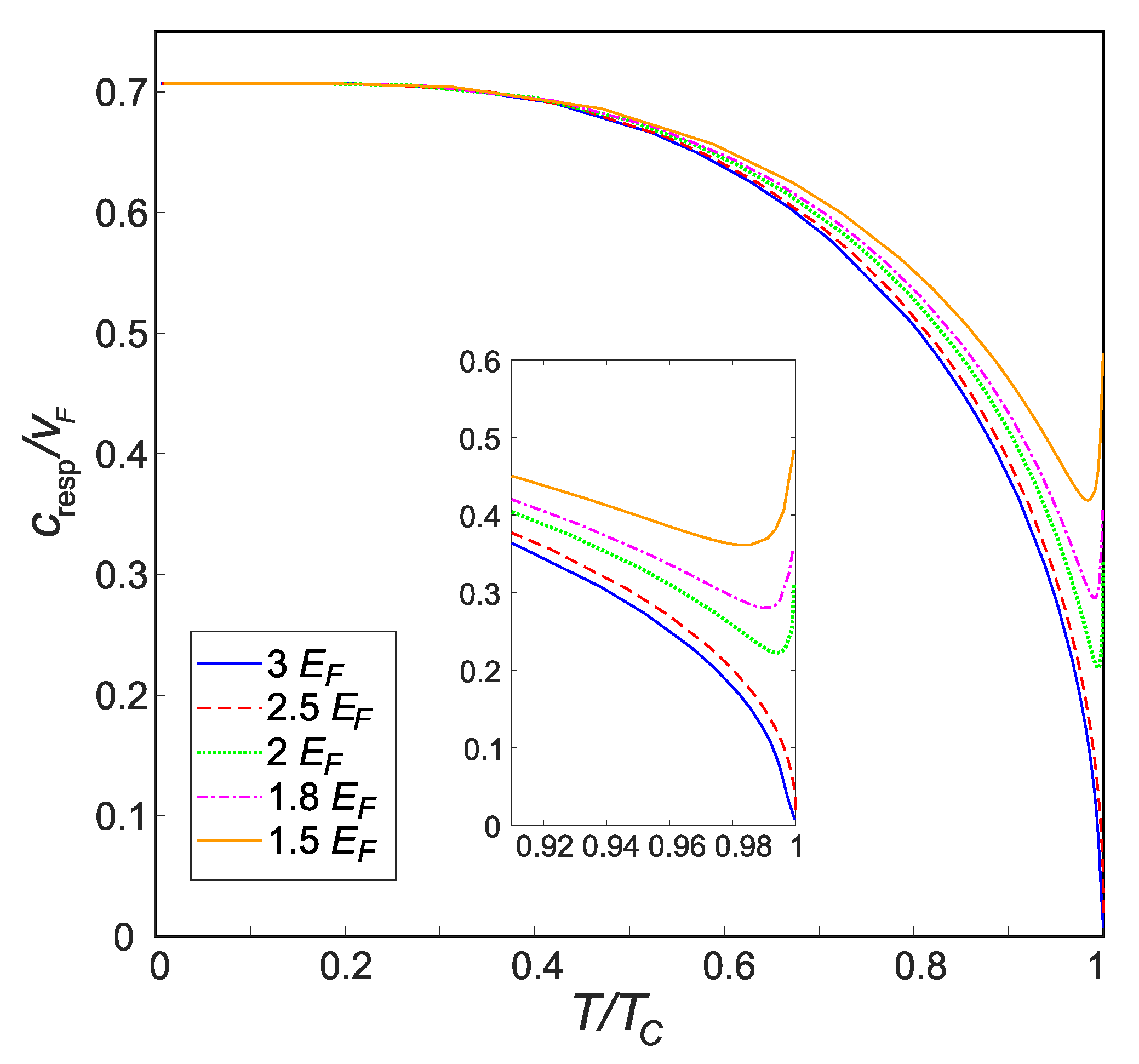
3.2. Response Function
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bartenstein, M.; Altmeyer, A.; Riedl, S.; Jochim, S.; Chin, C.; Denschlag, J.H.; Grimm, R. Collective Excitations of a Degenerate Gas at the BEC-BCS Crossover. Phys. Rev. Lett. 2004, 92, 203201. [Google Scholar] [CrossRef] [PubMed]
- Kinast, J.; Turlapov, A.; Thomas, J.E. Damping of a Unitary Fermi Gas. Phys. Rev. Lett. 2005, 94, 170404. [Google Scholar] [CrossRef] [PubMed]
- Altmeyer, A.; Riedl, S.; Kohstall, C.; Wright, M.J.; Geursen, R.; Bartenstein, M.; Chin, C.; Hecker Denschlag, J.; Grimm, R. Precision Measurements of Collective Oscillations in the BEC-BCS Crossover. Phys. Rev. Lett. 2007, 98, 040401. [Google Scholar] [CrossRef]
- Tey, M.K.; Sidorenkov, L.A.; Guajardo, E.R.S.; Grimm, R.; Ku, M.J.; Zwierlein, M.W.; Hou, Y.H.; Pitaevskii, L.; Stringari, S. Collective Modes in a Unitary Fermi Gas across the Superfluid Phase Transition. Phys. Rev. Lett. 2013, 110, 055303. [Google Scholar] [CrossRef]
- Sidorenkov, L.A.; Tey, M.K.; Grimm, R.; Hou, Y.H.; Pitaevskii, L.; Stringari, S. Second sound and the superfluid fraction in a Fermi gas with resonant interactions. Nature 2013, 498, 78. [Google Scholar] [CrossRef]
- Hoinka, S.; Dyke, P.; Lingham, M.G.; Kinnunen, J.J.; Bruun, G.M.; Vale, C.J. Goldstone mode and pair-breaking excitations in atomic Fermi superfluids. Nat. Phys. 2017, 13, 943. [Google Scholar] [CrossRef]
- Patel, P.B.; Yan, Z.; Mukherjee, B.; Fletcher, R.J.; Struck, J.; Zwierlein, M.W. Universal Sound Diffusion in a Strongly Interacting Fermi Gas. arXiv 2019, arXiv:1909.02555. [Google Scholar]
- Mukherjee, B.; Yan, Z.; Patel, P.B.; Hadzibabic, Z.; Yefsah, T.; Struck, J.; Zwierlein, M.W. Homogeneous Atomic Fermi Gases. Phys. Rev. Lett. 2017, 118, 123401. [Google Scholar] [CrossRef]
- Anderson, P.W. Random-Phase Approximation in the Theory of Superconductivity. Phys. Rev. 1958, 112, 1900. [Google Scholar] [CrossRef]
- Ohashi, Y.; Griffin, A. Superfluidity and collective modes in a uniform gas of Fermi atoms with a Feshbach resonance. Phys. Rev. A 2003, 67, 063612. [Google Scholar] [CrossRef]
- Combescot, R.; Kagan, M.Y.; Stringari, S. Collective mode of homogeneous superfluid Fermi gases in the BEC-BCS crossover. Phys. Rev. A 2006, 74, 042717. [Google Scholar] [CrossRef]
- Kurkjian, H.; Klimin, S.N.; Tempere, J.; Castin, Y. Pair-Breaking Collective Branch in BCS Superconductors and Superfluid Fermi Gases. Phys. Rev. Lett. 2019, 122, 093403. [Google Scholar] [CrossRef] [PubMed]
- Klimin, S.N.; Tempere, J.; Kurkjian, H. Phononic collective excitations in superfluid Fermi gases at nonzero temperatures. Phys. Rev. A 2019, 100, 063634. [Google Scholar] [CrossRef]
- Klimin, S.N.; Kurkjian, H.; Tempere, J. Leggett collective excitations in a two-band Fermi superfluid at finite temperatures. New J. Phys. 2019, 21, 113043. [Google Scholar] [CrossRef]
- De Melo, C.S.; Randeria, M.; Engelbrecht, J.R. Crossover from BCS to Bose superconductivity: Transition temperature and time-dependent Ginzburg-Landau theory. Phys. Rev. Lett. 1993, 71, 3202. [Google Scholar] [CrossRef] [PubMed]
- Engelbrecht, J.R.; Randeria, M.; Melo, C.S. BCS to Bose crossover: Broken-symmetry state. Phys. Rev. B 1997, 55, 15153. [Google Scholar] [CrossRef]
- Diener, R.B.; Sensarma, R.; Randeria, M. Quantum fluctuations in the superfluid state of the BCS-BEC crossover. Phys. Rev. A 2008, 77, 023626. [Google Scholar] [CrossRef]
- Adhikari, S.K.; Salasnich, L. Superfluid Bose-Fermi mixture from weak coupling to unitarity. Phys. Rev. A 2008, 78, 043616. [Google Scholar] [CrossRef]
- Gautam, S.; Adhikari, S.K. Weak coupling to unitarity crossover in Bose-Fermi mixtures: Mixing-demixing transition and spontaneous symmetry breaking in trapped systems. Phys. Rev. A 2019, 100, 023626. [Google Scholar] [CrossRef]
- Klimin, S.N.; Tempere, J.; Devreese, J.T.; Van Schaeybroeck, B. Collective modes of an imbalanced trapped Fermi gas in two dimensions at finite temperatures. Phys. Rev. A 2011, 83, 063636. [Google Scholar] [CrossRef]
- Feynman, R.P.; Hibbs, A.R.; Styer, D.F. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Randeria, M.; Duan, J.M.; Shieh, L.Y. Superconductivity in a two-dimensional Fermi gas: Evolution from Cooper pairing to Bose condensation. Phys. Rev. B 1990, 41, 327. [Google Scholar] [CrossRef] [PubMed]
- Hubbard, J. Calculation of Partition Functions. Phys. Rev. Lett. 1959, 3, 77. [Google Scholar] [CrossRef]
- Stratonovich, R.L. On a method of calculating quantum distribution functions. In Soviet Physics Doklady; American Institute of Physics: College Park, MD, USA, 1957; Volume 2, p. 416. [Google Scholar]
- Tempere, J.; Devreese, J.P. Path-Integral Description of Cooper Pairing. In Superconductors—Materials, Properties and Applications; Gabovich, A., Ed.; Institute of Physics: London, UK, 2012. [Google Scholar] [CrossRef]
- Nozières, P. Le problème à N corps: Propriétés générales des gaz de fermions; Dunod: Paris, France, 1963. [Google Scholar]
- Marini, M.; Pistolesi, F.; Strinati, G.C. Evolution from BCS superconductivity to Bose condensation: Analytic results for the crossover in three dimensions. Eur. Phys. J. B 1998, 1, 151. [Google Scholar] [CrossRef]
- Salasnich, L.; Marchetti, P.A.; Toigo, F. Superfluidity, sound velocity, and quasicondensation in the two-dimensional BCS-BEC crossover. Phys. Rev. A 2013, 88, 053612. [Google Scholar] [CrossRef]
- Bighin, G.; Salasnich, L. Finite-temperature quantum fluctuations in two-dimensional Fermi superfluids. Phys. Rev. B 2016, 93, 014519. [Google Scholar] [CrossRef]
- Chan, C.K.; Wu, C.; Lee, W.C.; Sarma, S.D. Anisotropic-Fermi-liquid theory of ultracold fermionic polar molecules: Landau parameters and collective modes. Phys. Rev. A 2010, 81, 023602. [Google Scholar] [CrossRef]
- Mulkerin, B.C.; Liu, X.J.; Hu, H. Leggett mode in a two-component Fermi gas with dipolar interactions. Phys. Rev. A 2019, 99, 023626. [Google Scholar] [CrossRef]
- Veljić, V.; Pelster, A.; Balaž, A. Stability of quantum degenerate Fermi gases of tilted polar molecules. Phys. Rev. Res. 2019, 1, 012009. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lumbeeck, L.-P.; Tempere, J.; Klimin, S. Dispersion and Damping of Phononic Excitations in Fermi Superfluid Gases in 2D. Condens. Matter 2020, 5, 13. https://doi.org/10.3390/condmat5010013
Lumbeeck L-P, Tempere J, Klimin S. Dispersion and Damping of Phononic Excitations in Fermi Superfluid Gases in 2D. Condensed Matter. 2020; 5(1):13. https://doi.org/10.3390/condmat5010013
Chicago/Turabian StyleLumbeeck, Lars-Paul, Jacques Tempere, and Serghei Klimin. 2020. "Dispersion and Damping of Phononic Excitations in Fermi Superfluid Gases in 2D" Condensed Matter 5, no. 1: 13. https://doi.org/10.3390/condmat5010013
APA StyleLumbeeck, L.-P., Tempere, J., & Klimin, S. (2020). Dispersion and Damping of Phononic Excitations in Fermi Superfluid Gases in 2D. Condensed Matter, 5(1), 13. https://doi.org/10.3390/condmat5010013





