Multi-Band Superconductivity and the Steep Band/Flat Band Scenario
Abstract
:1. Introduction
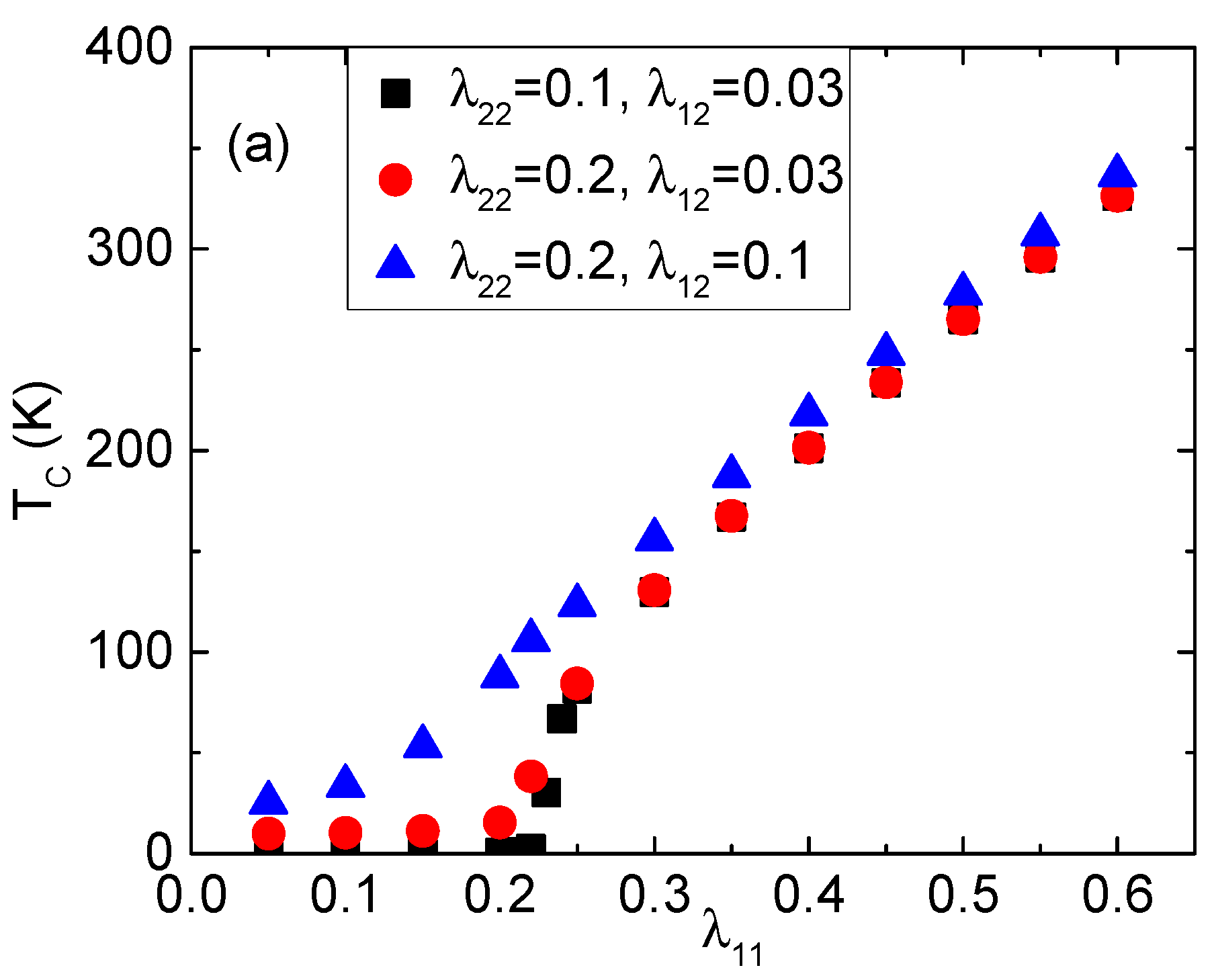
2. The Two-Band Model
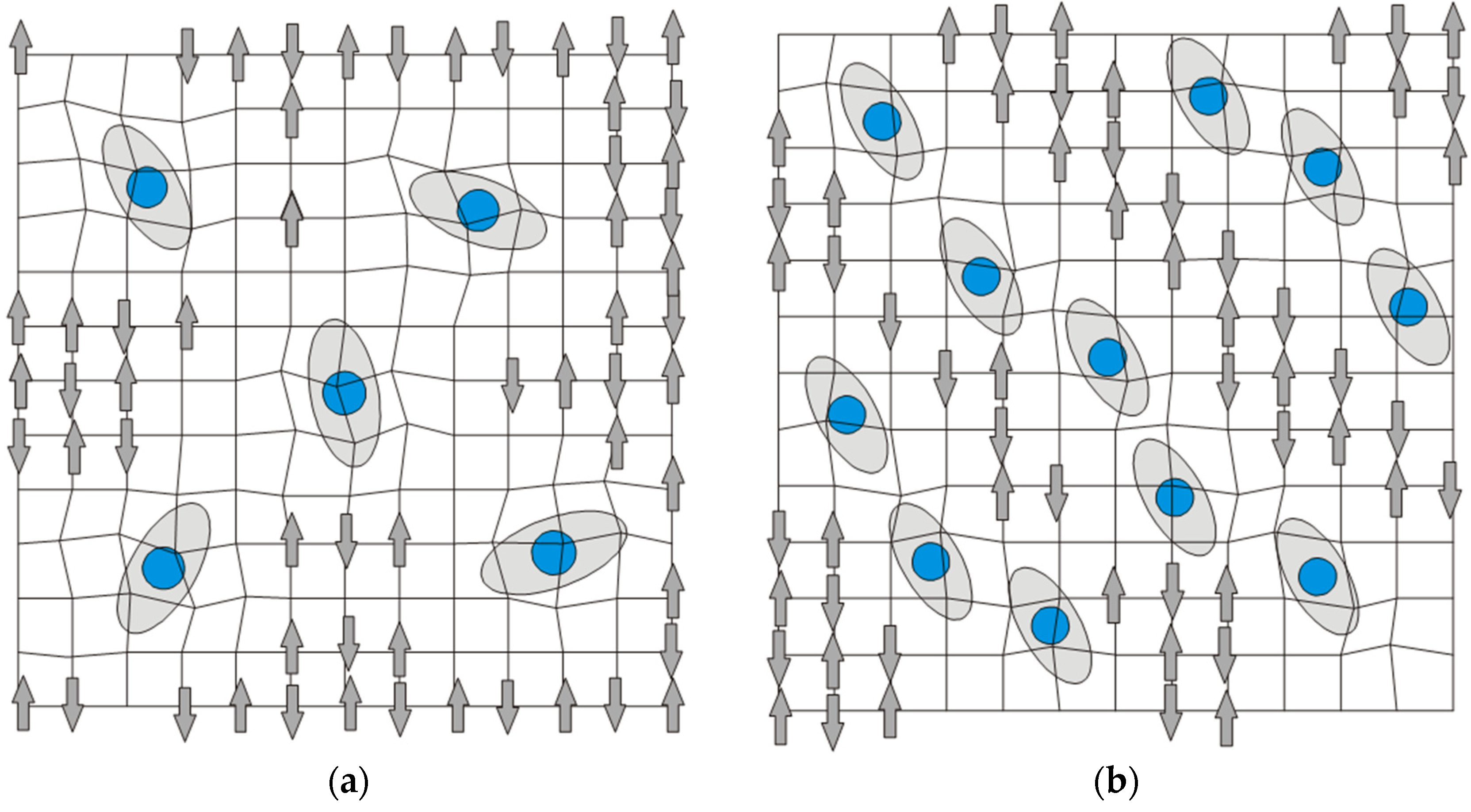
3. Polaron Effects
4. Isotope Effects
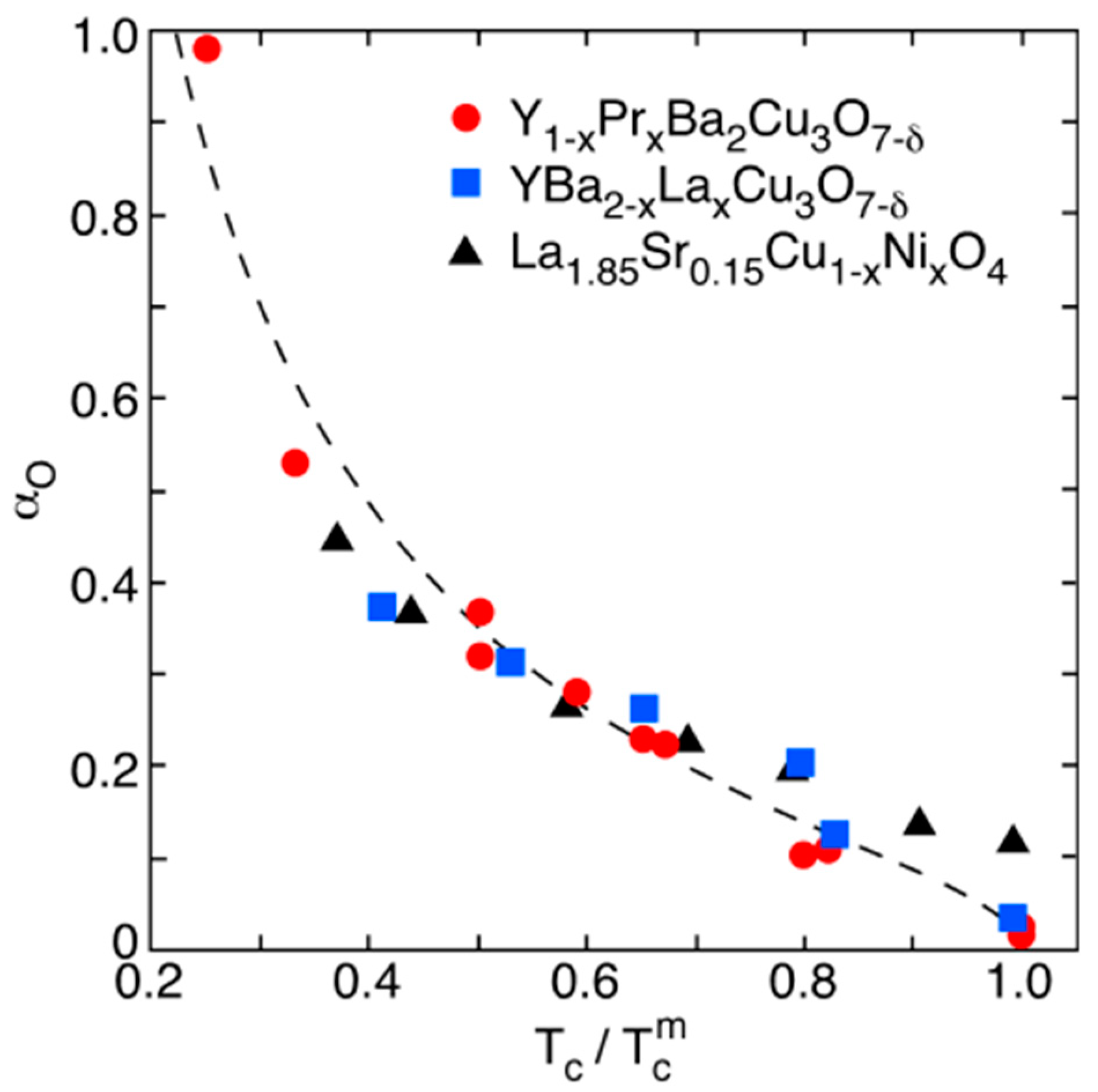
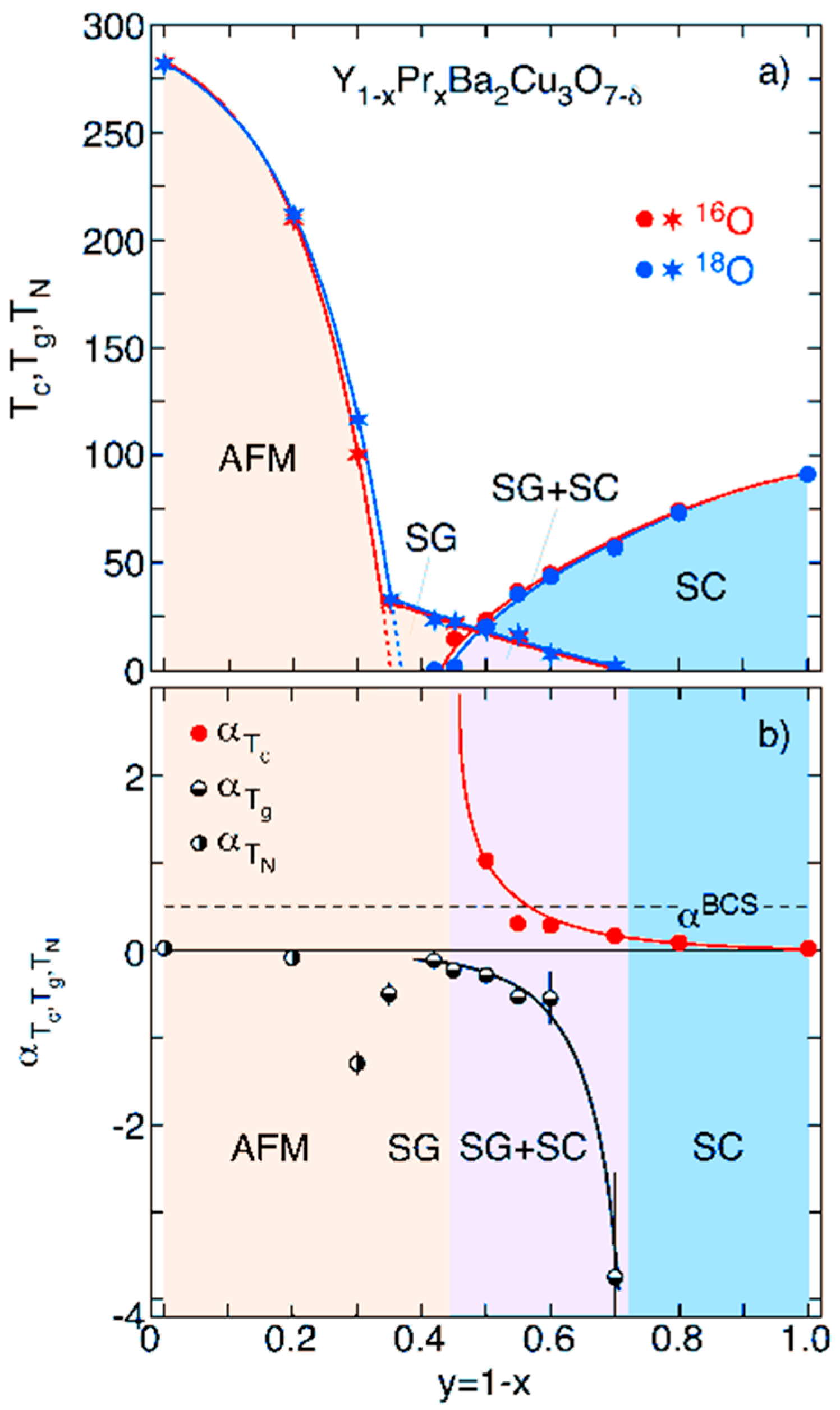
4.1. Cuprates
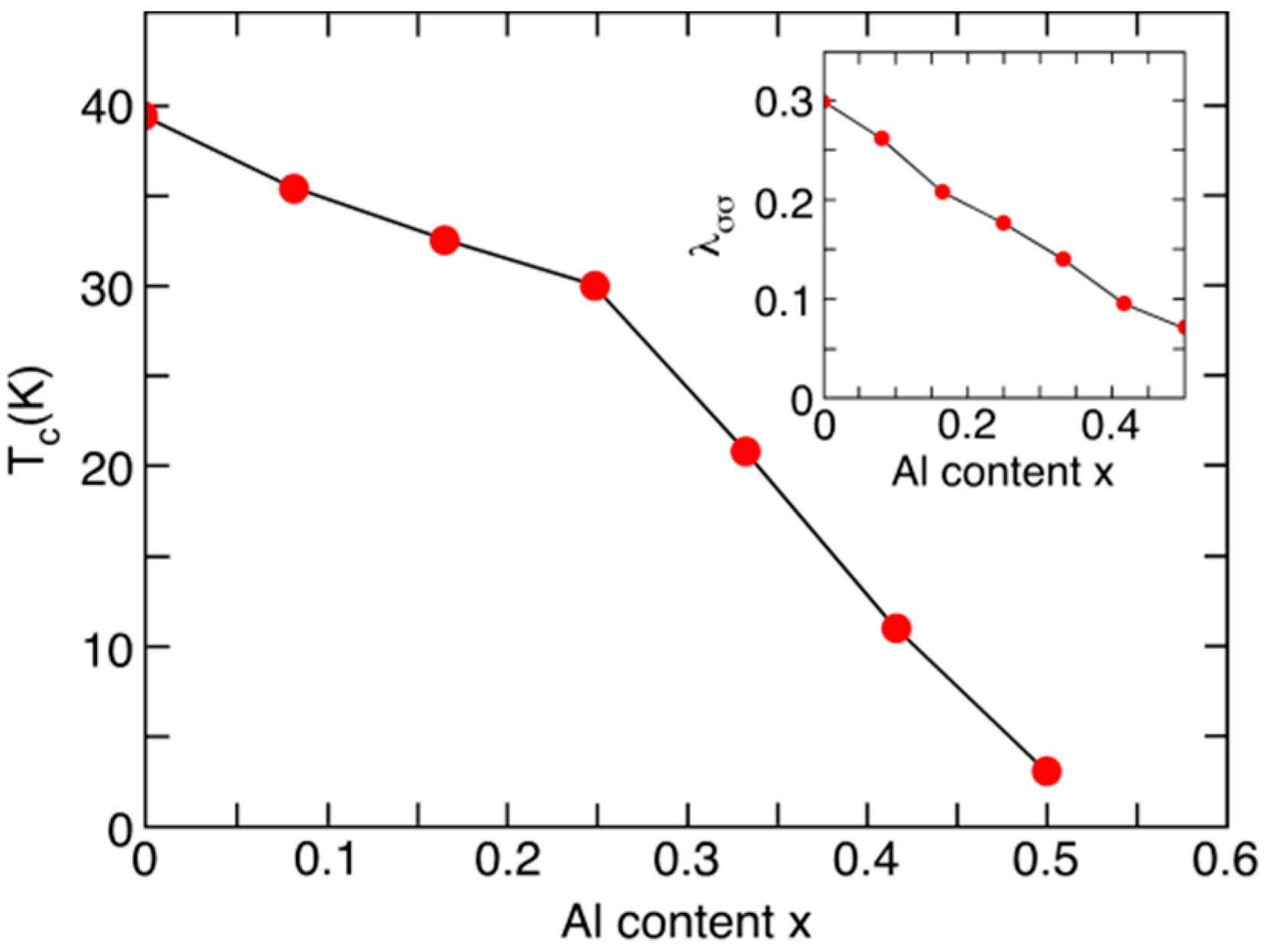
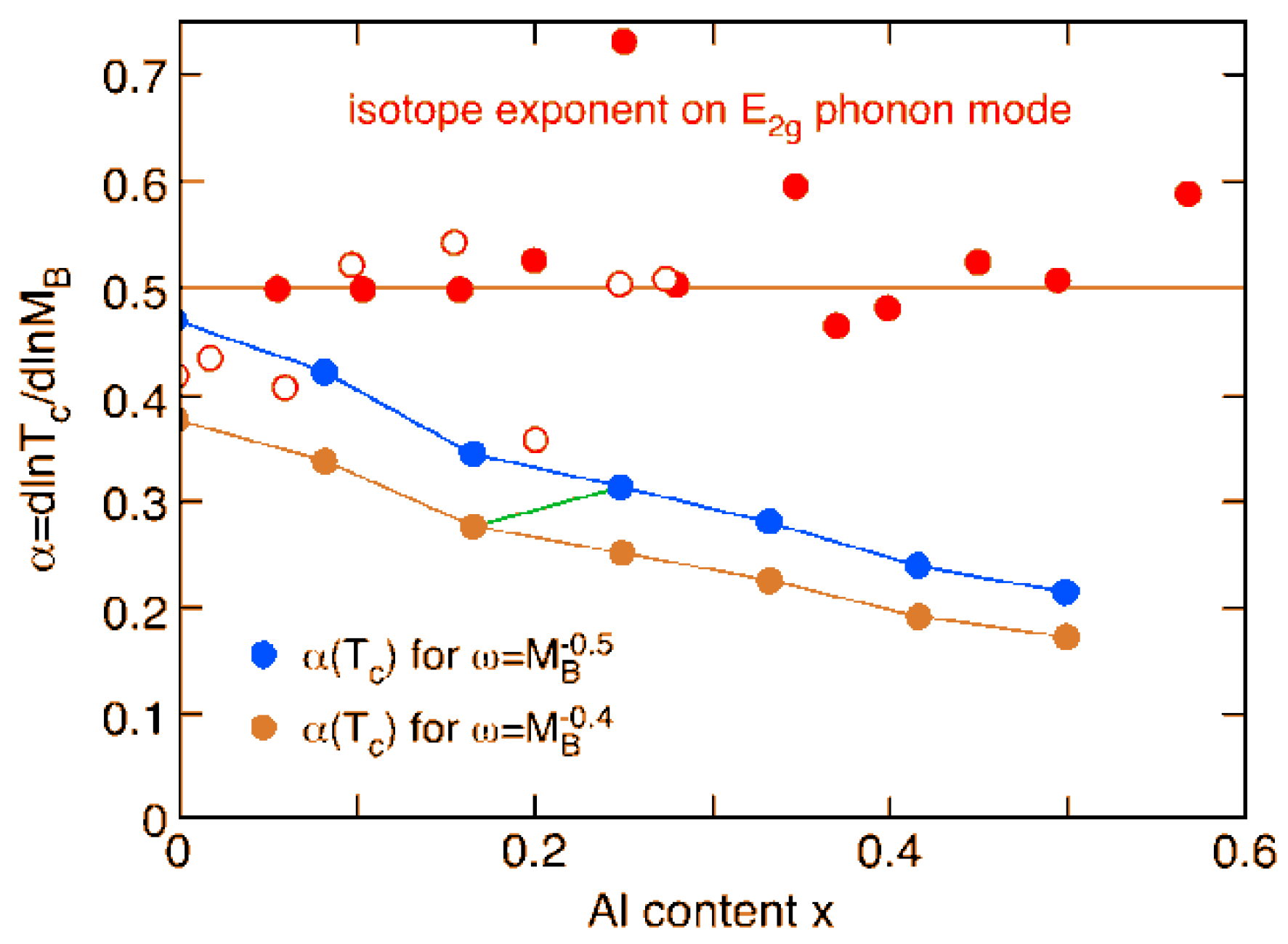
4.2. MgB2
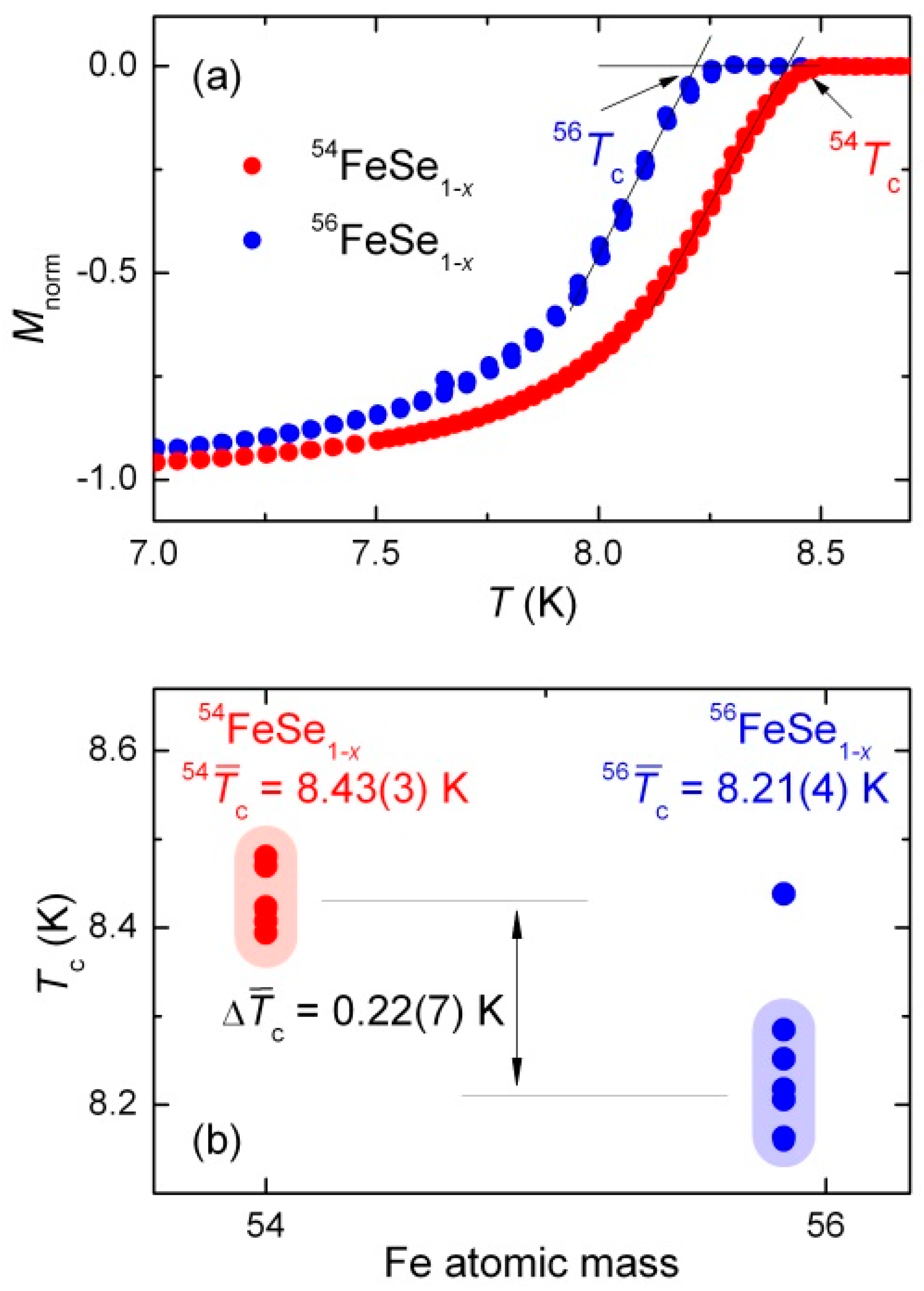
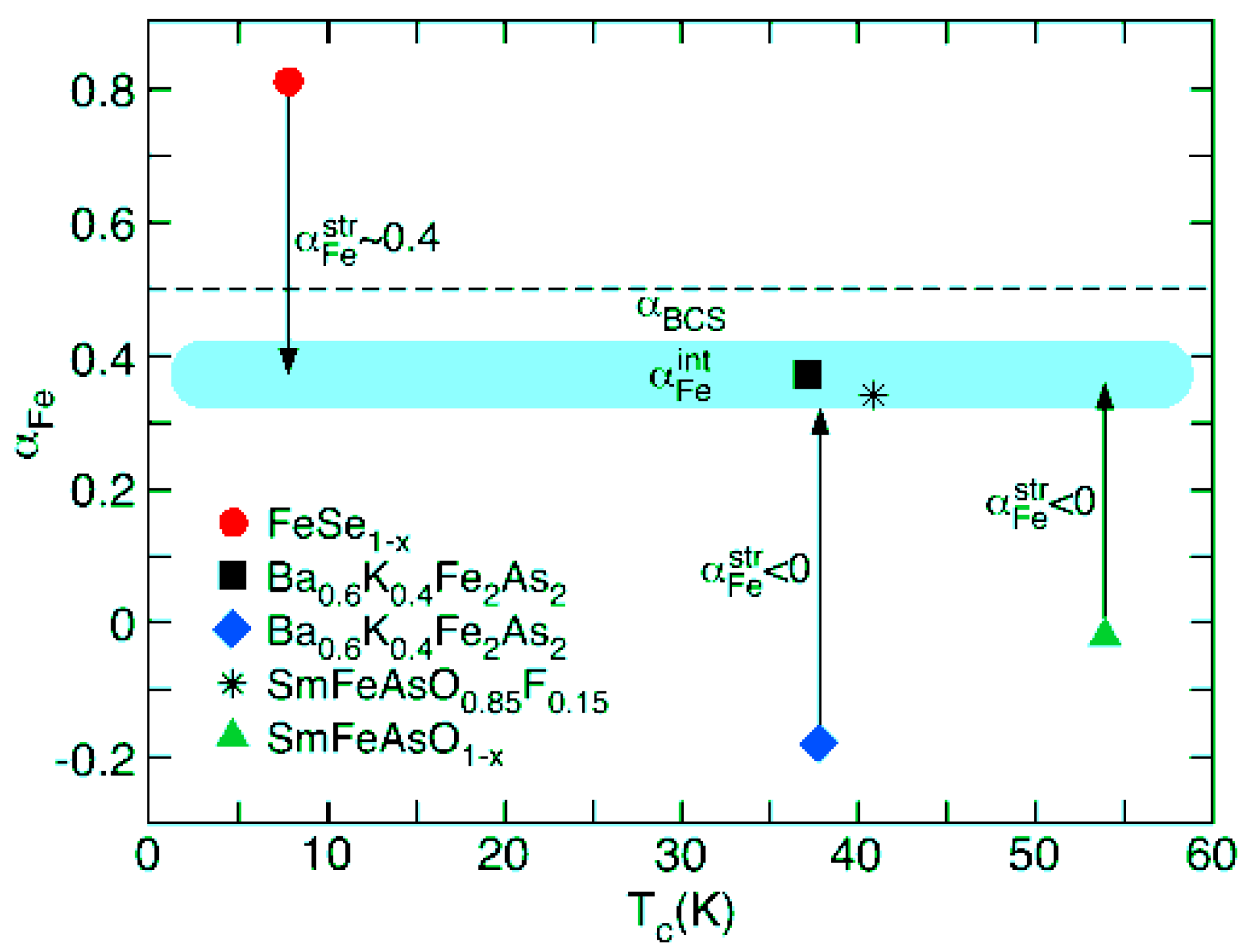
4.3. Fe Based Superconductors
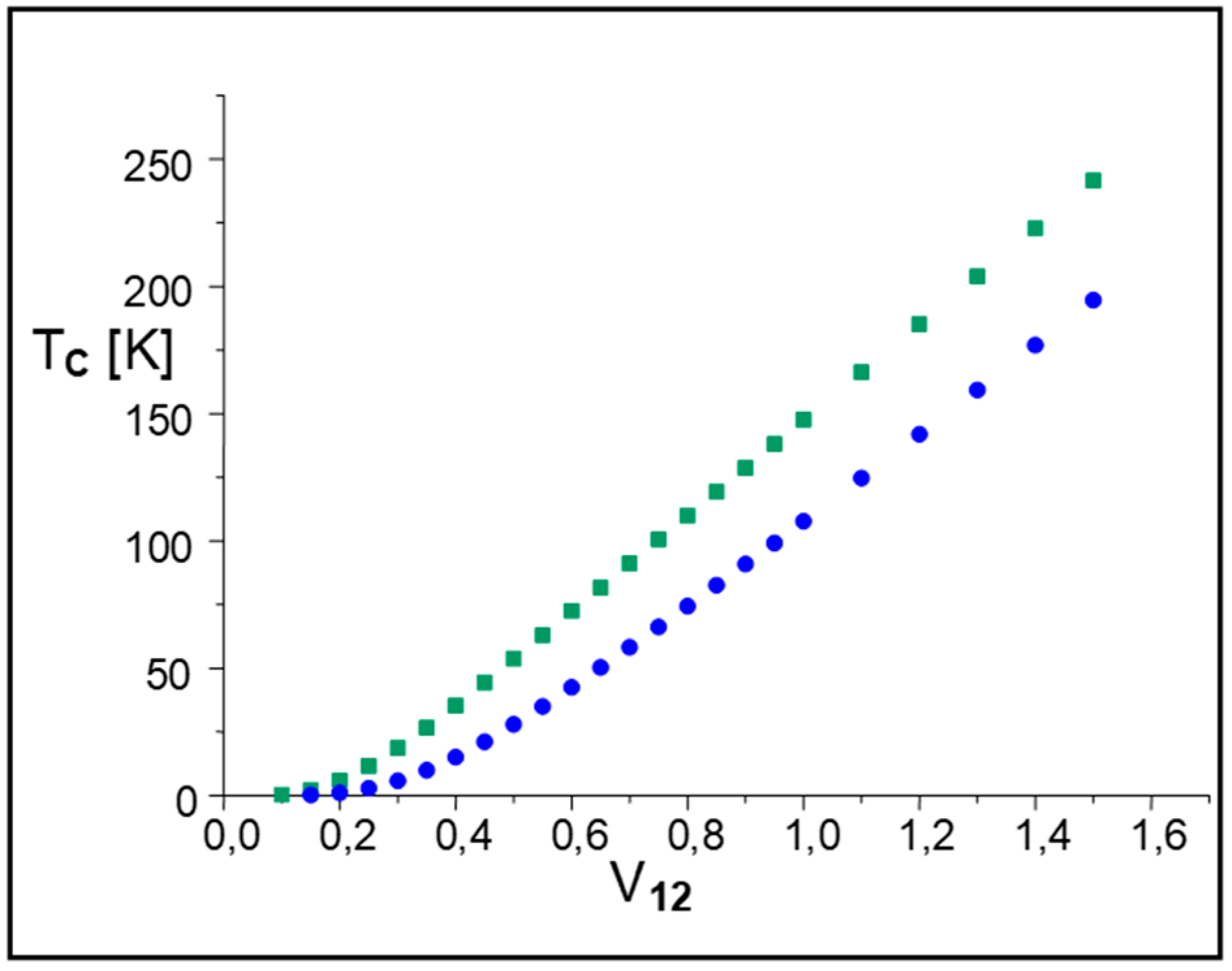
5. The Steep Band/Flat Band Model
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- Suhl, H.; Matthias, B.T.; Walker, L. Bardeen-Cooper-Schrieffer theory of superconductivity in the case of overlapping bands. Phys. Rev. Lett. 1959, 3, 552. [Google Scholar] [CrossRef]
- Moskalenko, V. Superconductivity in metals with overlapping energy bands. Fiz. Metal. Metallov. 1959, 8, 503. [Google Scholar]
- Binnig, G.; Baratoff, A.; Hoenig, H.E.; Bednorz, J.G. Two-band superconductivity in Nb-doped SrTiO3. Phys. Rev. Lett. 1980, 45, 1352. [Google Scholar] [CrossRef]
- Müller, K.A. Possible coexistence of s-and d-wave condensates in copper oxide superconductors. Nature 1995, 377, 133. [Google Scholar]
- Müller, K.A. Essential Heterogeneities in Hole-Doped Cuprate Superconductors. In Superconductivity in Complex Systems; Müller, K.A., Bussmann-Holder, A., Eds.; Springer: Berlin, Heidelberg, 2005. [Google Scholar]
- Bianconi, A.; Saini, N.L.; Lanzara, A.; Missori, M.; Rossetti, T.; Oyanagi, H.; Yamaguchi, H.; Oka, K.; Ito, T. Determination of the Local Lattice Distortions in the CuO2 Plane of La1.85 Sr0.15CuO4. Phys. Rev. Lett. 1996, 96, 3412. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, A.; Lusignoli, M.; Saini, N.L.; Bordet, P.; Kvick, Å.; Radaelli, P.G. Stripe structure of the CuO2 plane in Bi2 Sr2CaCu2O8+y by anomalous X-ray diffraction. Phys. Rev. B 1996, 54, 4310. [Google Scholar] [CrossRef]
- Nagamatsu, J.; Nakagawa, N.; Muranaka, T.; Zenitani, Y.; Akimitsu, J. Superconductivity at 39 K in magnesium diboride. Nature 2001, 410, 63–64. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Keller, H. Polarons in Advanced Materials; Sasha, A., Ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Simon, A. Superconductivity and chemistry. Angew. Chem. Int. Ed. 1997, 36, 1788. [Google Scholar] [CrossRef]
- Guidini, A.; Flammia, L.; Milošević, M.; Perali, A. BCS-BEC crossover in quantum confined superconductors. J. Supercond. Nov. Magn. 2016, 29, 711–715. [Google Scholar] [CrossRef]
- Bianconi, A. Feshbach shape resonance for high Tc pairing in superlattices of quantum stripes and quantum wells. Iran. J. Phys. Research 2006, 6, 139. [Google Scholar]
- Bednorz, J.G.; Müller, K.A. Perovskite-type oxides—The new approach to high-Tc superconductivity. Rev. Mod. Phys. 1988, 60, 585. [Google Scholar] [CrossRef]
- Bianconi, A.; Missori, M. The instability of a 2D electron gas near the critical density for a Wigner polaron crystal giving the quantum state of cuprate superconductors. Solid State Commun. 1994, 91, 287–293. [Google Scholar] [CrossRef]
- Bianconi, A.; Valletta, A.; Perali, A.; Saini, N.L. High Tc superconductivity in a superlattice of quantum stripes. Solid State Commun. 1997, 102, 369–374. [Google Scholar] [CrossRef]
- Lang, I.G.; Firsov, Y.A. Kinetic theory of semiconductors with low mobility. Sov. Phys. JETP 1963, 16, 1302. [Google Scholar]
- Keller, H.; Bussmann-Holder, A.; Müller, K.A. Jahn–Teller physics and high-Tc superconductivity. Mater. Today 2008, 11, 38–46. [Google Scholar] [CrossRef]
- Crawford, M.K.; Kunchur, M.N.; Farneth, W.E.; McCarron, E.M., III; Poon, S.J. Anomalous oxygen isotope effect in La2−xSrxCuO4. Phys. Rev. B 1990, 41, 282. [Google Scholar] [CrossRef]
- Ginsberg, D.M. Physical Properties of High Temperature Superconductors IV; World Scientifc: Singapore, 1994; p. 94. [Google Scholar]
- Perali, A.; Innocenti, D.; Valletta, A.; Bianconi, A. Anomalous isotope effect near a 2.5 Lifshitz transition in a multi-band multi-condensate superconductor made of a superlattice of stripes. Superconduct. Sci. Technol. 2012, 25, 124002. [Google Scholar] [CrossRef]
- Batlogg, B.; Cava, R.J.; Jayaraman, A.; van Dover, R.B.; Kourouklis, G.A.; Sunshine, S.; Murphy, D.W.; Rupp, L.W.; Chen, H.S.; White, A.; et al. Isotope Effect in the High-T c Superconductors Ba2YCu3O7 and Ba2EuCu3O7. Phys. Rev. Lett. 1987, 58, 2333. [Google Scholar] [CrossRef]
- Keller, H. Superconductivity in Complex Systems, Müller, K.A., Bussmann-Holder, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; p. 43. [Google Scholar]
- Zech, D.; Keller, H.; Conder, K.; Kaldis, E.; Liarokapis, E.; Poulakis, N.; Müller, K.A. Site-selective oxygen isotope effect in optimally doped YBa2Cu3O6+x. Nature 1994, 371, 681. [Google Scholar] [CrossRef]
- Thomsen, C.; Liu, R.; Bauer, M.; Wittlin, A.; Genzel, L.; Cardona, M.; Schönherr, E.; Bauhofer, W.; König, W. Systematic Raman and infrared studies of the superconductor YBa2Cu3O7-x as a function of oxygen concentration (0≦x≦1). Solid State Commun. 1988, 65, 55–58. [Google Scholar] [CrossRef]
- Khasanov, R.; Eshchenko, D.G.; Luetkens, H.; Morenzoni, E.; Prokscha, T.; Suter, A.; Garifianov, N.; Mali, M.; Roos, J.; Conder, K.; et al. Direct Observation of the Oxygen Isotope Effect on the In-Plane Magnetic Field Penetration Depth in Optimally Doped YBa2Cu3O7−δ. Phys. Rev. Lett. 2004, 92, 057602. [Google Scholar] [CrossRef] [PubMed]
- Schneider, T.; Keller, H. Schneider and Keller reply. Phys. Rev. Lett. 1994, 72, 1133. [Google Scholar] [CrossRef] [PubMed]
- Lanzara, A.; Zhao, G.M.; Saini, N.L.; Bianconi, A.; Conder, K.; Keller, H.; Müller, K.A. Oxygen-isotope shift of the charge-stripe ordering temperature in La2-xSrxCuO4 from x-ray absorption spectroscopy. J. Phys. Condens. Matter 1999, 11, L541. [Google Scholar] [CrossRef]
- Temprano, D.R.; Mesot, J.; Janssen, S.; Conder, K.; Furrer, A.; Mutka, H.; Müller, K.A. Large isotope effect on the pseudogap in the high-temperature superconductor HoBa2Cu4O8. Phys. Rev. Lett. 2000, 84, 1990. [Google Scholar] [CrossRef] [PubMed]
- Rubio Temprano, D.; Conder, K.; Furrer, A.; Mutka, H.; Trounov, V.; Müller, K.A. Oxygen and copper isotope effects on the pseudogap in the high-temperature superconductor La1.81Ho0.04Sr0.15CuO4 studied by neutron crystal-field spectroscopy. Phys. Rev. B 2002, 66, 184506. [Google Scholar] [CrossRef]
- Bendele, M.; von Rohr, F.; Guguchia, Z.; Pomjakushina, E.; Conder, K.; Bianconi, A.; Simon, A.; Bussmann-Holder, A.; Keller, H. Evidence for strong lattice effects as revealed from huge unconventional oxygen isotope effects on the pseudogap temperature in La2−xSrxCuO4. Phys. Rev. B 2017, 95, 014514. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Keller, H.; Bishop, A.R.; Simon, A.; Müller, K.A. Polaron coherence as origin of the pseudogap phase in high temperature superconducting cuprates. J. Supercond. Nov. Magn. 2008, 21, 353. [Google Scholar] [CrossRef]
- Madan, I.; Kurosawa, T.; Toda, Y.; Oda, M.; Mertelj, T.; Mihailovic, D. Evidence for carrier localization in the pseudogap state of cuprate superconductors from coherent quench experiments. Nat. Commun. 2015, 6, 6958. [Google Scholar] [CrossRef]
- Weyeneth, S.; Müller, K.A. Oxygen isotope effect in cuprates results from polaron-induced superconductivity. J. Supercond. Nov. Magn. 2011, 24, 1235. [Google Scholar] [CrossRef]
- Khasanov, R.; Shengelaya, A.; Di Castro, D.; Morenzoni, E.; Maisuradze, A.; Savić, I.M.; Conder, K.; Pomjakushina, E.; Bussmann-Holder, A.; Keller, H. Oxygen isotope effects on the superconducting transition and magnetic states within the phase diagram of Y1−xPr xBa2Cu3O7− δ. Phys. Rev. Lett. 2008, 101, 077001. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, A.; Di Castro, D.; Agrestini, S.; Campi, G.; Saini, N.L.; Saccone, A.; Negri, S.; Giovannini, M. A superconductor made by a metal heterostructure at the atomic limit tuned at the shape resonance’: MgB2. J. Phys. Conden. Matter 2001, 13, 7383. [Google Scholar] [CrossRef]
- Agrestini, S.; Di Castro, D.; Sansone, M.; Saini, N.L.; Saccone, A.; De Negri, S.; Giovannini, M.; Colapietro, M.; Bianconi, A. High Tc superconductivity in a critical range of micro-strain and charge density in diborides. J. Phys. Conden. Matter 2001, 13, 11689. [Google Scholar] [CrossRef]
- Choi, H.J.; Roundy, D.; Sun, H.; Cohen, M.L.; Louie, S.G. The origin of the anomalous superconducting properties of MgB2. Nature 2002, 418, 758. [Google Scholar] [CrossRef] [PubMed]
- Bussmann-Holder, A.; Bianconi, A. Raising the diboride superconductor transition temperature using quantum interference effects. Phys. Rev. B 2003, 67, 132509. [Google Scholar] [CrossRef] [Green Version]
- Simonelli, L.; Palmisano, V.; Fratini, M.; Filippi, M.; Parisiadis, P.; Lampakis, D.; Liarokapis, E.; Bianconi, A. Isotope effect on the E2g phonon and mesoscopic phase separation near the electronic topological transition in Mg1−xAlxB2. Phys. Rev. B 2009, 80, 014520. [Google Scholar] [CrossRef] [Green Version]
- De la Peña-Seaman, O.; de Coss, R.; Heid, R. Electron-phonon coupling and two-band superconductivity of Al-and C-doped MgB2. Phys. Rev. B 2010, 82, 224508. [Google Scholar] [CrossRef] [Green Version]
- Innocenti, D.; Poccia, N.; Ricci, A.; Valletta, A.; Caprara, S.; Perali, A.; Bianconi, A. Resonant and crossover phenomena in a multiband superconductor: Tuning the chemical potential near a band edge. Phys. Rev. B 2010, 82, 184528. [Google Scholar] [CrossRef] [Green Version]
- Bud’ko, S.L.; Lapertot, G.; Petrovic, C.; Cunningham, C.E.; Anderson, N.; Canfield, P.C. Boron isotope effect in superconducting MgB2. Phys. Rev. Lett. 2001, 86, 1877. [Google Scholar] [CrossRef] [Green Version]
- Hinks, D.G.; Jorgensen, J.D. The isotope effect and phonons in MgB2. Physica C 2003, 385, 98. [Google Scholar] [CrossRef]
- Di Castro, D.; Angst, M.; Eshchenko, D.G.; Khasanov, R.; Roos, J.; Savic, I.M.; Shengelaya, A.; Bud’ko, S.L.; Canfield, P.C.; Conder, K.; et al. Absence of a boron isotope effect in the magnetic penetration depth of MgB2. Phys. Rev. B 2004, 70, 014519. [Google Scholar] [CrossRef] [Green Version]
- Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H.J. Iron-based layered superconductor La [O1-x F x] FeAs (x= 0.05− 0.12) with T c= 26 K. Am. Chem. Soc. 2008, 130, 3296. [Google Scholar] [CrossRef] [PubMed]
- Khasanov, R.; Bendele, M.; Conder, K.; Keller, H.; Pomjakushina, E.; Pomjakushin, V. Iron isotope effect on the superconducting transition temperature and the crystal structure of FeSe1−x. New J. Phys. 2010, 12, 073024. [Google Scholar] [CrossRef]
- Liu, R.H.; Wu, T.; Wu, G.; Chen, H.; Wang, X.F.; Xie, Y.L.; Yin, J.J.; Yan, Y.J.; Li, Q.J.; Shi, B.C.; et al. A large iron isotope effect in SmFeAsO1-xFx and Ba1-x KxFe2As2. Nature 2009, 459, 64. [Google Scholar] [CrossRef]
- Shirage, P.M.; Kihou, K.; Miyazawa, K.; Lee, C.-H.; Kito, H.; Eisaki, H.; Yanagisawa, T.; Tanaka, Y.; Iyo, A. Inverse iron isotope effect on the transition temperature of the (Ba, K)Fe2As2 superconductor. Phys. Rev. Lett. 2009, 103, 257003. [Google Scholar] [CrossRef] [Green Version]
- Shirage, P.M.; Miyazawa, K.; Kihou, K.; Kito, H.; Yoshida, Y.; Tanaka, Y.; Eisaki, H.; Iyo, A. Absence of an appreciable iron isotope effect on the transition temperature of the optimally doped SmFeAsO1−y superconductor. Phys. Rev. Lett. 2010, 105, 037004. [Google Scholar] [CrossRef]
- Khasanov, R.; Bendele, M.; Bussmann-Holder, A.; Keller, H. Intrinsic and structural isotope effects in iron-based superconductors. Phys. Rev. B 2010, 82, 212505. [Google Scholar] [CrossRef] [Green Version]
- Khasanov, R. High Tc Copper Oxide Superconductors and Related Novel Materials; Bussmann-Holder, A., Keller, H., Bianconi, A., Eds.; Springer: Ney York, NY, USA, 2017; p. 15. [Google Scholar]
- Deng, S.; Simon, A.; Köhler, J. Superconductivity and chemical bonding in mercury. Angew. Chem. Int. Ed. 1998, 37, 640. [Google Scholar] [CrossRef]
- Deng, S.; Simon, A.; Köhler, J. Flat band-steep band scenario and superconductivity - The case of calcium. J. Solid State Sci. 2000, 2, 31. [Google Scholar] [CrossRef]
- Deng, S.; Simon, A.; Köhler, J. Chemical Bonding Variations and Electron− Phonon Interaction. J. Am. Chem. Soc. 2002, 124, 10712. [Google Scholar] [CrossRef]
- An, J.; Rosner, H.; Savrasov, S.Y.; Pickett, W.E. Extreme electron-phonon coupling in boron-based layered superconductors. Phys. Rev. B 2002, 66, 220502. [Google Scholar] [CrossRef] [Green Version]
- Deng, S.; Simon, A.; Köhler, J. The origin of a flat band. J. Solid State Chem. 2003, 176, 412. [Google Scholar] [CrossRef]
- Deng, S.; Simon, A.; Köhler, J. Pairing mechanisms viewed from physics and chemistry. In Superconductivity in Complex Systems; Springer: Berlin, Heidelberg, Germany, 2005; pp. 103–141. [Google Scholar]
- Deng, S.; Simon, A.; Köhler, J. A “flat/steep band” model for superconductivity. Int. J. Mod. Phys. B 2005, 19, 29. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Köhler, J.; Simon, A.; Whangbo, M.H.; Bianconi, A. The road map toward Room-Temperature superconductivity: Manipulating different pairing channels in systems composed of multiple electronic components. Condens. Matter 2017, 2, 24. [Google Scholar] [CrossRef]
- Müller, K.A. The unique properties of superconductivity in cuprates. J. Supercond. Nov. Magn. 2014, 27, 2163–2179. [Google Scholar] [CrossRef]
- Bianconi, A. On the Fermi liquid coupled with a generalized Wigner polaronic CDW giving high Tc superconductivity. Solid State Commun. 1994, 91, 1–5. [Google Scholar] [CrossRef]
- Bianconi, A.; Missori, M.; Oyanagi, H.; Yamaguchi, H.; Ha, D.H.; Nishiara, Y.; Della Longa, S. The measurement of the polaron size in the metallic phase of cuprate superconductors. EPL (Europhysics Letters) 1995, 31, 411. [Google Scholar] [CrossRef]
- Zhou, J.S.; Bersuker, G.I.; Goodenough, J.B. Non-adiabatic electron-lattice interactions in the copper-oxide superconductors. J. Supercond. 1995, 8, 541–544. [Google Scholar] [CrossRef]
- Oleś, A.M.; Wohlfeld, K.; Khaliullin, G. Orbital Symmetry and Orbital Excitations in High-Tc Superconductors. Condens. Matter 2019, 4, 46. [Google Scholar] [CrossRef] [Green Version]
- Kagan, M.Y.; Bianconi, A. Fermi-Bose mixtures and BCS-BEC crossover in high-Tc superconductors. Condens. Matter 2019, 4, 51. [Google Scholar] [CrossRef] [Green Version]
- Caprara, S. The ancient romans’ route to charge density waves in cuprates. Condens. Matter 2019, 4, 60. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, V.G.; Ivanov, A.A.; Menushenkov, A.P.; Joseph, B.; Bianconi, A. Fe–As Bond Fluctuations in a Double-Well Potential in LaFeAsO. J. Supercond. Nov. Magn. 2016, 29, 3035–3039. [Google Scholar] [CrossRef] [Green Version]
- Bianconi, A.; Menushenkov, A.P.; Ivanov, V.G.; Ivanov, A.A.; Joseph, B. Low-temperature anomalies of EXAFS at the K-edge of As in superconducting LaFe0. 89Co0.11AsO. J. Phys. Conf. Ser. 2017, 941, 012058. [Google Scholar] [CrossRef]
- Bauer, E.; Paul, C.; Berger, S.; Majumdar, S.; Michor, H.; Giovannini, M.; Saccone, A.; Bianconi, A. Thermal conductivity of superconducting MgB2. Phys. Condens. Matter 2001, 13, L487. [Google Scholar] [CrossRef]
- Campi, G.; Cappelluti, E.; Proffen, T.; Qiu, X.; Bozin, E.S.; Billinge, S.J.L.; Bianconi, A. Study of temperature dependent atomic correlations in MgB2. Eur. Phys. J. B Condens. Matter Complex Syst. 2006, 52, 15–21. [Google Scholar] [CrossRef]
- Agrestini, S.; Metallo, C.; Filippi, M.; Simonelli, L.; Campi, G.; Sanipoli, C.; Liarokapis, E.; De Negri, S.; Saccone, A.; Latini, A.; et al. Substitution of Sc for Mg in MgB2: effects on transition temperature and Kohn anomaly. Phys. Rev. B 2004, 70, 134514. [Google Scholar] [CrossRef] [Green Version]
- Bianconi, A. Feshbach shape resonance in multiband superconductivity in heterostructures. J. Supercond. 2005, 18, 625–636. [Google Scholar] [CrossRef] [Green Version]
- Bianconi, A. Multiband superconductivity in high Tc cuprates and diborides. J. Phys. Chem. Solids 2006, 67, 567–570. [Google Scholar] [CrossRef]
- Bianconi, A. Quantum materials: Shape resonances in superstripes. Nat. Phys. 2013, 9, 536–537. [Google Scholar] [CrossRef]
- Bianconi, A.; Jarlborg, T. Lifshitz transitions and zero point lattice fluctuations in sulfur hydride showing near room temperature superconductivity. Nov. Supercond. Mater. 2015, 1, 37–49. [Google Scholar] [CrossRef]
- Bianconi, A.; Jarlborg, T. Superconductivity above the lowest Earth temperature in pressurized sulfur hydride. EPL Europhys. Lett. 2015, 112, 37001. [Google Scholar] [CrossRef] [Green Version]
- Jarlborg, T.; Bianconi, A. Breakdown of the Migdal approximation at Lifshitz transitions with giant zero-point motion in H3S superconductor. Sci. Rep. 2016, 6, 24816. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Méndez-Moreno, R.M. A Schematic Two Overlapping-Band Model for Superconducting Sulfur Hydrides: The Isotope Mass Exponent. Adv. Condens. Matter Phys. 2019, 2019, 6795250. [Google Scholar] [CrossRef] [Green Version]
- Ashcroft, N.W. Symmetry and higher superconductivity in the lower elements in “Symmetry and Heterogeneity in High Temperature Superconductors”. In NATO Science Series, Springer Netherlands II Mathematics, Physics and Chemistry; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; p. 3. [Google Scholar]
- Bianconi, A. Feshbach shape resonances in multiband high Tc superconductors in “Symmetry and Heterogeneity in High Temperature Superconductors”. Symmetry and Heterogeneity in High Temperature Superconductors; NATO Science Series; Bianconi, A., Ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 214, p. 21. [Google Scholar]
- Campi, G.; Bianconi, A.; Poccia, N.; Bianconi, G.; Barba, L.; Arrighetti, G.; Innocenti, D.; Karpinski, J.; Zhigadlo, N.D.; Kazakov, S.M.; et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-Tc superconductor. Nature 2015, 525, 359–362. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bussmann-Holder, A.; Keller, H.; Simon, A.; Bianconi, A. Multi-Band Superconductivity and the Steep Band/Flat Band Scenario. Condens. Matter 2019, 4, 91. https://doi.org/10.3390/condmat4040091
Bussmann-Holder A, Keller H, Simon A, Bianconi A. Multi-Band Superconductivity and the Steep Band/Flat Band Scenario. Condensed Matter. 2019; 4(4):91. https://doi.org/10.3390/condmat4040091
Chicago/Turabian StyleBussmann-Holder, Annette, Hugo Keller, Arndt Simon, and Antonio Bianconi. 2019. "Multi-Band Superconductivity and the Steep Band/Flat Band Scenario" Condensed Matter 4, no. 4: 91. https://doi.org/10.3390/condmat4040091
APA StyleBussmann-Holder, A., Keller, H., Simon, A., & Bianconi, A. (2019). Multi-Band Superconductivity and the Steep Band/Flat Band Scenario. Condensed Matter, 4(4), 91. https://doi.org/10.3390/condmat4040091






