Probing Phase Separation and Local Lattice Distortions in Cuprates by Raman Spectroscopy
Abstract
:1. Introduction
2. The Yttrium Family Cuprates
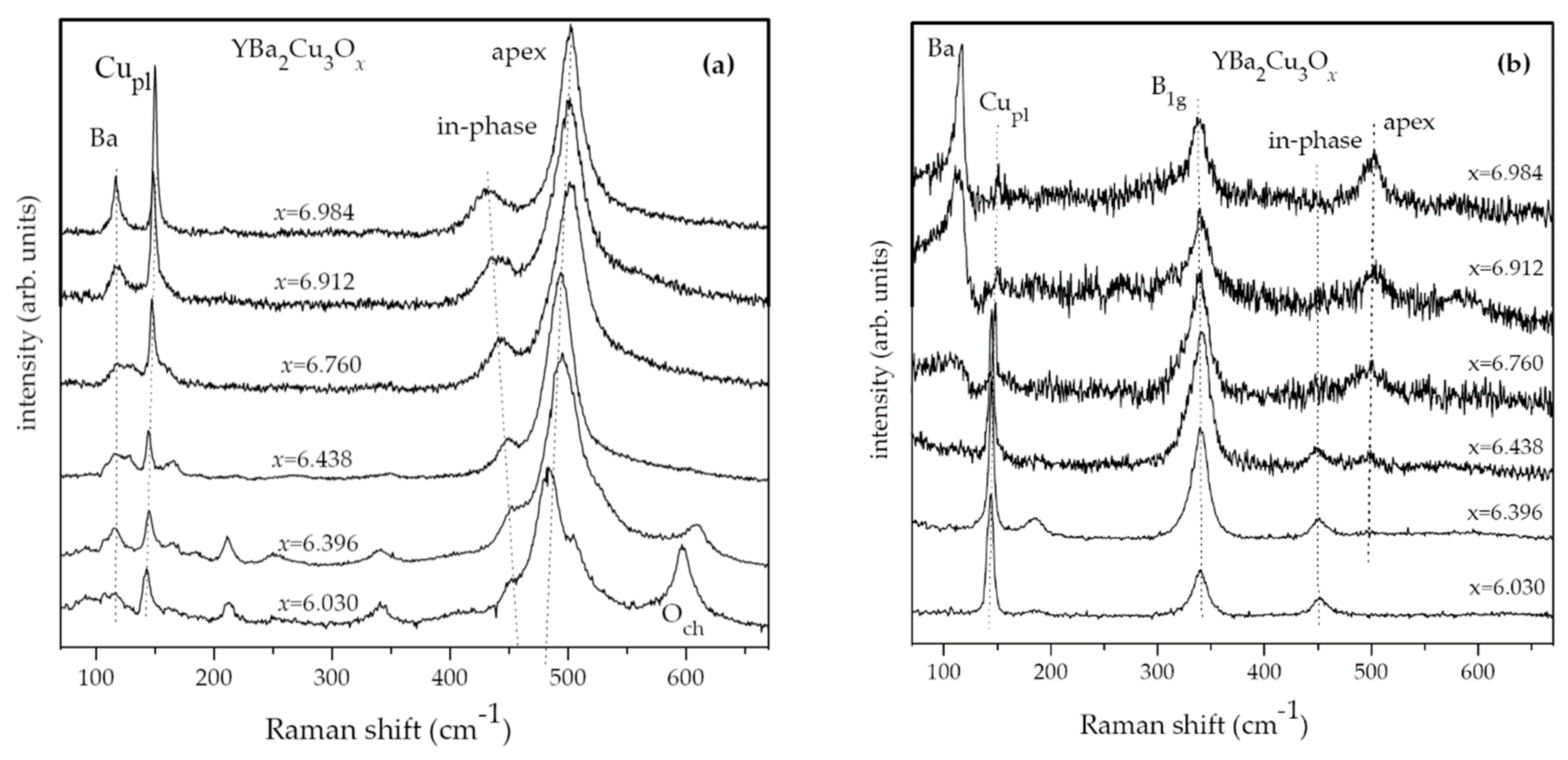
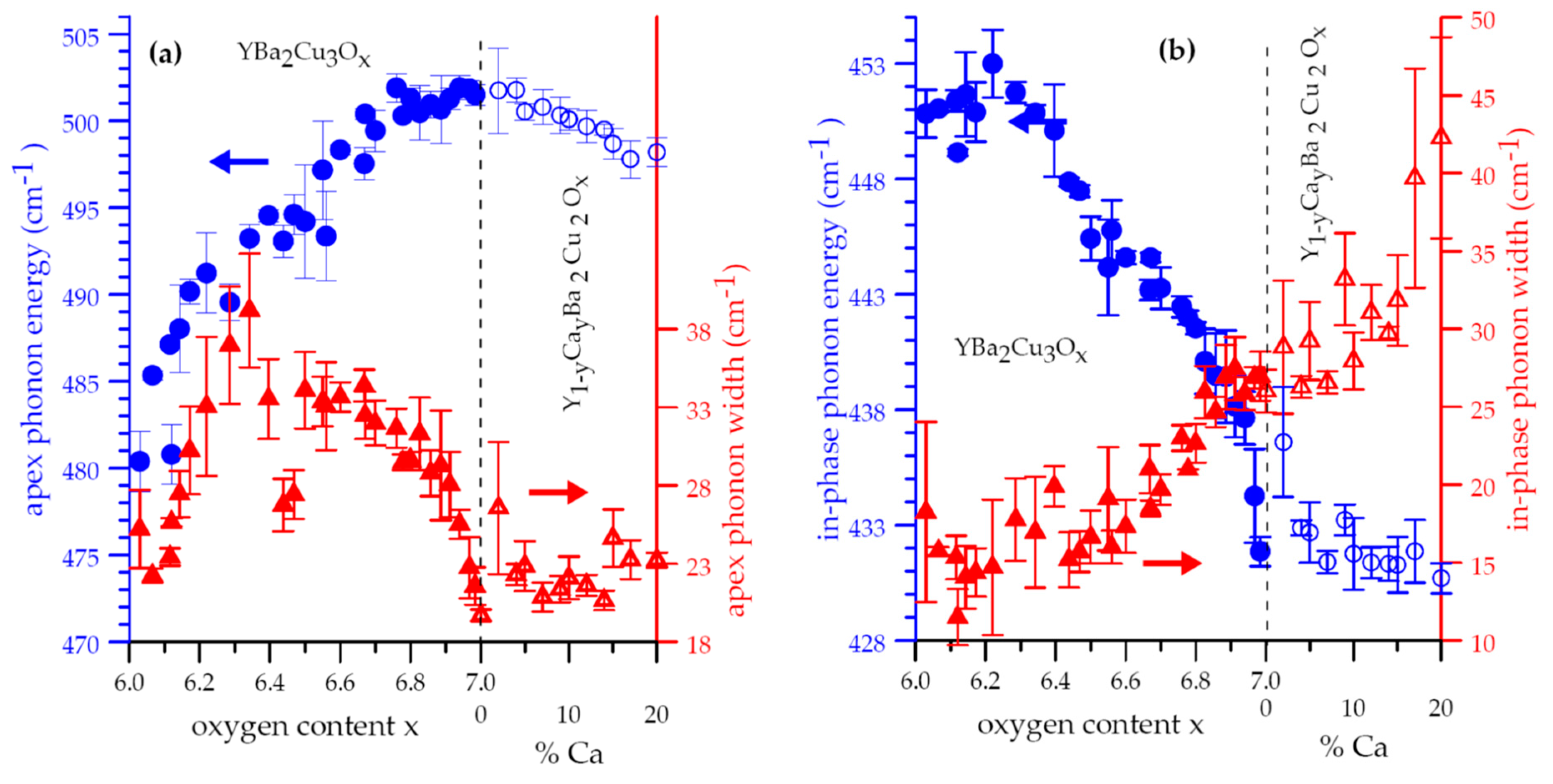
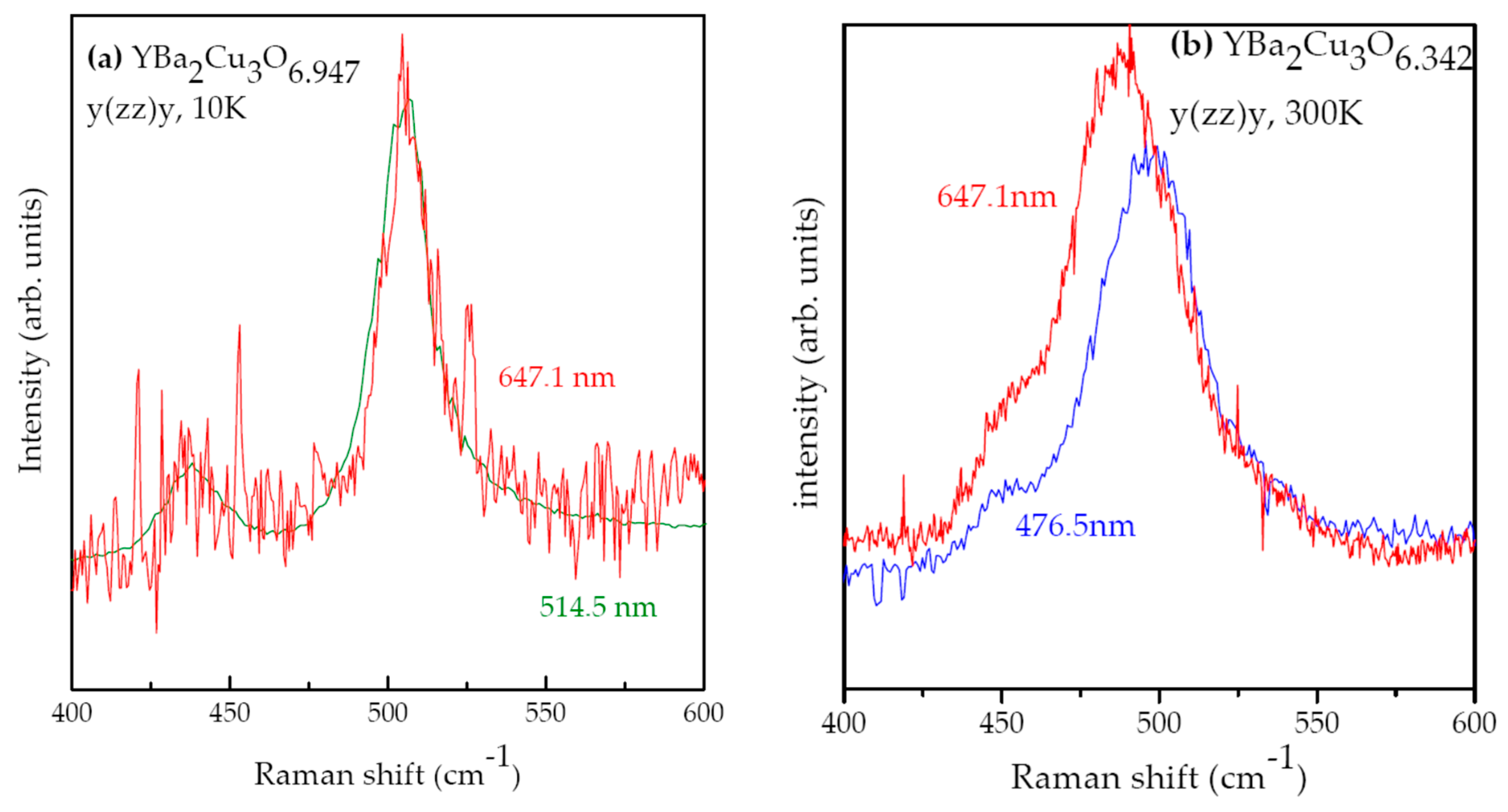
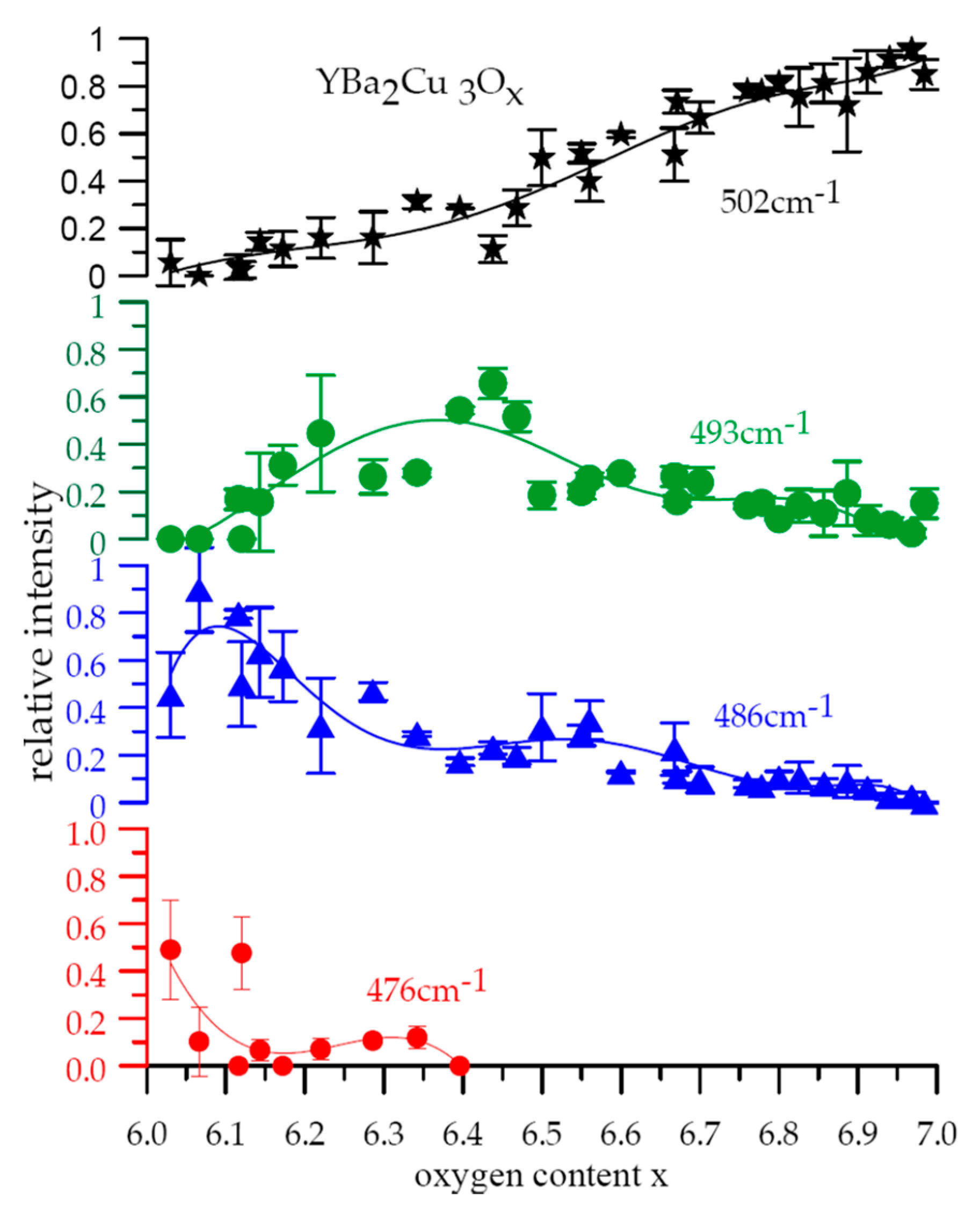
2.1. Phase Separation from Oxygen Doping
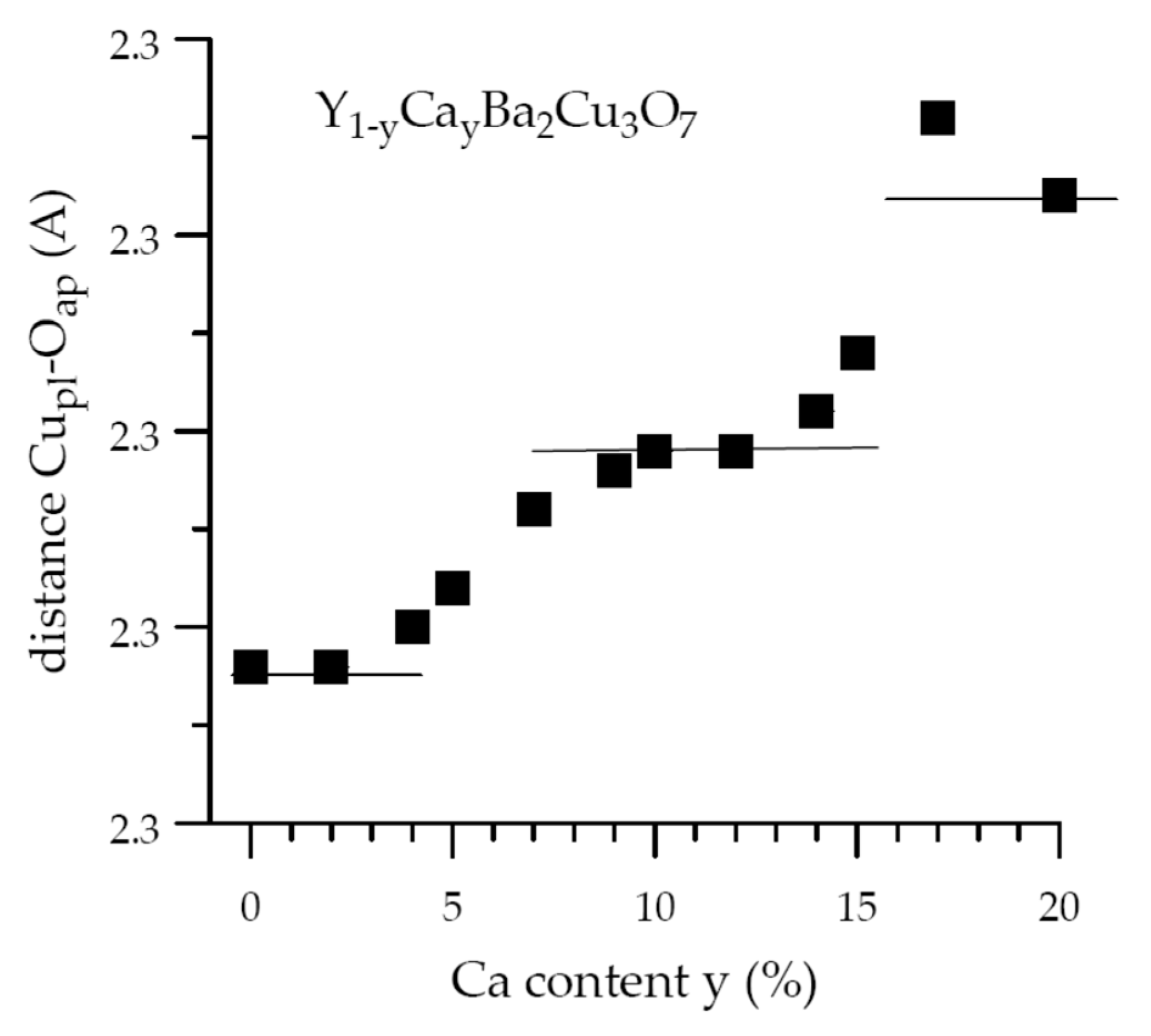
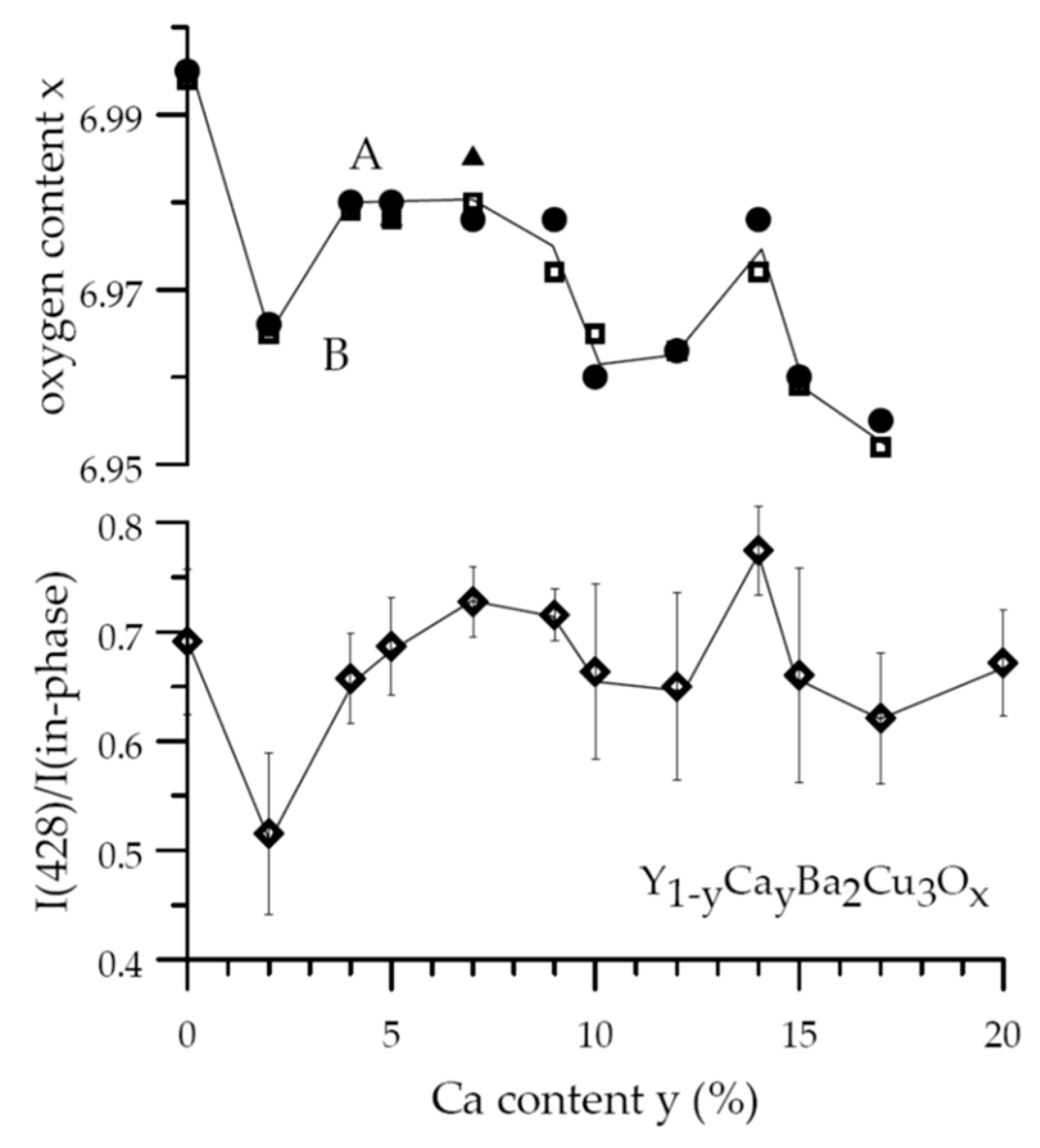
2.2. Phase Separation from Atomic Substitutions
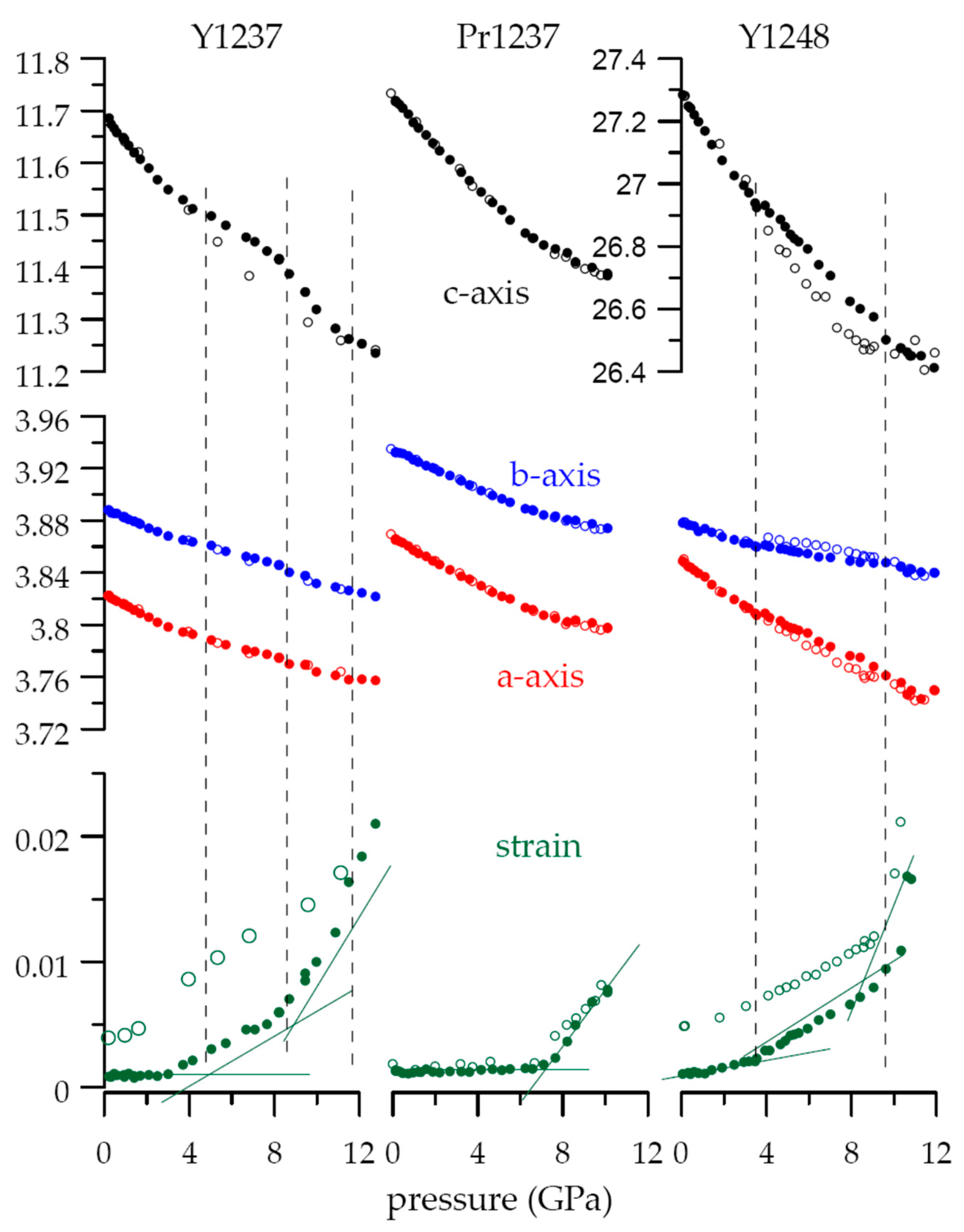
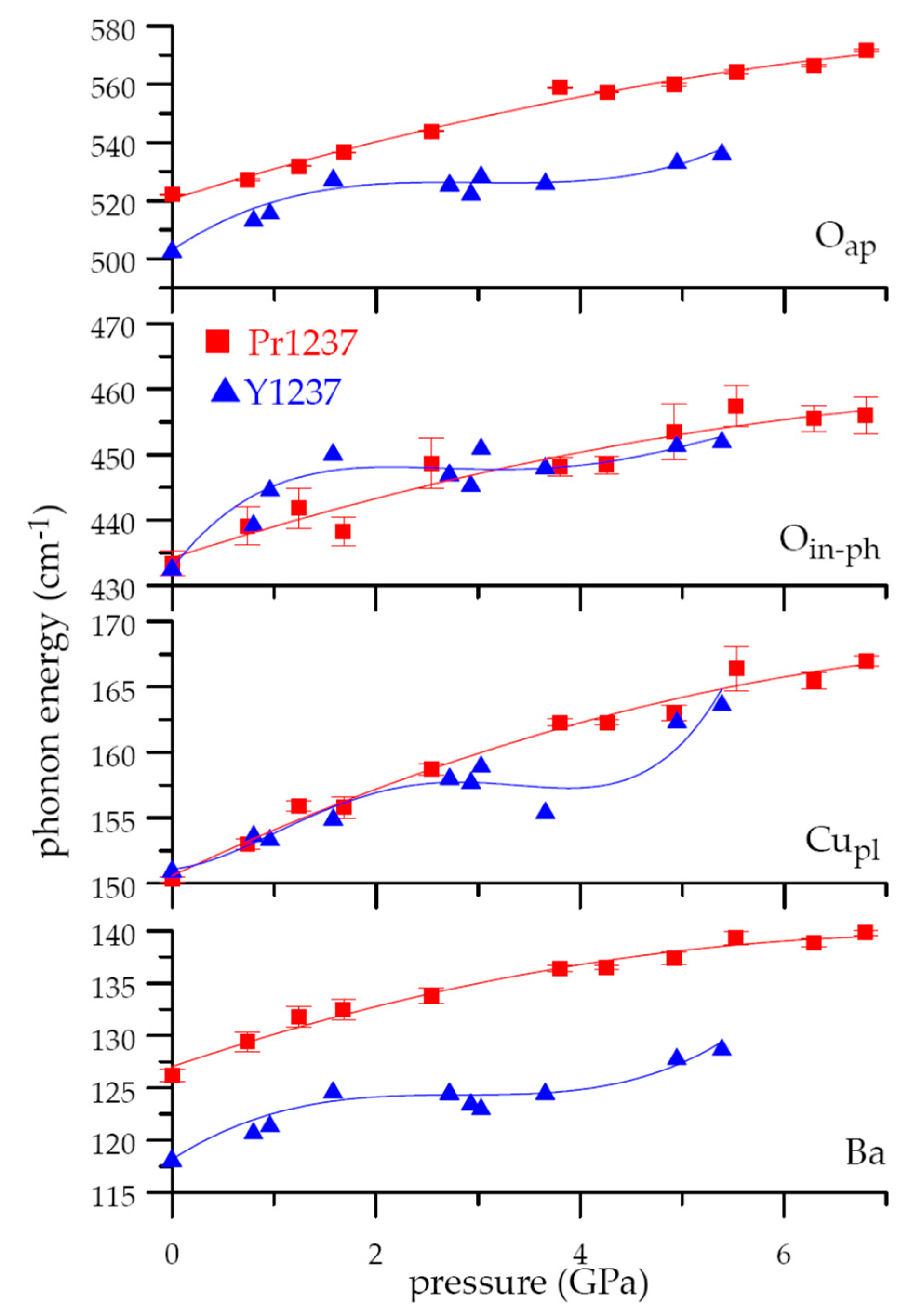
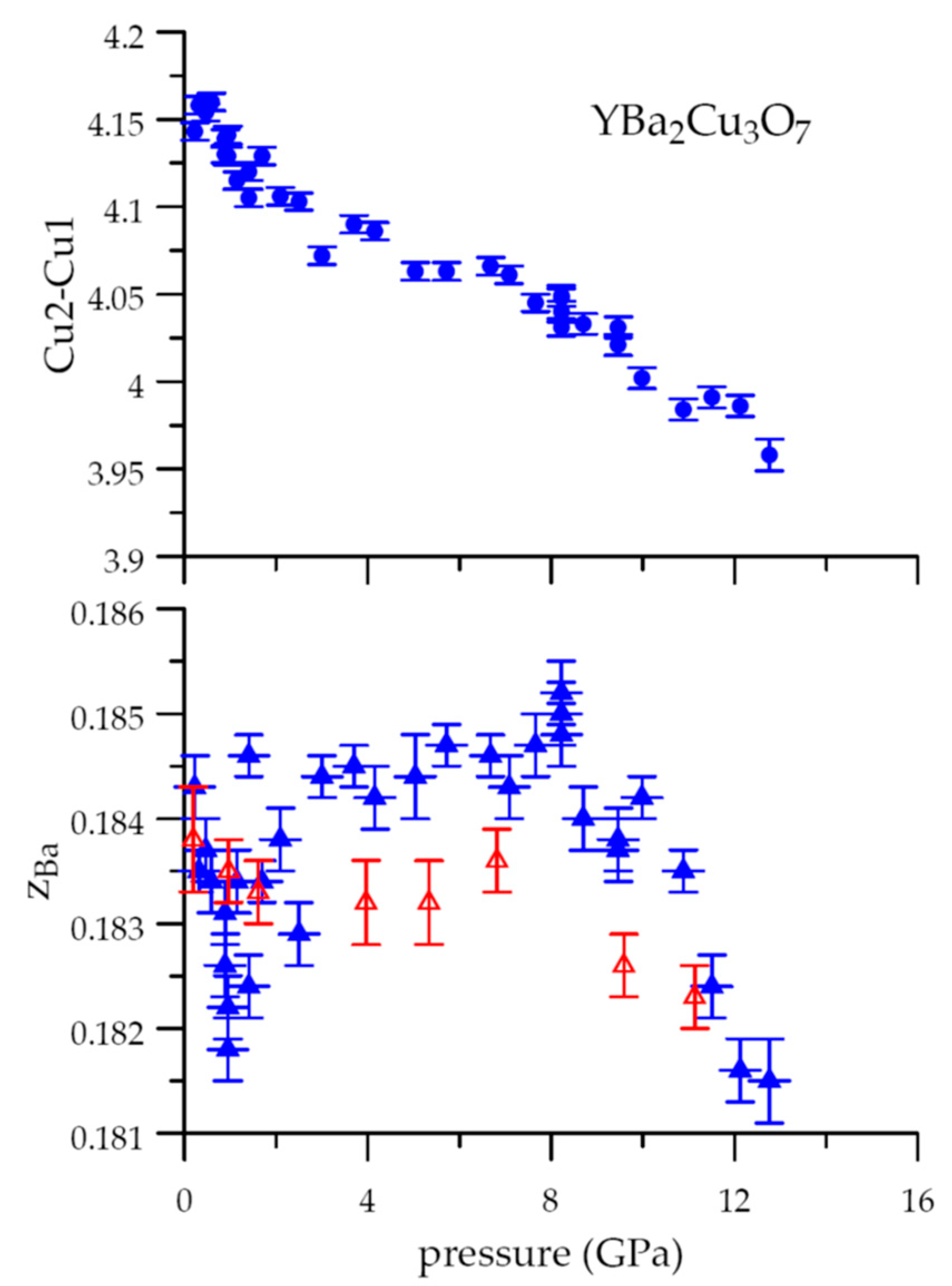
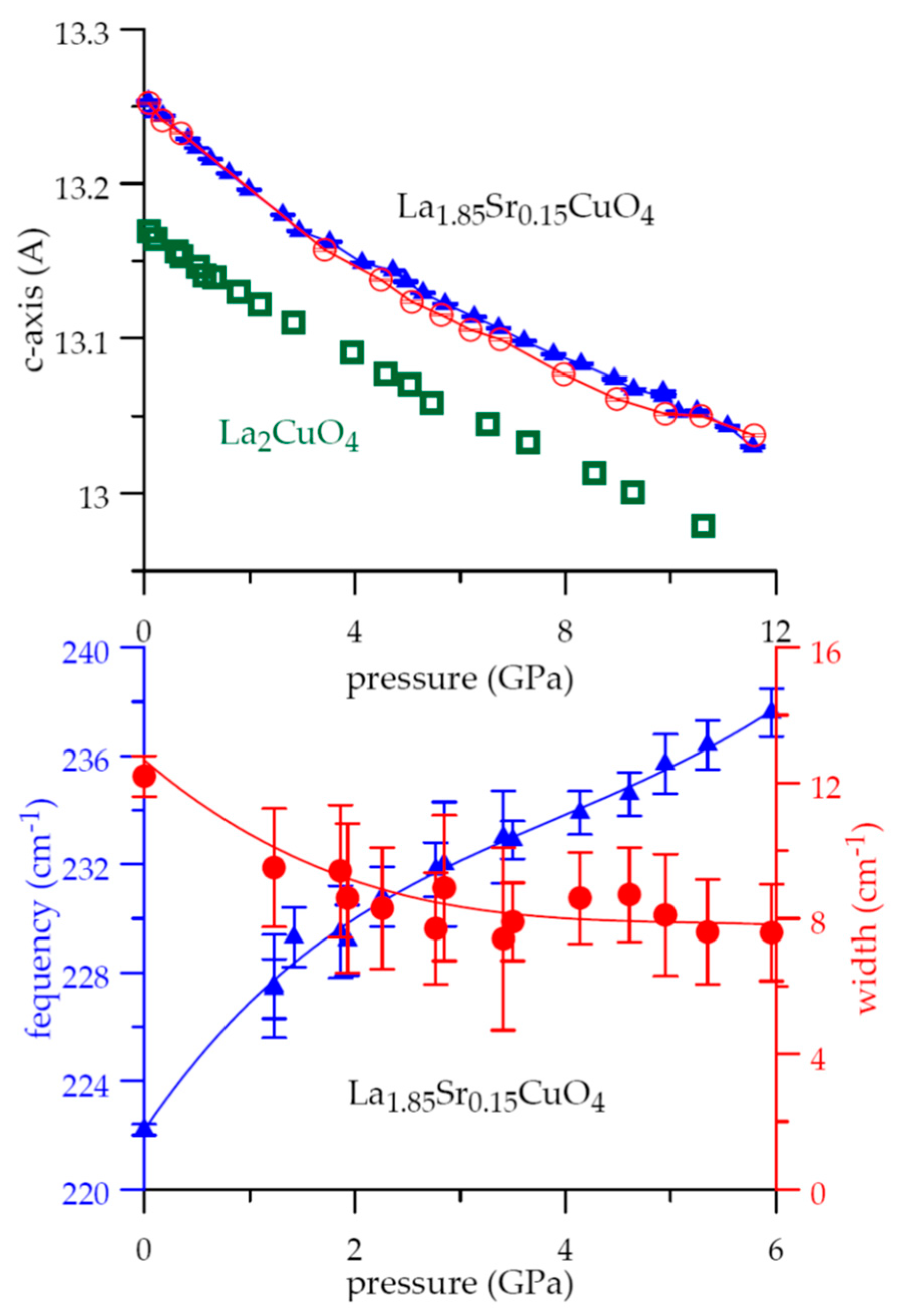
2.3. Pressure Induced Lattice Effects
3. Conclusions
Funding
Conflicts of Interest
References
- Yukalov, V.I. Heterophase fluctuations in ferroelectrics. Ferroelectrics 1988, 82, 11–24. [Google Scholar] [CrossRef]
- Yukalov, V.I. Phase transitions and heterophase fluctuations. Phys. Rep. 1991, 208, 395–489. [Google Scholar] [CrossRef]
- Nagaev, E.L. Phase-separation mechanism for giant magnetoresistance of lanthanum manganites. Phys. Lett. A 1996, 218, 367–372. [Google Scholar] [CrossRef]
- Lanzara, A.; Saini, N.L.; Brunelli, M.; Natali, F.; Bianconi, A.; Radaelli, P.G.; Cheong, S.W. Crossover from large to small polarons across the metal-insulator transition in manganites. Phys. Rev. Lett. 1998, 81, 878–881. [Google Scholar] [CrossRef]
- Yunoki, S.; Hu, J.; Malvezzi, A.L.; Moreo, A.; Furukawa, N.; Dagotto, E. Phase separation in electronic models for manganites. Phys. Rev. Lett. 1998, 80, 845–848. [Google Scholar] [CrossRef]
- Uehara, M.; Mori, S.; Chen, C.H.; Cheong, S.W. Percolative phase separation underlies colossal magnetoresistance in mixed-valent manganites. Nature 1999, 399, 560–563. [Google Scholar] [CrossRef]
- Kagan, M.Y.; Kugel, K.I. Inhomogeneous charge distributions and phase separation in manganites. Phys. Uspekhi 2001, 44, 553–570. [Google Scholar] [CrossRef]
- Kagan, M.Y.; Klaptsov, A.V.; Brodsky, I.V.; Kugel, K.I.; Sboychakov, A.O.; Rakhmanov, A.L. Nanoscale phase separation in manganites. J. Phys. A Math. Gen. 2003, 36, 9155–9164. [Google Scholar] [CrossRef]
- Dagotto, E.; Burgy, J.; Moreo, A. Nanoscale phase separation in colossal magnetoresistance materials: Lessons for the cuprates? Solid State Commum. 2003, 126, 9–22. [Google Scholar] [CrossRef]
- Dagotto, E. Complexity in strongly correlated electronic systems. Science 2005, 309, 257–262. [Google Scholar] [CrossRef]
- Tokura, Y. Critical features of colossal magnetoresistive manganites. Rep. Prog. Phys. 2006, 69, 797–851. [Google Scholar] [CrossRef]
- Hayden, S.M.; Lander, G.H.; Zaretsky, J.; Brown, P.J.; Stassis, C.; Metcalf, P.; Honig, J.M. Incommensurate magnetic correlations in La1.8Sr0.2NiO4. Phys. Rev. Lett. 1992, 68, 1061. [Google Scholar] [CrossRef] [PubMed]
- Campi, G.; Poccia, N.; Joseph, B.; Bianconi, A.; Mishra, S.; Lee, J.; Roy, S.; Nugroho, A.A.; Buchholz, M.; Braden, M.; et al. Direct Visualization of Spatial Inhomogeneity of Spin Stripes Order in La1.72Sr0.28NiO4. Condens. Matter 2019, 4, 77. [Google Scholar] [CrossRef]
- Testardi, L.R. Structural instability and superconductivity in A-15 compounds. Rev. Mod. Phys. 1975, 47, 637–648. [Google Scholar] [CrossRef]
- Bednorz, J.G.; Müller, K.A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. B Condens. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Jorgensen, A.J.; Dabrowski, B.; Pei, S.; Hinks, D.G.; Soderholm, L.; Morosin, B.; Schirber, E.L.; Venturini, E.L.; Ginley, D.S. Superconducting phase of La2CuO4+δ: A superconducting composition resulting from phase separation. Phys. Rev. B 1988, 38, 11337–11345. [Google Scholar] [CrossRef]
- Benedek, G.; Müller, K.A. Phase Separation in Cuprate Superconductors; World Scientific: Singapore, 1992. [Google Scholar]
- Bianconi, A. Phase Separation in Cuprate Superconductors; Müller, K.A., Benedek, G., Eds.; World Scientific: Singapore, 1993; pp. 125–138. [Google Scholar]
- Kremer, R.K.; Sigmund, E.; Hizhnyakov, V.; Hentsch, F.; Simon, A.; Müller, K.A.; Mehring, M. Percolative phase separation in La2CuO4+δ and La2−xSrxCuO4. Z. Phys. B Condens. Matter 1992, 86, 319–324. [Google Scholar] [CrossRef]
- Benedek, G.; Müller, K.A. Phase Separation in Cuprate Superconductors; Springer: Berlin/Herdelberg, Germany, 1994. [Google Scholar]
- Bianconi, A.; Missori, M. The Coupling of a Wigner Polaronic Charge Density Wave with a Fermi Liquid Arising from the Instability of a Wigner Polaron Crystal: A Possible Pairing Mechanism in High Tc Superconductors. In Phase Separation in Cuprate Superconductors; Springer: Berlin/Heidelberg, Germany, 1994; pp. 272–289. [Google Scholar]
- Bianconi, A. On the Fermi liquid coupled with a generalized Wigner polaronic CDW giving high Tc superconductivity. Solid State Commun. 1994, 91, 1–5. [Google Scholar] [CrossRef]
- Bianconi, A.; Missori, M. High Tc superconductivity by quantum confinement. J. Phys. 1994, 4, 361–365. [Google Scholar] [Green Version]
- Bianconi, A. On the possibility of new high Tc superconductors by producing metal heterostructures as in the cuprate perovskites. Solid State Commum. 1994, 89, 933–936. [Google Scholar] [CrossRef] [Green Version]
- Hizhnyakov, V.; Sigmund, E.; Seibold, G. Polaron formation and percolative phase separation in HTSC. In Phase Separation in Cuprate Superconductors; Springer: Berlin/Heidelberg, Germany, 1994; pp. 50–65. [Google Scholar]
- Bianconi, A.; Missori, M.; Oyanagi, H.; Yamaguchi, H.; Ha, D.H.; Nishiara, Y.; Della Longa, S. The measurement of the polaron size in the metallic phase of cuprate superconductors. Eur. Lett. 1995, 31, 411. [Google Scholar] [CrossRef]
- Nagaev, E.L. Phase separation in high-temperature superconductors and related magnetic materials. Uspekhi Fizicheskikh Nauk 1995, 165, 529–555. [Google Scholar] [CrossRef]
- Zech, D.; Conder, K.; Keller, H.; Kaldis, E.; Liarokapis, E.; Poulakis, N.; Müller, K.A. Anharmonic Properties of High-Tc Cuprates; Mihailovic, D., Ruani, G., Kaldis, E., Müller, K.A., Eds.; World Scientific: Singapore, 1995; pp. 18–29. [Google Scholar]
- Kusmartsev, F.V.; Di Castro, D.; Bianconi, G.; Bianconi, A. Transformation of strings into an inhomogeneous phase of stripes and itinerant carriers. Phys. Lett. A 2000, 275, 118–123. [Google Scholar] [CrossRef]
- Gor’kov, L.P. Phase separation in a two-component model for cuprates. J. Supercond. 2000, 13, 765–769. [Google Scholar] [CrossRef]
- Bianconi, A.; Di Castro, D.; Bianconi, G.; Pifferi, A.; Saini, N.L.; Chou, F.C.; Johnston, D.C.; Colapietro, M. Coexistence of stripes and superconductivity: Tc amplification in a superlattice of superconducting stripes. Phys. C 2000, 341, 1719–1722. [Google Scholar] [CrossRef]
- Coleman, A.J. Phase Transitions and Self-Organization in Electronic and Molecular Networks; Phillips, J.C., Thorpe, M.F., Eds.; Kluwer: New York, NY, USA, 2001; pp. 23–35. [Google Scholar]
- Phillips, J.C. Percolative model of nanoscale phase separation in high-temperature superconductors. Philos. Mag. B 2002, 82, 783–790. [Google Scholar] [CrossRef]
- Bishop, A.R.; Lookman, T.; Saxena, A.; Shenoy, S.R. Elasticity-driven nanoscale texturing in complex electronic materials. Eur. Phys. Lett. 2003, 63, 289–295. [Google Scholar] [CrossRef]
- Phillips, J.C.; Saxena, A.; Bishop, A.R. Pseudogaps, dopants, and strong disorder in cuprate high-temperature superconductors. Rep. Prog. Phys. 2003, 66, 2111–2182. [Google Scholar] [CrossRef]
- De Mello, E.V.L.; Caixeiro, E.S. Effects of phase separation in the cuprate superconductors. Phys. Rev. B 2004, 70, 224517. [Google Scholar] [CrossRef] [Green Version]
- Kugel, K.I.; Rakhmanov, A.L.; Sboychakov, A.O. Phase separation in Jahn-Teller systems with localized and itinerant electrons. Phys. Rev. Lett. 2005, 95, 267210. [Google Scholar] [CrossRef]
- De Mello, E.V.L.; Dias, D.H.N. Phase separation and the phase diagram of cuprate superconductors. J. Phys. Condens. Matter 2007, 19, 086218. [Google Scholar] [CrossRef]
- Fine, B.V.; Egami, T. Phase separation in the vicinity of quantum-critical doping concentration: Implications for high-temperature superconductors. Phys. Rev. B 2008, 77, 014519. [Google Scholar] [CrossRef] [Green Version]
- Kugel, K.I.; Rakhmanov, A.L.; Sboychakov, A.O.; Poccia, N.; Bianconi, A. Model for phase separation controlled by doping and the internal chemical pressure in different cuprate superconductors. Phys. Rev. B 2008, 78, 165124. [Google Scholar] [CrossRef] [Green Version]
- Fratini, M.; Poccia, N.; Bianconi, A. The Feshbach resonance and nanoscale phase separation in a polaron liquid near the quantum critical point for a polaron Wigner crystal. J. Phys. 2008, 108, 012036. [Google Scholar] [CrossRef]
- Innocenti, D.; Ricci, A.; Poccia, N.; Campi, G.; Fratini, M.; Bianconi, A. A model for liquid-striped liquid phase separation in liquids of anisotropic polarons. J. Supercond. Nov. Magn. 2009, 22, 529–533. [Google Scholar] [CrossRef]
- De Mello, E.V.L.; Kasal, R.B.; Passos, C.A.C. Electronic phase separation transition as the origin of the superconductivity and pseudogap phase of cuprates. J. Phys. Condens. Matter 2009, 21, 235701. [Google Scholar] [CrossRef] [Green Version]
- Fratini, M.; Poccia, N.; Ricci, A.; Campi, G.; Burghammer, M.; Aeppli, G.; Bianconi, A. Scale-free structural organization of oxygen interstitials in La2CuO4+y. Nature 2010, 466, 841–844. [Google Scholar] [CrossRef]
- Poccia, N.; Fratini, M.; Ricci, A.; Campi, G.; Barba, L.; Vittorini-Orgeas, A.; Bianconi, G.; Aeppli, G.; Bianconi, A. Evolution and control of oxygen order in a cuprate superconductor. Nat. Mater. 2011, 10, 733–736. [Google Scholar] [CrossRef]
- Poccia, N.; Ricci, A.; Campi, G.; Fratini, M.; Puri, A.; Di Gioacchino, D.; Marcelli, A.; Reynolds, M.; Burghammer, M.; Saini, N.L.; et al. Optimum inhomogeneity of local lattice distortions in La2CuO4+y. Proc. Natl. Acad. Sic. USA 2012, 109, 15685–15690. [Google Scholar] [CrossRef]
- Pinheiro, C.F.S.; De Mello, E.V.L. Random resistivity network calculations for cuprate superconductors with an electronic phase separation transition. Physica A 2012, 391, 1532–1539. [Google Scholar] [CrossRef]
- De Mello, E.V.L. Describing how the superconducting transition in La2CuO4+y is related to the iO phase separation. J. Supercond. Nov. Magn. 2012, 25, 1347–1350. [Google Scholar] [CrossRef]
- De Mello, E.V.L. Description and connection between the oxygen order evolution and the superconducting transition in La2CuO4+y. Eur. Phys. Lett. 2012, 98, 57008. [Google Scholar] [CrossRef]
- Phillips, J.C. Ineluctable complexity of high temperature superconductivity elucidated. J. Supercond. Nov. Magn. 2014, 27, 345–347. [Google Scholar] [CrossRef]
- Bianconi, A.; Poccia, N.; Sboychakov, A.O.; Rakhmanov, A.L.; Kugel, K.I. Intrinsic arrested nanoscale phase separation near a topological Lifshitz transition in strongly correlated two-band metals. Supercond. Sci. Technol. 2015, 28, 024005. [Google Scholar] [CrossRef] [Green Version]
- Campi, G.; Bianconi, A.; Poccia, N.; Bianconi, G.; Barba, L.; Arrighetti, G.; Innocenti, D.; Karpinski, J.; Zhigadlo, N.D.; Kazakov, S.M.; et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-Tc superconductor. Nature 2015, 525, 359–362. [Google Scholar] [CrossRef]
- Agrestini, S.; Saini, N.L.; Bianconi, G.; Bianconi, A. The strain of CuO2 lattice: The second variable for the phase diagram of cuprate perovskites. J. Phys. A Math. Gen. 2003, 36, 9133–9142. [Google Scholar] [CrossRef]
- Campi, G.; Ricci, A.; Poccia, N.; Fratini, M.; Bianconi, A. X-rays Writing/Reading of charge density waves in the CuO2 plane of a simple cuprate superconductor. Condens. Matter 2017, 2, 26. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A. Evolution of complexity in out-of-equilibrium systems by time-resolved or space-resolved synchrotron radiation techniques. Condens. Matter 2019, 4, 32. [Google Scholar] [CrossRef]
- Phillips, J.C. Physics of High-Tc Superconductors; Academic: Boston, MA, USA, 1989. [Google Scholar]
- Nagamatsu, J.; Nakagawa, N.; Muranaka, T.; Zenitani, Y.; Akimitsu, J. Superconductivity at 39 K in magnesium diboride. Nature 2001, 410, 63–64. [Google Scholar] [CrossRef]
- Bauer, E.; Paul, C.; Berger, S.; Majumdar, S.; Michor, H.; Giovannini, M.; Saccone, A.; Bianconi, A. Thermal conductivity of superconducting MgB2. J. Phys. Condens. Mat. 2001, 13, L487–L493. [Google Scholar] [CrossRef]
- Agrestini, S.; Di Castro, D.; Sansone, M.; Saini, N.L.; Saccone, A.; De Negri, S.; Giovannini, M.; Colapietro, M.; Bianconi, A. High Tc superconductivity in a critical range of micro-strain and charge density in diborides. J. Phys. Condens. Matter 2001, 13, 11689–11695. [Google Scholar] [CrossRef]
- Agrestini, S.; Metallo, C.; Filippi, M.; Siminelli, L.; Campi, G.; Sanipoli, C.; Liarokapis, E.; De Negri, S.; Giovannini, M.; Saccone, A.; et al. Substitution of Sc for Mg in MgB2: Effects on transition temperature and Kohn anomaly. Phys. Rev. B 2004, 70, 134514. [Google Scholar] [CrossRef]
- Palmisano, V.; Simonelli, L.; Puri, A.; Fratini, M.; Busby, Y.; Parisiades, P.; Liarokapis, E.; Brunelli, M.; Fitch, A.N.; Bianconi, A. Controlling mesoscopic phase separation near electronic topological transitions via quenched disorder in ternary diborides. J. Phys. Condens. Matter 2008, 20, 434222. [Google Scholar] [CrossRef]
- Simonelli, L.; Palmisano, V.; Fratini, M.; Paridiades, P.; Lampakis, D.; Liarokapis, E.; Bianconi, A. Isotope effect on the E2g phonon and mesoscopic phase separation near the electronic topological transition in Mg1−xAlxB2. Phys. Rev. B 2009, 80, 014520. [Google Scholar] [CrossRef]
- Parisiades, P.; Liarokapis, E. Lattice effects in diborides. J. Supercond. Nov. Magn. 2011, 24, 49–56. [Google Scholar] [CrossRef]
- Hebard, A.F.; Rosseinsky, M.J.; Haddon, R.C.; Murphy, D.W.; Glarum, S.H.; Palstra, T.T.M.; Ramirez, A.P.; Kortan, A.R. Superconductivity at 18 K in potassium doped C60. Nature 1991, 350, 600–601. [Google Scholar] [CrossRef]
- Zhou, O.; Zhu, Q.; Fischer, J.E.; Coustel, N.; Vaughan, G.B.M.; Heiney, P.A.; McCauley, J.P., Jr.; Smith, A.B. Compressibility of M3C60 fullerene superconductors: Relation between Tc and lattice parameter. Science 1992, 255, 833–835. [Google Scholar] [CrossRef]
- Palstra, T.T.M.; Zhou, O.; Iwasa, Y.; Sulewski, P.E.; Fleming, R.M.; Zegarski, B.R. Superconductivity at 40K in cesium doped C60. Solid State Commum. 1995, 93, 327–330. [Google Scholar] [CrossRef]
- Drozdov, A.P.; Eremets, M.I.; Troyan, I.A.; Ksenofontov, V.; Shylin, S.I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73–76. [Google Scholar] [CrossRef]
- Bianconi, A.; Jarlborg, T. Superconductivity above the lowest Earth temperature in pressurized sulfur hydride. Eur. Phys. Lett. 2015, 112, 37001. [Google Scholar] [CrossRef] [Green Version]
- Jarlborg, T.; Bianconi, A. Breakdown of the Migdal approximation at Lifshitz transitions with giant zero-point motion in the H3S superconductor. Sci. Rep. 2016, 6, 24816. [Google Scholar] [CrossRef] [Green Version]
- Bianco, R.; Errea, I.; Calandra, M.; Mauri, F. High-pressure phase diagram of hydrogen and deuterium sulfides from first principles: Structural and vibrational properties including quantum and anharmonic effects. Phys. Rev. B 2018, 97, 214101. [Google Scholar] [CrossRef] [Green Version]
- Bianconi, A.; Saini, N.L.; Lanzara, A.; Missori, M.; Rossetti, T.; Oyanagi, H.; Yamaguchi, H.; Oka, K.; Ito, T. Determination of the lattice Distortions in the CuO2 Plane of La1.85Sr0.15CuO4. Phys. Rev. Lett. 1996, 76, 3412–3415. [Google Scholar] [CrossRef] [PubMed]
- Lanzara, A.; Zhao, G.M.; Saini, N.L.; Bianconi, A.; Conder, K.; Keller, H.; Müller, K.A. Oxygen-isotope shift of the charge-stripe ordering temperature in La2−xSrxCuO4 from x-ray absorption spectroscopy. J. Phys. Condens. Matter 1999, 11, L541–L546. [Google Scholar] [CrossRef]
- Lanzara, A.; Bogdanov, P.V.; Zhou, X.J.; Kellar, S.A.; Feng, D.L.; Lu, E.D.; Yoshida, T.; Eisaki, H.; Fujimori, A.; Kishio, K.; et al. Evidence for ubiquitous strong electron-phonon coupling in high-temperature superconductors. Nature 2001, 412, 510–514. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.X.; Lanzara, A.; Ishihara, S.; Nagaosa, N. Role of the electron-phonon interaction in the strongly correlated cuprate superconductors. Philos. Mag. B 2002, 82, 1349–1368. [Google Scholar] [CrossRef]
- Gweon, G.H.; Sasagawa, T.; Zhou, S.Y.; Graf, J.; Takagi, H.; Lee, D.H.; Lanzara, A. An unusual isotope effect in a high-transition-temperature superconductor. Nature 2004, 430, 187–190. [Google Scholar] [CrossRef] [Green Version]
- Graf, J.; Jozwiak, C.; Smallwood, C.L.; Eisaki, H.; Kaindl, R.A.; Lee, D.H.; Lanzara, A. Nodal quasiparticle meltdown in ultrahigh-resolution pump-probe angle-resolved photoemission. Nat. Phys. 2011, 7, 805–809. [Google Scholar] [CrossRef]
- Perali, A.; Innocenti, D.; Valletta, A.; Bianconi, A. Anomalous isotope effect near a 2.5 Lifshitz transition in a multi-band multi-condensate superconductor made of a superlattice of stripes. Supercond. Sci. Technol. 2012, 25, 124002. [Google Scholar] [CrossRef]
- Guguchia, Z.; Khasanov, R.; Bendele, M.; Pomjakushina, E.; Conder, K.; Shengelaya, A.; Keller, H. Negative Oxygen Isotope Effect on the Static Spin Stripe Order in Superconducting La2−xBaxCuO4 (x = 1/8) Observed by Muon-Spin Rotation. Phys. Rev. Lett. 2014, 113, 057002. [Google Scholar] [CrossRef]
- Bendele, M.; von Rohr, F.; Guguchia, Z.; Pomjakushina, E.; Conder, K.; Bianconi, A.; Simon, A.; Bussmann-Holder, A.; Keller, H. Evidence for strong lattice effects as revealed from huge unconventional oxygen isotope effects on the pseudogap temperature in La2−xSrxCuO4. Phys. Rev. B 2017, 95, 014514. [Google Scholar] [CrossRef]
- Caivano, R.; Fratini, M.; Poccia, N.; Ricci, A.; Puri, A.; Ren, Z.A.; Dong, X.L.; Yang, J.; Lu, W.; Zhao, Z.X.; et al. Feshbach resonance and mesoscopic phase separation near a quantum critical point in multiband FeAs-based superconductors. Supercond. Sci. Technol. 2008, 22, 014004. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Campi, G.; Joseph, B.; Arrighetti, G.; Barba, L.; Reynolds, M.; Burghammer, M.; Takeya, H.; Mizuguchi, Y.; et al. Nanoscale phase separation in the iron chalcogenide superconductor K0.8Fe1.6Se2 as seen via scanning nanofocused x-ray diffraction. Phys. Rev. B 2011, 84, 060511. [Google Scholar] [CrossRef]
- Bianconi, A. Quantum materials: Shape resonances in superstripes. Nat. Phys. 2013, 9, 536–537. [Google Scholar] [CrossRef]
- Bendele, M.; Barinov, A.; Joseph, B.; Innocenti, D.; Iadecola, A.; Bianconi, A.; Takeya, H.; Mizuguchi, Y.; Takano, T.; Noji, T.; et al. Spectromicroscopy of electronic phase separation in KxFe2−ySe2 superconductor. Sci. Rep. 2014, 4, 5592. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Joseph, B.; Innocenti, D.; Campi, G.; Zozulya, A.; Westermeier, A.; Schavkan, A.; Coneri, F.; Bianconi, A.; et al. Direct observation of nanoscale interface phase in the superconducting chalcogenide KxFe2−ySe2 with intrinsic phase separation. Phys. Rev. B 2015, 91, 020503. [Google Scholar] [CrossRef]
- Simonelli, L.; Mizokawa, T.; Sala, M.M.; Takeya, H.; Mizuguchi, Y.; Takano, Y.; Garbarino, G.; Monaco, G.; Saini, N.L. Temperature dependence of iron local magnetic moment in phase-separated superconducting chalcogenide. Phys. Rev. B 2014, 90, 214516. [Google Scholar] [CrossRef]
- Mangelis, P.; Lei, H.; McDonnell, M.; Feygenson, M.; Petrovic, C.; Bozin, E.; Lappas, A. On the Nanoscale Structure of KxFe2−yCh2 (Ch=S, Se): A Neutron Pair Distribution Function View. Condens. Matter 2018, 3, 20. [Google Scholar] [CrossRef]
- Bianconi, A. Multiplet splitting of final-state configurations in x-ray-absorption spectrum of metal VO2: Effect of core-hole-screening, electron correlation, and metal-insulator transition. Phys. Rev. B 1982, 26, 2741. [Google Scholar] [CrossRef]
- Marcelli, A.; Coreno, M.; Stredansky, M.; Xu, W.; Zou, C.; Fan, L.; Wangsheng, C.; Wei, S.; Cossaro, A.; Ricci, A.; et al. Nanoscale phase separation and lattice complexity in VO2: The metal-insulator transition investigated by XANES via Auger electron yield at the vanadium L23-edge and resonant photoemission. Condens. Matter 2017, 2, 38. [Google Scholar] [CrossRef]
- Gioacchino, D.; Marcelli, A.; Puri, A.; Zou, C.; Fan, L.; Zeitler, U.; Bianconi, A. Metastability phenomena in VO2 thin films. Condens. Matter 2017, 2, 10. [Google Scholar] [CrossRef]
- Corder, S.N.G.; Jiang, J.; Chen, X.; Kittiwatanakul, S.; Tung, I.C.; Zhu, Y.; Zhang, J.; Bechtel, H.; Martin, M.C.; Carr, L.G.; et al. Controlling phase separation in vanadium dioxide thin films via substrate engineering. Phys. Rev. B 2017, 96, 161110. [Google Scholar] [CrossRef] [Green Version]
- Vidas, L.; Günther, C.M.; Miller, T.A.; Pfau, B.; Perez-Salinas, D.; Martínez, E.; Schneider, M.; Guhrs, E.; Gargiani, P.; Valvidares, M.; et al. Imaging Nanometer Phase Coexistence at Defects During the Insulator-Metal Phase Transformation in VO2 Thin Films by Resonant Soft X-ray Holography. Nano Lett. 2018, 18, 3449–3453. [Google Scholar] [CrossRef] [PubMed]
- Grandi, F.; Amaricci, A.; Fabrizio, M. Unraveling the Mott-Peierls intrigue in Vanadium dioxide. arXiv 2019, arXiv:1906.10632. [Google Scholar]
- Thomsen, C. Light Scattering in Solids; Cardona, M., Guntherodt, G., Eds.; Springer-Verlag: Berlin, Germany, 1991; Volume VI, pp. 285–359. [Google Scholar]
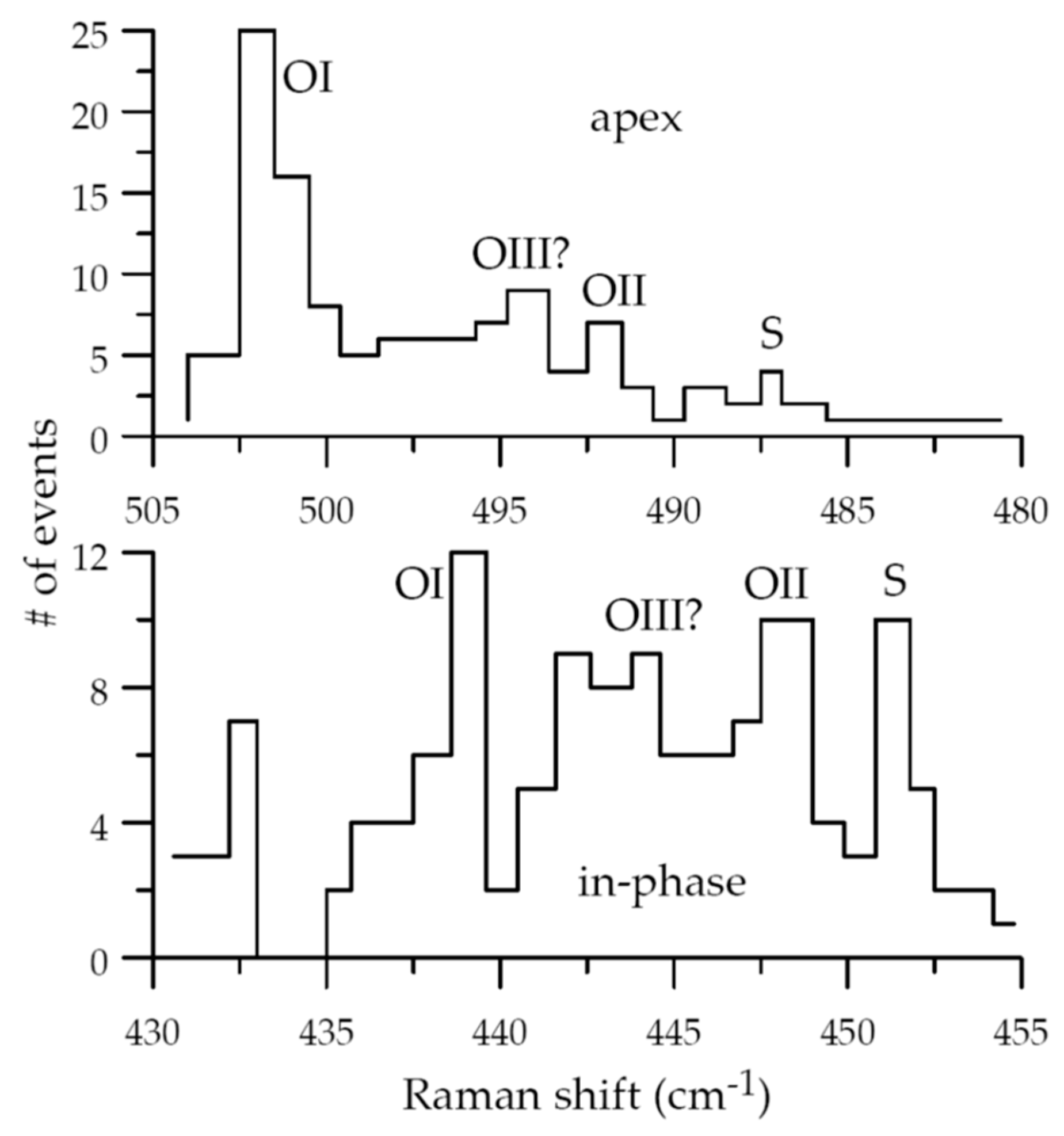
- Iliev, M.N.; Thomsen, C.; Hadjiev, V.; Cardona, M. Resonant Raman scattering of oxygen-deficient YBa2Cu3O7−δ: Evidence for the coexistence of ortho-I, ortho-II, and tetragonal microstructures. Phys. Rev. B 1993, 47, 12341–12344. [Google Scholar] [CrossRef]
- Poulakis, N.; Palles, D.; Liarokapis, E.; Conder, K.; Kaldis, E.; Müller, K.A. Phase separation and softening of the O2,3 in-phase mode in the YBa2Cu3Ox superconductors. Phys. Rev. B 1996, 53, 219–220. [Google Scholar] [CrossRef]
- Mihailovic, D.; McCarty, K.F.; Ginley, D.S. Anharmonic properties and the two-particle continuum in the Raman spectra of YBa2Cu3O6.9, TlBa2CaCu2O7, and Tl2Ba2CaCu2O8. Phys. Rev. B 1993, 47, 8910–8916. [Google Scholar] [CrossRef]
- Ruani, G.; Taliani, C.; Muccini, M.; Conder, K.; Kaldis, M.; Keller, H.; Zech, D.; Muller, K.A. Apex anharmonicity observed by Raman scattering in 18O substituted YBa2Cu3O6+x. Physica C 1994, 226, 101–105. [Google Scholar] [CrossRef]
- Palles, D.; Poulakis, N.; Liarokapis, E.; Conder, K.; Kaldis, E.; Muller, K.A. Raman study of the oxygen anharmonicity in YBa2Cu3Ox (6.4 < x < 7.0) superconductors. Phys. Rev. B 1996, 54, 6721–6727. [Google Scholar]
- Cooper, S.L.; Slakey, F.; Klein, M.V.; Rice, J.P.; Bukowski, E.D.; Ginsberg, D.M. Gap anisotropy and phonon self-energy effects in single-crystal YBa2Cu3O7−δ. Phys. Rev. B 1988, 38, 11934–11937. [Google Scholar] [CrossRef]
- Deveraux, T.P.; Einzel, D.; Stadlober, B.; Hackl, R.; Leach, D.H.; Neumeier, J.J. Electronic Raman scattering in high-Tc superconductors: A probe of dx2−y2 pairing. Phys. Rev. Lett. 1994, 72, 396–399. [Google Scholar] [CrossRef] [PubMed]
- Heyen, E.T.; Wegerer, R.; Schonherr, E.; Cardona, M. Raman study of the coupling of crystal-field excitations to phonons in NdBa2Cu3O7−δ. Phys. Rev. B 1991, 44, 10195–10205. [Google Scholar] [CrossRef] [PubMed]
- Parisiades, P.; Lampakis, D.; Palles, D.; Liarokapis, E.; Zhigadlo, N.D.; Katrysh, S.; Karpinski, J. Two-mode behavior for the E2g broad band in Mg(B1−xCx)2. Phys. C 2008, 468, 1064–1069. [Google Scholar] [CrossRef]
- Calamiotou, M.; Margiolaki, I.; Gantis, A.; Siranidi, E.; Ren, Z.A.; Zhao, Z.X.; Liarokapis, E. Lattice anomalies in the FeAs4 tetrahedra of the NdFeAsO0.85 superconductor that disappear at Tc. Eur. Phys. Lett. 2010, 91, 57005. [Google Scholar] [CrossRef]
- Liarokapis, E.; Calamiotou, M.; Zhigadlo, N.D.; Katrysh, S.; Karpinski, J. Non-linera lattice response of Sm oxypnictides to hydrostatic pressure. J. Phys. Chem. Solid 2013, 74, 1465–1469. [Google Scholar] [CrossRef]
- Calamiotou, M.; Lampakis, D.; Zhigadlo, N.D.; Katrysh, S.; Karpinski, J.; Fitch, A.; Tsiaklaganos, P.; Liarokapis, E. Local lattice distortions vs. structural phase transition in NdFeAsO1−xFx. Phys. C 2016, 527, 55–62. [Google Scholar] [CrossRef]
- Thomsen, C.; Cardona, M. Physical Properties of High Temperature Superconductors; Ginsberg, D.M., Ed.; World Scientific: Singapore, 1994; p. 409. [Google Scholar]
- Plakida, N.M. High Temperature Superconductivity; Springer-Verlag: Berlin, Germany, 1995. [Google Scholar]
- FacFarlane, R.M.; Rosen, H.J.; Engler, E.M.; Jacowitz, R.D.; Lee, V.Y. Raman study of the effect of oxygen stoichiometry on the phonon spectrum of the high-Tc superconductor YBa2Cu3Ox. Phys. Rev. B 1988, 38, 284–289. [Google Scholar] [CrossRef]
- Wille, L.T.; Berera, A.; deFontaine, D. Thermodynamics of oxygen ordering in YBa2Cu3Oz. Phys. Rev. Lett. 1988, 60, 1065–1068. [Google Scholar] [CrossRef]
- Cava, R.J.; Hewat, A.W.; Hewat, E.A.; Batlogg, B.; Marezio, M.; Rabe, K.M.; Krajewski, J.J.; Peck, W.F.; Rupp, L.W., Jr. Structural anomalies, oxygen ordering and superconductivity in oxygen deficient Ba2YCu3Ox. Physica C 1990, 165, 419–433. [Google Scholar] [CrossRef]
- Schleger, P.; Casalta, H.; Hadfield, R.; Poulsen, H.F.; von Zimmermann, M.; Andersen, N.H.; Schneider, J.R.; Liang, R.; Dosanjh, P.; Hardy, W.N. Observation of ortho-III correlations by neutron and hard X-ray scattering in an untwined YBa2Cu3O6.77 single crystal. Physica C 1995, 241, 103–110. [Google Scholar] [CrossRef]
- Dagotto, E. Correlated electrons in high-temperature superconductors. Rev. Mod. Phys. 1992, 66, 763–841. [Google Scholar] [CrossRef]
- Heyen, E.T.; Kircher, J.; Cardona, M. Resonant Raman scattering in insulating YBa2Cu3O6 as a probe of its electronic structure. Phys. Rev. B 1992, 45, 3037–3047, and references therein. [Google Scholar] [CrossRef] [PubMed]
- Denisov, V.N.; Taliani, C.; Mal’shukov, A.G.; Burlakov, V.M.; Schonherr, E.; Ruani, G. Infrared excited Raman scattering and photoluminescence of deep intragap states in semiconducting YBa2Cu3O6+x. Phys. Rev. B 1993, 48, 16714–16721. [Google Scholar] [CrossRef] [PubMed]
- Mesot, J.; Allenspach, P.; Staub, U.; Furrer, A.; Mutka, H. Neutron spectroscopic evidence for cluster formation and percolative superconductivity in ErBa2Cu3Ox. Phys. Rev. Lett. 1993, 70, 865–868. [Google Scholar] [CrossRef]
- Liarokapis, E. Raman spectroscopy, structural modifications and phase transitions in the high-temperature superconductors. J. Supercond. 2000, 13, 889–893. [Google Scholar] [CrossRef]
- Pintschovius, L.; Reichardt, W. Inelastic neutron scattering studies of the lattice vibrations of high Tc compounds. In Physical Properties of High Temperature Superconductors; Ginsberg, D.M., Ed.; World Scientific: Singapore, 1994; pp. 295–374. [Google Scholar]
- Reyes-Gasga, J.; Krekels, T.; van Tendeloo, G.; van Landuyt, J.; Amelinckx, S.; Bruggink, W.H.M.; Verweij, H. 3-d vacancy ordered superstructures in “homogeneous” YBa2Cu3O7−δ. Physica C 1989, 159, 831–848. [Google Scholar] [CrossRef]
- Alario-Franco, M.A.; Chaillout, C.; Capponi, J.J.; Chenavas, J.; Marezio, M. A family of non-stoichiometric phases based on Ba2YCu3O7−δ (0 ≤ δ ≤ 1). Physica C 1988, 156, 455–460. [Google Scholar] [CrossRef]
- Sonntag, R.; Hohlwein, D.; Brückel, T.; Collin, G. First observation of superstructure reflections by neutron diffraction due to oxygen ordering in YBa2Cu3O6.35. Phys. Rev. Lett. 1991, 66, 1497–1500. [Google Scholar] [CrossRef]
- Zimmermann, V.M.; Schneider, J.R.; Frello, T.; Andersen, N.H.; Madsen, J.; Käll, M.; Poulsen, H.F.; Liang, R.; Dosanjh, P.; Hardy, W.N. Oxygen-ordering superstructures in underdoped YBa2Cu3O6+x studied by hard x-ray diffraction. Phys. Rev. B 2003, 68, 104515. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Campi, G.; Coneri, F.; Caporale, A.S.; Innocenti, D.; Burghammer, M.V.; Zimmermann, M.; Bianconi, A. Multiscale distribution of oxygen puddles in 1/8 doped YBa2Cu3O6.67. Sci. Rep. 2013, 3, 2383. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Campi, G.; Coneri, F.; Barba, L.; Arrighetti, G.; Polentarutti, M.; Burghammer, M.; Sprung, M.V.; Zimmermann, M.; et al. Networks of superconducting nano-puddles in 1/8 doped YBa2Cu3O6.5+y controlled by thermal manipulation. New J. Phys. 2014, 16, 053030. [Google Scholar] [CrossRef]
- Campi, G.; Ricci, A.; Poccia, N.; Bianconi, A. Imaging Spatial Ordering of the Oxygen Chains in YBa2Cu3O6+y at the Insulator-to-Metal Transition. J. Supercond. Nov. Mater. 2014, 27, 987–990. [Google Scholar] [CrossRef]
- Rohler, J.; Loeffen, P.W.; Mullender, S.; Conder, K.; Kaldis, E. Local structure studies of the underdoped-overdoped transition in YBa2Cu3Ox. In High-Tc Superconductivity 1996: Ten Years after the Discovery; Kaldis, E., Liarokapis, E., Muller, K.A., Eds.; NATO ASI Series; Kluwer Academic Publ.: Dordrecht, The Netherlands, 1997; pp. 469–502. [Google Scholar]
- Conder, K.; Zech, D.; Kruger, C.H.; Kaldis, E.; Keller, H.; Hewat, A.W.; Jilek, E. Indications for a phase separation in YBa2Cu3O7−x. In Phase Separation in Cuprate Superconductors; Sigmund, E., Muller, K.A., Eds.; Springer: Berlin/Herdelberg, Germany, 1994; pp. 210–224. [Google Scholar]
- Kaldis, E.; Röhler, J.; Liarokapis, E.; Poulakis, N.; Conder, K.; Loeffen, P.W. A displacive structural transformation in the CuO2 planes of YBa2Cu3Ox at the underdoped-overdoped phase separation line. Phys. Rev. Lett. 1997, 79, 4894–4897. [Google Scholar] [CrossRef]
- Calamiotou, M.; Gantis, A.; Palles, D.; Lampakis, D.; Liarokapis, E.; Koufoudakis, A. Phase separation and internal strains in the mixed La0.5R0.5Ba2Cu3Oy compounds (R = rare-earth element). Phys. Rev. B 1998, 58, 15238–15246. [Google Scholar] [CrossRef]
- Bogachev, G.; Abrashev, M.; Iliev, M.N.; Poulakis, N.; Liarokapis, E.; Mitros, C.; Koufoudakis, A.; Psyharis, V. Raman study of R0.5Pr0.5Ba2Cu3O7−δ. Phys. Rev. B 1994, 49, 12151–12158. [Google Scholar] [CrossRef] [PubMed]
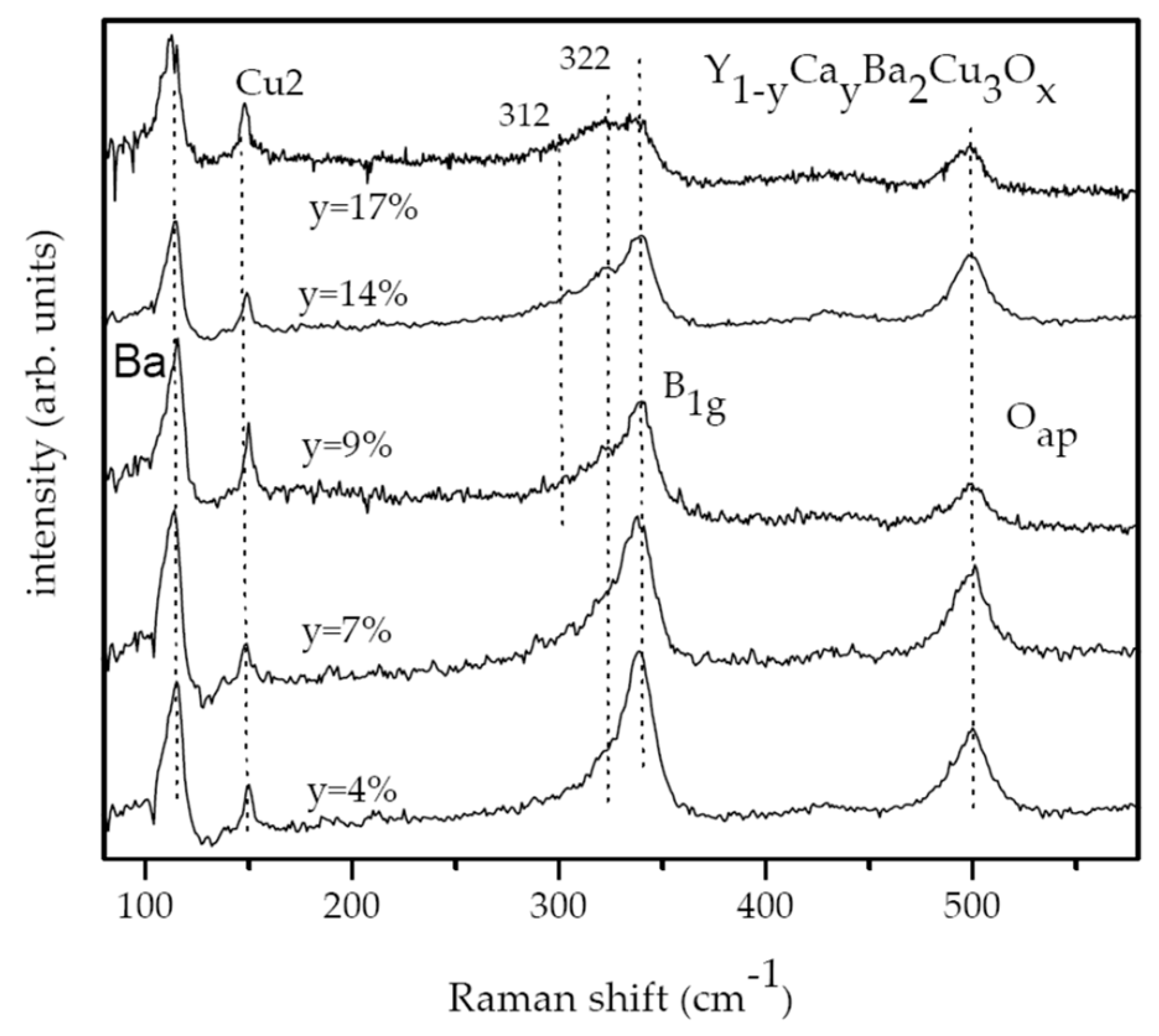
- Palles, D.; Liarokapis, E.; Leventouri, T.H.; Chakoumakos, B.C. The effect of Ca substitution on the structure and the Raman active phonons in Y1−xCaxBa2Cu3O7−δ. J. Phys. Condens. Matter 1998, 10, 2515–2524. [Google Scholar] [CrossRef]
- Friedl, B.; Thomsen, C.; Cardona, M. Determination of the superconducting gap in RBa2Cu3O7−δ. Phys. Rev. Lett. 1990, 65, 915–918. [Google Scholar] [CrossRef]
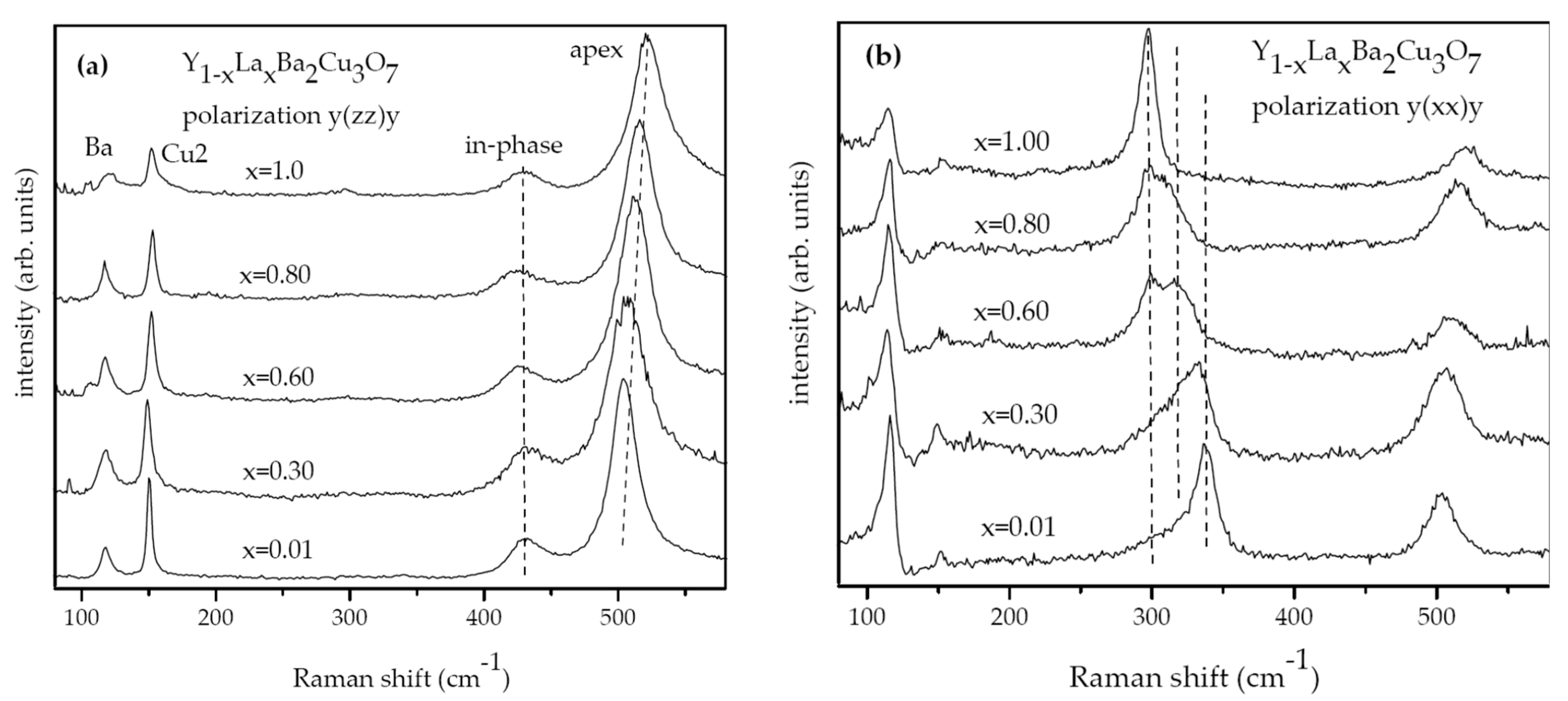
- Gantis, A.; Calamiotou, M.; Palles, D.; Lampakis, D.; Liarokapis, E. Phase formation and lattice strain in superconducting compound Y1−xLaxBa2Cu3Oy (0 ≤ x ≤ 1). Phys. Rev. B 2003, 68, 064502. [Google Scholar] [CrossRef]
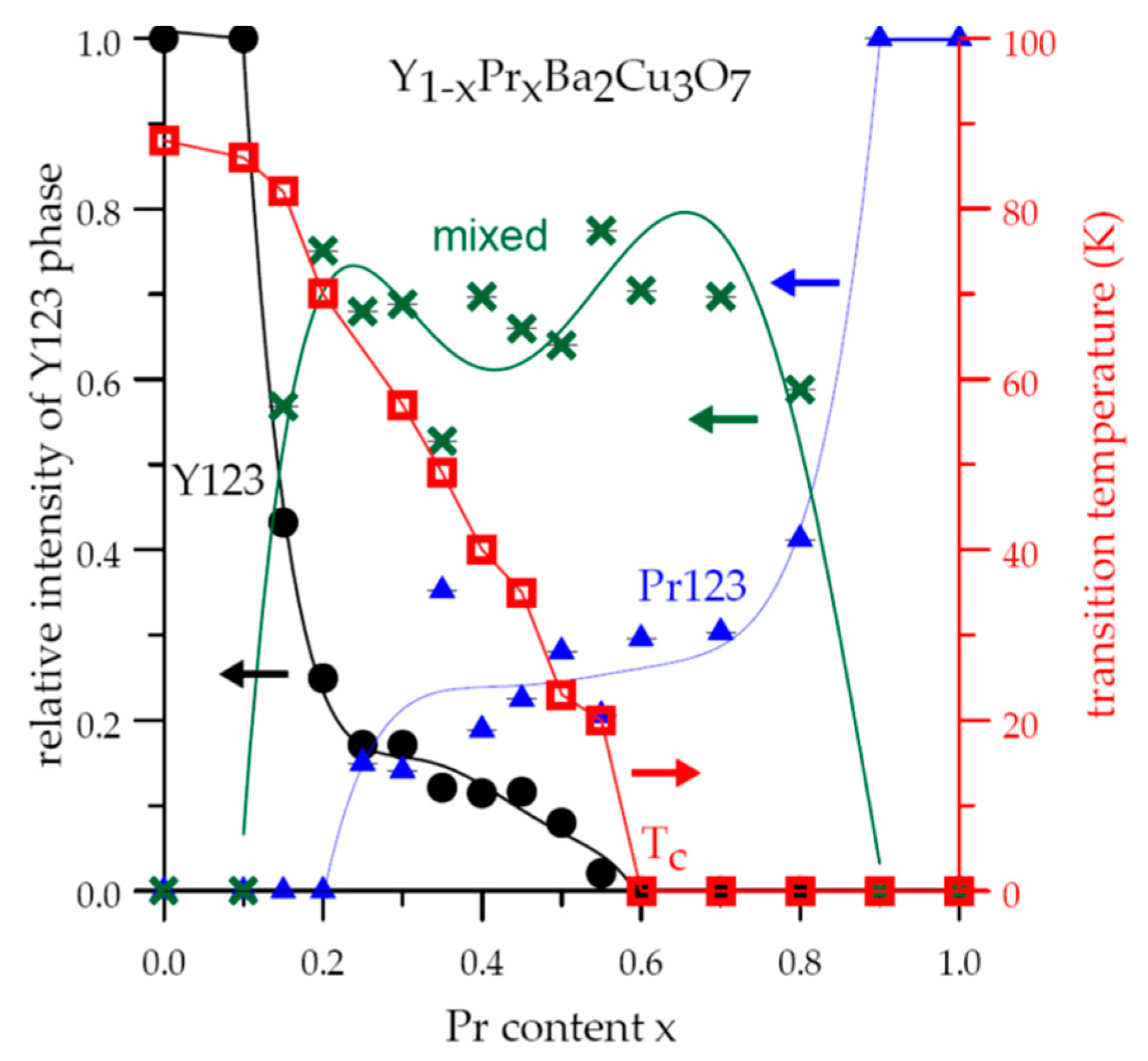
- Calamiotou, M.; Gantis, A.; Margiolaki, I.; Palles, D.; Siranidi, E.; Liarokapis, E. Phase separation, microstructure and superconductivity in the Y1−xPrxBa2Cu3Oy compounds. J. Condens. Matter 2008, 20, 395224. [Google Scholar] [CrossRef]
- Rosen, H.J.; Macfarlane, R.M.; Engler, E.M.; Lee, V.Y.; Jacowitz, R.D. Systematic Raman study of effects of rare-earth substitution on the lattice modes of high Tc superconductors. Phys. Rev. 1988, 38, 2460–2465. [Google Scholar] [CrossRef]
- Chang, I.F.; Mitra, S.S. Long wavelength optical phonons in mixed crystals. Adv. Phys. 1971, 20, 359–404. [Google Scholar] [CrossRef]
- Röhler, J.; Friedrich, C.; Granzow, T.; Kaldis, E.; Böttger, G. High Temperature Superconductivity; AIP Conf. Proc. No. 483; Barnes, S.E., Ed.; AIP: New York, NY, USA, 1999; pp. 320–323. [Google Scholar]
- Lampakis, D.; Liarokapis, E.; Karpinski, J.; Panagopoulos, C.; Nishizaki, T. Local lattice distortions and phase separation in cuprates. J. Supercond. 2004, 17, 121–125. [Google Scholar] [CrossRef]
- Liarokapis, E.; Lampakis, D.; Palles, D.; Karpinski, J.; Panagopoulos, C. A Raman view of lattice distortions an charge transfer in cuprates. J. Phys. Chem. Solid 2006, 67, 2065–2071. [Google Scholar] [CrossRef]
- Lampakis, D.; Palles, D.; Liarokapis, E.; Kazakov, S.M.; Karpinski, J. Hydrostatic pressure induced phase separation in the YBa2Cu4O8 superconductor. J. Phys. Rev. B 2005, 72, 014539. [Google Scholar] [CrossRef]
- Osada, M.; Kakihana, M.; Käll, M.; Börjesson, L. Pressure-induced effects in high-Tc superconductors: Raman scattering as a probe of charge-lattice dynamics under high pressure. Physica C 2001, 357–360, 142–145. [Google Scholar] [CrossRef]
- Liarokapis, E.; Lampakis, D.; Panagopoulos, C.; Nishizaki, T. High pressure study of Bi-2212. High Press. Res. 2003, 23, 111–115. [Google Scholar] [CrossRef]
- Orenstein, J.; Millis, A.J. Advances in the Physics of high-temperature superconductivity. Science 2000, 288, 468–474. [Google Scholar] [CrossRef]
- Lampakis, D.; Liarokapis, E.; Panagopoulos, C. Micro-Raman evidence for topological charge order across the superconducting dome of La2−xSrxCuO4. Phys. Rev. B 2006, 73, 174518. [Google Scholar] [CrossRef]
- Liarokapis, E.; Lampakis, D.; Nishizaki, T.; Panagopoulos, C. Raman studies of the high pressure effects in high Tc superconductors. High Press. Res. 2000, 18, 109–116. [Google Scholar] [CrossRef]
- Koch, U.; Lotter, N.; Wittig, J.; Assmus, W.; Gegenheimer, B.; Winzer, K. Pressure dependence of Tc for single crystal YBa2Cu3O7−x up to 10 GPa. Solid State Commum. 1988, 67, 959–963. [Google Scholar] [CrossRef]
- Scholtz, J.J.; van Eenige, E.N.; Wijngaarden, R.J.; Griessen, R. Pressure dependence of Tc and Hc2 of YBa2Cu3O8. Phys. Rev. B 1992, 45, 3077–3082. [Google Scholar] [CrossRef] [PubMed]
- Calamiotou, M.; Gantis, A.; Siranidi, E.; Lampakis, D.; Karpinski, J.; Liarokapis, E. Pressure-induced lattice instabilities and superconductivity in YBa2Cu4O8 and optimally doped YBa2Cu3O7−δ. Phys. Rev. B 2009, 80, 214517. [Google Scholar] [CrossRef]
- Karpinski, J.; Kazakov, S.M.; Angst, M.; Mironov, A.; Mali, M.; Roos, J. Influence of Sr substitution on the structure, charge distribution, and critical temperature of Y(Ba1−xSrx)2Cu4O8 single crystals. Phys. Rev. B 2001, 64, 094518. [Google Scholar] [CrossRef]
- Calamiotou, M.; Gantis, A.; Lampakis, D.; Siranidi, E.; Liarokapis, E.; Margiolaki, I.; Conder, K. Pressure-induced phase separation in the Y123 superconductor. Eur. Phys. Lett. 2009, 85, 26004. [Google Scholar] [CrossRef]
- Kenichi, T. Evaluation of the hydrostaticity of a helium-pressure medium with powder x-ray diffraction techniques. J. Appl. Phys. 2001, 89, 662–668. [Google Scholar]
- Calamiotou, M.; Parisiades, P.; Siranidi, E.; Lampakis, D.; Conder, K.; Liarokapis, E. Pressure induced lattice effects in pure and near optimally doped La2−xSrxCuO4. Physica C 2019, 565, 1353516. [Google Scholar] [CrossRef]
- Ohtani, T.; Himeda, Y.; Norimatsu, Y.; Akiyama, N. Tc increase of Bi2212 induced by exposure to organic liquids or by photocatalytic effect using TiO2. Bull. Okayama Univ. Sci. 2016, 52, 35–44. [Google Scholar]
- Raghuveer, V.; Thampi, R.; Xanthopoulos, N.; Mathieu, H.J.; Viswanathan, B. Rare earth cuprates as electrocatalysts for ethanol oxidation. Solid State Ion. 2001, 140, 263–274. [Google Scholar] [CrossRef]
- Gupta, M.; Gupta, R. Pressure dependence of the hole concentration in superconducting La1.85Sr0.15CuO4. Physica C 1991, 173, 381–386. [Google Scholar] [CrossRef]
- Ganguly, P.; Shah, N.; Phadke, M.; Ramaswamy, V.; Mulla, I.S. Deviations from Vegard’s law: Charges in the c-axis parameter in La2−xSrxCuO4−d in relation to the insulator-superconductor-metal transition. Phys. Rev. B 1993, 47, 991–995. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liarokapis, E. Probing Phase Separation and Local Lattice Distortions in Cuprates by Raman Spectroscopy. Condens. Matter 2019, 4, 87. https://doi.org/10.3390/condmat4040087
Liarokapis E. Probing Phase Separation and Local Lattice Distortions in Cuprates by Raman Spectroscopy. Condensed Matter. 2019; 4(4):87. https://doi.org/10.3390/condmat4040087
Chicago/Turabian StyleLiarokapis, Efthymios. 2019. "Probing Phase Separation and Local Lattice Distortions in Cuprates by Raman Spectroscopy" Condensed Matter 4, no. 4: 87. https://doi.org/10.3390/condmat4040087
APA StyleLiarokapis, E. (2019). Probing Phase Separation and Local Lattice Distortions in Cuprates by Raman Spectroscopy. Condensed Matter, 4(4), 87. https://doi.org/10.3390/condmat4040087




