Dzyaloshinskii–Moriya Coupling in 3d Insulators
Abstract
:1. Introduction
2. Microscopic Theory of the Isotropic Superexchange Coupling
3. Microscopic Theory of the DM Coupling
3.1. Moriya’s Microscopic Theory
- When C is a center of inversion: .
- When a mirror plane ⊥AB passes through C, mirror plane or AB.
- When there is a mirror plane including A and B, mirror plane.
- When a twofold rotation axis ⊥ AB passes through C, twofold axis.
- When there is an n-fold axis (n ≥ 2) along AB, AB.
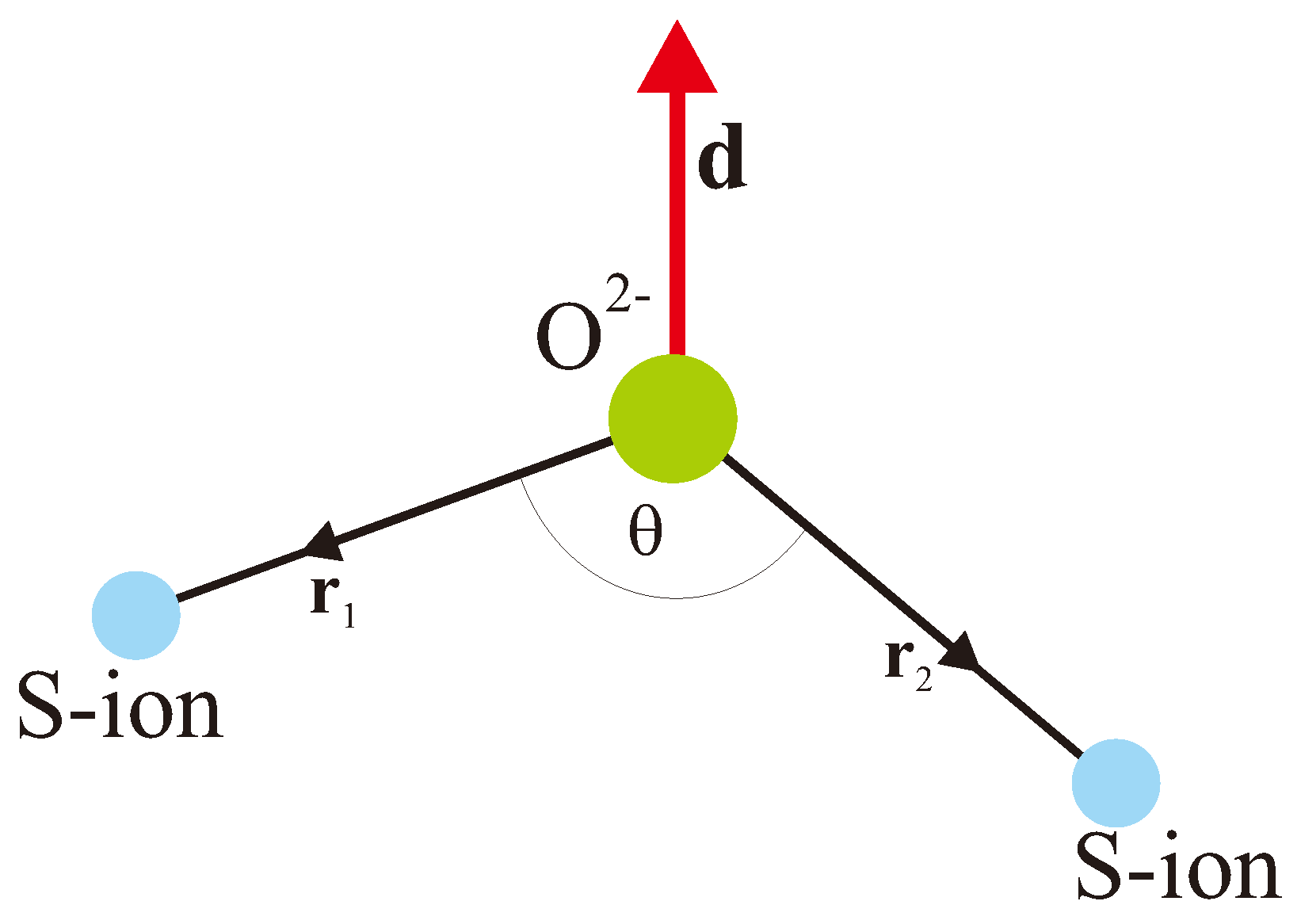
3.2. Microscopic Theory of the DM Coupling: Direct Exchange Interaction of the S-Type Ions
3.3. Microscopic Theory of the DM Coupling: Superexchange Interaction of the S-Ions
3.4. Microscopic Theory of the DM Coupling: Superexchange Interaction of the S-Type Ions in a Strong Cubic Crystal Field
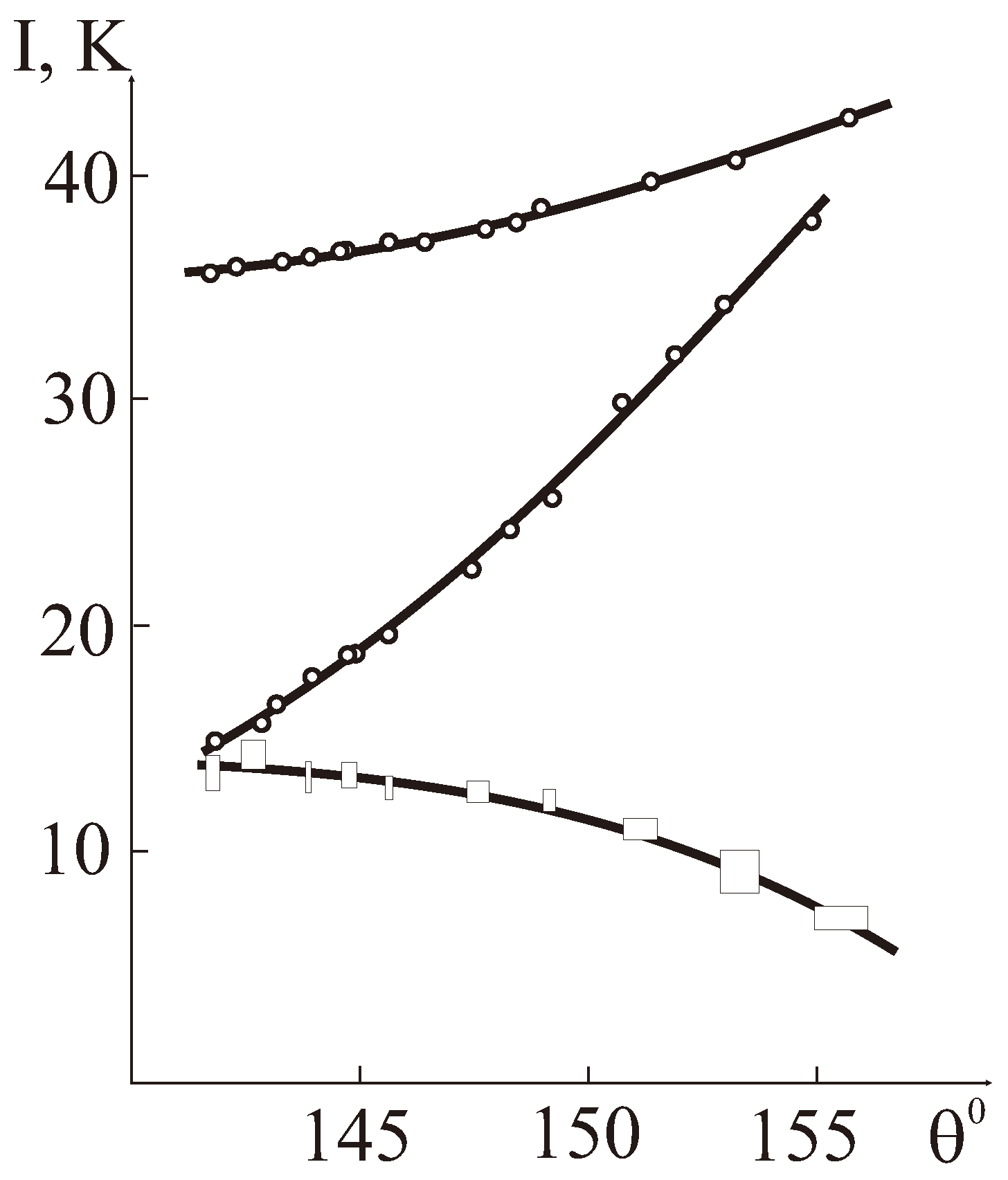
3.5. DM Coupling in Trigonal Hematite -
3.6. DM Coupling with Participation of Rare-Earth Ions
4. Theoretical Predictions as Compared with Experiment
4.1. Overt and Hidden Canting in Orthoferrites
4.2. The DM Coupling and Effective Magnetic Anisotropy
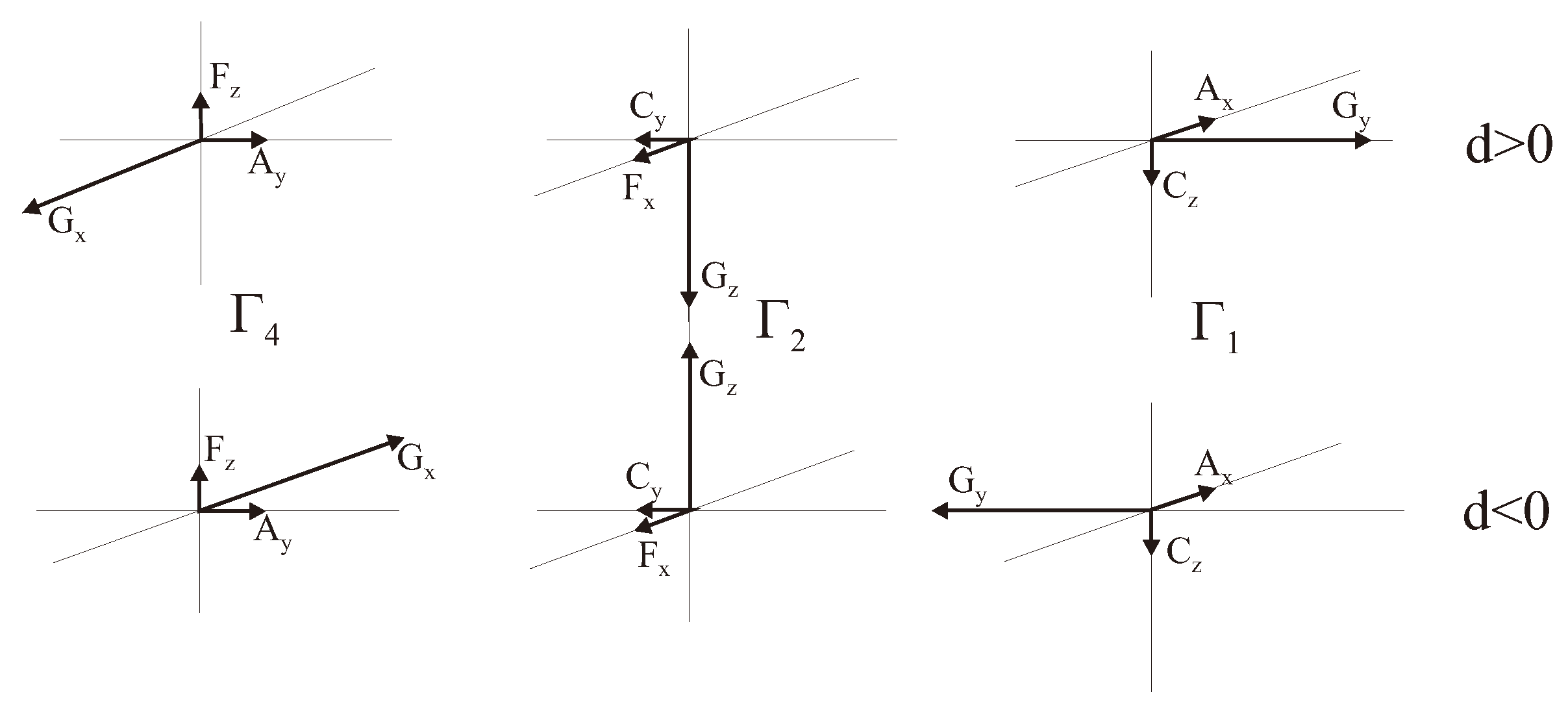
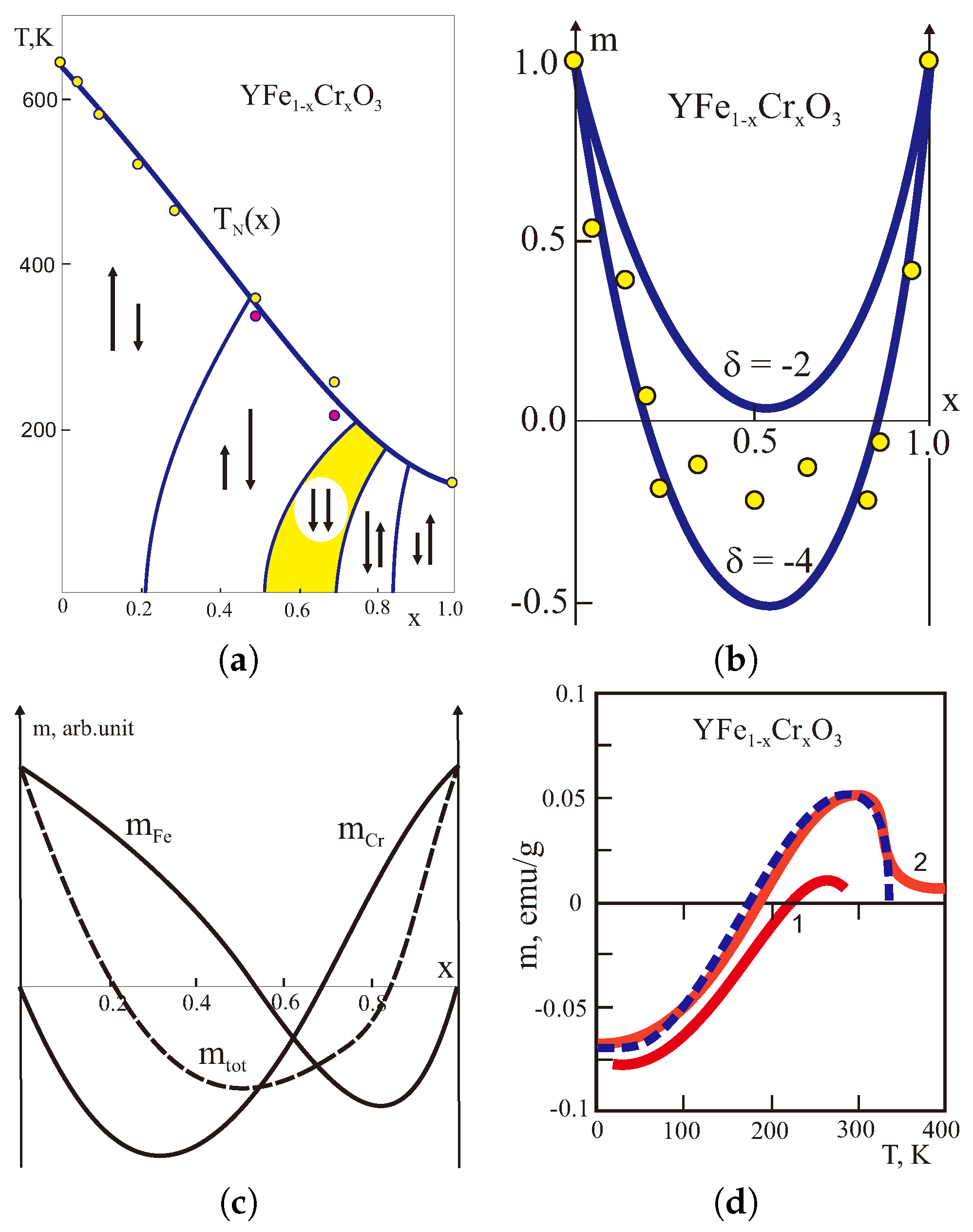
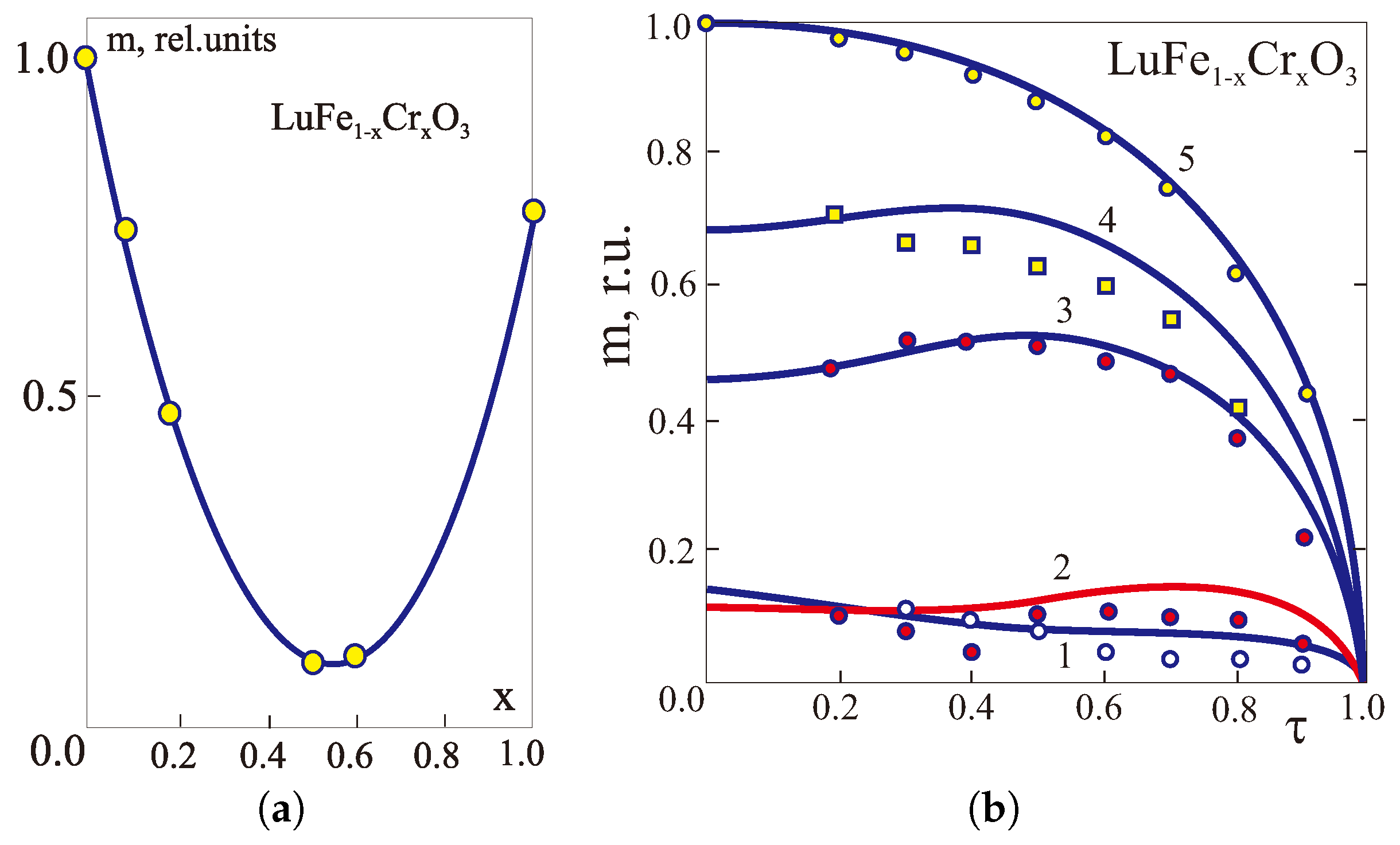
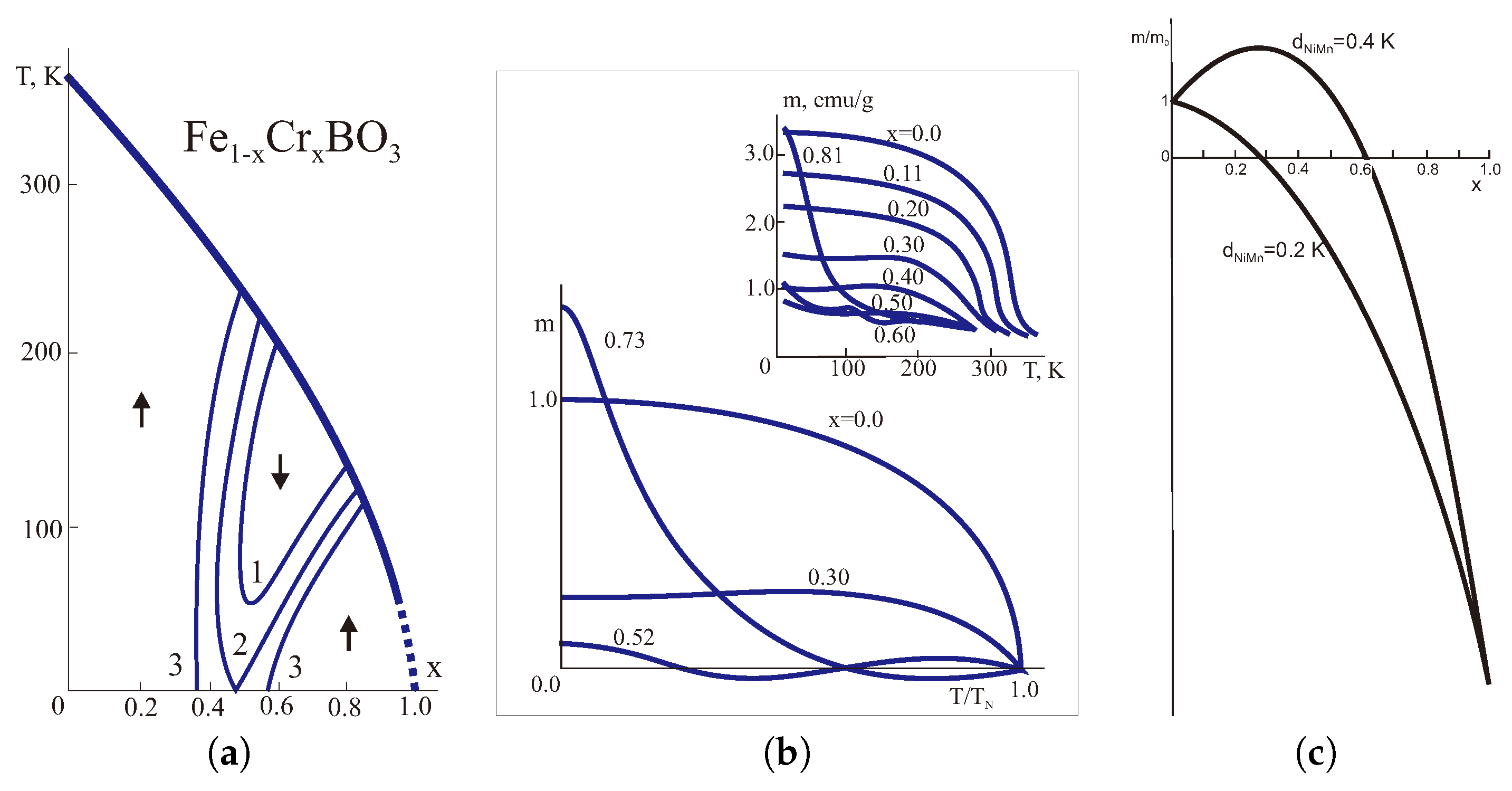
4.3. Weak Ferrimagnetism as a Novel Type of Magnetic Ordering in Systems with Competing Signs of the Dzyaloshinskii Vector
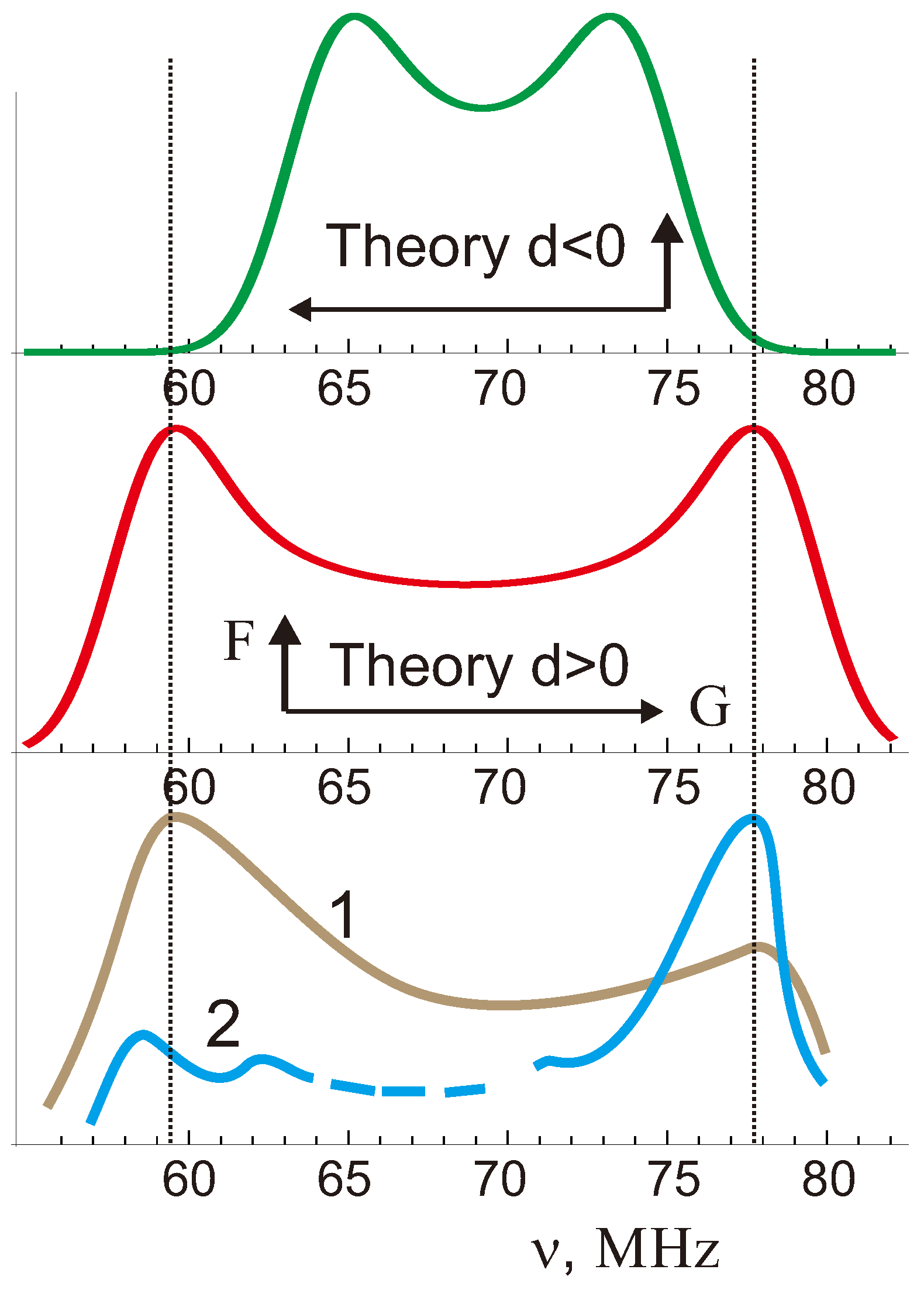
5. Determination of the Sign of the Dzyaloshinskii Vector
5.1. Ligand NMR in Weak Ferromagnets and First Determination of the Sign of the Dzyaloshinskii Vector
5.2. Sign of the Dzyaloshinskii Vector in FeBO and -FeO
6. DM Coupling in the Three-Center Two-Electron/Hole System: Cuprates
6.1. Effective Hamiltonian
6.2. DM Coupling
6.2.1. Copper Contribution
6.2.2. Ligand Contribution
6.2.3. DM Coupling in LaCuO and Related Cuprates
6.3. DM Coupled Cu-O-Cu Bond in External Fields
7. The O NMR in LCO: Field-Induced Staggered Magnetization
8. DM Coupling in Helimagnetic CsCuCl3
9. Effective Two-Ion Symmetric Spin Anisotropy Due to DM Coupling
10. “First-Principles” Calculations of the DM Coupling
11. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Smith, T. The magnetic properties of hematite. Phys. Rev. 1916, 8, 721–737. [Google Scholar] [CrossRef]
- Matarrese, L.M.; Stout, J.W. Magnetic Anisotropy of NiF2. Phys. Rev. 1954, 94, 1792–1793. [Google Scholar] [CrossRef]
- Borovik-Romanov, A.S.; Orlova, M.P. Magnetic Properties of Cobalt and Manganese Carbonates. Sov. Phys. JETP 1956, 4, 531–534. [Google Scholar]
- Dzyaloshinskii, I.E. Thermodynamic theory of weak ferromagnetism in antiferromagnetic substances. Sov. Phys. JETP 1957, 5, 1259–1272. [Google Scholar]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. New Mechanism of Anisotropic Superexchange Interaction. Phys. Rev. Lett. 1960, 4, 228–230. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 1960, 120, 91–98. [Google Scholar] [CrossRef]
- Keffer, F. Moriya Interaction and the Problem of the Spin Arrangements in β MnS. Phys. Rev. 1962, 126, 896–900. [Google Scholar] [CrossRef]
- Moskvin, A.S. Many-electron theory of superexchange. Fizika Tverdogo Tela 1970, 12, 3209–3220, (Sov. Phys. Solid State USSR 1971, 12, 2593–2604). [Google Scholar]
- Moskvin, A.S.; Sinitsyn, E.V. Magnetic interactions in rare-earth orthoferrites. Fizika Tverdogo Tela 1972, 14, 2535–2543. [Google Scholar]
- Moskvin, A.S.; Sinitsyn, E.V. Antisymmetrical exchange and four-sublattice model in orthoferrites. Fizika Tverdogo Tela 1975, 17, 2495–2497, (Sov. Phys. Solid State USSR 1975, 17, 2495–2497). [Google Scholar]
- Moskvin, A.S.; Bostrem, I.G. Some Peculiarities of Exchange Interactions in Orthoferrite-Orthochromites. Fizika Tverdogo Tela 1977, 19, 1616–1626, (Sov. Phys. Solid State USSR 1977, 19, 1532–1542). [Google Scholar]
- Moskvin, A.S. Antisimmetrichniy Obmen i Magnitnaya Anizotropiya v Slabyh Ferromagnetikah (Antisymmetric Exchange and Magnetic Anisotropy in Weak Ferromagnets). Ph.D. Dissertation, Lomonosov Moscow State University, Moscow, Russia, 1984. (In Russian). [Google Scholar]
- Flanders, P.J.; Remeika, J.P. Magnetic properties of hematite single crystals. Philos. Mag. 1965, 11, 1271–1288. [Google Scholar] [CrossRef]
- Bodker, F.; Hansen, M.F.; Koch, C.B.; Lefmann, K.; Morup, S. Magnetic properties of hematite nanoparticles. Phys. Rev. B 2000, 61, 6826–6838. [Google Scholar] [CrossRef] [Green Version]
- Thio, T.; Thurster, T.R.; Preyer, N.W.; Picone, P.J.; Kastner, M.A.; Jenssen, H.P.; Gabbe, D.R.; Chen, C.Y.; Birgeneau, R.J.; Aharony, A. Antisymmetric exchange and its influence on the magnetic structure and conductivity of La2CuO4. Phys. Rev. B 1988, 38, R905–R908. [Google Scholar] [CrossRef] [PubMed]
- Kastner, M.A.; Birgeneau, R.J.; Thurston, T.R.; Picone, P.J.; Jenssen, H.P.; Gabbe, D.R.; Sato, M.; Fukuda, K.; Shamoto, S.; Endoh, Y.; et al. Neutron-scattering study of the transition from antiferromagnetic to weak ferromagnetic order in La2CuO4. Phys. Rev. B 1988, 38, 6636–6640. [Google Scholar] [CrossRef]
- Kotyuzhanskii, B.Y.; Prozorova, L.A. Parametric excitation of spin waves in antiferromagnetic FeF3. Izv. Akad. Nauk SSSR Seriya Fiz. 1980, 44, 1409–1412. [Google Scholar]
- Jacobs, S.; Burne, H.F.; Levinson, L.M. Field-Induced Spin Reorientation in YFeO3 and YCrO3. J. Appl. Phys. 1971, 42, 1631. [Google Scholar] [CrossRef]
- Kotyuzhanskii, B.Y.; Prozorova, L.A. Parametric excitation of spin waves in the antiferromagnet FeBO3. Zh. Eksp. Teor. Fiz. 1981, 81, 1913–1924. [Google Scholar]
- Ozhogin, V.I.; Yakimov, S.S.; Voskanyan, R.A.; Gamlitskii, V.Y. Experimental determination of sign of Dzyaloshinskii interaction in an antiferromagnet. Pis’ma Zh. Eksp. Teor. Fiz. 1968, 8, 256–260, (JETP Lett. 1968, 8, 157–161). [Google Scholar]
- Moskvin, A.S. 19F NMR in the weak ferromagnet FeF3 and deterrmination of the sign of the Dzyaloshinskii vector. Fizika Tverdogo Tela 1990, 32, 1644–1652, (Sov. Phys. Solid State 1990, 32, 959–967). [Google Scholar]
- Kadomtseva, A.M.; Moskvin, A.S.; Bostrem, I.G.; Wanklyn, B.M.; Khafizova, N.A. Nature of anomalous magnetic properties of yttrium ferrite-chromites. Zhurnal Exp. I Teor. Fiz. 1977, 72, 2286–2298. [Google Scholar]
- Kadomtseva, A.M.; Milov, V.N.; Moskvin, A.S.; Pardavi-Horvath, M. On compensation of weak-ferrimagnetic moments in yttrium ferrite-chromite. Fizika Tverdogo Tela 1978, 20, 817–820, (Sov. Phys. Solid State 1978, 20, 474–477). [Google Scholar]
- Luetgemeier, H.; Bohn, H.G.; Brajczewska, M. NMR observation of the spin structure and field induced spin reorientation in YFeO3. J. Magn. Magn. Mater. 1980, 21, 289–296. [Google Scholar] [CrossRef]
- Plakhtii, V.P.; Chernenkov, Y.P.; Schweizer, J.; Bedrizova, M.N. Experimental proof of the existence of a weak antiferromagnetic component in yttrium orthoferrite. JETP 1981, 53, 1291–1296. [Google Scholar]
- Plakhtii, V.P.; Chernenkov, Y.P.; Bedrizova, M.N.; Schweizer, J. Neutron diffraction study of the weak antiferromagnetism in orthoferrites. AIP Conf. Proc. 1982, 89, 330–332. [Google Scholar]
- Plakhtii, V.P.; Chernenkov, Y.P.; Bedrizova, M.N. Neutron diffraction study of weak antiferromagnetism in ytterbium orthoferrite. Solid State Commun. 1983, 47, 309–312. [Google Scholar] [CrossRef]
- Oshikawa, M.; Affleck, I. Field-Induced Gap in S=1/2 Antiferromagnetic Chains. Phys. Rev. Lett. 1997, 79, 2883–2886. [Google Scholar] [CrossRef]
- Affleck, I.; Oshikawa, M. Field-induced gap in Cu benzoate and other S=1/2 antiferromagnetic chains. Phys. Rev. B 1999, 60, 1038–1056. [Google Scholar] [CrossRef]
- Coffey, D.; Rice, T.M.; Zhang, F.C. Dzyaloshinskii-Moriya interaction in the cuprates. Phys. Rev. B 1991, 44, 10112–10116. [Google Scholar] [CrossRef]
- Bonesteel, N.E.; Rice, T.M.; Zhang, F.C. Spin-orbit coupling and spirals in doped La2CuO4. Phys. Rev. Lett. 1992, 68, 2684–2687. [Google Scholar] [CrossRef]
- Bonesteel, N.E. Theory of anisotropic superexchange in insulating cuprates. Phys. Rev. B 1993, 47, 11302–11313. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koshibae, W.; Ohta, Y.; Maekawa, S. Electronic and magnetic structures of cuprates with spin-orbit interaction. Phys. Rev. B 1993, 47, 3391–3400. [Google Scholar] [CrossRef] [PubMed]
- Koshibae, W.; Ohta, Y.; Maekawa, S. Theory of Dzyaloshinski-Moriya antiferromagnetism in distorted CuO2 and NiO2 planes. Phys. Rev. B 1994, 50, 3767–3778. [Google Scholar] [CrossRef] [PubMed]
- Shekhtman, L.; Entin-Wohlman, O.; Aharony, A. Moriya’s anisotropic superexchange interaction, frustration, and Dzyaloshinsky’s weak ferromagnetism. Phys. Rev. Lett. 1992, 69, 836–839. [Google Scholar] [CrossRef] [PubMed]
- Koshibae, W.; Ohta, Y.; Maekawa, S. Comment on ”Moriya’s anisotropic superexchange interaction, frustration, and Dzyaloshinsky’s weak ferromagnetism”. Phys. Rev. Lett. 1993, 71, 467. [Google Scholar] [CrossRef]
- Shekhtman, L.; Entin-Wohlman, O.; Aharony, A. Shekhtman, Entin-Wohlman, and Aharony reply. Phys. Rev. Lett. 1993, 71, 468. [Google Scholar] [CrossRef]
- Tsukada, I.; Sun, X.F.; Komiya, S.; Lavrov, A.N.; Ando, Y. Significant suppression of weak ferromagnetism in (La1.8Eu0.2)CuO4. Phys. Rev. B 2003, 67, 224401. [Google Scholar] [CrossRef]
- Hücker, M.; Kataev, V.; Pommer, J.; Ammerahl, U.; Revcolevschi, A.; Tranquada, J.M.; Büchner, B. Dzyaloshinsky-Moriya spin canting in the low-temperature tetragonal phase of La2−x−yEuySrxCuO4. Phys. Rev. B 2004, 70, 214515. [Google Scholar] [CrossRef]
- Walstedt, R.E.; Shastry, B.S.; Cheong, S.W. NMR, neutron scattering, and the one-band model of La2−xSrxCuO4. Phys. Rev. Lett. 1994, 72, 3610–3613. [Google Scholar] [CrossRef]
- Walstedt, R.E.; Cheong, S.W. Covalency in La2CuO4: A study of 17O hyperfine couplings in the paramagnetic phase. Phys. Rev. B 2001, 64, 014404. [Google Scholar] [CrossRef]
- Sergienko, I.E.; Sȩn, C.; Dagotto, E. Role of the Dzyaloshinskii-Moriya interaction in multiferroic perovskites. Phys. Rev. B 2006, 73, 094434. [Google Scholar] [CrossRef] [Green Version]
- Moskvin, A.S.; Drechsler, S.-L. Microscopic mechanisms of spin-dependent electric polarization in 3d oxides. Phys. Rev. B 2008, 78, 024102. [Google Scholar] [CrossRef]
- Zvezdin, A.K.; Pyatakov, A.P. On the problem of coexistence of the weak ferromagnetism and the spin flexoelectricity in multiferroic bismuth ferrite. EPL 2012, 99, 57003. [Google Scholar] [CrossRef]
- Rössler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797–801. [Google Scholar] [CrossRef] [Green Version]
- Dzyaloshinskii, I.E. Theory of helicoidal structures in antiferromagnets. I. Nonmetals. Sov. Phys. JETP 1964, 19, 960–971. [Google Scholar]
- Anderson, P.W. Antiferromagnetism. Theory of superexchange interaction. Phys. Rev. 1950, 79, 350–356. [Google Scholar] [CrossRef]
- Anderson, P.W. New approach to the theory of superexchange interactions. Phys. Rev. 1959, 115, 2–13. [Google Scholar] [CrossRef]
- Anderson, P.W. Theory of magnetic exchange interactions: exchange in insulators and semiconductors. Solid State Phys. 1963, 14, 99–214. [Google Scholar]
- Druzhinin, V.V.; Moskvin, A.S. Theory of direct exchange interacton. Phys. Met. Metallogr.-USSR 1968, 26, 32. [Google Scholar]
- Levy, P.M. Anisotropy in two-center exchange interactions. Phys. Rev. 1969, 177, 509. [Google Scholar] [CrossRef]
- Copland, G.M.; Levy, P.M. Direct Exchange between d Electrons. Phys. Rev. B 1970, 1, 3043. [Google Scholar] [CrossRef]
- Veltrusky, I. On superexchange interaction between orbitally degenerate ions. Czechoslov. J. Phys. 1975, 25, 101–114. [Google Scholar] [CrossRef]
- Sidorov, A.A.; Moskvin, A.S.; Popkov, V.V. Superexchange interaction in strong crystalline field. Fizika Tverdogo Tela 1976, 18, 3005–3013. [Google Scholar]
- Moskvin, A.S.; Druzhinin, V.V. Mechanism of excitation transfer in ionic pairs. Opt. Spectrosc.-USSR 1970, 29, 478. [Google Scholar]
- Moskvin, A.S.; Luk’yanov, A.S. Theory of potential exchange in magnetic dielectrics. Fizika Tverdogo Tela 1977, 19, 1199–1201. [Google Scholar]
- Freeman, S. Molecular-Orbital Theory of the Excited-State Exchange Interaction. Phys. Rev. B 1973, 7, 3960–3986. [Google Scholar] [CrossRef]
- Moskvin, A.S.; Ovanesyan, N.S.; Trukhtanov, V.A. Angular dependence of the superexchange interaction Fe3+-O2−-Cr3+. Hyperfine Interact. 1975, 1, 265–281. [Google Scholar] [CrossRef]
- Hornreich, R.M.; Shtrikman, S.; Wanklyn, B.M.; Yaeger, I. Magnetization studies in rare-earth orthochromites. VII. LuCrO3. Phys. Rev. B 1976, 13, 4046–4052. [Google Scholar] [CrossRef]
- Bloch, D. The 10/3 law for the volume dependence of superexchange. J. Phys. Chem. Solids 1966, 27, 881. [Google Scholar] [CrossRef]
- Dmitrienko, V.E.; Ovchinnikova, E.N.; Kokubun, J.; Ishida, K. Dzyaloshinskii-Moriya interaction: How to measure its sign in weak ferromagnets? JETP Lett. 2010, 92, 383–387. [Google Scholar] [CrossRef]
- Moskvin, A.S. Atomy v kristallah (Atoms in Crystals), Ural Federal University. 2018. Available online: elar.urfu.ru/bitstream/10995/65226/1/978-5-7996-2377-7_2018.pdf (accessed on 9 October 2019). (In Russian).
- Sobelman, I.I. Introduction to the Theory of Atomic Spectra; Pergamon Press: Oxford, UK; New York, NY, USA, 1972; 609p. [Google Scholar]
- Varshalovich, D.A.; Moskalev, A.N.; Khersonskii, V.K. Quantum Theory of Angular Momentum; World Scientific: Singapore, 1988. [Google Scholar]
- Moskvin, A.S. The Lowdin orthogonalization and magnetoelectric coupling for noncentrosymmetric ions. Magn. Reson. Solids 2019, 21, 19409. [Google Scholar] [CrossRef]
- Sugano, S.; Tanabe, Y.; Kamimura, H. Multiplets of Transition-Metal Ions in Crystals; Academic Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Kahn, F.J.; Pershan, P.S.; Remeika, J.P. Ultraviolet magneto-optical properties of single-crystal orthoferrites, garnets, and other ferric oxide compounds. Phys. Rev. 1969, 186, 891. [Google Scholar] [CrossRef]
- Moskvin, A.S. Microscopic theory of Dzyaloshinskii-Moriya coupling and related exchange-relativistic effects. JMMM 2016, 400, 117–120. [Google Scholar] [CrossRef]
- Tofield, B.C.; Fender, B.F.E. Covalency parameters for Cr3+, Fe3+ and Mn4+ in an oxide environment. J. Phys. Chem. Solids 1970, 31, 2741–2749. [Google Scholar] [CrossRef]
- Hollebone, B.R.; Donini, J.C. The coupling algebra of trigonally subduced crystal field eigenvectors. Theor. Chem. Acta 1975, 37, 233–250. [Google Scholar] [CrossRef]
- Belov, D.V.; Zvezdin, A.K.; Kadomtseva, A.M.; Krynetski, I.B.; Moskvin, A.S.; Mukhin, A.A. Anisotripy of R-Fe interaction in gadolinium ortho-ferrite. Fizika Tverdogo Tela 1981, 23, 2831–2841, (Sov. Phys. Solid State 1981, 23, 1654–1664). [Google Scholar]
- Marezio, M.; Remeika, J.P.; Dernier, P.D. The crystal chemistry of the rare earth orthoferrites. Acta Crystallogr. 1970, 26, 2008–2022. [Google Scholar] [CrossRef]
- Georgieva, D.G.; Krezhov, K.A.; Nietza, V.V. Weak antiferromagnetism in YFeO3 and HoFeO3. Solid State Commun. 1995, 96, 535–537. [Google Scholar] [CrossRef]
- Kadomtseva, A.M.; Agafonov, A.P.; Lukina, M.M.; Milov, V.N.; Moskvin, A.S.; Semenov, V.A.; Sinitsyn, E.V. Nature of magnetic anisotropy and magnetostriction of orthoferrites and orthochromites. Zhurnal Exp. I Teor. Fiz. 1981, 81, 700–703, (JETP 1981, 81, 374–377). [Google Scholar]
- Zalesskii, A.V.; Savvinov, A.M.; Zheludev, I.S.; Lvashchenko, A.N. NMR of 57Fe nuclei reorientation of spins in domains and domain walls of ErFeO3 and DyFeO3 crystals. JETP 1975, 41, 723–728. [Google Scholar]
- Moskvin, A.S.; Vigura, M.A.; Agafonov, A.P. Competing antisymmetric exchange and weak ferrimagnetism in Mn1−xNixCO3. Fizika Tverdogo Tela 1986, 28, 2902–2904, (Sov. Phys. Solid State 1986, 28, 1631–1633). [Google Scholar]
- Moskvin, A.S.; Vigura, M.A. Competing antisymmetric exchange and weak ferrimagnetism in Fe1−xCrxBO3. Fizika Tverdogo Tela 1986, 28, 2259–2261. [Google Scholar]
- Dasari, N.; Mandal, P.; Sundaresan, A.; Vidhyadhiraja, N.S. Weak ferromagnetism and magnetization reversal in YFe1−xCrxO3. Europhys. Lett. 2012, 99, 17008. [Google Scholar] [CrossRef]
- Sinitsyn, E.V.; Kadomtseva, A.M.; Moskvin, A.S.; Bostrem, I.G.; Timofeeva, V.A.; Kazakevich, O.V. Weak ferromagnetism of mixed yttrium and lutecium orthoferrite-orthochromites. Sov. Phys. Solid State 1983, 25, 161–163. [Google Scholar]
- O’Horo, M.P.; Muller, O. Magnetization studies in the system Fe1−xCrxBO3. J. Appl. Phys. 1978, 49, 1516–1518. [Google Scholar] [CrossRef]
- Vorob’ev, G.P.; Kadomtseva, A.M.; Moskvin, A.S.; Popov, Y.F.; Timofeeva, V.A. Aspects of magnetic ordering in the system (FexCr1−x)2O3. Phys. Solid State 1997, 39, 97–98. [Google Scholar] [CrossRef]
- Dmitrienko, V.E.; Krasnoyarsk, Russia. Private communication, 2016.
- Kadomtseva, A.M.; Agafonov, A.P.; Zorin, I.A.; Moskvin, A.S.; Ovchinnikova, T.L.; Timofeeva, V.A. Features of f-d exchange in weak ferrimagnets. Zhurnal Exp. I Teor. Fiz. 1983, 84, 1432–1439, (JETP 1983, 57, 833–840). [Google Scholar]
- Kadomtseva, A.M.; Moskvin, A.S. Features of the f-d –interaction in orthoferrites with competing antisymmetric exchange. Acta Phys. Polonica 1985, 68, 303. [Google Scholar]
- Kadomtseva, A.M.; Bostrem, I.G.; Vasil’eva, L.M.; Krynetskii, I.B.; Lukina, M.M.; Moskvin, A.S. Antisymmetric exchange in some fluoro-substituted ortho-ferrites. Fizika Tverdogo Tela 1980, 22, 1965–1970, (Sov. Phys. Solid State 1980, 22, 1146–1151). [Google Scholar]
- Bostrem, I.G.; Moskvin, A.S.; Sinitsyn, E.V. Antisymmetric exchange in disordered magnetic oxides. Fizika Tverdogo Tela 1981, 23, 1535–1537, (Sov. Phys. Solid State 1981, 23, 899–901). [Google Scholar]
- Mao, J.; Sui, Y.; Zhang, X.; Su, Y.; Wang, X.; Liu, Z.; Wang, Y.; Zhu, R.; Wang, Y.; Liu, W.; et al. Temperature- and magnetic-field-induced magnetization reversal in perovskite YFe0.5Cr0.5O3. Appl. Phys. Lett. 2011, 98, 192510. [Google Scholar] [CrossRef]
- Fita, I.; Markovich, V.A.; Moskvin, S.; Wisniewski, A.; Puzniak, R.; Iwanowski, P.; Martin, C.; Maignan, A.; Carbonio, R.E.; Gutowska, M.U.; et al. Reversed exchange-bias effect associated with magnetization reversal in the weak ferrimagnet LuFe0.5Cr0.5O3. Phys. Rev. B 2018, 97, 104416. [Google Scholar] [CrossRef]
- Moskvin, A.S. Weak ferrimagnets with competing Dzyaloshinskii-Moriya coupling are perspective for the exchange-bias effect materials. JMMM 2018, 463, 50–56. [Google Scholar] [CrossRef]
- Bora, T.; Saravanan, P.; Ravi, S. Antiferromagnetism and the Effect of Exchange Bias in LaCr1−xFexO3 (x = 0.40 to 0.60). J. Supercond. Nov. Magn. 2013, 26, 1645–1648. [Google Scholar] [CrossRef]
- Kumar, A.; Yusuf, S.M. The phenomenon of negative magnetization and its implications. Phys. Rep. 2015, 556, 1–34. [Google Scholar] [CrossRef]
- Grigoriev, S.V.; Potapova, N.M.; Siegfried, S.-A.; Dyadkin, V.A.; Moskvin, E.V.; Dmitriev, V.; Menzel, D.; Dewhurst, C.D.; Chernyshov, D.; Sadykov, R.A.; et al. Chiral Properties of Structure and Magnetism in Mn1−xFexGe Compounds: When the Left and the Right are Fighting, Who Wins? Phys. Rev. Lett. 2013, 110, 207201. [Google Scholar] [CrossRef]
- Chepurnykh, G.K.; Medvedovskaya, O.G.; Nikitina, O.A. Phase transitions in antiferromagnetic cobalt fluoride. Fiz. Nizk. Temp. 2000, 26, 108–111, (Low Temp. Phys. 2000, 26, 81–83). [Google Scholar]
- Dmitrienko, V.E.; Ovchinnikova, E.N.; Collins, S.P.; Nisbet, G.; Beutier, G.; Kvashnin, Y.O.; Mazurenko, V.V.; Lichtenstein, A.I.; Katsnelson, M.I. Measuring the Dzyaloshinskii-Moriya interaction in a weak ferromagnet. Nat. Phys. 2014, 10, 202–206. [Google Scholar] [CrossRef]
- Hepworth, M.A.; Jack, K.H.; Peacock, R.D.; Westland, G.J. The crystal structures of the trifluorides of iron, cobalt, ruthenium, rhodium, palladium and iridium. Acta Crystallogr. 1957, 10, 63–69. [Google Scholar] [CrossRef]
- Turov, E.A.; Petrov, M.P. Nuclear Magnetic Resonance in Ferro and Antiferromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 1972; 206p. [Google Scholar]
- Hall, T.P.P.; Hayes, W.; Stevenson, R.W.H.; Wilkens, J. Investigation of the bonding of iron-group ions in fluoride crystals. I. J. Chem. Phys. 1963, 38, 1977–1984. [Google Scholar] [CrossRef]
- Adam, C.D. ENDOR determination of covalency in K2NaAlF6:Fe3+, Cr3+. J. Phys. C Solid State Phys. 1981, 14, L105–L110. [Google Scholar] [CrossRef]
- Jacobson, A.J.; McBridge, L.; Fender, B.E.F. A neutron diffraction determination of covalency parameters for Fe3+ and Cr3+ in FeF3 and CrF3. J. Phys. C Solid State Phys. 1974, 7, 783. [Google Scholar] [CrossRef]
- Wolfe, R.; Kurtzig, A.G.; Crow, R.C.L. Room-temperature ferromagnetic materials transparent in the visible. J. Appl. Phys. 1970, 41, 1218–1224. [Google Scholar] [CrossRef]
- Petrov, M.P.; Paugurt, A.P.; Smolenskii, G.A. Nuclear Echo in the Transparent Antiferromagnet FeF3. JETP Lett.-USSR 1972, 15, 214–216. [Google Scholar]
- Zalesskii, A.V.; Vanchikov, V.V.; Krivenko, V.G.; Ivashchenko, A.N. Spin Echo Spectra of 57Fe and 19F Nuclei in a Canted Antiferromagnet FeF3. Phys. Status Solid 1979, 54, 471–476. [Google Scholar] [CrossRef]
- Diehl, R. Crystal structure refinement of ferric borate, FeBO3. Solid State Commun. 1975, 17, 743–745. [Google Scholar] [CrossRef]
- Moskvin, A.S. Dzyaloshinsky-Moriya antisymmetric exchange coupling in cuprates: Oxygen effects. JETP 2007, 104, 911–927. [Google Scholar] [CrossRef]
- Moskvin, A.S. Field-induced staggered magnetization and 17O Knight shift anomaly in La2CuO4. Phys. Rev. B 2007, 75, 054505. [Google Scholar] [CrossRef]
- Shekhtman, L.; Aharony, A.; Entin-Wohlman, O. Bond-dependent symmetric and antisymmetric superexchange interactions in La2CuO4. Phys. Rev. B 1993, 47, 174–182. [Google Scholar] [CrossRef]
- Low, W. Paramagnetic Resonance in Solids, in Solid State Physics, Suppl. II; Academic Press: New York, NY, USA; London, UK, 1960. [Google Scholar]
- Yildirim, T.; Harris, A.B.; Entin-Wohlman, O.; Aharony, A. Symmetry, Spin-Orbit Interactions, and Spin Anisotropies. Phys. Rev. Lett. 1994, 73, 2919–2922. [Google Scholar] [CrossRef] [Green Version]
- Yildirim, T.; Harris, A.B.; Aharony, A.; Entin-Wohlman, O. Anisotropic spin Hamiltonians due to spin-orbit and Coulomb exchange interactions. Phys. Rev. B 1995, 52, 10239–10267. [Google Scholar] [CrossRef] [Green Version]
- Tornow, S.; Entin-Wohlman, O.; Aharony, A. Anisotropic superexchange for nearest and next-nearest coppers in chain, ladder, and lamellar cuprates. Phys. Rev. B 1999, 60, 10206–10215. [Google Scholar] [CrossRef] [Green Version]
- Herzberg, G. Ionization Potentials and Lamb Shifts of the Ground States of 4He and 3He. Proc. R. Soc. Ser. A 1958, 248, 309–332. [Google Scholar]
- Veseth, L. Many body calculations of atomic properties: II. Spin-orbit coupling. J. Phys. B At. Mol. Phys. 1983, 16, 2713–2720. [Google Scholar] [CrossRef]
- Renold, S.; Pliberŝek, S.; Stoll, E.P.; Claxton, T.A.; Meier, P.F. First-principles calculation of electric field gradients and hyperfine couplings in YBa2Cu3O7. Eur. Phys. J. B 2001, 23, 3–15. [Google Scholar] [CrossRef]
- These equalities are true to within a replacement δ1↔δ2. It should be noted that the probability amplitudes for triplet 200 and 002 configurations are of the same sign due to double-minus effect: (1) θ↔−θ replacement, and (2) the antisymmetry of orbital functions: 200-function ∝dx2−y2(1)dxy(2), while 002-function ∝dx2−y2(2)dxy(1).
- Eskes, H.; Tjeng, L.H.; Sawatzky, G.A. Cluster-model calculation of the electronic structure of CuO: A model material for the high-Tc superconductors. Phys. Rev. B 1990, 41, 288. [Google Scholar] [CrossRef]
- Chung, E.M.L.; McIntyre, G.J.; Paul, D.M.; Balakrishnan, G.; Lees, M.R. Oxygen moment formation and canting in Li2CuO2. Phys. Rev. B 2003, 68, 144410. [Google Scholar] [CrossRef]
- Ozhogin, V.I.; Cherepanov, V.M.; Yakimov, S.S. Effect of anisotropy on field-induced antiferromagnetism in YFeO3. JETP 1975, 40, 517–520. [Google Scholar]
- Wolter, A.U.B.; Wzietek, P.; Sullow, S.; Litterst, F.J.; Honecker, A.; Brenig, W.; Feyerherm, R.; Klauss, H.-H. Giant Spin Canting in the S=1/2 Antiferromagnetic Chain [CuPM(NO3)2(H2O)2]n Observed by 13C-NMR. Phys. Rev. Lett. 2005, 94, 057204. [Google Scholar] [CrossRef]
- Achiwa, N. Linear Antiferromagnetic Chains in Hexagonal ABCl3-Type Compounds (A; Cs, or Rb, B; Cu, Ni, Co, or Fe). J. Phys. Soc. Jpn. 1969, 27, 561–574. [Google Scholar] [CrossRef]
- Hirotsu, S. Jahn-Teller induced phase transition in CsCuCl3: Structural phase transition with helical atomic displacements. J. Phys. C Solid State Phys. 1977, 10, 967–986. [Google Scholar] [CrossRef]
- Schlueter, A.W.; Jacobson, R.A.; Rundle, R.E. A Redetermination of the Crystal Structure of CsCuCl3. Inorg. Chem. 1966, 5, 277–280. [Google Scholar] [CrossRef]
- Plakhty, V.P.; Wosnitza, J.; Kulda, J.; Brückel, T.; Schweika, W.; Visser, D.; Gavrilov, S.V.; Moskvin, E.V.; Kremer, R.K.; Banks, M.G. Polarized neutron scattering studies of chiral criticality, and new universality classes of phase transitions. Physica B 2006, 385, 288–294. [Google Scholar] [CrossRef]
- Adachi, K.; Achiwa, N.; Mekata, M. Helical Magnetic Structure in CsCuCl3. J. Phys. Soc. Jpn. 1980, 49, 545–553. [Google Scholar] [CrossRef]
- Kubo, H.; Yahara, I.; Hirakawa, K. Nuclear Magnetic Resonance of Cu Nuclei in CsCuCl3—A Screw Spin Arrangement in the Ordered State. J. Phys. Soc. Jpn. 1976, 40, 591–592. [Google Scholar] [CrossRef]
- Dang, K.L.; Vefflet, P.; Renard, J.-P. NMR study in a single crystal of the one-dimensional antiferromagnet CsCuCl3. Solid State Commun. 1977, 24, 313–316. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, 864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, J.L. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Kryachko, E.S.; Ludena, E.V. Density functional theory: Foundations reviewed. Phys. Rep. 2014, 544, 123–239. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Izyumov, Y.A. Electronic Structure of Strongly Correlated Materials; Springer: Berlin, Germany, 2010. [Google Scholar]
- Ghijsen, J.; Tjeng, L.H.; van Elp, J.; Eskes, H.; Westerink, J.; Sawatzky, G.A.; Czyzyk, M.T. Electronic structure of Cu2O and CuO. Phys. Rev. B 1988, 38, 11322–11330. [Google Scholar] [CrossRef]
- Sandratskii, L.M. Symmetry analysis of electronic states for crystals with spiral magnetic order. II. Connection with limiting cases. J. Phys. Condens. Matter 1991, 3, 8565–8585. [Google Scholar] [CrossRef]
- Sandratskii, L.M. Magnetic structure of relativistic systems with low symmetry. Phys. Rev. B 2001, 64, 134402. [Google Scholar] [CrossRef]
- Mazurenko, V.V.; Anisimov, V.I. Weak ferromagnetism in antiferromagnets: α-Fe2O3 and La2CuO4. Phys. Rev. B 2005, 71, 184434. [Google Scholar] [CrossRef]
- Moskvin, A.S.; Drechsler, S.-L. Multiferroicity due to nonstoichiometry in the chain cuprate LiVCuO4. Europhys. Lett. 2008, 81, 57004. [Google Scholar] [CrossRef]
- Moskvin, A.S.; Panov, Y.D.; Drechsler, S.-L. Nonrelativistic multiferrocity in the nonstoichiometric spin-1/2 spiral-chain cuprate LiCu2O2. Phys. Rev. B 2009, 79, 104112. [Google Scholar] [CrossRef]
- Panov, Y.D.; Moskvin, A.S.; Fedorova, N.S.; Drechsler, S.-L. Nonstoichiometry Effect on Magnetoelectric Coupling in Cuprate Multiferroics. Ferroelectrics 2013, 442, 27–41. [Google Scholar] [CrossRef]
- Liu, J.; Koo, H.; Xiang, H.; Kremer, R.K.; Whangbo, M. Most spin-1/2 transition-metal ions do have single ion anisotropy. J. Chem. Phys. 2014, 141, 124113. [Google Scholar] [CrossRef] [Green Version]
- Katsnelson, M.I.; Kvashnin, Y.O.; Mazurenko, V.V.; Lichtenstein, A.I. Correlated band theory of spin and orbital contributions to Dzyaloshinskii-Moriya interactions. Phys. Rev. B 2010, 82, 100403R. [Google Scholar] [CrossRef]
- Secchi, A.; Lichtenstein, A.I.; Katsnelson, M.I. Magnetic interactions in strongly correlated systems: Spin and orbital contributions. Ann. Phys. 2015, 360, 61–97. [Google Scholar] [CrossRef] [Green Version]
- Secchi, A.; Lichtenstein, A.I.; Katsnelson, M.I. Spin and orbital exchange interactions from Dynamical Mean Field Theory. J. Magn. Magn. Mater. 2016, 400, 112–116. [Google Scholar] [CrossRef]
- Haverkort, M.W.; Zwierzycki, M.; Andersen, O.K. Multiplet ligand-field theory using Wannier orbitals. Phys. Rev. B 2012, 85, 165113. [Google Scholar] [CrossRef]
- Agrestini, S.; Saini, N.L.; Bianconi, G.; Bianconi, A. The strain of CuO2 lattice: The second variable for the phase diagram of cuprate perovskites. J. Phys. A Math. Gener. 2003, 36, 9133. [Google Scholar] [CrossRef]
- Gavrichkov, V.A.; Shan’ko, Y.; Zamkova, N.G.; Bianconi, A. Is there any hidden symmetry in the stripe structure of perovskite high temperature superconductors? J. Phys. Chem. Lett. 2019, 10, 1840–1844. [Google Scholar] [CrossRef] [PubMed]
- Ivashko, O.; Horio, M.; Wan, W.; Christensen, N.B.; McNally, D.E.; Paris, E.; Tseng, Y.; Shaik, N.E.; Rønnow, H.M.; Wei, H.I.; et al. Strain-engineering Mott-insulating La2CuO4. Nat. Commun. 2019, 10, 786. [Google Scholar] [CrossRef] [PubMed]
- Liao, Z.; Skoropata, E.; Freeland, J.W.; Guo, E.-J.; Desautels, R.; Gao, X.; Sohn, C.; Rastogi, A.; Ward, T.Z.; Zou, T.; et al. Large orbital polarization in nickelate-cuprate heterostructures by dimensional control of oxygen coordination. Nat. Commun. 2019, 10, 589. [Google Scholar] [CrossRef] [PubMed]
- Campi, G.; Bianconi, A.; Poccia, N.; Bianconi, G.; Barba, L.; Arrighetti, G.; Innocenti, D.; Karpinski, J.; Zhigadlo, N.D.; Kazakov, S.M.; et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-Tc superconductor. Nature 2015, 525, 359. [Google Scholar] [CrossRef] [PubMed]
- Seino, Y.; Kotani, A.; Bianconi, A. Effect of Rhombic Distortion on the Polarized X-Ray Absorption Spectra in High Tc Superconductors. J. Phys. Soc. Jpn. 1990, 59, 815–818. [Google Scholar] [CrossRef]
- Oleś, A.M.; Wohlfeld, K.; Khaliullin, G. Orbital Symmetry and Orbital Excitations in High-Tc Superconductors. Condens. Matter 2019, 4, 46. [Google Scholar] [Green Version]
- Moskvin, A.S.; Bostrem, I.G.; Sidorov, M.A. Two-ion exchange-relativistic anisotropy—The tensor form, temperature dependence, and numerical value. JETP 1993, 77, 127–137. [Google Scholar]
- Zenkov, A.V.; Krichevtsov, B.B.; Moskvin, A.S.; Mukimov, K.M.; Pisarev, R.V.; Ruvinshtein, M.M. Anisotropry of the Faraday effect in the weak ferromagnet YFeO3. Zhurnal Exp. I Teor. Fiz. 1989, 96, 1397–1401, (JETP 1989, 69, 792–796). [Google Scholar]
- Gaydukov, Y.P.; Zenkov, A.V.; Koptsik, S.V.; Krinchik, G.S.; Moskvin, A.S. Nature of high magnetooptic activity of crystals with Fe3+ ions. JETP Lett. 1990, 51, 228–231. [Google Scholar]
- Krinchik, G.S.; Moskvin, A.S.; Ganshina, E.A.; Koptsik, S.V.; Trifonov, A.Y.; Zenkov, A.V. Origin of high magnetooptical activity in weak ferromagnets. Fizika Nizkih Temperatur 1992, 18 (Suppl. S1), 5–8. [Google Scholar]
- Gan’shina, E.A.; Zenkov, A.V.; Krinchik, G.S.; Moskvin, A.S.; Trifonov, A.Y. Exchange–relativistic interactions and characteristics of magnetooptic properties of orthoferrites. Fizika Tverdogo Tela 1991, 33, 1122–1133, (Sov. Phys. Solid State 1991, 33, 637–647). [Google Scholar]
- Gan’shina, E.A.; Zenkov, A.V.; Krinchik, G.S.; Moskvin, A.S.; Nishanova, M.M. Exchange-relativistic interactions and anisotropy of circular magnetooptics of Er and Ho orthoferrites. Fizika Tverdogo Tela 1992, 34, 3319–3322, (Sov. Phys. Solid State 1992, 34, 1776–1779). [Google Scholar]
- Moskvin, A.S.; Zenkov, A.V.; Ganshina, E.A.; Krinchik, G.S.; Nishanova, M.M. Anisotropy of the circular magneto-optics of orthoferrites: A theoretical consideration on the basis of the charge-transfer transitions and exchange-relativistic concept. J. Phys. Chem. Solids 1993, 54, 101–105. [Google Scholar] [CrossRef]
- Moskvin, A.S. Exchange and Exchange-Relativistic Effects in the Excited States of 3d Ions in Crystals. Phys. Solid State 2019, 61, 887–893. [Google Scholar] [CrossRef]
- Moskvin, A.S. Dzyaloshinskii-Moriya electron-nuclear interaction in orthoferrites. JETP 1986, 63, 1015–1017. [Google Scholar]
- Rokeakh, A.I.; Moskvin, A.S.; Legkikh, N.V.; Sherstkov, Y.A. Experimental observation of the Dzyaloshinskii-Moriya electron-nuclear interaction by the electron-nuclear double resonance method. JETP 1987, 66, 1021–1027. [Google Scholar]
- Yang, H.; Thiaville, A.; Rohart, S.; Fert, A.; Chshiev, M. Anatomy of Dzyaloshinskii-Moriya Interaction at Co/Pt Interfaces. Phys. Rev. Lett. 2015, 115, 267210. [Google Scholar] [CrossRef]
- Yang, H.; Boulle, O.; Cros, V.; Fert, A.; Chshiev, M. Controlling Dzyaloshinskii-Moriya Interaction via Chirality Dependent Atomic-Layer Stacking, Insulator Capping and Electric Field. Sci. Rep. 2018, 8, 12356. [Google Scholar] [CrossRef]
- Jadaun, P.; Register, L.F.; Banerjee, S.K. The microscopic origin of DMI in magnetic bilayers and prediction of giant DMI in new bilayers. arXiv 1903, arXiv:1903.09345. [Google Scholar]
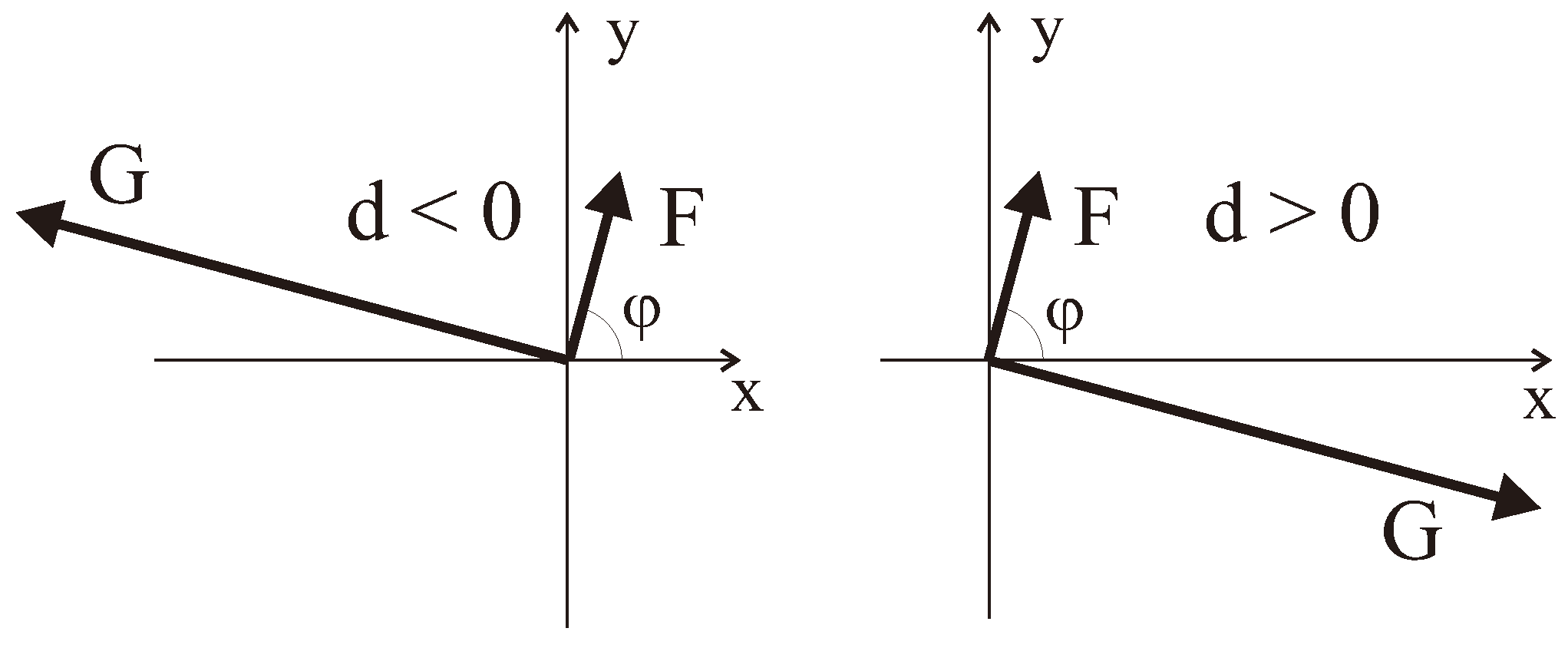
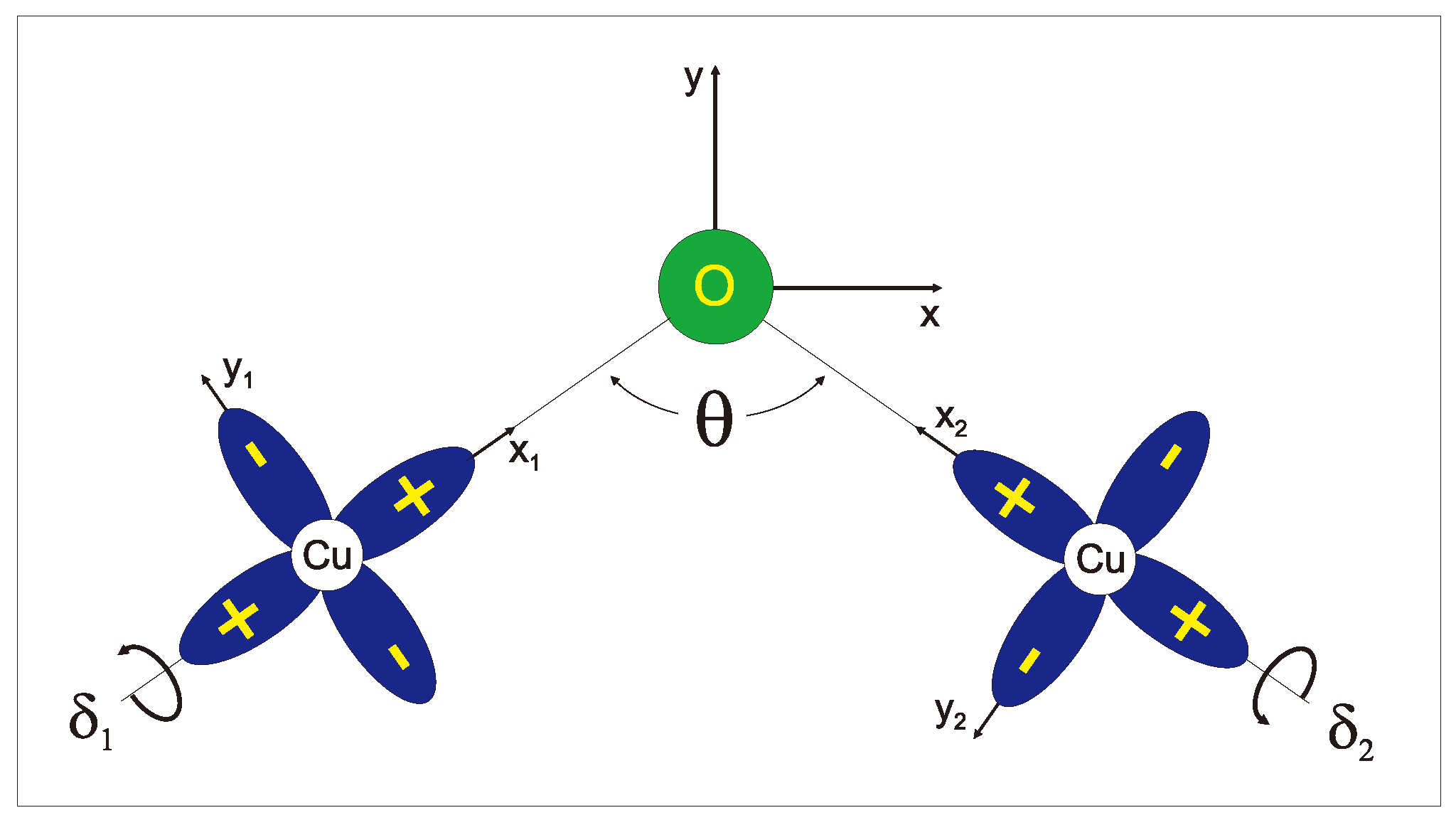
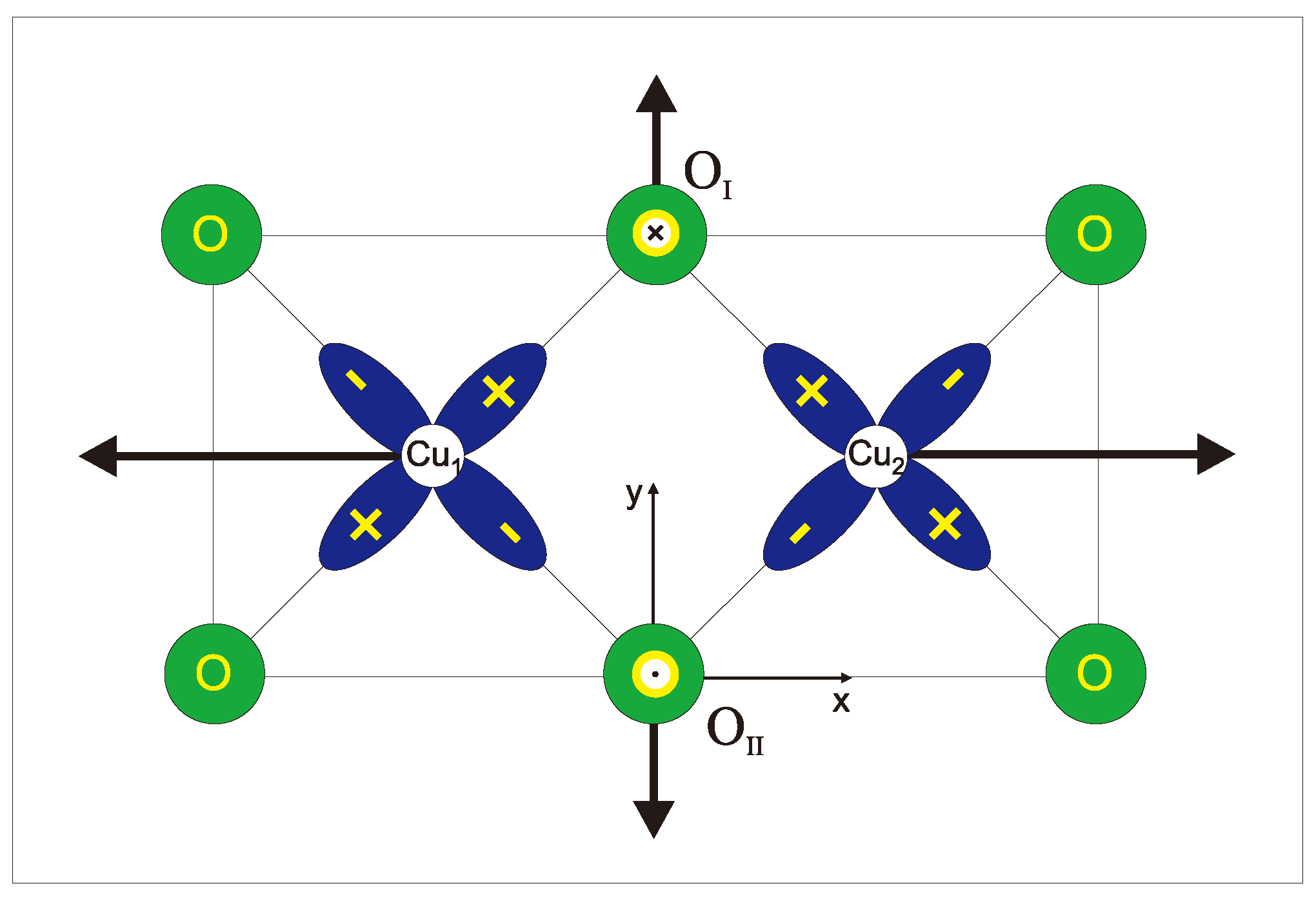
| WFM | , Å | , K | I, K (MFA) | , Tesla | , Tesla | d(), K | ||
|---|---|---|---|---|---|---|---|---|
| -FeO [14,15] | 2.111 | 145 | 948 | 54.2 | 870–920 | 1.9–2.2 | 2.3 | |
| YFeO [19] | 2.001 (×2) | 145 | 640 | 36.6 | 640 | 14 | 3.2 | |
| FeBO [20] | 2.028 | 126 | 348 | 19.9 | 300 | 10 | 2.3 | |
| FeF [18] | 1.914 | 153 | 363 | 20.7 | 440 | 4.88 | 1.1 |
| Ground Sate Configuration | X | Sign X | Y | Sign Y | Excited State Configuration |
|---|---|---|---|---|---|
| (): , , | + | + | |||
| (): , | − | − | − | − | , |
| (): , | − | + |
| () | () | () | |
|---|---|---|---|
| () | + | − | + |
| () | − | + | + |
| () | + | + | − |
| 1a | = −0.31 | = −0.29 | = 0.41 |
| 1b | = 0.31 | = −0.29 | = 0.41 |
| 3a | = 0.20 | = −0.55 | 0 |
| Orthoferrite | /, Theory [11] | /, exp | /, Theory [11] | /, Exp |
|---|---|---|---|---|
| YFeO | 1.10 | 1.10 ± 0.03 [25] 1.4 ± 0.2 [26,27] 1.1 ± 0.1 [74] | 2.04 | ? |
| HoFeO | 1.16 | 0.85 ± 0.10 [74] | 2.00 | ? |
| TmFeO | 1.10 | 1.25 ± 0.05 [25] | 1.83 | ? |
| YbFeO | 1.11 | 1.22 ± 0.05 [28] | 1.79 | 2.0 ± 0.2 [25] |
| 0 | |||
| 0 | |||
| 0 | 0 | 0 | |
| 0 | |||
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moskvin, A. Dzyaloshinskii–Moriya Coupling in 3d Insulators. Condens. Matter 2019, 4, 84. https://doi.org/10.3390/condmat4040084
Moskvin A. Dzyaloshinskii–Moriya Coupling in 3d Insulators. Condensed Matter. 2019; 4(4):84. https://doi.org/10.3390/condmat4040084
Chicago/Turabian StyleMoskvin, Alexander. 2019. "Dzyaloshinskii–Moriya Coupling in 3d Insulators" Condensed Matter 4, no. 4: 84. https://doi.org/10.3390/condmat4040084





