3.1. Lithiated System
The GB construction starts by selecting the tilt axis. We take [010] (perpendicular to the structure mirrors with the coordinates
y = ¼ and ¾), which is in fact parallel with the LFP crystallographic axis
b. Such an axis allows us to construct GBs with Li atoms at the GB plane in order to be able to study Li diffusion at this GB and its neighborhood in a follow-up study. By trying various tilt/rotation angles along the chosen axis and selecting the Li atom at the (0, 0, 0) position as the origin, a nearly perfect coincidence occurs at ~48.3° for a near-CSL GB with a {101} plane. The CSL is determined by translation vectors
a −
c,
b, and 3
c, which implicates that the CSL unit cell volume is three times more than that of the original lattice determined by vectors
a,
b, and
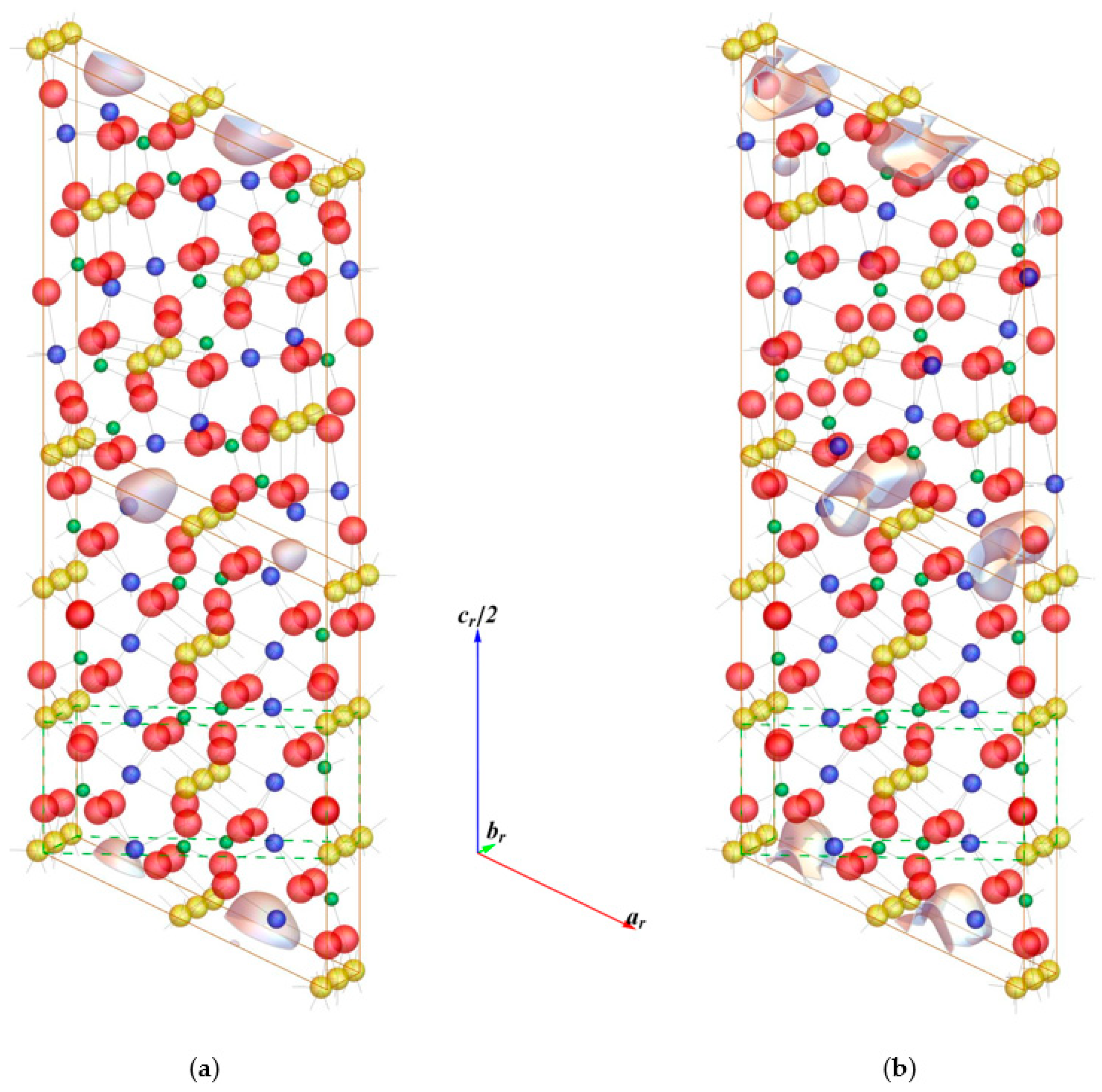
c. Thus, the complete designation is (near-CSL) symmetrical Σ 3 (101)/[010] GB, with Σ specifying the ratio of volumes. The total volume of the GB box is then six times the LFP unit cell volume (the lower part is not rotated, and the upper part is rotated by 48.3° degrees along the [010] axis). In this way, each box contains two GB boundaries (one is in the middle and the other one at the upper and lower faces). It is useful to note that Li ions lie on the (101) GB plane, and since this plane is not a mirror, the GB lacks mirror symmetry. The result of the construction procedure called further configuration 1 (or C1) is shown in
Figure 1a. The GB box (unit cell/supercell) is not orthogonal anymore, and contains 168 atoms. In fact,
Figure 1a presents the structure whose last dimension (along the original lattice vector 6
c) is already relaxed; atomic positions in the whole box are also allowed to relax to minimize the total energy. A closer inspection unveils that bonds of atoms near the interface are somewhat distorted, and dangling bonds are also present. Especially, four pairs of Fe atoms become mutually very close, which results in their repulsion because of the differently positioned O atoms that do not screen such repulsion well compared to the bulk regions. The octahedral coordination of Fe (and Li) atoms is lowered in the GB regions (though one could also see it as a disruption of oxygen cationic coordination).
Since the GB construction procedure described above is based on a geometrical concept, it might not necessarily lead to the best chemical bonding of atoms at the interface (after ‘cutting’ and ‘welding’ two pieces of crystal together). In order to better bond the atoms at the GB regions, we shift the upper grain along the [010] direction (
b axis) by
b/2, which is what a detailed examination of the interfaces suggests. In this way, the coherence/’matching’ of both interfaces could be improved. No atoms are added or removed in the present GB configuration, which was constructed to be charge neutral (the same holds for C1). The result of this transformation (including the relaxation of atoms and the last cell dimension) is shown in
Figure 1b, and it is called configuration 2 (or C2). From the viewpoint of the magnetic structure, we keep the magnetic moments opposite for Fe atoms with
y = ¼ and ¾, having effectively an AF structure. In the relaxed structure C2, the coordination number of Fe atoms close to the GB reaches 4–6, whereas the C1 structure yields 4–5 only. This means that some Fe atoms close to the interfaces in C2 exhibit the same (octahedral) coordination as in the bulk regions. The oxygen coordination is also modified at the GB region and increased slightly upon the shift performed to obtain configuration C2. The coordination of P ions is not affected at the GB regions. Regardless of configuration, Li atoms are fivefold coordinated at all the GB interfaces. These findings indicate that the presence of cations at the studied GBs is important in order to maintain cohesion at these interfaces.
The final C1 and C2 structures (shown in
Figure 1a,b) were both relaxed with respect to atomic coordinates as well as the supercell last dimension. This procedure is now explained in more detail as follows. The ‘bulk’ supercell (not shown here), in which the upper part/grain is not rotated, is relaxed with respect to all its cell dimensions (including atomic positions). The corresponding lattice vectors are
ar,
br, and
cr and it holds approximately that
ar ≈
a −
c,
br ≈
b, and
cr ≈ 6
c. In this way, we obtain the supercell containing no GB/interface, and this supercell is used as a reference for GB energy calculations (the corresponding total energy is denoted as
Etot(bulk)). First, two box dimensions along cell vectors
ar and
br are taken to be the corresponding dimensions of supercells for configurations C1 and C2. The last cell dimension, called further
zc, was taken initially to be
cr, and its size was then optimized to obtain the lowest energy,
Etot(GB). The final/equilibrium value of
zc is larger than
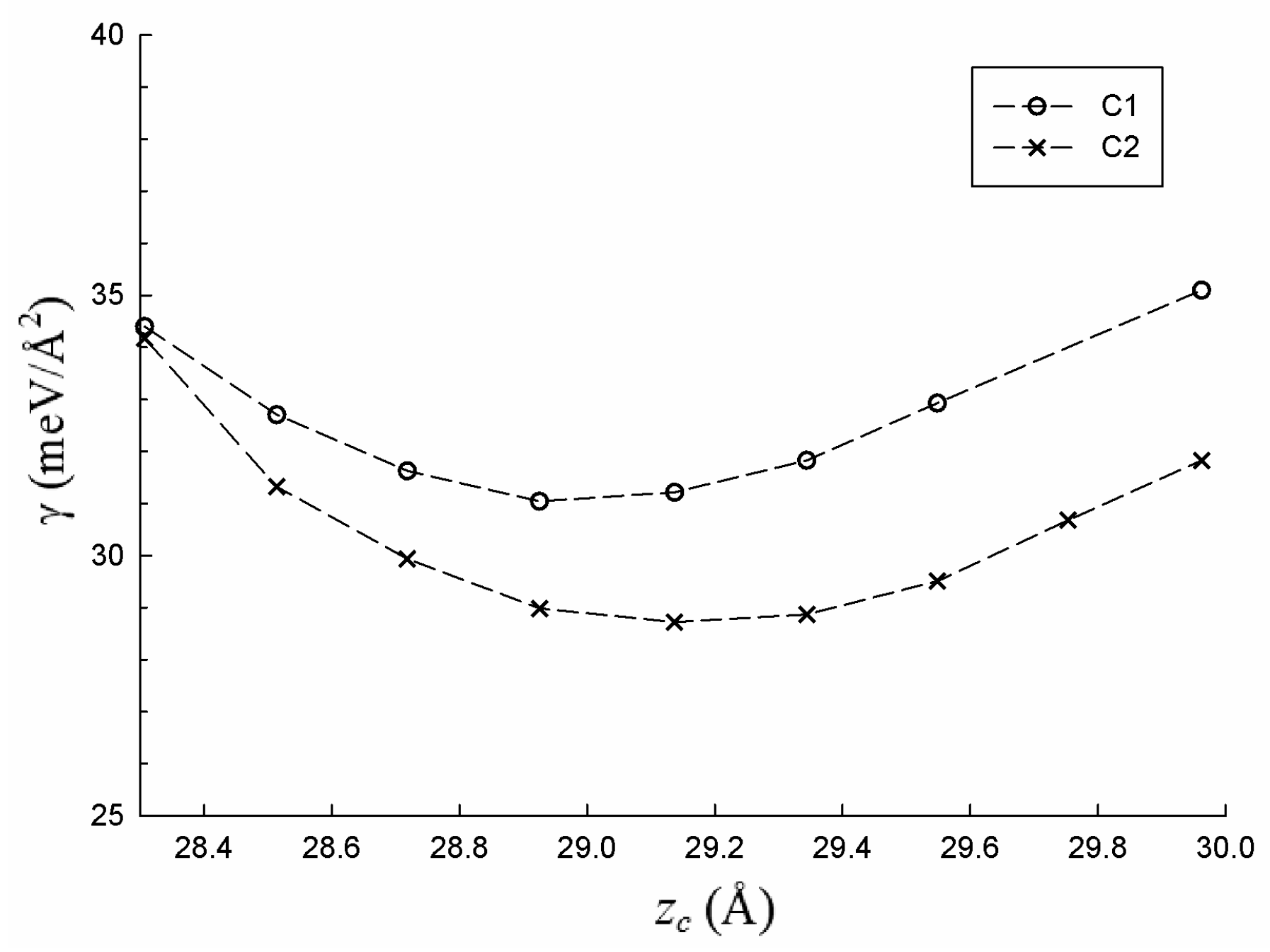
cr, since the cells expand along the last cell vector (the adaptation of the structure at the grain interfaces takes normally larger volume compared to bulk). Whereas dimensions parallel to the interface are not changed, as the same type of periodicity is kept as in the bulk. The curves showing how the cells’ energy is changed with the dimension
zc are presented in
Figure 2. In fact, the grain boundary energy, γ, is plotted here against
zc for both GB configurations, and the minimum corresponds to equilibrium, i.e., the optimal dimension. The GB energy (or interface energy) is given by relation:
where
A is the area of the GB in the supercell/box, considering that there are two GBs in each supercell. Using the dimensions
ar,
br, and
cr of the relaxed bulk supercell,
A can be calculated as
arbr ≈
b (
a2 +
c2)
1/2 when we relate it to the original primitive lattice dimensions. The minimum along this relaxation path corresponds to the equilibrium volume. Our results on the GB interface energy are given in
Table 1. One can see that the GB energies are quite low compared to a typical GB energy around 1 J/m
2, which indicates that the studied interfaces should be relatively easy to form. It also holds that γ (C1) > γ (C2), showing that the configuration C2 is more energetically favorable than C1 even if the difference is smaller than 10%. This is an expected result, since C2 exhibits better coherence than C1, as discussed above.
Table 1 contains γ values both in J/m
2 and meV/Å
2 units, since the latter is more suitable for considerations at the atomic level (1 J/m
2 corresponds to 62.4 meV/Å
2). In principle, the GB energy can be recalculated to the excess energy per one atom/ion at the interface (here ~0.5 eV/Li), which could be related, for example, to the point defect formation energies that are of the same order.
Another observation is that C2 expands more than C1, as it is reflected by the GB excess free volumes δ
V(C1) = 0.26 Å
3/Å
2 and δ
V (C2) = 0.36 Å
3/Å
2. This quantity can be determined as an extra volume due to the introduction of the GB into the bulk related to the GB area (units are usually expressed in the form volume per area), and can be easily calculated using Equation (1) where energies are replaced by cell volumes. The property δ
V should be viewed as an increase in the interstitial space at the GB regions. The GB excess free volumes can be also connected to positron characteristics, especially regarding the lifetime. The bulk positron lifetime for the LFP structure was calculated in Refs. [
28,
29] and amounts to 157.5 ps (LDA) and 169.7 ps (GGA) considering the room temperature lattice parameters. Here, we are getting [
30] slightly longer values—159 ps and 171 ps—for respective treatments of electron–positron correlations, considering the relaxed lattice parameters for which the volume per formula unit is larger (and consequently is the positron lifetime). We give both LDA and GGA values, even if the latter one is more realistic for comparison with experiment, to evaluate the effect of gradient corrections, which is apparently quite large because of the open-type crystal structure and ionic character of interatomic bonds. As for GBs,
Figure 1a,b clearly show positron density isosurfaces at about 55% of the maximum value are displayed, in which the positron presence is enhanced at the GB regions, especially in the interstitial channels between Li chains along the [010] direction. This is also reflected by the positron lifetime, τ
GB, which is 10–20 ps longer than its bulk counterpart. In particular, we obtain τ
GB = 177 ps (LDA) and 190 ps (GGA) for C1, whereas the values were τ
GB = 169 ps (LDA) and 182 ps (GGA) for C2. Small differences in positron density distributions between the middle and bottom/top GB are likely due to not exact site coincidence at the GBs mentioned above. Surprisingly, δ
V (C2) > δ
V(C1), but τ
GB(C2) < τ
GB(C1). In principle, a larger (excess) free volume should result in a larger positron lifetime, but in this case, a complex morphology of the GB interstitial space also plays a role, which likely reverses the expected trend (compare
Figure 1a,b). In any case, we can state that positrons trap at the studied GB in the LFP material. Interestingly, our recent experiment [
31] provides the positron lifetime data of a LiFePO
4 powder sample with the average grain size of about 100 nm. A lifetime component of 188 ps was detected and assigned to the annihilation of free positrons. Considering the above-calculated values of the bulk positron lifetime, we rather suggest that the component 188 ps more probably corresponds to the annihilation at grain boundaries because of similarity with lifetimes for the GBs calculated here (GGA case). Clearly, more types of GBs need to be examined to see how the lifetime depends on the GB geometry. Positrons stay in the interstitial space, but they are affected by ions forming an interstitial space ‘boundary’. Positrons are attracted to negative ions and repulsed from the positive ones.
The atom/ion charge analysis after Bader [
19] allows assigning charges to ions in a physically plausible way using the concept of ‘zero flux surface’ of the electron density around ions. Then, Bader charges correspond to the electron density integrated inside the (Bader) volumes bounded by zero-flux surfaces. Using the implementation [
20] for VASP, we found that in the bulk cell average charges, the
q values, which are related to neutral atoms for all atomic/crystallographic species, are:
q(Li) = +0.88
e,
q(Fe) = +1.40
e,
q(P) = +3.63
e,
q(O(1)) = −1.50
e,
q(O(2)) = −1.50
e, and
q(O(3)) = −1.46
e (with
e being the elementary charge). Summing them for the formula unit, i.e.,
q(Li) +
q(Fe) +
q(P) +
q(O(1)) +
q(O(2)) + 2
q(O(3)), gives −0.01
e, which is effectively zero considering the rounding errors. The charge neutrality is preserved, as expected, and the charges are not too far from the nominal valence charges assumed for LFP (note that the phosphate group, nominally (PO
4)
3−, has a charge of −2.29
e). Concerning the GB configuration C1, the average ionic charges almost do not change (at most, they are 0.02
e in both directions), but the charge of Fe ions close to the GB interfaces is lowered by 0.14
e on average (there are eight such Fe ions). For other atomic species, the changes are apparently smaller, although they must compensate for the lowered Fe charges in the whole cell. The detailed examination of atomic clusters making ‘formula units’ (i.e., LiFePO (1) O (2) O (3)
2) reveals that both GB interfaces in the cell are slightly negatively charged. In particular, the atomic clusters close to the interface have a charge between −0.12
e and −0.16
e, whereas clusters in the bulk regions have about half of these charges with the opposite sign. In the case of configuration C2, the charges of Fe ions close to the interface are almost unchanged compared to those in bulk, and the effect of GB charging is almost negligible (about −0.02
e on average per cluster). This shows that a better matching in bonds, appearing for the configuration C2, can make the charges almost the same as in the perfect crystal. Another aspect is that positrons are attracted to negatively charged regions (GBs). This effect may affect the positron lifetime already discussed, although a detailed analysis is needed. Similarly to charge, one can integrate spin-up and spin-down charge densities in the same Bader volumes to get magnetic moments (μ): μ(Li) = 0.00 μ
B, μ(Fe) = 3.59 μ
B, μ(P) = 0.00 μ
B, μ(O(1)) = 0.04 μ
B, μ(O(2)) = 0.05 μ
B, and μ(O(3)) = 0.03 μ
B (μ
B is the Bohr magneton; only magnitudes are given). The net magnetic moment of the supercell is zero, as required for an AF order. The magnetic moment of Fe is close to the anticipated value of 4 μ
B (spin-only contribution). The magnetic moments of oxygen ions are nearly negligible. Concerning the GB configurations, both C1 and C2 have average Fe and O magnetic moments that are nearly the same as those in bulk within 0.02 μ
B. In the case of C1, Fe atoms close to the interface have magnetic moments that are about 0.12 μ
B smaller than those farther from the interfaces (magnitude is considered). This is related to the effect of diminished charge at such Fe ions. When C2 is considered, Fe atoms with sixfold coordination at the GB interfaces have their magnetic moment with the same value as that in the bulk regions, but those with a lower coordination number have their moment lowered by about 0.02 μ
B compared to the average value. This indicates that a better coherency of C2 is also detectable via the magnetic moments. The net magnetic moment of the whole supercell is negligible (~0.01 μ
B) for both configurations, confirming an AF magnetic state.
3.2. Delithiated System
In the case of a delithiated system, i.e., FPO
4 or FP, we proceed in a similar way to that employed for LFP. Even if the lattice parameters
a,
b, and
c do not change much when going from LFP to FP by removing Li atoms, the
c/
a ratio important for CSL construction varies more significantly (increases by ~7%). This change affects the tilt angle, becoming now ~51.4°, and increases the Σ parameter to 4, since Σ 3 yields poor coincidence (certainly, the tilt angle and Σ are correlated). The result is a near-CSL symmetrical tilt Σ4 (101)/[010] GB for FP [
32]. For this reason, there are more atoms in the boxes/supercells than before, even if Li is not present. The supercells now contain 192 atoms (32× Fe, 32× P, 128× O). Nevertheless, a comparison of constructed GBs in LFP and FP still makes sense, since the GB planes (and tilt axes) are the same, and thereby, the geometrical relationship of the lower and upper blocks (expressed by the tilt angle) is very similar in both cases. However, we have no atoms/cations lying on the GB planes—in contrast to the LFP case, which may pose some problems related to the GB cohesion. In any case, this GB model for FP may be ideal to study Li GB diffusion at a later stage. As in the case of LFP, we construct a GB configuration shifted along [010] by
b/2 (configuration 2) in order to improve the GB coherence compared to the configuration 1 obtained just by rotation along the tilt axis. The perfect bulk box was constructed and relaxed as well, and its
ar,
br, and
cr translation vectors were used to make initial configurations of GBs similar to those for LFP. The magnetic order was again considered to be antiferromagnetic, and the directions of magnetic moments of Fe atoms were arranged in the same way as in LFP. While checking the atomic neighborhood of interfaces, one can notice that the rebonding of atoms at the bottom/top interface might be impeded by the matching plane of the rotated part being shifted by
ar/2, which does not happen for the middle interface. This is an effect of having a Σ4 GB for FP, and it does not happen for the Σ 3 GB studied in LFP.
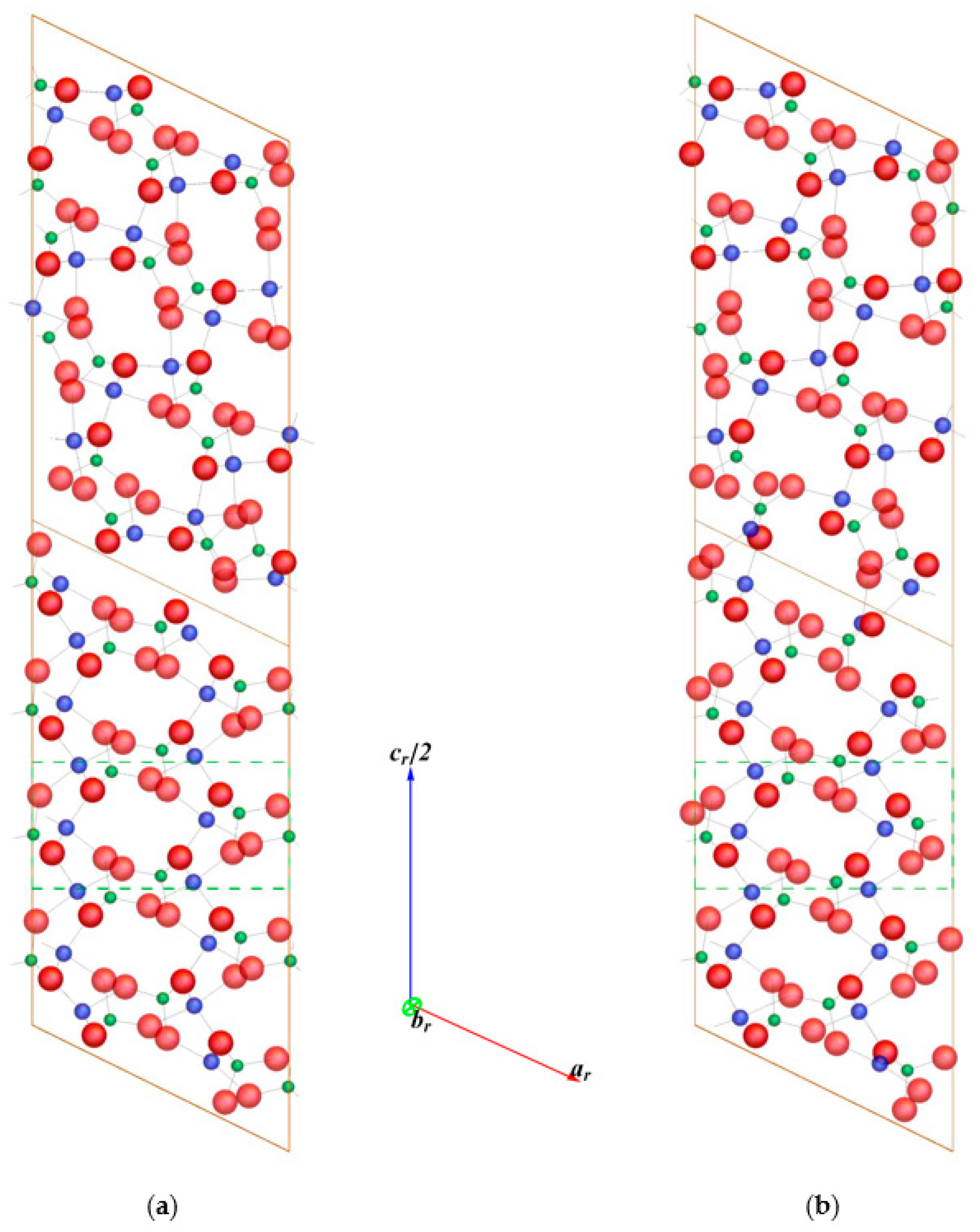
Figure 3 displays en face the relaxed GB configuration 1 (C1) and configuration 2 (C2) of FP without performing box dimension optimization (it has length
cr, as in the bulk box). The reason is that we need to examine first the GB structure before proceeding further, given the difficulty with the rebonding process mentioned above. Configuration 1 (
Figure 3a) clearly has no bonds across the interfaces, showing also large interstitial space at these regions. In contrast, configuration 2 exhibits Fe–O bonding across the middle GB, whereas bonding across the bottom/top GB appears weak. This might indicate an insufficient GB cohesion in FP, at least for the GB type studied. Preliminary calculations show that increasing the last box dimension leads to upper and lower grain separation at both interfaces for C1. In the case of C2, only the bottom/top interface splits. Concerning the coordination of Fe atoms close to the interfaces, C1 shows fourfold or fivefold coordination at both interfaces, whereas in C2, Fe is fourfold or sixfold coordinated in the middle, and fourfold to sixfold coordinated at the bottom/top, which is similar to that observed in LFP. GB energies are calculated formally according to Equation (1). The results are reported in
Table 1, and provide the first idea regarding interface energies for the delithiated system. These values correspond to boxes with the last dimension unrelaxed. We can see that C1 has a larger interface energy compared to C2, which is again an expected trend. Both γ’s—to be considered as a first guess only—are about twice as large as those for LFP. Obviously, the FP GB energies may still change when the studied GB is further elaborated to be better suitable for the Li diffusion study envisaged. Some ideas in this direction are given in the next section.
Let us now discuss other properties of the studied GB in the FP material, even if they should be considered as preliminary. Bader charge analysis shows that for the bulk cell, charges are as follows:
q(Fe) = +1.76
e,
q(P) = +3.55
e,
q(O(1)) = −1.32
e,
q(O(2)) = −1.34
e, and
q(O(3)) = −1.32
e. The sum of charges in the formula unit, i.e.,
q(Fe) +
q(P) +
q(O(1)) +
q(O(2)) + 2
q(O(3)), results in +0.01
e, which is again practically zero, taking into account rounding errors. With the charge neutrality being fulfilled, one can observe that the FP system becomes more covalent bonded compared to LFP (see also the discussion in Ref. [
5]), since the magnitude of ionic charges diminishes (except for Fe, which is assumed to be an Fe
3+ ion); the phosphate group has the charge −1.76
e. This indicates that in LFP, the Li electron—which is supposed to be transferred solely to the Fe ion—is partially transferred also to the phosphate group (thereby oxygen anions). The more open FP structure with respect to LFP (see
Figure 1 and
Figure 3) is also an indication of more covalent bonds in FP. In the case of the C1 GB, average ionic charges change slightly only (0.01–0.02
e), but Fe ions close to the interface have a lower charge by about 0.04
e (the largest changes occur for Fe ions with fourfold coordination). The C2 GB behaves in about the same way as the C1 GB concerning ionic charges, but for Fe ions with fourfold coordination, the charge decreases even by 0.11
e on average compared to the reference bulk system. Clusters of atoms were also investigated, but for the FP GB configurations, we chose a somewhat different approach because of a less regular GB structure compared to LFP. Namely, 24 atom clusters (four formula units) were considered (instead of six atom clusters) forming just one unit cell of FePO
4. Such 24 atom clusters are ‘parallel’ with the GB interface, and are located on either side of the interfaces, as well as in the bulk-like regions. There are totally eight clusters in the supercell of each configuration. For both cases, there is a charge modulation going along the last supercell dimension. At the interfaces, one side is charged positively, and the other one is charged negatively. The magnitudes of the cluster charges peak at 0.10
e for C1 and 0.03
e for C2. The overall charge is, of course, zero, since the boxes have neutral charge. Again, the GB C2 interface with a better coherence exhibits lower cluster charges.
The magnetic moments of all the atomic species in the reference bulk box are μ(Fe) = 4.01 μ
B, μ(P) = 0.01 μ
B, μ(O(1)) = 0.18 μ
B, μ(O(2)) = 0.16 μ
B, and μ(O(3)) = 0.00 μ
B (magnitudes are given). Due to an AF order, the total magnetic moment of the cell is zero. The magnetic moment of iron ions is slightly increased over the value for bulk LFP, but it does not reach the value 5 μ
B, which is expected for a free Fe
3+ ion in the high spin state. As for GB configurations, the magnetic moments of Fe atoms in configuration 1 are modified slightly only—usually within 0.02 μ
B—regardless of the atomic positions (close to the interface or in bulk-like regions). The magnetic moments of oxygen atoms are also affected when they are close to the interface (and have dangling bonds). The size of the total magnetic moment is 0.08 μ
B, indicating slight disturbances in the AF order. An examination of configuration 2 reveals less expected behavior. Namely, three Fe ions close to the interfaces have their magnetic moments diminished to about 3.33 μ
B, while the remaining Fe ions are almost unchanged. O ions with dangling bonds (i.e., those close to interfaces) have their magnetic moments also changed compared to bulk-like regions. The total magnetic moment of C2 is 1.16 μ
B, suggesting a strong disturbance of the AF order. We mention that a GGA+
U approach (see e.g., Ref. [
33]) applied to the Fe 3
d electrons can help to increase slightly the Fe ionic charge and magnetic moment in the FP compound.
Concerning the positron behavior at the studied C1 and C2 configurations, preliminary calculations carried out using the so-called atomic superposition method [
34]—being part of our computational approach [
22]—indicate that positrons are trapped at the grain boundary studied. The estimated lifetimes exceed the bulk lifetime by about 40 ps and 10 ps for the C1 and C2 configurations, respectively. This is an interesting observation, since there is no excess free volume for the examined boxes. Still the structure at the GBs provides more interstitial space compared to bulk (as seen in
Figure 3), which explains this effect. The positron density (not shown here) shows only a maximum at the middle GB for both configurations, in contrast to LFP (see
Figure 1). The calculated bulk FP lifetime amounts to 207.2 ps (GGA value) [
28,
29], and this value also reflects the more open structure of FP compared to LFP. A recent positron annihilation study of the FP system [
35] suggests again that one lifetime component detected in measured spectra could correspond to positron annihilation at grain interfaces.