Instabilities of the Vortex Lattice and the Peak Effect in Single Crystal YBa2Cu4O8
Abstract
1. Introduction
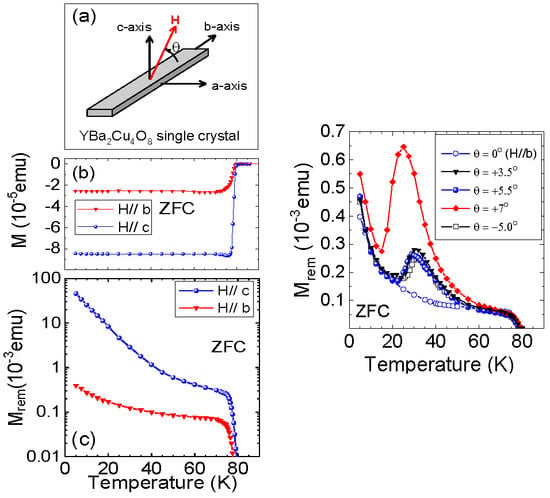
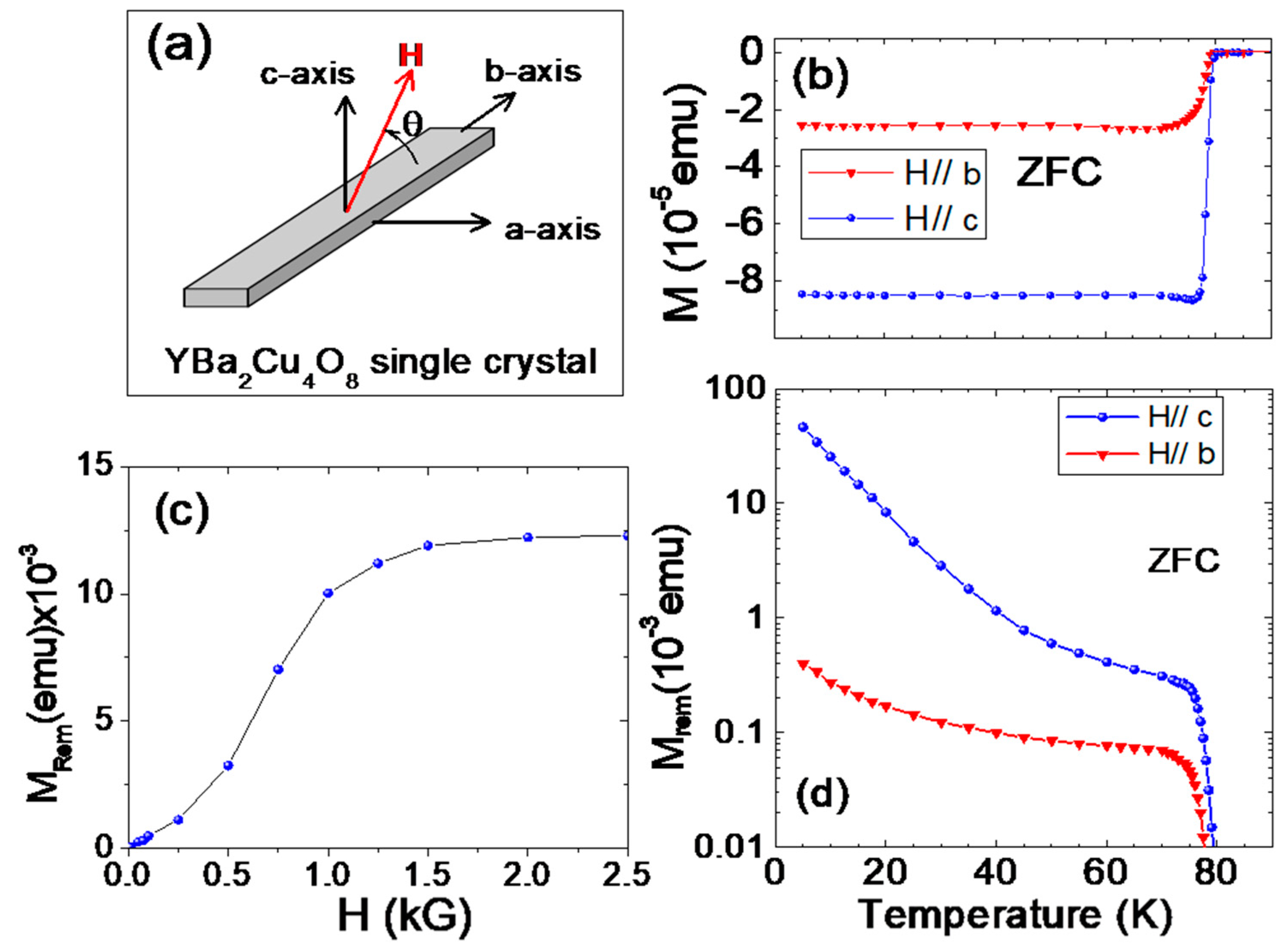
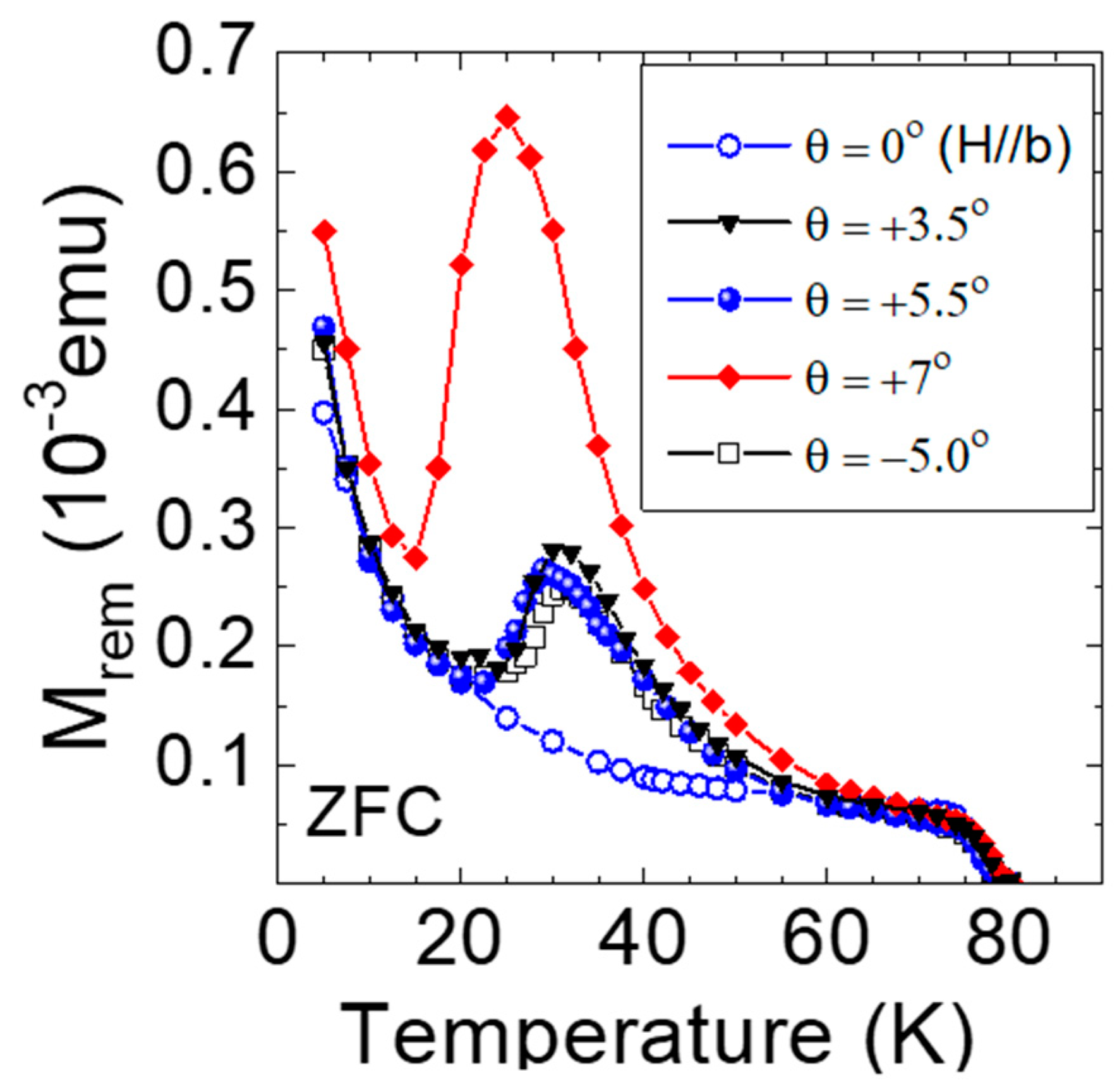
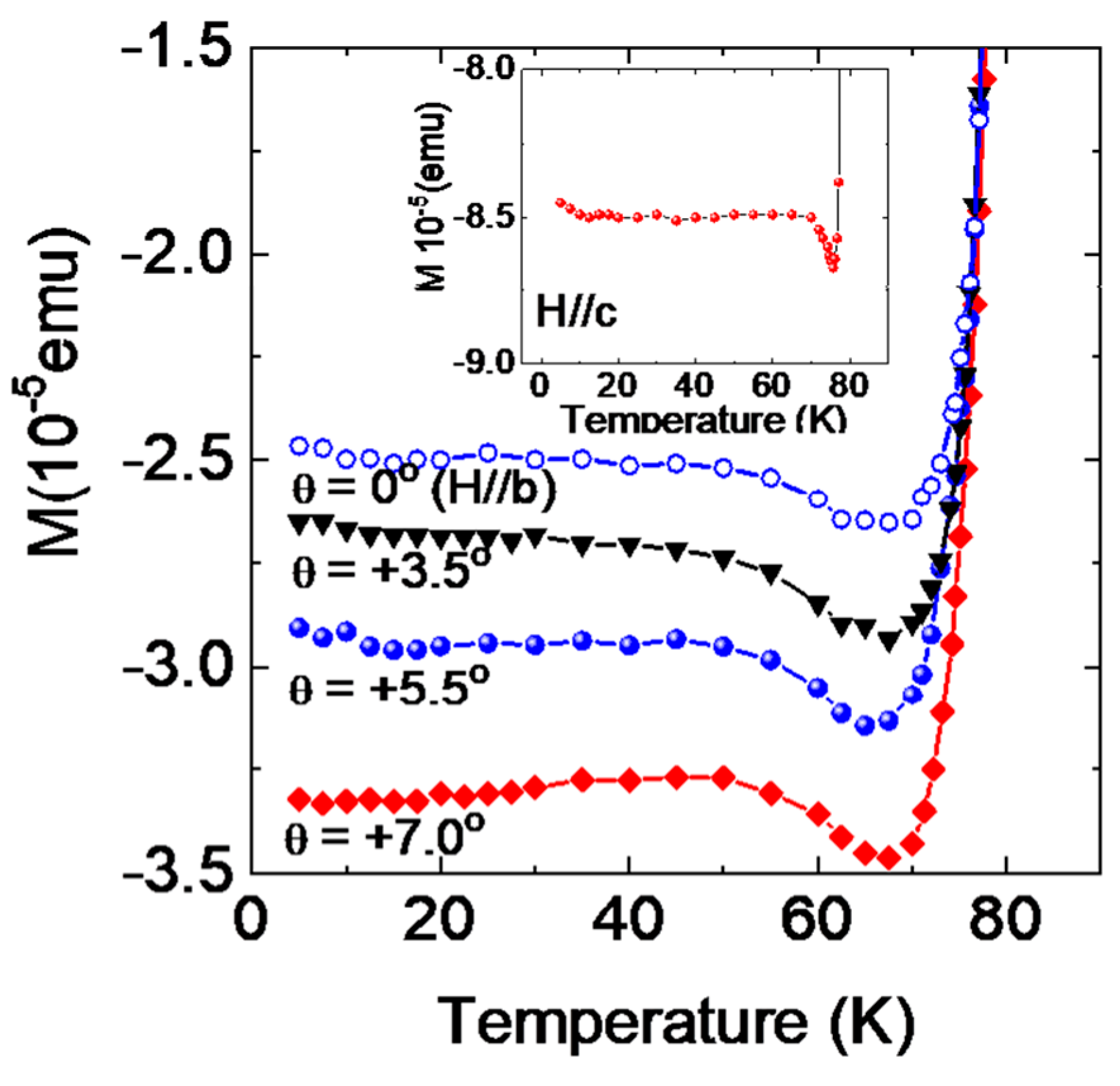
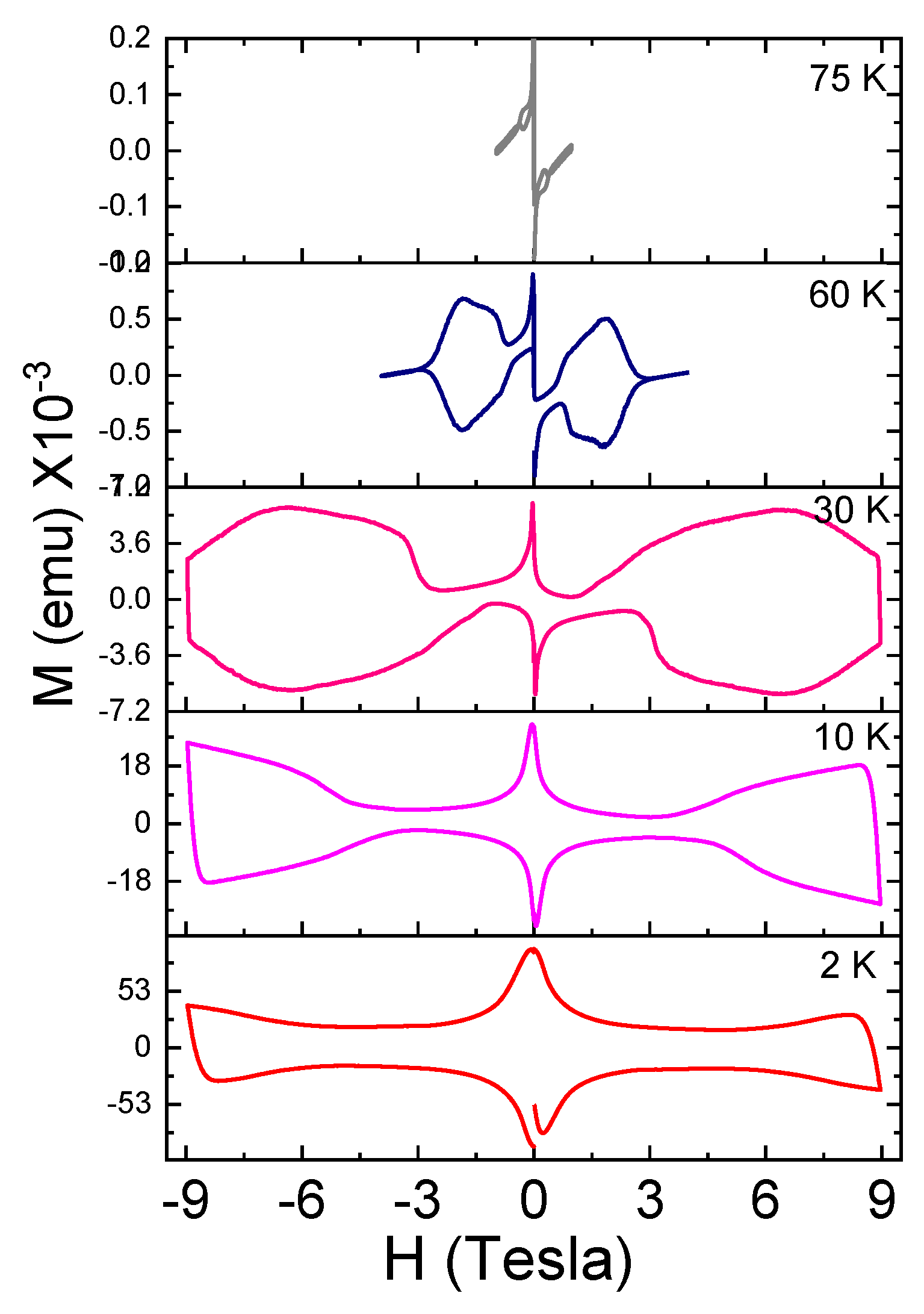
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Glatz, A.; Vlasko-Vlasov, V.K.; Kwok, W.K.; Crabtree, G.W. Vortex cutting in superconductors. Phys. Rev. B 2016, 94, 064505. [Google Scholar] [CrossRef]
- Toft-Petersen, R.; Abrahamsen, A.B.; Balog, S.; Porcar, L.; Laver, M. Decomposing the Bragg glass and the peak effect in a Type-II superconductor. Nat. Commun. 2018, 9, 901. [Google Scholar] [CrossRef] [PubMed]
- Tachiki, M.; Takahashi, S. Strong vortex pinning intrinsic in high-Tc oxide superconductors. Solid State Commun. 1989, 70, 291. [Google Scholar] [CrossRef]
- Feinberg, D.; Villard, C. Intrinsic pinning and lock-in transition of flux lines in layered type-II superconductors. Phys. Rev. Lett. 1990, 65, 919. [Google Scholar] [CrossRef] [PubMed]
- Blatter, G.; Rhyner, J.; Vinokur, V.M. Vortex pinning by twin boundaries in copper oxide superconductors. Phys. Rev. B 1991, 43, 7826. [Google Scholar] [CrossRef]
- Ivlev, B.I.; Ovchinnikov, Y.N.; Pokrovsky, V.L. The kinked vortices in layered superconductors in the presence of a tilted magnetic field. Mod. Phys. Lett. B 1991, 5, 73. [Google Scholar] [CrossRef]
- Koshelev, A.E. Kink walls and critical behavior of magnetization near the lock-in transition in layered superconductors. Phys. Rev. B 1993, 48, 1180. [Google Scholar] [CrossRef]
- Koshelev, A.E. Vortex-chain phases in layered superconductors. Phys. Rev. B 2005, 71, 174507. [Google Scholar] [CrossRef]
- Bulaevskii, N.L.; Ledvij, M.; Kogan, V.G. Vortices in layered superconductors with Josephson coupling. Phys. Rev. B 1992, 46, 366. [Google Scholar] [CrossRef]
- Kwok, W.K.; Welp, U.; Vinokur, V.M.; Fleshler, S.; Downey, J.; Crabtree, G.W. Direct observation of intrinsic pinning by layered structure in single-crystal YBa2Cu3O7−δ. Phys. Rev. Lett. 1991, 67, 390. [Google Scholar] [CrossRef]
- Sudbo, A.; Brandt, E.H.; Huse, D.A. Multiple coexisting orientations of flux lines in superconductors with uniaxial anisotropy. Phys. Rev. Lett. 1993, 71, 1451. [Google Scholar] [CrossRef] [PubMed]
- Sardella, E.; Moore, M.A. Tilt-wave instability of the flux-line lattice in anisotropic superconductors. Phys. Rev. B 1993, 48, 9664. [Google Scholar] [CrossRef] [PubMed]
- Thompson, A.M.; Moore, M.A. Instabilities in the flux-line lattice of anisotropic superconductors. Phys. Rev. B 1997, 55, 3856. [Google Scholar] [CrossRef]
- Machida, M.; Kaburaki, H. Structure of flux lines in three-dimensional layered type-II superconductor: Numerical experiments. Phys. Rev. Lett. 1995, 74, 1434. [Google Scholar] [CrossRef] [PubMed]
- Bending, S.J.; Dodgson, M.W. Vortex chains in anisotropic superconductors. J. Phys. Condens. Matter 2005, 17, 955R. [Google Scholar] [CrossRef]
- Karpinski, J.; Kaldis, E.; Jilek, E.; Rusiecki, S.; Bucher, B. Bulk synthesis of the 81-K superconductor YBa2Cu4O8 at high oxygen pressure. Nature 1988, 336, 660. [Google Scholar] [CrossRef]
- Qiu, X.G.; Moshchalkov, V.V.; Bruynseraede, Y.; Karpinski, J. Vortex lattice melting into a disentangled liquid followed by the 3D-2D decoupling transition in YBa2Cu4O8 single crystals. Phys. Rev. B 1998, 58, 8826. [Google Scholar] [CrossRef]
- Iwasawa, H.; Dudin, P.; Inui, K.; Masui, T.; Kim, T.K.; Cacho, C.; Hoesch, M. Buried double CuO chains in YBa2Cu4O8 uncovered by nano-ARPES. Phys. Rev. B 2019, 99, 140510. [Google Scholar] [CrossRef]
- Hussey, N.E.; Takagi, H.; Mori, N.; Takeshita, N.; Iye, Y.; Adachi, S.; Tanabe, K. Vortex Lattice Melting in YBa2Cu4O8 with H||ab. J. Supercond. 1999, 12, 583. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Sannikov, I.I.; Ivanov, A.A.; Menushenkov, A.P. Temperature dependence of the critical current of YBa2Cu3O7−δ films. JETP Lett. 2017, 106, 324. [Google Scholar] [CrossRef]
- Lairson, B.M.; Sun, J.Z.; Bravman, J.C.; Geballe, T.H. Reduction of the magnetization decay rate in high-Tc superconductors. Phys. Rev. B 1990, 42, 1008. [Google Scholar] [CrossRef] [PubMed]
- Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H.J. Iron-Based Layered Superconductor La[O1-xFx]FeAs (x = 0.05−0.12) with Tc = 26 K. Am. Chem. Soc. 2008, 130, 3296. [Google Scholar] [CrossRef] [PubMed]
- Mohan, S.; Sinha, J.; Banerjee, S.S.; Myasoedov, Y. Instabilities in the Vortex Matter and the Peak Effect Phenomenon. Phys. Rev. Lett. 2007, 98, 027003. [Google Scholar] [CrossRef] [PubMed]
- Kwok, W.K.; Fendrich, J.A.; van der Beek, C.J.; Crabtree, G.W. Peak Effect as a Precursor to Vortex Lattice Melting in Single Crystal YBa2Cu3O7−δ. Phys. Rev. Lett. 1994, 73, 2614. [Google Scholar] [CrossRef] [PubMed]
- Kupfer, H.; Wolf, T.; Lessing, C.; Zhukov, A.A.; ̧Lanc ̧on, X.L.; Meier-Hirmer, R.; Schauer, W.; Wuhl, H. Peak effect and its evolution from oxygen deficiency in YBa2Cu3O7−δ single crystals. Phys. Rev. B 1998, 58, 2886. [Google Scholar] [CrossRef]
- Gozzelino, L.; Botta, D.; Chiodoni, A.; Gerbaldo, R.; Ghigo, G.; Laviano, F.; Mezzetti, E. Magneto-optical analysis of second-peak effect in BSCCO single crystals. Europhys. Lett. 2002, 60, 910. [Google Scholar] [CrossRef]
- Terashima, T.; Kikugawa, N.; Kiswandhi, A.; Choi, Eu.; Kihou, K.; Ishida, S.; Lee, Ch.; Iyo, A.; Eisaki, H.; Uji, S. Anomalous peak effect in iron-based superconductors Ba1−xKxFe2As2 (x ≈ 0.69 and 0.76) for magnetic-field directions close to the ab plane and its possible relation to the spin paramagnetic effect. Phys. Rev. B 2019, 99, 094508. [Google Scholar] [CrossRef]
- Kokubo, N.; Kadowaki, K.; Takita, K. Peak Effect and Dynamic Melting of Vortex Matter in NbSe2. Phys. Rev. Lett. 2005, 95, 177005. [Google Scholar] [CrossRef]
- Abulafia, Y.; Shaulov, A.; Wolfus, Y.; Prozorov, R.; Burlachkov, L.; Yeshurun, Y.; Majer, D.; Zeldov, E.; Wühl, H.; Geshkenbein, V.B. Plastic Vortex Creep in YBa2Cu3O7−x Crystals. Phys. Rev. Lett. 1996, 77, 1596. [Google Scholar] [CrossRef]
- Nishizaki, T.; Naito, T.; Kobayashi, N. Anomalous magnetization and field-driven disordering transition of a vortex lattice in untwinned YBa2Cu3Oy. Phys. Rev. B 1998, 58, 11169. [Google Scholar] [CrossRef]
- Rosenstein, B.; Shapiro, B.Y.; Shapiro, I.; Bruckental, Y.; Shaulov, A.; Yeshurun, Y. Peak effect and square-to-rhombic vortex lattice transition in La2−xSrxCuO4. Phys. Rev. B 2005, 72, 144512. [Google Scholar] [CrossRef]
- Kopylov, V.N.; Koshelev, A.E.; Schegolev, F.; Togonidze, T.G. The role of surface effects in magnetization of high-Tc superconductors. Phys. C 1990, 170, 291. [Google Scholar] [CrossRef]
- Zhou, W.; Xing, X.; Wu, W.; Zhao, H.; Shi, Z. Second magnetization peak effect, vortex dynamics, and flux pinning in 112-type superconductor Ca0.8La0.2Fe1−xCoxAs2. Sci. Rep. 2016, 6, 22278. [Google Scholar] [CrossRef]
- Jackson, D.K.; Nicodemi, M.; Perkins, G.K.; Lindop, N.A.; Jensen, H.J. Vortex clustering: The origin of the second peak in the magnetisation loops of type-two superconductors. Europhys. Lett. 2000, 52, 210. [Google Scholar] [CrossRef]
- Zech, D.; Keller, H.; Warden, M.; Simmler, H.; Stäuble-Pümpin, B.; Zimmermann, P.; Kaldis, E.; Karpinski, J. Angle-dependent magnetic-relaxation studies in single-crystal YBa2Cu4O8. Phys. Rev. B 1993, 48, 6533. [Google Scholar] [CrossRef]
- Katayama, K.; Yoshida, Y.; Kawamata, S.; Ishida, T.; Shibata, K.; Sasaki, T.; Kobayashi, N.; Adachi, S.; Tajima, S. Peak effect and vortex phase diagram of YBa2Cu4O8. Phys. C 2003, 392, 382. [Google Scholar] [CrossRef]
- Harrison, N.; Vanacken, J.; Lagutin, A.S.; Hrlach, F. Observation of the peak effect at high fields in single crystalline YBa2Cu4O8. Phys. B 1995, 211, 251. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Egilmez, M.; Isaac, I.; Alnaser, A.S.; Bukowski, Z.; Karpinski, J.; Chow, K.H.; Jung, J. Instabilities of the Vortex Lattice and the Peak Effect in Single Crystal YBa2Cu4O8. Condens. Matter 2019, 4, 74. https://doi.org/10.3390/condmat4030074
Egilmez M, Isaac I, Alnaser AS, Bukowski Z, Karpinski J, Chow KH, Jung J. Instabilities of the Vortex Lattice and the Peak Effect in Single Crystal YBa2Cu4O8. Condensed Matter. 2019; 4(3):74. https://doi.org/10.3390/condmat4030074
Chicago/Turabian StyleEgilmez, Mehmet, Isaac Isaac, Ali S. Alnaser, Zbigniew Bukowski, Janusz Karpinski, Kim H. Chow, and Jan Jung. 2019. "Instabilities of the Vortex Lattice and the Peak Effect in Single Crystal YBa2Cu4O8" Condensed Matter 4, no. 3: 74. https://doi.org/10.3390/condmat4030074
APA StyleEgilmez, M., Isaac, I., Alnaser, A. S., Bukowski, Z., Karpinski, J., Chow, K. H., & Jung, J. (2019). Instabilities of the Vortex Lattice and the Peak Effect in Single Crystal YBa2Cu4O8. Condensed Matter, 4(3), 74. https://doi.org/10.3390/condmat4030074