Tc and Other Cuprate Properties in Relation to Planar Charges as Measured by NMR
Abstract
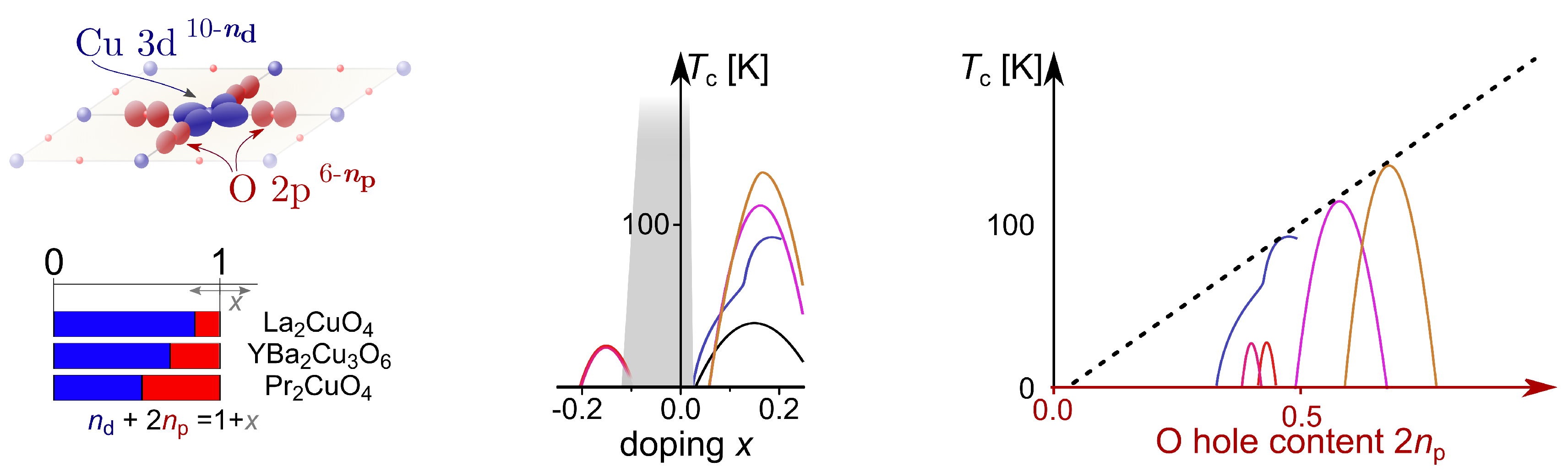
1. Introduction
2. NMR of Charges in the Cuprate Plane
3. Planar Charges and Electronic Properties
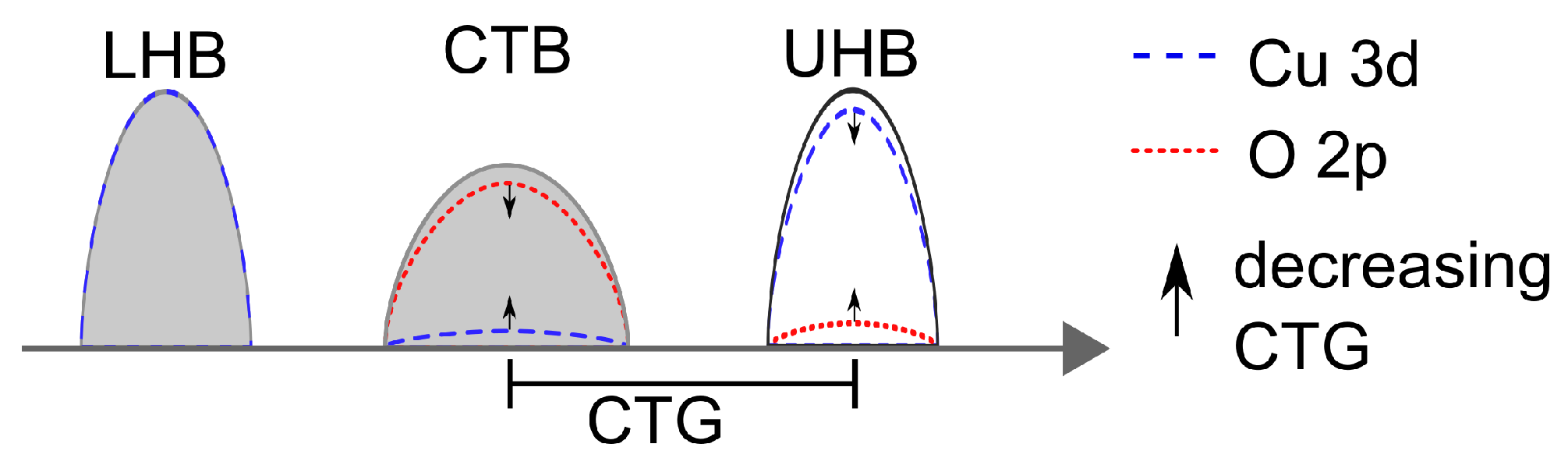
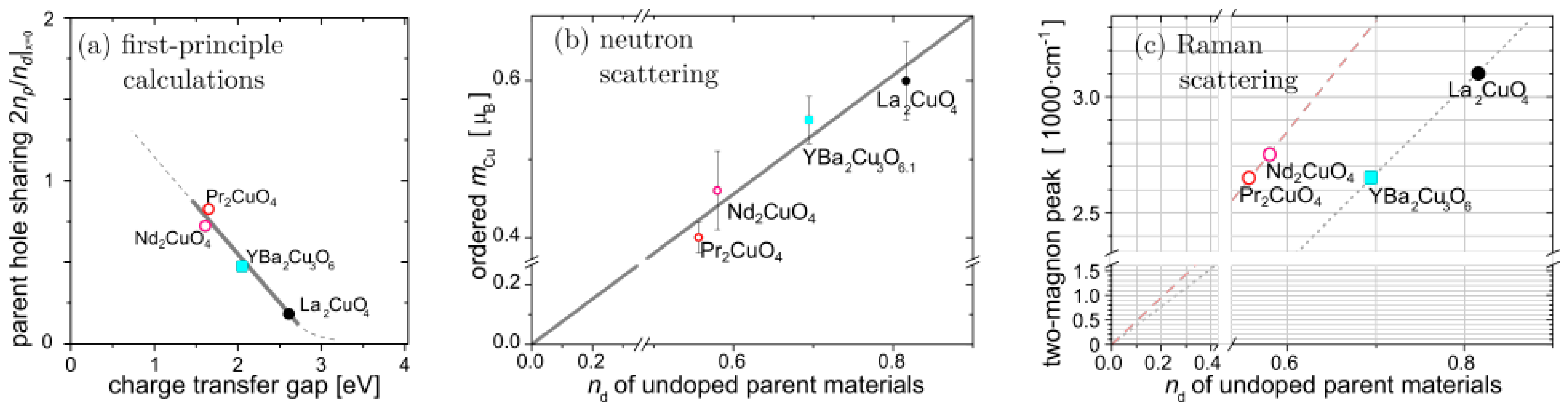
3.1. Parent Materials
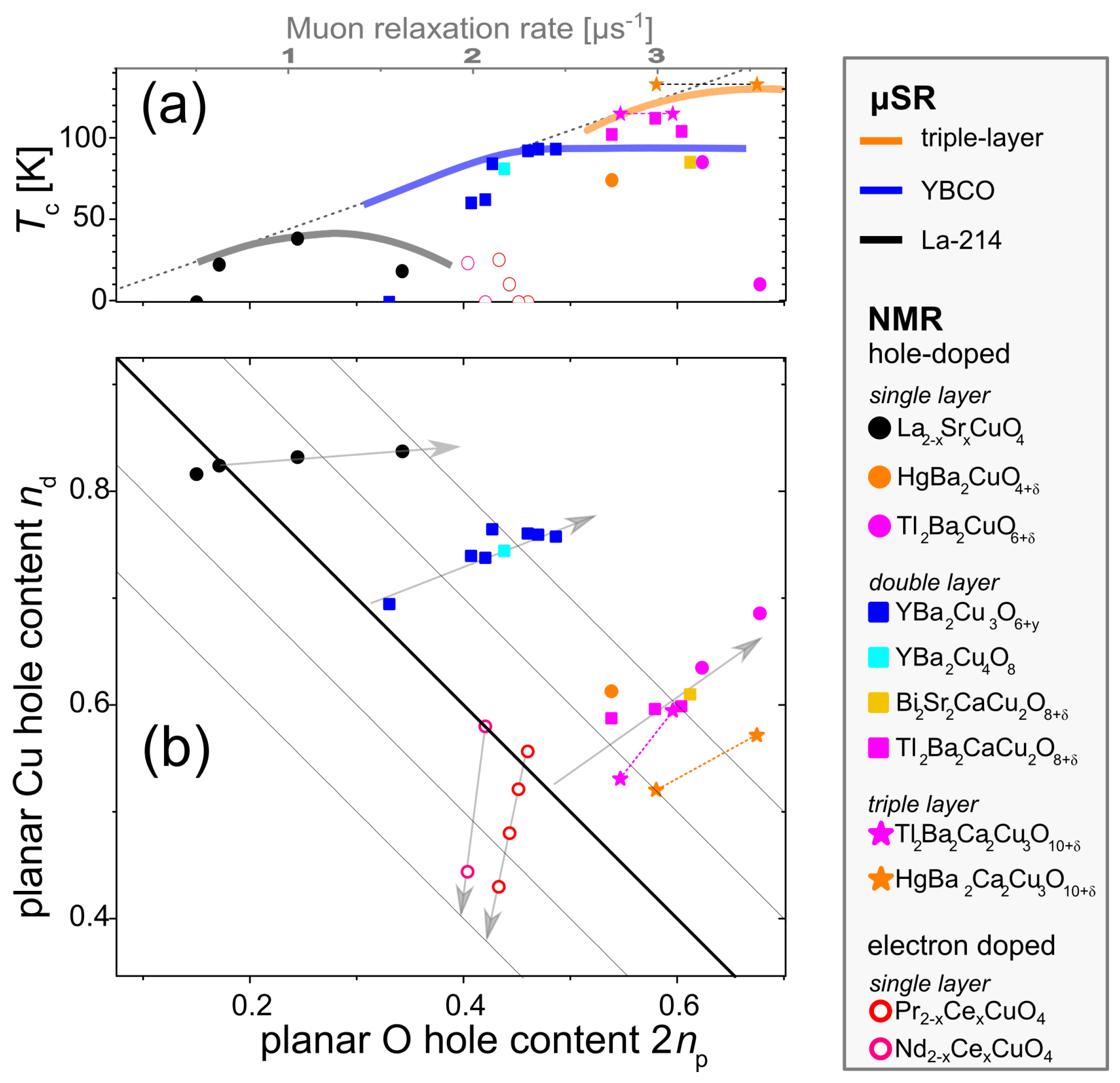
3.2. Underdoped Cuprates
3.3. Optimal Doping
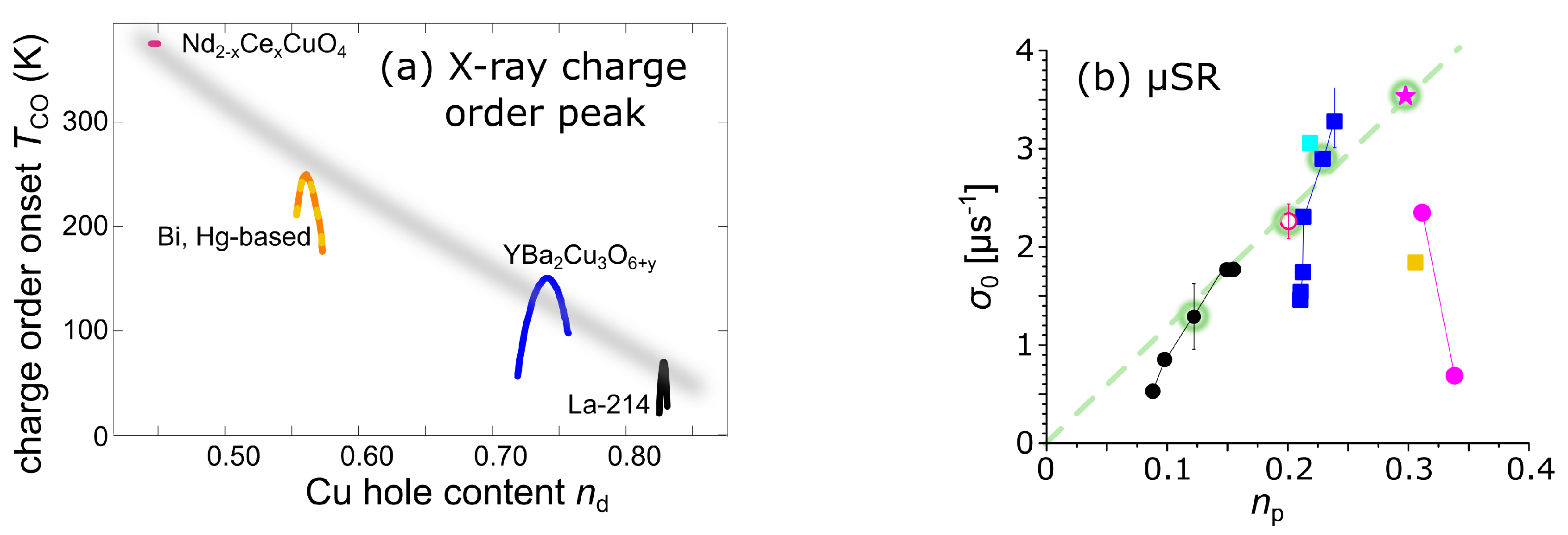
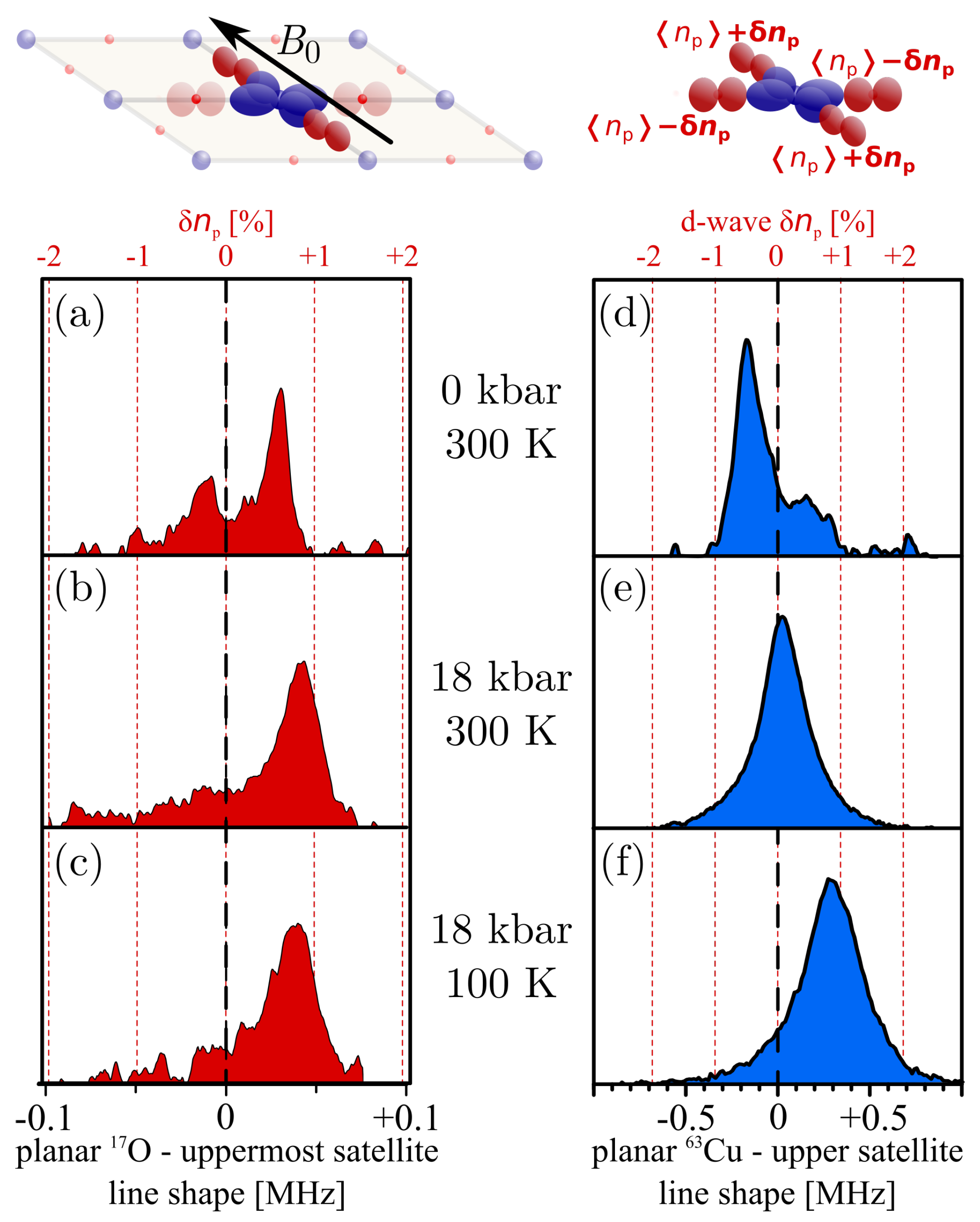
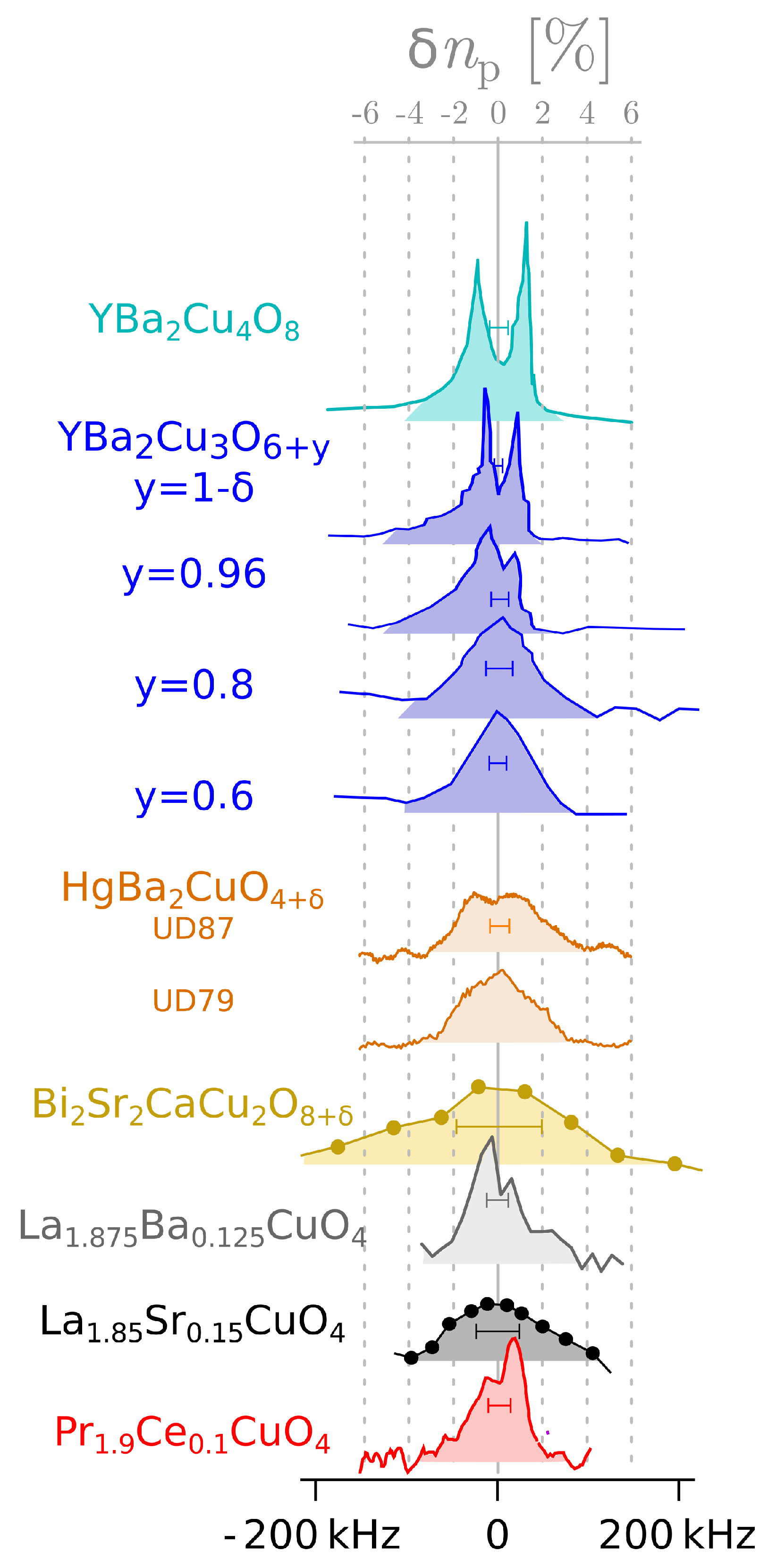
4. Planar Charge Density Variations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Slichter, C.P. Principles of Magnetic Resonance, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Slichter, C.P. Magnetic Resonance Studies of High Temperature Superconductors. In Handbook of High-Temperature Superconductivity; Schrieffer, J.R., Brooks, J.S., Eds.; Springer: New York, NY, USA, 2007; pp. 215–256. [Google Scholar]
- Walstedt, R.E. The NMR Probe of High-Tc Materials; Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 228, p. 273. [Google Scholar]
- Jurkutat, M.; Kohlrautz, J.; Reichardt, S.; Erb, A.; Williams, G.V.M.; Haase, J. NMR of Cuprate Superconductors: Recent Developments. In High-Tc Copper Oxide Superconductors and Related Novel Materials: Dedicated to Prof. K. A. Müller on the Occasion of His 90th Birthday; Bussmann-Holder, A., Keller, H., Bianconi, A., Eds.; Springer International Publishing: Cham, Switzerlands, 2017; pp. 77–97. [Google Scholar]
- Haase, J.; Jurkutat, M.; Kohlrautz, J. Contrasting Phenomenology of NMR Shifts in Cuprate Superconductors. Condens. Matter 2017, 2, 16. [Google Scholar] [CrossRef]
- Jurkutat, M.; Avramovska, M.; Williams, G.V.M.; Dernbach, D.; Pavićević, D.; Haase, J. Phenomenology of 63Cu nuclear relaxation in cuprate superconductors. arXiv 2019, arXiv:1902.10625. [Google Scholar]
- Avramovska, M.; Pavićević, D.; Haase, J. Properties of the electronic fluid of superconducting cuprates from 63Cu NMR shift and relaxation. J. Supercond. Nov. Magn. 2019. [Google Scholar] [CrossRef]
- Zheng, G.Q.; Mito, T.; Kitaoka, Y.; Asayama, K.; Kodama, Y. 63Cu NMR and NQR studies of high-Tc cuprates under pressure. Phys. C Supercond. 1995, 243, 337–341. [Google Scholar] [CrossRef]
- Haase, J.; Sushkov, O.P.; Horsch, P.; Williams, G.V.M. Planar Cu and O hole densities in high-Tc cuprates determined with NMR. Phys. Rev. B 2004, 69, 94504. [Google Scholar] [CrossRef]
- Jurkutat, M.; Rybicki, D.; Sushkov, O.P.; Williams, G.V.M.; Erb, A.; Haase, J. Distribution of electrons and holes in cuprate superconductors as determined from 17O and 63Cu nuclear magnetic resonance. Phys. Rev. B 2014, 90, 140504. [Google Scholar] [CrossRef]
- Rybicki, D.; Jurkutat, M.; Reichardt, S.; Kapusta, C.; Haase, J. Perspective on the phase diagram of cuprate high-temperature superconductors. Nat. Commun. 2016, 7, 1–6. [Google Scholar] [CrossRef]
- Reichardt, S.; Jurkutat, M.; Guehne, R.; Kohlrautz, J.; Erb, A.; Haase, J. Bulk Charge Ordering in the CuO2 Plane of the Cuprate Superconductor YBa2Cu3O6.9 by High-Pressure NMR. Condens. Matter 2018, 3, 23. [Google Scholar] [CrossRef]
- Ishida, K.; Kitaoka, Y.; Asayama, K. Nuclear Quadrupole Resonance of Cu in Superconducting (La0.925Sr0.075)2CuO4. JPSJ 1989, 58, 36–38. [Google Scholar] [CrossRef]
- Abe, M.; Kumagai, K.; Awaji, S.; Fujita, T. Cu-NMR studies of Nd2−xCexCuO4−y. Phys. C Supercond. 1989, 160, 8–16. [Google Scholar] [CrossRef]
- Martin, R.L. Nuclear Quadrupole Resonance Spectrum of La2CuO4. Phys. Rev. Lett. 1995, 75, 744–747. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, K.; Ambrosch-Draxl, C.; Blaha, P. Charge distribution and electric-field gradients in YBa2Cu3O7−x. Phys. Rev. B 1990, 42, 2051–2061. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Novák, P. Electric field gradients in cuprates: Does LDA+U give the correct charge distribution? Int. J. Quantum Chem. 2005, 101, 550–556. [Google Scholar] [CrossRef]
- Shimizu, T. On the Electric Field Gradient at Copper Nuclei in Oxides. JPSJ 1993, 62, 772–778. [Google Scholar] [CrossRef]
- Bianconi, A.; Castellano, A.; Santis, M.D.; Rudolf, P.; Lagarde, P.; Flank, A.; Marcelli, A. L2,3 xanes of the high Tc superconductor YBa2Cu3O7 with variable oxygen content. Solid State Commun. 1987, 63, 1009–1013. [Google Scholar] [CrossRef]
- Uemura, Y.J.; Luke, G.M.; Sternlieb, B.J.; Brewer, J.H.; Carolan, J.F.; Hardy, W.N.; Kadono, R.; Kempton, J.R.; Kiefl, R.F.; Kreitzman, S.R.; et al. Universal Correlations between Tc and (Carrier Density over Effective Mass) in High-Tc Cuprate Superconductors. Phys. Rev. Lett. 1989, 62, 2317. [Google Scholar] [CrossRef] [PubMed]
- Pavarini, E.; Dasgupta, I.; Saha-Dasgupta, T.; Jepsen, O.; Andersen, O.K. Band-Structure Trend in Hole-Doped Cuprates and Correlation with Tc,max. Phys. Rev. Lett. 2001, 87, 047003. [Google Scholar] [CrossRef] [PubMed]
- Agrestini, S.; Saini, N.L.; Bianconi, G.; Bianconi, A. The strain of CuO2 lattice: The second variable for the phase diagram of cuprate perovskites. J. Phys. A 2003, 36, 9133–9142. [Google Scholar] [CrossRef]
- Weber, C.; Yee, C.; Haule, K.; Kotliar, G. Scaling of the transition temperature of hole-doped cuprate superconductors with the charge-transfer energy. Eur. Phys. Lett. 2012, 100, 37001. [Google Scholar] [CrossRef]
- Weber, C.; Haule, K.; Kotliar, G. Strength of correlations in electron- and hole-doped cuprates. Nat. Phys. 2010, 6, 574–578. [Google Scholar] [CrossRef]
- Lorenzana, J.; Seibold, G.; Coldea, R. Sum rules and missing spectral weight in magnetic neutron scattering in the cuprates. Phys. Rev. B 2005, 72, 224511. [Google Scholar] [CrossRef]
- Tranquada, J.M. Neutron Scattering Studies of Antiferromagnetic Correlations in Cuprates. In Handbook of High-Temperature Superconductivity: Theory and Experiment; Schrieffer, J.R., Brooks, J.S., Eds.; Springer: New York, NY, USA, 2007; pp. 257–298. [Google Scholar]
- Walters, A.C.; Perring, T.G.; Caux, J.S.; Savici, A.T.; Gu, G.D.; Lee, C.C.; Ku, W.; Zaliznyak, I.A. Effect of covalent bonding on magnetism and the missing neutron intensity in copper oxide compounds. Nat. Phys. 2009, 5, 867–872. [Google Scholar] [CrossRef]
- Tomeno, I.; Yoshida, M.; Ikeda, K.; Tai, K. Raman scattering from spin fluctuations in Pr2−xCexCuO4−y, Nd2−xCexCuO4−y, and Sm2−xCexCuO4−y. Phys. Rev. B 1991, 43, 3009–3019. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, M.; Tajima, S.; Koshizuka, N.; Tanaka, S.; Uchida, S.; Itoh, T. Two-magnon and two-phonon excitations in some parent insulating compounds of the high-Tc cuprates. Phys. Rev. B 1992, 46, 6505–6510. [Google Scholar] [CrossRef] [PubMed]
- Honma, T.; Hor, P.H. Unified electronic phase diagram for hole-doped high-Tc cuprates. Phys. Rev. B 2008, 77, 184520. [Google Scholar] [CrossRef]
- Alloul, H.; Ohno, T.; Mendels, P. 89Y NMR evidence for a Fermi-liquid behavior in YBa2Cu3O6+x. Phys. Rev. Lett. 1989, 63, 1700. [Google Scholar] [CrossRef] [PubMed]
- Comin, R.; Damascelli, A. Resonant X-Ray Scattering Studies of Charge Order in Cuprates. Annu. Rev. Condens. Matter Phys. 2016, 7, 369–405. [Google Scholar] [CrossRef]
- Wu, T.; Mayaffre, H.; Krämer, S.; Horvatić, M.; Berthier, C.; Hardy, W.N.; Liang, R.; Bonn, D.A.; Julien, M.H. Magnetic-field-induced charge-stripe order in the high-temperature superconductor YBa2Cu3Oy. Nature 2011, 477, 191–194. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Mayaffre, H.; Krämer, S.; Horvatić, M.; Berthier, C.; Kuhns, P.L.; Reyes, A.P.; Liang, R.; Hardy, W.N.; Bonn, D.A.; et al. Emergence of charge order from the vortex state of a high-temperature superconductor. Nat. Commun. 2013, 4, 2113. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Mayaffre, H.; Krämer, S.; Horvatić, M.; Berthier, C.; Hardy, W.; Liang, R.; Bonn, D.A.; Julien, M.H. Incipient charge order observed by NMR in the normal state of YBa2Cu3Oy. Nat. Commun. 2015, 6, 6438. [Google Scholar] [CrossRef] [PubMed]
- Chang, J.; Blackburn, E.; Holmes, A.T.; Christensen, N.B.; Larsen, J.; Mesot, J.; Liang, R.; Bonn, D.A.; Hardy, W.N.; Watenphul, A.; et al. Direct observation of competition between superconductivity and charge density wave order in YBa2Cu3O6.67. Nat. Phys. 2012, 8, 871–876. [Google Scholar] [CrossRef]
- Da Silva Neto, E.H.; Aynajian, P.; Frano, A.; Comin, R.; Schierle, E.; Weschke, E.; Gyenis, A.; Wen, J.; Schneeloch, J.; Xu, Z.; et al. Ubiquitous Interplay Between Charge Ordering and High-Temperature Superconductivity in Cuprates. Science 2014, 343, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Poccia, N.; Ricci, A.; Campi, G.; Fratini, M.; Puri, A.; Gioacchino, D.D.; Marcelli, A.; Reynolds, M.; Burghammer, M.; Saini, N.L.; et al. Optimum inhomogeneity of local lattice distortions in La2CuO4+y. Proc. Natl. Aacd. Sci. USA 2012, 109, 15685–15690. [Google Scholar] [CrossRef] [PubMed]
- Campi, G.; Bianconi, A.; Poccia, N.; Bianconi, G.; Barba, L.; Arrighetti, G.; Innocenti, D.; Karpinski, J.; Zhigadlo, N.D.; Kazakov, S.M.; et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-Tc superconductor. Nature 2015, 525, 359–362. [Google Scholar] [CrossRef] [PubMed]
- Campi, G.; Bianconi, A. High-Temperature Superconductivity in a Hyperbolic Geometry of Complex Matter from Nanoscale to Mesoscopic Scale. J. Supercond. Nov. Magn. 2016, 29, 627–631. [Google Scholar] [CrossRef]
- Da Silva Neto, E.H.; Comin, R.; He, F.; Sutarto, R.; Jiang, Y.; Greene, R.L.; Sawatzky, G.A.; Damascelli, A. Charge ordering in the electron-doped superconductor Nd2−xCexCuO4. Science 2015, 347, 282–285. [Google Scholar] [CrossRef] [PubMed]
- Fratini, M.; Poccia, N.; Ricci, A.; Campi, G.; Burghammer, M.; Aeppli, G.; Bianconi, A. Scale-free structural organization of oxygen interstitials in La2CuO4+y. Nature 2010, 466, 841–844. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Campi, G.; Coneri, F.; Caporale, A.S.; Innocenti, D.; Burghammer, M.; Zimmermann, M.V.; Bianconi, A. Multiscale distribution of oxygen puddles in 1/8 doped YBa2Cu3O6.67. Sci. Rep. 2013, 3, 2383. [Google Scholar] [CrossRef]
- Chiciak, A.; Vitali, E.; Shi, H.; Zhang, S. Magnetic orders in the hole-doped three-band Hubbard model: Spin spirals, nematicity, and ferromagnetic domain walls. Phys. Rev. B 2018, 97, 235127. [Google Scholar] [CrossRef]
- Niedermayer, C.; Bernhard, C.; Binninger, U.; Glückler, H.; Tallon, J.L.; Ansaldo, E.J.; Budnick, J.I. Muon spin rotation study of the correlation between Tc and ns/m* in overdoped Tl2Ba2CuO6+δ. Phys. Rev. Lett. 1993, 71, 1764–1767. [Google Scholar] [CrossRef]
- Khasanov, R.; Shengelaya, A.; Conder, K.; Morenzoni, E.; Savić, I.M.; Karpinski, J.; Keller, H. Correlation between oxygen isotope effects on transition temperature and magnetic penetration depth in high-temperature superconductors close to optimal doping. Phys. Rev. B 2006, 74, 4–9. [Google Scholar] [CrossRef]
- Shengelaya, A.; Khasanov, R.; Eshchenko, D.G.; Di Castro, D.; Savić, I.M.; Park, M.S.; Kim, K.H.; Lee, S.I.; Müller, K.A.; Keller, H. Muon-Spin-Rotation Measurements of the Penetration Depth of the Infinite-Layer Electron-Doped Sr0.9La0.1CuO2 Cuprate Superconductor. Phys. Rev. Lett. 2005, 94, 127001. [Google Scholar] [CrossRef] [PubMed]
- Schilling, J.S. High-Pressure Effects. In Handbook of High-Temperature Superconductivity; Schrieffer, J.R., Ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Meissner, T.; Goh, S.K.; Haase, J.; Williams, G.V.M.; Littlewood, P.B. High-pressure spin shifts in the pseudogap regime of superconducting YBa2Cu4O8 as revealed by 17O NMR. Phys. Rev. B 2011, 83, 220517. [Google Scholar] [CrossRef]
- Rybicki, D.; Kohlrautz, J.; Haase, J.; Greven, M.; Zhao, X.; Chan, M.K.; Dorow, C.J.; Veit, M.J. Electronic spin susceptibilities and superconductivity in HgBa2CuO4+δ from nuclear magnetic resonance. Phys. Rev. B 2015, 92, 081115. [Google Scholar] [CrossRef]
- Jurkutat, M.; Haase, J.; Erb, A. Charge Inhomogeneity in Electron-Doped Pr1.85Ce0.15CuO4 Determined with 63Cu NMR. J. Supercond. Nov. Magn. 2013, 26, 2685–2688. [Google Scholar] [CrossRef]
- Haase, J. Charge density variation in YBa2Cu3O6+y. Phys. Rev. Lett. 2003, 91, 189701. [Google Scholar] [CrossRef] [PubMed]
- Haase, J.; Slichter, C.P. Charge Density Variations or Stripes in YBa2Cu3O6+y. J. Supercond. 2003, 16, 473–475. [Google Scholar] [CrossRef]
- Reichardt, S.; Jurkutat, M.; Erb, A.; Haase, J. Charge Variations in Cuprate Superconductors from Nuclear Magnetic Resonance. J. Supercond. Nov. Magn. 2016, 29, 3017–3022. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jurkutat, M.; Erb, A.; Haase, J. Tc and Other Cuprate Properties in Relation to Planar Charges as Measured by NMR. Condens. Matter 2019, 4, 67. https://doi.org/10.3390/condmat4030067
Jurkutat M, Erb A, Haase J. Tc and Other Cuprate Properties in Relation to Planar Charges as Measured by NMR. Condensed Matter. 2019; 4(3):67. https://doi.org/10.3390/condmat4030067
Chicago/Turabian StyleJurkutat, Michael, Andreas Erb, and Jürgen Haase. 2019. "Tc and Other Cuprate Properties in Relation to Planar Charges as Measured by NMR" Condensed Matter 4, no. 3: 67. https://doi.org/10.3390/condmat4030067
APA StyleJurkutat, M., Erb, A., & Haase, J. (2019). Tc and Other Cuprate Properties in Relation to Planar Charges as Measured by NMR. Condensed Matter, 4(3), 67. https://doi.org/10.3390/condmat4030067




