1. Introduction
Lattice gas cellular automata are some of the simplest models of physical phenomena. The microscopic state of a lattice gas is given by particles (possibly of more than one type) occupying a set of lattice vectors at each site of a lattice. The time evolution of a lattice gas model proceeds in two substeps. First, in the propagation step, the particles propagate along their lattice vectors to a neighboring site, retaining their direction of motion. Secondly, in the collision step, the particles are rearranged amongst the lattice vectors at each site. For hydrodynamic lattice gases, these collisions preserve one or more local densities.
It has been known since the 1980s that the bulk behavior of certain lattice-gases may be governed by some of the most sophisticated equations of mathematical physics, including,
inter alia, the equations governing hydrodynamics [
1,
2], magnetohydrodynamics [
3,
4,
5,
6] and the Burger’s equation [
7,
8]. Equivalently, this means that lattice-gases can be used to simulate such equations on a classical computer; the lattice gas is evolved, and the desired dynamics are
emergent. The demonstration that the bulk behavior of a lattice-gas obeys a certain equation of mathematical physics is usually carried out with the machinery of classical kinetic theory, including the Chapman-Enskog analysis and kinetic ring theory [
2,
9,
10].
The HPP model was the first hydrodynamic lattice gas studied, and was shown to reproduce many features of continuum kinetic theory: in particular the existence of sound waves and viscosity [
11,
12]. The HPP collision rules are reversible in time (the propagation step is always trivially reversible in time) and so this model provided a simple arena in which to study irreversible kinetic phenomenon arising from a reversible microscopic model. While interesting from a fundamental perspective, the HPP model is not a useful model of a fluid. Momentum in the North-South and East-West directions is separately conserved, and relaxes via a one-dimensional diffusive process. The average momentum of the particles does not satisfy a two dimensional Navier-Stokes equation.
Intuitively, one would not expect such lattice models to reproduce all features of continuum dynamics, as the isotropy of the continuum is broken by the lattice. It was not until 1986, 13 years after the HPP model was discovered, that Frisch, Hasslacher and Pomeau, and independently Wolfram, showed that a lattice gas on the triangular lattice could reproduce isotropic two-dimensional Navier Stokes behavior [
1,
13]. While it is clear that adding more directions to a discrete lattice model will enable one to more accurately approximate an isotropic system, it is a remarkable fact that only six directions are necessary to exactly reproduce the isotropic Navier-Stokes equations in two dimensions.
Quantum generalizations of cellular automata [
14,
15,
16] and lattice gases [
10,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26] appeared in the late 1990s. These models propagate amplitudes for particle occupations and in their single particle sectors are equivalent to discrete-time quantum random walks [
27]. Quantum lattice gas models are exactly unitary, and possess both the Dirac and Schroedinger equations as different continuum limits [
17,
21]. At the same time, the analogy between the derivation of the Navier stokes equations from the Boltzmann equation, and the derivation of the Schroedinger equation from the Dirac equation led to the formulation of quantum lattice-Boltzmann models [
28,
29]. These provide numerical schemes for quantum mechanics on a classical computer. Because the lattice gas of Meyer [
21] can be shown to obey the Dirac equation in the continuum limit through an evaluation of the discrete path integral, the quantum lattice-Boltzmann treatment can be seen as providing the map from this Dirac dynamics to the Schroedinger dynamics analogous to the way that the Navier Stokes equations arise from the Boltzmann equation.
Quantum cellular automata models as originally defined in [
14,
15,
16] may not obey causality [
30]. This required a reformulation of quantum cellular automata [
31], and these models are now completely classified in one dimension [
32,
33]. The correspondence between quantum cellular automata and quantum lattice gases is also well understood [
34]. Quantum cellular automata can be used to simulate quantum random walks, which have many quantum algorithmic applications. This connection is explored in detail in [
35].
Classical cellular automata and lattice-gas models are natural models for implementation on parallel supercomputers [
36]. They also led to the construction of special-purpose hardware for their simulation [
37,
38,
39]. These cellular automata machines (CAM) reproduced in silico the features of lattice-gas cellular automata (LGCA) models—spatial locality and simple bitwise collision rules resulted in fast hardware [
40,
41]. Simulation of quantum systems is a central application of quantum computation [
42]. Given the simplicity of quantum lattice gas methods, one might imagine similar advantages from the construction of special purpose quantum hardware. Indeed, some of the earliest specific proposals for quantum simulation architectures had the features of a quantum cellular automata machine [
43]. However, large scale quantum computation requires quantum error correction, and the architectural constraints of large scale quantum computation will likely be set by the requirements of fault tolerance rather than the requirements of the target application. The prospects for a quantum analogue of the CAM have receded for this reason. It seems likely that we will have to wait for the advent of large scale error corrected quantum computers before large scale quantum lattice gas simulations are feasible. One may ask: are there semiclassical limits of quantum lattice gases, or minimal quantum extensions of classical lattice gases, that still permit efficient classical simulation? The efficient classical simulation of subclasses of quantum computation is an active area of study, with a number of well-defined types of efficiently simulable quantum computations known including matchgate computation [
44,
45] and the stabilizer formalism [
46,
47,
48] being notable examples. An overview of these models and their relations is given in [
49].
The Clifford subtheory is an example of a classically simulable subtheory comprised of stabilizer states Clifford gates and preparation and measurement in the logical basis. A stabilizer state is the common eigenvalue one eigenstate of an abelian group of signed tensor products of Pauli matrices. Clifford operations are actions on
n qubits generated by the controlled-NOT (CNOT), Hadamard and Phase gates [
48]. Clifford operations map stabilizer states to stabilizer states. In spite of the fact that stabilizer states can be highly entangled, the dynamics of stabilizer states under the action of Clifford operations can be efficiently classically simulated [
50].
A Clifford quantum cellular automata has a microdynamics described by stabilizer states, and a dynamics described in terms of Clifford operations. In spite of the fact that these stabilizer states are elements of a Hilbert space whose dimensions are exponential in the number of sites of the quantum cellular automataon (QCA), such models still admit an efficient classical simulation. Indeed, they are directly equivalent to some classical cellular automata [
51,
52,
53]. Are there any efficiently classically simulable subtheories of quantum mechanics that possess classical hydrodynamics as a limit? Such a theory would enable us to study the transition from classical to quantum behavior in the same setting as the transition from reversible or unitary microdynamics to irreversible macroscopic hydrodynamics.
A hydrodynamic lattice gas imposes two requirements on such automata. Firstly we require the dynamics be expressed as into a propagation step and a collision step. Secondly we require the model to possess local conserved quantities. In the present paper we ask whether efficiently simulable quantum extensions of classical hydrodynamic lattice gases exist. Previous connections between quantum automata and hydrodynamics have been made through the Madelung transformation [
54]. Consideration of this transformation for the quaternionic schroedinger equation leads to interesting equations for non-abelian fluids [
55,
56]. Recently, a relativistic Madelung transformation has been used to obtain hydrodynamic equations for a two-dimensional quantum walk [
57].
The structure of the paper is as follows. In
Section 2 we give reversible circuits for the propagation step of lattice gases. In
Section 3 we give constraints on observables that can represent local conserved quantities in lattice gases. We use the
notation to denote our models, in which
n is the spatial dimension of the lattice and
v is the number of lattice vectors at a site. We then consider the D1Q3, D1Q4, D2Q4 (HPP) and D2Q7 (FHP) models. We show that quantum extensions in which some lattice vector occupancies are encoded in different bases are possible. However, while classically simulable, these extensions are rather trivial. We also consider the case in which any occupancy may be encoded and measured in one of two bases. We show how this causes entanglement production when particles collide. For the HPP and FHP models, which are capable of universal classical computation [
58,
59], we argue that such extensions are unlikely to be amenable to efficient classical simulation.
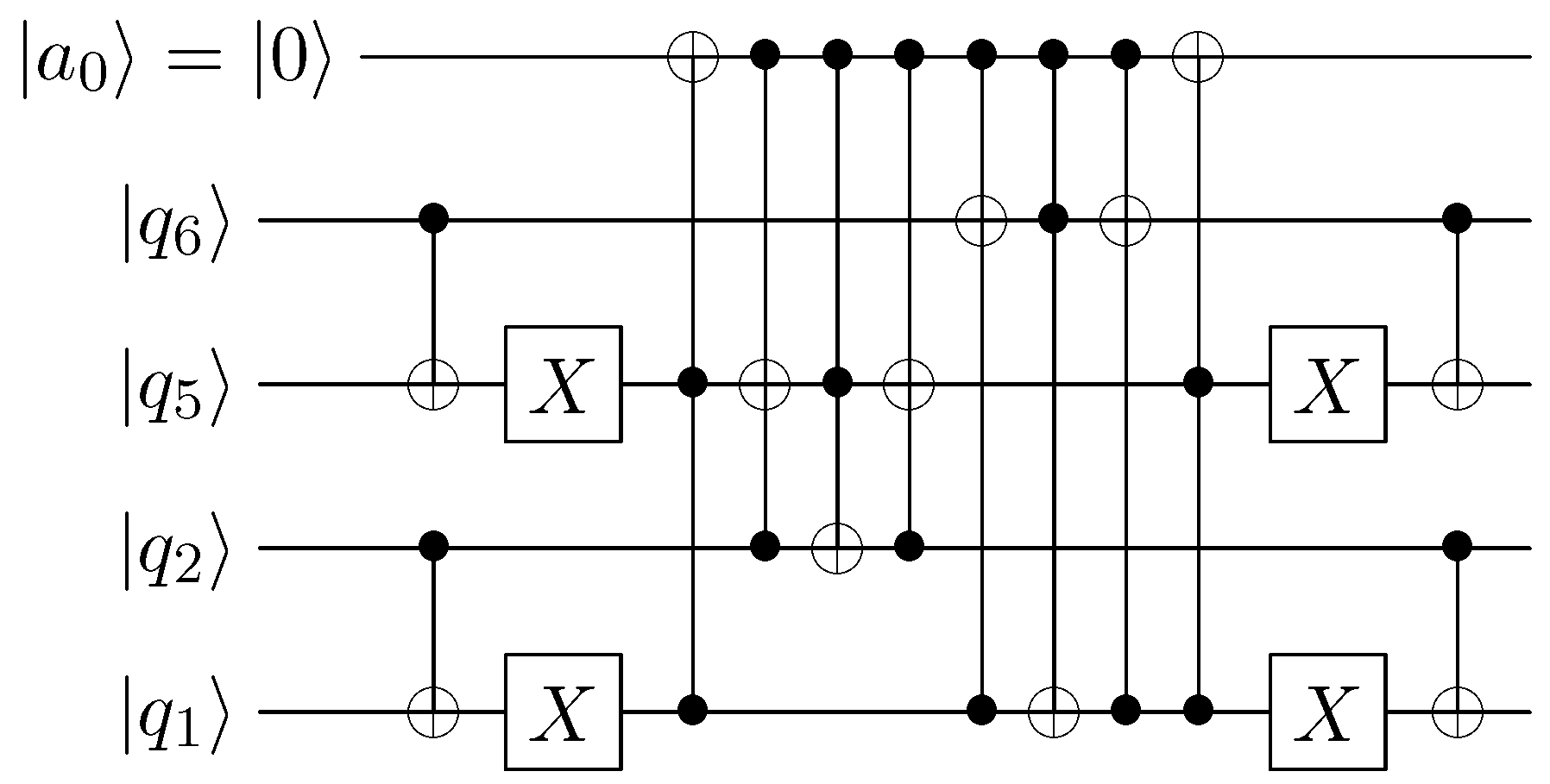
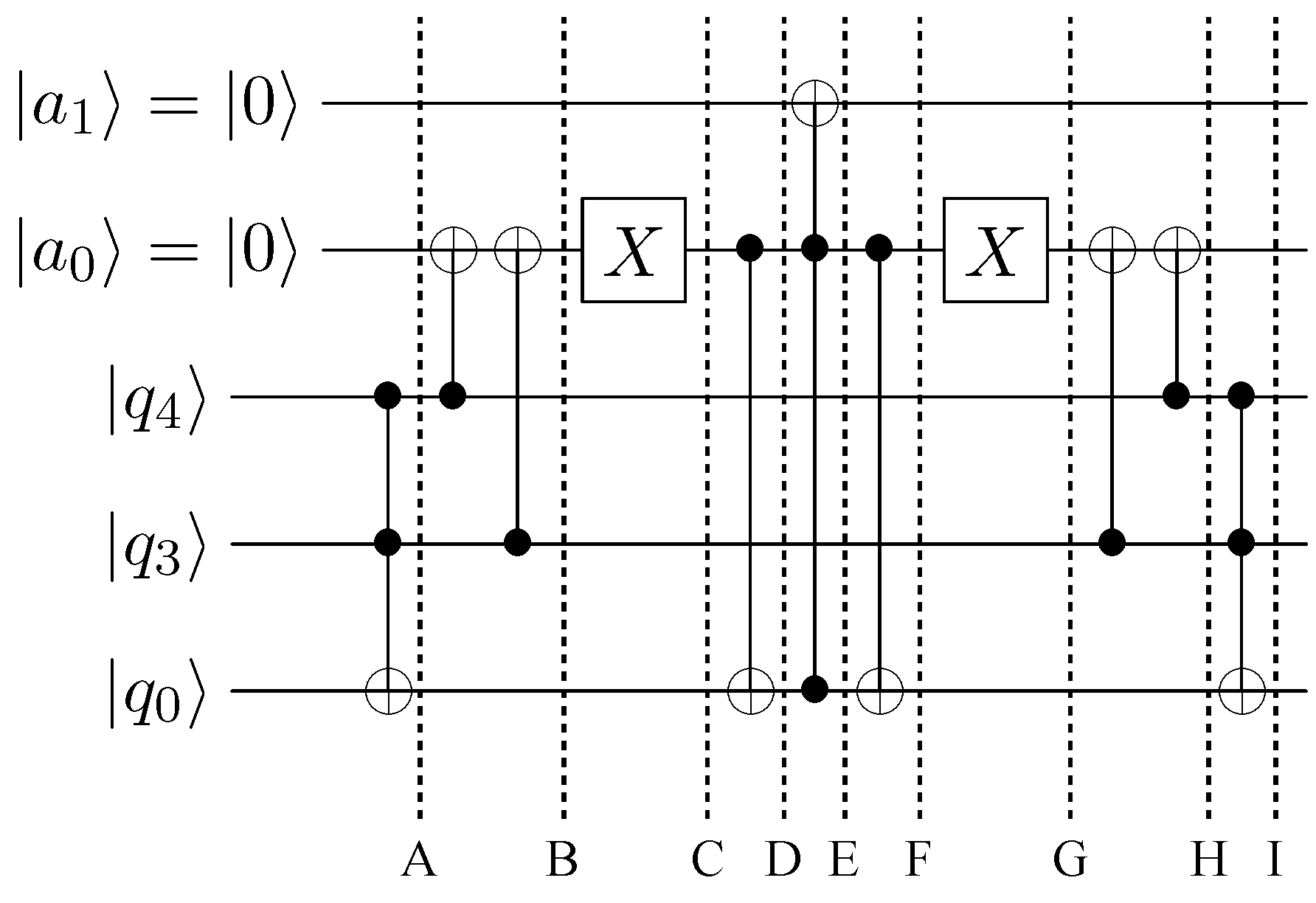
2. Propagation
In this section we describe reversible circuits over CNOT gates that implement the propagation step for models defined on lattices in which the vectors appear in antipodal pairs, possibly with the addition of rest states. We will begin with the D1Q2 model.
The D1Q2 model has two lattice vectors at each site of a one-dimensional lattice. The state of such a model with three sites and periodic boundary conditions may be written: where . We consider the trivial collision rule at a site: . The propagation rule is given by: . Written in terms of bits for N sites: where indicates i is taken modulo . The preservation of the parity of the bit labels here is a consequence of the fact that propagation maps left (right) moving particles to left (right) moving particles.
Consider the following sequence of swaps:
The first swap for N sites is: , in terms of bits this is so that: and . The second swap for N sites is so that: and . Combining this with the result of the first swap gives a bitwise expression for propagation in a single step: , .
Formulation of propagation as a pair of unconditional swaps enables us to immediately write propagation as a circuit over CNOTS. For
N sites each propagation step is composed of two rounds of
CNOT gates, and hence the cost of propagation in the D1Q2 is
CNOT gates, and the propagation step is therefore a round of only Clifford gates. The example propagation for three sites is shown in
Figure 1.
Having constructed propagation in the D1Q2 model, the propagation circuits for other models follow trivially. Propagation always occurs along straight lines in the lattice composed of
vectors for some
N. The operator for the D1Q2 model may therefore be directly applied to this subset of bits. Even for models in which the underlying geometry is dynamical [
60,
61], or not a lattice [
62], propagation occurs on a subset of the variables composed of an even number of the bits and the D1Q2 model operator can be applied.
3. Local Conserved Quantities
A local observable is a Hermitian operator which is a sum of operators acting on the Hilbert space of a single site. For the simplest models, each lattice vector has two states, occupied or empty, and the dimension of the local Hilbert space is
. If the model is translation invariant the operators on the local Hilbert space must be identical. The exploration of the evolution of local operators is the principle subject of the literature defining causal cellular automata and lattice gases in general [
30,
31,
34].
For a conserved quantity of a lattice gas model, the local operator must be preserved by propagation and by collision. Propagation preserves the identity of the lattice vectors but changes the lattice site. This immediately implies that local operators representing conserved quantities must be the sum of operators acting nontrivially on only one lattice vector, as in the classical case. The question of conserved quantities becomes the question of what subset of these operators, if any, commutes with the global evolution. In turn, this becomes the question of which operators commute with both the propagation and collision operators.
We can write the most general such operator as follows:
Here x labels the lattice sites and l labels the lattice vectors. The individual operators act on two dimensional subspaces of the Hilbert space and hence may be expanded in terms of the Pauli matrices. Translational invariance implies that the do not depend on x. The propagation step changes x but not l and so leaves invariant. We therefore only need to consider the commutation of with the collision step.
As the collision operator
acts locally at a site
x we require:
Next consider the symmetry properties of conserved quantities. The models we considered here are one- and two-dimensional with lattice vectors that occur in antipodal pairs. There is therefore a lattice symmetry corresponding to exchanging the elements of each pair of antipodal vectors. Scalar conserved quantities should be invariant under this operator, whereas vector conserved quantities should be negated. For fluid models we are interested in two scalars (mass and energy density) and one vector (momentum).
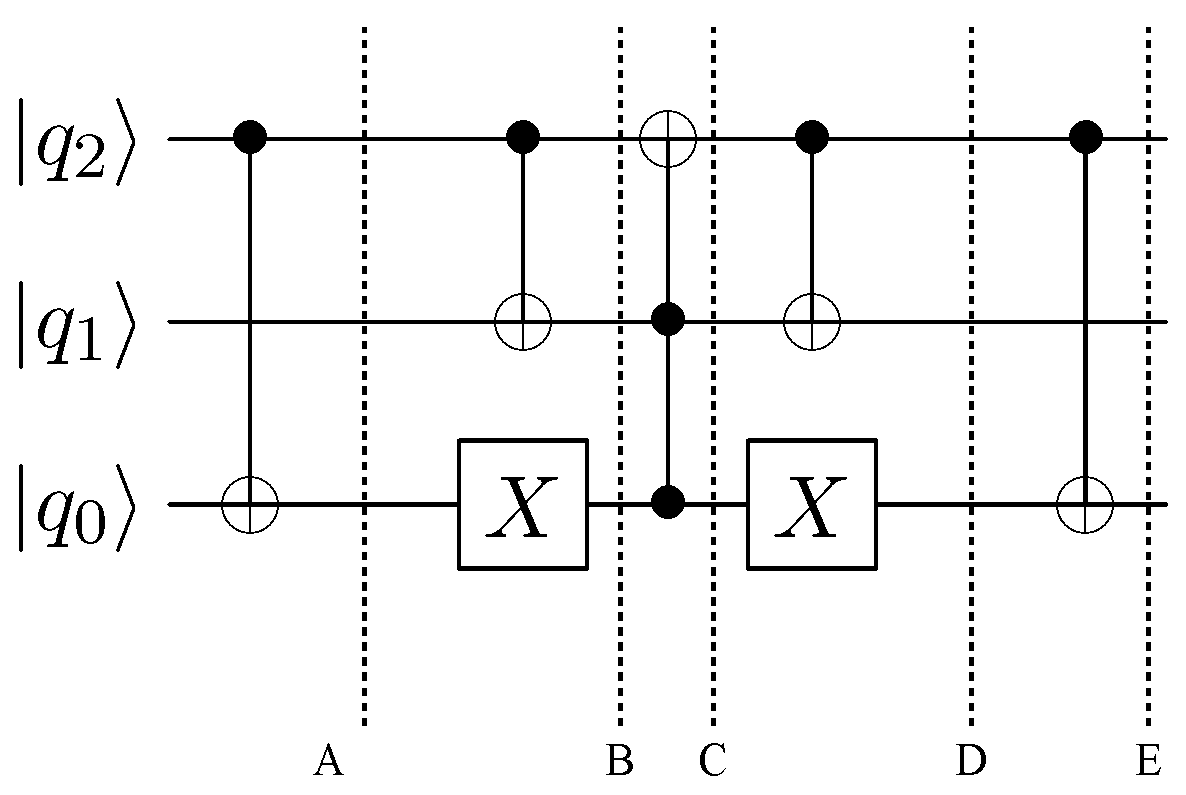
4. The D1Q3 Model
We consider a lattice gas in one dimension with a left moving particle of mass one, right moving particle of mass one and rest particle of mass two. The model has three bits per site and has a conserved mass and momentum. The conserved quantities partition the states into distinct sets that the permutation defined by the collision rule cannot mix. For the D1Q3 model every state is specified uniquely by its mass and momentum except states and which both have mass two and momentum zero. Hence the conservation laws in this case determine the only allowed collision rules—either the model is trivial with no collisions, or the collision operator must exchange states and .
We can use the conserved quantities to obtain a circuit for the collision rule. The collision rule only acts nontrivially on a two-dimensional subspace of the zero momentum subspace. We calculate the magnitude of the momentum by performing a controlled-NOT operation on the high and low qubits. This maps the four zero momentum states to states with the low bit equal to zero. The two high bits have odd parity in the states exchanged by the collision. A controlled-NOT conditioned on the high bit and acting on the central bit maps the target states of the collision to the two states of the high bit. If we now perform a Toffoli gate conditioned on zero on the low qubit and one on the central qubit, we obtain the target collision rule. This circuit is shown in
Figure 2 and the truth table is given in
Table 1.
The action on the nine single qubit Pauli operators is:
The classical conserved quantities give the only combinations of single qubit Pauli operators that are preserved by the collision operator:
The only quantum extensions of the classical collision operator which also preserve these densities are conjugations by single-qubit Clifford operations. However, this corresponds to a choice of which states in which to encode the presence or absence of a particle. One could, for example, encode the rest particle in the eigenstates of the Pauli
X operator and write:
The collision operator would then be conjugated by an additional Hadamard gate on the rest bit. However, all these gates except the first and the last would cancel, and so this modified model corresponds to initially encoding the occupancies of rest particles in the eigenstates of Pauli X but then immediately converting this choice back to the classical encoding, performing the classical evolution and then measuring the rest particles in the X basis. In this example we see that it is the absence of conserved quantities beyond mass and momentum in the classical model that restrict possible Clifford extensions with conserved densities.
One might ask how the dynamics of the model changes if one makes an arbitrary choice of initial encoding of the occupancy? That is, I take the classical circuit defined by the propagation operator and the collision operator defined in
Figure 2 and allow it to act on separable initial conditions comprised of tensor products of
. These separable states propagate through the evolution unchanged until they participate in a collision. The three new collisions are shown below:
In each case a Bell pair on the right and left moving state is created by the collision of a conjugate encoded state. Subsequent collision with other conjugate encoded states will generate further entanglement.
If we were to measure the results of this evolution only in the
Z basis, the entire dynamics could be simulated efficiently by the methods of [
49]. This is because the separable input states are, in the terminology of [
49], computationally tractable (CT), and the classical evolution, being basis preserving, is also CT. However, if we measure some of the output qubits in the
X basis we are composing CT and non-CT operations and the methods of [
49] are no longer sufficient. In this case the cicuit is composed of a round of Hadamard gates, a round of reversible classical computation expressed in terms of Toffoli gates and a further round of Hadamard gates followed by measurement in the
Z basis. Such circuits are sufficient to express quantum algorithms, such as Simon’s algorithm, which are not believed to be amenable to efficient classical simulation. It is an interesting open question whether the structure of the D1Q3 model is simple enough to admit an efficient classical simulation algorithm when supplemented by pre- and post- rounds of Hadamard, or whether D1Q3 enables us to encode quantum algorithms that rule out classical simulation.
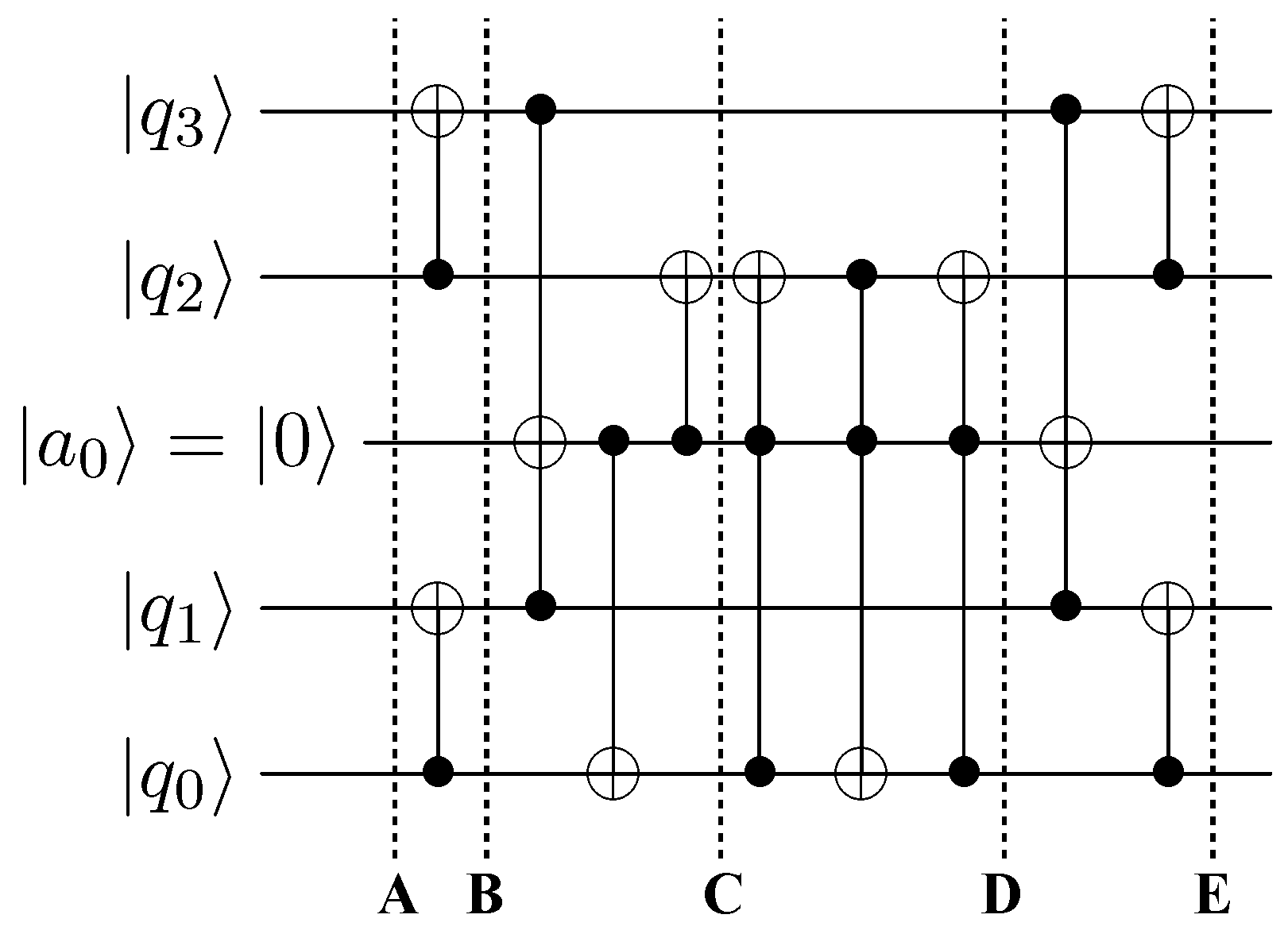
5. The D1Q4 Model
Next we consider the one-dimensional, multi-speed model of Qian, d’Humieres and Lallemand [
63]. This model has four velocity vectors at a site, two with speed one and two with speed two. The particles of speed two have mass one and the particles with speed one have mass two. That is, the particles are either light and fast, or heavy and slow. We encode occupancy of these states in a bitstring
where
and
are the fast, light particles and
and
are the slow, heavy particles. The nontrivial collision is 0101 maps to 1010, and the reversible circuit and its truth table are given in
Figure 3 and
Table 2. This model is of interest as a deterministic reversible model that yields diffusive behavior in the continuum limit [
63].
The classical conserved densities include mass, momentum and energy:
This model does have conserved quantities beyond mass, momentum and energy [
63,
64]. However, these quantities are staggered in space or in space and time. We do not consider these extra conserved quantities here. Writing mass, momentum and energy as operators gives:
The map induced on the Pauli observables by the classical collision operator is:
Because this model has two scalar conserved quantities we can consider collision rules that conserve a different basis for this space of operators. First rewrite the mass and energy in terms of the masses of the fast, light particles
and the slow heavy particles
. Then:
and
are separately conserved by the classical collision operator.
We may choose to encode the population of fast, light particles in the states , by conjugating the classical collision operator with (We could choose the slow, heavy particles instead by conjugating with , of course). In this case the first and last vectors of the model would be in states . These states would be mapped back to classical states for by the Hadamard gates and then the classical collision operator would act. The first and last vectors of the output would then be mapped back to states . The propagation step only propagates fast vectors to fast vectors and so an initial condition in which the first and last (fast, light) vectors are always in state retains this property through the evolution.
The conserved local densities then become:
The evolution described has the same property as our deformation of the D1Q3 model. We are able in this model to consistently encode a subset of the vectors in the x-basis rather than the z-basis, and this choice is then preserved by the evolution. Unlike the D1Q3 model, in the D1Q4 model our differently encoded states now propagate across the system.
We again may ask: what happens if a particle enters in the wrong encoding? Consider the state
for
. This becomes
before entering the classical collision operator. The two terms in the superposition are unaffected by the collision operator unless they are equal to 0101 or 1010 and hence the state emerges unchanged as
. Therefore, we only need to consider:
Incorrectly encoded states therefore propagate unaffected until they participate in a nontrivial collision, when they result in a state which is an entangled superposition of at most four correctly encoded states. This superposition subsequently propagates through the evolution until it meets another incorrectly encoded particle in which case the support of the superposition will again grow by a factor of at most four. In spite of the generation of entanglement in these collisions, if the final measurements occur in the correct basis then the evolution will be efficiently classically simulable by the methods of [
49], using the same argument that we invoked for the D1Q3 model.
If both preparation and measurement of the state can occur in the incorrect basis, the simulation complexity is less clear. As noted in [
49], circuits composed of a round of Hadamard gates (which in this case would generate defects) followed by a reversible computation, followed by another round of Hadamard gates can be difficult to classically simulate because several notable quantum algorithms take this form. It is an interesting question whether the restricted form of the collision operator here (and in the D1Q3 case) in fact allows efficient classical simulation. If so we could use the conjugate coded extension of the model to implement Simon’s algorithm which would provide strong evidence that even these simple modifications of classical automata are not amenable to efficient classical simulation. We now move on to consider lattice gas models whose classical computational complexity is large enough for us to make more definitive statements concerning their quantum complexity.
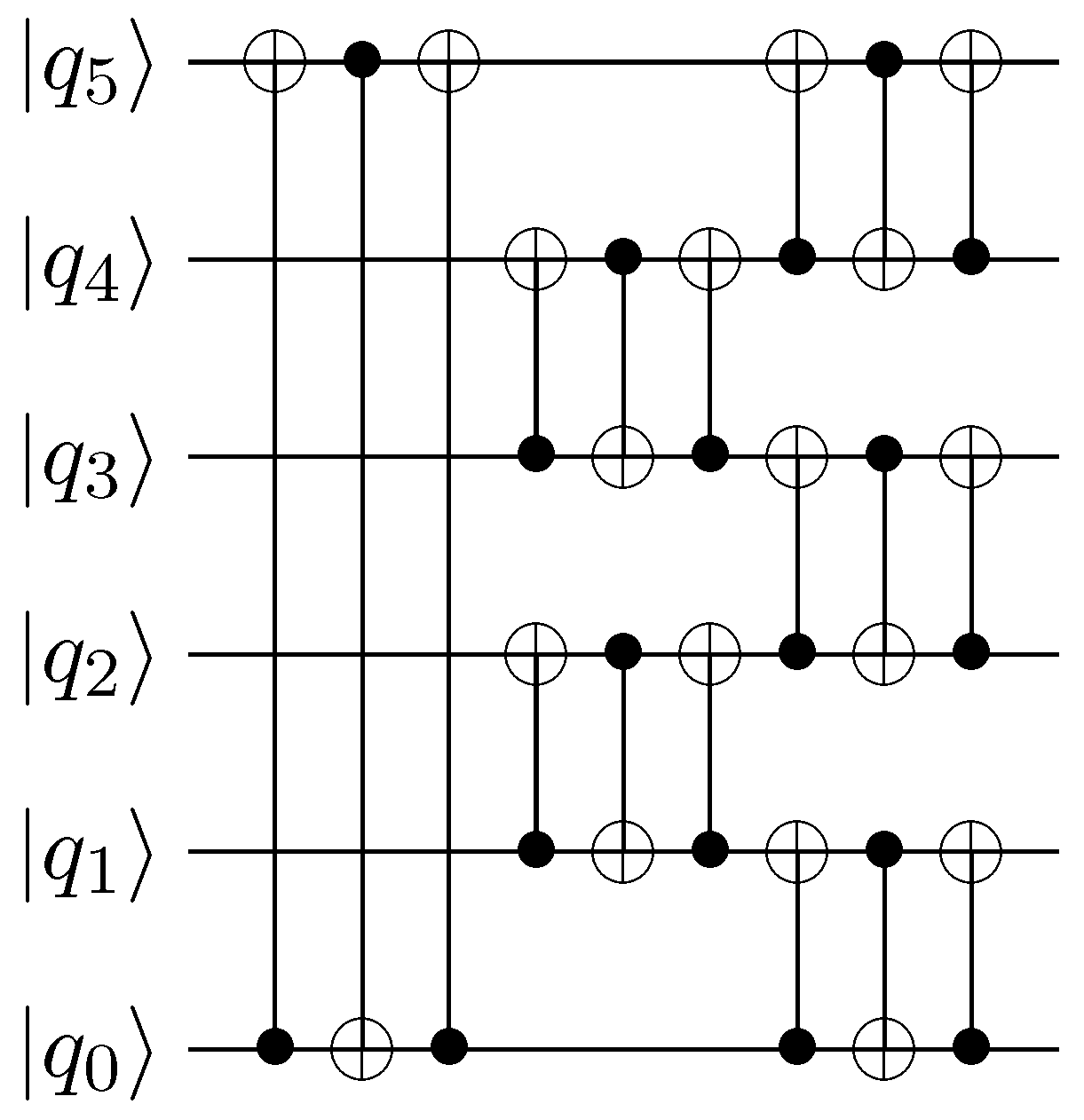
6. The HPP Model
The HPP model is defined on a Cartesian lattice in two-dimensions, giving four lattice directions per site. We encode the occupancies of the lattice vectors in a bitstring in the order . The only nontrivial collision is , just as for the D1Q4 model discussed in the previous section. We can therefore use the circuit to implement this collision as only the interpretation of the bits has changed. The propagation step will differ to reflect the two-dimensional geometry. This provides the simplest two dimensional example of a reversible model, however, despite conserving mass and momentum this model does not have hydrodynamic macroscopic behaviour as the cartesian lattice is insufficiently symmetric to reproduce isotropic fluid behaviour.
Because the collision rules for HPP are identical to those already given for D1Q4, all the results may be immediately taken over from the one dimensional model to HPP. The two scalar conserved quantities in D1Q4,
and
are the sum of occupancies of the
and
vectors of the model, which are preserved by the HPP rules. The previous discussion of the computational difficulty of this model with arbitrary encodings and measurements of occupancy in
x or
z bases carries over to the HPP model. However, in the case of the HPP model we can say a little more because predicting the output of the HPP lattice gas is a P-complete problem [
59]. Therefore, we can encode, for example, the function evaluation step of Simon’s algorithm [
65] in the HPP evolution using the techniques of [
59]. This presents an obstacle to efficient classical simulation of the HPP model with arbitrary
x or
z encodings and measurements. That is, unless Simon’s algorithm can be efficiently classically simulated, neither can this model.
8. Conclusions and Future Work
We have considered simple quantum extensions of four hydrodynamic lattice gas automata in one and two dimensions. The models of [
1,
11,
12,
63] all simulate important physical phenomona in the continuum limit, and the models of [
1,
11,
12] are P-complete and computationally universal. The existence of local conserved quantities in these models strongly constrains quantum deformations of the models. The simplest such deformations are obtained by simply changing the encoding of occupancies for a subset of the lattice vectors. This leads to classically simulable models, however, their dynamics will be the same as the classical model.
Finally, we consider the evolution given by allowing the input state of the model to be coded in either the X or Z basis, while remaining separable. The output can they be measured in either the Z or the X basis. This is equivalent to conjugating the classical evolution by a hadamard operation on a subset of the qubits. The incorrectly coded state propagates freely until it participates in a collision, when it generates entanglement between different branches of the evolution.
The complexity of simulation of these models is interesting. Many quantum algorithms, including Simon’s algorithm [
65] can be realized in a framework where a classical reversible circuit is supplemented by rounds of Hadamard gates. In the case of the HPP and FHP models we can use the fact that they are known to be P-complete and computationally universal, respectively, to immediately show that they can realize Simon’s algorithm and therefore are unlikely to admit efficient classical simulation.
In the last decade, a weaker criterion for the separation between classical and quantum computation has been established. Instead of demanding a separation between quantum and classical algorithms for a specific computational task, one may instead ask if a given quantum device can draw samples from a distribution which is hard to sample from classically. This is termed quantum computational supremacy [
66]. It is an interesting open question as to whether the models of [
1,
11,
12,
63], conjugated by rounds of Hadamard gates, can exhibit quantum supremacy, and how such a demonstration would differ from existing supremacy schemes.