Superconducting Properties of 3D Low-Density TI-Bipolaron Gas in Magnetic Field
Abstract
1. Introduction
2. Pekar-Froehlich Hamiltonian. Canonical Transformations
3. Energy Spectrum of a TI-Bipolaron
4. Statistical Thermodynamics of Low-Density TI Bipolarons without Magnetic Field
5. Current States of a TI-Bipolaron Gas
6. Thermodynamic Properties of a TI-Bipolaron Gas in a Magnetic Field
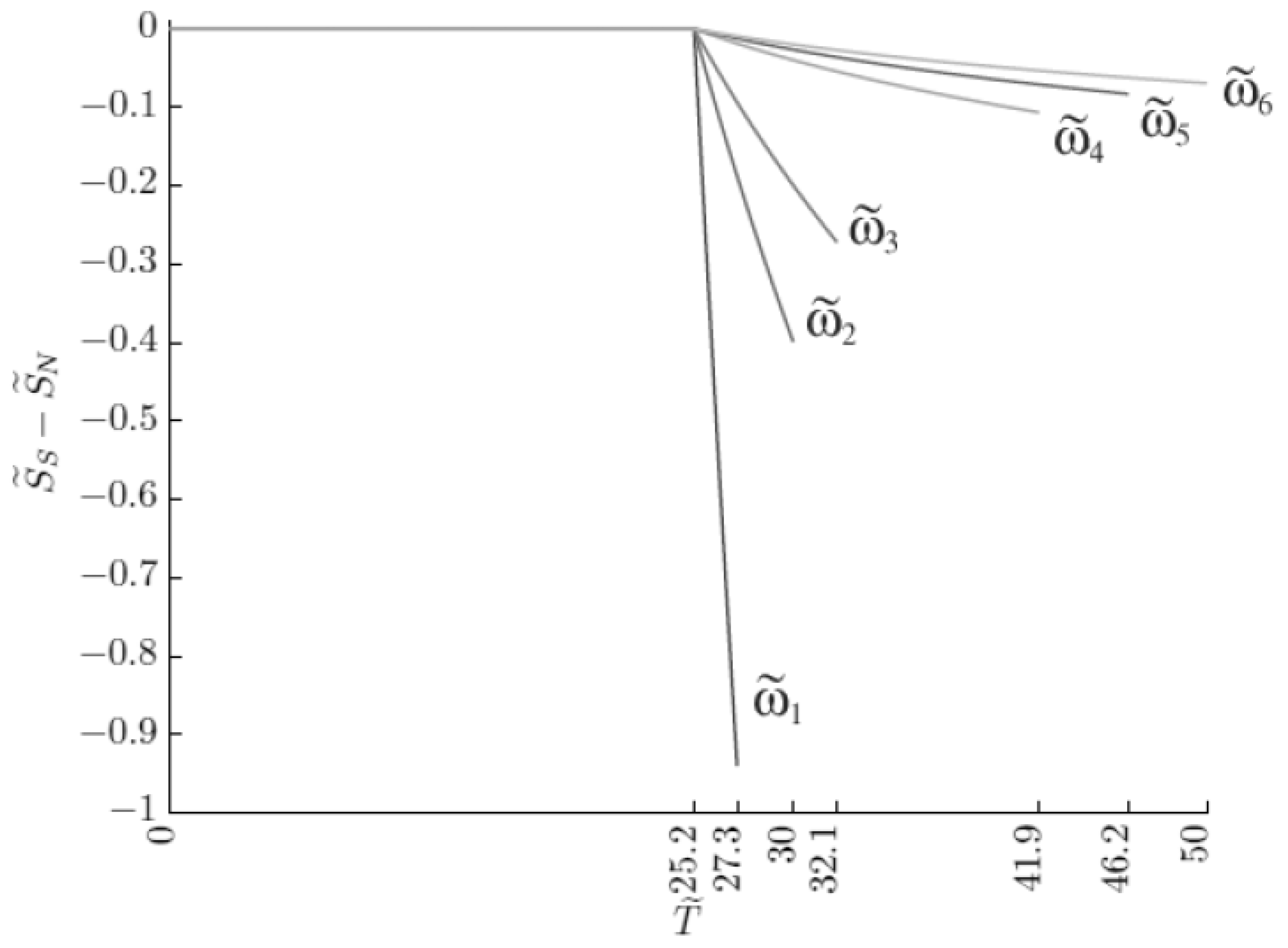
- In BCS and Ginzburg-Landau theory at the most critical point the difference of entropies becomes zero in accordance with Rutgers formula. In Figure 5 entropy is a monotonous function which does not vanish for .
- Second, in absolute terms, the difference , when approaching the limit point , which corresponds to the value , as it can be seemed should decrease rather than increase vanishing at .
- The curve of the dependence (Figure 3) for has a zero derivative, accordingly for . This result is consistent with Nernst theorem which implies that entropy determined by (41) is equal to zero for .
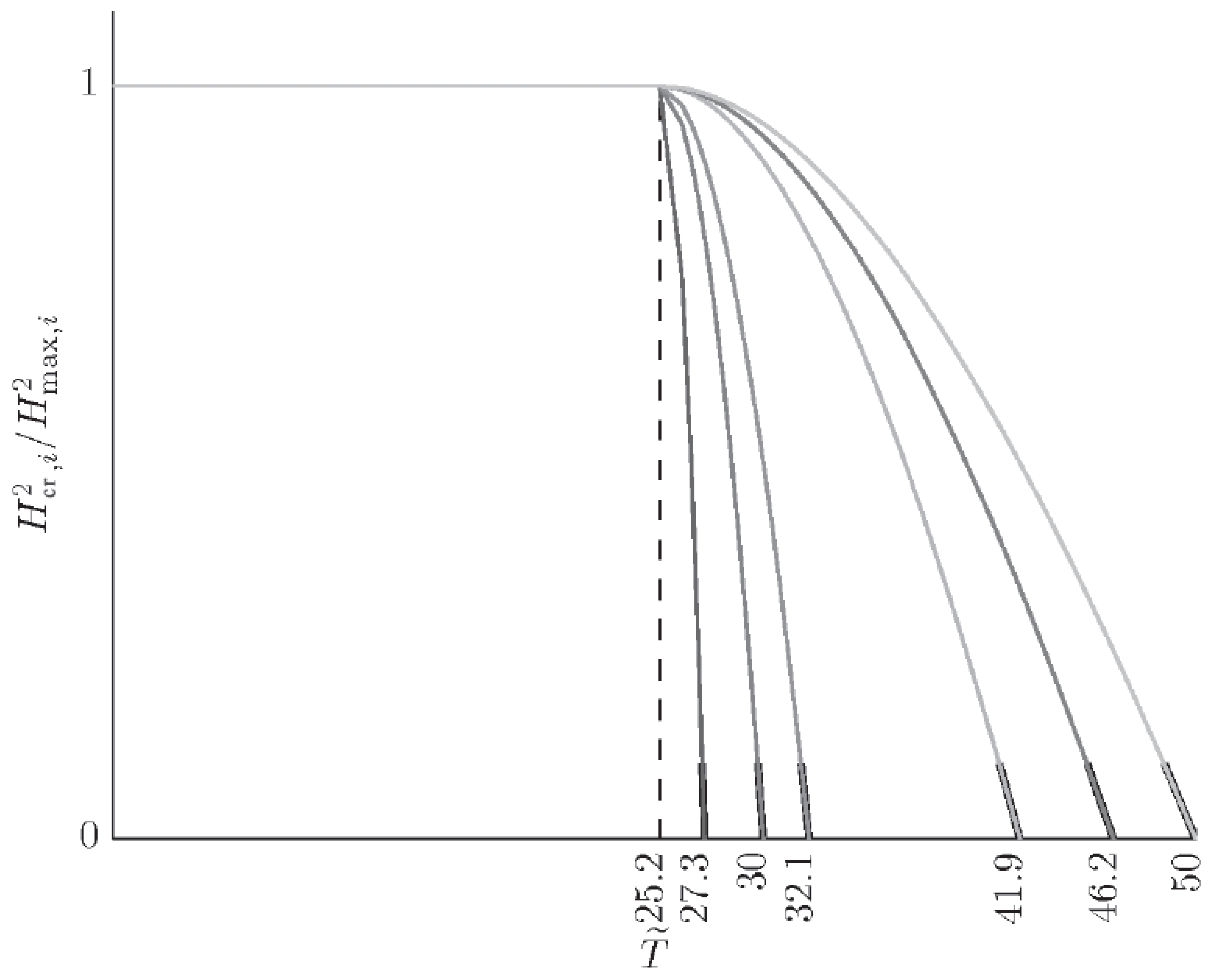
- According to Figure 3, is a curve monotonously drooping with increasing T for , and a constant value for . Hence for . Therefore on the temperature interval and on the interval .
- Transition on the interval occurs without absorption or release of latent heat since in this case . Experimentally it will be seen as a phase transition of the second kind. Actually, in the region , a phase transition into a superconducting state is a phase transition of infinite kind, since in this region, according to (40) and Figure 3, any-order derivatives of the difference of free energies , become zero.
- Passing in a magnetic field from a superconducting state to a normal one on the interval , which corresponds to , occurs with absorption of latent heat. On the contrary, passing from a normal state to a superconducting one takes place with release of latent heat. The phase transition on the interval is not attended by absorption or release of the latent heat being the phase transition of infinite kind.
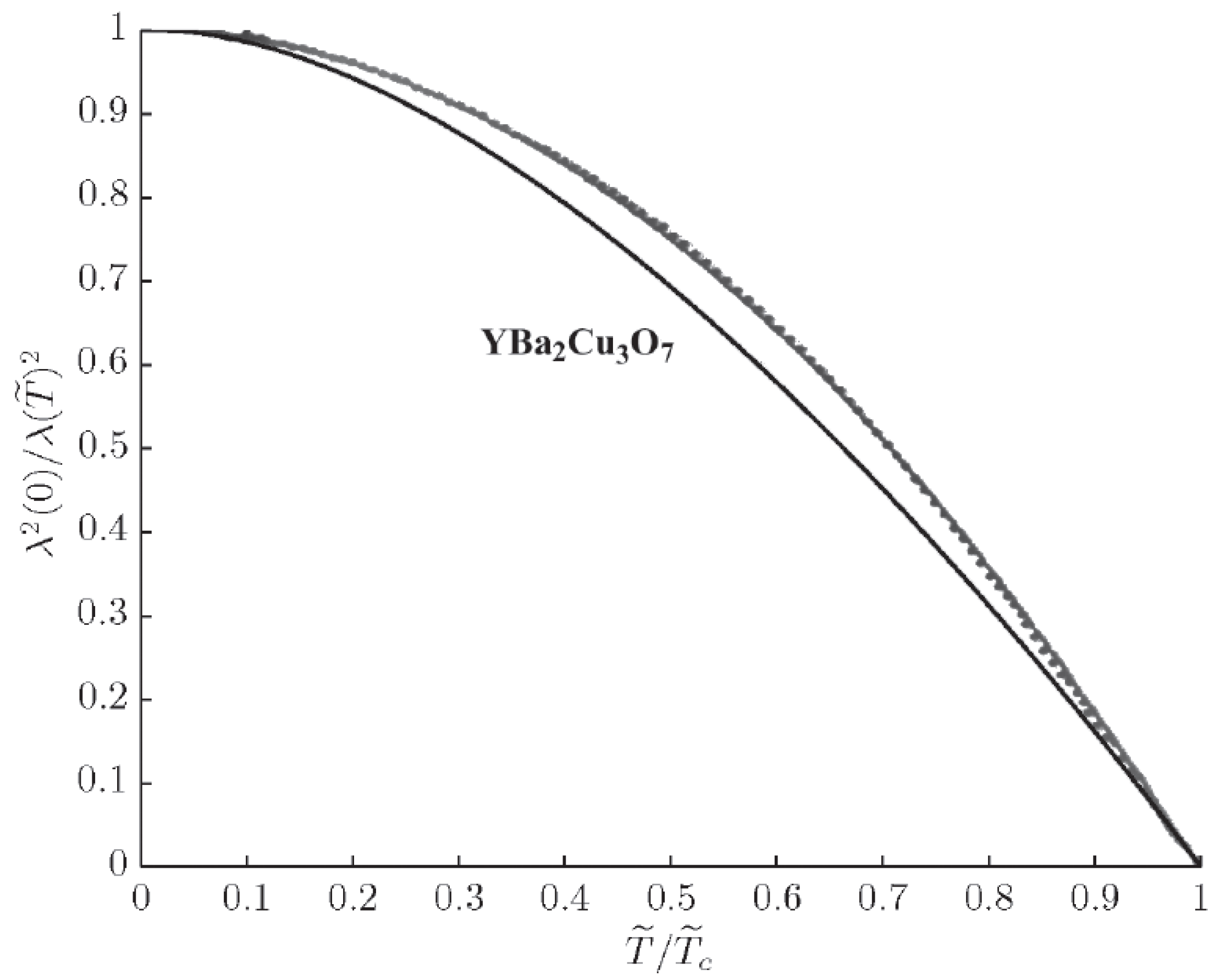
7. Comparison with the Experiment
8. Scaling Relations
- Alexandrov’s formula As was mentioned in [39], in an anisotropic case formula (49) takes on the form:It is convenient to pass on in formula (52) from quantities , , which can hardly be determined in experiments to quantities which are easily measured experimentally:where , are London lengths of penetration into the planes of layers and in perpendicular direction, respectively; is Hall coefficient. In expressions (53) the light velocity is assumed to be equal to unity: . With the use of relations (53) and (52) we get:In formula (54) the quantity is measured in cm, , in cm, in Kelvin.Taking into account that in most HTSC materials and the function changes near only slightly, with the use of the value and expression (53) we present in the form:Formula (55) differs from Alexandrov’s formula [69,70] only in numerical coefficient which in [69,70] is equal to 1.64. As is shown in [69,70], formula (55) practically always properly describes relation between the parameters for all known HTSC materials. In [69,70] it is also shown that Uemura relation [71,72] is a particular case of formula (55).
- Homes’s law Homes’s law holds that scaling relation are valid for superconducting materials [73,74]:where is the density of a superfluid component for , is the conductivity of direct current for , C is a constant equal to cm for ordinary superconductors and HTSC materials for a current running in the plane of layers.The quantity involved in (56) is related to plasma frequency (where is a concentration of superconducting charge carriers; , are a mass and charge of superconducting charge carriers) by a well-known expression [75]. Using this expression, relation (where is the concentration of charge carriers for ), , are the mass and the charge of charge carriers, relation (where is the minimum Planck time for scattering of electrons at the critical point [75]) and also expression (56), on the assumption , , we get:This result is confirmed by experimental data [76].In our scenario of Bose-condensation of TI-bipolarons, Homes’s law in the form of (57) becomes almost obvious. Indeed, for TI-bipolarons are stable formations (they decay at temperature equal to the pseudogap energy which considerably exceeds ). Their concentration for is equal to and therefore these bipolarons for start forming condensate whose concentration reaches its maximum for (i.e., when bipolarons fully pass on to condensed state) which corresponds to relation (57). Notice that in the framework of BCS theory Homes’s law can hardly be explained.
9. Summary
- It is shown that the occurrence of a gap in the spectrum of TI-bipolarons makes possible their condensation in a magnetic field.
- It is demonstrated that there exists a critical value of the magnetic field above which homogeneous Bose-condensation becomes impossible.
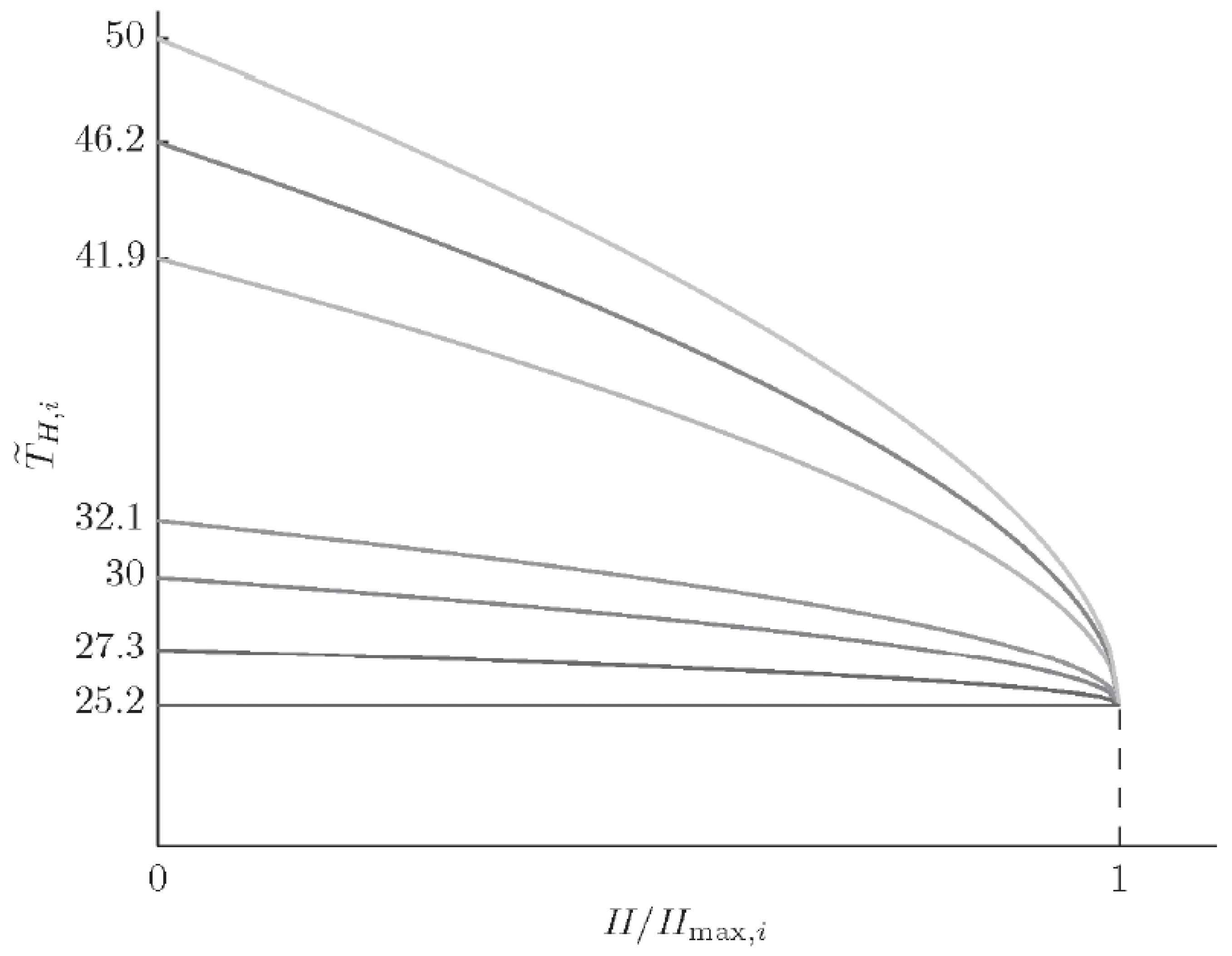
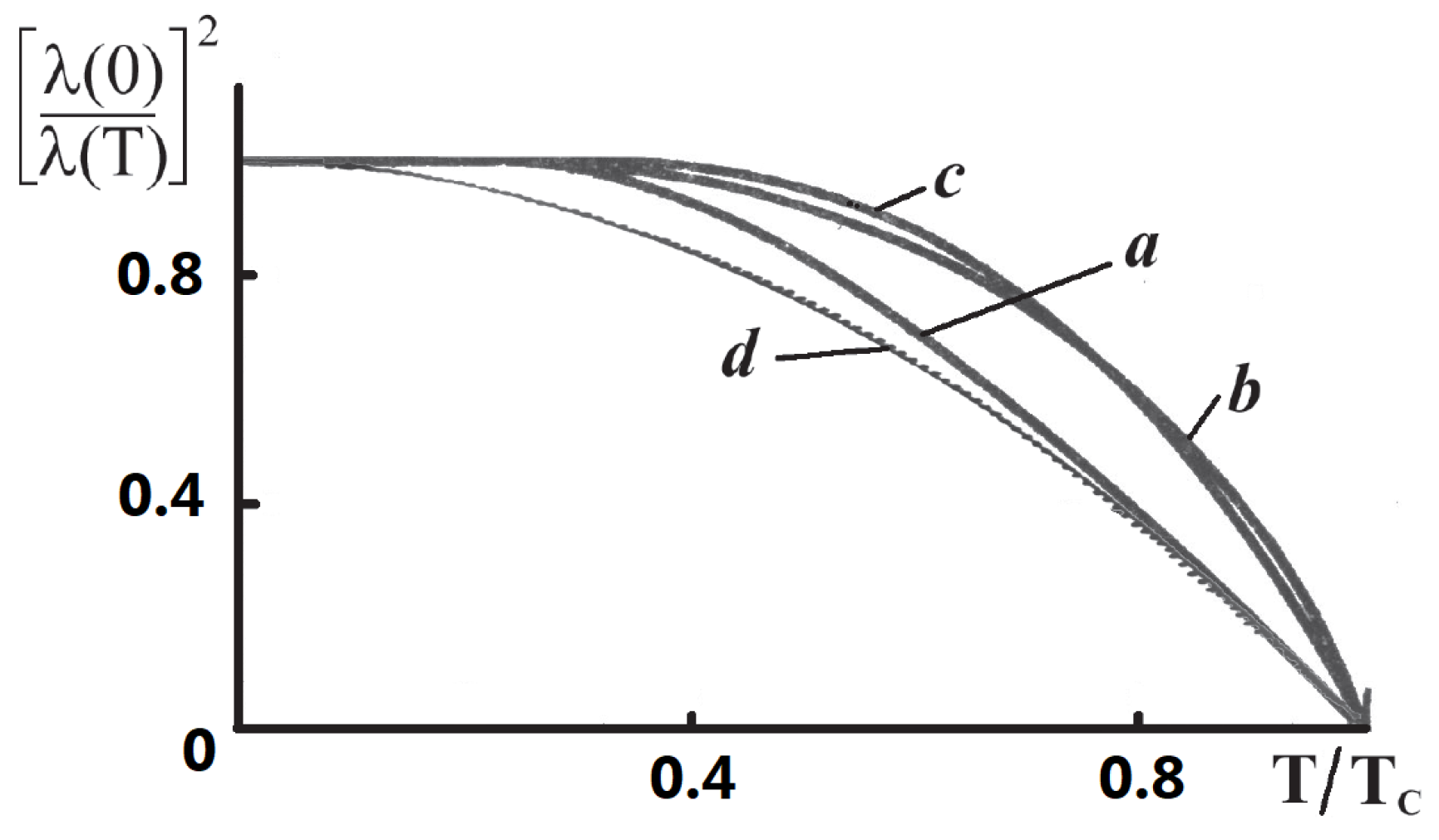
- The temperature dependence of the critical magnetic field and London penetration depth obtained in the paper are in good agreement with the experiment.
- Rutgers formula cannot be applied to describe Bose-condensation of TI-bipolarons.
- Ginzburg-Landau expansions do not suit to describe Bose-condensation of TI-bipolarons.
- Isotopic effect for a jump of heat capacity in passing from the normal phase to superconducting one.
- A possibility of the existence of a phase transition of infinite kind in a magnetic field at low temperatures.
- Identity of the energy gap with phonon frequency.
- Existence of superconducting TI-bipolarons whose concentration is much less than the total concentration of charge carriers.
Funding
Conflicts of Interest
Appendix A
References
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- Schrieffer, J.R. Theory of Superconductivity; Westview Press: Oxford, UK, 1999. [Google Scholar]
- Moriya, T.; Ueda, K. Spin fluctuations and high temperature superconductivity. Adv. Phys. 2000, 49, 555–606. [Google Scholar] [CrossRef]
- Sinha, K.P.; Kakani, S.L. Fermion local charged boson model and cuprate superconductors. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2002, 72, 153–214. [Google Scholar]
- Alexandrov, A.S. Theory of Superconductivity from Weak to Strong Coupling; IoP Publishing: Bristol, UK, 2003. [Google Scholar]
- Manske, D. Theory of Unconventional Superconductors; Springer: Heidelberg, Germany, 2004. [Google Scholar]
- Benneman, K.H.; Ketterson, J.B. (Eds.) Superconductivity: Conventional and Unconventional Superconductors 1–2; Springer: New York, NY, USA; Berlin, Germany, 2008. [Google Scholar]
- Gunnarsson, O.; Rösch, O. Interplay between electron-phonon and coulomb interactions in cuprates. J. Phys. 2008, 20, 043201. [Google Scholar] [CrossRef]
- Kakani, S.L.; Kakani, S. Superconductivity; Anshan: Kent, UK, 2009. [Google Scholar]
- Plakida, N.M. High Temperature Cuprate Superconductors: Experiment, Theory and Applications; Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Cooper, L.N.; Feldman, D. (Eds.) BCS: 50 Years; World Sci. Publ. Co.: Singapore, 2011. [Google Scholar]
- Tohyama, T. Recent progress in physics of high-temperature superconductors. Jpn. J. Appl. Phys. 2012, 51, 010004. [Google Scholar] [CrossRef]
- Askerzade, I. Unconventional Superconductors: Anisotropy and Multiband Effects; Springer: Berlin, Germany, 2012. [Google Scholar]
- Bardeen, J. Developments of concepts in superconductivity. Phys. Today 1963, 16, 19. [Google Scholar] [CrossRef]
- Keldysh, L.V.; Kozlov, A.N. Collective Properties of Excitons in Semiconductors. Sov. Phys. JETP 1968, 27, 521. [Google Scholar]
- Eagles, D.M. Possible Pairing without Superconductivity at Low Carrier Concentrations in Bulk and Thin-Film Superconducting Semiconductors. Phys. Rev. 1969, 186, 456. [Google Scholar] [CrossRef]
- Nozières, P.; Schmitt-Rink, S. Propagation of Second sound in a superfluid Fermi gas in the unitary limit. J. Low Temp. Phys. 1985, 59, 195. [Google Scholar] [CrossRef]
- Loktev, V.M. Mechanisms of high-temperature superconductivity of Copper oxides. Fizika Nizkih Temperatur 1996, 22, 3. [Google Scholar]
- Randeria, M. Precursor Pairing Correlations and Pseudogaps. arXiv 1997, arXiv:cond-mat/9710223. [Google Scholar]
- Uemura, Y.J. Bose-Einstein to BCS crossover picture for high-Tc cuprates. Phys. C Supercond. 1997, 282, 194–197. [Google Scholar] [CrossRef]
- Drechsler, M.; Zwerger, W. Crossover from BCS-superconductivity to Bose-condensation. Ann. Phys. 1992, 1, 15. [Google Scholar] [CrossRef]
- Griffin, A.; Snoke, D.W.; Stringari, S. (Eds.) Bose-Einstein Condensation; Cambridge University Press: New York, NY, USA, 1996. [Google Scholar]
- Eliashberg, G.M. Interactions between Electrons and Lattice Vibrations in a Superconductor. Sov. Phys. JETP 1960, 11, 696. [Google Scholar]
- Marsiglio, F.; Carbotte, J.P. Gap function and density of states in the strong-coupling limit for an electron-boson system. Phys. Rev. B 1991, 43, 5355. [Google Scholar] [CrossRef]
- Micnas, R.; Ranninger, J.; Robaszkiewicz, S. Superconductivity in narrow-band systems with local nonretarded attractive interactions. Rev. Mod. Phys. 1990, 62, 113. [Google Scholar] [CrossRef]
- Zwerger, W. (Ed.) The BCS-BEC Crossover and the Unitary Fermi Gas. In Lecture Notes in Physics; Springer: Berlin, Heidelberg, 2012. [Google Scholar]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885. [Google Scholar] [CrossRef]
- Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of ultracold atomic Fermi gases. Rev. Mod. Phys. 2008, 80, 1215. [Google Scholar] [CrossRef]
- Chen, Q.; Stajic, J.; Tan, S.; Levin, K. BCS-BEC crossover: From high temperature superconductors to ultracold superfluids. Phys. Rep. 2005, 412, 1–88. [Google Scholar] [CrossRef]
- Ketterle, W.; Zwierlein, M.W. Making, probing and understanding ultracold Fermi gases. In Ultra-cold Fermi Gases; Inguscio, M., Ketterle, W., Salomon, C., Eds.; IOS Press: Amsterdam, The Netherlands, 2007; p. 95. [Google Scholar]
- Pieri, P.; Strinati, G.C. Strong-coupling limit in the evolution from BCS superconductivity to Bose-Einstein condensation. Phys. Rev. B 2000, 61, 15370. [Google Scholar] [CrossRef]
- Gerlach, B.; Löwen, H. Analytical properties of polaron systems or: Do polaronic phase transitions exist or not? Rev. Mod. Phys. 1991, 63, 63. [Google Scholar] [CrossRef]
- Lakhno, V.D. Translation invariant theory of polaron (bipolaron) and the problem of quantizing near the classical solution. JETP 2013, 116, 892–896. [Google Scholar] [CrossRef]
- Gor’kov, L.P. Microscopic derivation of the Ginzburg-Landau equations in the theory of superconductivity. Sov. Phys. JETP 1959, 9, 1364–1367. [Google Scholar]
- Lakhno, V.D. Energy and Critical Ionic-Bond Parameter of a 3D Large-Radius Bipolaron. J. Exp. Theor. Phys. 2010, 110, 811–815. [Google Scholar] [CrossRef]
- Lakhno, V.D. Translation-invariant bipolarons and the problem of high-temperature superconductivity. Sol. State Commun. 2012, 152, 621–623. [Google Scholar] [CrossRef][Green Version]
- Kashirina, N.I.; Lakhno, V.D.; Tulub, A.V. The Virial Theorem and the Ground State Problem in Polaron Theory. J. Exp. Theor. Phys. 2012, 114, 867–869. [Google Scholar] [CrossRef]
- Lakhno, V.D. Pekar’s ansatz and the strong coupling problem in polaron theory. Phys. Usp. 2015, 58, 295. [Google Scholar] [CrossRef]
- Lakhno, V.D. Superconducting Properties of 3D Low-Density Translation-Invariant Bipolaron Gas. Adv. Condens. Matter Phys. 2018, 2018, 1380986. [Google Scholar] [CrossRef]
- Lakhno, V.D. Superconducting properties of a nonideal bipolaron gas. Phys. C Supercond. Its Appl. 2019, 561, 1–8. [Google Scholar] [CrossRef]
- Lakhno, V.D. Spin wave amplification in magnetically ordered crystals. Phys. Usp. 1996, 39, 669. [Google Scholar] [CrossRef]
- Tulub, A.V. Slow Electrons in Polar Crystals. Sov. Phys. JETP 1962, 14, 1301. [Google Scholar]
- Heisenberg, W. Die selbstenergie des elektrons. Z. Phys. 1930, 65, 4–13. [Google Scholar] [CrossRef]
- Rosenfeld, L. Über eine mögliche Fassung des Diracschen Programms zur Quantenelektrodynamik und deren formalen Zusammenhang mit der Heisenberg-Paulischen Theorie. Z. Phys. 1932, 76, 729–734. [Google Scholar] [CrossRef]
- Lee, T.D.; Low, F.; Pines, D. The motion of electrons in a polar crystal. Phys. Rev. 1953, 90, 297. [Google Scholar] [CrossRef]
- Tyablikov, S.V. Methods in the Quantum Theory of Magnetism; Plenum Press: New York, NY, USA, 1967. [Google Scholar]
- Miyake, S.J. Bound Polaron in the Strong-coupling Regime. In Polarons and Applications; Lakhno, V.D., Ed.; Wiley: Leeds, UK, 1994; p. 219. [Google Scholar]
- Levinson, I.B.; Rashba, E.I. Threshold phenomena and bound states in the polaron problem. Sov. Phys. Usp. 1974, 16, 892–912. [Google Scholar] [CrossRef]
- Porsch, M.; Röseler, J. Recoil Effects in the Polaron Problem. Phys. Status Solidi B 1967, 23, 365–376. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Mott, N. Polarons & Bipolarons; World Sci. Pub. Co.: Singapore, 1996. [Google Scholar]
- Alexandrov, A.S.; Krebs, A.B. Polarons in high-temperature superconductors. Sov. Phys. Usp. 1992, 35, 345–383. [Google Scholar] [CrossRef]
- Ogg, R.A., Jr. Superconductivity in solid metal-ammonia solutions. Phys. Rev. 1946, 70, 93. [Google Scholar] [CrossRef]
- Vinetskii, V.L.; Pashitskii, E.A. Superfluidity of charged Bose-gas and bipolaron mechanism of superconductivity. Ukr. J. Phys. 1975, 20, 338. [Google Scholar]
- Pashitskii, E.A.; Vinetskii, V.L. Plasmon and bipolaron mechanisms of high-temperature superconductivity. JETP Lett. 1987, 46, 124–127. [Google Scholar]
- Emin, D. Formation, motion, and high-temperature superconductivity of large bipolarons. Phys. Rev. Lett. 1989, 62, 1544. [Google Scholar] [CrossRef] [PubMed]
- Vinetskii, V.L.; Kashirina, N.I.; Pashitskii, E.A. Bipolaron states in ion crystals and the problem of high temperature superconductivity. Ukr. J. Phys. 1992, 37, 76. [Google Scholar]
- Emin, D. In-plane conductivity of a layered large-bipolaron liquid. Philos. Mag. 2015, 95, 918–934. [Google Scholar] [CrossRef][Green Version]
- Schmidt, V.V. The Physics of Superconductors; Muller, P., Ustinov, A.V., Eds.; Springer: Berlin/Heidelberg, Germnay, 1997. [Google Scholar]
- Pippard, A.B. Field variation of the superconducting penetration depth. Proc. Roy. Soc. (Lond.) 1950, A203, 210–223. [Google Scholar]
- Schafroth, M.R. Superconductivity of a Charged Ideal Bose Gas. Phys. Rev. 1955, 100, 463. [Google Scholar] [CrossRef]
- Gor’kov, L.P.; Kopnin, N.B. High-Tc superconductors from the experimental point of view. Sov. Phys. Usp. 1988, 31, 850. [Google Scholar] [CrossRef]
- Buckel, W.; Kleiner, R. Superconductivity: Fundamentals and Applications, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2004. [Google Scholar]
- Edstam, J.; Olsson, H.K. London penetration depth of YBCO in the frequency range 80-700 GHz. Phys. B 1994, 194–196 Pt 2, 1589–1590. [Google Scholar] [CrossRef]
- Panagopoulos, C.; Cooper, J.R.; Xiang, T. Systematic behavior of the in-plane penetration depth in d-wave cuprates. Phys. Rev. B 1998, 57, 13422. [Google Scholar] [CrossRef]
- Pereg-Barnea, T.; Turner, P.J.; Harris, R.; Mullins, G.K.; Bobowski, J.S.; Raudsepp, M.; Liang, R.; Bonn, D.A.; Hardy, W.N. Absolute values of the London penetration depth in YBa2Cu3O6+y measured by zero field ESR spectroscopy on Gd doped single crystals. Phys. Rev. B 2004, 69, 184513. [Google Scholar] [CrossRef]
- Bonn, D.A.; Liang, R.; Riseman, T.M.; Baar, D.J.; Morgan, D.C.; Zhang, K.; Dosanjh, P.; Duty, T.L.; MacFarlane, A.; Morris, G.D.; et al. Microwave determination of the quasiparticle scattering time in YBa2Cu3O6.95. Phys. Rev. B 1993, 47, 11314. [Google Scholar] [CrossRef]
- Madelung, O. Festkörpertheorie I, II; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1972. [Google Scholar]
- Wu, D.H.; Sridhar, S. Pinning forces and lower critical fields in YBa2Cu3Oy crystals: Temperature dependence and anisotropy. Phys. Rev. Lett. 1990, 65, 2074. [Google Scholar] [CrossRef] [PubMed]
- Alexandrov, A.S. Comment on Experimental and Theoretical Constraints of Bipolaronic Superconductivity in High Tc Materials: An Impossibility. Phys. Rev. Lett. 1999, 82, 2620. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Kabanov, V.V. Parameter-free expression for superconducting Tc in cuprates. Phys. Rev. B 1999, 59, 13628. [Google Scholar] [CrossRef]
- Uemura, Y.J.; Luke, G.M.; Sternlieb, B.J.; Brewer, J.H.; Carolan, J.F.; Hardy, W.N.; Kadono, R.; Kempton, J.R.; Kiefl, R.F.; Kreitzman, S.R.; et al. Universal correlations between Tc and ns/m (carrier density over effective mass) in high-Tc cuprate superconductors. Phys. Rev. Lett. 1989, 62, 2317. [Google Scholar] [CrossRef] [PubMed]
- Uemura, Y.J.; Le, L.P.; Luke, G.M.; Sternlieb, B.J.; Wu, W.D.; Brewer, J.H.; Riseman, T.M.; Seaman, C.L.; Maple, M.B.; Ishikawa, M.; et al. Basic similarities among cuprate, bismuthate, organic, Chevrel-phase, and heavy-fermion superconductors shown by penetration-depth measurements. Phys. Rev. Lett. 1991, 66, 2665. [Google Scholar] [CrossRef]
- Homes, C.C.; Dordevic, S.V.; Strongin, M.; Bonn, D.A.; Liang, R.; Hardy, W.N.; Komiya, S.; Ando, Y.; Yu, G.; Kaneko, N.; et al. A universal scaling relation in high-temperature superconductors. Nature 2004, 430, 539. [Google Scholar] [CrossRef]
- Zaanen, J. Superconductivity: Why the temperature is high. Nature 2004, 430, 512. [Google Scholar] [CrossRef]
- Erdmenger, J.; Kerner, P.; Müller, S. Towards a holographic realization of Homes law. J. High Energy Phys. 2012, 10, 21. [Google Scholar] [CrossRef]
- Balakirev, F.F.; Betts, J.B.; Migliori, A.; Ono, S.; Ando, Y.; Boebinger, G.S. Signature of optimal doping in Hall-effect measurements on a high-temperature superconductor. Nature 2003, 424, 912–915. [Google Scholar] [CrossRef]
- Lakhno, V.D. A Translation invariant bipolaron in the Holstein model and superconductivity. SpringerPlus 2016, 5, 1277. [Google Scholar] [CrossRef][Green Version]
- Drozdov, A.P.; Eremets, M.I.; Troyan, I.A.; Ksenofontov, V.; Shylin, S.I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73–76. [Google Scholar] [CrossRef] [PubMed]
- Somayazulu, M.; Ahart, M.; Mishra, A.K.; Geballe, Z.M.; Baldini, M.; Meng, Y.; Struzhkin, V.V.; Hemley, R.J. Evidence for Superconductivity above 260 K in Lanthanum Superhydride at Megabar Pressures. Phys. Rev. Lett. 2019, 122, 027001. [Google Scholar] [CrossRef] [PubMed]
- Drozdov, A.P.; Kong, P.P.; Minkov, V.S.; Besedin, S.P.; Kuzovnikov, M.A.; Mozaffari, S.; Balicas, L.; Balakirev, F.; Graf, D.; Prakapenka, V.B.; et al. Superconductivity at 250 K in lanthanum hydride under high pressures. arXiv 2018, arXiv:1812.01561. [Google Scholar]



| i | , Oe | ||||
|---|---|---|---|---|---|
| 0 | 0 | 25.2 | 0 | 0 | 0 |
| 1 | 0.2 | 27.3 | −0.94 | −11.54 | 2.27 |
| 2 | 1 | 30 | −0.4 | −2.18 | 7.8 |
| 3 | 2 | 32.1 | −0.27 | −1.05 | 13.3 |
| 4 | 10 | 41.9 | −0.1 | −0.19 | 47.1 |
| 5 | 15 | 46.2 | −0.08 | −0.12 | 64.9 |
| 6 | 20 | 50 | −0.07 | −0.09 | 81.5 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lakhno, V.D. Superconducting Properties of 3D Low-Density TI-Bipolaron Gas in Magnetic Field. Condens. Matter 2019, 4, 43. https://doi.org/10.3390/condmat4020043
Lakhno VD. Superconducting Properties of 3D Low-Density TI-Bipolaron Gas in Magnetic Field. Condensed Matter. 2019; 4(2):43. https://doi.org/10.3390/condmat4020043
Chicago/Turabian StyleLakhno, Victor D. 2019. "Superconducting Properties of 3D Low-Density TI-Bipolaron Gas in Magnetic Field" Condensed Matter 4, no. 2: 43. https://doi.org/10.3390/condmat4020043
APA StyleLakhno, V. D. (2019). Superconducting Properties of 3D Low-Density TI-Bipolaron Gas in Magnetic Field. Condensed Matter, 4(2), 43. https://doi.org/10.3390/condmat4020043





