Geometric Effects of a Quarter of Corrugated Torus
Abstract
:1. Introduction
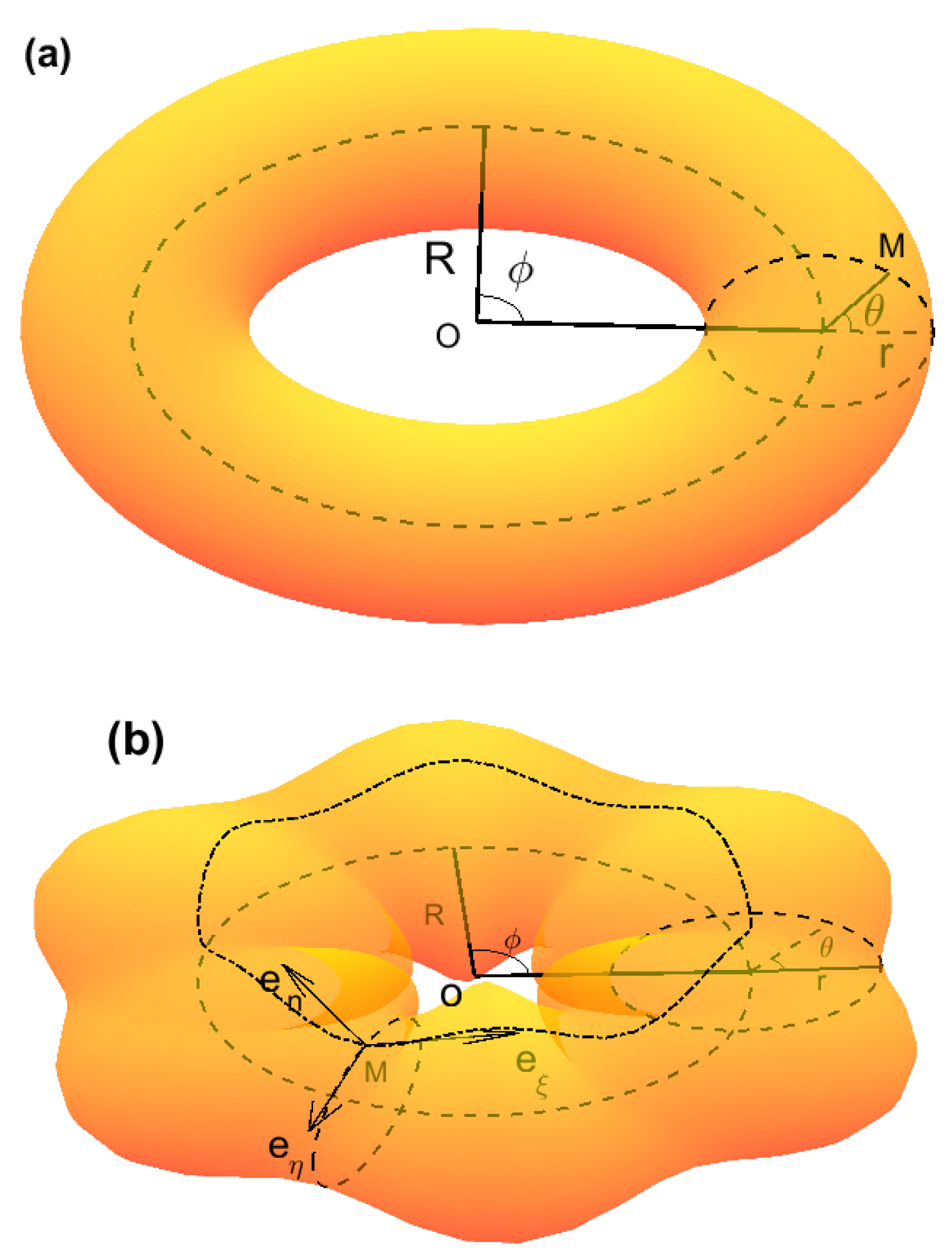
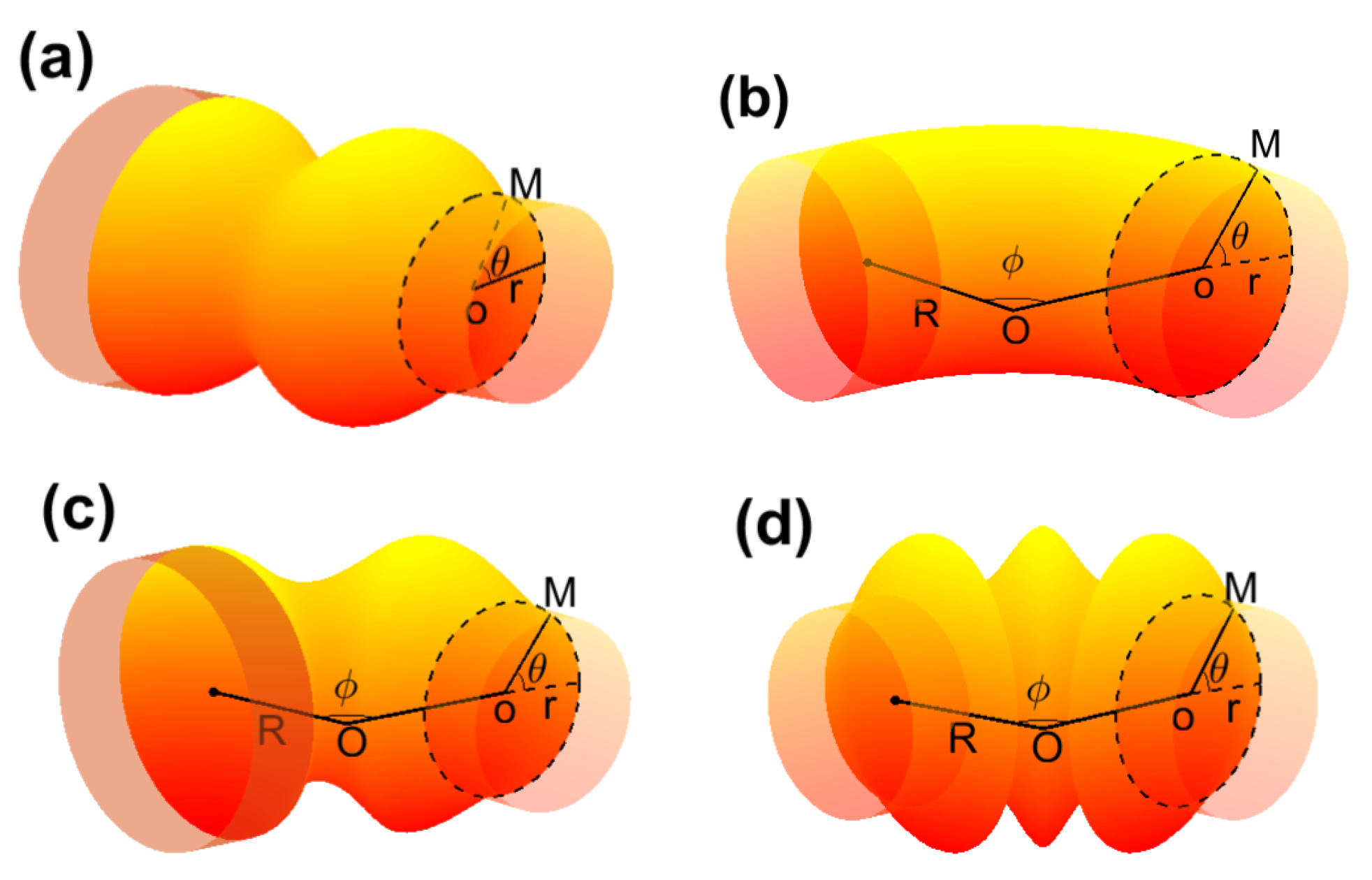
2. Quantum Dynamics of a Particle Confined to a Periodically Corrugated Torus
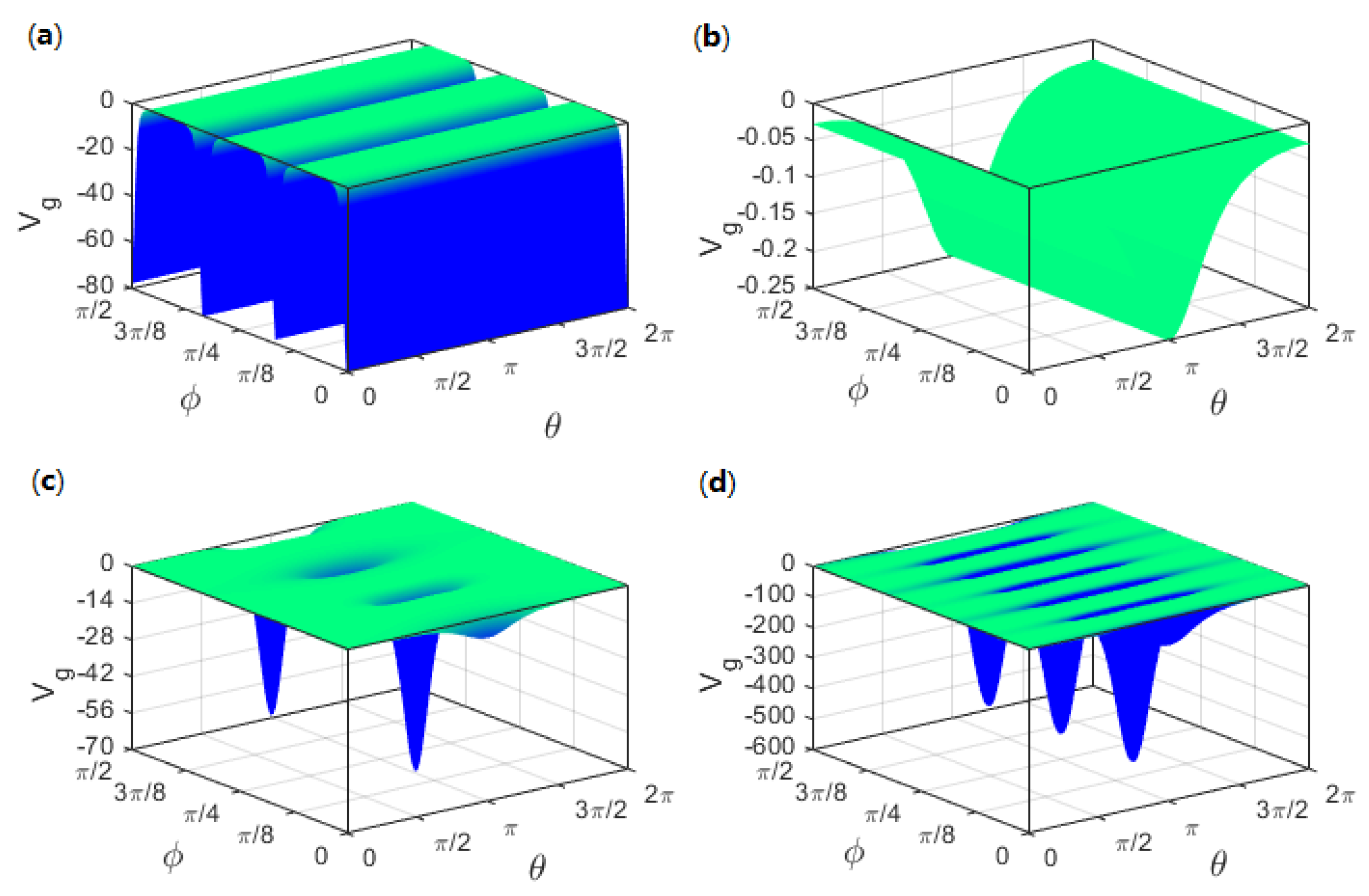
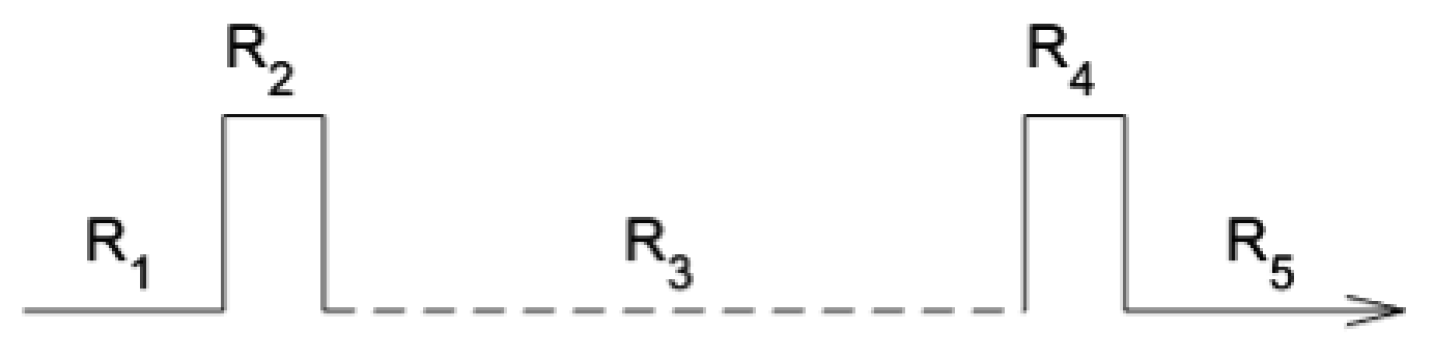
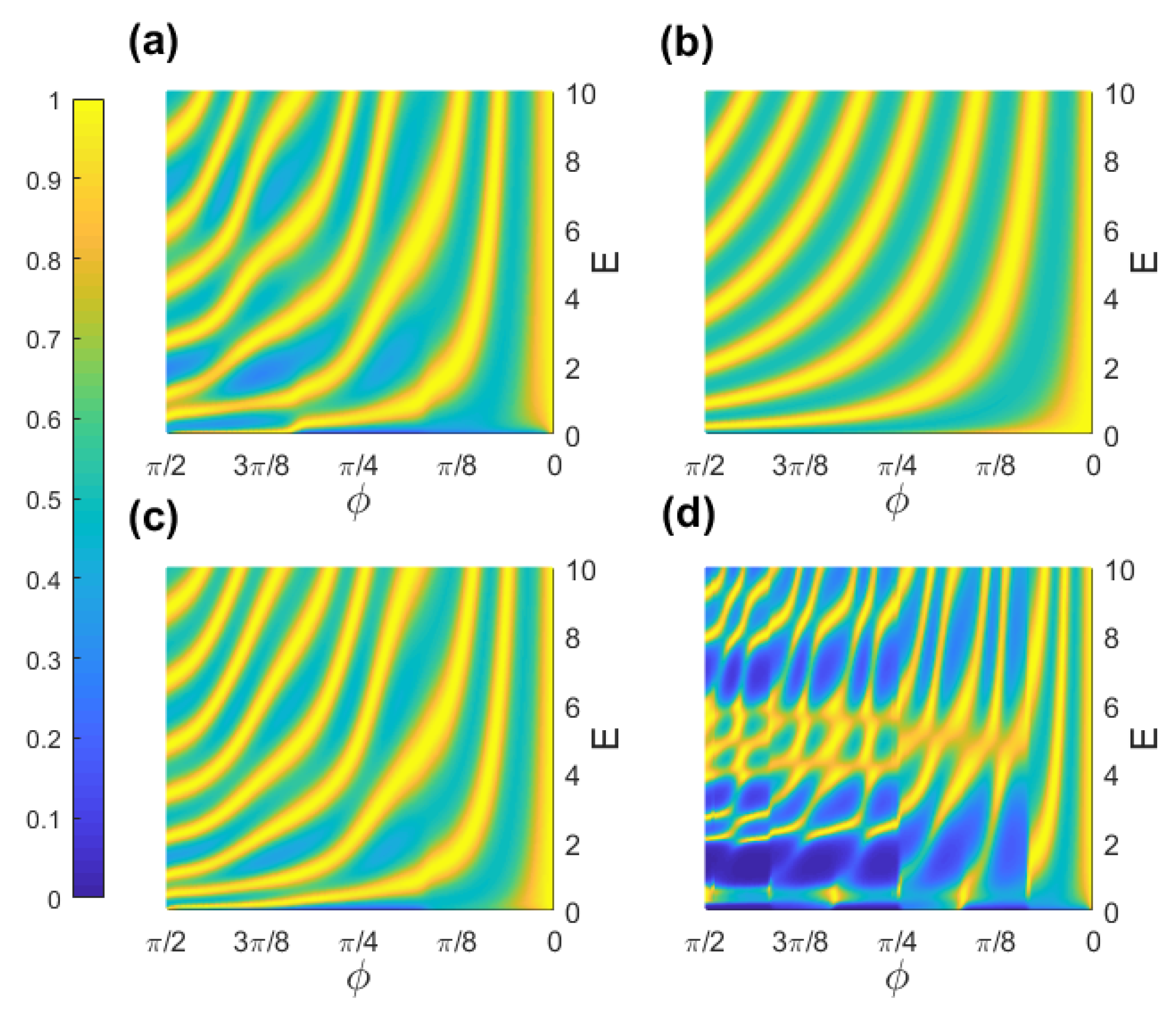
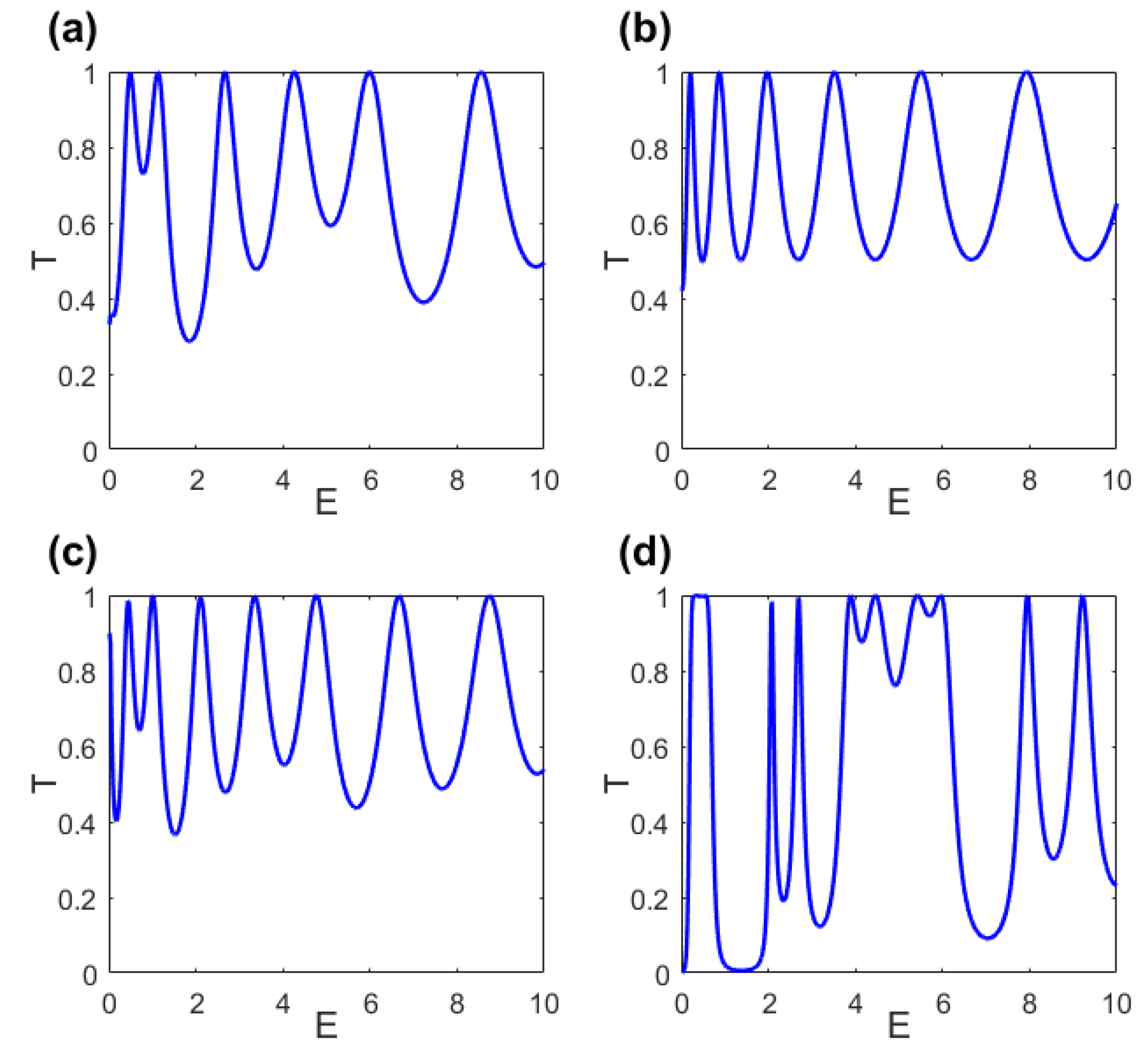
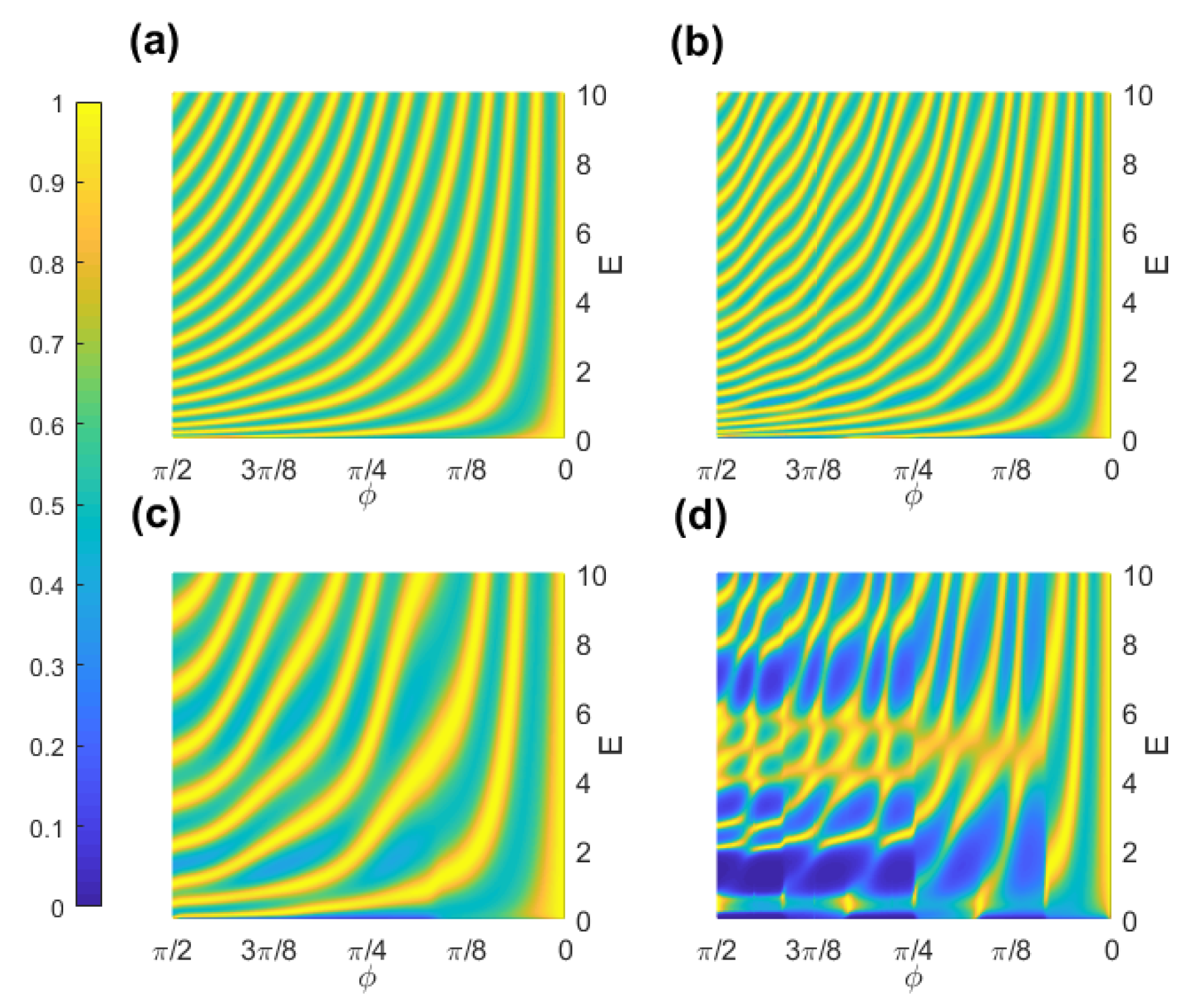
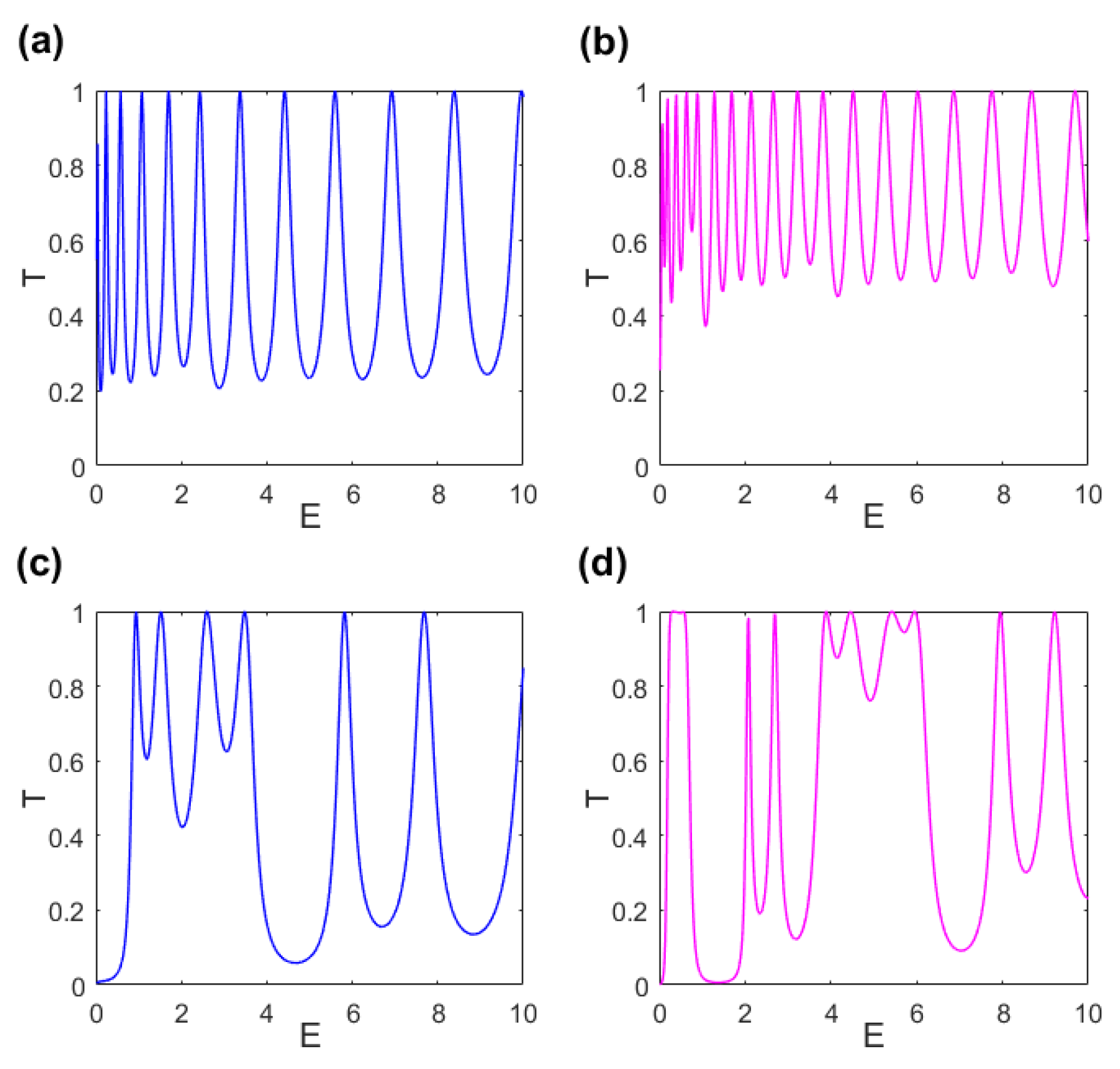
3. Transmission Probability in Periodically Corrugated Toruses
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, P.; Cottrill, A.L.; Kozawa, D.; Koman, V.B.; Parviz, D.; Liu, A.T.; Yang, J.; Tran, T.Q.; Wong, M.H.; Wang, S.; et al. Emerging trends in 2D nanotechnology that are redefining our understanding of “Nanocomposites”. Nano Today 2018, 21, 18–40. [Google Scholar] [CrossRef]
- Khoshnevis, H.; Tran, T.Q.; Mint, S.M.; Zadhoush, A.; Duong, H.M.; Youssefi, M. Effect of alignment and packing density on the stress relaxation process of carbon nanotube fibers spun from floating catalyst chemical vapor deposition method. Colloids Surf. A 2018, 588, 570–578. [Google Scholar] [CrossRef]
- Da Costa, R.C.T. Quantum mechanics of a constrained particle. Phys. Rev. A 1981, 23, 1982–1987. [Google Scholar] [CrossRef]
- Schuster, P.; Jaffe, R. Quantum mechanics on manifolds embedded in Euclidean space. Ann. Phys. 2003, 307, 132–143. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.H.; Tong, C.L.; Lai, M.M. Constraint-induced mean curvature dependence of Cartesian momentum operators. J. Phys. A Math. Theor. 2007, 40, 4161. [Google Scholar] [CrossRef]
- Liu, Q.H.; Tang, L.H.; Xun, D.M. Geometric momentum: The proper momentum for a free particle on a two-dimensional sphere. Phys. Rev. A 2011, 84, 042101. [Google Scholar] [CrossRef]
- Wang, Y.L.; Jiang, H.; Zong, H.S. Geometric influences of a particle confined to a curved surface embedded in three-dimensional Euclidean space. Phys. Rev. A 2017, 96, 022116. [Google Scholar] [CrossRef]
- Wang, Y.L.; Lai, M.Y.; Wang, F.; Zong, H.S.; Chen, Y.F. Geometric effects resulting from square and circular confinements for a particle constrained to a space curve. Phys. Rev. A 2018, 97, 042108. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.L.; Lai, M.Y.; Wang, F.; Zong, H.S.; Chen, Y.F. Erratum: Geometric effects resulting from square and circular confinements for a particle constrained to a space curve. Phys. Rev. A 2018, 97, 069904. [Google Scholar] [CrossRef]
- Brandt, F.T.; Sánchez-Monroy, J.A. Induced magnetic moment for a spinless charged particle in the thin-layer approach. EPL 2015, 111, 67004. [Google Scholar] [CrossRef] [Green Version]
- Aoki, H.; Koshino, M.; Takeda, D.; Morise, H.; Kuroki, K. Electronic structure of periodic curved surfaces: Topological band structure. Phys. Rev. B 2001, 65, 035102. [Google Scholar] [CrossRef]
- Fujita, N.; Terasaki, O. Band structure of the P, D, and G surfaces. Phys. Rev. B 2005, 72, 085459. [Google Scholar] [CrossRef] [Green Version]
- Koshino, M.; Aoki, H. Electronic structure of an electron on the gyroid surface: A helical labyrinth. Phys. Rev. B 2005, 71, 073405. [Google Scholar] [CrossRef]
- Goldstone, J.; Jaffe, R.L. Bound states in twisting tubes. Phys. Rev. B 1992, 45, 14100–14107. [Google Scholar] [CrossRef]
- Cantele, G.; Ninno, D.; Iadonisi, G. Topological surface states in deformed quantum wires. Phys. Rev. B 2000, 61, 13730–13736. [Google Scholar] [CrossRef]
- Encinosa, M.; Mott, L. Curvature-induced toroidal bound states. Phys. Rev. A 2003, 68, 014102. [Google Scholar] [CrossRef]
- Taira, H.; Shima, H. Electronic States in Cylindrical Surfaces with Local Deformation. J. Phys. Conf. Ser. 2007, 61, 1142. [Google Scholar] [CrossRef]
- Taira, H.; Shima, H. Curvature effects on surface electron states in ballistic nanostructures. Surf. Sci. 2007, 601, 5270–5275. [Google Scholar] [CrossRef] [Green Version]
- Ortix, C.; van den Brink, J. Effect of curvature on the electronic structure and bound-state formation in rolled-up nanotubes. Phys. Rev. B 2010, 81, 165419. [Google Scholar] [CrossRef]
- Encinosa, M.; Etemadi, B. Energy shifts resulting from surface curvature of quantum nanostructures. Phys. Rev. A 1998, 58, 77–81. [Google Scholar] [CrossRef]
- Shima, H.; Yoshioka, H.; Onoe, J. Geometry-driven shift in the Tomonaga-Luttinger exponent of deformed cylinders. Phys. Rev. B 2009, 79, 201401. [Google Scholar] [CrossRef]
- Marchi, A.; Reggiani, S.; Rudan, M.; Bertoni, A. Coherent electron transport in bent cylindrical surfaces. Phys. Rev. B 2005, 72, 035403. [Google Scholar] [CrossRef]
- Zhang, E.; Zhang, S.; Wang, Q. Quantum transport in a curved one-dimensional quantum wire with spin-orbit interactions. Phys. Rev. B 2007, 75, 085308. [Google Scholar] [CrossRef]
- Cuoghi, G.; Ferrari, G.; Bertoni, A. Surface carrier transport in Y nanojunctions: Signatures of the geometric potential. Phys. Rev. B 2009, 79, 073410. [Google Scholar] [CrossRef]
- Szameit, A.; Dreisow, F.; Heinrich, M.; Keil, R.; Nolte, S.; Tünnermann, A.; Longhi, S. Geometric Potential and Transport in Photonic Topological Crystals. Phys. Rev. Lett. 2010, 104, 150403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spittel, R.; Uebel, P.; Bartelt, H.; Schmidt, M.A. Curvature-induced geometric momenta: the origin of waveguide dispersion of surface plasmons on metallic wires. Opt. Express 2015, 23, 12174. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, P.; Mohta, V.; Jaffe, R. Dirac Particles in Twisted Tubes. Ann. Phys. 1999, 275, 297–313. [Google Scholar] [CrossRef] [Green Version]
- Novakovic, B.; Akis, R.; Knezevic, I. Transport in curved nanoribbons in a magnetic field. Phys. Rev. B 2011, 84, 195419. [Google Scholar] [CrossRef]
- Santos, F.; Fumeron, S.; Berche, B.; Moraes, F. Geometric effects in the electronic transport of deformed nanotubes. Nanotechnology 2016, 27, 135302. [Google Scholar] [CrossRef] [Green Version]
- Sakurai, J.J.; Kirkner, D.J. Modern Quantum Mechanics; Addison-Wesley: Reading, MA, USA, 1993. [Google Scholar]
- Li, X. Strain induced semiconductor nanotubes: from formation process to device applications. J. Phys. D Appl. Phys. 2008, 41, 193001. [Google Scholar] [CrossRef]
- Turner, A.M.; Vitelli, V.; Nelson, D.R. Vortices on curved surfaces. Rev. Mod. Phys. 2010, 82, 1301–1348. [Google Scholar] [CrossRef] [Green Version]
- Mutilin, S.V.; Soots, R.A.; Vorob’ev, A.B.; Ikusov, D.G.; Prinz, V.Y. Microtubes and corrugations fabricated from strained ZnTe/CdHgTe/HgTe/CdHgTe heterofilms with 2D electron–hole gas in the HgTe quantum well. J. Phys. D Appl. Phys. 2014, 47, 295301. [Google Scholar] [CrossRef]
- Wang, Y.L.; Liang, G.H.; Jiang, H.; Lu, W.T.; Zong, H.S. Transmission gaps from corrugations. J. Phys. D Appl. Phys. 2016, 49, 295103. [Google Scholar] [CrossRef] [Green Version]
- Maraner, P. A complete perturbative expansion for quantum mechanics with constraints. J. Phys. A Math. Gen. 1995, 28, 2939–2951. [Google Scholar] [CrossRef] [Green Version]
- Jensen, H.; Koppe, H. Quantum mechanics with constraints. Ann. Phys. 1971, 63, 586–591. [Google Scholar] [CrossRef]
- Encinosa, M. Surface geometric effects on tunneling rates. IEEE Trans. Electron. Devices 2000, 47, 878. [Google Scholar] [CrossRef]
- Li, Y.P.; Zaslavsky, A.; Tsui, D.C.; Santos, M.; Shayegan, M. Noise characteristics of double-barrier resonant-tunneling structures below 10 kHz. Phys. Rev. B 1990, 41, 8388–8391. [Google Scholar] [CrossRef]
- Chen, L.Y.; Ting, C.S. Theoretical investigation of noise characteristics of double-barrier resonant-tunneling systems. Phys. Rev. B 1991, 43, 4534–4537. [Google Scholar] [CrossRef]
- Chen, L.Y.; Ting, C.S. Dynamic properties of double-barrier resonant-tunneling structures. Phys. Rev. B 1991, 43, 2097–2105. [Google Scholar] [CrossRef]
- Kane, C.L.; Fisher, M.P.A. Transmission through barriers and resonant tunneling in an interacting one-dimensional electron gas. Phys. Rev. B 1992, 46, 15233–15262. [Google Scholar] [CrossRef]
- Doering, C.R.; Gadoua, J.C. Resonant activation over a fluctuating barrier. Phys. Rev. Lett. 1992, 69, 2318–2321. [Google Scholar] [CrossRef]
- Nguyen, H.S.; Vishnevsky, D.; Sturm, C.; Tanese, D.; Solnyshkov, D.; Galopin, E.; Lemaître, A.; Sagnes, I.; Amo, A.; Malpuech, G.; et al. Realization of a Double-Barrier Resonant Tunneling Diode for Cavity Polaritons. Phys. Rev. Lett. 2013, 110, 236601. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.X.; Zhan, A.; Xu, Y.D.; Chen, H.Y.; You, W.L.; Majumdar, A.; Jiang, J.H. Quantum many-body simulation using monolayer exciton-polaritons in coupled-cavities. J. Phys. Condens. Matter 2017, 29, 445703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khelif, A.; Djafari-Rouhani, B.; Vasseur, J.O.; Deymier, P.A. Transmission and dispersion relations of perfect and defect-containing waveguide structures in phononic band gap materials. Phys. Rev. B 2003, 68, 024302. [Google Scholar] [CrossRef]
- Chen, X.; Wang, L.G.; Li, C.F. Transmission gap, Bragg-like reflection, and Goos-Hänchen shifts near the Dirac point inside a negative-zero-positive index metamaterial slab. Phys. Rev. A 2009, 80, 043839. [Google Scholar] [CrossRef]
- Chen, X.; Tao, J.W. Design of electron wave filters in monolayer graphene by tunable transmission gap. Appl. Phys. Lett. 2009, 94, 262102. [Google Scholar] [CrossRef]
- Liu, X.W.; Stamp, A.P. Resonance splitting effect in multibarrier tunneling. Phys. Rev. B 1993, 47, 16605–16607. [Google Scholar] [CrossRef]
- Guo, Y.; Gu, B.L.; Li, Z.Q.; Yu, J.Z.; Kawazoe, Y. Resonance splitting effect and wave-vector filtering effect in magnetic superlattices. J. Appl. Phys. 1998, 83, 367218. [Google Scholar] [CrossRef]
- Zeng, Z.Y.; Zhang, L.D.; Yan, X.H.; You, J.Q. Resonant peak splitting for ballistic conductance in magnetic superlattices. Phys. Rev. B 1999, 60, 1515–1518. [Google Scholar] [CrossRef] [Green Version]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, R.; Wang, Y.-L.; Jiang, H.; Liu, X.-J.; Zong, H.-S. Geometric Effects of a Quarter of Corrugated Torus. Condens. Matter 2019, 4, 3. https://doi.org/10.3390/condmat4010003
Cheng R, Wang Y-L, Jiang H, Liu X-J, Zong H-S. Geometric Effects of a Quarter of Corrugated Torus. Condensed Matter. 2019; 4(1):3. https://doi.org/10.3390/condmat4010003
Chicago/Turabian StyleCheng, Run, Yong-Long Wang, Hua Jiang, Xiao-Jun Liu, and Hong-Shi Zong. 2019. "Geometric Effects of a Quarter of Corrugated Torus" Condensed Matter 4, no. 1: 3. https://doi.org/10.3390/condmat4010003
APA StyleCheng, R., Wang, Y.-L., Jiang, H., Liu, X.-J., & Zong, H.-S. (2019). Geometric Effects of a Quarter of Corrugated Torus. Condensed Matter, 4(1), 3. https://doi.org/10.3390/condmat4010003




