Experimental Observation of Temperature-Driven Topological Phase Transition in HgTe/CdHgTe Quantum Wells
Abstract
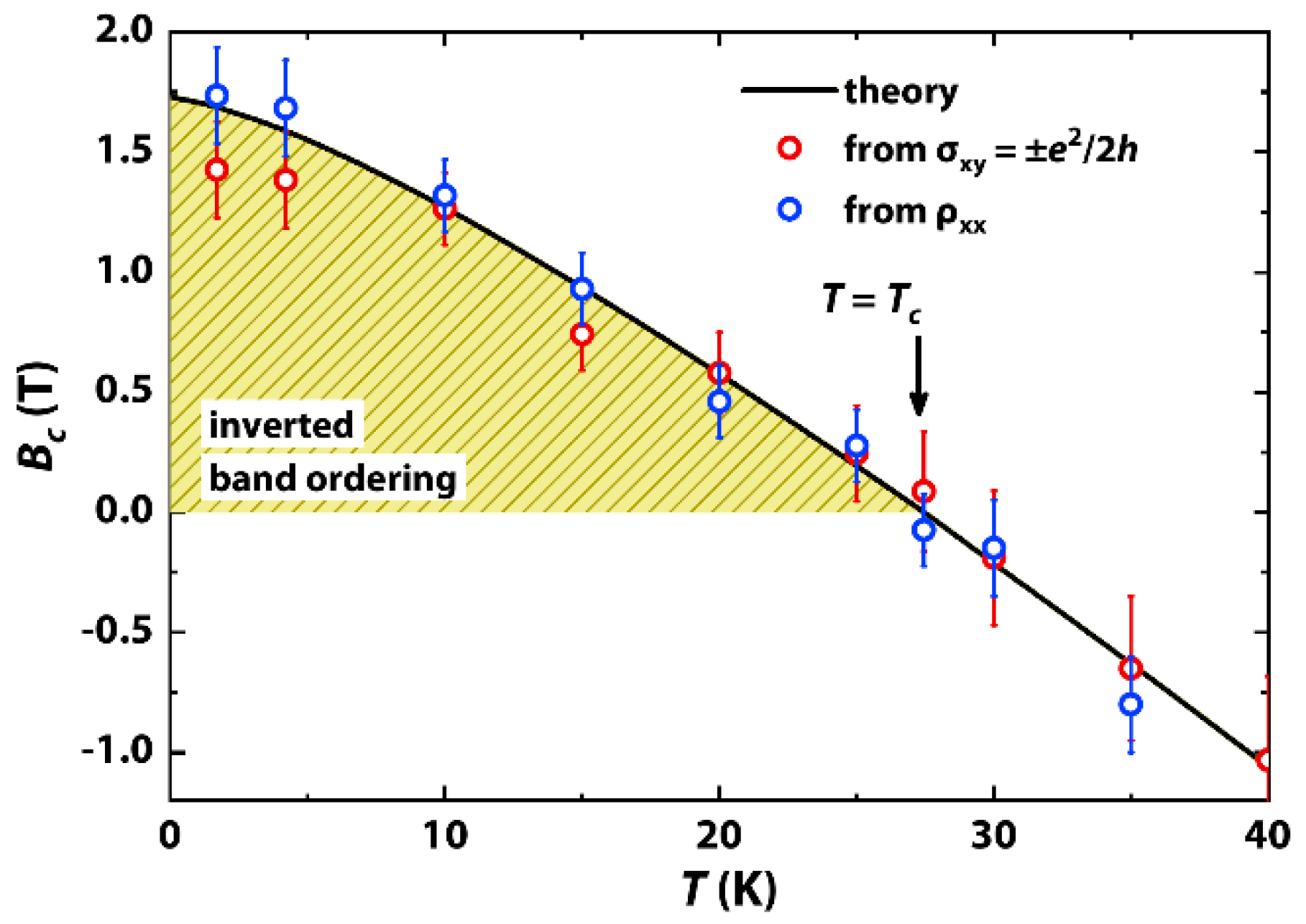
:1. Introduction
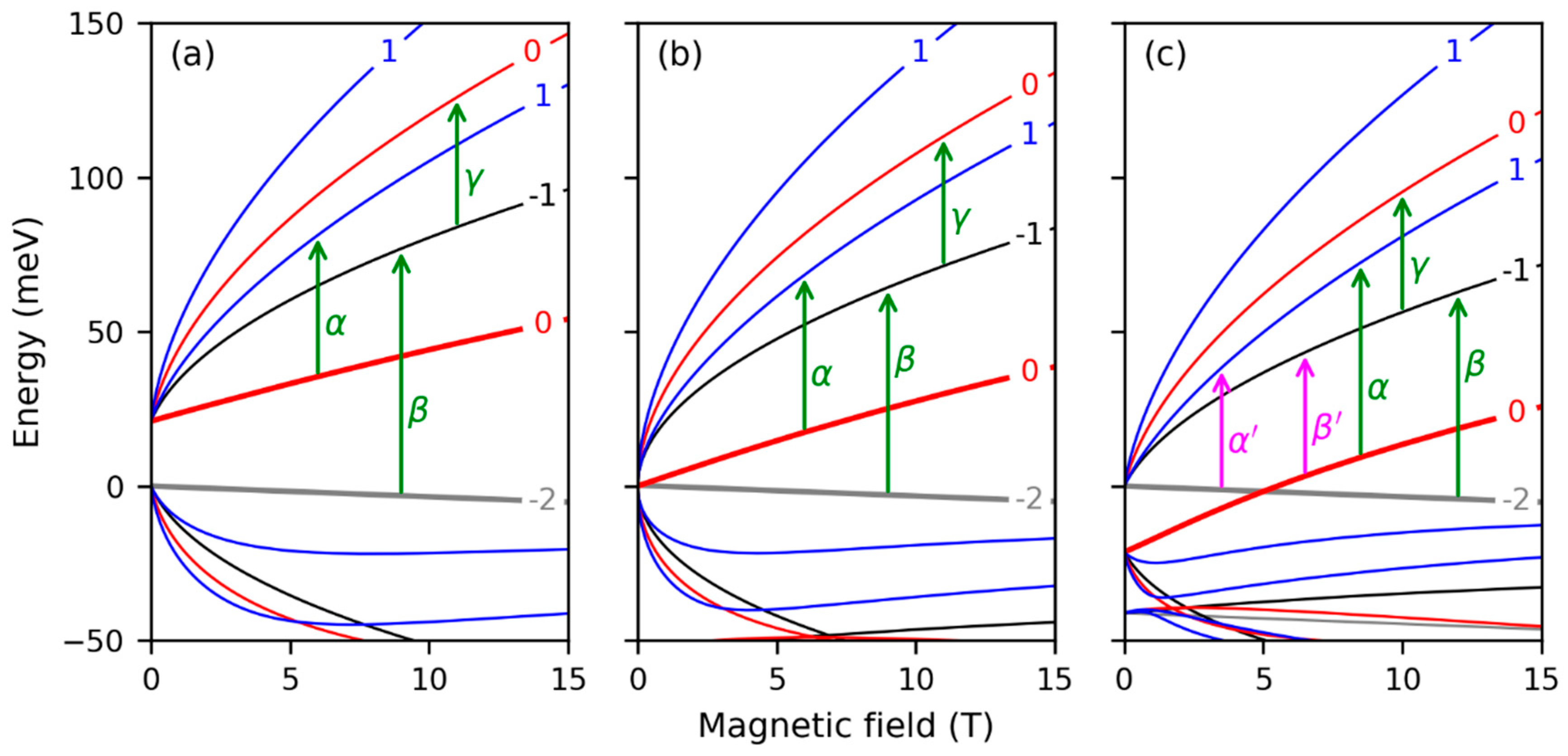
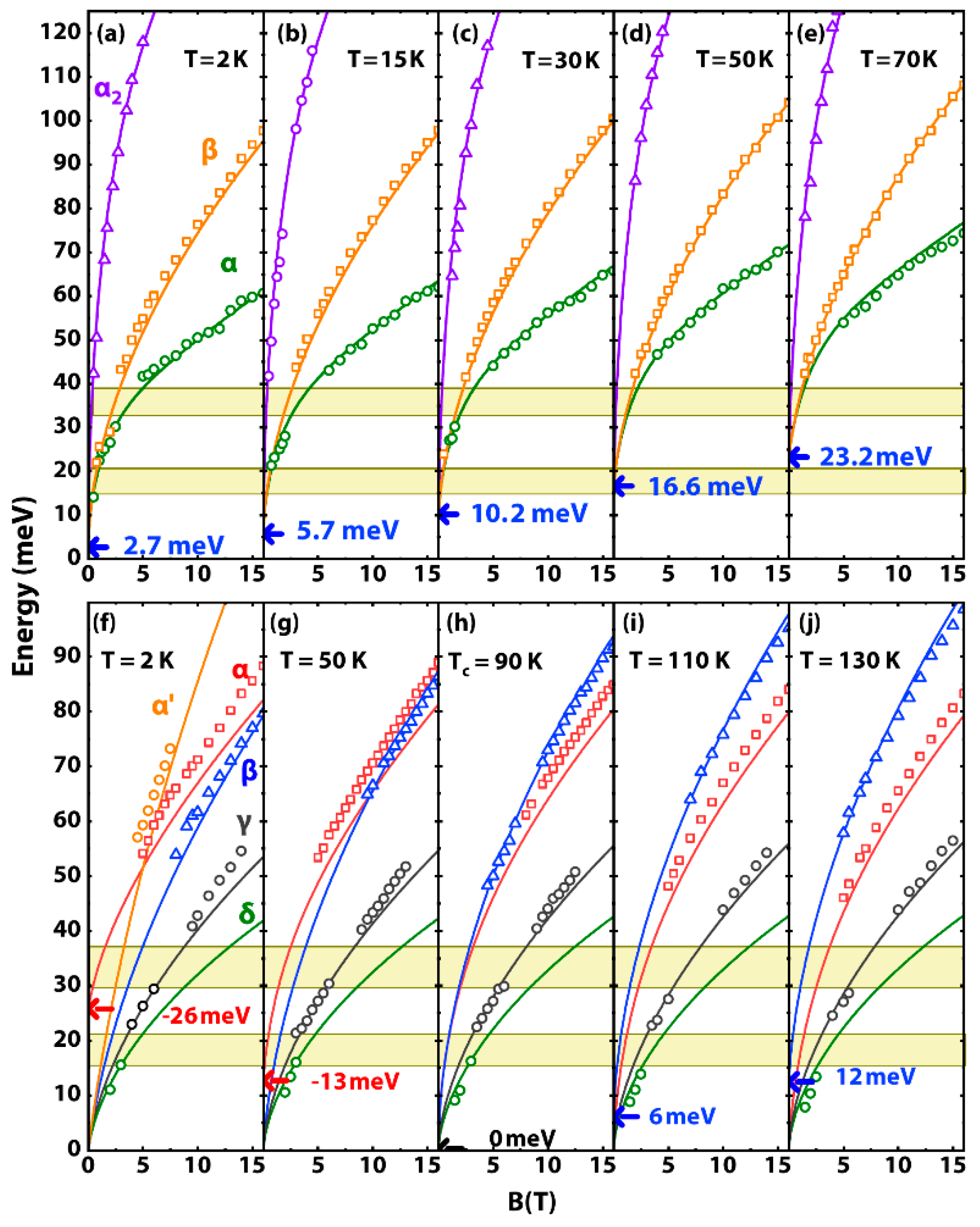
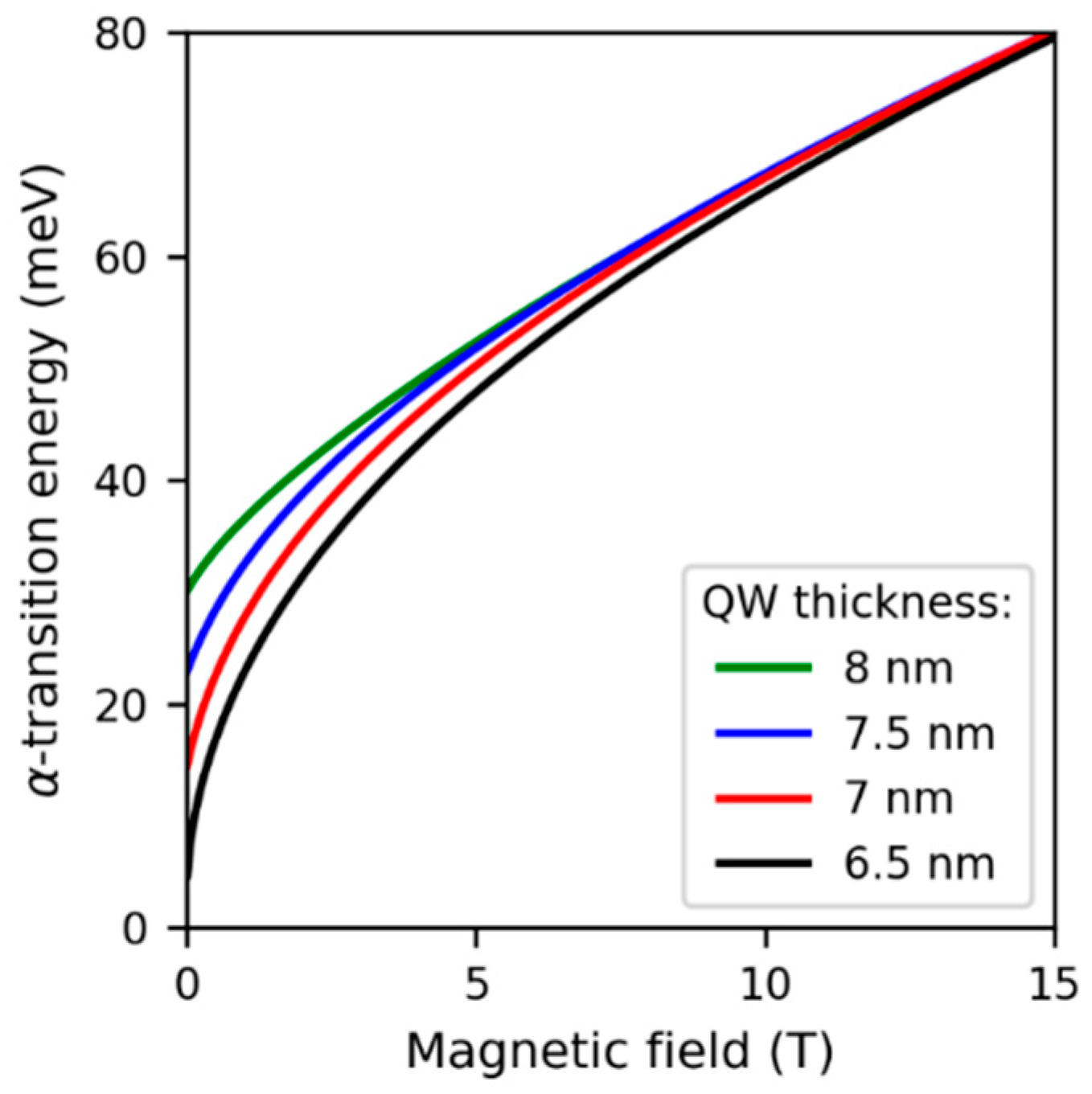
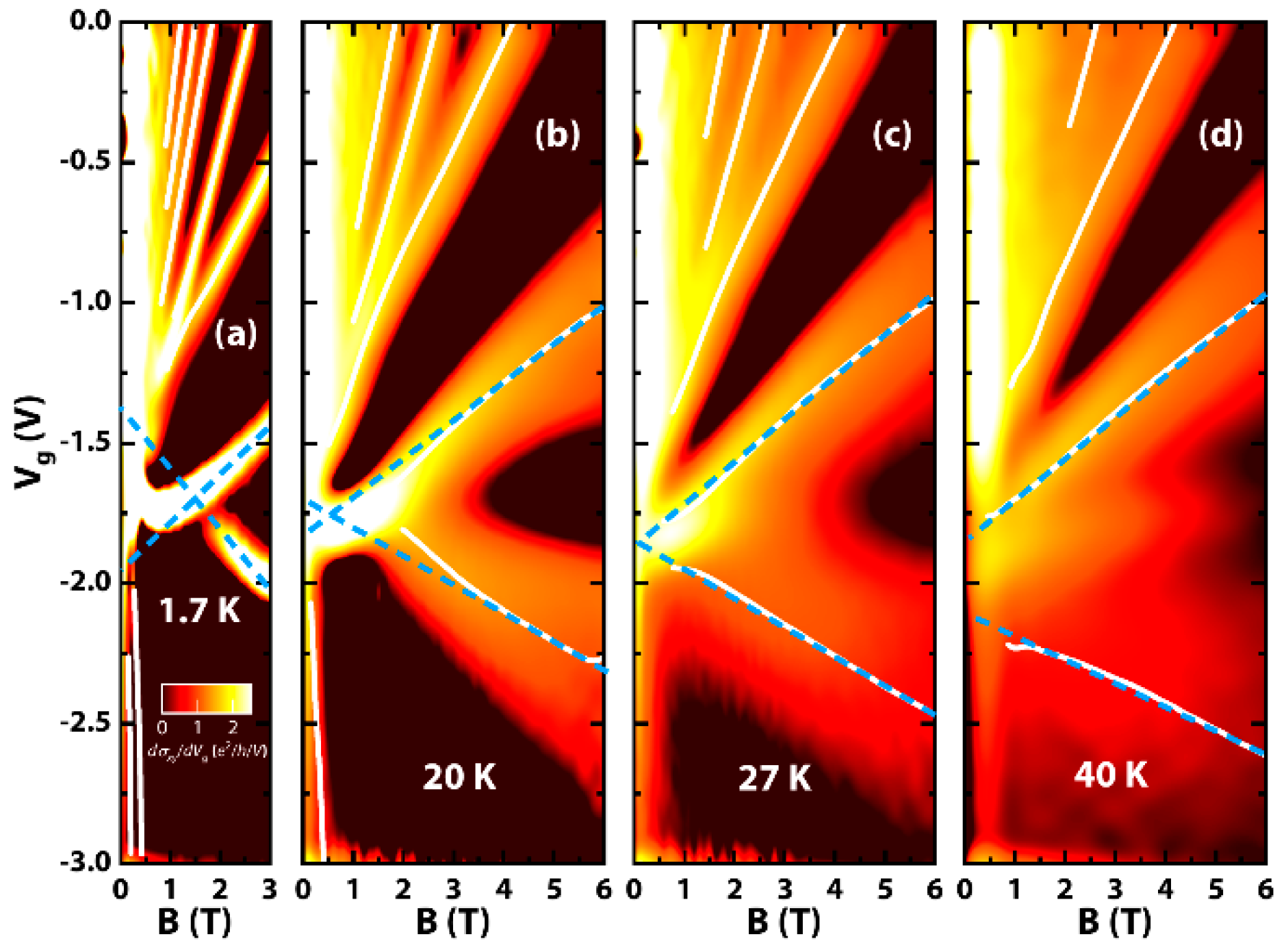
2. Results
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 2006, 314, 1757–1761. [Google Scholar] [CrossRef] [PubMed]
- Konig, M.; Wiedmann, S.; Brune, C.; Roth, A.; Buhmann, H.; Molenkamp, L.W.; Qi, X.-L.; Zhang, S.-C. Quantum spin Hall insulator state in HgTe quantum wells. Science 2007, 318, 766–770. [Google Scholar] [CrossRef] [PubMed]
- Büttner, B.; Liu, C.X.; Tkachov, G.; Novik, E.G.; Brüne, C.; Buhmann, H.; Hankiewicz, E.M.; Recher, P.; Trauzettel, B.; Zhang, S.C.; et al. Single valley Dirac fermions in zero-gap HgTe quantum wells. Nat. Phys. 2011, 7, 418–422. [Google Scholar] [CrossRef]
- Sengupta, P.; Kubis, T.; Tan, Y.; Povolotskyi, M.; Klimeck, G. Design principles for HgTe based topological insulator devices. J. Appl. Phys. 2013, 114, 043702. [Google Scholar] [CrossRef]
- Wiedmann, S.; Jost, A.; Thienel, C.; Brüne, C.; Leubner, P.; Buhmann, H.; Molenkamp, L.W.; Maan, J.C.; Zeitler, U. Temperature-driven transition from a semiconductor to a topological insulator. Phys. Rev. B 2015, 91, 205311. [Google Scholar] [CrossRef]
- Krishtopenko, S.S.; Yahniuk, I.; But, D.B.; Gavrilenko, V.I.; Knap, W.M.; Teppe, F. Pressure- and temperature-driven phase transitions in HgTe quantum wells. Phys. Rev. B 2016, 94, 245402. [Google Scholar] [CrossRef]
- Teppe, F.; Marcinkiewicz, M.; Krishtopenko, S.S.; Ruffenach, S.; Consejo, C.; Kadykov, A.M.; Desrat, W.; But, D.; Knap, W.M.; Ludwig, J.; et al. Temperature-driven massless Kane fermions in HgCdTe crystals. Nat. Commun. 2016, 7, 12576. [Google Scholar] [CrossRef] [PubMed]
- Orlita, M.; Masztalerz, K.; Faugeras, C.; Potemski, M.; Novik, E.G.; Brüne, C.; Buhmann, H.; Molenkamp, L.W. Fine structure of zero-mode Landau levels in HgTe/HgxCd1−xTe quantum wells. Phys. Rev. B 2011, 83, 115307. [Google Scholar] [CrossRef]
- Zholudev, M.S.; Teppe, F.; Orlita, M.; Consejo, C.; Torres, J.; Dyakonova, N.; Czapkiewicz, M.; Wróbel, J.; Grabecki, G.; Mikhailov, N.N.; et al. Magnetospectroscopy of two-dimensional HgTe-based topological insulators around the critical thickness. Phys. Rev. B 2012, 86, 205420. [Google Scholar] [CrossRef]
- Ikonnikov, A.V.; Krishtopenko, S.S.; Drachenko, O.; Goiran, M.; Zholudev, M.S.; Platonov, V.V.; Kudasov, Y.B.; Korshunov, A.S.; Maslov, D.A.; Makarov, I.V.; et al. Temperature-dependent magnetospectroscopy of HgTe quantum wells. Phys. Rev. B 2016, 94, 155421. [Google Scholar] [CrossRef]
- Marcinkiewicz, M.; Ruffenach, S.; Krishtopenko, S.S.; Kadykov, A.M.; Consejo, C.; But, D.B.; Desrat, W.; Knap, W.M.; Torres, J.; Ikonnikov, A.V.; et al. Temperature-driven single-valley Dirac fermions in HgTe quantum wells. Phys. Rev. B 2017, 96, 035405. [Google Scholar] [CrossRef]
- Kadykov, A.M.; Torres, J.; Krishtopenko, S.S.; Consejo, C.; Ruffenach, S.; Marcinkiewicz, M.; But, D.; Knap, W.M.; Morozov, S.V.; Gavrilenko, V.I.; et al. Terahertz imaging of Landau levels in HgTe-based topological insulators. Appl. Phys. Lett. 2016, 108, 262102. [Google Scholar] [CrossRef]
- Kadykov, A.M.; Krishtopenko, S.S.; Jouault, B.; Desrat, W.; Knap, W.M.; Ruffenach, S.; Consejo, C.; Torres, J.; Morozov, S.V.; Mikhailov, N.N.; et al. Temperature-Induced Topological Phase Transition in HgTe Quantum Wells. Phys. Rev. Lett. 2018, 120, 086401. [Google Scholar] [CrossRef] [PubMed]
- Bovkun, L.S.; Ikonnikov, A.V.; Aleshkin, V.Y.; Spirin, K.E.; Gavrilenko, V.I.; Mikhailov, N.N.; Dvoretskii, S.A.; Teppe, F.; Piot, B.A.; Potemski, M.; et al. Landau level spectroscopy of valence bands in HgTe quantum wells: Effects of symmetry lowering. J. Phys. Condens. Matter 2019, 31, 145501. [Google Scholar] [CrossRef]
- Zholudev, M.S.; Teppe, F.; Morozov, S.V.; Orlita, M.; Consejo, C.; Ruffenach, S.; Knap, W.M.; Gavrilenko, V.I.; Dvoretskii, S.A.; Mikhailov, N.N. Anticrossing of Landau levels in HgTe/CdHgTe (013) quantum wells with an inverted band structure. JETP Lett. 2015, 100, 790–794. [Google Scholar] [CrossRef]
- Supplemental Material of [13]. Available online: http://link.aps.org/supplemental/10.1103/PhysRevLett.120.086401 (accessed on 28 January 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zholudev, M.S.; Kadykov, A.M.; Fadeev, M.A.; Marcinkiewicz, M.; Ruffenach, S.; Consejo, C.; Knap, W.; Torres, J.; Morozov, S.V.; Gavrilenko, V.I.; et al. Experimental Observation of Temperature-Driven Topological Phase Transition in HgTe/CdHgTe Quantum Wells. Condens. Matter 2019, 4, 27. https://doi.org/10.3390/condmat4010027
Zholudev MS, Kadykov AM, Fadeev MA, Marcinkiewicz M, Ruffenach S, Consejo C, Knap W, Torres J, Morozov SV, Gavrilenko VI, et al. Experimental Observation of Temperature-Driven Topological Phase Transition in HgTe/CdHgTe Quantum Wells. Condensed Matter. 2019; 4(1):27. https://doi.org/10.3390/condmat4010027
Chicago/Turabian StyleZholudev, Maksim S., Aleksandr M. Kadykov, Mikhail A. Fadeev, Michal Marcinkiewicz, Sandra Ruffenach, Christophe Consejo, Wojciech Knap, Jeremie Torres, Sergey V. Morozov, Vladimir I. Gavrilenko, and et al. 2019. "Experimental Observation of Temperature-Driven Topological Phase Transition in HgTe/CdHgTe Quantum Wells" Condensed Matter 4, no. 1: 27. https://doi.org/10.3390/condmat4010027
APA StyleZholudev, M. S., Kadykov, A. M., Fadeev, M. A., Marcinkiewicz, M., Ruffenach, S., Consejo, C., Knap, W., Torres, J., Morozov, S. V., Gavrilenko, V. I., Mikhailov, N. N., Dvoretskii, S. A., & Teppe, F. (2019). Experimental Observation of Temperature-Driven Topological Phase Transition in HgTe/CdHgTe Quantum Wells. Condensed Matter, 4(1), 27. https://doi.org/10.3390/condmat4010027




