Nematic Superconductivity in Doped Bi2Se3 Topological Superconductors
Abstract
1. Introduction
2. Nematic Superconductivity: Rotational Symmetry Breaking in the Gap Amplitude
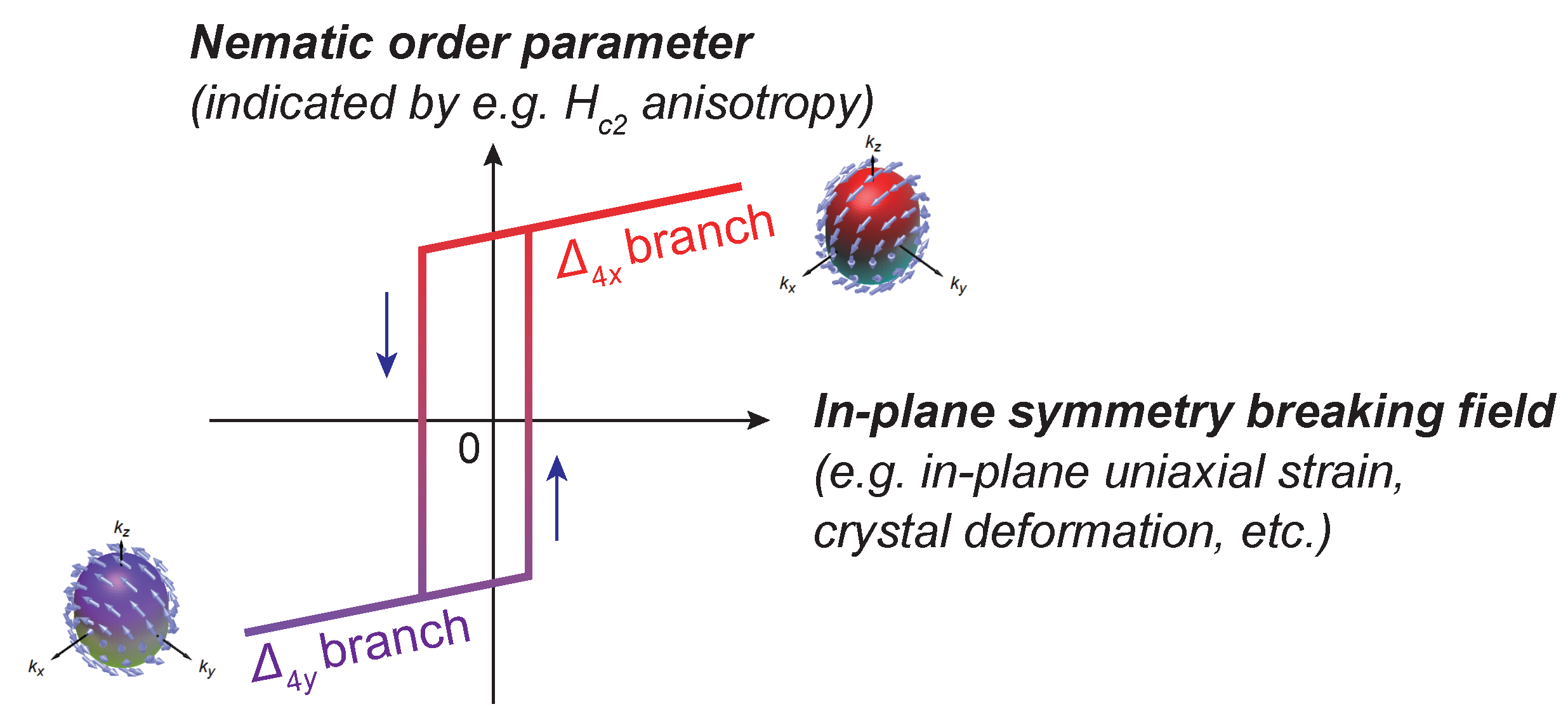
2.1. Symmetry Breaking in Superconductivity
2.2. Gap-Nematic and Spin-Nematic Superconductivity
3. Superconductivity in Doped BiSe
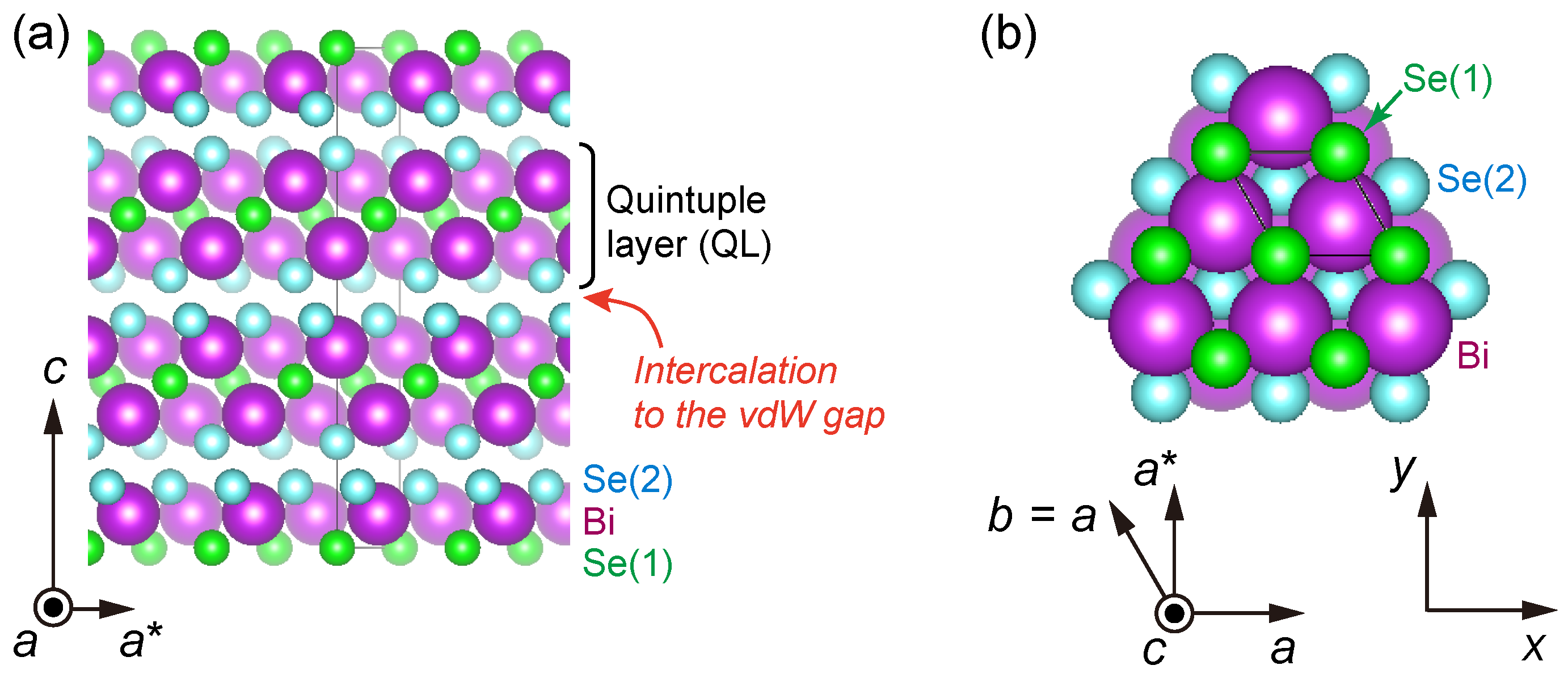
3.1. Crystal Structure of the Mother Compound BiSe
3.2. Basic Properties of Doped BiSe Superconductors
3.3. Possible Superconducting States
3.4. Early Experiments on the Superconducting State in Doped BiSe
4. Recent Experiments on Nematic Superconducting Behavior
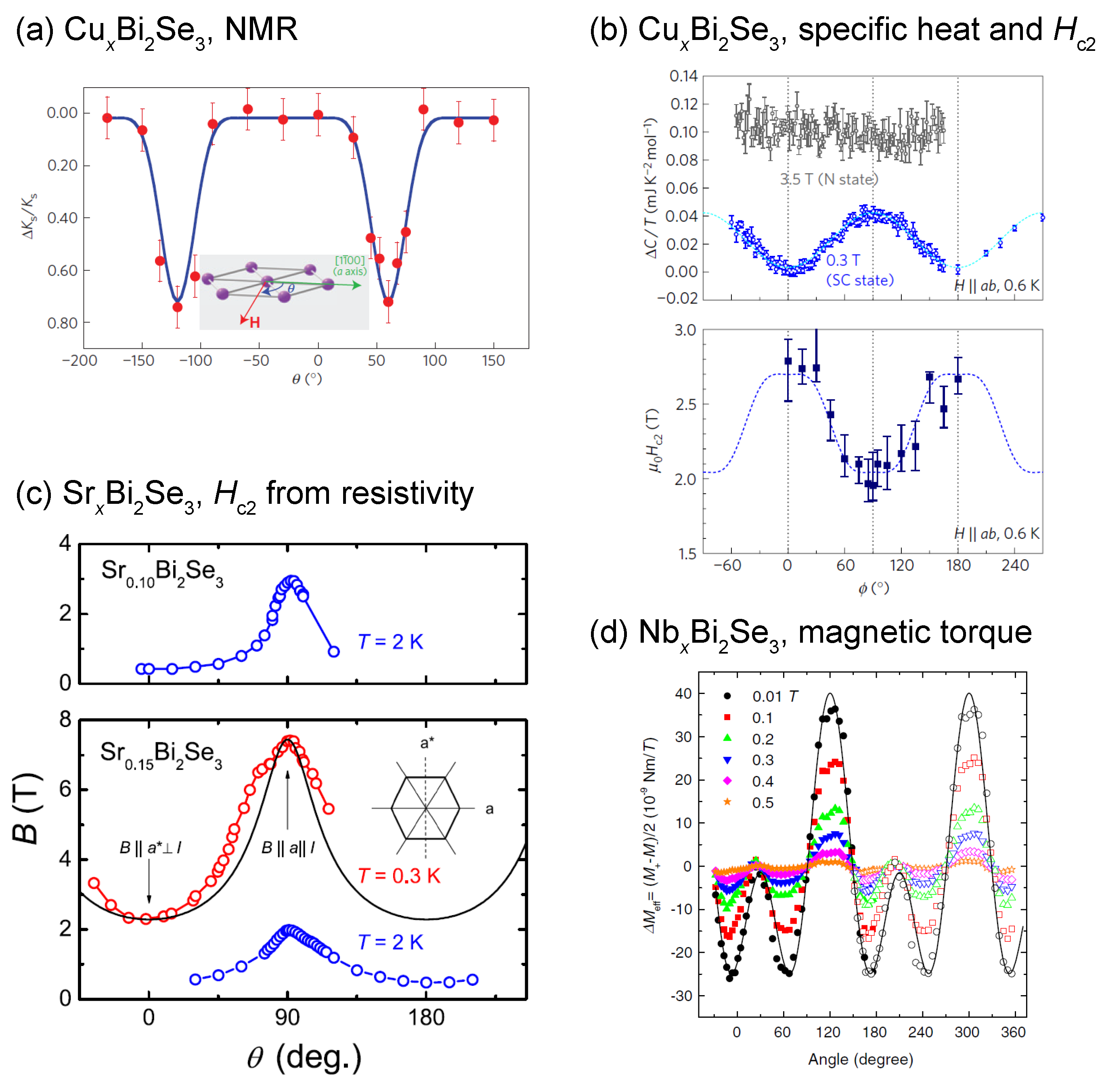
4.1. Beginning of the Story: Nuclear Magnetic Resonance
4.2. Pioneering Reports of Bulk Properties
4.3. Recent Reports
4.4. Direct Visualization
5. Known Issues
5.1. Which of or Is Realized?
5.2. Normal-State and Superconducting-State Nematicities
5.3. Nematic Domains
5.4. Possible Nematic Superconductivity in Other Systems
6. Summary and Perspectives
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AMR | Angular magnetoresistance |
| ARPES | Angle-resolved photoemission spectroscopy |
| BCS | Bardeen–Cooper–Schrieffer |
| BG | Bridgman method |
| BW | Balian–Werthamer |
| ECI | Electrochemical intercalation |
| MBE | Molecular-beam epitaxy |
| MG | Melt growth |
| NMR | Nuclear magnetic resonance |
| QL | Quintuple layer |
| SC | Superconducting |
| STM | Scanning tunneling microscope |
| vdW | van der Waals |
References
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef]
- Ando, Y. Topological Insulator Materials. J. Phys. Soc. Jpn. 2013, 82, 102001. [Google Scholar] [CrossRef]
- Schnyder, A.P.; Brydon, P.M.R. Topological surface states in nodal superconductors. J. Phys. Condens. Matter 2015, 27, 243201. [Google Scholar] [CrossRef] [PubMed]
- Sato, M.; Ando, Y. Topological superconductors: A review. Rep. Prog. Phys. 2017, 80, 076501. [Google Scholar] [CrossRef]
- Wilczek, F. Majorana returns. Nat. Phys. 2009, 5, 614. [Google Scholar] [CrossRef]
- Yonezawa, S. Bulk Topological Superconductors. AAPPS Bull. 2016, 26, 3. [Google Scholar] [CrossRef]
- Matano, K.; Kriener, M.; Segawa, K.; Ando, Y.; Zheng, G.-Q. Spin-rotation symmetry breaking in the superconducting state of CuxBi2Se3. Nat. Phys. 2016, 12, 852. [Google Scholar] [CrossRef]
- Yonezawa, S.; Tajiri, K.; Nakata, S.; Nagai, Y.; Wang, Z.; Segawa, K.; Ando, Y.; Maeno, Y. Thermodynamic evidence for nematic superconductivity in CuxBi2Se3. Nat. Phys. 2017, 13, 123. [Google Scholar] [CrossRef]
- Pan, Y.; Nikitin, A.M.; Araizi, G.K.; Huang, Y.K.; Matsushita, Y.; Naka, T.; de Visser, A. Rotational symmetry breaking in the topological superconductor SrxBi2Se3 probed by upper-critical field experiments. Sci. Rep. 2016, 6, 28632. [Google Scholar] [CrossRef]
- Asaba, T.; Lawson, B.; Tinsman, C.; Chen, L.; Corbae, P.; Li, G.; Qiu, Y.; Hor, Y.; Fu, L.; Li, L. Rotational Symmetry Breaking in a Trigonal Superconductor Nb-doped Bi2Se3. Phys. Rev. X 2017, 7, 011009. [Google Scholar] [CrossRef]
- Fu, L. Odd-parity topological superconductor with nematic order: Application to CuxBi2Se3. Phys. Rev. B 2014, 90, 100509(R). [Google Scholar] [CrossRef]
- Fu, L.; Berg, E. Odd-Parity Topological Superconductors: Theory and Application to CuxBi2Se3. Phys. Rev. Lett. 2010, 105, 097001. [Google Scholar] [CrossRef] [PubMed]
- Ando, Y.; Fu, L. Topological Crystalline Insulators and Topological Superconductors: From Concepts to Materials. Annu. Rev. Condens. Matter Phys. 2015, 6, 361. [Google Scholar] [CrossRef]
- Sasaki, S.; Mizushima, T. Superconducting doped topological materials. Physica C 2015, 514, 206. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- Luke, G.M.; Fudamoto, Y.; Kojima, K.M.; Larkin, M.I.; Merrin, J.; Nachumi, B.; Uemura, Y.J.; Maeno, Y.; Mao, Z.Q.; Mori, Y.; et al. Time-reversal symmetry-breaking superconductivity in Sr2RuO4. Nature 1998, 394, 558. [Google Scholar] [CrossRef]
- Xia, J.; Maeno, Y.; Beyersdorf, P.T.; Fejer, M.M.; Kapitulnik, A. High Resolution Polar Kerr Effect Measurements of Sr2RuO4: Evidence for Broken Time-Reversal Symmetry in the Superconducting State. Phys. Rev. Lett. 2006, 97, 167002. [Google Scholar] [CrossRef] [PubMed]
- Yamashita, T.; Shimoyama, Y.; Haga, Y.; Matsuda, T.D.; Yamamoto, E.; Onuki, Y.; Sumiyoshi, H.; Fujimoto, S.; Levchenko, A.; Shibauchi, T.; et al. Colossal thermomagnetic response in the exotic superconductor URu2Si2. Nat. Phys. 2015, 11, 17. [Google Scholar] [CrossRef]
- Schemm, E.R.; Baumbach, R.E.; Tobash, P.H.; Ronning, F.; Bauer, E.D.; Kapitulnik, A. Evidence for broken time-reversal symmetry in the superconducting phase of URu2Si2. Phys. Rev. B 2015, 91, 140506(R). [Google Scholar] [CrossRef]
- Schemm, E.R.; Gannon, W.J.; Wishne, C.M.; Halperin, W.P.; Kapitulnik, A. Observation of broken time-reversal symmetry in the heavy-fermion superconductor UPt3. Science 2014, 345, 190. [Google Scholar] [CrossRef] [PubMed]
- Anderson, P.W.; Morel, P. Generalized Bardeen-Cooper-Schrieffer States and the Proposed Low-Temperature Phase of Liquid 3He. Phys. Rev. 1961, 123, 1911–1934. [Google Scholar] [CrossRef]
- Balian, R.; Werthamer, N.R. Superconductivity with Pairs in a Relative p Wave. Phys. Rev. 1963, 131, 1553. [Google Scholar] [CrossRef]
- Leggett, A.J. A theoretical description of the new phases of liquid 3He. Rev. Mod. Phys. 1975, 47, 331. [Google Scholar] [CrossRef]
- Mizushima, T.; Tsutsumi, Y.; Kawakami, T.; Sato, M.; Ichioka, M.; Machida, K. Symmetry-Protected Topological Superfluids and Superconductors—From the Basics to 3He. J. Phys. Soc. Jpn. 2016, 85, 022001. [Google Scholar] [CrossRef]
- Mackenzie, A.P.; Maeno, Y. The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing. Rev. Mod. Phys. 2003, 75, 657–712. [Google Scholar] [CrossRef]
- Maeno, Y.; Kittaka, S.; Nomura, T.; Yonezawa, S.; Ishida, K. Evaluation of Spin-Triplet Superconductivity in Sr2RuO4. J. Phys. Soc. Jpn. 2012, 81, 011009. [Google Scholar] [CrossRef]
- Mackenzie, A.P.; Scaffidi, T.; Hicks, C.W.; Maeno, Y. Even odder after twenty-three years: The superconducting order parameter puzzle of Sr2RuO4. npj Quantum Mater. 2017, 2, 40. [Google Scholar] [CrossRef]
- Izawa, K.; Machida, Y.; Itoh, A.; So, Y.; Ota, K.; Haga, Y.; Yamamoto, E.; Kimura, N.; Onuki, Y.; Tsutsumi, Y.; et al. Pairing Symmetry of UPt3 Probed by Thermal Transport Tensors. J. Phys. Soc. Jpn. 2014, 83, 061013. [Google Scholar] [CrossRef]
- Sato, M. Topological odd-parity superconductors. Phys. Rev. B 2010, 81, 220504(R). [Google Scholar] [CrossRef]
- Van Harlingen, D.J. Phase-sensitive tests of the symmetry of the pairing state in the high-temperature superconductors—Evidence for dx2−y2 symmetry. Rev. Mod. Phys. 1995, 67, 515. [Google Scholar] [CrossRef]
- Tsuei, C.C.; Kirtley, J.R. Pairing symmetry in cuprate superconductors. Rev. Mod. Phys. 2000, 72, 969. [Google Scholar] [CrossRef]
- Ando, Y.; Segawa, K.; Komiya, S.; Lavrov, A.N. Electrical Resistivity Anisotropy from Self-Organized One Dimensionality in High-Temperature Superconductors. Phys. Rev. Lett. 2002, 88, 137005. [Google Scholar] [CrossRef] [PubMed]
- Vojta, M. Lattice symmetry breaking in cuprate superconductors: Stripes, nematics, and superconductivity. Adv. Phys. 2009, 58, 699–820. [Google Scholar] [CrossRef]
- Kasahara, S.; Shi, H.J.; Hashimoto, K.; Tonegawa, S.; Mizukami, Y.; Shibauchi, T.; Sugimoto, K.; Fukuda, T.; Terashima, T.; Nevidomskyy, A.H.; et al. Electronic nematicity above the structural and superconducting transition in BaFe2(As1−xPx)2. Nature 2012, 486, 382. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, R.M.; Chubukov, A.V.; Schmalian, J. What drives nematic order in iron-based superconductors? Nat. Phys. 2014, 10, 97. [Google Scholar] [CrossRef]
- Borzi, R.A.; Grigera, S.A.; Farrell, J.; Perry, R.S.; Lister, S.J.S.; Lee, S.L.; Tennant, D.A.; Maeno, Y.; Mackenzie, A.P. Formation of a Nematic Fluid at High Fields in Sr3Ru2O7. Science 2007, 315, 214. [Google Scholar] [CrossRef] [PubMed]
- Murakawa, H.; Ishida, K.; Kitagawa, K.; Mao, Z.Q.; Maeno, Y. Measurement of the 101Ru-Knight Shift of Superconducting Sr2RuO4 in a Parallel Magnetic Field. Phys. Rev. Lett. 2004, 93, 167004. [Google Scholar] [CrossRef] [PubMed]
- Tou, H.; Kitaoka, Y.; Ishida, K.; Asayama, K.; Kimura, N.; Ōnuki, Y.; Yamamoto, E.; Haga, Y.; Maezawa, K. Nonunitary Spin-Triplet Superconductivity in UPt3: Evidence from 195Pt Knight Shift Study. Phys. Rev. Lett. 1998, 80, 3129. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, C.X.; Qi, X.L.; Dai, X.; Fang, Z.; Zhang, S.C. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 438. [Google Scholar] [CrossRef]
- Xia, Y.; Qian, D.; Hsieh, D.; Wray, L.; Pal, A.; Lin, H.; Bansil, A.; Grauer, D.; Hor, Y.S.; Cava, R.J.; et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 398. [Google Scholar] [CrossRef]
- Nakajima, S. The crystal structure of Bi2Te3−xSex. J. Phys. Chem. Solids 1963, 24, 479. [Google Scholar] [CrossRef]
- Li, Z.; Wang, M.; Zhang, D.; Feng, N.; Jiang, W.; Han, C.; Chen, W.; Ye, M.; Gao, C.; Jia, J.; et al. Possible structural origin of superconductivity in Sr-doped Bi2Se3. Phys. Rev. Materials 2018, 2, 014201. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272. [Google Scholar] [CrossRef]
- Hor, Y.S.; Williams, A.J.; Checkelsky, J.G.; Roushan, P.; Seo, J.; Xu, Q.; Zandbergen, H.W.; Yazdani, A.; Ong, N.P.; Cava, R.J. Superconductivity in CuxBi2Se3 and its Implications for Pairing in the Undoped Topological Insulator. Phys. Rev. Lett. 2010, 104, 057001. [Google Scholar] [CrossRef] [PubMed]
- Kriener, M.; Segawa, K.; Ren, Z.; Sasaki, S.; Ando, Y. Bulk Superconducting Phase with a Full Energy Gap in the Doped Topological Insulator CuxBi2Se3. Phys. Rev. Lett. 2011, 106, 127004. [Google Scholar] [CrossRef]
- Kriener, M.; Segawa, K.; Ren, Z.; Sasaki, S.; Wada, S.; Kuwabata, S.; Ando, Y. Electrochemical synthesis and superconducting phase diagram of CuxBi2Se3. Phys. Rev. B 2011, 84, 054513. [Google Scholar] [CrossRef]
- Liu, Z.; Yao, X.; Shao, J.; Zuo, M.; Pi, L.; Tan, S.; Zhang, C.; Zhang, Y. Superconductivity with Topological Surface State in SrxBi2Se3. J. Am. Chem. Soc. 2015, 137, 10512. [Google Scholar] [CrossRef]
- Shruti; Maurya, V.K.; Neha, P.; Srivastava, P.; Patnaik, S. Superconductivity by Sr intercalation in the layered topological insulator Bi2Se3. Phys. Rev. B 2015, 92, 020506(R). [Google Scholar] [CrossRef]
- Qiu, Y.; Sanders, K.N.; Dai, J.; Medvedeva, J.E.; Wu, W.; Ghaemi, P.; Vojta, T.; Hor, Y.S. Time reversal symmetry breaking superconductivity in topological materials. arXiv, 2015; arXiv:1512.03519. [Google Scholar]
- Lahoud, E.; Maniv, E.; Petrushevsky, M.S.; Naamneh, M.; Ribak, A.; Wiedmann, S.; Petaccia, L.; Salman, Z.; Chashka, K.B.; Dagan, Y.; et al. Evolution of the Fermi surface of a doped topological insulator with carrier concentration. Phys. Rev. B 2013, 88, 195107. [Google Scholar] [CrossRef]
- Lawson, B.J.; Corbae, P.; Li, G.; Yu, F.; Asaba, T.; Tinsman, C.; Qiu, Y.; Medvedeva, J.E.; Hor, Y.S.; Li, L. Multiple Fermi surfaces in superconducting Nb-doped Bi2Se3. Phys. Rev. B 2016, 94, 041114. [Google Scholar] [CrossRef]
- Shen, J.; He, W.Y.; Yuan, N.F.Q.; Huang, Z.; Cho, C.-W.; Lee, S.H.; Hor, Y.S.; Law, K.T.; Lortz, R. Nematic topological superconducting phase in Nb-doped Bi2Se3. npj Quantum Mater. 2017, 2, 59. [Google Scholar] [CrossRef]
- Kriener, M.; (Center for Emergent Matter Science (CEMS), Riken, Wako-shi, Saitama, Japan). Private communication, 2018.
- Du, G.; Shao, J.; Yang, X.; Du, Z.; Fang, D.; Wang, J.; Ran, K.; Wen, J.; Zhang, C.; Yang, H.; et al. Drive the Dirac electrons into Cooper pairs in SrxBi2Se3. Nat. Commun. 2017, 8, 14466. [Google Scholar] [CrossRef]
- Hashimoto, T.; Yada, K.; Yamakage, A.; Sato, M.; Tanaka, Y. Bulk Electronic State of Superconducting Topological Insulator. J. Phys. Soc. Jpn. 2013, 82, 044704. [Google Scholar] [CrossRef]
- Hashimoto, T.; Yada, K.; Yamakage, A.; Sato, M.; Tanaka, Y. Effect of Fermi surface evolution on superconducting gap in superconducting topological insulator. Supercond. Sci. Technol. 2014, 27, 104002. [Google Scholar] [CrossRef]
- Sun, Y.; Maki, K. Impurity effects in d-wave superconductors. Phys. Rev. B 1995, 51, 6059. [Google Scholar] [CrossRef]
- Mackenzie, A.P.; Haselwimmer, R.K.W.; Tyler, A.W.; Lonzarich, G.G.; Mori, Y.; Nishizaki, S.; Maeno, Y. Extremely Strong Dependence of Superconductivity on Disorder in Sr2RuO4. Phys. Rev. Lett. 1998, 80, 161. [Google Scholar] [CrossRef]
- Joo, N.; Auban-Senzier, P.; Pasquier, C.R.; Monod, P.; Jérome, D.; Bechgaard, K. Suppression of superconductivity by non-magnetic disorder in the organic superconductor (TMTSF)2(ClO4)(1−x)(ReO4)x. Eur. Phys. J. B 2004, 40, 43. [Google Scholar] [CrossRef]
- Yonezawa, S.; Marrache-Kikuchi, C.A.; Bechgaard, K.; Jérome, D. Crossover from impurity-controlled to granular superconductivity in (TMTSF)2ClO4. Phys. Rev. B 2018, 97, 014521. [Google Scholar] [CrossRef]
- Michaeli, K.; Fu, L. Spin-Orbit Locking as a Protection Mechanism of the Odd-Parity Superconducting State against Disorder. Phys. Rev. Lett. 2012, 109, 187003. [Google Scholar] [CrossRef]
- Nagai, Y. Robust superconductivity with nodes in the superconducting topological insulator CuxBi2Se3: Zeeman orbital field and nonmagnetic impurities. Phys. Rev. B 2015, 91, 060502(R). [Google Scholar] [CrossRef]
- Kriener, M.; Segawa, K.; Sasaki, S.; Ando, Y. Anomalous suppression of the superfluid density in the CuxBi2Se3 superconductor upon progressive Cu intercalation. Phys. Rev. B 2012, 86, 180505. [Google Scholar] [CrossRef]
- Bay, T.; Naka, T.; Huang, Y.K.; Luigjes, H.; Golden, M.S.; de Visser, A. Superconductivity in the Doped Topological Insulator CuxBi2Se3 under High Pressure. Phys. Rev. Lett. 2012, 108, 057001. [Google Scholar] [CrossRef]
- Kita, T.; Arai, M. Ab initio calculations of Hc2 in type-II superconductors: Basic formalism and model calculations. Phys. Rev. B 2004, 70, 224522. [Google Scholar] [CrossRef]
- Sasaki, S.; Kriener, M.; Segawa, K.; Yada, K.; Tanaka, Y.; Sato, M.; Ando, Y. Topological Superconductivity in CuxBi2Se3. Phys. Rev. Lett. 2011, 107, 217001. [Google Scholar] [CrossRef]
- Yamakage, A.; Yada, K.; Sato, M.; Tanaka, Y. Theory of tunneling conductance and surface-state transition in superconducting topological insulators. Phys. Rev. B 2012, 85, 180509(R). [Google Scholar] [CrossRef]
- Mizushima, T.; Yamakage, A.; Sato, M.; Tanaka, Y. Dirac-fermion-induced parity mixing in superconducting topological insulators. Phys. Rev. B 2014, 90, 184516. [Google Scholar] [CrossRef]
- Tao, R.; Yan, Y.J.; Liu, X.; Wang, Z.W.; Ando, Y.; Wang, Q.H.; Zhang, T.; Feng, D.L. Direct Visualization of the Nematic Superconductivity in CuxBi2Se3. Phys. Rev. X 2018, 8, 041024. [Google Scholar] [CrossRef]
- Nikitin, A.M.; Pan, Y.; Huang, Y.K.; Naka, T.; de Visser, A. High-pressure study of the basal-plane anisotropy of the upper critical field of the topological superconductor SrxBi2Se3. Phys. Rev. B 2016, 94, 144516. [Google Scholar] [CrossRef]
- Du, G.; Li, Y.; Schneeloch, J.; Zhong, R.D.; Gu, G.; Yang, H.; Lin, H.; Wen, H.H. Superconductivity with two-fold symmetry in topological superconductor SrxBi2Se3. Sci. China Phys. Mech. Astron. 2017, 60, 037411. [Google Scholar] [CrossRef]
- Smylie, M.P.; Willa, K.; Claus, H.; Koshelev, A.E.; Song, K.W.; Kwok, W.K.; Islam, Z.; Gu, G.D.; Schneeloch, J.A.; Zhong, R.D.; et al. Superconducting and normal-state anisotropy of the doped topological insulator Sr0.1Bi2Se3. Sci. Rep. 2018, 8, 7666. [Google Scholar] [CrossRef] [PubMed]
- Kuntsevich, A.; Bryzgalov, M.A.; Prudkoglyad, V.A.; Martovitskii, V.P.; Selivanov, Y.G.; Chizhevskii, E.G. Structural distortion behind the nematic superconductivity in SrxBi2Se3. New J. Phys. 2018, 20, 103022. [Google Scholar] [CrossRef]
- Willa, K.; Willa, R.; Song, K.W.; Gu, G.D.; Schneeloch, J.A.; Zhong, R.; Koshelev, A.E.; Kwok, W.K.; Welp, U. Nanocalorimetric evidence for nematic superconductivity in the doped topological insulator Sr0.1Bi2Se3. Phys. Rev. B 2018, 98, 184509. [Google Scholar] [CrossRef]
- Andersen, L.; Wang, Z.; Lorenz, T.; Ando, Y. Nematic Superconductivity in Cu1.5(PbSe)5(Bi2Se3)6. arXiv, 2018; arXiv:1811.00805. [Google Scholar]
- Chen, M.; Chen, X.; Yang, H.; Du, Z.; Wen, H.H. Superconductivity with twofold symmetry in Bi2Te3/FeTe0.55Se0.45 heterostructures. Sci. Adv. 2018, 4. [Google Scholar] [CrossRef] [PubMed]
- Tou, H.; Kitaoka, Y.; Asayama, K.; Kimura, N.; Ōnuki, Y.; Yamamoto, E.; Maezawa, K. Odd-Parity Superconductivity with Parallel Spin Pairing in UPt3: Evidence from 195Pt Knight Shift Study. Phys. Rev. Lett. 1996, 77, 1374. [Google Scholar] [CrossRef] [PubMed]
- Ishida, K.; Mukuda, H.; Kitaoka, Y.; Asayama, K.; Mao, Z.Q.; Mori, Y.; Maeno, Y. Spin-triplet superconductivity in Sr2RuO4 identified by 17O Knight shift. Nature 1998, 396, 658. [Google Scholar] [CrossRef]
- Tien, C.; Jiang, I.M. Magnetic resonance of heavy-fermion superconductors and high-Tc superconductors. Phys. Rev. B 1989, 40, 229. [Google Scholar] [CrossRef]
- Shinagawa, J.; Kurosaki, Y.; Zhang, F.; Parker, C.; Brown, S.E.; Jérome, D.; Bechgaard, K.; Christensen, J.B. Superconducting State of the Organic Conductor (TMTSF)2ClO4. Phys. Rev. Lett. 2007, 98, 147002. [Google Scholar] [CrossRef]
- Nagai, Y.; Nakamura, H.; Machida, M. Rotational isotropy breaking as proof for spin-polarized Cooper pairs in the topological superconductor CuxBi2Se3. Phys. Rev. B 2012, 86, 094507. [Google Scholar] [CrossRef]
- Sullivan, P.F.; Seidel, G. Steady-State, ac-Temperature Calorimetry. Phys. Rev. 1968, 173, 679. [Google Scholar] [CrossRef]
- Deguchi, K.; Ishiguro, T.; Maeno, Y. Field-orientation dependent heat capacity measurements at low temperatures with a vector magnet system. Rev. Sci. Instrum. 2004, 75, 1188. [Google Scholar] [CrossRef]
- Smylie, M.P.; Willa, K.; Claus, H.; Snezhko, A.; Martin, I.; Kwok, W.K.; Qiu, Y.; Hor, Y.S.; Bokari, E.; Niraula, P.; et al. Robust odd-parity superconductivity in the doped topological insulator NbxBi2Se3. Phys. Rev. B 2017, 96, 115145. [Google Scholar] [CrossRef]
- Sasaki, S.; Segawa, K.; Ando, Y. Superconductor derived from a topological insulator heterostructure. Phys. Rev. B 2014, 90, 220504(R). [Google Scholar] [CrossRef]
- Nakayama, K.; Kimizuka, H.; Tanaka, Y.; Sato, T.; Souma, S.; Takahashi, T.; Sasaki, S.; Segawa, K.; Ando, Y. Observation of two-dimensional bulk electronic states in the superconducting topological insulator heterostructure Cux(PbSe)5(Bi2Se3)6: Implications for unconventional superconductivity. Phys. Rev. B 2015, 92, 100508(R). [Google Scholar] [CrossRef]
- Venderbos, J.W.F.; Kozii, V.; Fu, L. Identification of nematic superconductivity from the upper critical field. Phys. Rev. B 2016, 94, 094522. [Google Scholar] [CrossRef]
- Venderbos, J.W.F.; Kozii, V.; Fu, L. Odd-parity superconductors with two-component order parameters: Nematic and chiral, full gap, and Majorana node. Phys. Rev. B 2016, 94, 180504. [Google Scholar] [CrossRef]
- Walko, D.A.; Hong, J.I.; Rao, T.V.C.; Wawrzak, Z.; Seidman, D.N.; Halperin, W.P.; Bedzyk, M.J. Crystal structure assignment for the heavy-fermion superconductor UPt3. Phys. Rev. B 2001, 63, 054522. [Google Scholar] [CrossRef]
- Aeppli, G.; Bucher, E.; Broholm, C.; Kjems, J.K.; Baumann, J.; Hufnagl, J. Magnetic order and fluctuations in superconducting UPt3. Phys. Rev. Lett. 1988, 60, 615. [Google Scholar] [CrossRef]
- Machida, Y.; Itoh, A.; So, Y.; Izawa, K.; Haga, Y.; Yamamoto, E.; Kimura, N.; Onuki, Y.; Tsutsumi, Y.; Machida, K. Twofold Spontaneous Symmetry Breaking in the Heavy-Fermion Superconductor UPt3. Phys. Rev. Lett. 2012, 108, 157002. [Google Scholar] [CrossRef]
- Izawa, K.; Nakajima, Y.; Goryo, J.; Matsuda, Y.; Osaki, S.; Sugawara, H.; Sato, H.; Thalmeier, P.; Maki, K. Multiple Superconducting Phases in New Heavy Fermion Superconductor PrOs4Sb12. Phys. Rev. Lett. 2003, 90, 117001. [Google Scholar] [CrossRef]
- Sakakibara, T.; Yamada, A.; Custers, J.; Yano, K.; Tayama, T.; Aoki, H.; Machida, K. Nodal Structures of Heavy Fermion Superconductors Probed by the Specific-Heat Measurements in Magnetic Fields. J. Phys. Soc. Jpn. 2007, 76, 051004. [Google Scholar] [CrossRef]
- Kittaka, S.; An, K.; Sakakibara, T.; Haga, Y.; Yamamoto, E.; Kimura, N.; Ōnuki, Y.; Machida, K. Anomalous Field-Angle Dependence of the Specific Heat of Heavy-Fermion Superconductor UPt3. J. Phys. Soc. Jpn. 2013, 82, 024707. [Google Scholar] [CrossRef]
- Machida, K. Spin Triplet Nematic Pairing Symmetry and Superconducting Double Transition in U1−xThxBe13. J. Phys. Soc. Jpn. 2018, 87, 033703. [Google Scholar] [CrossRef]
- Roy, B.; Ghorashi, S.A.A.; Foster, M.S.; Nevidomskyy, A.H. Topological superconductivity of spin-3/2 carriers in a three-dimensional doped Luttinger semimetal. arXiv, 2017; arXiv:1708.07825. [Google Scholar]
- Venderbos, J.W.F.; Savary, L.; Ruhman, J.; Lee, P.A.; Fu, L. Pairing States of Spin-3/2 Fermions: Symmetry-Enforced Topological Gap Functions. Phys. Rev. X 2018, 8, 011029. [Google Scholar] [CrossRef]
- Agterberg, D.F. Vortex Lattice Structures of Sr2RuO4. Phys. Rev. Lett. 1998, 80, 5184. [Google Scholar] [CrossRef]
- Yonezawa, S.; Kajikawa, T.; Maeno, Y. First-Order Superconducting Transition of Sr2RuO4. Phys. Rev. Lett. 2013, 110, 077003. [Google Scholar] [CrossRef]
- Yonezawa, S.; Kajikawa, T.; Maeno, Y. Specific-Heat Evidence of the First-Order Superconducting Transition in Sr2RuO4. J. Phys. Soc. Jpn. 2014, 83, 083706. [Google Scholar] [CrossRef]
- Hicks, C.W.; Brodsky, D.O.; Yelland, E.A.; Gibbs, A.S.; Bruin, J.A.N.; Barber, M.E.; Edkins, S.D.; Nishimura, K.; Yonezawa, S.; Maeno, Y.; et al. Strong Increase of Tc of Sr2RuO4 Under Both Tensile and Compressive Strain. Science 2014, 344, 283. [Google Scholar] [CrossRef]
- Steppke, A.; Zhao, L.; Barber, M.E.; Scaffidi, T.; Jerzembeck, F.; Rosner, H.; Gibbs, A.S.; Maeno, Y.; Simon, S.H.; et al. Strong peak in Tc of Sr2RuO4 under uniaxial pressure. Science 2017, 355, eaaf9398. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Yao, H. Possible Three-Dimensional Nematic Odd-Parity Superconductivity in Sr2RuO4. Phys. Rev. Lett. 2018, 121, 157002. [Google Scholar] [CrossRef]
- Hecker, M.; Schmalian, J. Vestigial nematic order and superconductivity in the doped topological insulator CuxBi2Se3. npj Quantum Mater. 2018, 3, 26. [Google Scholar] [CrossRef]
- Uematsu, H.; Mizushima, T.; Tsuruta, A.; Fujimoto, S.; Sauls, J.A. Chiral Higgs Mode in Nematic Superconductors. arXiv, 2018; arXiv:1809.06989. [Google Scholar]
- Nagai, Y.; Nakamura, H.; Machida, M. Spin-Polarized Majorana Bound States inside a Vortex Core in Topological Superconductors. J. Phys. Soc. Jpn. 2014, 83, 064703. [Google Scholar] [CrossRef]
- Zyuzin, A.A.; Garaud, J.; Babaev, E. Nematic Skyrmions in Odd-Parity Superconductors. Phys. Rev. Lett. 2017, 119, 167001. [Google Scholar] [CrossRef] [PubMed]

| Irreducible representation | ||||||
| Pairing potential | ||||||
| -vector | - | - | ||||
| Parity | even | even | odd | odd | odd | |
| Topo.SC | no | no | yes | yes | yes | |
| Nematic SC | no | no | no | no | yes | |
Schematic -vector/gap structures  |  | 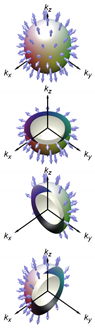 | 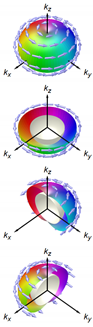 | 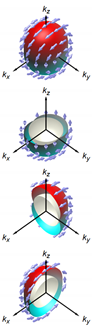 | 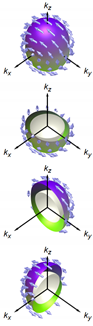 | |
| Material | Reference | Growth Method | Doping Level x | Probe | Large | Suggested State |
|---|---|---|---|---|---|---|
| CuBiSe | Matano 2016 [8] | MG + ECI | 0.29–0.31 | NMR | y | |
| Yonezawa 2017 [9] | MG + ECI | 0.3 | C | x | ||
| Tao 2018 [70] | MG + ECI | 0.31 | STM | - | ||
| SrBiSe | Pan 2016 [10] | MG | 0.10, 0.15 | x | ||
| Nikitin 2016 [71] | MG | 0.15 | in P | x | ||
| Du 2017 [72] | MG | NA | x (#1, #2) | |||
| y (#3) | ||||||
| Smylie 2018 [73] | MG | 0.1 | , M | x | ||
| Kuntsevich 2018 [74] | BG | 0.10–0.20 | x (some) | |||
| y (others) | ||||||
| Willa 2018 [75] | MG | 0.1 | C | y | ||
| NbBiSe | Asaba 2017 [11] | MG | NA | torque | - | |
| Shen 2017 [53] | MG | 0.25 | , M | y | ||
| Cu(PbSe)(BiSe) | Andersen 2018 [76] | BG + ECI | 1.5 | , , C | x | |
| BiTe/Fe(Se, Te) | Chen 2018 [77] | MBE | - | STM | - |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yonezawa, S. Nematic Superconductivity in Doped Bi2Se3 Topological Superconductors. Condens. Matter 2019, 4, 2. https://doi.org/10.3390/condmat4010002
Yonezawa S. Nematic Superconductivity in Doped Bi2Se3 Topological Superconductors. Condensed Matter. 2019; 4(1):2. https://doi.org/10.3390/condmat4010002
Chicago/Turabian StyleYonezawa, Shingo. 2019. "Nematic Superconductivity in Doped Bi2Se3 Topological Superconductors" Condensed Matter 4, no. 1: 2. https://doi.org/10.3390/condmat4010002
APA StyleYonezawa, S. (2019). Nematic Superconductivity in Doped Bi2Se3 Topological Superconductors. Condensed Matter, 4(1), 2. https://doi.org/10.3390/condmat4010002





