Abstract
This paper presents a computational study of non-stoichiometric nickel oxide in a 64-cell NiO system to model and validate localized heating effects due to nanosecond laser irradiation. Variation in the Bandgap of NiO is studied as a function of varying concentrations of native defects, ranging from 0 to 25%. It is observed that there is a slight increase in the bandgap from 3.80 eV for stoichiometric NiO to 3.86 eV for Ni-rich NiO and to 3.95 eV for O-rich NiO. It is hence deduced that the experimental laser irradiation leads to simultaneous reduction of Ni2+ ions and the oxidation of NiO as the number of laser pulses increase. As well, a detailed study on the effects of doping nickel family elements, i.e., palladium (Pd) and platinum (Pt), in stoichiometric NiO is presented. A bandgap decrease from 3.8 eV for pure NiO to 2.5 eV for Pd-doping and 2.0 eV for Pt-doping for varying doping concentrations ranging from 0–25% Pd, Pt, respectively, is observed.
1. Introduction
Transition metal oxides (TMOs) establish an important section of semiconducting materials which exhibit a variety of electronic and magnetic properties that depend on the nature of their respective outer d-shell configurations [1]. Point defects in TM oxides, such as vacancies and interstitials, play a crucial role in determining the behavior of such oxides. Nickel Oxide (NiO) is one such challenging transition metal oxide (TMO) that has been studied rigorously to establish an accurate theoretical analysis of its electronic structure [2,3,4,5,6,7,8]. NiO was first recognized as a Mott insulator in [2], where, until then, the perceptions of transition metal oxides were as conductors (according to band theory). It was initially suggested that band structures of such semiconductors with incomplete d-bands cannot be explained in terms of potential barriers, instead, adding or removing of metal d-electrons could lead to the formation of discrete energy bands. Hence, the electrostatic interaction as well as the role of electron correlation was thoroughly discussed. In [3], the many-body effects in NiO measured by O-k edge XANES spectrum revealed the first experimental evidence that NiO was not a Mott type insulator with Hubbard gap U with a correlation gap between the initial state {E [Ni(3d8)] + E[Ni(3d8)]} and the final state {E [Ni(3d7)] + E[Ni(3d9)]}, but it was a charge transfer insulator with a correlation gap between the initial state{E [Ni(3d8)] + E[Ni(3d8)]} and the final state {E [Ni(3d8 O(2p5)] + E[Ni(3d9)]} where the configuration [Ni(3d8 O(2p5)] is called 3d8L where L is the ligand hole. This experimental evidence was strongly supported by researchers in [4], when defects in stoichiometric NiO were evaluated by observing the charge-transfer gap (i.e., observing changes in the relative configuration weight in O k-XANES).
Density functionaltheory (DFT) study on undoped NiO was first reported in detail in [1], wherein the electron correlations in the 3d shell of metal ions in nickel oxide were computed using a combination of local spin density approximation (LSDA) and unrestricted Hartree-Fock approximation (U) techniques. This method was fit to calculate the total energy of crystalline nickel oxide and validate the obtained results by measuring the electron energy loss spectra. The local-density approximation (LDA) plus Hubbard model was implemented in [5] to compute the insulating antiferromagnetic ground state of NiO and its optical properties. It is observed that charge transfer was a result of the enhancement of O 2p character at the top of the valence state rather than Ni d-d LSDA-type band gap. In [6], an ab initio study of NiO at the Pd (100) surface was studied and observed that a Ni3O4 phase existed with rhombic distribution of Ni vacancies. A preferential formation due to surface reaction of O and NiO was shown to be thermodynamically possible along with some peculiar aspects resulting from a strong bond formation between Ni and O and Pd and O simultaneously. In [7], the magnetism of uniform porous NiO showed a distorted structure with an ordering temperature of 3K, and a paramagnetic ordering temperature of 13K. NiO clusters of less than 1nm in size displayed ferromagnetic interactions. The stability and magnetism that are associated with vacancy in NiO are studied using GGA+U in [8]. The role of oxygen vacancies and mechanism of oxide reduction were dealt with in [9] and the electronic structure of oxygen and nickel vacancies at the surface of NiO (100) were investigated in [10] using hybrid DFT calculations. General gradient approximation (GGA) technique was used to study the defect formation energies under different conditions and inducted magnetism by vacancies in [8]. The results indicated that the dominant defect is Ni vacancy under oxygen-rich condition and the most suitable oxidation state varies with varying Fermi level.
The stoichiometric NiO is a Mott insulator with conductivity of 10−13 S/cm, while non-stoichiometric NiOx is a wide-band-gap p-type semiconductor. The p-type conductivity of NiOx originates from two positive charge compensation, which favors Ni2+ vacancies [11]. Several methods have been used for growing NiO films, including sputtering [12,13,14,15], e-beam evaporation [16,17], chemical and plasma-enhanced chemical vapor methods [18,19,20], pulsed laser deposition [21], and spray pyrolysis [22,23]. Among the above-mentioned techniques, sputtering is one of the preferred due to its industrial scalability, even though the composition of sputtered films varies slightly to significantly from equilibrium [24,25]. Lattice defects are not well-defined in NiO films with high oxygen content [26,27]. From [28,29], it is observed that high energy laser irradiation causes a change in the chemical composition as well as the electrical properties of NiO, but a thorough computational analysis has not been presented to date. Because of its peculiar mechanism, nickel vacancy and/or interstitial oxygen are commonly used to describe the electrical properties of NiO films. To facilitate this study, density functional theory offers the right platform for defect analysis in terms of minimal errors, full convergence, and k-point integration.
Recent studies indicate an enormous work in doped NiO to enhance room temperature ferromagnetism for multiferroic devices [30], supercapacitor applications [31], and resistive switching [32]. Dopants, such Cu [32] and Li [33] enhance the p-type conductivity of NiO films and have been studied extensively, both theoretically and experimentally. Doping NiO with metals in the nickel family, i.e., Palladium (Pd) and Platinum (Pt), have gained attention, owing to their Electrochromic, supercapacitor, and gas-sensing applications and studied extensively experimentally [34,35,36,37,38,39,40], but no theoretical analysis has been investigated in knowing the vacancy and interstitial behavior in doped NiO. In this paper, we also study the effect of doping Pd and Pton the bandgap of NiO by varying doping concentrations from 0 to 25% in a 32 atom NiO.
2. Computational Method
All of the computations are performed based on the generalized gradient (GGA) and local density approximations (LDA) to DFT using the Vienna ab initio simulation package (VASP) [41,42,43]. 4 k-points in the irreducible part of the Brilliouin zone is a result of test of convergence in the 32-atom primitive cell. The single particle wave functions are expanded in a plane-wave basis using a 420 eV energy cutoff for LDA and 460 eV for GGA. Full relaxation of ions is performed for undoped NiO to find the minimum energy of each configuration. The absolute minimum in total energy was obtained by varying the lattice constant.
The density of states (DOS) calculations were performed using Methfessel-Paxton scheme for the energy [44]. Computations of dopants (Pd, Pt) were performed by substituting Ni positions in the 64 cell NiO with varying doping concentrations ranging from 0–25%. Similarly, native defects (Ni, O) were introduced at interstitial sites in the 64 cell NiO with varying concentrations from 0–25%, i.e., introducing 0 to 8 Ni or O interstitials, respectively.
3. Results and Discussion
Pure nickel oxide belongs to the space group Fm-3m with the space number 225. The primitive cell of NiO consists of a Ni16O16 unit of 32 atoms in a rock-salt structure. Positions of the 32-atom basis in this cell are obtained from international tables for crystallography [45]. The Ni atoms forming the fcc lattice occupy the Wyckoff position 4a. For a crystal lattice equivalent to an elastic medium, the change of the lattice constant is proportional to the concentration of the dopant and hence, Vegard’s law is obeyed. Therefore, to examine the influence of doping on the lattice constant is examined, it is important to know the concentration of native defects.
3.1. Density of States (DOS)–Excess Ni Occupying Interstitial Sites inNiO
The GGA calculations imply that Ni interstitials play a dominating role under Ni-rich conditions, as depicted in Figure 1a–d, which is correlated with observed Ni deficiency and n-type behavior of NiO. The results show O interstitials as unstable and that O vacancies are the lowest energy defects near the Fermi level. As a result, from [29], it is experimentally observed that Ni-rich NiO is typically n-type semiconductor. There is also a slight increase in the bandgap for increasing % doping of excess of Ni in the NiO system (Figure 1a–d). Table 1 summarizes the extent of increase and it is comparable to the ellipsometric analysis that was established in [29].
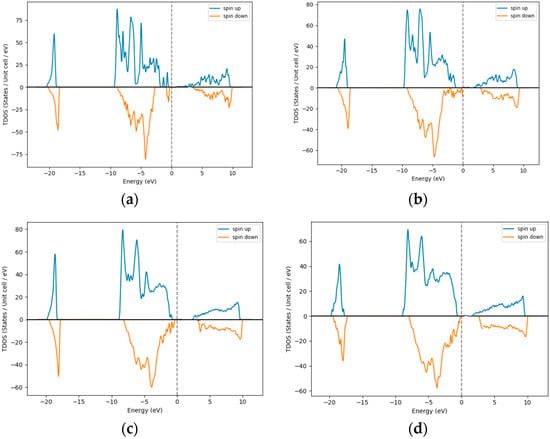
Figure 1.
Density of States for excess Ni in NiO (a) 3%, (b) 12%, (c) 18%, and (d) 25% Ni.

Table 1.
Bandgap of excess Ni in NiO with respect to % doping.
3.2. Density of States (DOS)—Excess O Occupying Interstitial Sites in NiO
The computational analysis, as shown in Figure 2a–d, reveals that Ni vacancies dominate under excess O conditions, which is usually the case with sputtered NiO films being Ni-deficient and p-type semiconducting in nature. From [29], it is observed experimentally that O-rich NiO is typically a p-type semiconductor. Table 2 depicts the increasing trend in bandgap with an increase in O concentration.
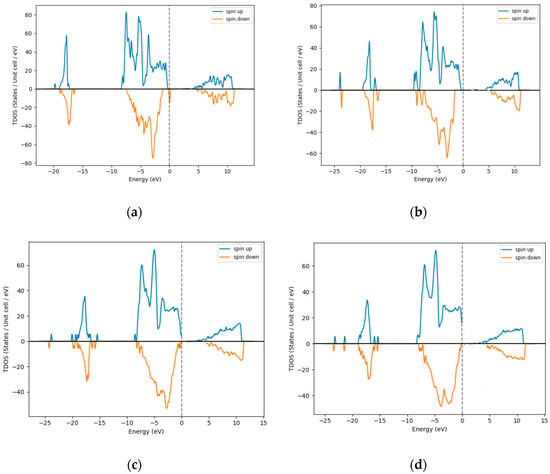
Figure 2.
Density of States for excess O in NiO (a) 3%, (b) 12%, (c) 18%, and (d) 25% O.

Table 2.
Bandgap of excess O in NiO with respect to % doping.
3.3. Formation energies of oxides of Pd and Pt
The formation energies of the oxides of nickel family elements (Pd, Pt) are calculated as:
where µ(M1−xOx) is the energy per formula unit M1−xOx (M= Ni, Pd, Pt).
Eform(M1−xOx) = µ(M1−xOx) − (1−x) µM− xµO
The formation energy of PdO is 2.52 eV [46] and the formation energy of PtO is −0.49 eV [47].
Many approaches to fabricate p-doped NiO are gaining attention among researchers. The nickel family elements Pd and Pt are studied as a single atom defect in the 32-cell NiO. The formation energies of Pd-/Pt-doped NiO as an uncharged defect at various substitutional sites were computed from Equation (2).
Eform(D,0) = Edef(D,0)− Epure(NiO)−(−1)x[(µpure(NiO)−µO] − (+1)xµDMax
From Table 3, the defect formation energies for PdNiand PtNi reach minima at O-rich condition, which suggest that both Pd-doped NiO and Pt-doped NiO show affinity to behave as p-type semiconductors.

Table 3.
Formation energies of single Pd, Pt atom defects (i.e., single atom in 32 atom NiO cell) as interstitials or substitutional defects in NiO.
3.4. Density of States (DOS) - Pd as Dopant Occupying Interstitial Sites inNiO
Figure 3a–dpresents DOS for 3%–12% doping of Pd in NiO. A band gap of 3.8 eV is observed for 3% Pd doping. As the doping increases, there is a decrease in the bandgap of Pd-doped NiO up to 12% doping. It is plausible to explain that the bandgap has a negligible effect on doping up to 12% Pd, because these Pd atoms occupy only interstitial sites in the 64-cell NiO system. Table 4 summarizes the bandgap versus % doping in Pd-NiO system.
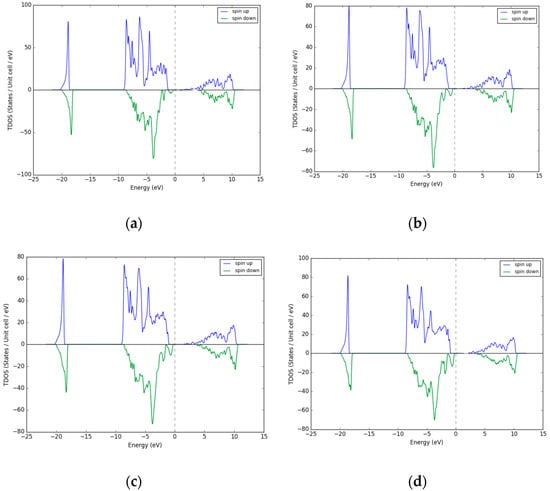
Figure 3.
Density of States for Pd- doped NiO (a) 3% (b) 6% (c) 9%, and (d) 12% Pd.

Table 4.
Bandgap of Pd –doped NiO with respect to % doping.
For higher doping percentage of Pd in NiO (Figure 4a–d), there is a further decrease in the bandgap of Pd doped NiO from 2.95 eV to 2.5 eV. This arises from the Pd2+ substituting Ni2+ sites, resulting in an increase in the lattice constant and overall volume of the cubic cell. The Pd2+ atoms reorganize and stabilize the NiO units with increase in dopant concentration. The nonstoichiometric phase of NiOx goes through a phase of oxygen reduction (i.e., electrons), thus keeping the Fermi level that is close to the valence band [32]. Hence, it can be deduced that Pd-NiO is p-type in nature.
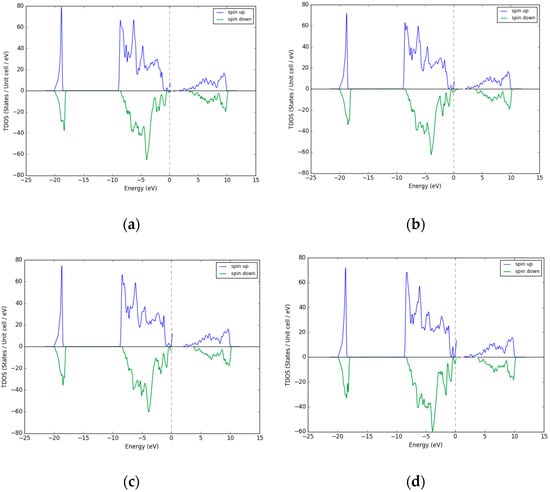
Figure 4.
Densityof States for Pd- doped NiO (a) 15%, (b) 18%, (c) 21%, and (d) 25% Pd.
3.5. Density of States (DOS)—Pt as Dopant Occupying Interstitial Sites inNiO
Density of States for various % doping of Pt in NiO is shown in Figure 5a–d. A band gap of 2.5 eV is observed for 3% Pt2+ doping. It can be observed that, as the doping increases, there is a slight change in the bandgap of Pt-doped NiO upto 12% doping. Due to the large size of Pt atom, there is some amount of distortion in the lattice arrangement resulting in a dominant Pt2+ vacancy occupying the previously held Ni2+ in the cubic lattice.
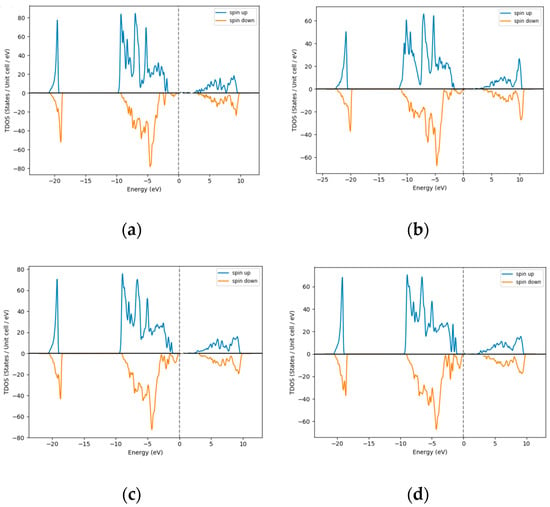
Figure 5.
Density of States for Pt- doped NiO (a) 3% Pt, (b) 6% Pt, (c) 9% Pt, and (d) 12% Pt.
For higher doping percentage of Pt in NiO, there is a further decrease in the bandgap of Pt doped NiO from 2.5 eV to 2.0 eV, as shown in Figure 6a–d. This arises from the Pd2+ substituting Ni2+ sites resulting in an increase in the lattice constant and overall volume of the cubic cell. Table 5 summarizes the bandgap versus % doping in the Pt-NiO system.
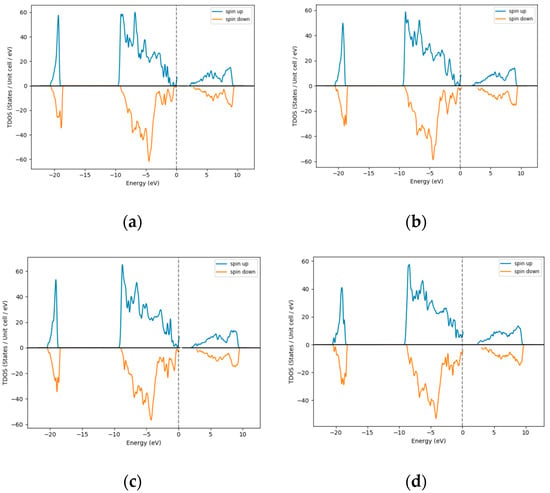
Figure 6.
Density of States for Pt- doped NiO (a) 15%, (b) 18%, (c) 21%, and (d) 25% Pt.

Table 5.
Bandgap of Pt–doped NiO with respect to % doping.
4. Conclusions
Bandgap calculations have been performed on nonstoichiometric NiO with excess native defects and it is observed that there is a slight increase in the bandgap of NiO. This study also validates that O-rich NiO is p-type in nature; whereas, Ni-rich NiO is n-type. Also, doping NiOwith nickel family elements i.e., Pd and Pt by varying the doping concentration from 0–25% is studied. It is observed that there is a decrease in bandgap from 3.8 eV for pure NiO to 2.5 eV for 25% Pd doping. Similarly, there is a decrease in bandgap to 2 eV for 25% Pt doping. The density of state calculations suggests that both Pd-and Pt-doped NiO are p-type in nature.
Author Contributions
S.I. conceptualized, conceived and formally analyzed the computational study; V.B. and F.M. curated the data; S.I. and V.B. validated and drafted the original manuscript; F.M contributed resources; S.I., V.B. and F.M. reviewed and edited the paper.
Funding
This research received no external funding
Acknowledgments
The authors like to thank the facilities in the College of Engineering and the College of Physics and Astronomy at the University of Toledo to carry out this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide:An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Mott, N.F.; Peierls, R. Discussion on the paper by de Boer and Verwey. Proc. Phys. Soc. 1937, 49, 72–73. [Google Scholar] [CrossRef]
- Davoli, I.; Marcelli, A.; Bianconi, A.; Tomellini, M.; Fanfoni, M. Multi-electron configurations in the X-ray absorption near-edge structure of NiO at the oxygen K threshold. Phys. Rev. B 1986, 33, 2979–2982. [Google Scholar] [CrossRef]
- Tomellini, M.; Gozzi, D.; Bianconi, A.; Davoli, I. Local structure of nickel oxide grown at high temperatures in ceramic electrolyte cells. J. Chem. Soc. Faraday Trans. 1987, 83, 289–298. [Google Scholar] [CrossRef]
- Bengone, O.; Alouani, M.; Blöchl, P.; Hugel, J. Implementation of the projector augmented-wave LDA+U method: Application to the electronic structure of NiO. Phys. Rev. B 2000, 62, 16392–16401. [Google Scholar] [CrossRef]
- Ferrari, A.M.; Ferrero, M.; Pisani, C. An ab Initio Periodic Study of NiO Supported at the Pd(100) Surface. Part 2: The Nonstoichiometric Ni3O4 Phase. J. Phys. Chem. B 2006, 110, 7918–7927. [Google Scholar] [CrossRef]
- Yi, J.B.; Ding, J.; Feng, Y.P.; Peng, G.W.; Chow, G.M.; Kawazoe, Y.; Liu, B.H.; Yin, J.H.; Thongmee, S. Size-dependent magnetism and spin-glass behavior of amorphous NiO bulk, clusters, and nanocrystals: Experiments and first-principles calculations. Phys. Rev. B 2007, 76, 224402. [Google Scholar] [CrossRef]
- Zhang, W.-B.; Yu, N.; Yu, W.-Y.; Tang, B.-Y. Stability and magnetism of vacancy in NiO: A GGA+U study. Eur. Phys. J. B 2008, 64, 153–158. [Google Scholar] [CrossRef]
- Park, S.; Ahn, H.-S.; Lee, C.-K.; Kim, H.; Jin, H.; Lee, H.-S.; Seo, S.; Yu, J.; Han, S. Interaction and ordering of vacancy defects in NiO. Phys. Rev. B 2008, 77, 134103. [Google Scholar] [CrossRef]
- Rodriguez, J.A.; Hanson, J.C.; Frenkel, A.I.; Kim, J.Y.; Pérez, M. Experimental and Theoretical Studies on the Reaction of H2 with NiO: Role of O Vacancies and Mechanism for Oxide Reduction. J. Am. Chem. Soc. 2001, 124, 346–354. [Google Scholar] [CrossRef]
- Ferrari, A.M.; Pisani, C.; Cinquini, F.; Giordano, L.; Pacchioni, G. Cationic and anionic vacancies on the NiO(100) surface: DFT+U and hybrid functional density functional theory calculations. J. Chem. Phys. 2007, 127, 174711. [Google Scholar] [CrossRef] [PubMed]
- Manders, J.R.; Tsang, S.-W.; Hartel, M.J.; Lai, T.-H.; Chen, S.; Amb, C.M.; Reynolds, J.R.; So, F. Solution-Processed Nickel Oxide Hole Transport Layers in High Efficiency Polymer Photovoltaic Cells. Adv. Funct. Mater. 2013, 23, 2993–3001. [Google Scholar] [CrossRef]
- Chen, S.C.; Kuo, T.Y.; Sun, T.H. Microstructures, electrical and optical properties of non-stoichiometric p-type nickel oxide films by radio frequency reactive sputtering. Surf. Coat. Technol. 2010, 205, S236–S240. [Google Scholar] [CrossRef]
- Sato, H.; Minami, T.; Takata, S.; Yamada, T. Transparent conducting p-type NiO thin films prepared by magnetron sputtering. Thin Solid Films 1993, 236, 27–31. [Google Scholar] [CrossRef]
- Chen, H.-L.; Lu, Y.-M.; Hwang, W.-S. Characterization of sputtered NiO thin films. Surf. Coat. Technol. 2005, 198, 138–142. [Google Scholar] [CrossRef]
- Reddy, Y.A.K. Influence of Growth Temperature on the Properties of DC Reactive Magnetron Sputtered NiO Thin Films. Int. J. Curr. Eng. Technol. 2013, 2, 351–357. [Google Scholar] [CrossRef]
- Subramanian, B.; Ibrahim, M.M.; Murali, K.R.; Vidhya, V.S.; Sanjeeviraja, C.; Jayachandran, M. Structural, optoelectronic and electrochemical properties of nickel oxide films. J. Mater. Sci. Mater. Electron. 2009, 20, 953–957. [Google Scholar] [CrossRef]
- Agrawal, A.; Habibi, H.R.; Agrawal, R.K.; Cronin, J.P.; Roberts, D.M.; Caron-Popowich, R.; Lampert, C.M. Effect of deposition pressure on the microstructure and electrochromic properties of electron-beam-evaporated nickel oxide films. Thin Solid Films 1992, 221, 239–253. [Google Scholar] [CrossRef]
- Yeh, W.; Matsumura, M. Chemical Vapor Deposition of Nickel Oxide Films from Bis-π-Cyclopentadienyl-Nickel. Jpn. J. Appl. Phys. 1997, 36, 6884–6887. [Google Scholar] [CrossRef]
- Raut, B.T.; Pawar, S.G.; Chougule, M.A.; Sen, S.; Patil, V.B. New process for synthesis of nickel oxide thin films and their characterization. J. Alloys Compd. 2011, 509, 9065–9070. [Google Scholar] [CrossRef]
- Guo, W.; Hui, K.N.; Hui, K.S. High conductivity nickel oxide thin films by a facile sol–gel method. Mater. Lett. 2013, 92, 291–295. [Google Scholar] [CrossRef]
- Tanaka, M.; Mukai, M.; Fujimori, Y.; Kondoh, M.; Tasaka, Y.; Baba, H.; Usami, S. Transition metal oxide films prepared by pulsed laser deposition for atomic beam detection. Thin Solid Films 1996, 281, 453–456. [Google Scholar] [CrossRef]
- Reguig, B.A.; Khelil, A.; Cattin, L.; Morsli, M.; Bernède, J.C. Properties of NiO thin films deposited by intermittent spray pyrolysis process. Appl. Surf. Sci. 2007, 253, 4330–4334. [Google Scholar] [CrossRef]
- Kang, J.-K.; Rhee, S.-W. Chemical vapor deposition of nickel oxide films from Ni(C5H5)2/O2. Thin Solid Films 2001, 391, 57–61. [Google Scholar] [CrossRef]
- Liu, H.; Zheng, W.; Yan, X.; Feng, B. Studies on electrochromic properties of nickel oxide thin films prepared by reactive sputtering. J. Alloys Compd. 2008, 462, 356–361. [Google Scholar] [CrossRef]
- Brückner, W.; Kaltofen, R.; Thomas, J.; Hecker, M.; Uhlemann, M.; Oswald, S.; Elefant, D.; Schneider, C.M. Stress development in sputtered NiO thin films during heat treatment. J. Appl. Phys. 2003, 94, 4853. [Google Scholar] [CrossRef]
- Kuzmin, A.; Purans, J.; Rodionov, A. X-ray absorption spectroscopy study of the Ni K edge in magnetron-sputtered nickel oxide thin films. J. Phys. Condens. Matter 1997, 9, 6979–6993. [Google Scholar] [CrossRef]
- Itapu, S.; Khan, K.; Georgiev, D.G. Effect of UV Laser Irradiation on the properties of NiO films and ZnO/NiO Heterostructures. MRS Adv. 2016, 1, 293–298. [Google Scholar] [CrossRef]
- Itapu, S.; Georgiev, D.G.; Uprety, P.; Podraza, N.J. Modification of reactively sputtered NiOx thin films by pulsed UV laser irradiation. Phys. Status Solidi 2017, 214, 1600414. [Google Scholar] [CrossRef]
- He, J.H.; Yuan, S.L.; Yin, Y.S.; Tian, Z.M.; Li, P.; Wang, Y.Q.; Liu, K.L.; Wang, C.H. Exchange bias and the origin of room-temperature ferromagnetism in Fe-doped NiO bulk samples. J. Appl. Phys. 2008, 103, 23906. [Google Scholar] [CrossRef]
- Han, D.; Jing, X.; Wang, J.; Yang, P.; Song, D.; Liu, J. Porous lanthanum doped NiO microspheres for supercapacitor application. J. Electroanal. Chem. 2012, 682, 37–44. [Google Scholar] [CrossRef]
- Li, J.-C.; Hou, X.-Y.; Cao, Q. Effect of Cu doping on the resistive switching of NiO thin films. J. Appl. Phys. 2014, 115, 164507. [Google Scholar] [CrossRef]
- Dutta, T.; Gupta, P.; Gupta, A.; Narayan, J. Effect of Li doping in NiO thin films on its transparent and conducting properties and its application in heteroepitaxial p-n junctions. J. Appl. Phys. 2010, 108, 83715. [Google Scholar] [CrossRef]
- Li, G.; Li, L.; Jiang, D.; Shi, J. Design of a meso-structured Pd/NiO catalyst for highly efficient low temperature CO oxidation under ambient conditions. RSC Adv. 2015, 5, 40352–40357. [Google Scholar] [CrossRef]
- Sambi, M.; Sensolo, R.; Rizzi, G.A.; Petukhov, M.; Granozzi, G. Growth of NiO ultrathin films on Pd(100) by post-oxidation of Ni films: The effect of pre-adsorbed oxygen. Surf. Sci. 2003, 537, 36–54. [Google Scholar] [CrossRef]
- Zou, X.; Rui, Z.; Ji, H. Core–Shell NiO@PdO Nanoparticles Supported on Alumina as an Advanced Catalyst for Methane Oxidation. ACS Catal. 2017, 7, 1615–1625. [Google Scholar] [CrossRef]
- Huang, S.; Zhu, X.; Cheng, B.; Yu, J.; Jiang, C. Flexible nickel foam decorated with Pt/NiO nanoflakes with oxygen vacancies for enhanced catalytic formaldehyde oxidation at room temperature. Environ. Sci. Nano 2017, 4, 2215–2224. [Google Scholar] [CrossRef]
- Nie, L.; Meng, A.; Teng, F.; Cheng, B. Hierarchically macro-mesoporous flowerlike Pt/NiO composite microspheres for efficient formaldehyde oxidation at room temperature. RSC Adv. 2015, 5, 83997–84003. [Google Scholar] [CrossRef]
- Qi, L.; Cheng, B.; Ho, W.; Liu, G.; Yu, J. Hierarchical Pt/NiO Hollow Microspheres with Enhanced Catalytic Performance. ChemNanoMat 2015, 1, 58–67. [Google Scholar] [CrossRef]
- Walker, M.; Parkinson, C.R.; Draxler, M.; Brown, M.G.; Mcconville, C.F. Initial growth of platinum on oxygen-covered Ni(1 1 0) surfaces. Surf. Sci. 2006, 600, 3327–3336. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Av, G.K.; Furthmiiller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar]
- Kresse, G.; Hafner, J. Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements. J. Phys. Condens. Matter. 1994, 6, 8245–8257. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef]
- Hahn, T. (Ed.) International Tables for Crystallography Volume A: Space-Group Symmetry, 5th ed.; Springer: Amsterdam, The Netherlands, 2002; p. 688. [Google Scholar]
- Bruska, M.K.; Czekaj, I.; Delley, B.; Mantzaras, J.; Wokaun, A. Electronic structure and oxygen vacancies in PdO and ZnO: Validation of DFT models. Phys. Chem. Chem. Phys. 2011, 13, 15947–15954. [Google Scholar] [CrossRef] [PubMed]
- Jacob, T. Theoretical investigations on the potential-induced formation of Pt-oxide surfaces. J. Electroanal. Anal. Chem. 2007, 607, 158–166. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).