Exponents of Spectral Functions in the One-Dimensional Bose Gas

Abstract

The one-dimensional gas of bosons interacting via a repulsive contact potential was solved long ago via Bethe’s ansatz by Lieb and Liniger (Exact Analysis of an Interacting Bose Gas. I. The General Solution and the Ground State). The low energy excitation spectrum is a Luttinger liquid parametrized by a conformal field theory with conformal charge $c=1$. For higher energy excitations the spectral function displays deviations from the Luttinger behavior arising from the curvature terms in the dispersion. Adding a corrective term of the form of a mobile impurity coupled to the Luttinger liquid modes corrects this problem. The “impurity” term is an irrelevant operator, which if treated non-perturbatively, yields the threshold singularities in the one-particle and one-hole Green’s function correctly. We show that the exponents obtained via the finite size corrections to the ground state energy are identical to those obtained through the shift function.

1. Introduction

The one-dimensional Bose gas with a repulsive $\delta$ function was one of the first models exactly solved via Bethe’s ansatz [1,2]. Its properties are those of a Luttinger liquid [3], i.e., as a consequence of the reduced phase space in 1D, the quasi-particle pole in the one-particle Green’s function for a three dimensional Fermi liquid is replaced by an asymmetric power-law singularity at the excitation energy with an exponent that depends on the interaction strength [4].

For a Luttinger liquid the energy of the low-energy excitations is linearized in the momentum about the Fermi points. The spectrum can be described by the conformal tower in terms of four quantum numbers. The correlation functions, determined by the low-energy excitations of the system and the conformal space-time invariance, display power-law divergences. Conformal field theory only yields asymptotically exact correlation functions for long times and long distances, since the curvature of the dispersion is being neglected. These curvature terms in the Hamiltonian are formally irrelevant in the field theory [5], but modify the position of the singularity and the critical exponent.

The exact exponents of the edge singularities in dynamical correlation functions of the 1D Bose gas have been calculated by Imambekov and Glazman [6]. They obtained the phase shifts through the so-called shift function derived from the Bethe ansatz solution. Carmelo and Sacramento [7] used a simplified version of the pseudofermion dynamical theory previously employed for the Hubbard model to derive the phase shifts and exponents. Both methods have been shown to be equivalent approaches [7] yielding the same results. An alternative method consists in calculating the finite size corrections of the ground state energy in the presence of the nonlinear excitation, i.e., the conformal tower in the presence of the excitation. In this paper we use the latter method and show that the outcome for the critical exponents is the same as for the shift function [6] and the pseudofermion dynamical theory [7].

In a series of papers [8,9,10,11,12,13,14,15,16,17,18,19,20], it was shown for several models that neglecting curvature terms in the dispersion leads to incorrect results for the threshold singularities in response functions. This problem is solved by adding a corrective term of the form of a mobile impurity that is coupled to the Luttinger liquid modes. Although formally irrelevant operators, the impurity terms if treated nonperturbatively, yield the correct threshold singularities in the one-particle and one-hole Green’s function. The method is not limited to weak interactions. The procedure is analogous to the X-ray edge divergence in metals [21,22], which arises from the perturbation of the Fermi surface when a core electron is promoted (the impurity). The exact critical exponents are determined by the scattering phase shifts of the electrons off the impurity and for integrable models they can be extracted from the Bethe ansatz solution. This has been demonstrated in several cases, e.g., for spinless fermions with nearest neighbor interactions (anisotropic Heisenberg chain) [10], the Hubbard model (spinfull fermions) [16], for an ultracold gas of fermionic atoms of arbitrary spin S confined to an one-dimensional optical trap interacting via an attractive contact potential [18], and the spinless Bose-Fermi mixture in 1D with contact potential [20].

Previous work on mobile impurities embedded into a Fermi gas should be pointed out [23,24,25,26,27,28,29,30,31,32]. However, in contrast to the present work and References [8,9,10,11,12,13,14,15,16,17,18,19,20,33,34,35,36], where the “impurity” is just an excitation of the interacting 1D gas, there the impurity refers to a foreign particle dragging through the Luttinger liquid.

In this paper we study the one-hole (particle) Green’s function for the boson gas by introducing a “mobile impurity” for the high energy excitation. In Section 2 we restate the results from the Bethe ansatz that are necessary for this paper. In Section 3 the effective field-theoretical Hamiltonian (bosonized model) is introduced, as well as the mobile impurity term due to the high-energy mode. The field theoretical model is diagonalized via a canonical transformation leading to boundary terms for the bosonic field. In Section 4 we use the Euler-MacLaurin summation formula to derive the finite size corrections to the ground state energy using the discrete Bethe ansatz equation including the high-energy mode. The relation of the finite size terms to the scattering phase shifts and the critical exponents of the spectral function is established. The equivalence of the finite size effect and shift function methods is shown. Conclusions follow in Section 5.

2. Model and Bethe Ansatz Equation

2.1. The Model

We consider the 1D Bose gas with repulsive contact potential as solved by Lieb and Liniger [1,2]. The Hamiltonian is given by

$$\mathcal{H}=-\sum _{i=1}^N\frac{{\partial }^2}{\partial x_i^2}+2c\sum _{i<j}\delta (x_i-x_j),$$

(1)

where $x_i$ are the coordinates, N is the total number of bosons and the interaction strength is c. We assume periodic boundary conditions in a system of length L. Here the quantities $\mathcal{H}$ and c have either been scaled by the constant ${\hslash }^2/2m$, where m is the particle mass, or alternatively we equated ${\hslash }^2/2m$ to 1.

2.2. Bethe Ansatz Equations

In the coordinate Bethe ansatz the wave functions are piecewise plane waves connected by the continuity of the wave function and the discontinuity of its first derivative. The Bethe ansatz solution consists then of a set of rapidities, parametrizing the momenta, denoted with $\left\{k_j\right\}$, $j=1,\dots ,N$. To ensure linearly independent solutions for the wave functions, all rapidities within the set have to be different. Choosing periodic boundary conditions for the wave functions, the rapidities are determined by the following equations [1]

$$exp\left(i{k}_{j}L\right)=\prod _{\alpha =1;\alpha \ne j}^N\frac{k_j-k_{\alpha }+ic}{k_j-k_{\alpha }-ic},j=1,\cdots ,N,$$

(2)

The solutions of the above equations determine all the states of the Bose gas. All rapidity solutions of Equation (2) are real [37]. This can be shown by assuming an imaginary component for $k_j$. The equations then have no solution in the thermodynamic limit ($L\to \infty$).

The energy and the momentum of the gas are given by

$$E=\sum _{j=1}^N{k}_j^2-\mu N,P=\sum _{j=1}^N{k}_j,$$

(3)

where $\mu$ is the chemical potential.

2.3. Dressed Energy Potential and Density

In the ground state the set of rapidities $\left\{k_j\right\}$ is densely distributed in the interval $[-Q,Q]$. The dressed energy, denoted with $\epsilon \left(k\right)$, is a monotonically increasing function of $\left|k\right|$ and satisfies the following integral equation in the ground state [37]

$$\epsilon \left(k\right)=k^2-\mu +{\int }_{-Q}^{Q}d{k}^{\prime }\frac{1}{\pi }\frac{c}{{(k-k^{\prime })}^2+c^2}\epsilon \left(k^{\prime }\right),$$

(4)

The condition determining the integration limit Q as a function of $\mu$ is $\epsilon (\pm Q)=0$. Consequently, $\pm Q$ are the Fermi points of the system, i.e., where the dressed energy changes sign. Occupied states correspond to a negative potential and for empty states the dressed energy is positive. $\mu$ is the Lagrange multiplier corresponding to the conservation of the number of bosons.

We denote with $\rho \left(k\right)$ and ${\rho }_h\left(k\right)$ the density distribution functions for particles and holes of k. The density functions for the rapidities are obtained by differentiating $\epsilon$ with respect to $\mu$, i.e., [38]

$${\rho }_h\left(k\right)+\rho \left(k\right)=-\frac{1}{2\pi }\frac{\partial \epsilon \left(k\right)}{\partial \mu },$$

(5)

and satisfy the following integral equation [1,2]

$$\rho \left(k\right)+{\rho }_h\left(k\right)=\frac{1}{2\pi }+{\int }_{-Q}^{Q}d{k}^{\prime }\rho \left(k^{\prime }\right)\frac{1}{\pi }\frac{c}{{(k-k^{\prime })}^2+c^2}.$$

(6)

The total number of particles and the energy of the system are given by

$$\frac{N}{L}={\int }_{-Q}^{Q}dk\rho \left(k\right),\frac{E}{L}={\int }_{-Q}^Q{k}^2\rho \left(k\right)-\mu \frac{N}{L}.$$

(7)

2.4. Particle and Hole Excitations

Elementary particle (hole) excitations are obtained by adding (removing) a boson to (from) the system. Denoting the rapidity of the removed or added boson with $k_0$ the energy of the excitation is given by $\epsilon \left(k_0\right)$, i.e., the dressed energy potential. For particle excitations the energy is ${\epsilon }_p\left(k_0\right)=\epsilon \left(k_0\right)$ with $|k_0|>Q$, while hole excitations correspond to $|k_0|<Q$ and their energy is ${\epsilon }_h\left(k_0\right)=-\epsilon \left(k_0\right)$. Hence, $\Delta E_{exc}\left(k_0\right)=\left|\epsilon \left(k_0\right)\right|$ for all $k_0$ and since $\epsilon (\pm Q)=0$ the excitation energy vanishes at the Fermi points. The momentum of the excitation is given by

$$p_{exc}\left(k_0\right)=2\pi {\int }_0^{k_0}dk[\rho \left(k\right)+{\rho }_h\left(k\right)],$$

(8)

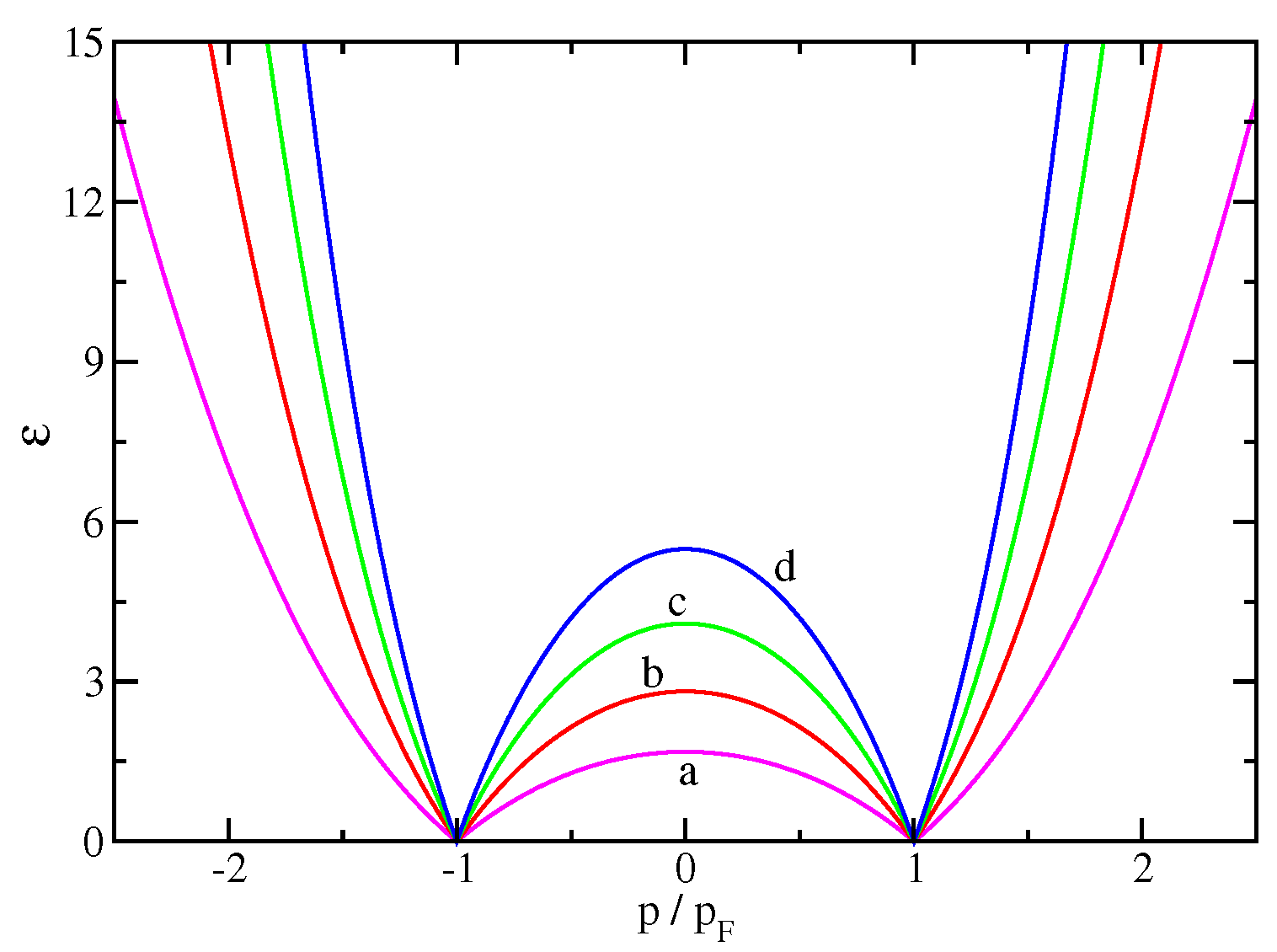
leading to the Fermi momentum $p_F=\pi n=\pi N/L$. Hence, $p_F$ is completely determined by the band occupation and the excitations at low energies form a simple Dirac sea with two Fermi points at $k_0=\pm Q$ or $p=\pm p_F$. The dispersion of the excitations for $c=1$ and $N/L=0.400$ is shown in Figure 1.

Figure 1. Elementary excitations for particles and holes as a function of the momentum for $c=1$ and four sets of parameters: (a) (magenta) $N/L=0.740$, $\mu =1.0$, and $Q=1.175$; (b) (red) $N/L=1.045$, $\mu =1.5$, and $Q=1.470$; (c) (green) $N/L=1.333$, $\mu =2.0$, and $Q=1.715$; (d) (blue) $N/L=1.620$, $\mu =2.5$, and $Q=1.935$.

2.5. Group Velocities

In the Luttinger limit, where the dispersion of the excitations is linear with the momentum, the group velocity is given by [2]

$$v_F=\left(\frac{d\epsilon \left(k\right)}{dk}{|}_{k=Q}\right)/\left(2\pi \rho \left(Q\right)\right).$$

(9)

The group velocity away from the linear dispersion regime is

$$u\left(k_0\right)=\left(\frac{d\epsilon \left(k_0\right)}{d{k}_0}\right)/\left[2\pi (\rho \left(k_0\right)+{\rho }_h\left(k_0\right))\right],$$

(10)

and corresponds to the slope of the dispersion in Figure 1. Note that for hole excitations $\left|u\right|$ is always smaller than the respective Fermi velocity.

2.6. Conformal Towers

In the Luttinger limit the model has excitations with energy proportional to the momentum with Fermi velocity $v_F$. The finite size corrections to the ground state energy determine the energies of the low-lying excitations [39]. The ground state energy, $E_{GS}$, is an extensive quantity given by Equation (7). The excitations, on the other hand, are mesoscopic corrections, i.e., of order $1/L$, where L is the length of the system. These mesoscopic corrections depend on the boundary conditions employed, in our case periodic boundary conditions. Four quantum numbers determine the finite size corrections, namely, $\Delta N$ corresponds to the number of removed or added of rapidities and D is the parity variable, i.e., $2D$ is the difference between the number of forward and backward movers. In addition, the quantum numbers $n^{\pm }$ count the number of particle and hole excitations about each Fermi point (“+” for forward movers and “−” for backward movers). The ground state energy with finite size corrections is given by [38,39]

$$\begin{array}{ccc}\hfill E=E_{GS}& +& \frac{\pi v_F}{2L}{\left[\frac{\Delta N}{L}\right]}^2+\frac{2\pi v_F}{L}\left[{\left(zD\right)}^2+n^{+}+n^{-}-\frac{1}{12}\right],\hfill \end{array}$$

(11)

and assuming that the momentum of the ground state is zero, the excitations change the momentum by [38]

$$\Delta P=\frac{2\pi }{L}\left[D\Delta N+n^{+}-n^{-}\right]+2p_{F}D.$$

(12)

The quantity z in Equation (11) is the generalized dressed charge, which determines the interaction between the two Fermi points, i.e., how the energy is affected by a change of a quantum number, e.g., $\Delta N$ or D. The periodic boundary conditions for the discrete Bethe ansatz equations restrict the values of the backscattering quantum number D to be an integer. The dressed generalized charge is determined by $z=\Xi \left(Q\right)$, where $\Xi$ is the solution of

$$\Xi \left(k\right)=1+{\int }_{-Q}^{Q}d{k}^{\prime }\frac{1}{\pi }\frac{c}{{(k-k^{\prime })}^2+c^2}\Xi \left(k^{\prime }\right).$$

(13)

Comparing Equations (6) and (13), we conclude that $z=2\pi \rho \left(Q\right)$.

2.7. Correlation Functions

Consider now a conformal field operator $\mathcal{O}$ characterized by a set of quantum numbers $\Delta N$, D and $n^{\pm }$. The conformal dimensions, defined as [40,41]

$$2{\Delta }^{\pm }=2n^{\pm }+{\left[zD\pm \frac{\Delta N}{2z}\right]}^2,$$

(14)

determine the critical exponents of asymptotes of the $\mathcal{O}$ correlation function. Conformal field theory then yields for the asymptote of $⟨{\mathcal{O}}^{†}(x,t)\mathcal{O}(0,0)⟩$

$$⟨{\mathcal{O}}^{†}(x,t)\mathcal{O}(0,0)⟩\propto \frac{exp[-2iD{p}_{F}x]}{{(x-i{v}_{F}t)}^{2{\Delta }^{+}}{(x+i{v}_{F}t)}^{2{\Delta }^{-}}}.$$

(15)

The correlation function consists of two factors corresponding to forward and backward movers, respectively. Each of these factors gives rise to a power-law singularity. The main assumption here is the linearized spectrum of the Luttinger liquid, which leads to an approximate position and exponent of the singularity for excitations beyond the linear regime.

2.8. Luttinger Parameter

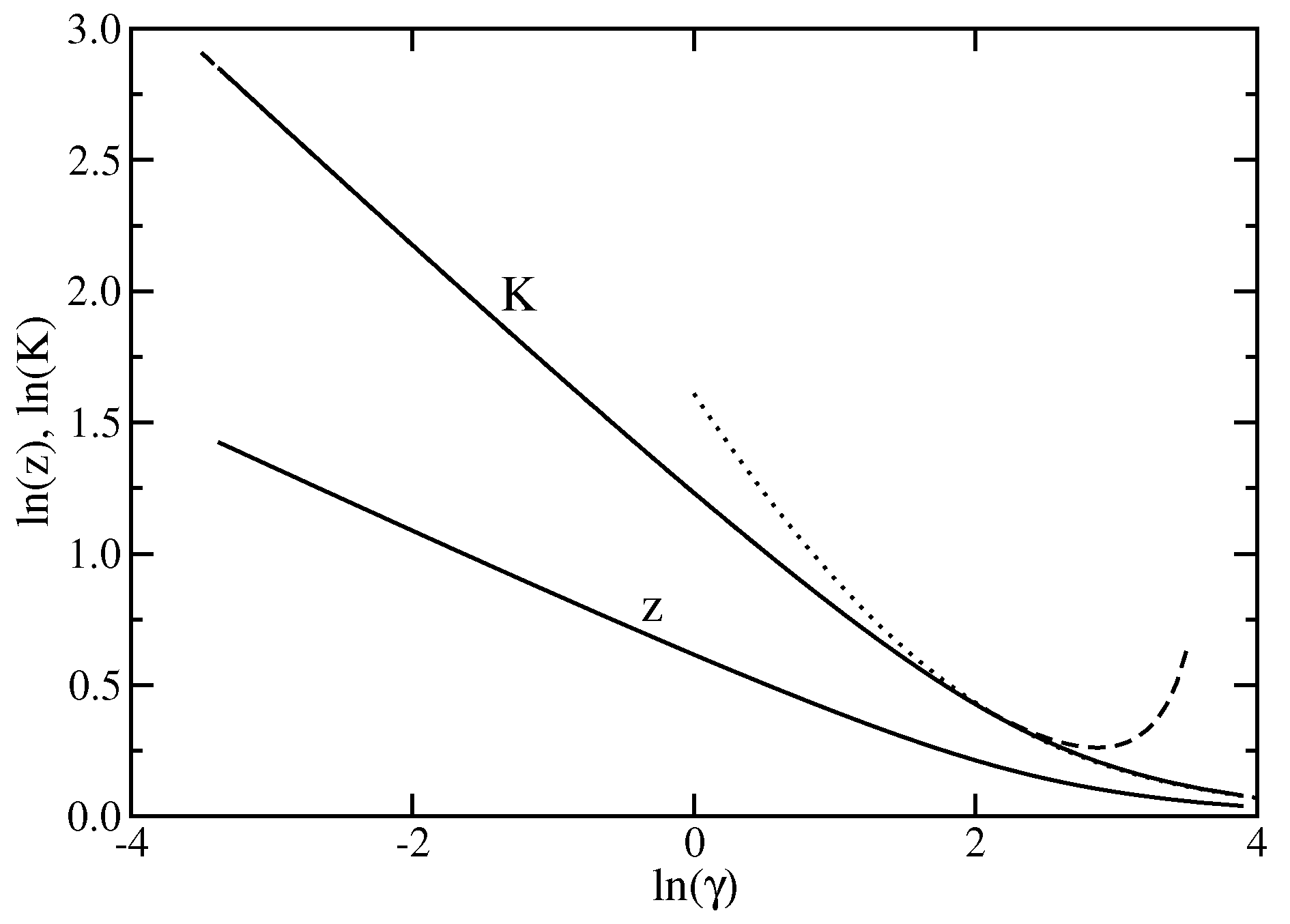
To parametrize the interaction strength in the field theory model for the Luttinger liquid we need the Luttinger parameter K in terms of the Bethe ansatz quantities. To determine K we consider the equal time hole boson propagator for which the quantum numbers are $\Delta N=-1$ and $D=0$. The correlation function decreases with a power law of the distance x, $1/{\left|x\right|}^{\theta }$, where $\theta =1/\left(2z^2\right)$ [20,42]. The field-theoretical approach yields through bosonization $\theta =1/\left(2K\right)$ [3]. Hence, we expect $K=z^2$, in agreement with previous results [42]. A double logarithmic plot of z and K vs. $\gamma =c/(N/L)$ is shown in Figure 2. According to Cazalilla [3] asymptotically for high densities (small $\gamma$) the Luttinger parameter K is $(\pi /\sqrt{\gamma })/{[1-\sqrt{\gamma }/\left(2\pi \right)]}^{1/2}$, while for low densities (large $\gamma$), $K=(1+4/\gamma )$. The agreement of these expressions with the present results is very good.

Figure 2. Dressed generalized charge z and the Luttinger parameter K vs. $\gamma =c/(N/L)$ on a double logarithmic scale. The dashed line is the high density approximation $K=(\pi /\sqrt{\gamma })/{[1-\sqrt{\gamma }/\left(2\pi \right)]}^{1/2}$ and the dotted line is the low density approximation $K=(1+4/\gamma )$ [3].

To obtain $K=1$ one could naively consider the limit $\gamma =c/(N/L)\to 0$. This limit corresponds to a gas of non-interacting bosons which, however, would condensate at $T=0$ into the ground state. In this limit K becomes arbitrarily large. On the other hand, for $\gamma \to \infty$ the bosons become “hard-core” bosons, i.e., they act as non-interacting fermions. Hence, in this limit $K=1$ [3].

3. Field Theory Model for the Luttinger Liquid with Mobile Impurity

The field theory for the Luttinger liquid, i.e., the model with the linear dispersion in the momentum is parametrized by a Bose field, $\Phi \left(x\right)$, and its dual field, $\Theta \left(x\right)$, which satisfy the commutation relation [5]

$$\left[\Phi \left(x\right),\frac{\partial \Theta \left(y\right)}{\partial y}\right]=i\pi \delta (x-y).$$

(16)

The Luttinger liquid Hamiltonian is given by

$${\mathcal{H}}_{LL}=\frac{v_F}{2\pi }\int dx\left[\frac{1}{K}{\left(\frac{\partial \Phi \left(x\right)}{\partial x}\right)}^2+K{\left(\frac{\partial \Theta \left(x\right)}{\partial x}\right)}^2\right],$$

(17)

where irrelevant operators have been neglected. Here K is the Luttinger parameter, which determines the strength of the interaction. For a noninteracting system $K=1$.

The deviations from linearity of the dispersion lead in general to incorrect results in the threshold position and the exponents in response functions [6,8,9,10,11,12,15,16,18,20,33,34,35,36]. A high energy excitation from the nonlinear portion of the spectrum can be included by coupling the Luttinger liquid to a mobile impurity. This mobile impurity, if treated nonperturbatively, leads to singularities in the response function with the correct energy and momentum-dependent exponent.

A boson with energy $\epsilon \left(p\right)$ added to the system is emulated by the following mobile impurity Hamiltonian (see, e.g., References [6,8,9,10,11,15,16,18,20])

$${\mathcal{H}}_d=\int dx{d}^{†}\left(x\right)\left[\epsilon \left(p\right)-iu\frac{\partial }{\partial x}\right]d\left(x\right),$$

(18)

where $d^{†}$ and d are the creation and annihilation operators of the mobile impurity, p is the momentum and u the group velocity of the excitation. The interaction of the Luttinger liquid with the mobile impurity is linear through coupling parameters $V_R$ and $V_L$

$${\mathcal{H}}_{int}=\int dx\left[\frac{V_L-V_R}{2\pi }\frac{\partial \Theta \left(x\right)}{\partial x}+\frac{V_L+V_R}{2\pi }\frac{\partial \Phi \left(x\right)}{\partial x}\right]d^{†}\left(x\right)d\left(x\right).$$

(19)

In Section 4 the parameters in Equations (17)–(19) are related to quantities from the Bethe ansatz.

We now consider $\mathcal{H}={\mathcal{H}}_{LL}+{\mathcal{H}}_{imp}+{\mathcal{H}}_{int}$ and to eliminate the terms linear in the fields ${\partial }_x\Theta$ and ${\partial }_x\Phi$ we apply a canonical transformation U to all operators [10,11,16],

$$U=exp\left\{-\frac{i}{2\pi }\int dx\left[-\sqrt{K}({\phi }_{+}-{\phi }_{-})\Theta \left(x\right)+\frac{{\phi }_{+}+{\phi }_{-}}{\sqrt{K}}\Phi \left(x\right)\right]d^{†}\left(x\right)d\left(x\right)\right\},$$

(20)

where the parameters ${\phi }_{+}$ and ${\phi }_{-}$ are to be determined. The transformed quantities are denoted by $\overline{d}=Ud{U}^{†}$, $\overline{\Phi }=U\Phi U^{†}$ and $\overline{\Theta }=U\Theta U^{†}$ so that

$$\begin{array}{ccc}\hfill {\partial }_x\Theta & =& {\partial }_x\overline{\Theta }-\frac{1}{2\sqrt{K}}({\phi }_{+}+{\phi }_{-}){\overline{d}}^{†}\overline{d},\hfill \\ \hfill {\partial }_x\Phi & =& {\partial }_x\overline{\Phi }+\frac{\sqrt{K}}{2}({\phi }_{+}-{\phi }_{-}){\overline{d}}^{†}\overline{d},\hfill \\ \hfill d& =& \overline{d}exp\left\{-\frac{i}{2\pi }\left[-\sqrt{K}({\phi }_{+}-{\phi }_{-})\overline{\Theta }+\frac{1}{\sqrt{K}}({\phi }_{+}+{\phi }_{-})\overline{\Phi }\right]\right\}.\hfill \end{array}$$

(21)

The unwanted linear terms disappear if [10,11,16]

$$\begin{array}{ccc}\hfill -\frac{(V_L-V_R)}{\sqrt{K}}& =& (v_F-u){\phi }_{+}+(v_F+u){\phi }_{-},\hfill \\ \hfill -(V_L+V_R)\sqrt{K}& =& -(v_F-u){\phi }_{+}+(v_F+u){\phi }_{-}\hfill \end{array}$$

(22)

and the transformed Hamiltonian becomes noninteracting

$${\mathcal{H}}_{tran}=\frac{v_F}{2\pi }\int dx\left[\frac{1}{K}{\left(\frac{\partial \overline{\Phi }\left(x\right)}{\partial x}\right)}^2+K{\left(\frac{\partial \overline{\Theta }\left(x\right)}{\partial x}\right)}^2\right]+\int dx{\overline{d}}^{†}\left(x\right)\left[\epsilon \left(p\right)-iu\frac{\partial }{\partial x}\right]\overline{d}\left(x\right).$$

(23)

As a consequence of the transformation boundary terms are introduced for the boson fields, $\Phi \left(x\right)$ and $\Theta \left(x\right)$, which are obtained by taking expectation values in Equation (21) [10,11]

$$\begin{array}{ccc}\hfill -\Delta N& =& \frac{1}{\pi }{\int }_0^{L}dx⟨{\partial }_x\Phi ⟩=\frac{1}{\pi }{\int }_0^{L}dx⟨{\partial }_x\overline{\Phi }⟩+\frac{\sqrt{K}}{2\pi }({\phi }_{+}-{\phi }_{-}),\hfill \\ \hfill D& =& -\frac{1}{\pi }{\int }_0^{L}dx⟨{\partial }_x\Theta ⟩=-\frac{1}{\pi }{\int }_0^{L}dx⟨{\partial }_x\overline{\Theta }⟩+\frac{1}{2\pi \sqrt{K}}({\phi }_{+}+{\phi }_{-}),\hfill \end{array}$$

(24)

where $2D$ is the current quantum number (backscattering).

4. Relation to the Bethe Ansatz Results

We now calculate the finite size corrections to the ground state energy in the presence of a high energy excitation using the Bethe ansatz equations. The results for hole and particle excitations are similar, so that here we consider holes. Removing a rapidity introduces a small asymmetry in the integration limits, which were symmetric at $\pm Q$ without excitation. We denote the new integration limits with $Q_{+}$ and $Q_{-}$.

4.1. Densities

In close analogy to References [16,41] we start with the discrete Bethe ansatz equations, $\mathcal{Z}\left(k_j\right)=2\pi J_j/L$,

$$\mathcal{Z}\left(k\right)=k+\frac{2}{L}\sum _{\alpha =1}^{N}arctan\left(\frac{(k-k_{\alpha })}{c}\right)-\frac{2}{L}arctan\left(\frac{(k-k_L^{\left(h\right)})}{c}\right).$$

(25)

The term with $k_L^{\left(h\right)}$ is the term of the excitation with the removed quantum number $J^{\left(h\right)}$ and $\mathcal{Z}\left(k_L^{\left(h\right)}\right)=2\pi J^{\left(h\right)}/L$. The subindex L indicates that $k_L^{\left(h\right)}$ depends on the size of the system. With the aid of the Euler-MacLaurin sum formula the discrete equations can be transformed into an integral form for large L

$$\begin{array}{ccc}\hfill \mathcal{Z}\left(k\right)& =& k+2{\int }_{Q_{-}}^{Q_{+}}d{k}^{\prime }\rho \left(k^{\prime }\right)arctan\left(\frac{(k-k^{\prime })}{c}\right)-\frac{2}{L}arctan\left(\frac{(k-k_L^{\left(h\right)})}{c}\right)\hfill \\ & -& \frac{1}{12L^2}\left[\frac{1}{2\pi \rho \left(Q_{+}\right)}\frac{c}{{(k-Q_{+})}^2+c^2}-\frac{1}{2\pi \rho \left(Q_{-}\right)}\frac{c}{{(k-Q_{-})}^2+c^2}\right].\hfill \end{array}$$

(26)

The integration boundaries are fixed by $\mathcal{Z}\left(Q_{\pm }\right)=\frac{2\pi J_{\pm }}{L}$, where $J_{\pm }=\pm (N_{GS}-1)/2$ with $N_{GS}$ being the number of bosons in the ground state.

Dividing Equation (26) by $2\pi$ and differentiating with respect to k the integral equation for $\rho$ for the finite system of length L is obtained. Expanding $\rho$ in powers of $1/L$, i.e., ${\rho }_0\left(k\right)+{\rho }_1\left(k\right)/L+{\rho }_2\left(k\right)/L^2+\mathcal{O}\left(L^{-3}\right)$, we obtain for ${\rho }_0\left(k\right)$

$${\rho }_0\left(k\right)=\frac{1}{2\pi }+{\int }_{Q_{-}}^{Q_{+}}d{k}^{\prime }{\rho }_0(\Lambda )\frac{1}{\pi }\frac{c}{{(k-\Lambda )}^2+c^2}.$$

(27)

This corresponds to the thermodynamic limit and except for the integration limits this equation is identical to Equation (6).

The integral equation for ${\rho }_1\left(k\right)$ is essentially the change in the density function due to a “hole” excitation, again except for the integration limits, i.e.,

$${\rho }_1\left(k\right)=-\frac{1}{\pi }\frac{c}{{(k-k_L^{\left(h\right)})}^2+c^2}+{\int }_{Q_{-}}^{Q_{+}}d{k}^{\prime }{\rho }_1\left(k^{\prime }\right)\frac{1}{\pi }\frac{c}{{(k-k^{\prime })}^2+c^2}.$$

(28)

Finally, the last driving terms in Equation (26) determine the integral equation for ${\rho }_2\left(k\right)$, i.e.,

$$\begin{array}{ccc}\hfill {\rho }_2\left(k\right)& =& -\frac{1}{48{\pi }^2}\left[\frac{1}{{\rho }_0\left(Q_{+}\right)}\frac{c}{{(k-Q_{+})}^2+c^2}-\frac{1}{{\rho }_0\left(Q_{-}\right)}\frac{c}{{(k-Q_{-})}^2+c^2}\right]\hfill \\ & +& {\int }_{Q_{-}}^{Q_{+}}d{k}^{\prime }{\rho }_2\left(k^{\prime }\right)\frac{1}{\pi }\frac{c}{{(k-k^{\prime })}^2+c^2}.\hfill \end{array}$$

(29)

4.2. Energy

In terms of discrete rapidities the system’s energy is expressed as

$$E=\sum _{j=1}^N{k}_j^2-{\left(k_L^{\left(h\right)}\right)}^2-(N-1)\mu .$$

(30)

Employing once again the Euler-MacLaurin sum formula this expression reduces to [16,41]

$$\begin{array}{ccc}\hfill \frac{E}{L}& =& {\int }_{Q_{-}}^{Q_{+}}dk(k^2-\mu ){\rho }_0\left(k\right)-\frac{1}{L}[{\left(k_L^{\left(h\right)}\right)}^2-\mu ]+\frac{1}{L}{\int }_{Q_{-}}^{Q_{+}}dk(k^2-\mu ){\rho }_1\left(k\right)\hfill \\ & +& \frac{1}{L^2}{\int }_{Q_{-}}^{Q_{+}}dk(k^2-\mu ){\rho }_2\left(k\right)-\frac{1}{24L^2}\left[\frac{{(Q_{+}^2-\mu )}^{\prime }}{2\pi {\rho }_0\left(Q_{+}\right)}-\frac{{(Q_{-}^2-\mu )}^{\prime }}{2\pi {\rho }_0\left(Q_{-}\right)}\right],\hfill \end{array}$$

(31)

where derivative is denoted with a prime.

Defining ${\epsilon }^{\left(0\right)}\left(k\right)=k^2-\mu$ the ground state energy density in the thermodynamic limit is

$${ϵ}_{GS}\left(Q_{\pm }\right)={\int }_{Q_{-}}^{Q_{+}}dk(k^2-\mu ){\rho }_0\left(k\right)={\int }_{Q_{-}}^{Q_{+}}dk{\epsilon }^{\left(0\right)}\left(k\right){\rho }_0\left(k\right),$$

(32)

and the energy of the finite system can be written as

$$\begin{array}{ccc}\hfill E& =& L{ϵ}_{GS}\left(Q_{\pm }\right)-{\epsilon }^{\left(0\right)}\left(k_L^{\left(h\right)}\right)+{\int }_{Q_{-}}^{Q_{+}}dk{\epsilon }^{\left(0\right)}\left(k\right){\rho }_1\left(k\right)+\frac{1}{L}{\int }_{Q_{-}}^{Q_{+}}dk{\epsilon }^{\left(0\right)}\left(k\right){\rho }_2\left(k\right)\hfill \\ & -& \frac{1}{24L}\left[\frac{{\epsilon }^{\left(0\right)}\left(Q_{+}\right)}{2\pi {\rho }_0\left(Q_{+}\right)}-\frac{{\epsilon }^{\left(0\right)}\left(Q_{-}\right)}{2\pi {\rho }_0\left(Q_{-}\right)}\right].\hfill \end{array}$$

(33)

After a tedious calculation the $L^{-1}$-terms reduce to $-(\pi /6L)v_F$.

Next we simplify the impurity terms in the expression for the energy. The rapidity of the “impurity”, $k_L^{\left(h\right)}$, is dependent on the size of the system and can be expanded in powers of $1/L$ as $k_L^{\left(h\right)}=k^{\left(h\right)}+\delta k^{\left(h\right)}/L$. The terms of order $L^0$, i.e., the second and third terms in Equation (33), reduce to the dressed energy of the hole, $\epsilon \left(k_L^{\left(h\right)}\right)$, but with integration limits $Q_{\pm }$

$$-{\epsilon }^{\left(0\right)}\left(k_L^{\left(h\right)}\right)+{\int }_{Q_{-}}^{Q_{+}}dk{\epsilon }^{\left(0\right)}\left(k\right){\rho }_1\left(k\right)=-\epsilon \left(k_L^{\left(h\right)}\right)=-\epsilon \left(k^{\left(h\right)}\right)-{\epsilon }^{\prime }\left(k^{\left(h\right)}\right)\delta k^{\left(h\right)}/L,$$

(34)

where the prime again represents derivative with respect to k. The quantity $\delta k^{\left(h\right)}/L$ can in principle be calculated, but plays no significant role in the remainder of the paper.

The energy of the system is now given by

$$E=L{ϵ}_{GS}\left(Q_{\pm }\right)-\epsilon \left(k^{\left(h\right)}\right)-{\epsilon }^{\prime }\left(k^{\left(h\right)}\right)\delta k^{\left(h\right)}/L-\pi v_F/\left(6L\right).$$

(35)

4.3. Integration Limits

The quantities $(Q_{\pm }\mp Q)$ are of the order of $1/L$. We now expand ${ϵ}_{GS}\left(Q_{\pm }\right)$ to second order in these differences. The linear term vanishes, i.e., ${[\delta {ϵ}_{GS}\left(Q_{\pm }\right)/\delta Q_{\pm }]}_{Q_{\pm }=\pm Q}=0$, because the excitations at the Fermi points vanish, i.e., $\epsilon (\pm Q)=0$.

Hence, the first term corresponds to the equilibrium energy density in the ground state and the first corrections are quadratic,

$${ϵ}_{GS}\left(Q_{\pm }\right)={ϵ}_{GS}(\pm Q)+\frac{1}{2}\sum _{\sigma \tau }\frac{{\delta }^2{ϵ}_{GS}\left(Q_{\pm }\right)}{\delta Q_{\sigma }\delta Q_{\tau }}{|}_{Q_{\sigma }=\sigma Q;Q_{\tau }=\tau Q}\left[(Q_{\sigma }-\sigma Q)(Q_{\tau }-\tau Q)\right].$$

(36)

After lengthy algebra we obtain

$$\frac{{\delta }^2{ϵ}_{GS}\left(Q_{\pm }\right)}{\delta Q_{\sigma }\delta Q_{\tau }}{|}_{Q_{\sigma }=\sigma Q;Q_{\tau }=\tau Q}={\delta }_{\sigma \tau }2\pi v_F{\left[{\rho }_0\left(Q\right)\right]}^2.$$

(37)

The ${\delta }_{\sigma \tau }$ arises since the two Fermi points are independent [16,41].

In summary, the corrections to the energy due to the finite size of the system are

$$\begin{array}{ccc}\hfill E& =& L{ϵ}_{GS}(\pm Q)+L\pi v_F{\left[{\rho }_0\left(Q\right)\right]}^2\left[{(Q_{+}-Q)}^2+{(Q_{-}+Q)}^2\right]-\epsilon (k^{\left(h\right)},Q_{\pm })\hfill \\ & -& {\epsilon }^{\prime }(k^{\left(h\right)},Q_{\pm })\delta k^{\left(h\right)}/L+\pi v_F/\left(6L\right).\hfill \end{array}$$

(38)

4.4. Relation to Quantum Numbers

The change of the integration limits due to the high energy excitation can be related to the quantum numbers of the excitation. We obtain the changes for the density and current density to order $1/L$

$$\begin{array}{ccc}\hfill \frac{N}{L}& =& \frac{J_{+}-J_{-}}{L}=\frac{1}{2\pi }[\mathcal{Z}\left(Q_{+}\right)-\mathcal{Z}\left(Q_{-}\right)]={\int }_{Q_{-}}^{Q_{+}}dk\rho \left(k\right)={\int }_{Q_{-}}^{Q_{+}}dk{\rho }_0\left(k\right)+\frac{1}{L}{\int }_{Q_{-}}^{Q_{+}}dk{\rho }_1\left(k\right),\hfill \\ \hfill \frac{2D}{L}& =& \frac{J_{+}+J_{-}}{L}=\frac{1}{2\pi }\left[\mathcal{Z}\left(Q_{+}\right)+\mathcal{Z}\left(Q_{-}\right)\right]={\int }_{-\infty }^{Q_{+}}dk\rho \left(k\right)-{\int }_{Q_{-}}^{\infty }dk\rho \left(k\right)\hfill \\ & =& {\int }_{-\infty }^{Q_{+}}dk\left[{\rho }_0\left(k\right)+\frac{1}{L}{\rho }_1\left(k\right)\right]-{\int }_{Q_{-}}^{\infty }dk\left[{\rho }_0\left(k\right)+\frac{1}{L}{\rho }_1\left(k\right)\right].\hfill \end{array}$$

(39)

We denote with $N_{imp}$ and $D_{imp}$ the quantities related to the high energy excitations (mobile impurities)

$$N_{imp}={\int }_{Q_{-}}^{Q_{+}}dk{\rho }_1\left(k\right),2D_{imp}={\int }_{-\infty }^{Q_{+}}dk{\rho }_1\left(k\right)-{\int }_{Q_{-}}^{\infty }dk{\rho }_1\left(k\right).$$

(40)

Note that in Equation (40) the integration limits $Q_{\pm }$ can be replaced by $\pm Q$. It is convenient to rewrite $D_{imp}$ as follows

$$\begin{array}{ccc}\hfill 2D_{imp}& =& -\frac{1}{\pi }arctan((Q-k^{\left(h\right)})/c)+\frac{1}{\pi }arctan((Q+k^{\left(h\right)})/c)\hfill \\ & +& \frac{1}{\pi }{\int }_{-Q}^{Q}d{k}^{\prime }{\rho }_1\left(k^{\prime }\right)\left[arctan((Q-k^{\prime })/c)-arctan((Q+k^{\prime })/c)\right].\hfill \end{array}$$

(41)

The shift of $Q_{\pm }$ with $N/L$ to leading order in $L^{-1}$ is given by $\partial Q_{\pm }/\partial (N/L)=\pm 1/\left[2z{\rho }_0\left(Q\right)\right]$ and the one of $Q_{\pm }$ with $D/L$ is $\partial Q_{\pm }/\partial (D/L)=z/{\rho }_0\left(Q\right)$. It now follows that

$$Q_{\pm }\mp Q=\pm \frac{1}{2z{\rho }_0\left(Q\right)L}\left[\Delta N-N_{imp}\right]+\frac{z}{{\rho }_0\left(Q\right)L}\left[\Delta D-D_{imp}\right].$$

(42)

We denote with $\Delta \tilde{N}=\Delta N-N_{imp}\left(p\right)$ and $\Delta \tilde{D}=\Delta D-D_{imp}\left(p\right)$. $N_{imp}$ and $D_{imp}$ do not necessarily vanish at the Fermi level. The corrections to the energy due to finite size take the form

$$\begin{array}{ccc}\hfill E& =& L{ϵ}_{GS}\left(Q\right)-\epsilon \left(k^{\left(h\right)}\right)-\frac{1}{L}{\epsilon }^{\prime }\left(k^{\left(h\right)}\right)\delta k^{\left(h\right)}+\frac{\pi v_F}{6L}+\frac{2\pi v_F}{L}\left\{{\left(z\tilde{D}\right)}^2+\frac{1}{4}{\left[\frac{\Delta \tilde{N}}{z}\right]}^2\right\}.\hfill \end{array}$$

(43)

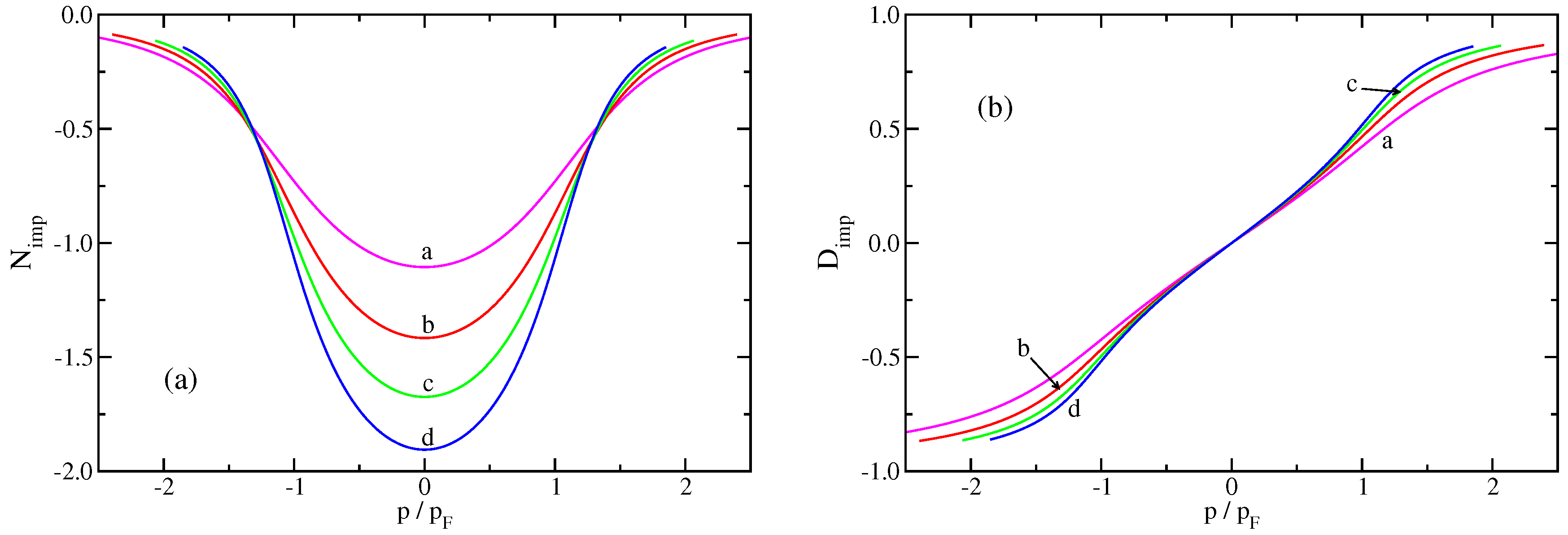
All of the above considerations for “hole” excitations are straightforwardly extended to “particle” excitations. In panel (a) of Figure 3 we show $N_{imp}$ and in panel (b) $D_{imp}$ as a function of the momentum of the excitation for several band fillings. Note that $N_{imp}$ is an even function of the momentum of the excitation, while $D_{imp}$ is an odd function of p.

Figure 3. (a) “Impurity” density $N_{imp}$ and (b) current density $D_{imp}$ as a function of the momentum for a high energy excitation. Note that $N_{imp}$ is an even function of the momentum and $D_{imp}$ is an odd function of the momentum. Here $c=1$ and the remaining parameters are (a) (magenta) $N/L=0.740$, $\mu =1.0$, and $Q=1.175$; (b) (red) $N/L=1.045$, $\mu =1.5$, and $Q=1.470$; (c) (green) $N/L=1.333$, $\mu =2.0$, and $Q=1.715$; (d) (blue) $N/L=1.620$, $\mu =2.5$, and $Q=1.935$.

4.5. Relation of the Bethe Ansatz with the Field Theoretical Quantities

We can now establish the relation between the field-theoretical and the Bethe ansatz approaches. For simplicity we are going to consider “holes”, for which $\Delta N=-1$, $D=0$. In Equation (24) the overlined quantities are proportional to $\Delta \tilde{N}$ and $\tilde{D}$. It follows that

$$N_{imp}\left(p\right)+\frac{\sqrt{K}}{2\pi }\left({\phi }_{+}-{\phi }_{-}\right)=0,-1+D_{imp}\left(p\right)+\frac{1}{2\pi \sqrt{K}}\left({\phi }_{+}+{\phi }_{-}\right),$$

(44)

or inverting these equations we have

$$\frac{{\phi }_{+}-{\phi }_{-}}{2\pi }=-\frac{N_{imp}\left(p\right)}{\sqrt{K}},\frac{{\phi }_{+}+{\phi }_{-}}{2\pi }=\sqrt{K}(1-D_{imp}\left(p\right)).$$

(45)

According to Reference [6] the critical exponent for the hole excitation is

$$\begin{array}{ccc}\hfill \underline{\mu }& =& 1-\frac{1}{2}{\left(\frac{2}{\sqrt{K}}+\frac{{\phi }_{+}-{\phi }_{-}}{2\pi }\right)}^2-\frac{1}{2}{\left(\frac{{\phi }_{+}+{\phi }_{-}}{2\pi }\right)}^2\hfill \\ & =& 1-\frac{1}{2K}{(2-N_{imp}\left(p\right))}^2-\frac{K}{2}{(1-D_{imp}\left(p\right))}^2,\hfill \end{array}$$

(46)

while for a particle excitation

$$\begin{array}{ccc}\hfill \overline{\mu }& =& 1-\frac{1}{2}{\left(\frac{{\phi }_{+}-{\phi }_{-}}{2\pi }\right)}^2-\frac{1}{2}{\left(\frac{{\phi }_{+}+{\phi }_{-}}{2\pi }\right)}^2\hfill \\ & =& 1-\frac{1}{2K}{N}_{imp}{\left(p\right)}^2-\frac{K}{2}{(1-D_{imp}\left(p\right))}^2.\hfill \end{array}$$

(47)

The values of the exponents at some special points have been established in Reference [6], e.g.,

$$\begin{array}{ccc}\hfill \overline{\mu }(p\to \infty )& =& 1.0,\overline{\mu }\left(p_F\right)=\frac{1}{\sqrt{K}}-\frac{1}{2K},\overline{\mu }(-p_F)=-2K+2\sqrt{K}+\frac{1}{\sqrt{K}}-\frac{1}{2K},\hfill \\ \hfill \underline{\mu }(p\to \infty )& =& 1-\frac{2}{K},\underline{\mu }\left(p_F\right)=-\frac{1}{\sqrt{K}}-\frac{1}{2K},\underline{\mu }(-p_F)=-2K+2\sqrt{K}-\frac{1}{\sqrt{K}}-\frac{1}{2K}.\hfill \end{array}$$

(48)

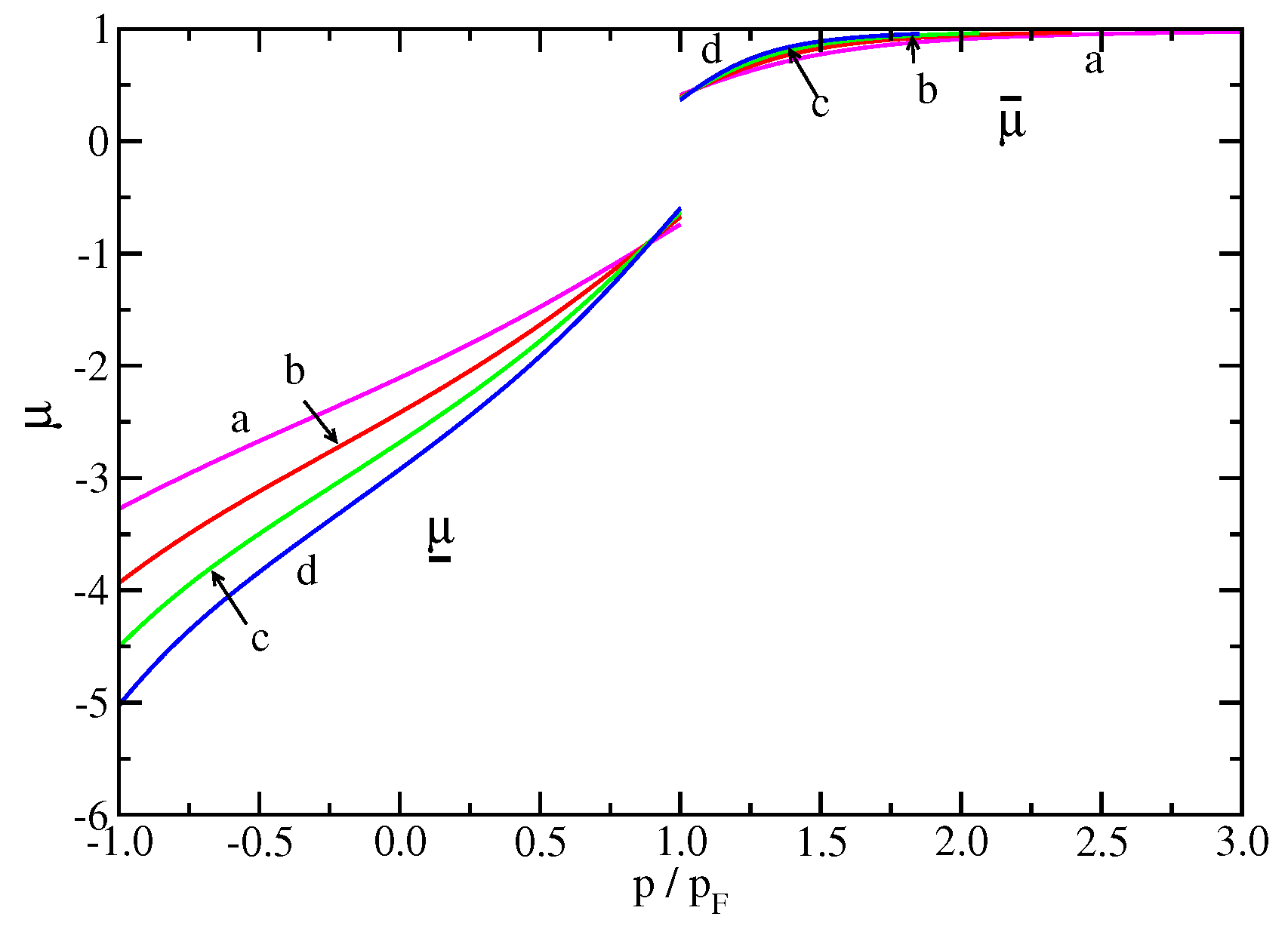
The critical exponents for particles and holes, $\overline{\mu }$ and $\underline{\mu }$, can now be evaluated and are shown in Figure 4. Note that the exponent for the particles in the regime $p\ge p_F$ is always positive indicating a divergence of the spectral function, while the one for the holes is negative for $-p_F\le p\le p_F$ and the spectral function tends to zero.

Figure 4. Critical exponents of the spectral function as a function of momentum for particles ($p\ge p_F$) and holes ($-p_F\le p\le p_F$). Here $c=1$ and the remaining parameters are (a) (magenta) $N/L=0.740$, $\mu =1.0$, and $Q=1.175$; (b) (red) $N/L=1.045$, $\mu =1.5$, and $Q=1.470$; (c) (green) $N/L=1.333$, $\mu =2.0$, and $Q=1.715$; (d) (blue) $N/L=1.620$, $\mu =2.5$, and $Q=1.935$.

The spectral function is then proportional to the following general form

$${\left|\frac{1}{\omega -\epsilon \left(p\right)}\right|}^{\mu },$$

(49)

where $\epsilon \left(p\right)>0$ with $\mu =\overline{\mu }$ for particles and $\epsilon \left(p\right)<0$ with $\mu =\underline{\mu }$ for holes. As noted by Imambekov and Glazman [6] the exponents show markedly non-Luttinger liquid behavior in the immediate vicinity of the edges. For the Luttinger liquid ${\mu }_{LL}=1-1/\left(4K\right)$ and $\epsilon \left(p\right)=v_F(p-p_F)$. Note that the conformal towers cannot give rise to a $\sqrt{K}$ dependence [6]. The difference between the exact results and the Luttinger liquid arises from the fact that $N_{imp}$ and $D_{imp}$ are not zero at the Fermi surface.

4.6. Agreement Between Phase Shifts From the Finite Size Corrections and the Shift Function

The phase shifts ${\phi }_{\pm }\left(p\right)$ can be obtained by more than one method, e.g., in Reference [7] the pseudofermion dynamical theory was employed, while in Reference [6] the phase shifts were obtained through the shift function. These two methods have been shown to be equivalent in Reference [7]. The shift function is defined as

$$F_B(k,k^{\left(h\right)})-\frac{1}{\pi }{\int }_{-Q}^{Q}d{k}^{\prime }\frac{c}{{(k-k^{\prime })}^2+c^2}{F}_B(k^{\prime },k^{\left(h\right)})=\frac{1}{2}+\frac{1}{\pi }arctan((k-k^{\left(h\right)})/c)$$

(50)

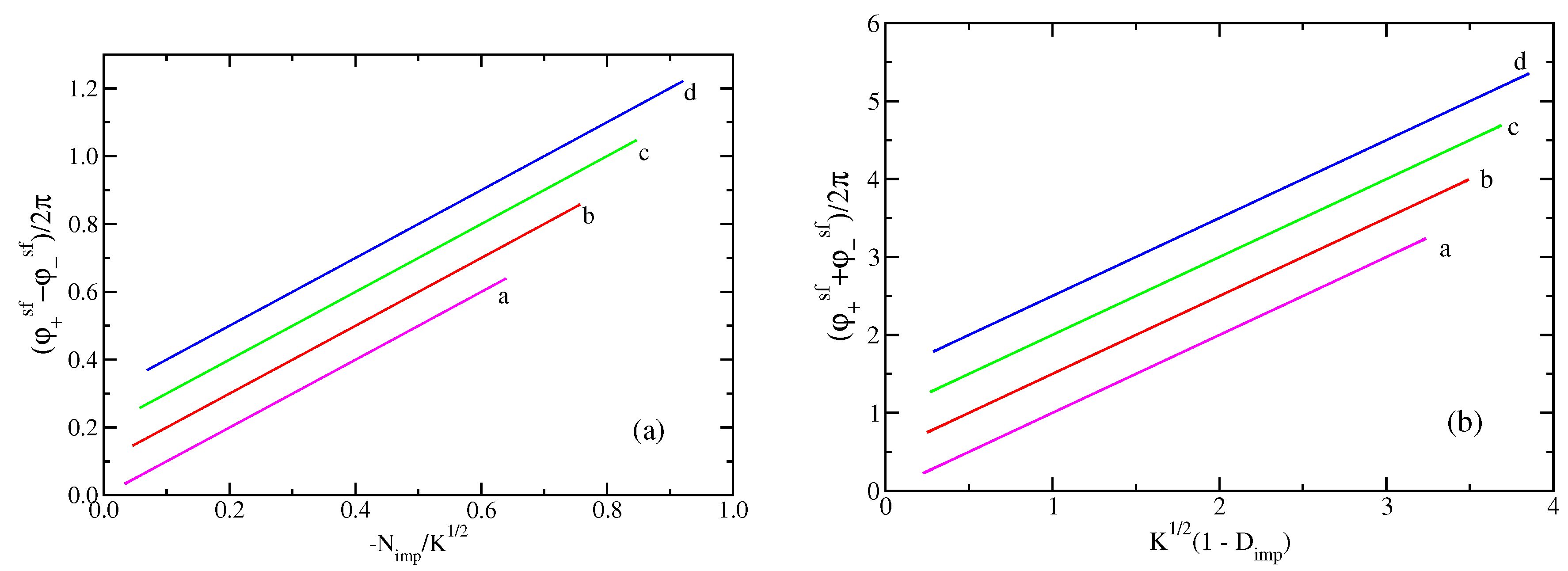
and the phase shifts are given by ${\phi }_{\pm }^{sf}\left(k^{\left(h\right)}\right)=2\pi F_B(\pm Q,k^{\left(h\right)})$. In Figure 5 we plot ${\phi }_{+}^{sf}\left(k^{\left(h\right)}\right)\pm {\phi }_{-}^{sf}\left(k^{\left(h\right)}\right)$ vs. the corresponding quantities in Equation (45) for four band fillings. The result is a straight line of slope one passing through the origin. For clarity, the lines for three of the band fillings are shown offset, namely lines (b), (c) and (d). This proves that the finite size correction method leads to results equivalent to those in References [6,7].

Figure 5. (a) Phase shift obtained from the shift function, ${\phi }_{+}^{sf}\left(k^{\left(h\right)}\right)-{\phi }_{-}^{sf}\left(k^{\left(h\right)}\right)$ vs. the “impurity” density, $-N_{imp}/\sqrt{K}$ and (b) phase shift obtained from the shift function, ${\phi }_{+}^{sf}\left(k^{\left(h\right)}\right)+{\phi }_{-}^{sf}\left(k^{\left(h\right)}\right)$ vs. the “impurity” current density $D_{imp}$, $\sqrt{K}(1-D_{imp})$. The corresponding expressions are equal, i.e., these are all straight lines with slope one that pass through the origin. For clarity, the red, green and blue lines have been offset. This proves that the methods are all equivalent. Here $c=1$ and the remaining parameters are (a) (magenta) $N/L=0.740$, $\mu =1.0$, and $Q=1.175$; (b) (red) $N/L=1.045$, $\mu =1.5$, and $Q=1.470$; (c) (green) $N/L=1.333$, $\mu =2.0$, and $Q=1.715$; (d) (blue) $N/L=1.620$, $\mu =2.5$, and $Q=1.935$.

5. Conclusions

We consider a 1D Bose gas interacting via a repulsive contact potential. This model is integrable and has been solved via Bethe’s ansatz [1,2,3]. Using a combination of the Bethe ansatz solution and field theory methods we derived the spectral function for particle and hole excitations with high energy. In analogy to other models investigated previously [6,8,9,10,11,12,15,16,33,34,35,36], we consider an effective model consisting of the Luttinger liquid coupled to a mobile impurity to obtain the time-dependence of the single particle Green’s function. The parametrization of the high energy-excited state as a mobile impurity allows to incorporate the exact excitation energy. Linearly coupling the impurity to the Luttinger liquid is analogous to the x-ray-threshold problem [21,22] and the arising power-law singularity in frequency or time is then the consequence of Anderson’s “infrared orthogonality catastrophe” [43]. As in Reference [10,11,16,18,20] the mobile impurity is justified via the exact the Bethe ansatz solution of the model. The phenomenological parameters of the field theoretical model are this way determined from the Bethe ansatz. The Luttinger liquid parameter K is related to the generalized dressed charge z ($K=z^2$). In addition, we obtain from the Bethe ansatz solution the exact energy of the excitation, and the momentum-dependent scattering phase shifts.

We employed a procedure consisting of calculating the $\mathcal{O}(1/L)$ terms of the energy using the discrete Bethe ansatz equations. The finite size corrections are evaluated for the system in the ground state including a high-energy particle or hole excitation. The conformal towers describe the low-energy excitations in a Luttinger liquid about the Fermi points. The present procedure extends the standard finite size terms to arbitrary excitations and consequently goes beyond the bosonization of fermions [4] and conformal field theory. By numerical comparison we have shown that the method is equivalent to calculating the phase shifts through the shift function [6] or the pseudofermion dynamical theory [7].