Abstract
The ferroelectric phase transition in RMnO3 breaks both Z3 and Z2 symmetries, giving rise to 6 structural domains. Topological protected vortices are formed at the junctions of all 6 domains, and the ferroelectric phase transition is closely related to these Z6 vortices. In this work, Monte-Carlo studies on both the ferroelectric and magnetic transition have been performed on RMnO3 system. The magnetic simulation results on lattices with different structural domain distributions induced by external electric field and simulated quenching show different magnetic transition temperature , indicating that the coupling of magnetism and ferroelectricity is through the Z6 structural domain. At extreme case, lattice quenched from above the ferroelectric transition results in high vortex density, which can drive the system into spin glass.
Multiferroics are materials that host magnetism and ferroelectricity in a single phase [1]. The potential of having magnetism and ferroelectricity coupling makes these materials of great importance both technologically and scientifically. Judging by the source of magnetism and ferroelectricity, multiferroics can be categorized into type-I and type-II: in type-I multiferroics the magnetism and ferroelectricity have different origins and are often well separated in transition temperatures, whereas in type-II multiferroics the magnetism is the cause of ferroelectricity [2,3,4]. As a typical type-I multiferroic, the hexagonal RMnO3 (R = Y, Lu, Sc, ⋯) becomes ferroelectric below 570–990 K when the crystal breaks the Z3 symmetry of the high temperature P63mmc phase through a structural instability of the Mn and O atoms due to trimerization [5,6,7]. The trimerization then leads to the rare earth atom splitting into two atomic sites which breaks the Z2 symmetry and gives rise to polarization, as illustrated in Figure 1b. The space group of the ferroelectric phase is P63cm [8]. Since the Mn atoms form triangular lattice in the xy-plane, the system becomes geometrically frustrated [9]. Below TN ∼ 90 K, the magnetic moment of Mn orders in a 120° arrangement [8,10]. The weak interaction between magnetism and ferroelectricity in RMnO3 was observed through in-plane dielectric anomaly [11].
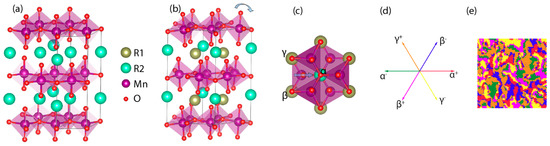
Figure 1.
(Color online.) Shown in (a,b) are the crystal structures of RMnO3 above and below the ferroelectric transition temperature TC, respectively. The arrow in (b) indicates the direction of the MnO5 bipyramid tilting (a.k.a. trimerization). In (c) shows the 6-symmetry equivalent trimerization directions, which correspond to the 6 structural domains as labeled in (d). Shown in (e) is a typical simulated lattice below TC.
The Z3 × Z2 symmetry breaking in the ferroelectric transition of RMnO3 creates 6 structural domains. As shown in Figure 1a–c, RMnO3 consists of corner sharing MnO5 bipyramid layers separated by the rare earth atom layers. From the top view, each MnO5 bipyramid is surrounded by 3 rare earth atoms (, , ). The trimerization involves tilting of the bipyramids towards one of the 6 symmetry equivalent directions: , , , , , , each of which corresponds to a structural domain [6]. This has been confirmed by observations using optics second harmonic generation, SEM, STM and AFM [6,12,13,14,15,16]. Both the magnetic and ferroelectric order parameters are confined in the xy-plane due to the crystal geometry [17]. Based on this feature, a 2D 6-fold clock model without microscopical details can be built for Monte-Carlo study of RMnO3 system [18]. Without external electric field, the Hamiltonian of the model has the following form:
Here represents direction of the bipyramid tilting on the ith unit cell, is the structural anisotropy coefficient, and is the coupling constant between the nearest neighbor . To simulate the hexagonal crystal structure of RMnO3, the Hamiltonian is defined on a triangular lattice. The first term determines 6 minima of the simulated variable: with , each corresponding to one of the 6 structural domains, as illustrated in Figure 1d. The second term introduces ferroelectric coupling between nearest neighbors with positive value of . The Metropolis Monte-Carlo algorithm is used to simulate the system. In each iteration, a unit cell i is chosen randomly. A random change is proposed to be added on , and will be accepted with probability , with being the corresponding change of the total energy and . A typical simulated lattice in the ferroelectric phase is shown in Figure 1e, where different domains are painted in different colors. The domain walls always cross at the junctions of all 6 domains, forming vortices, which are direct results of the Z3 × Z2 symmetry breaking. In the simulation the vortices always appear in two low-energy cyclic sequences: , , , , , and , , , , , , in agreement with the experimental observations [13,15,16]. In 3D the vortices in each xy-plane are connected, forming vortex loops [17,18].
The order parameter of this Z6 symmetry breaking transition is defined as:
If the variable goes through or across the 6 nearest neighbors of a site i, this site is classified as a vortex with positive or negative cyclic sequence. With this definition, the high temperature phase consists of high density of vortices. The polarization per site of the simulated lattice is calculated by:
Here is the unit dipole moment of a unit cell. With that the Hamiltonian with external electric field can be defined as:
The ferroelectric transition with different lattice sizes is simulated under zero electric field with , . The Z6 order parameter , the polarization P, the heat capacity C and the density of Z6 vortices are plotted as functions of simulated temperature in Figure 2a,b,d,e, respectively. The simulation clearly showed two transitions: T1.8 marks the temperature where the vortex density drops, and T0.7 is associated with the onset of polarization. It is known that a 2D xy model does not yield any 1st or 2nd order phase transition, but can give rise to the Kosterliz-Thouless (KT) transition [19]. Previous theoretical works have shown that the 2D 6-state clock model can go from disorder to order through either an Ising transition plus a 3-state Potts transition or two KT transitions [20]. Numerical study on systems with similar Z6 symmetry breaking shows evidence of 2 KT transitions with a critical phase in between [21,22]. As shown in Figure 2a,b,d,e, the two transitions we observed exhibit little lattice-size dependence. Finite size scaling analysis on these two transitions supports neither Ising transition nor Potts transition. Therefore the two ferroelectric transitions in our model are most likely KT transitions. Shown in Figure 2c are the simulation results of polarization as a function of the electric field E in a temperature range of 0.26∼2.51 on a lattice. Initially the lattice was fully polarized by negative field. The external electric field was then gradually increased. The simulated lattice reached equilibrium at each field point. Below the system shows a clear ferroelectric hysteresis. Between and the system shows paraelectric behavior with a non-linear P-E curve, similar to the superparaelectric P-E curve observed in relaxor ferroelectrics [23,24]. Above the system becomes a normal paraelectric with linear P-E curve. The superparaelectric behavior between and suggest that the system is in a critical phase with infinite correlation length, which further supports that the two observed transition is KT type. The results of the simulation on the ferroelectric variable with zero electric field demonstrate that the Z6 symmetry breaking in our model is achieved through two KT transitions. First the system breaks Z3 symmetry, indicated by the decrease of vortex density, then the system breaks Z2 symmetry, leading to non-zero polarization. This two-step nature of the ferroelectric transition in RMnO3 has been observed experimentally [25]. The lattice responds to external electric field is in agreement with experimental results [15,16,26].
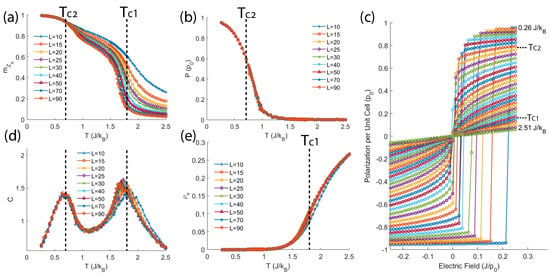
Figure 2.
(Color online.) Above shows the simulation results on the ferroelectric part of the model. First, the ferroelectric transition with different lattice sizes is simulated under zero electric field. The Z6 order parameter , the polarization P, the heat capacity C and the density of Z6 vortices are plotted as functions of simulated temperature in (a,b,d,e), respectively. Second, the responds of an lattice to the external electric field in temperature range of 0.26∼2.51 are demonstrated in (c).
On top of the 6-fold clock model for ferroelectricity of the system, a 2D xy model for spin order can be added by introducing the following Hamiltonian [27]:
Here the variable represents the magnetic ordering within the ith unit cell, and the variable takes the ferroelectric domain of that unit cell into account. represents the single-ion anisotropy for spin, and is the coupling constant between the nearest neighbor . The magnetization per site in the jth structural domain is calculated by:
with representing the magnetic moment within a unit cell, and being the size of the jth domain. If fixing the ferroelectric variable across the whole lattice, the spin part of the model is equivalent to a 2D Ising model under strong anisotropy term . By averaging among different structural domains the magnetic order parameter of the whole lattice is defined as:
With only one structural domain, the magnetic order parameter is Ising like with reasonably large anisotropy . It is then interesting to study how the magnetic transition behaves when the lattice exhibits different level of complexity in structural domain distribution. Since the ferroelectric transition temperature of RMnO3 is an order of magnitude larger than its magnetic transition temperature, the value of the parameters in were chosen to be . Shown in Figure 3a are six simulated lattices with different structural domain distributions. The ‘slow cooled’ lattice was simulated by gradually decreasing the temperature from above to . The ‘quenched’ lattices were simulated by abruptly changing the temperature from the labeled values to . The ‘polarized’ lattice was created by applying positive electric field on the ‘slow cooled’ lattice. The simulation results of the magnetic order on these lattices plus a trivial single domain case are shown in Figure 3b,c in the form of magnetization and magnetic susceptibility. With increased structural domain complexity and decreased average domain size, the magnetic moments order with a lower transition temperature and a lower saturated magnetization at base temperature. Previous works have shown coupling between magnetoelastic coupling in this system using inelastic neutron scattering and ultrasonic measurements [28,29]. In our model, the only thing that couples the magnetism and ferroelectricity is the term in Equation (3), where the first nearest neighbor coupling of the magnetic moment is weakened if the two neighbors belong to different ferroelectric domains. When the structural domain becomes more complex, the frequently changing induces disorder in the coupling constant , which drives the system towards the Edwards-Anderson model for spin glass [30]. In fact, the magnetic susceptibility curves of the ‘quenched at 1.7 ’ and ‘quenched at 1.9 ’ lattices shown in the inset of Figure 3c is very similar to the no-field-cooling curve of a spin glass. In conclusion, our Monte-Carlo simulation work demonstrates that the magnetism and the ferroelectricity in the type-I multiferroic material RMnO3 can still be coupled through the structural domains, and that in extreme case the high vortex density can drive the system into a spin glass state.
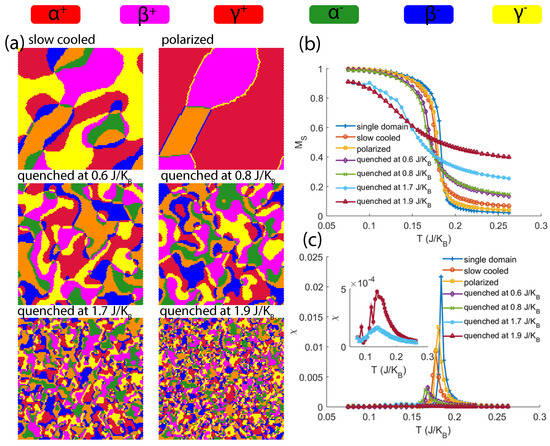
Figure 3.
(Color online.) Shown in (a) are six simulated lattices with different structural domain distributions. The magnetic order parameters and susceptibilities of the six lattices plus a single domain case are plotted in (b,c) as functions of temperature. The inset in (c) are zoomed-in plot of the susceptibility curves of the last two quenched lattices.
Author Contributions
Conceptualization, D.L., G.-W.C. and C.D.; methodology, G.-W.C.; data curation, C.D.; formal analysis, C.D.; writing—original draft, C.D.; writing—review & editing, G.-W.C., D.L.; supervision, D.L.
Funding
This research was funded by the US Department of Energy, Office of Basic Energy Science, DE-FG02-01ER45927.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Spaldin, N.A. MATERIALS SCIENCE: The Renaissance of Magnetoelectric Multiferroics. Science 2005, 309, 191–192. [Google Scholar] [CrossRef] [PubMed]
- Kimura, T.; Goto, T.; Shintani, H.; Ishizaka, K.; Arima, T.; Tokura, Y. Magnetic Control of Ferroelectric Polarization. Nature 2003, 426, 55–58. [Google Scholar] [CrossRef] [PubMed]
- Hur, N.; Park, S.; Sharma, P.A.; Ahn, J.S.; Guha, S.; Cheong, S.W. Electric Polarization Reversal and Memory in a Multiferroic Material Induced by Magnetic Fields. Nature 2004, 429, 392–395. [Google Scholar] [CrossRef] [PubMed]
- Khomskii, D. Classifying Multiferroics: Mechanisms and Effects. Physics 2009, 2, 20. [Google Scholar] [CrossRef]
- Yakel, H.L., Jr.; Koehler, W.C.; Bertaut, E.F.; Forrat, E.F. On the Crystal Structure of the Manganese(III) Trioxides of the Heavy Lanthanides and Yttrium. Acta Crystallograph. 1963, 16, 957–962. [Google Scholar] [CrossRef]
- Choi, T.; Horibe, Y.; Yi, H.T.; Choi, Y.J.; Wu, W.; Cheong, S.W. Insulating Interlocked Ferroelectric and Structural Antiphase Domain Walls in Multiferroic YMnO3. Nat. Mater. 2010, 9, 253–258. [Google Scholar] [CrossRef] [PubMed]
- Aikawa, Y.; Katsufuji, T.; Arima, T.; Kato, K. Effect of Mn Trimerization on the Magnetic and Dielectric Properties of Hexagonal YMnO3. Phys. Rev. B 2005, 71, 184418. [Google Scholar] [CrossRef]
- Tomuta, D.G.; Ramakrishnan, S.; Nieuwenhuys, G.J.; Mydosh, J.A. The Magnetic Susceptibility, Specific Heat and Dielectric Constant of Hexagonal YMnO3, LuMnO3 and ScMnO3. J. Phys. Condens. Matter 2001, 13, 4543–4552. [Google Scholar] [CrossRef]
- Katsufuji, T.; Mori, S.; Masaki, M.; Moritomo, Y.; Yamamoto, N.; Takagi, H. Dielectric and Magnetic Anomalies and Spin Frustration in Hexagonal RMnO3 (R = Y, Yb, and Lu). Phys. Rev. B 2001, 64, 104419. [Google Scholar] [CrossRef]
- Muñoz, A.; Alonso, J.A.; Martínez-Lope, M.J.; Casáis, M.T.; Martínez, J.L.; Fernández-Díaz, M.T. Magnetic Structure of Hexagonal RMnO3 (R = Y, Sc): Thermal Evolution From Neutron Powder Diffraction Data. Phys. Rev. B 2000, 62, 9498–9510. [Google Scholar] [CrossRef]
- Tian, W.; Tan, G.; Liu, L.; Zhang, J.; Winn, B.; Hong, T.; Fernandez-Baca, J.A.; Zhang, C.; Dai, P. Influence of Doping on the Spin Dynamics and Magnetoelectric Effect in Hexagonal Y0.7Lu0.3MnO3. Phys. Rev. B 2014, 89, 144417. [Google Scholar] [CrossRef]
- Fiebig, M.; Lottermoser, T.; Fröhlich, D.; Goltsev, A.V.; Pisarev, R.V. Observation of Coupled Magnetic and Electric Domains. Nature 2002, 419, 818–820. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Yang, H.X.; Tian, H.F.; Ma, C.; Zhang, S.; Zhao, Y.G.; Li, J.Q. Scanning Secondary-Electron Microscopy on Ferroelectric Domains and Domain Walls in YMnO3. Appl. Phys. Lett. 2012, 100, 152903. [Google Scholar] [CrossRef]
- Lottermoser, T.; Lonkai, T.; Amann, U.; Hohlwein, D.; Ihringer, J.; Fiebig, M. Magnetic Phase Control by an Electric Field. Nature 2004, 430, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Chae, S.C.; Lee, N.; Horibe, Y.; Tanimura, M.; Mori, S.; Gao, B.; Carr, S.; Cheong, S.W. Direct Observation of the Proliferation of Ferroelectric Loop Domains and Vortex-Antivortex Pairs. Phys. Rev. Lett. 2012, 108, 167603. [Google Scholar] [CrossRef] [PubMed]
- Chae, S.C.; Horibe, Y.; Jeong, D.Y.; Lee, N.; Iida, K.; Tanimura, M.; Cheong, S.W. Evolution of the Domain Topology in a Ferroelectric. Phys. Rev. Lett. 2013, 110, 167601. [Google Scholar] [CrossRef] [PubMed]
- Rowley, S.E.; Lonzarich, G.G. Ferroelectrics in a Twist. Nat. Phys. 2014, 10, 907–908. [Google Scholar] [CrossRef]
- Lin, S.; Wang, X.; Kamiya, Y.; Chern, G.W.; Fan, F.; Fan, D.; Casas, B.; Liu, Y.; Kiryukhin, V.; Zurek, W.H.; et al. Topological Defects as Relics of Emergent Continuous Symmetry and Higgs Condensation of Disorder in Ferroelectrics. Nat. Phys. 2014, 10, 970–977. [Google Scholar] [CrossRef]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, Metastability and Phase Transitions in Two-dimensional Systems. J. Phys. C Solid State Phys. 1973, 6, 1181. [Google Scholar] [CrossRef]
- Cardy, J.L. General Discrete Planar Models in Two Dimensions: Duality Properties and Phase Diagrams. J. Phys. A Math. Gener. 1980, 13, 1507–1515. [Google Scholar] [CrossRef]
- Chern, G.W.; Tchernyshyov, O. Magnetic Charge and Ordering in Kagome Spin Ice. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2012, 370, 5718–5737. [Google Scholar] [CrossRef] [PubMed]
- Challa, M.S.; Landau, D.P. Critical Behavior of the Six-state Clock Model in Two Dimensions. Phys. Rev. B 1986, 33, 437–443. [Google Scholar] [CrossRef]
- Skulski, R. Superparaelectric Behaviours of Relaxor Ferroelectrics. Mater. Sci. Eng. B 1999, 64, 39–43. [Google Scholar] [CrossRef]
- Cross, L.E. Relaxor Ferroelectrics. Ferroelectrics 1987, 76, 241–267. [Google Scholar] [CrossRef]
- Skjærvø, S.H.; Meier, Q.; Feygenson, M.; Spaldin, N.A.; Billinge, S.J.L.; Bozin, E.S.; Selbach, S.M. Unconventional Order-disorder Phase Transition in Improper Ferroelectric Hexagonal Manganites. arXiv, 2017; arXiv:1707.09649. [Google Scholar]
- Wang, X.; Mostovoy, M.; Han, M.G.; Horibe, Y.; Aoki, T.; Zhu, Y.; Cheong, S.W. Unfolding of Vortices into Topological Stripes in a Multiferroic Material. Phys. Rev. Lett. 2014, 112, 247601. [Google Scholar] [CrossRef] [PubMed]
- Artyukhin, S.; Delaney, K.T.; Spaldin, N.A.; Mostovoy, M. Landau Theory of Topological Defects in Multiferroic Hexagonal Manganites. Nat. Mater. 2013, 13, 42–49. [Google Scholar] [CrossRef] [PubMed]
- Poirier, M.; Laliberté, F.; Pinsard-Gaudart, L.; Revcolevschi, A. Magnetoelastic Coupling in Hexagonal Multiferroic YMnO3 Using Ultrasound Measurements. Phys. Rev. B 2007, 76, 174426. [Google Scholar] [CrossRef]
- Petit, S.; Moussa, F.; Hennion, M.; Pailhès, S.; Pinsard-Gaudart, L.; Ivanov, A. Spin Phonon Coupling in Hexagonal Multiferroic YMnO3. Phys. Rev. Lett. 2007, 99, 266604. [Google Scholar] [CrossRef] [PubMed]
- Edwards, S.F.; Anderson, P.W. Theory of Spin Glasses. J. Phys. F Met. Phys. 1975, 5, 965. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).