Suppression of Quantum-Mechanical Collapse in Bosonic Gases with Intrinsic Repulsion: A Brief Review
Abstract
:1. Introduction
2. The Basic Three- and Two-Dimensional Models
2.1. The Quantum Collapse in the Linear Schrödinger Equation
2.2. The Three-Dimensional Ground State (GS) Created by the Cubic Self-Repulsive Nonlinearity
2.3. The Quantum Phase Transition Induced by the Lee–Huang–Yang (LHY) Correction to the Mean-Field Theory
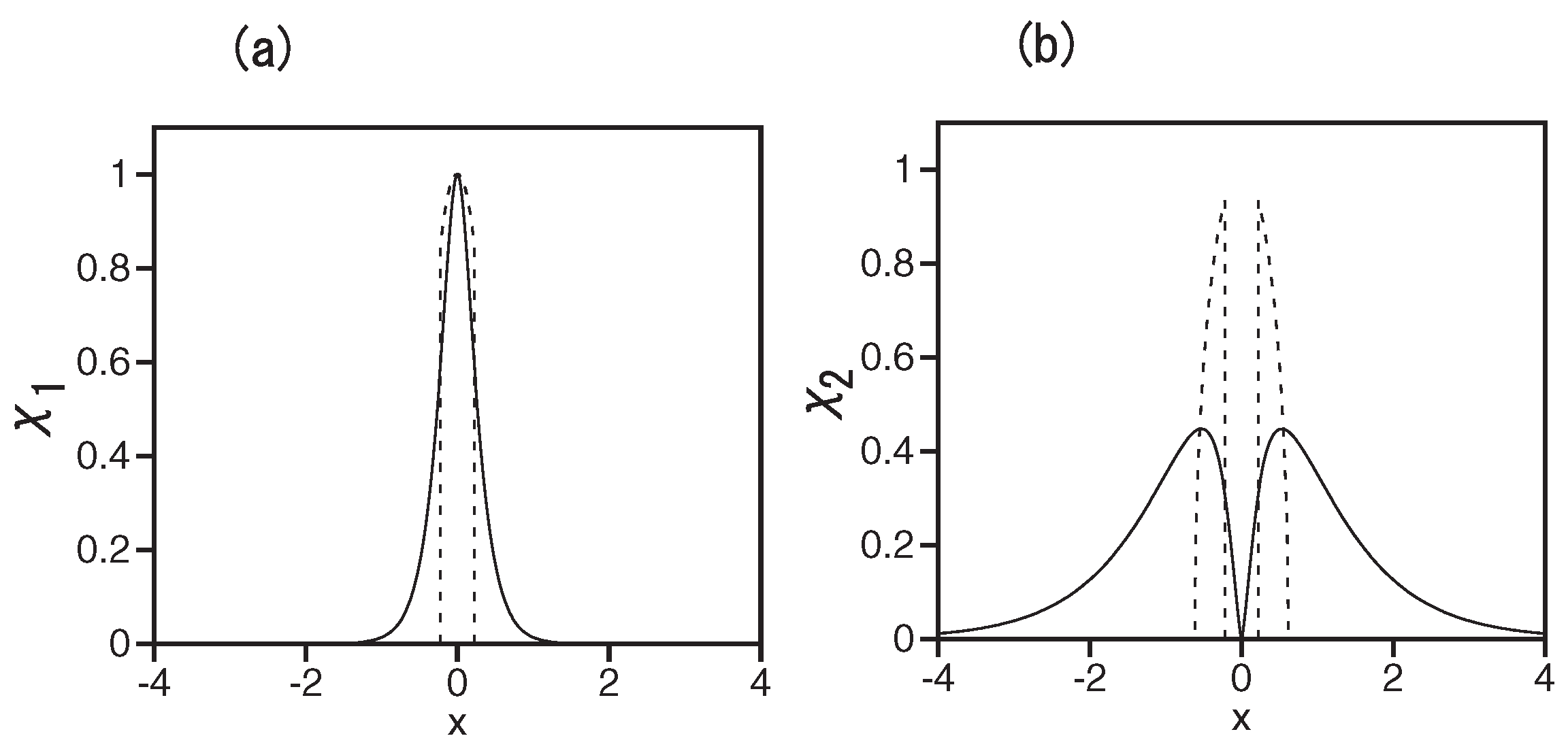
2.4. The Two-Dimensional Ground State Created by the Quintic Self-Repulsive Nonlinearity
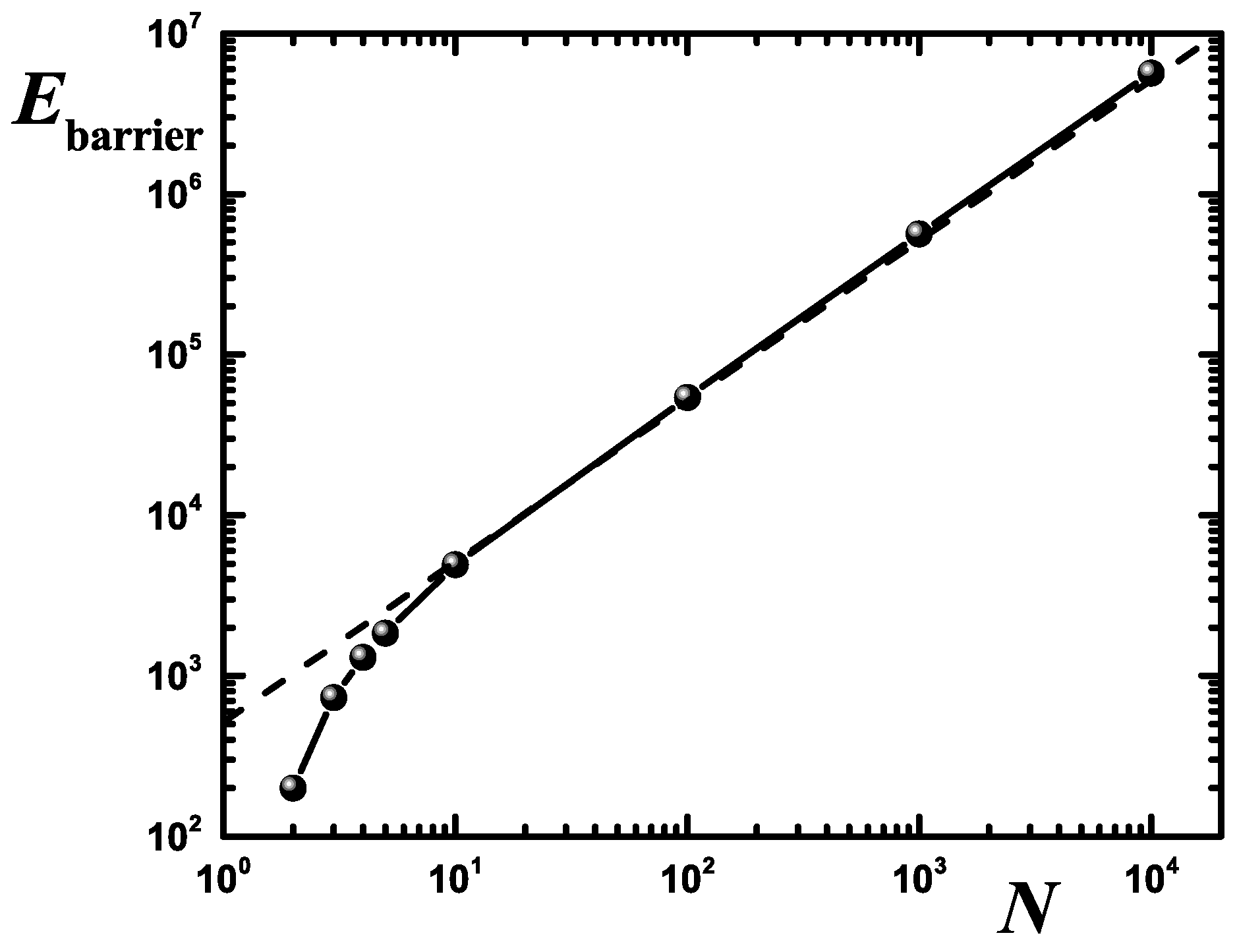
2.5. A Challenging Issue: The Fermi Gas Pulled to the Center
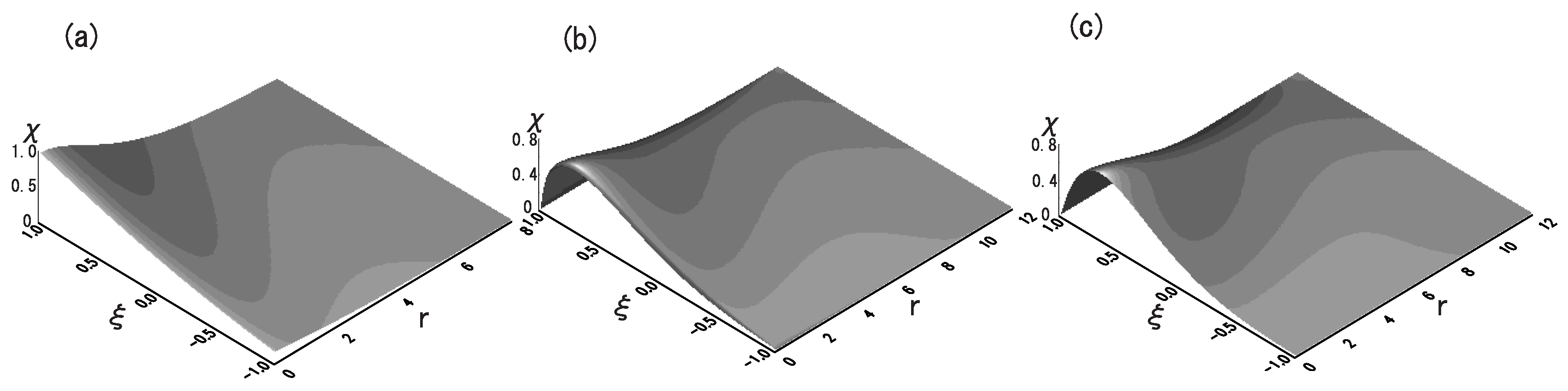
3. The Three-Dimensional Model with Cylindrical Symmetry
3.1. Formulation of the Model
3.2. The Linear Schrödinger Equation with Cylindrical Symmetry
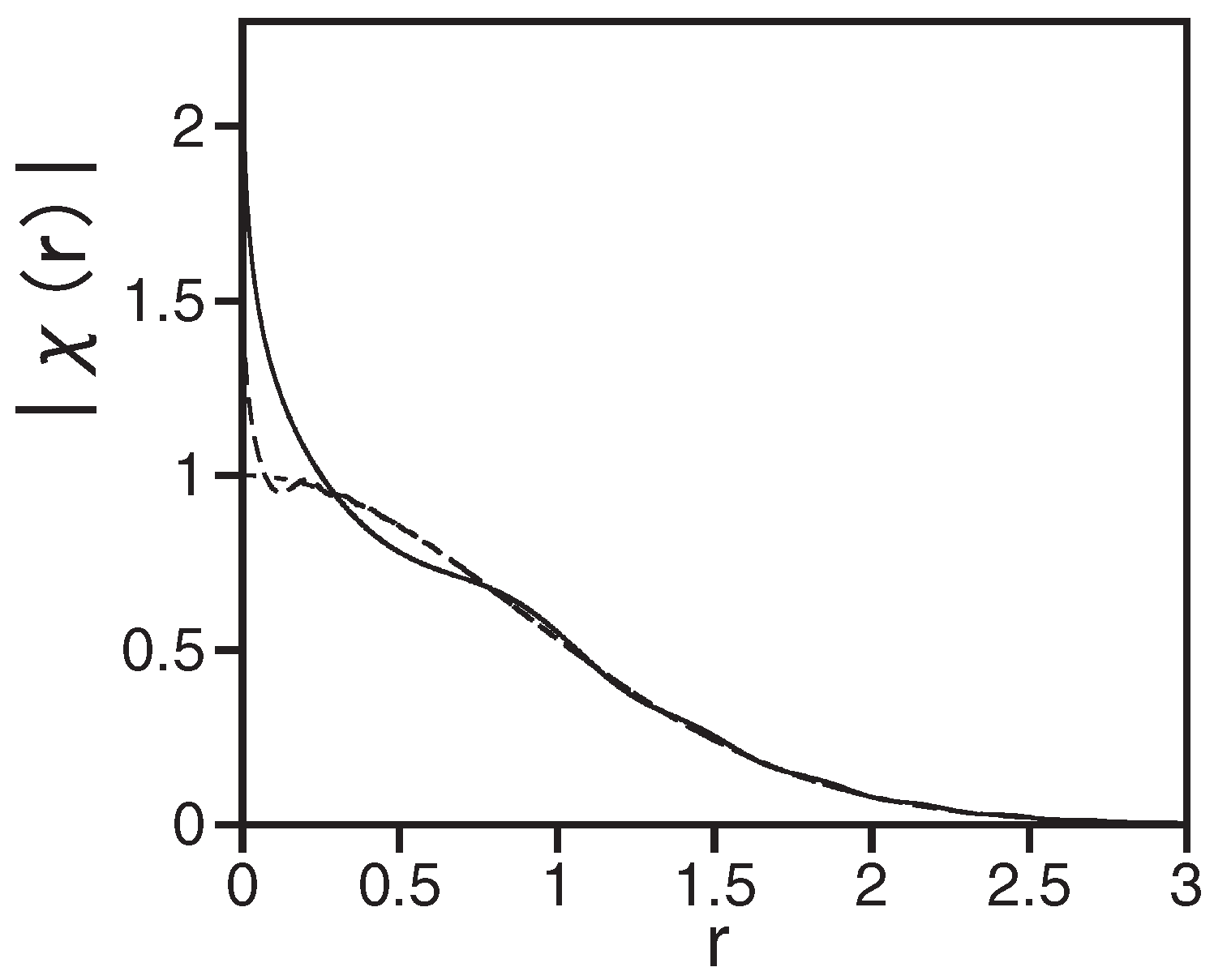
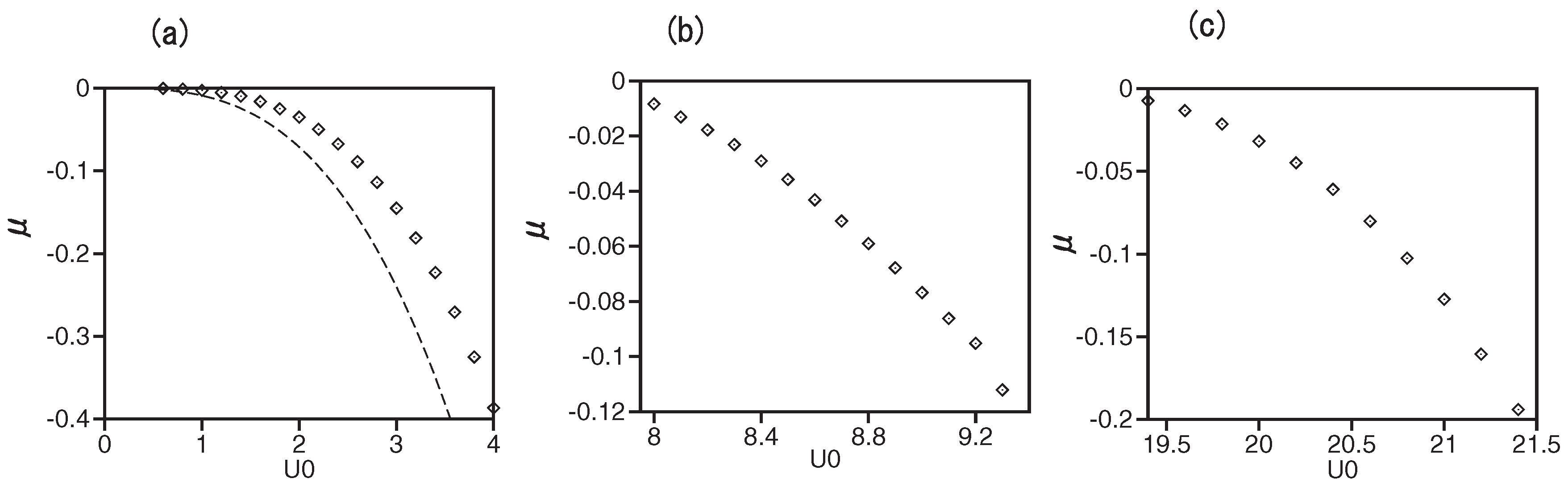
3.3. Suppression of the Quantum Collapse by the Repulsive Nonlinearity under the Cylindrical Symmetry
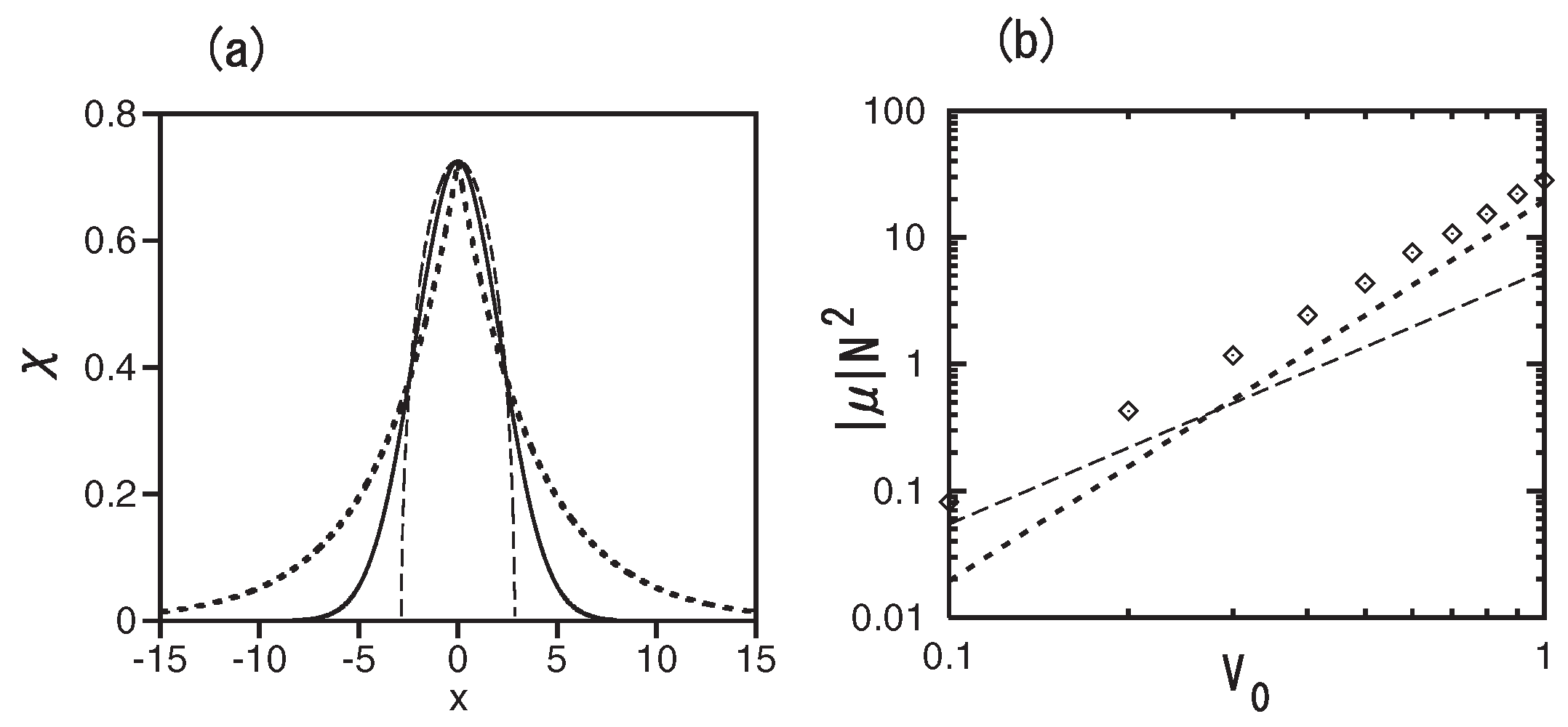
4. The Two-Component System in Three Dimensions: The Suppression of Quantum Collapse in Miscible and Immiscible Settings
4.1. The Formulation of the Model and Analytical Considerations
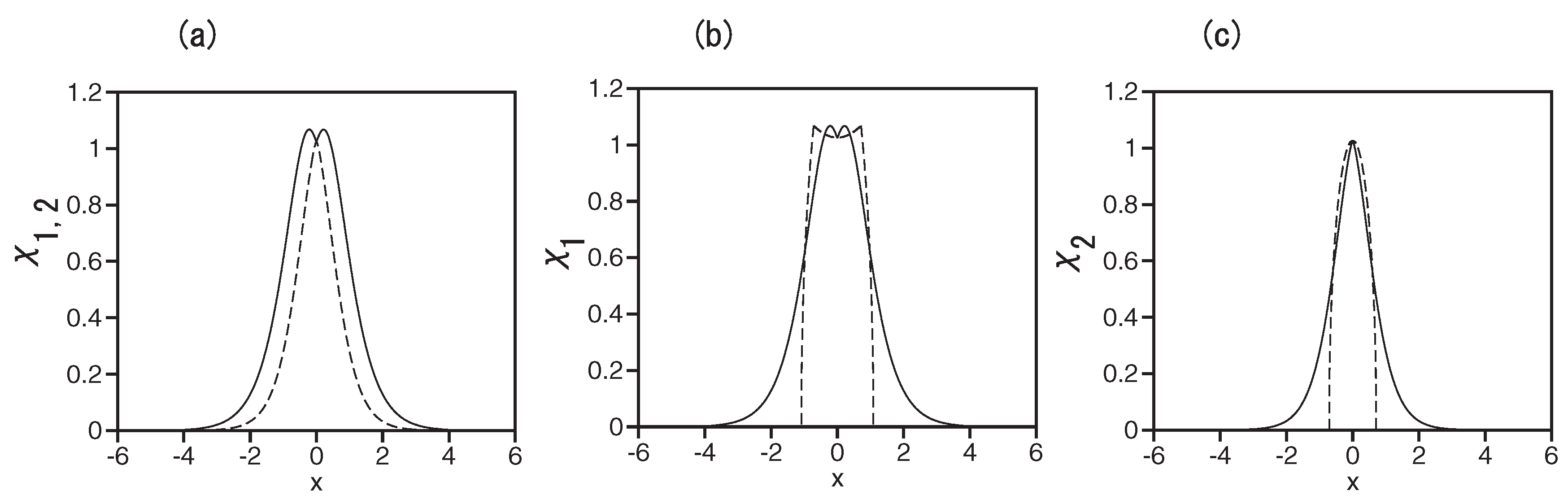
4.2. Numerical and Additional Analytical Results for Trapped Binary Modes
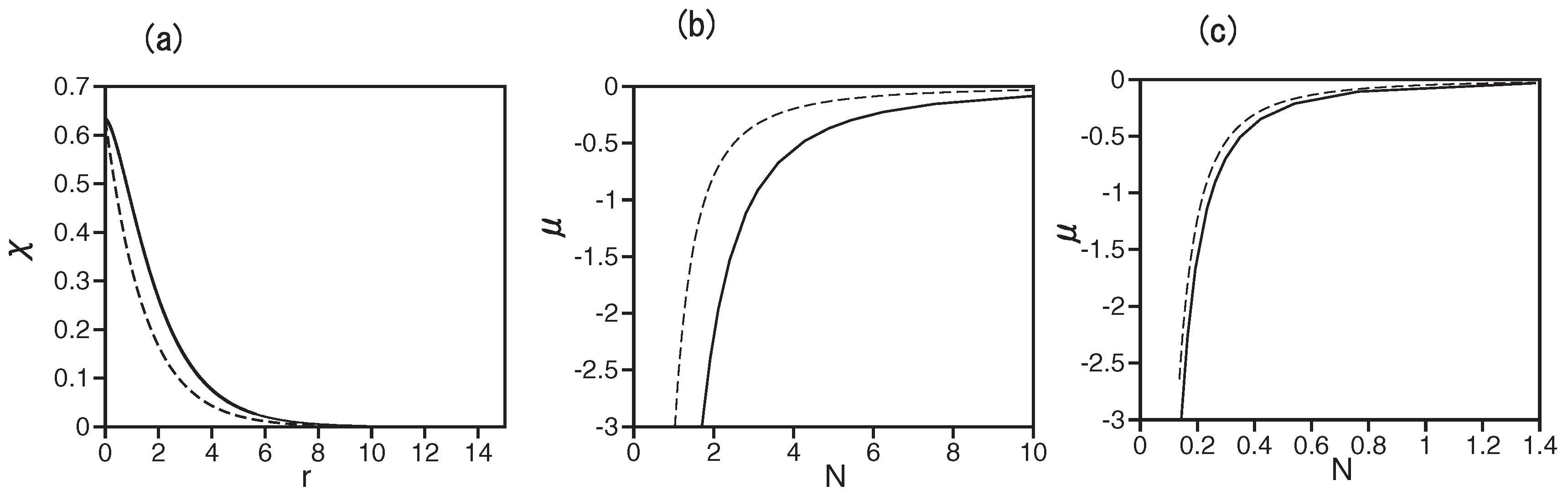
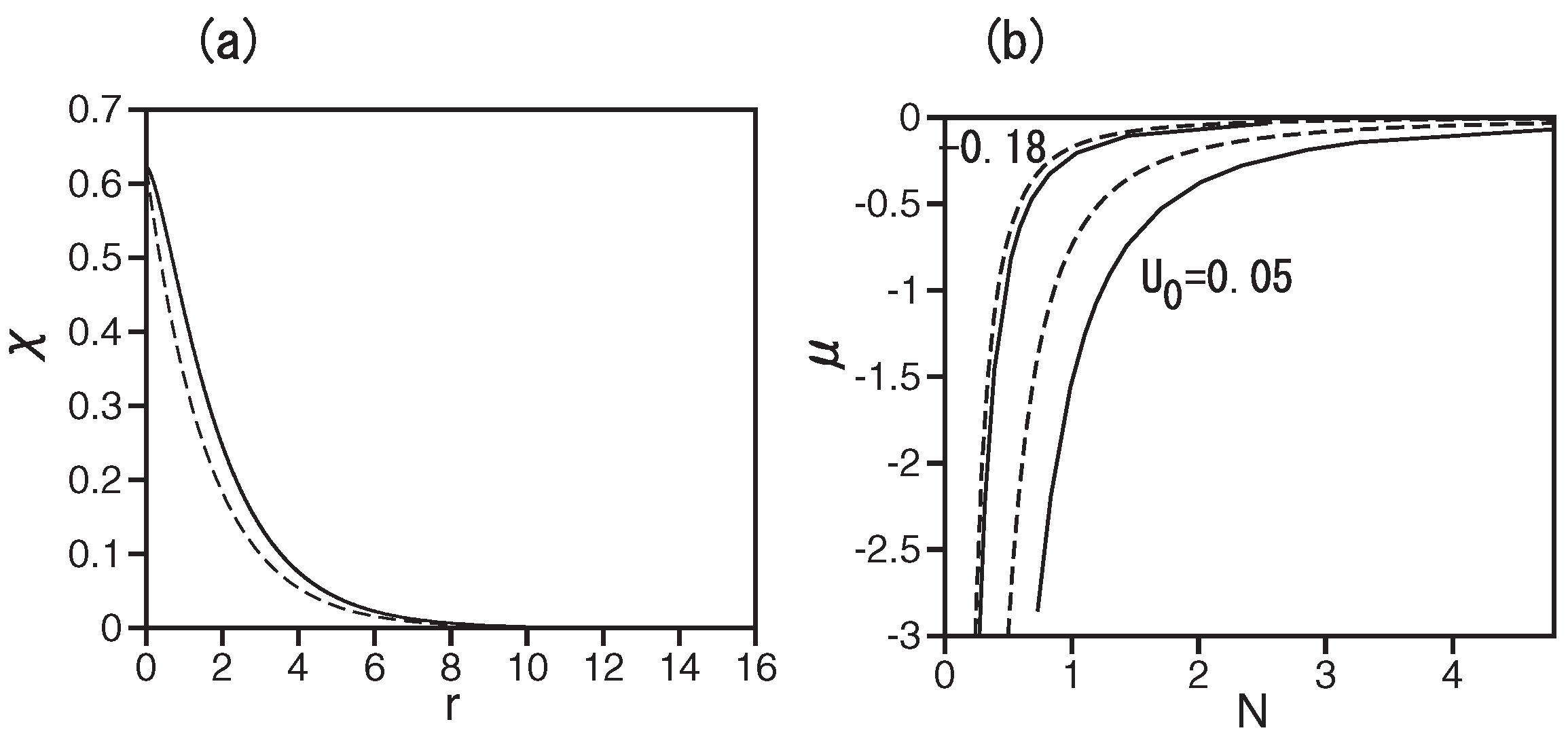
4.2.1. Mixed Ground States
4.2.2. The Immiscible Ground State
5. The Mean-Field Predictions versus the Many-Body Quantum Theory
5.1. Introduction to the Section
5.2. The Single-Particle Solution
5.3. The Monte-Carlo Method
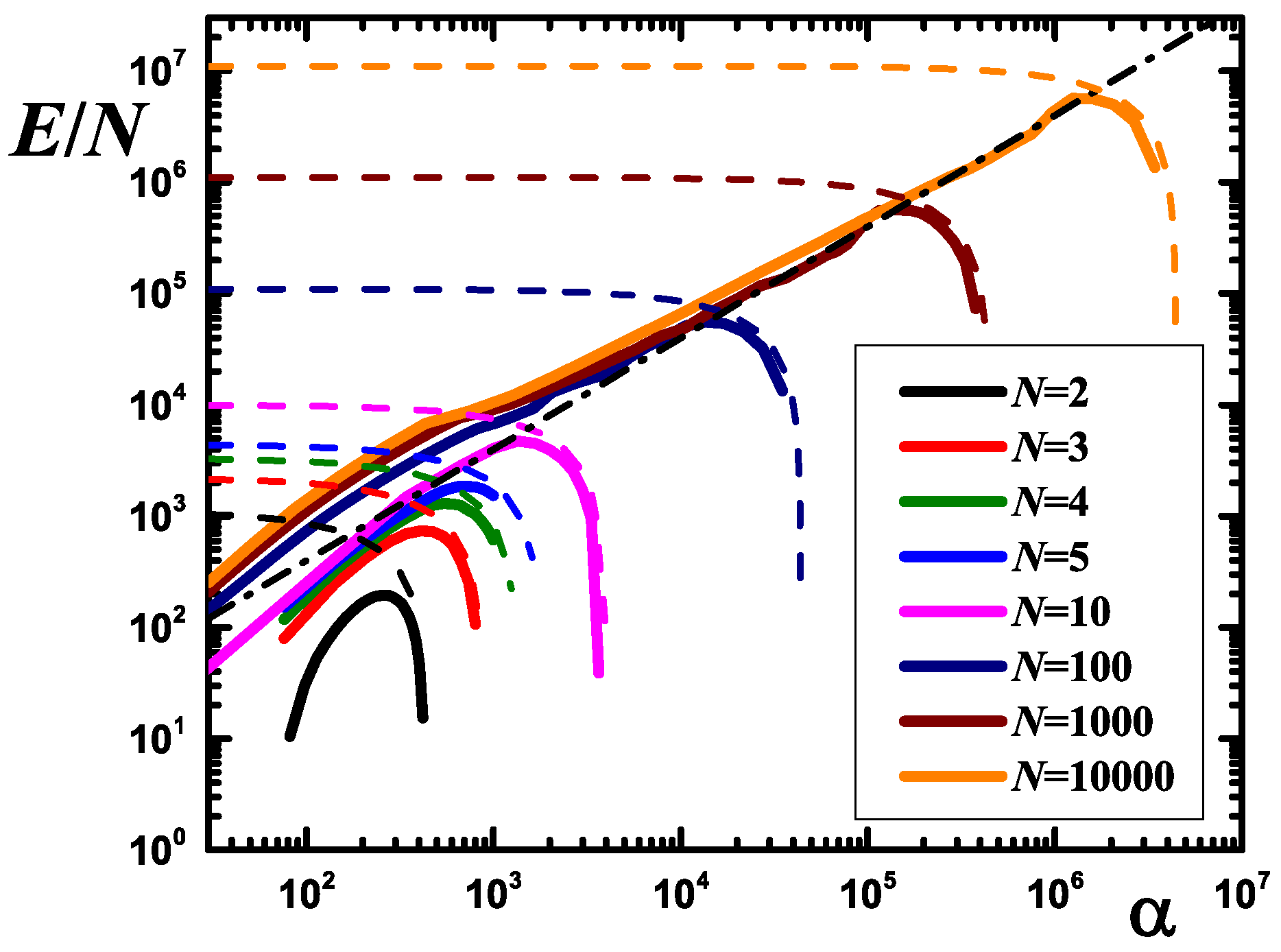
5.4. Numerical Results for the Many-Body System
6. Discussion and Conclusions
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | two-dimensional |
| 3D | three-dimensional |
| BEC | Bose–Einstein condensate |
| GPE | Gross–Pitaevskii equation |
| LHY | Lee–Huang–Yang (correction to the mean-field theory) |
| GS | ground state |
| rms | root-mean-square (value) |
| TFA | Thomas–Fermi approximation |
References
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Nonrelativistic Theory; Nauka Publishers: Moscow, Russia, 1974. [Google Scholar]
- Gupta, K.S.; Rajeev, S.G. Renormalization in quantum mechanics. Phys. Rev. D 1993, 48, 5940–5945. [Google Scholar] [CrossRef]
- Camblong, H.E.; Epele, L.N.; Fanchiotti, H.; Canal, C.A.G. Renormalization of the Inverse Square Potential. Phys. Rev. Lett. 2000, 85, 1590–1593. [Google Scholar] [CrossRef] [PubMed]
- Ávila-Aoki, M.; Cisneros, C.; Martínez-y-Romero, R.P.; Núñez-Yepez, H.N.; Salas-Brito, A.L. Classical and quantum motion in an inverse square potential. Phys. Lett. A 2009, 373, 418–421. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Suppression of the quantum-mechanical collapse by repulsive interactions in a quantum gas. Phys. Rev. A 2011, 83, 013607. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Suppression of the quantum collapse in an anisotropic gas of dipolar bosons. Phys. Rev. A 2011, 84, 033616. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Suppression of the quantum collapse in binary bosonic gases. Phys. Rev. A 2013, 88, 043638. [Google Scholar] [CrossRef]
- Pitaevskii, L.; Stringari, S. Bose–Einstein Condensation; Clarendon: Oxford, UK, 2003. [Google Scholar]
- Schmid, S.; Härter, A.; Denschlag, J.H. Dynamics of a cold trapped Ion in a Bose–Einstein condensate. Phys. Rev. Lett. 2010, 105, 133202. [Google Scholar] [CrossRef] [PubMed]
- Deiglmayr, J.; Grochola, A.; Repp, M.; Mörtlbauer, K.; Glück, C.; Lange, J.; Dulieu, O.; Wester, R.; Weidemüller, M. Formation of ultracold polar molecules in the rovibrational ground state. Phys. Rev. Lett. 2008, 101, 133004. [Google Scholar] [CrossRef] [PubMed]
- Ospelkaus, S.; Ni, K.-K.; Quéméner, G.; Neyenhuis, B.; Wang, D.; de Miranda, M.H.G.; Bohn, J.L.; Ye, J.; Jin, D.S. Controlling the hyperfine state of rovibronic ground-state polar molecules. Phys. Rev. Lett. 2010, 104, 030402. [Google Scholar] [CrossRef] [PubMed]
- Posazhennikova, A. Colloquium: Weakly interacting, dilute Bose gases in 2D. Rev. Mod. Phys. 2006, 78, 1111–1134. [Google Scholar] [CrossRef]
- Denschlag, J.; Schmiedmayer, J. Scattering a neutral atom from a charged wire. Europhys. Lett. 1997, 38, 405–410. [Google Scholar] [CrossRef]
- Olshanii, M.; Perrin, H.; Lorent, V. Example of a quantum anomaly in the physics of ultracold gases. Phys. Rev. Lett. 2010, 105, 095302. [Google Scholar] [CrossRef] [PubMed]
- Bergé, L. Wave collapse in physics: Principles and applications to light and plasma waves. Phys. Rep. 1998, 303, 259–370. [Google Scholar] [CrossRef]
- Dodd, R.J. Approximate solutions of the nonlinear Schrödinger equation for ground and excited states of Bose–Einstein condensates. J. Res. Natl. Inst. Stand. Technol. 1996, 101, 545–552. [Google Scholar] [CrossRef] [PubMed]
- Dalfovo, F.; Stringari, S. Bosons in anisotropic traps: Ground state and vortices. Phys. Rev. A 1996, 53, 2477–2485. [Google Scholar] [CrossRef] [PubMed]
- Alexander, T.J.; Bergé, L. Ground states and vortices of matter-wave condensates and optical guided waves. Phys. Rev. E 2002, 65, 026611. [Google Scholar] [CrossRef] [PubMed]
- Malomed, B.A.; Lederer, F.; Mazilu, D.; Mihalache, D. On stability of vortices in three-dimensional self-attractive Bose–Einstein condensates. Phys. Lett. A 2007, 361, 336–340. [Google Scholar] [CrossRef]
- Lee, T.D.; Huang, K.; Yang, C.N. Eigenvalues and eigenfunctions of a Bose system of hard spheres and its low-temperature properties. Phys. Rev. 1957, 106, 1135–1145. [Google Scholar] [CrossRef]
- Astrakharchik, G.E.; Malomed, B.A. Quantum versus mean-field collapse in a many-body system. Phys. Rev. A 2015, 92, 043632. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Solitons in combined linear and nonlinear lattice potentials. Phys. Rev. A 2010, 81, 013624. [Google Scholar] [CrossRef]
- Vakhitov, M.; Kolokolov, A. Stationary solutions of the wave equation in a medium with nonlinearity saturation. Radiophys. Quantum Electron. 1973, 16, 783–789. [Google Scholar] [CrossRef]
- Petrov, D.S. Quantum mechanical stabilization of a collapsing Bose-Bose mixture. Phys. Rev. Lett. 2015, 115, 155302. [Google Scholar] [CrossRef] [PubMed]
- Petrov, D.S.; Astrakharchik, G.E. Ultradilute low-dimensional liquids. Phys. Rev. Lett. 2016, 117, 100401. [Google Scholar] [CrossRef] [PubMed]
- Astrakharchik, G.E.; Gangardt, D.M.; Lozovik, Y.E.; Sorokin, I.A. Off-diagonal correlations of the Calogero-Sutherland model. Phys. Rev. E 2006, 74, 021105. [Google Scholar]
- Chubukov, A.V.; Pépin, C.; Rech, J. Instability of the quantum-critical point of itinerant ferromagnets. Phys. Rev. Lett. 2004, 92, 147003. [Google Scholar] [CrossRef] [PubMed]
- De Oliveira, T.R.; Rigolin, G.; de Oliveira, M.C.; Miranda, E. Multipartite entanglement signature of quantum phase transitions. Phys. Rev. Lett. 2007, 97, 170401. [Google Scholar] [CrossRef] [PubMed]
- Mazzanti, F.; Astrakharchik, G.E.; Boronat, J.; Casulleras, J. Off-diagonal ground-state properties of a one-dimensional gas of Fermi hard rods. Phys. Rev. A 2008, 77, 043632. [Google Scholar] [CrossRef]
- Zhao, J.-H.; Zhou, H.-Q. Singularities in ground-state fidelity and quantum phase transitions for the Kitaev model. Phys. Rev. B 2009, 80, 014403. [Google Scholar] [CrossRef]
- Yao, Y.; Li, H.W.; Zhang, C.-M.; Yin, Z.Q.; Chen, W.C.; Guo, G.-C.; Han, Z.-F. Performance of various correlation measures in quantum phase transitions using the quantum renormalization-group method. Phys. Rev. A 2012, 86, 042102. [Google Scholar] [CrossRef]
- Cabrera, C.R.; Tanzi, L.; Sanz, J.; Naylor, B.; Thomas, P.; Cheiney, P.; Tarruell, L. Quantum liquid droplets in a mixture of Bose–Einstein condensates. Science 2018, 359, 301–304. [Google Scholar] [CrossRef] [PubMed]
- Cheiney, P.; Cabrera, C.R.; Sanz, J.; Naylor, B.; Tanzi, L.; Tarruell, L. Bright soliton to quantum droplet transition in a mixture of Bose–Einstein condensates. Phys. Rev. Lett. 2018, 120, 135301. [Google Scholar] [CrossRef]
- Semeghini, G.; Ferioli, G.; Masi, L.; Mazzinghi, C.; Wolswijk, L.; Minardi, F.; Modugno, M.; Modugno, G.; Inguscio, M.; Fattori, M. Self-bound quantum droplets in atomic mixtures. arXiv, 2017; arXiv:1710.10890. [Google Scholar]
- Abdullaev, F.K.; Gammal, A.; Tomio, L.; Frederico, T. Stability of trapped Bose–Einstein condensates. Phys. Rev. A 2001, 63, 043604. [Google Scholar] [CrossRef]
- Abdullaev, F.K.; Salerno, M. Gap-Townes solitons and localized excitations in low-dimensional Bose–Einstein condensates in optical lattices. Phys. Rev. A 2005, 72, 033617. [Google Scholar] [CrossRef]
- Petrov, D.S.; Holzmann, M.; Shlyapnikov, G.V. Bose–Einstein condensation in quasi-2D trapped gases. Phys. Rev. Lett. 2000, 84, 2551–2555. [Google Scholar] [CrossRef] [PubMed]
- Salasnich, L.; Parola, A.; Reatto, L. Effective wave equations for the dynamics of cigar-shaped and disk-shaped Bose condensates. Phys. Rev. A 2002, 65, 043614. [Google Scholar] [CrossRef]
- Muñoz Mateo, A.; Delgado, V. Effective mean-field equations for cigar-shaped and disk-shaped Bose–Einstein condensates. Phys. Rev. A 2008, 77, 013617. [Google Scholar] [CrossRef]
- Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of ultracold atomic Fermi gases. Rev. Mod. Phys. 2008, 80, 1215–1273. [Google Scholar] [CrossRef]
- Capuzzi, P.; Minguzzi, A.; Tosi, M.P. Collective excitations of a trapped boson-fermion mixture across demixing. Phys. Rev. A 2003, 67, 053695. [Google Scholar] [CrossRef]
- Adhikari, S.K. Fermionic bright soliton in a boson-fermion mixture. Phys. Rev. A 2005, 72, 053608. [Google Scholar] [CrossRef]
- Manini, N.; Salasnich, L. Bulk and collective properties of a dilute Fermi gas in the BCS-BEC crossover. Phys. Rev. A 2005, 71, 033625. [Google Scholar] [CrossRef]
- Bulgac, A. Local-density-functional theory for superfluid fermionic systems: The unitary gas. Phys. Rev. A 2007, 76, 040502. [Google Scholar] [CrossRef]
- Góral, K.; Santos, L. Ground state and elementary excitations of single and binary Bose–Einstein condensates of trapped dipolar gases. Phys. Rev. A 2002, 66, 023613. [Google Scholar] [CrossRef]
- Deconinck, B.; Kevrekidis, P.G.; Nistazakis, H.E.; Frantzeskakis, D.J. Linearly coupled Bose–Einstein condensates: From Rabi oscillations and quasiperiodic solutions to oscillating domain walls and spiral waves. Phys. Rev. A 2004, 70, 063605. [Google Scholar] [CrossRef]
- Adhikari, S.K.; Malomed, B.A. Two-component gap solitons with linear interconversion. Phys. Rev. A 2009, 79, 015602. [Google Scholar] [CrossRef]
- Wen, L.; Liu, W.M.; Cai, Y.; Zhang, J.M.; Hum, J. Controlling phase separation of a two-component Bose–Einstein condensate by confinement. Phys. Rev. A 2012, 85, 043602. [Google Scholar] [CrossRef]
- Mineev, V.P. Theory of solution of two almost perfect Bose gases. JETP Lett. 1974, 67, 263–272. [Google Scholar]
- Wang, J.; Cerdeiriña, C.A.; Anisimov, M.A.; Sengers, J.V. Principle of isomorphism and complete scaling for binary-fluid criticality. Phys. Rev. E 2008, 77, 031127. [Google Scholar] [CrossRef] [PubMed]
- Roeksabutr, A.; Mayteevarunyoo, T.; Malomed, B.A. Symbiotic two-component gap solitons. Opt. Exp. 2012, 20, 24559–24574. [Google Scholar] [CrossRef] [PubMed]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087. [Google Scholar] [CrossRef]
- Jastrow, R. Many-body problem with strong forces. Phys. Rev. 1955, 98, 1479–1484. [Google Scholar] [CrossRef]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malomed, B.A. Suppression of Quantum-Mechanical Collapse in Bosonic Gases with Intrinsic Repulsion: A Brief Review. Condens. Matter 2018, 3, 15. https://doi.org/10.3390/condmat3020015
Malomed BA. Suppression of Quantum-Mechanical Collapse in Bosonic Gases with Intrinsic Repulsion: A Brief Review. Condensed Matter. 2018; 3(2):15. https://doi.org/10.3390/condmat3020015
Chicago/Turabian StyleMalomed, Boris A. 2018. "Suppression of Quantum-Mechanical Collapse in Bosonic Gases with Intrinsic Repulsion: A Brief Review" Condensed Matter 3, no. 2: 15. https://doi.org/10.3390/condmat3020015
APA StyleMalomed, B. A. (2018). Suppression of Quantum-Mechanical Collapse in Bosonic Gases with Intrinsic Repulsion: A Brief Review. Condensed Matter, 3(2), 15. https://doi.org/10.3390/condmat3020015