Electronic Properties of Curved Few-Layers Graphene: A Geometrical Approach
Abstract
1. Introduction
2. Galilean Fermions in Few Layers Graphene
2.1. Bilayer Graphene
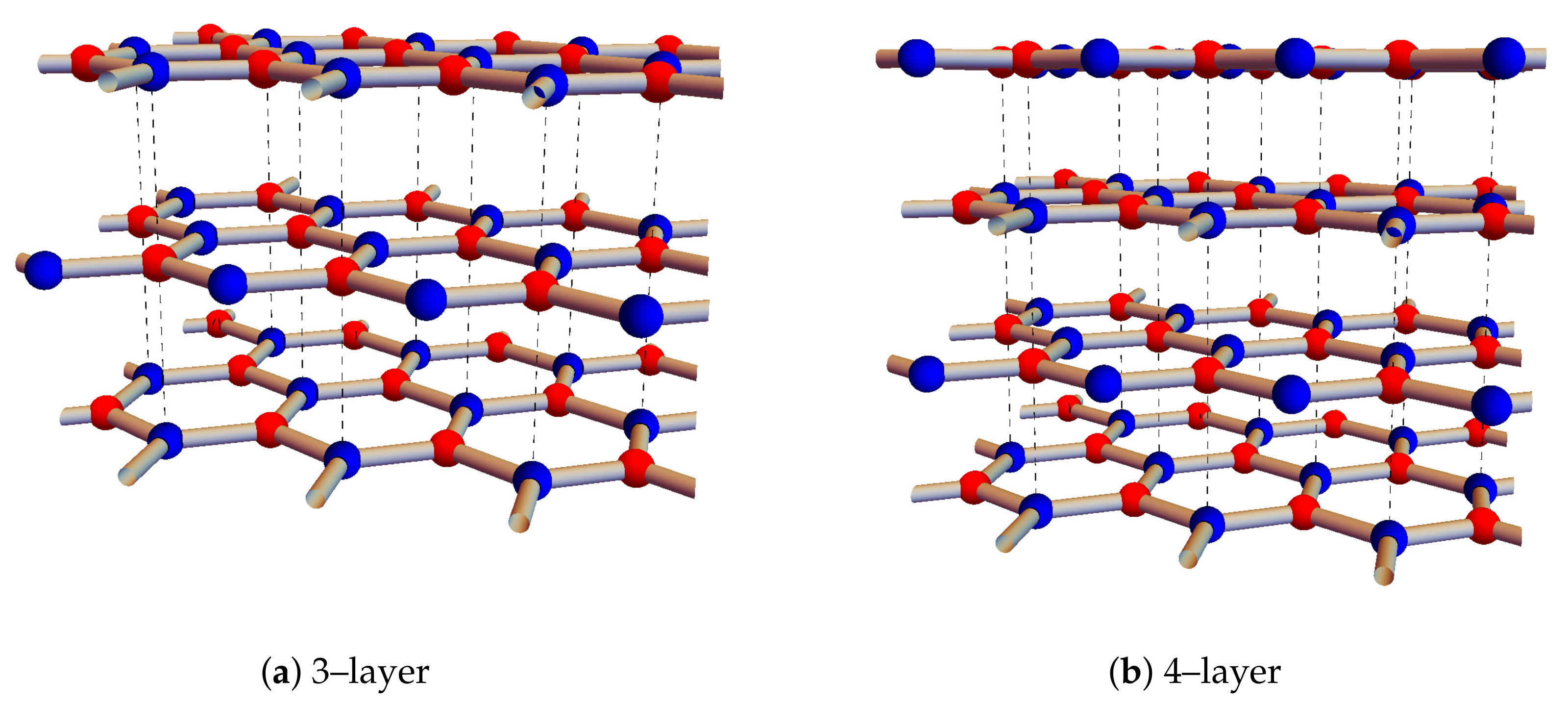
2.2. Three-Layer Graphene
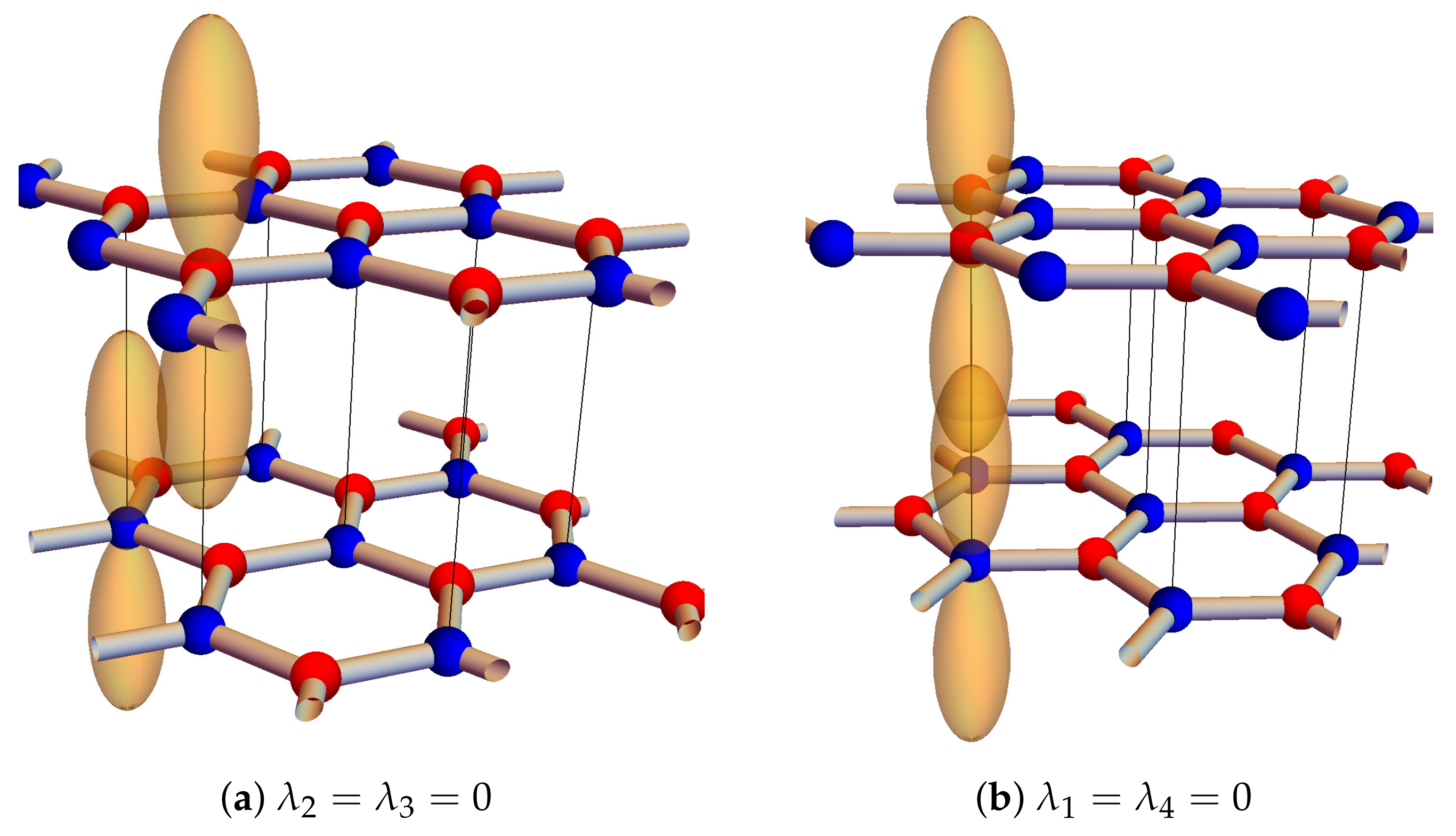
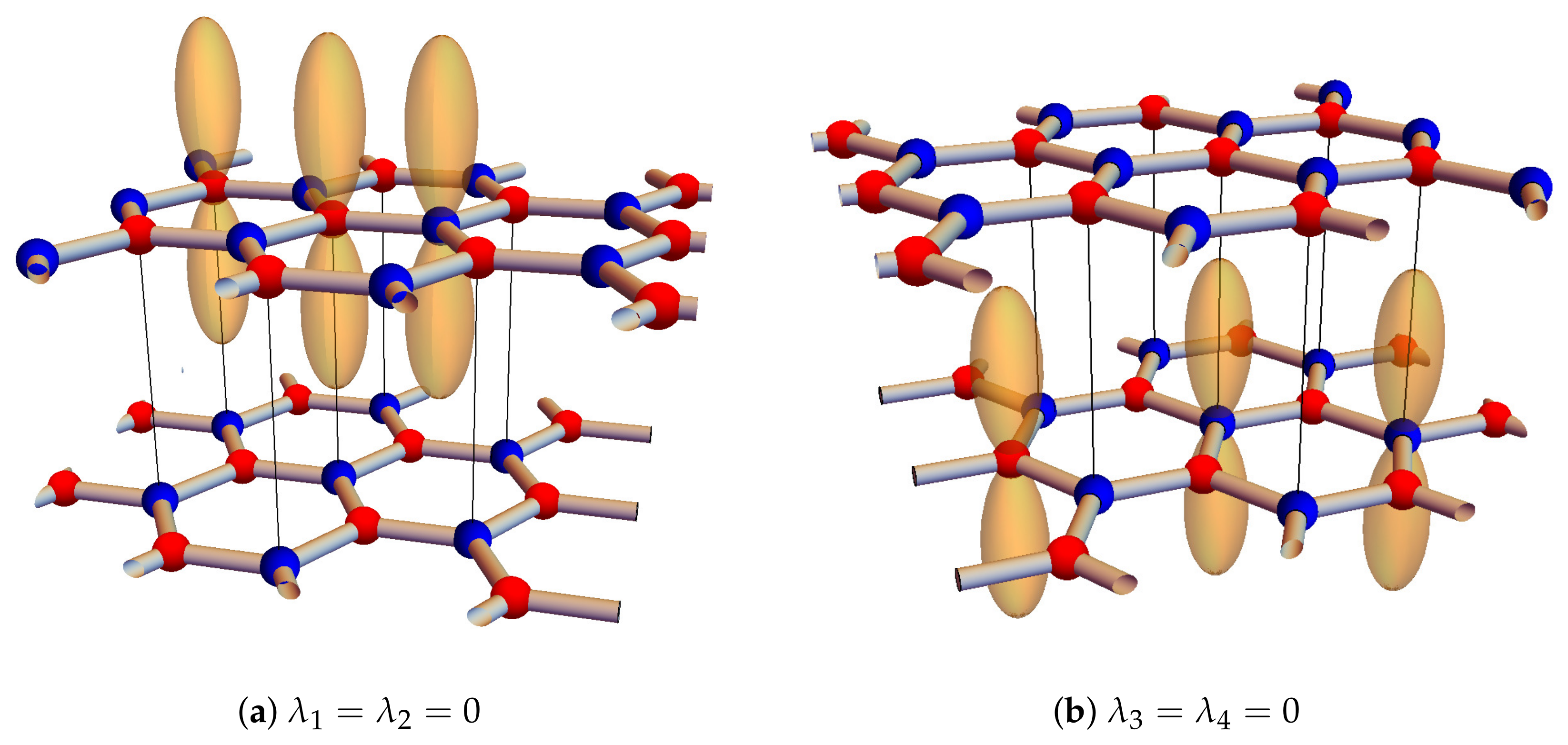
2.3. Four-Layer Graphene
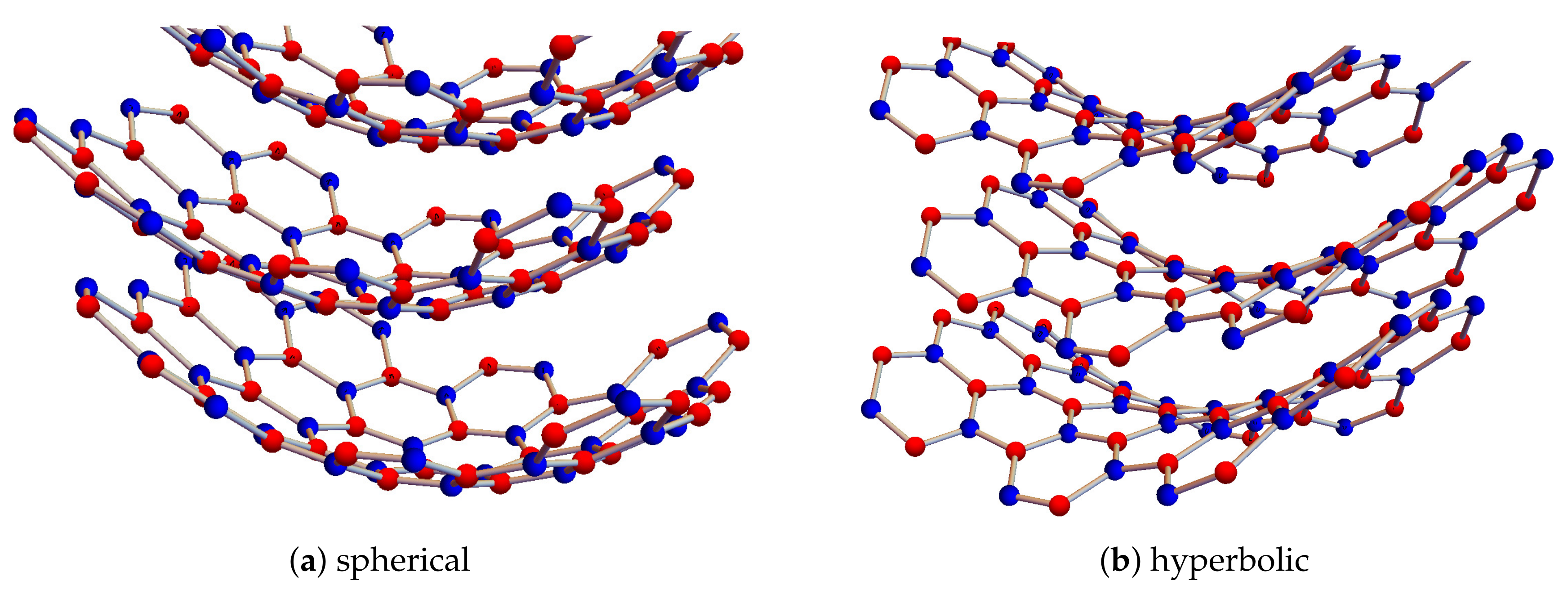
3. The Curved Case
3.1. The Lévy-Leblond Equation
3.2. The Role of Curvature
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Geim, A.K.; Grigorieva, I.V. Van der Waals heterostructures. Nature 2013, 499, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Perali, A.; Neilson, D.; Hamilton, A.R. High-Temperature Superfluidity in Double-Bilayer Graphene. Phys. Rev. Lett. 2013, 110, 146803. [Google Scholar] [CrossRef] [PubMed]
- Zarenia, M.; Perali, A.; Neilson, D.; Peeters, F.M. Enhancement of electron-hole superfluidity in double few-layer graphene. Sci. Rep. 2014, 4, 7319. [Google Scholar] [CrossRef] [PubMed]
- McCann, E.; Fal’ko, V.I. Landau-Level Degeneracy and Quantum Hall Effect in a Graphite Bilayer. Phys. Rev. Lett. 2006, 96, 086805. [Google Scholar] [CrossRef] [PubMed]
- Min, H.; MacDonald, A.H. Electronic Structure of Multilayer Graphene. Prog. Theor. Phys. Suppl. 2008, 176, 227–252. [Google Scholar] [CrossRef]
- Koshino, M.; McCann, E. Trigonal warping and Berry’s phase Nπ in ABC-stacked multilayer graphene. Phys. Rev. B 2009, 80, 165409. [Google Scholar] [CrossRef]
- Zhang, F.; Sahu, B.; Min, H.; MacDonald, A.H. Band structure of ABC-stacked graphene trilayers. Phys. Rev. B 2010, 82, 035409. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Meyer, J.C.; Scardaci, V.; Casiraghi, C.; Lazzeri, M.; Mauri, F.; Piscanec, S.; Jiang, D.; Novoselov, K.S.; Roth, S.; et al. Raman Spectrum of Graphene and Graphene Layers. Phys. Rev. Lett. 2006, 97, 187401. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Small, J.P.; Pontius, W.V.; Kim, P.H. Fabrication and electric-field-dependent transport measurements of mesoscopic graphite devices. Appl. Phys. Lett. 2005, 86, 073104. [Google Scholar] [CrossRef]
- Berger, C.; Song, Z.; Li, T.; Li, X.; Ogbazghi, A.Y.; Feng, R.; Dai, Z.; Marchenkov, A.N.; Conrad, E.H.; First, P.N.; et al. Ultrathin Epitaxial Graphite: 2D Electron Gas Properties and a Route toward Graphene-based Nanoelectronics. J. Phys. Chem. B 2004, 108, 19912–19916. [Google Scholar] [CrossRef]
- Shih, C.J.; Vijayaraghavan, A.; Krishnan, R.; Sharma, R.; Han, J.; Ham, M.; Jin, Z.; Lin, S.; Paulus, G.L.C.; Reuel, N.F.; et al. Bi- and trilayer graphene solutions. Nat. Nanotechnol. 2011, 6, 439–445. [Google Scholar] [CrossRef] [PubMed]
- Mahanandia, P.; Simon, F.; Heinrich, G.; Nanda, K.K. An electrochemical method for the synthesis of few layer graphene sheets for high temperature applications. Chem. Commun. 2014, 50, 4613–4615. [Google Scholar] [CrossRef] [PubMed]
- Craciun, M.F.; Russo, S.; Yamamoto, M.; Oostinga, J.B.; Morpurgo, A.F.; Tarucha, S. Trilayer graphene is a semimetal with a gate-tunable band overlap. Nat. Nanotechnol. 2009, 4, 383–388. [Google Scholar] [CrossRef] [PubMed]
- Bao, W.; Jing, L.; Velasco, J., Jr.; Lee, Y.; Liu, G.; Tran, D.; Standley, B.; Aykol, M.; Cronin, S.B.; Smirnov, D.; et al. Stacking-dependent band gap and quantum transport in trilayer graphene. Nat. Phys. 2011, 7, 948–952. [Google Scholar] [CrossRef]
- Mak, K.F.; Shan, J.; Heinz, T.F. Electronic Structure of Few-Layer Graphene: Experimental Demonstration of Strong Dependence on Stacking Sequence. Phys. Rev. Lett. 2010, 104, 176404. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Tang, T.; Girit, C.; Hao, Z.; Martin, M.C.; Zettl, A.; Crommie, M.F.; Shen, Y.R.; Wang, F. Direct observation of a widely tunable bandgap in bilayer graphene. Nature 2009, 459, 820–823. [Google Scholar] [CrossRef] [PubMed]
- Lui, C.H.; Li, Z.; Mak, K.F.; Cappelluti, E.; Heinz, T.F. Observation of an electrically tunable band gap in trilayer graphene. Nat. Phys. 2011, 7, 944–947. [Google Scholar] [CrossRef]
- Zou, K.; Zhang, F.; Clapp, C.; MacDonald, A.H.; Zhu, J. Transport Studies of Dual-Gated ABC and ABA Trilayer Graphene: Band Gap Opening and Band Structure Tuning in Very Large Perpendicular Electric Fields. Nano Lett. 2013, 13, 369–373. [Google Scholar] [CrossRef] [PubMed]
- Avetisyan, A.A.; Partoens, B.; Peeters, F.M. Stacking order dependent electric field tuning of the band gap in graphene multilayers. Phys. Rev. B 2010, 81, 115432. [Google Scholar] [CrossRef]
- Poccia, N.; Ricci, A.; Bianconi, A. Misfit strain in superlattices controlling the Electron-Lattice interaction via microstrain in active layers. Adv. Condens. Matter Phys. 2010, 2010, 261849. [Google Scholar] [CrossRef]
- Agrestini, S.; Saini, N.L.; Bianconi, G.; Bianconi, A. The strain of CuO2 lattice: the second variable for the phase diagram of cuprate perovskites. J. Phys. A Math. Gen. 2003, 36, 9133. [Google Scholar] [CrossRef]
- Agrestini, S.; Di Castro, D.; Sansone, M.; Saini, N.L.; Saccone, A.; De Negri, S.; Giovannini, M.; Colapietro, M.; Bianconi, A. High Tc superconductivity in a critical range of micro-strain and charge density in diborides. J. Phys. Condens. Matter 2001, 13, 11689. [Google Scholar] [CrossRef]
- Bianconi, A.; Lusignoli, M.; Saini, N.L.; Bordet, P.; Kvick, Å.; Radaelli, P.G. Stripe structure of the CuO2 plane in Bi2Sr2CaCu2O8+y by anomalous x-ray diffraction. Phys. Rev. B 1996, 54, 4310–4314. [Google Scholar] [CrossRef]
- Bianconi, A.; Saini, N.L.; Rossetti, T.; Lanzara, A.; Perali, A.; Missori, M.; Oyanagi, H.; Yamaguchi, H.; Nishihara, Y.; Ha, D.H. Stripe structure in the CuO2 plane of perovskite superconductors. Phys. Rev. B 1996, 54, 12018–12021. [Google Scholar] [CrossRef]
- Lévy-Leblond, J.M. Nonrelativistic particles and Wave Equations. Commun. Math. Phys. 1967, 6, 287–311. [Google Scholar] [CrossRef]
- Cariglia, M.; Giambò, R.; Perali, A. Curvature-tuned electronic properties of bilayer graphene in an effective four-dimensional spacetime. Phys. Rev. B 2017, 95, 245426. [Google Scholar] [CrossRef]
- Sitenko, Y.A.; Vlasii, N.D. Electronic properties of graphene with a topological defect. Nucl. Phys. B 2007, 787, 241–259. [Google Scholar] [CrossRef]
- Cortijo, A.; Vozmediano, M.A.H. Effects of topological defects and local curvature on the electronic properties of planar graphene. Nucl. Phys. B 2007, 763, 293–308, Erratum: Nucl. Phys. B 2009, 807, 659–660. [Google Scholar] [CrossRef]
- De Juan, F.; Cortijo, A.; Vozmediano, M.A.H. Charge inhomogeneities due to smooth ripples in graphene sheets. Phys. Rev. B 2007, 76, 165409. [Google Scholar] [CrossRef]
- Cortijo, A.; Vozmediano, M.A.H. Electronic properties of curved graphene sheets. EPL 2007, 77, 47002. [Google Scholar] [CrossRef]
- Vozmediano, M.A.H.; Katsnelson, M.I.; Guinea, F. Gauge fields in graphene. Phys. Rep. 2010, 496, 109–148. [Google Scholar] [CrossRef]
- Arias, E.; Hernández, A.R.; Lewenkopf, C. Gauge fields in graphene with nonuniform elastic deformations: A quantum field theory approach. Phys. Rev. B 2015, 92, 245110. [Google Scholar] [CrossRef]
- Amorim, B.; Cortijo, A.; de Juan, F.; Grushin, A.G.; Guinea, F.; Gutiérrez-Rubio, A.; Ochoa, H.; Parente, V.; Roldán, R.; San-Jose, P.; et al. Novel effects of strains in graphene and other two dimensional materials. Phys. Rep. 2016, 617, 1–54. [Google Scholar] [CrossRef]
- Sepehri, A.; Pincak, R.; Bamba, K.; Capozziello, S.; Saridakis, E.N. Current density and conductivity through modified gravity in the graphene with defects. Int. J. Mod. Phys. D 2017, 26, 17500948. [Google Scholar] [CrossRef]
- Capozziello, S.; Pincak, R.; Saridakis, E.N. Constructing superconductors by graphene Chern–Simons wormholes. Ann. Phys. 2018, 390, 303–333. [Google Scholar] [CrossRef]
- Weyl, H. Elektron und gravitation. I. Z. Phys. 1929, 56, 330–352. [Google Scholar] [CrossRef]
- Wan, X.; Turner, A.M.; Vishwanath, A.; Savrasov, S.Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 2011, 83, 205101. [Google Scholar] [CrossRef]
- Doria, M.M.; Perali, A. Weyl states and Fermi arcs in parabolic bands. Eur. Phys. Lett. 2017, 119, 21001. [Google Scholar] [CrossRef][Green Version]
- Rodrigues, E.I.B.; Doria, M.M.; Vargas-Paredes, A.A.; Cariglia, M.; Perali, A. Zero Helicity States in the LaAlO3-SrTiO3 Interface: The Origin of the Mass Anisotropy. J. Superconduc. Novel Magn. 2017, 30, 145–150. [Google Scholar] [CrossRef]
- Jung, J.; MacDonald, A.H. Accurate tight-binding models for the π bands of bilayer graphene. Phys. Rev. B 2014, 89, 035405. [Google Scholar] [CrossRef]
- Yuan, S.; Roldán, R.; Katsnelson, M.I. Landau level spectrum of ABA-and ABC-stacked trilayer graphene. Phys. Rev. B 2011, 84, 125455. [Google Scholar] [CrossRef]
- Duval, C. The dirac & Lévy-leblond equations and geometric quantization. In Differential Geometric Methods in Mathematical Physics; García, P.L., Pérez-Rendon, A., Eds.; Springer: Berlin/Heidelberg, Germany, 1987; p. 205. [Google Scholar]
- Duval, C.; Horváthy, P.A.; Palla, L. Spinor vortices in nonrelativistic Chern-Simons theory. Phys. Rev. D 1995, 52, 4700–4703. [Google Scholar] [CrossRef]
- Duval, C.; Horváthy, P.A.; Palla, L. Spinors in nonrelativistic Chern-Simons electrodynamics. Ann. Phys. 1996, 249, 265–297. [Google Scholar] [CrossRef]
- Cariglia, M. Hidden symmetries of Eisenhart-Duval lift metrics and the Dirac equation with flux. Phys. Rev. D 2012, 86, 084050. [Google Scholar] [CrossRef]
- Eisenhart, L.P. Dynamical trajectories and geodesics. Ann. Math. 1928, 30, 591–606. [Google Scholar] [CrossRef]
- Duval, C.; Burdet, G.; Künzle, H.P.; Perrin, M. Bargmann structures and Newton-Cartan theory. Phys. Rev. D 1985, 31, 1841. [Google Scholar] [CrossRef]
- Duval, C.; Gibbons, G.W.; Horváthy, P. Celestial mechanics, conformal structures and gravitational waves. Phys. Rev. D 1991, 43, 3907–3922. [Google Scholar] [CrossRef]
- Hladnik, M.; Omladič, M. Spectrum of the product of operators. Proc. Am. Math. Soc. 1988, 102, 300–302. [Google Scholar] [CrossRef]
- Westström, A.; Ojanen, T. Designer Curved-Space Geometry for Relativistic Fermions in Weyl Metamaterials. Phys. Rev. X 2017, 7, 041026. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cariglia, M.; Giambò, R.; Perali, A. Electronic Properties of Curved Few-Layers Graphene: A Geometrical Approach. Condens. Matter 2018, 3, 11. https://doi.org/10.3390/condmat3020011
Cariglia M, Giambò R, Perali A. Electronic Properties of Curved Few-Layers Graphene: A Geometrical Approach. Condensed Matter. 2018; 3(2):11. https://doi.org/10.3390/condmat3020011
Chicago/Turabian StyleCariglia, Marco, Roberto Giambò, and Andrea Perali. 2018. "Electronic Properties of Curved Few-Layers Graphene: A Geometrical Approach" Condensed Matter 3, no. 2: 11. https://doi.org/10.3390/condmat3020011
APA StyleCariglia, M., Giambò, R., & Perali, A. (2018). Electronic Properties of Curved Few-Layers Graphene: A Geometrical Approach. Condensed Matter, 3(2), 11. https://doi.org/10.3390/condmat3020011





