Role of H Distribution on Coherent Quantum Transport of Electrons in Hydrogenated Graphene
Abstract
1. Introduction
2. Results
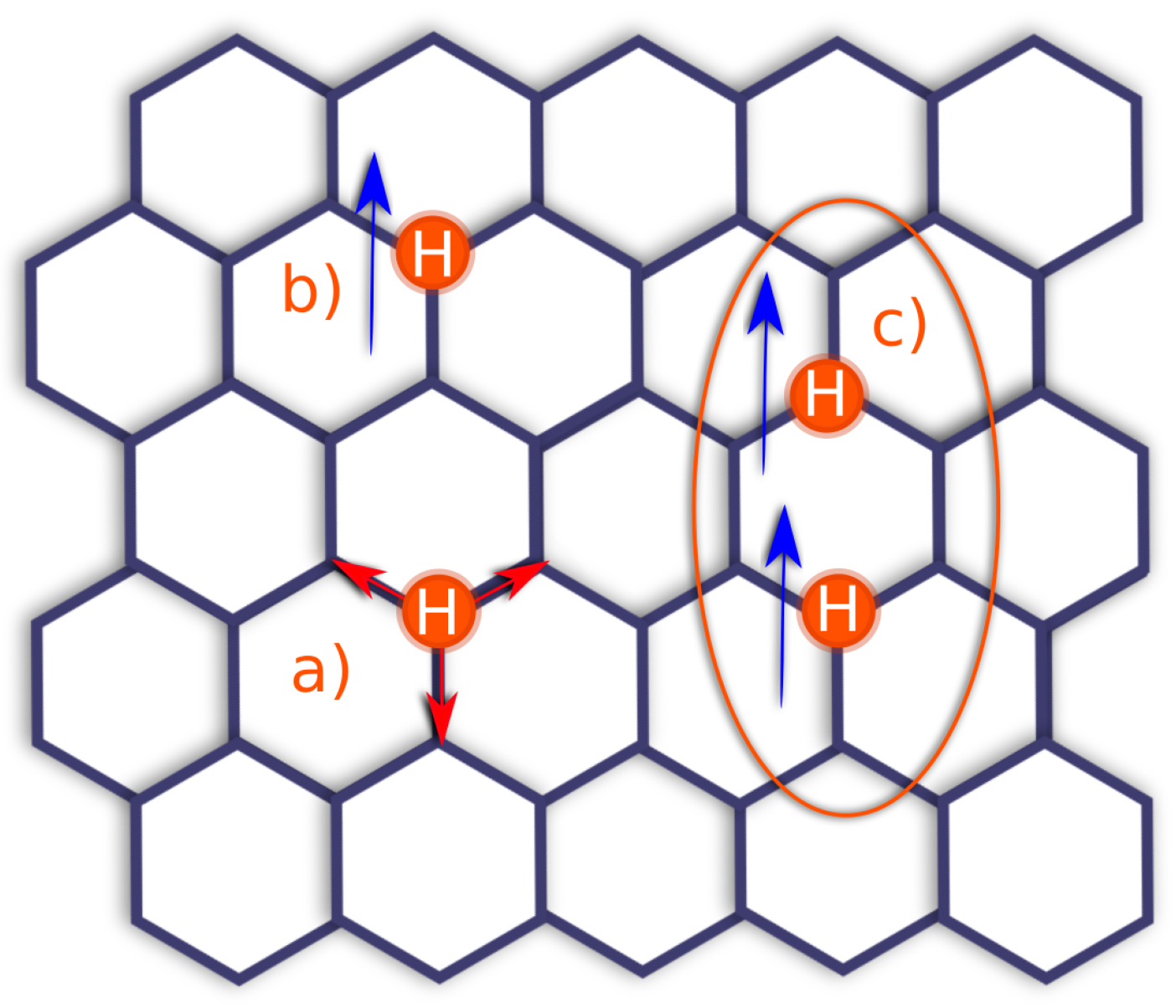
2.1. Adatoms Interactions
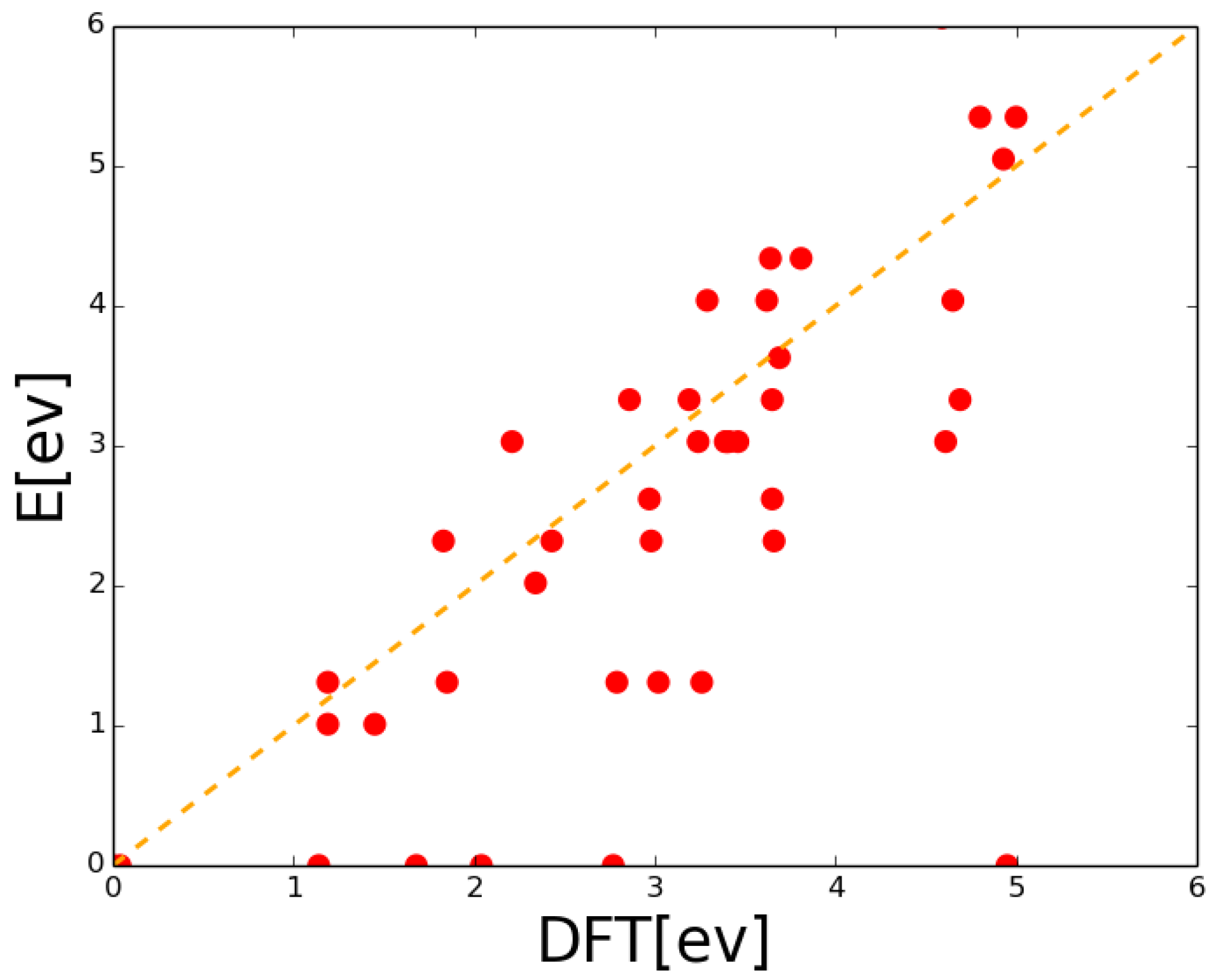
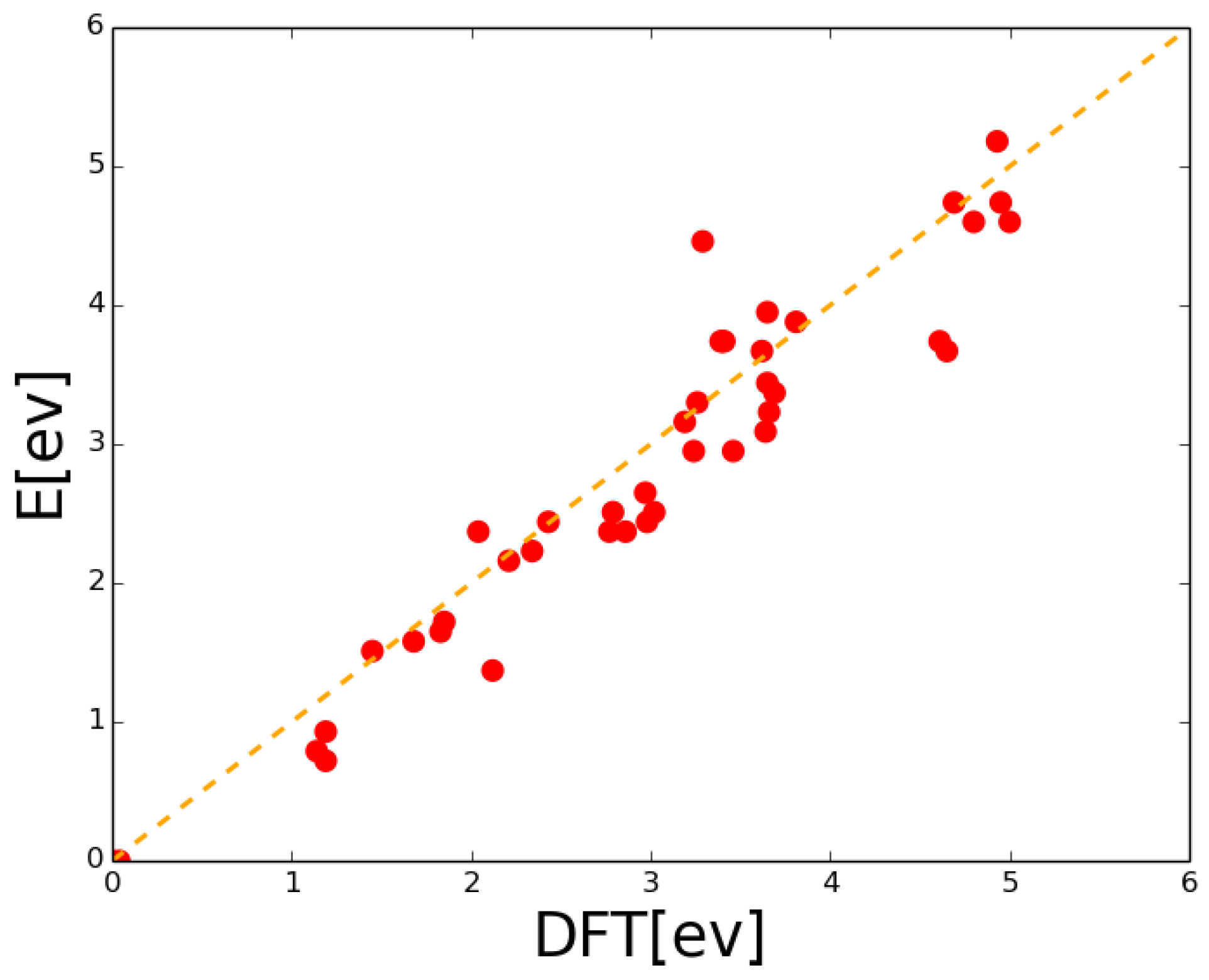
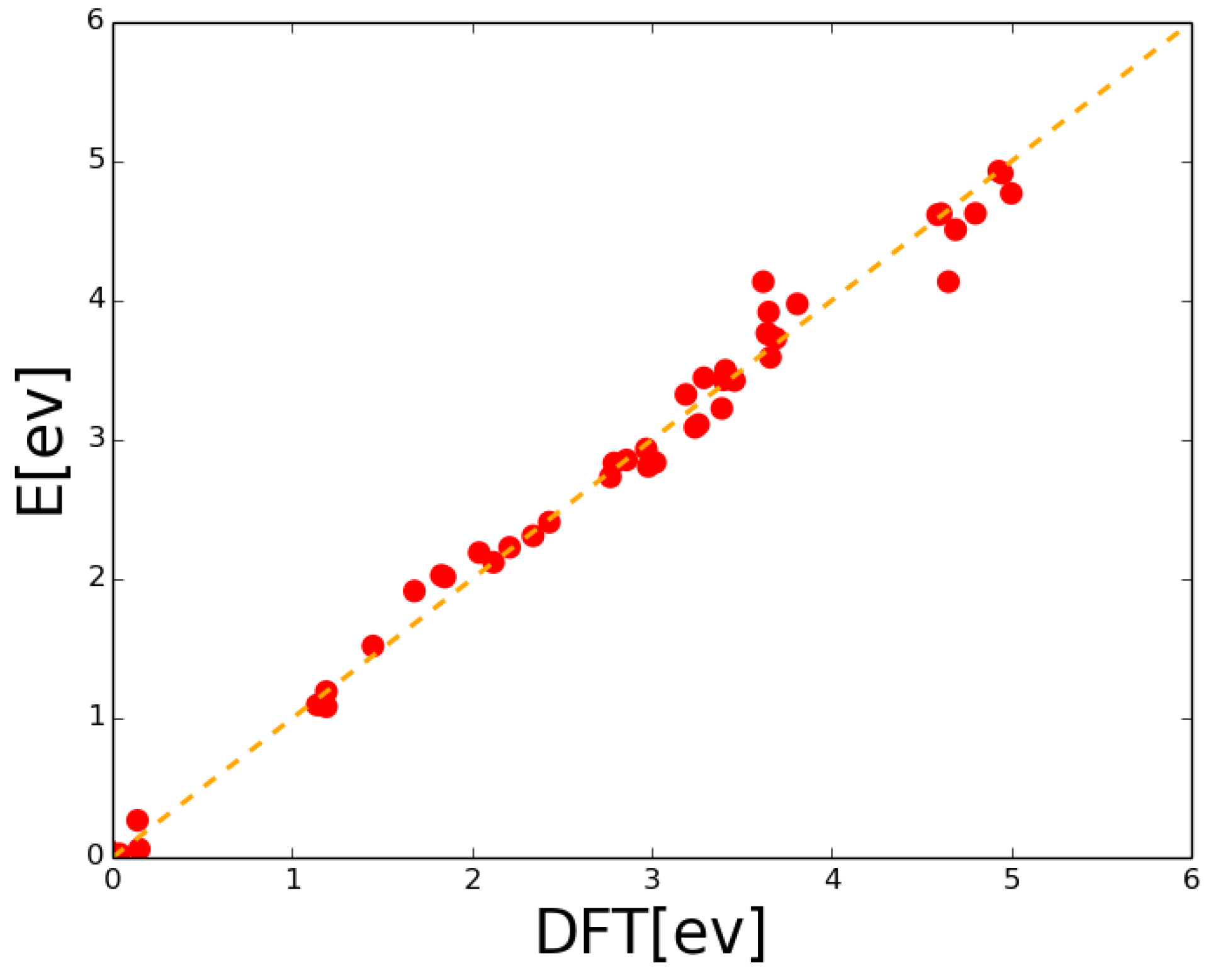
2.2. Lattice Kinetic Monte Carlo Energetic Effects
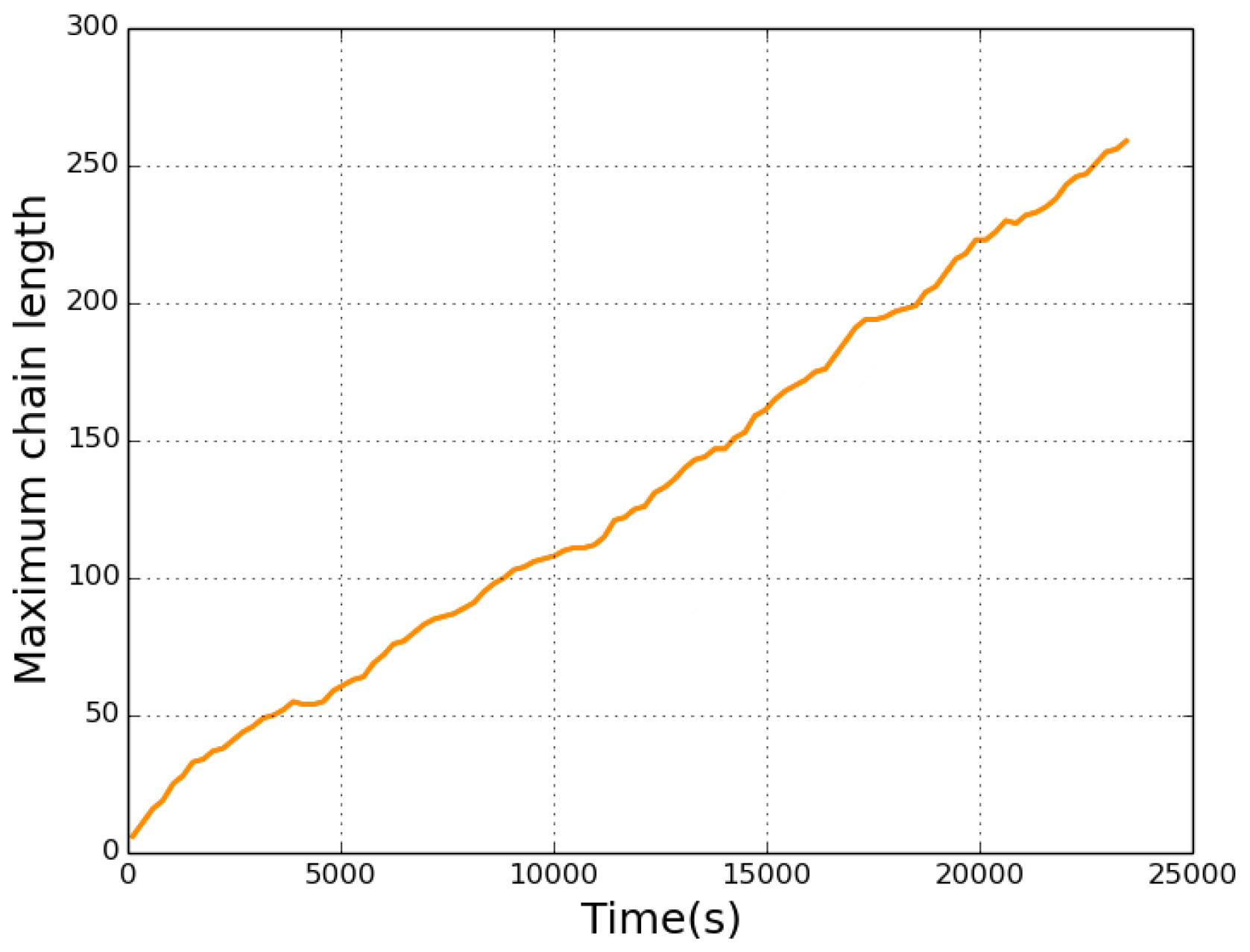
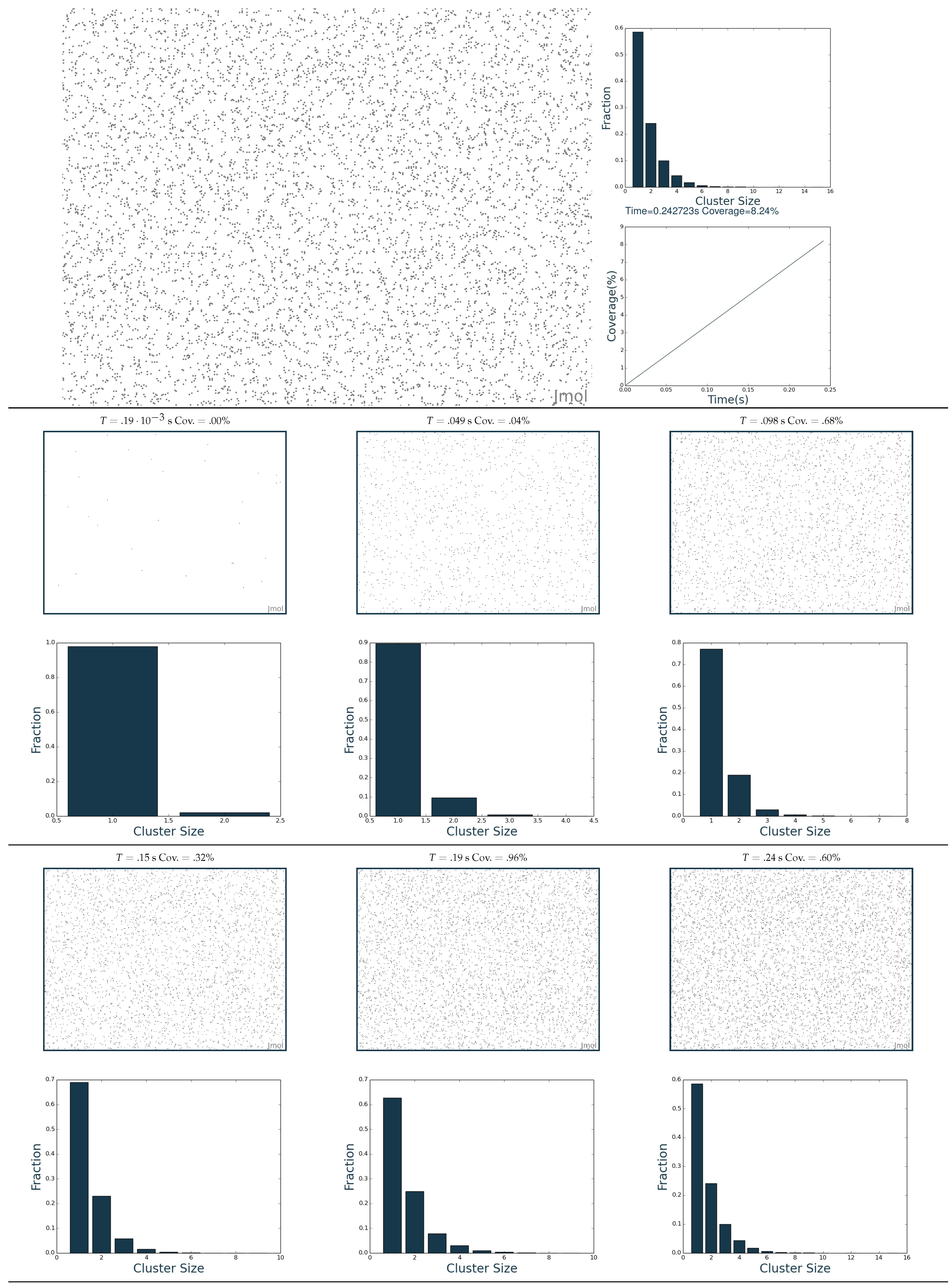
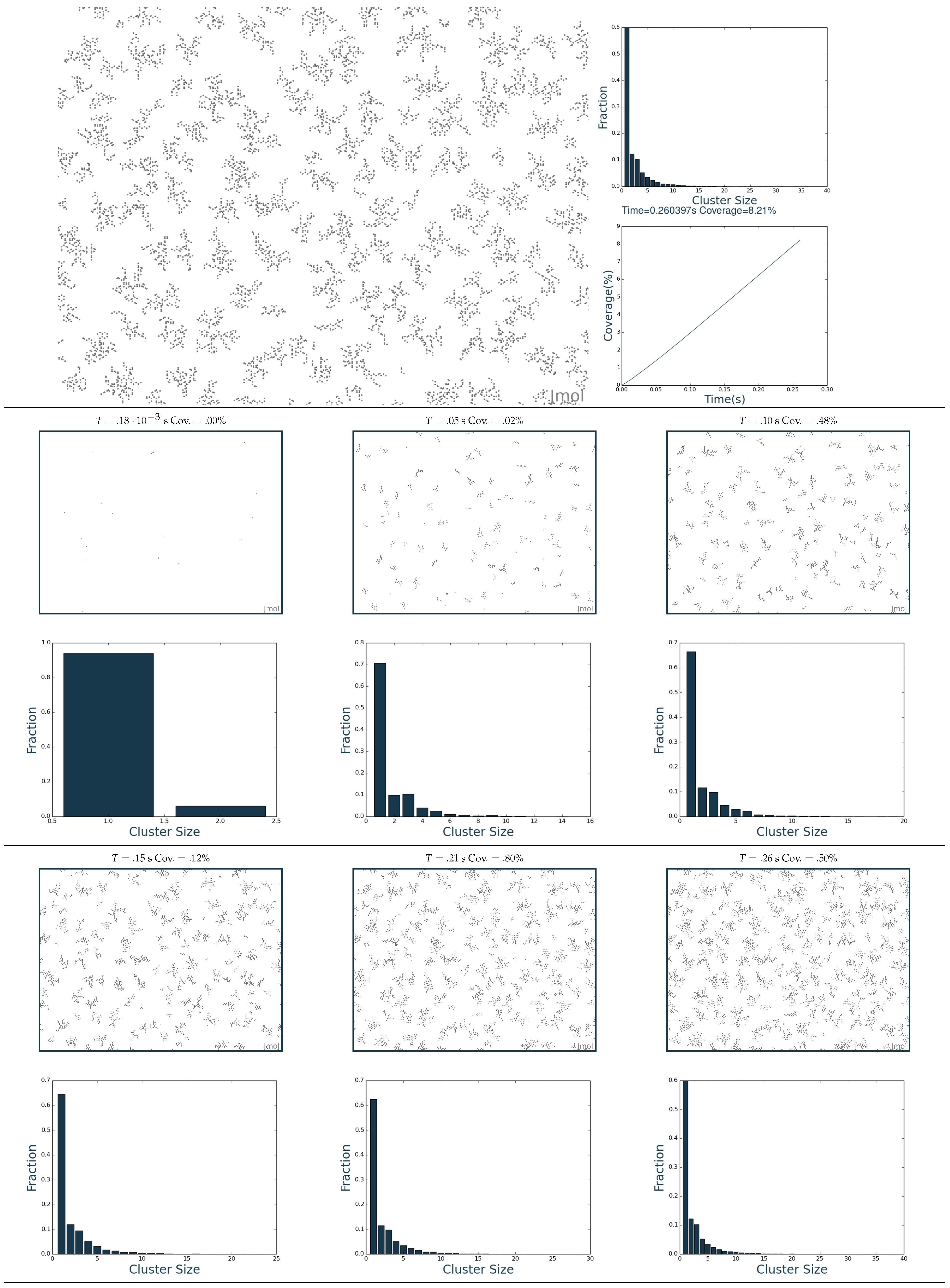
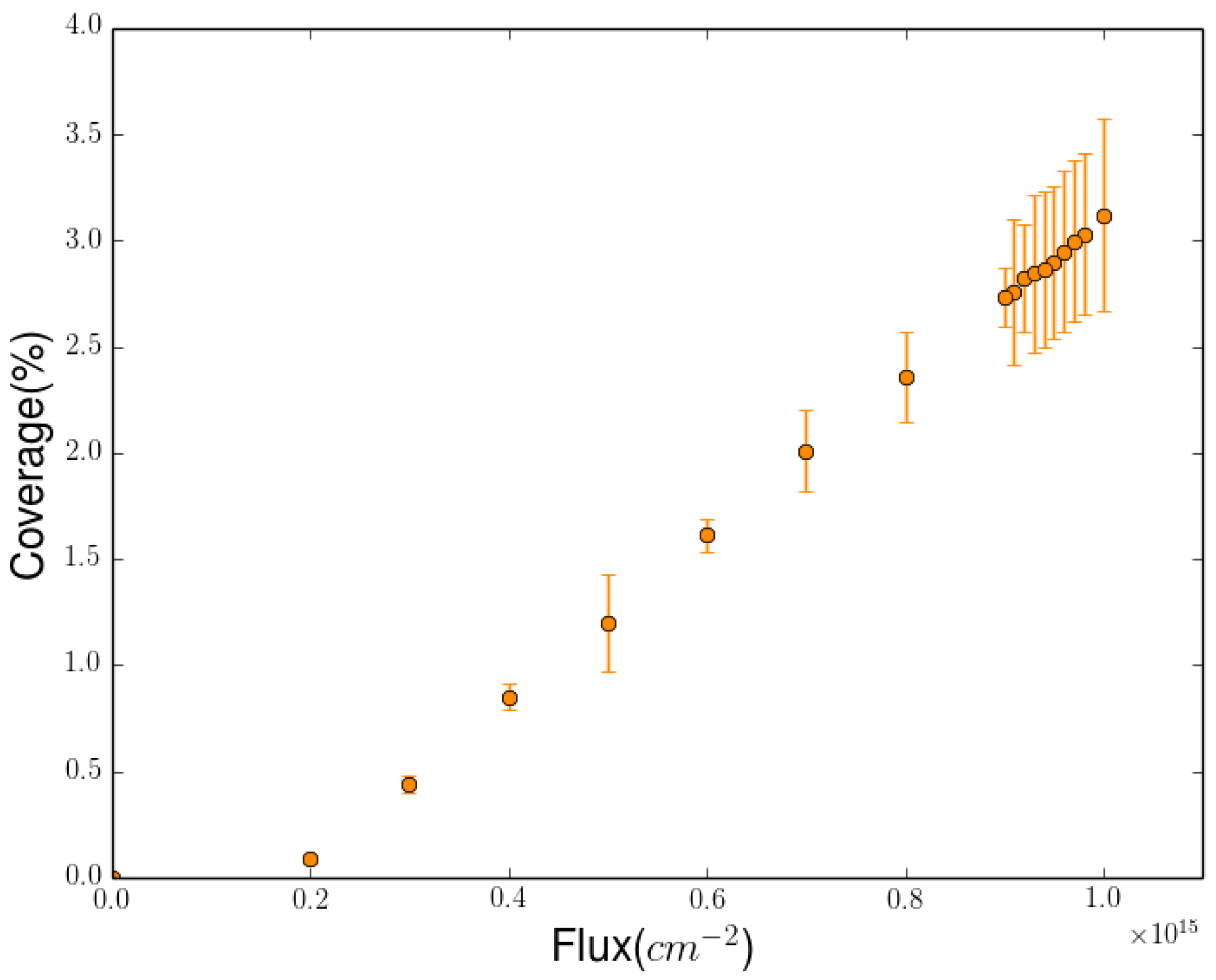
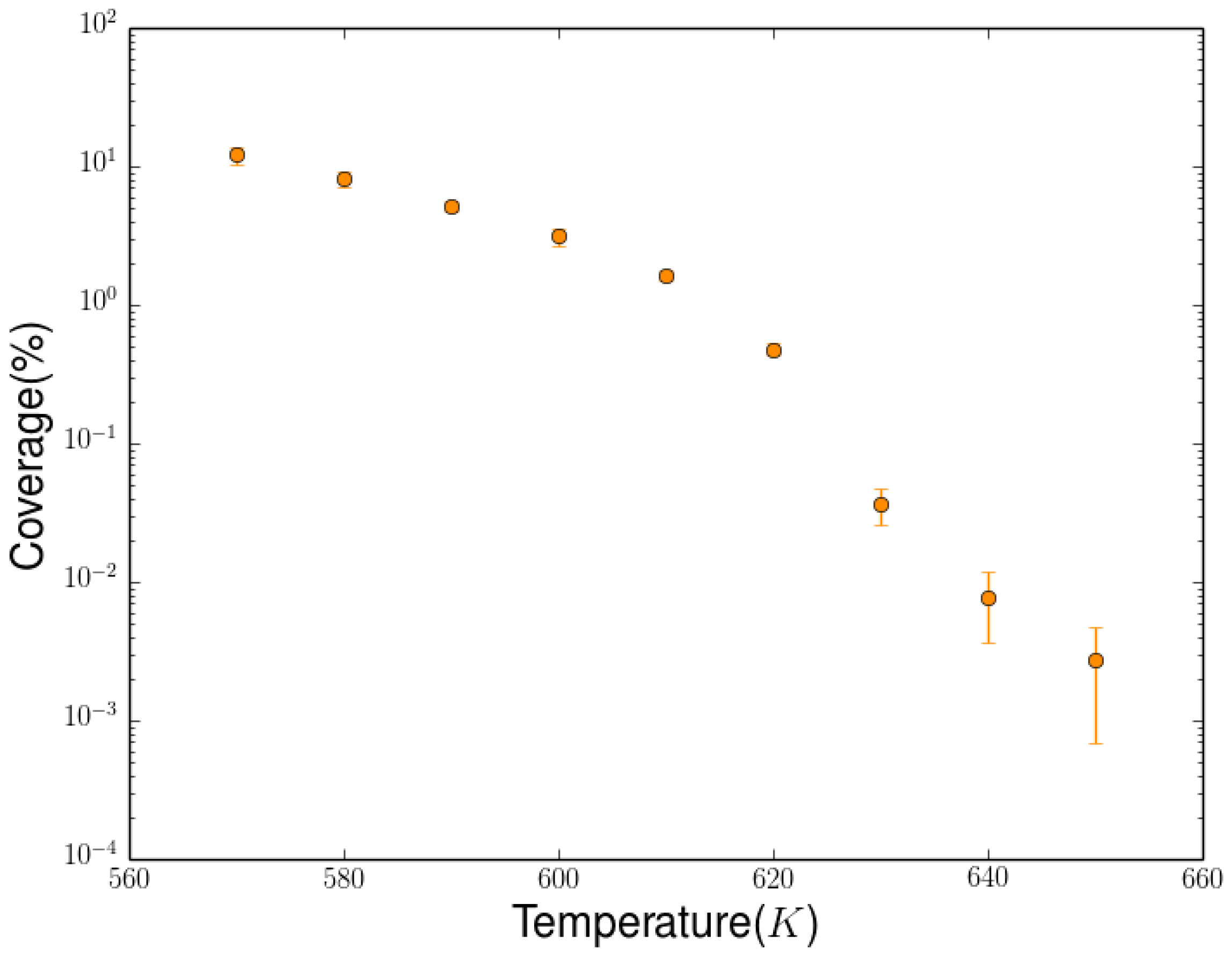
2.3. Simulation of the Hydrogenation Process
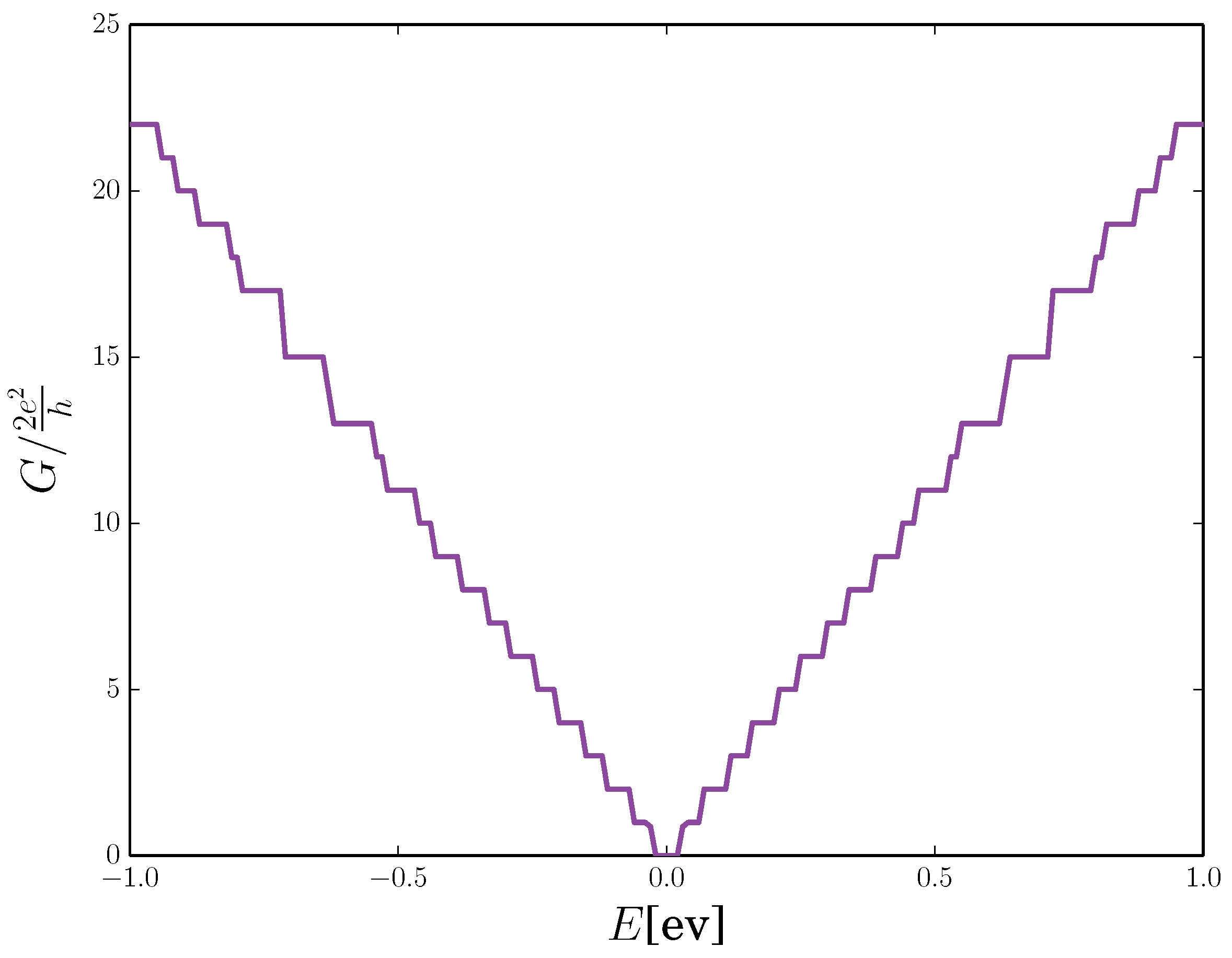
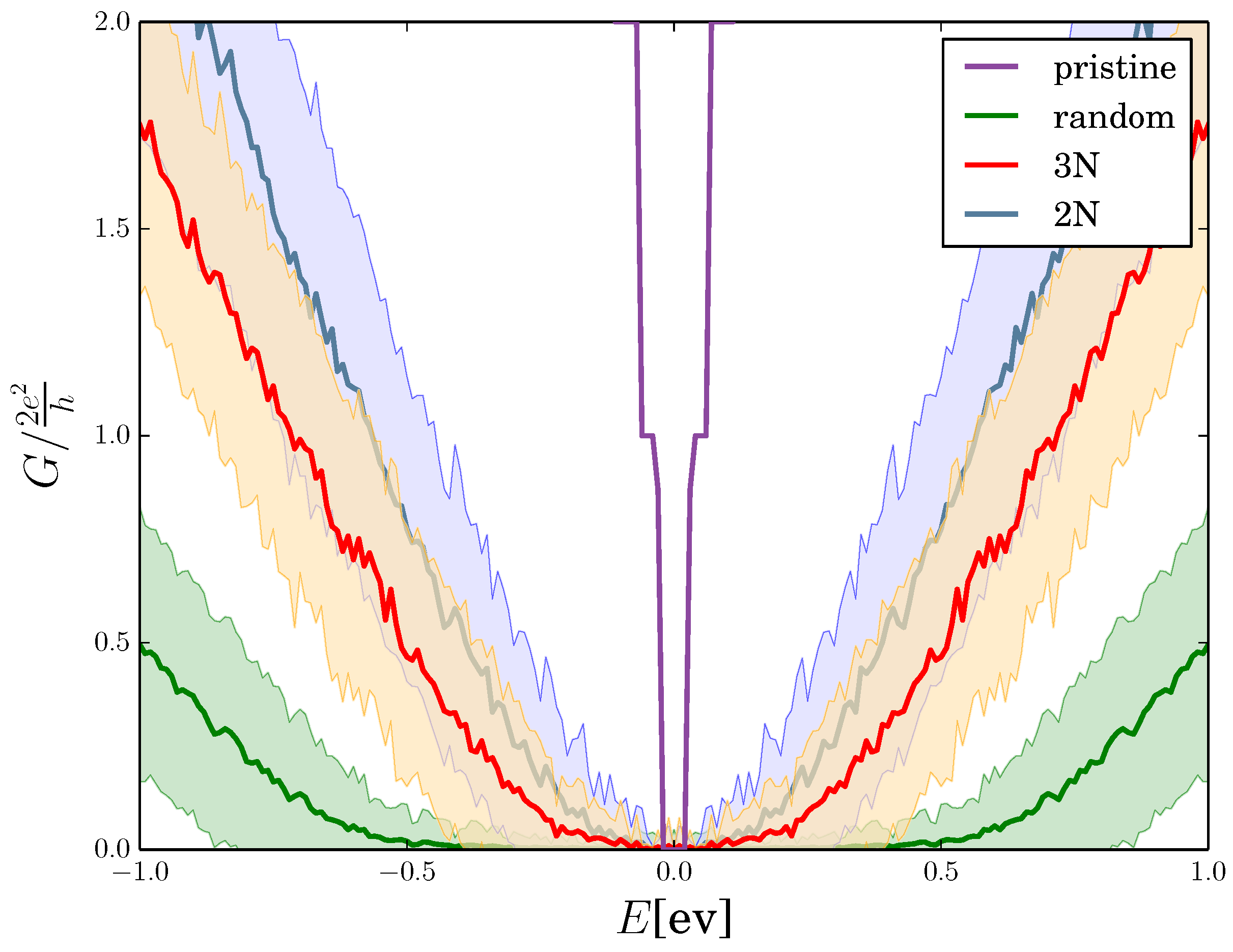
2.4. Quantum Conductance of Hydrogenated Graphene
3. Discussion
4. Methods
4.1. Lattice Kinetic Monte Carlo
4.2. Lattice Kinetic Monte Carlo Events
Configuration Redundancy
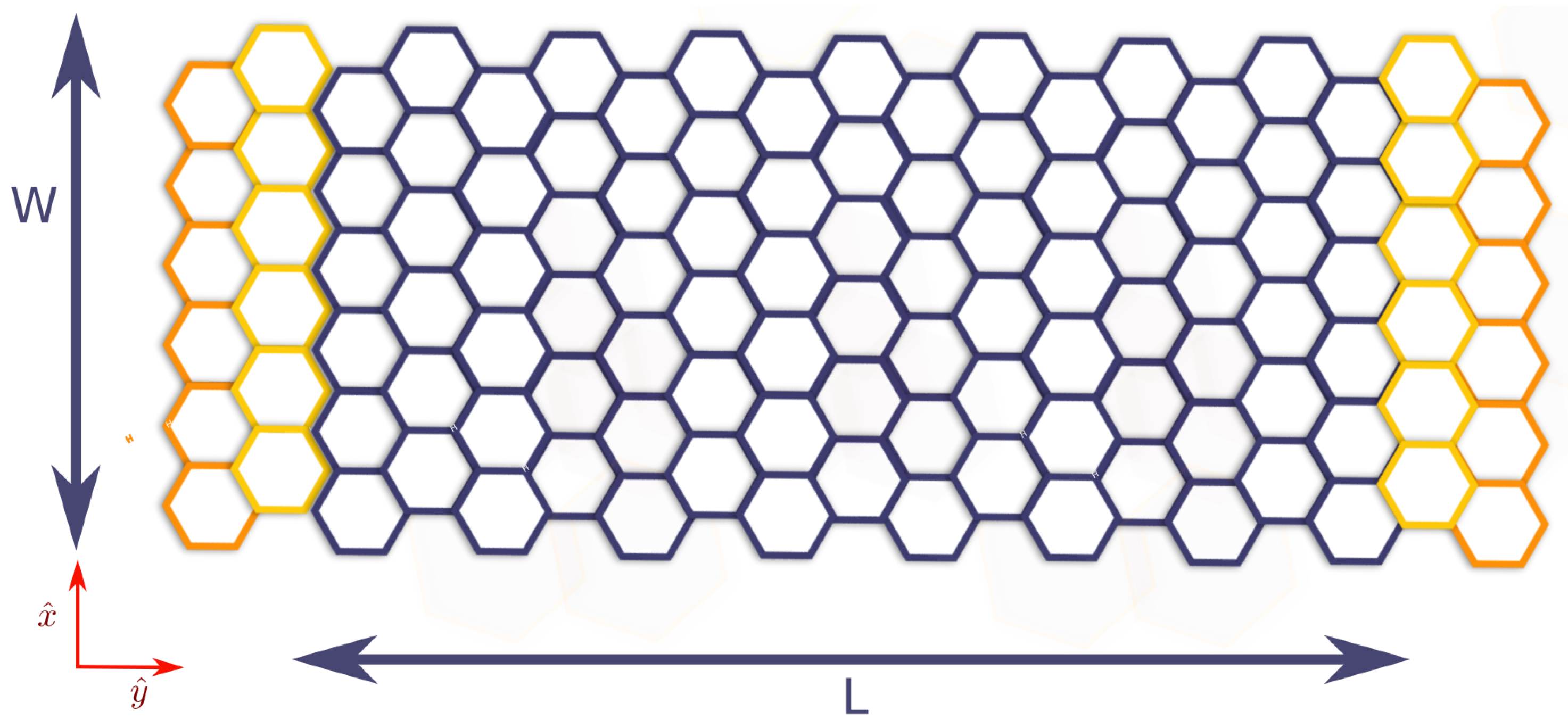
4.3. Non-Equilibrium Green’s Function
Author Contributions
Conflicts of Interest
Abbreviations
| 2N | next-nearest-neighbor (interactions) |
| 3N | third-nearest-neighbor (interactions) |
| AMC | absorbing Markov chain |
| DFT | density functional theory |
| G | graphene |
| HG | hydrogenated graphene |
| LKMC | lattice kinetic Monte Carlo |
| MC | Monte Carlo |
| NEB | nudged elastic band |
| NEGF | non-equilibrium Green’s function |
| QED | quantum electrodynamics |
| QT | quantum technology |
| TST | transition state theory |
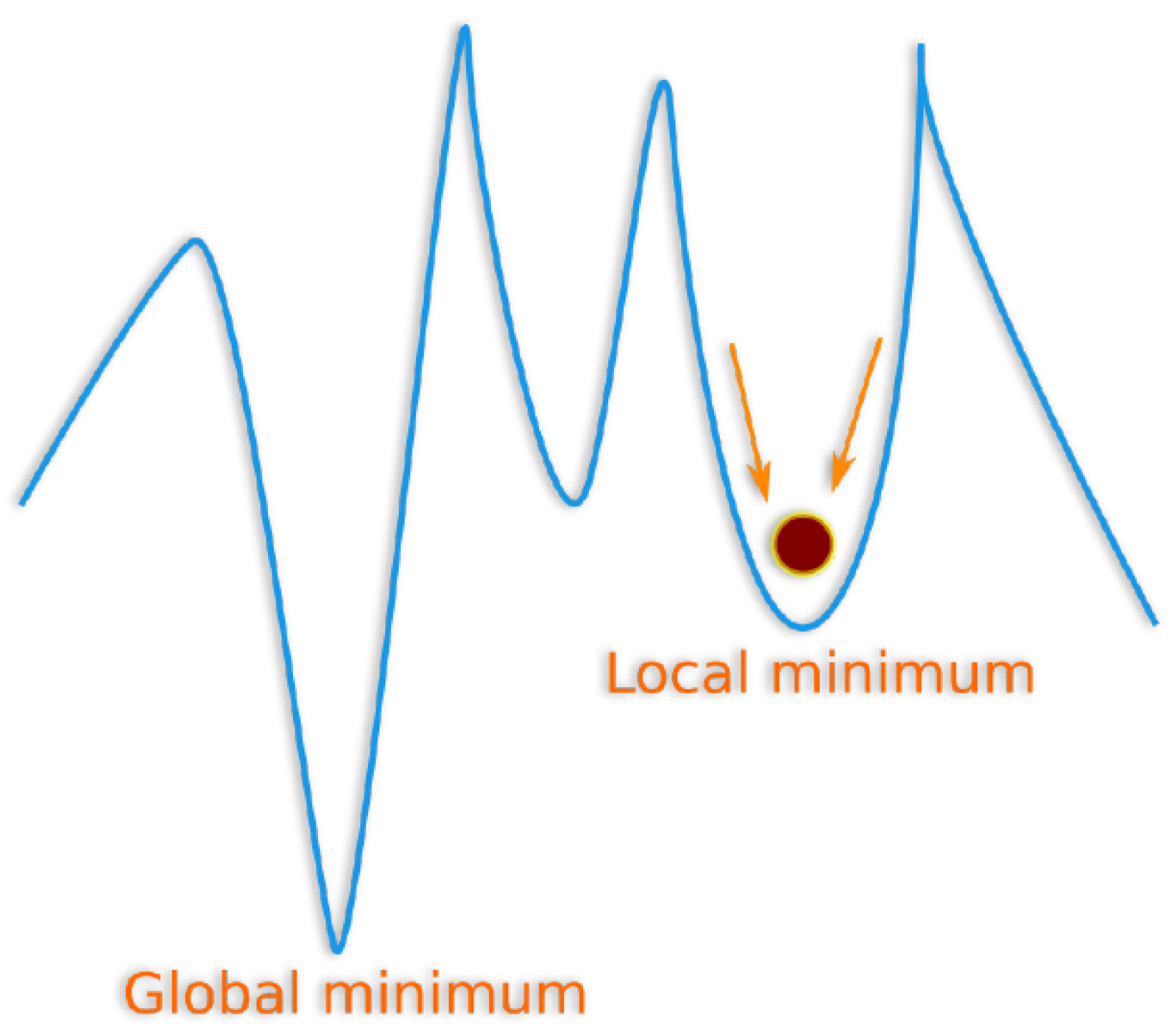
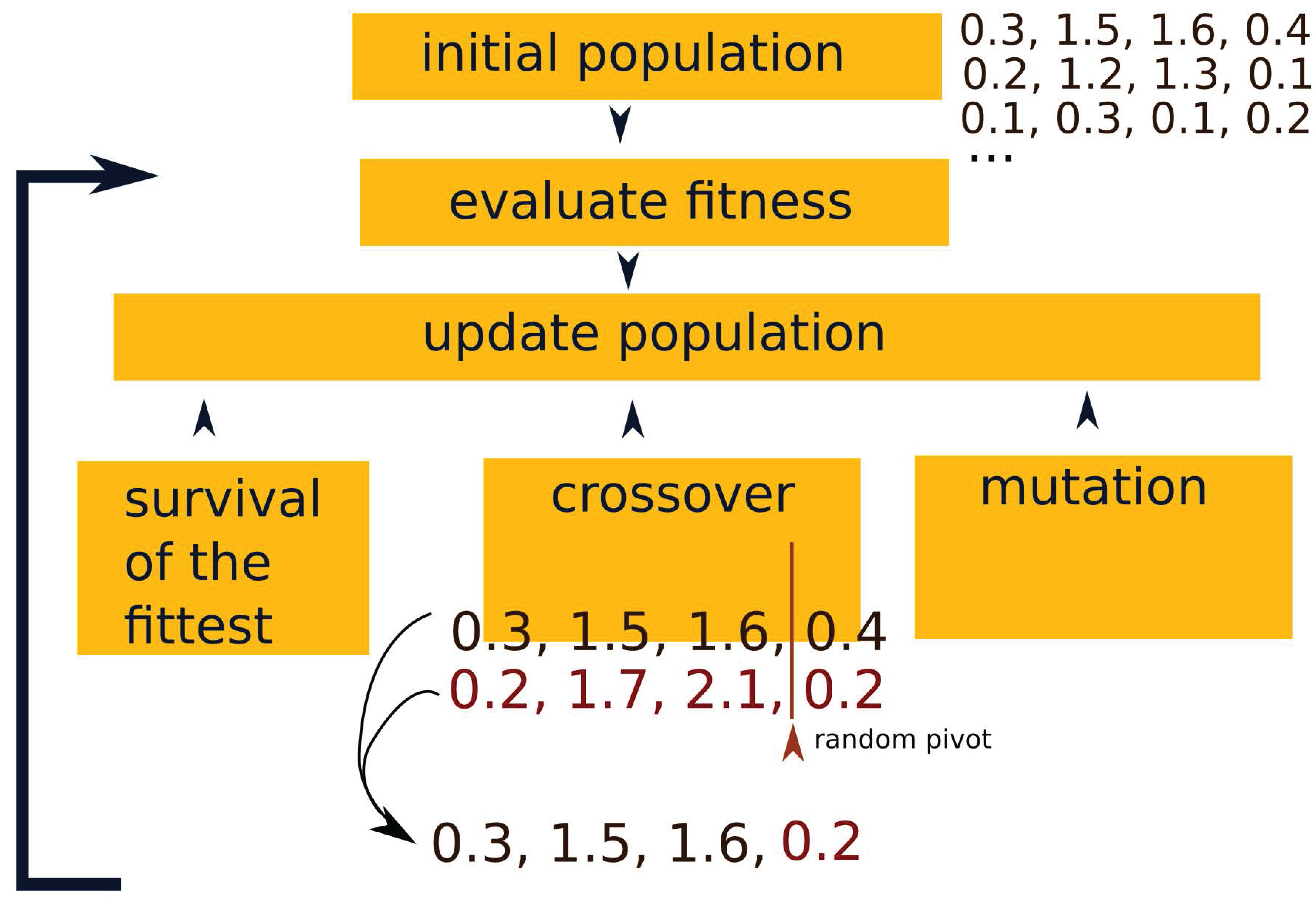
Appendix A. Genetic Algorithms for the LKMC Calibration
| 0 | 0 | 0 | 0.0269 | 1 | 2 | 1 | 0.6618 | 2 | 4 | 2 | 0.7802 |
| 0 | 0 | 1 | 1.0836 | 1 | 2 | 2 | 0.8664 | 2 | 4 | 3 | 0.5641 |
| 0 | 0 | 2 | 1.5875 | 1 | 2 | 3 | 0.2523 | 2 | 5 | 0 | 0.6506 |
| 0 | 0 | 3 | 1.0028 | 1 | 3 | 0 | 0.4692 | 2 | 5 | 1 | 0.5304 |
| 0 | 1 | 0 | 0.1327 | 1 | 3 | 1 | 0.0512 | 2 | 5 | 2 | 0.7571 |
| 0 | 1 | 1 | 0.4247 | 1 | 3 | 2 | 0.4164 | 2 | 5 | 3 | 0.3987 |
| 0 | 1 | 2 | 1.9331 | 1 | 3 | 3 | 0.7304 | 2 | 6 | 0 | 0.2445 |
| 0 | 1 | 3 | 0.1619 | 1 | 4 | 0 | 0.4583 | 2 | 6 | 1 | 0.9874 |
| 0 | 2 | 0 | 1 | 4 | 1 | 0.6692 | 2 | 6 | 2 | 0.1629 | |
| 0 | 2 | 1 | 0.7918 | 1 | 4 | 2 | 0.7061 | 2 | 6 | 3 | 0.0280 |
| 0 | 2 | 2 | 0.6347 | 1 | 4 | 3 | 0.1311 | 3 | 0 | 0 | 6.4501 |
| 0 | 2 | 3 | 0.1706 | 1 | 5 | 0 | 0.1462 | 3 | 0 | 1 | 0.6706 |
| 0 | 3 | 0 | 0.3160 | 1 | 5 | 1 | 0.6872 | 3 | 0 | 2 | 0.7434 |
| 0 | 3 | 1 | 0.2604 | 1 | 5 | 2 | 0.2335 | 3 | 0 | 3 | 0.2740 |
| 0 | 3 | 2 | 0.5545 | 1 | 5 | 3 | 0.3379 | 3 | 1 | 0 | 4.9250 |
| 0 | 3 | 3 | 0.9167 | 1 | 6 | 0 | 0.5991 | 3 | 1 | 1 | 0.4324 |
| 0 | 4 | 0 | 0.6187 | 1 | 6 | 1 | 0.6379 | 3 | 1 | 2 | 0.3590 |
| 0 | 4 | 1 | 0.4000 | 1 | 6 | 2 | 0.7474 | 3 | 1 | 3 | 0.2727 |
| 0 | 4 | 2 | 0.0157 | 1 | 6 | 3 | 0.9152 | 3 | 2 | 0 | 3.1747 |
| 0 | 4 | 3 | 0.0617 | 2 | 0 | 0 | 2.1957 | 3 | 2 | 1 | 0.0603 |
| 0 | 5 | 0 | 2 | 0 | 1 | 0.6159 | 3 | 2 | 2 | 0.8733 | |
| 0 | 5 | 1 | 0.3609 | 2 | 0 | 2 | 0.0350 | 3 | 2 | 3 | 0.2785 |
| 0 | 5 | 2 | 2 | 0 | 3 | 0.7425 | 3 | 3 | 0 | 0.9470 | |
| 0 | 5 | 1 | 0.3609 | 2 | 1 | 0 | 1.9977 | 3 | 3 | 1 | 0.9201 |
| 0 | 5 | 3 | 0.3821 | 2 | 1 | 1 | 1.9263 | 3 | 3 | 2 | 0.9011 |
| 0 | 6 | 0 | 0.0557 | 2 | 1 | 2 | 0.3083 | 3 | 3 | 3 | 0.8078 |
| 0 | 6 | 1 | 0.6402 | 2 | 1 | 3 | 1.1571 | 3 | 4 | 0 | 0.8892 |
| 0 | 6 | 2 | 0.3567 | 2 | 2 | 0 | 1.7397 | 3 | 4 | 1 | 0.1157 |
| 0 | 6 | 3 | 0.3289 | 2 | 2 | 1 | 1.5419 | 3 | 4 | 2 | 0.3957 |
| 1 | 0 | 0 | 1.2079 | 2 | 2 | 2 | 0.8053 | 3 | 4 | 3 | 0.5538 |
| 1 | 0 | 1 | 1.6966 | 2 | 2 | 3 | 0.7230 | 3 | 5 | 0 | 0.1971 |
| 1 | 0 | 2 | 0.6769 | 2 | 3 | 0 | −0.0081 | 3 | 5 | 1 | 0.0778 |
| 1 | 0 | 3 | 0.4641 | 2 | 3 | 1 | 0.9847 | 3 | 5 | 2 | 0.1401 |
| 1 | 1 | 0 | 0.8549 | 2 | 3 | 2 | 0.3008 | 3 | 5 | 3 | 0.5883 |
| 1 | 1 | 1 | 1.3669 | 2 | 3 | 3 | 0.3298 | 3 | 6 | 0 | 0.3159 |
| 1 | 1 | 2 | 1.3645 | 2 | 4 | 0 | 0.2410 | 3 | 6 | 1 | 0.2322 |
| 1 | 1 | 3 | 2 | 4 | 1 | 0.3460 | 3 | 6 | 2 | 0.2416 | |
| 1 | 2 | 0 | 3 | 6 | 3 | 0.0972 |
Appendix B. Accelerating Kinetic Monte Carlo
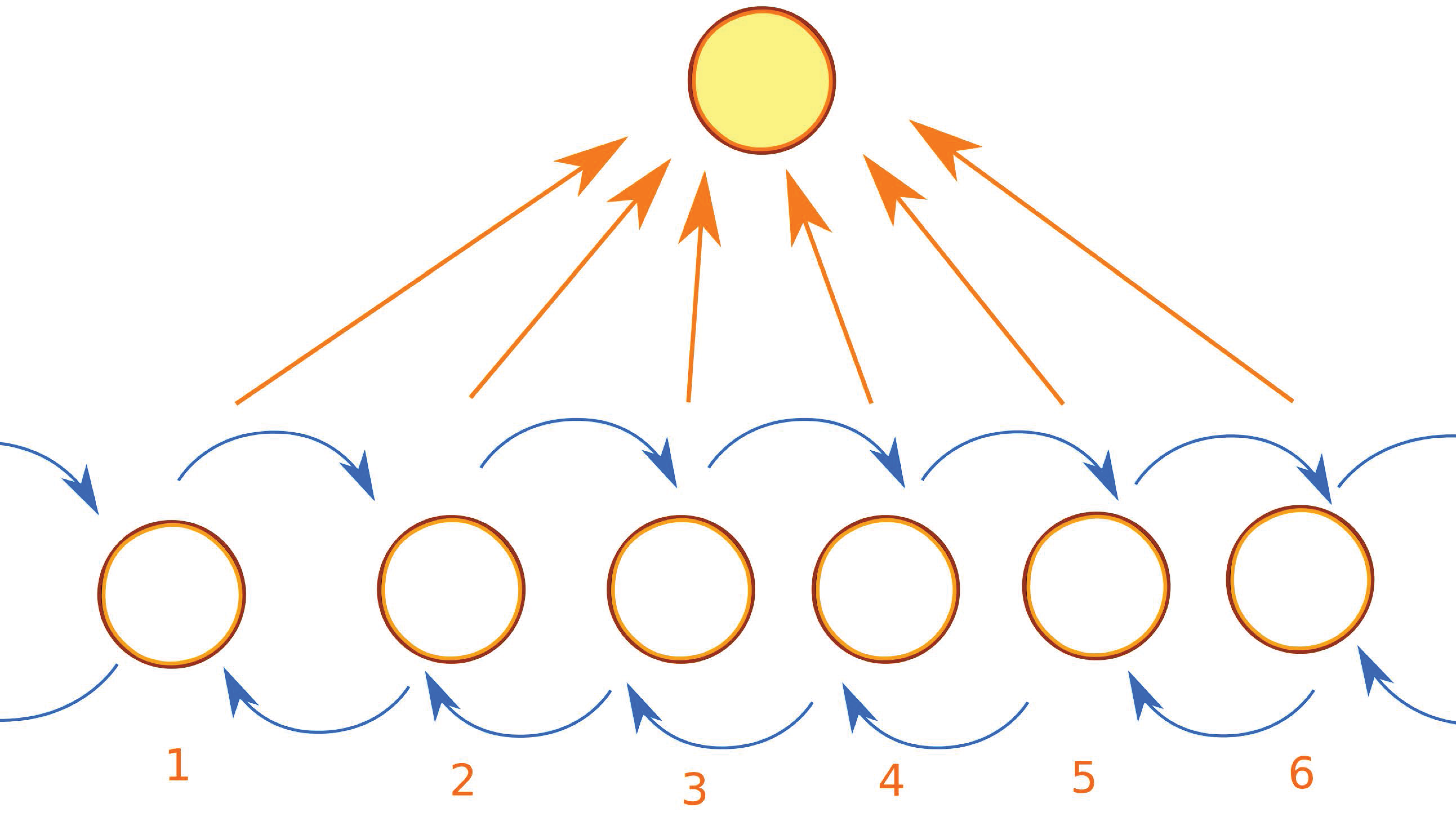
- recognize when the LKMC algorithm revisits the same configurations many times;
- when some configuration is repeated too many times, we pause the regular LKMC algorithm; we then proceed as in the regular LKMC algorithm, but performing all possible events with a barrier less than some limiting barrier , instead of just selecting the most probable move, allowing us to build the matrix T and the vector R;
- estimate the time and configuration when the system exits the basin using AMC theory;
- accordingly update the simulation time and the current configuration;
- resume the regular LKMC algorithm.
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Butler, S.Z.; Hollen, S.M.; Cao, L.; Cui, Y.; Gupta, J.A.; Gutiérrez, H.R.; Heinz, T.F.; Hong, S.S.; Huang, J.; Ismach, A.F.; et al. Progress, Challenges, and Opportunities in Two-Dimensional Materials Beyond Graphene. ACS Nano 2013, 7, 2898–2926. [Google Scholar] [CrossRef] [PubMed]
- Boukhvalov, D.W.; Katsnelson, M.I.; Lichtenstein, A.I. Hydrogen on graphene: Electronic structure, total energy, structural distortions and magnetism from first-principles calculations. Phys. Rev. B 2008, 77, 035427. [Google Scholar] [CrossRef]
- Forte, G.; Grassi, A.; Lombardo, G.M.; La Magna, A.; Angilella, G.G.N.; Pucci, R.; Vilardi, R. Modeling vacancies and hydrogen impurities in graphene: A molecular point of view. Phys. Lett. A 2008, 372, 6168–6174. [Google Scholar] [CrossRef]
- Pellegrino, F.M.D.; Angilella, G.G.N.; Pucci, R. Effect of impurities in high-symmetry lattice positions on the local density of states and conductivity of graphene. Phys. Rev. B 2009, 80, 094203. [Google Scholar] [CrossRef]
- Ulybyshev, M.V.; Katsnelson, M.I. Magnetism and Interaction-Induced Gap Opening in Graphene with Vacancies or Hydrogen Adatoms: Quantum Monte Carlo Study. Phys. Rev. Lett. 2015, 114, 246801. [Google Scholar] [CrossRef] [PubMed]
- Aréou, E.; Cartry, G.; Layet, J.M.; Angot, T. Hydrogen-graphite interaction: Experimental evidences of an adsorption barrier. J. Chem. Phys. 2011, 134, 014701. [Google Scholar] [CrossRef] [PubMed]
- Šljivančanin, Ž.; Rauls, E.; Hornekaer, L.; Xu, W.; Besenbacher, F.; Hammer, B. Extended atomic hydrogen dimer configurations on the graphite(0001) surface. J. Chem. Phys. 2009, 131, 084706. [Google Scholar] [CrossRef] [PubMed]
- González-Herrero, H.; Gómez-Rodríguez, J.M.; Mallet, P.; Moaied, M.; Palacios, J.J.; Salgado, C.; Ugeda, M.M.; Veuillen, J.Y.; Yndurain, F.; Brihuega, I. Atomic-scale control of graphene magnetism by using hydrogen atoms. Science 2016, 352, 437–441. [Google Scholar] [CrossRef] [PubMed]
- Lehtinen, P.O.; Foster, A.S.; Ma, Y.; Krasheninnikov, A.V.; Nieminen, R.M. Irradiation-Induced Magnetism in Graphite: A Density Functional Study. Phys. Rev. Lett. 2004, 93, 187202. [Google Scholar] [CrossRef] [PubMed]
- Yazyev, O.V.; Helm, L. Defect-induced magnetism in graphene. Phys. Rev. B 2007, 75, 125408. [Google Scholar] [CrossRef]
- Palacios, J.J.; Fernández-Rossier, J.; Brey, L. Vacancy-induced magnetism in graphene and graphene ribbons. Phys. Rev. B 2008, 77, 195428. [Google Scholar] [CrossRef]
- Nair, R.R.; Sepioni, M.; Tsai, I.L.; Lehtinen, O.; Keinonen, J.; Krasheninnikov, A.V.; Thomson, T.; Geim, A.K.; Grigorieva, I.V. Spin-half paramagnetism in graphene induced by point defects. Nat. Phys. 2012, 8, 199–202. [Google Scholar] [CrossRef]
- McCreary, K.M.; Swartz, A.G.; Han, W.; Fabian, J.; Kawakami, R.K. Magnetic Moment Formation in Graphene Detected by Scattering of Pure Spin Currents. Phys. Rev. Lett. 2012, 109, 186604. [Google Scholar] [CrossRef] [PubMed]
- Tao, C.; Jiao, L.; Yazyev, O.V.; Chen, Y.C.; Feng, J.; Zhang, X.; Capaz, R.B.; Tour, J.M.; Zettl, A.; Louie, S.G.; et al. Spatially resolving edge states of chiral graphene nanoribbons. Nat. Phys. 2011, 7, 616–620. [Google Scholar] [CrossRef]
- Nair, R.R.; Tsai, I.L.; Sepioni, M.; Lehtinen, O.; Keinonen, J.; Krasheninnikov, A.V.; Castro Neto, A.H.; Katsnelson, M.I.; Geim, A.K.; Grigorieva, I.V. Dual origin of defect magnetism in graphene and its reversible switching by molecular doping. Nat. Commun. 2013, 4, 2010. [Google Scholar] [CrossRef] [PubMed]
- Moaied, M.; Alvarez, J.V.; Palacios, J.J. Hydrogenation-induced ferromagnetism on graphite surfaces. Phys. Rev. B 2014, 90, 115441. [Google Scholar] [CrossRef]
- Sha, X.; Jackson, B. First-principles study of the structural and energetic properties of H atoms on a graphite (0001) surface. Surf. Sci. 2002, 496, 318–330. [Google Scholar] [CrossRef]
- Chen, L.; Cooper, A.C.; Pez, G.P.; Cheng, H. Mechanistic Study on Hydrogen Spillover onto Graphitic Carbon Materials. J. Phys. Chem. C 2007, 111, 18995–19000. [Google Scholar] [CrossRef]
- Denis, P.A.; Iribarne, F. On the hydrogen addition to graphene. J. Mol. Struct. 2009, 907, 93–103. [Google Scholar] [CrossRef]
- Kerwin, J.; Jackson, B. The sticking of H and D atoms on a graphite (0001) surface: The effects of coverage and energy dissipation. J. Chem. Phys. 2008, 128, 084702. [Google Scholar] [CrossRef] [PubMed]
- Moaied, M.; Moreno, J.A.; Caturla, M.J.; Ynduráin, F.; Palacios, J.J. Theoretical study of the dynamics of atomic hydrogen adsorbed on graphene multilayers. Phys. Rev. B 2015, 91, 155419. [Google Scholar] [CrossRef]
- Casolo, S.; Løvvik, O.M.; Martinazzo, R.; Tantardini, G.F. Understanding adsorption of hydrogen atoms on graphene. J. Chem. Phys. 2009, 130, 054704. [Google Scholar] [CrossRef] [PubMed]
- Hornekær, L.; Rauls, E.; Xu, W.; Šljivančanin, Ž.; Otero, R.; Stensgaard, I.; Lægsgaard, E.; Hammer, B.; Besenbacher, F. Clustering of Chemisorbed H(D) Atoms on the Graphite (0001) Surface due to Preferential Sticking. Phys. Rev. Lett. 2006, 97, 186102. [Google Scholar] [CrossRef] [PubMed]
- Jeloaica, L.; Sidis, V. DFT investigation of the adsorption of atomic hydrogen on a cluster-model graphite surface. Chem. Phys. Lett. 1999, 300, 157–162. [Google Scholar] [CrossRef]
- Forte, G.; Grassi, A.; Lombardo, G.M.; Pucci, R.; Angilella, G.G.N. From molecules and clusters of atoms to solid state properties. In Many-Body Approaches at Different Scales: A Tribute to Norman H. March on the Occasion of His 90th Birthday; Angilella, G.G.N., Amovilli, C., Eds.; Springer: New York, NY, USA, 2018; Chapter 19; pp. 239–248. [Google Scholar]
- Soriano, D.; Leconte, N.; Ordejón, P.; Charlier, J.C.; Palacios, J.J.; Roche, S. Magnetoresistance and Magnetic Ordering Fingerprints in Hydrogenated Graphene. Phys. Rev. Lett. 2011, 107, 016602. [Google Scholar] [CrossRef] [PubMed]
- Leconte, N.; Soriano, D.; Roche, S.; Ordejon, P.; Charlier, J.C.; Palacios, J.J. Magnetism-Dependent Transport Phenomena in Hydrogenated Graphene: From Spin-Splitting to Localization Effects. ACS Nano 2011, 5, 3987–3992. [Google Scholar] [CrossRef] [PubMed]
- Soriano, D.; Van Tuan, D.; Dubois, S.M.M.; Gmitra, M.; Cummings, A.W.; Kochan, D.; Ortmann, F.; Charlier, J.C.; Fabian, J.; Roche, S. Spin transport in hydrogenated graphene. 2D Mater. 2015, 2, 022002. [Google Scholar] [CrossRef]
- Jayasingha, R.; Sherehiy, A.; Wu, S.Y.; Sumanasekera, G.U. In Situ Study of Hydrogenation of Graphene and New Phases of Localization between Metal–Insulator Transitions. Nano Lett. 2013, 13, 5098–5105. [Google Scholar] [CrossRef] [PubMed]
- Cresti, A.; Louvet, T.; Ortmann, F.; Van Tuan, D.; Lenarczyk, P.; Huhs, G.; Roche, S. Impact of Vacancies on Diffusive and Pseudodiffusive Electronic Transport in Graphene. Crystals 2013, 3, 289–305. [Google Scholar] [CrossRef]
- Roche, S.; Leconte, N.; Ortmann, F.; Lherbier, A.; Soriano, D.; Charlier, J.C. Quantum transport in disordered graphene: A theoretical perspective. Solid State Commun. 2012, 152, 1404–1410. [Google Scholar] [CrossRef]
- Chuang, C.; Puddy, R.K.; Lin, H.D.; Lo, S.T.; Chen, T.M.; Smith, C.G.; Liang, C.T. Experimental evidence for Efros–Shklovskii variable range hopping in hydrogenated graphene. Solid State Commun. 2012, 152, 905–908. [Google Scholar] [CrossRef]
- Leconte, N.; Lherbier, A.; Varchon, F.; Ordejon, P.; Roche, S.; Charlier, J.C. Quantum transport in chemically modified two-dimensional graphene: From minimal conductivity to Anderson localization. Phys. Rev. B 2011, 84, 235420. [Google Scholar] [CrossRef]
- Saloriutta, K.; Uppstu, A.; Harju, A.; Puska, M.J. Ab initio transport fingerprints for resonant scattering in graphene. Phys. Rev. B 2012, 86, 235417. [Google Scholar] [CrossRef]
- Deretzis, I.; Giannazzo, F.; Angilella, G.G.N.; Parisi, L.; Magna, A.L. Atom by atom simulations of nano-materials processing. In Proceedings of the 2016 IEEE Nanotechnology Materials and Devices Conference (NMDC), Toulouse, France, 9–12 October 2016; pp. 1–2. [Google Scholar]
- Parisi, L.; Di Giugno, R.; Deretzis, I.; Angilella, G.G.N.; La Magna, A. Kinetic Monte Carlo simulations of vacancy evolution in graphene. Mater. Sci. Semicond. Process. 2016, 42, 179–182. [Google Scholar] [CrossRef]
- Datta, S. Electronic Transport in Mesoscopic Systems; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Šljivančanin, Ž.; Andersen, M.; Hornekaer, L.; Hammer, B.; Andersen, M. Structure and stability of small H clusters on graphene. Phys. Rev. B 2011, 83, 205426. [Google Scholar] [CrossRef]
- Gargiulo, F.; Autés, G.; Virk, N.; Barthel, S.; Rösner, M.; Toller, L.R.M.; Wehling, T.O.; Yazyev, O.V. Electronic Transport in Graphene with Aggregated Hydrogen Adatoms. Phys. Rev. Lett. 2014, 113, 246601. [Google Scholar] [CrossRef] [PubMed]
- La Magna, A.; Coffa, S.; Colombo, L. Role of extended vacancy-vacancy interaction on the ripening of voids in silicon. Phys. Rev. Lett. 1999, 82, 1720. [Google Scholar] [CrossRef]
- La Magna, A.; Coffa, S. Accelerated Monte Carlo algorithms for defect diffusion and clustering. Comput. Mater. Sci. 2000, 17, 21–33. [Google Scholar] [CrossRef]
- Lieb, E.H. Two Theorems on the Hubbard Model. Phys. Rev. Lett. 1989, 62, 1201–1204. [Google Scholar] [CrossRef] [PubMed]
- Lieb, E.H. Two Theorems on the Hubbard Model. Phys. Rev. Lett. 1989, 62, 1927. [Google Scholar] [CrossRef]
- Petersen, D.E.; Sørensen, H.H.B.; Hansen, P.C.; Skelboe, S.; Stokbro, K. Block tridiagonal matrix inversion and fast transmission calculations. J. Comput. Phys. 2008, 227, 3174–3190. [Google Scholar] [CrossRef]
- La Magna, A.; Deretzis, I.; Forte, G.; Pucci, R. Conductance distribution in doped and defected graphene nanoribbons. Phys. Rev. B 2009, 80, 195413. [Google Scholar] [CrossRef]
- Deretzis, I.; Fiori, G.; Iannaccone, G.; La Magna, A. Effects due to backscattering and pseudogap features in graphene nanoribbons with single vacancies. Phys. Rev. B 2010, 81, 085427. [Google Scholar] [CrossRef]
- Camarda, M.; La Magna, A.; La Via, F. A kinetic Monte Carlo method on super-lattices for the study of the defect formation in the growth of close packed structures. J. Comput. Phys. 2007, 227, 1075–1093. [Google Scholar] [CrossRef]
- Deretzis, I.; La Magna, A. Interaction between hydrogen flux and carbon monolayer on SiC(0001): Graphene formation kinetics. Nanoscale 2013, 5, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Campo, A.; Lombardo, S.F.; Deretzis, I.; Garozzo, G.; Angilella, G.G.N.; La Magna, A. Atom by Atom simulation of nano-materials manipulation: The plasma etching case. IEEE Trans. Nanotechnol. 2017, 16, 790–797. [Google Scholar] [CrossRef]
- Herrero, C.P.; Ramírez, R. Vibrational properties and diffusion of hydrogen on graphene. Phys. Rev. B 2009, 79, 115429. [Google Scholar] [CrossRef]
- Tozzini, V.; Pellegrini, V. Prospects for hydrogen storage in graphene. Phys. Chem. Chem. Phys. 2013, 15, 80–89. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Novotny, M.A. Monte Carlo Algorithms with Absorbing Markov Chains: Fast Local Algorithms for Slow Dynamics. Phys. Rev. Lett. 1995, 74, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Fichthorn, K.A.; Lin, Y. A local superbasin kinetic Monte Carlo method. J. Chem. Phys. 2013, 138, 164104. [Google Scholar] [CrossRef] [PubMed]
- Mason, D.; Hudson, T.; Sutton, A. Fast recall of state-history in kinetic Monte Carlo simulations utilizing the Zobrist key. Comput. Phys. Commun. 2005, 165, 37–48. [Google Scholar] [CrossRef]





| Event | Configuration | Prefactor | Barrier |
|---|---|---|---|
| Migration | eV + | ||
| Atomic desorption | 1 eV | ||
| Associative desorption | eV |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parisi, L.; Angilella, G.G.N.; Deretzis, I.; Pucci, R.; La Magna, A. Role of H Distribution on Coherent Quantum Transport of Electrons in Hydrogenated Graphene. Condens. Matter 2017, 2, 37. https://doi.org/10.3390/condmat2040037
Parisi L, Angilella GGN, Deretzis I, Pucci R, La Magna A. Role of H Distribution on Coherent Quantum Transport of Electrons in Hydrogenated Graphene. Condensed Matter. 2017; 2(4):37. https://doi.org/10.3390/condmat2040037
Chicago/Turabian StyleParisi, Luca, Giuseppe G. N. Angilella, Ioannis Deretzis, Renato Pucci, and Antonio La Magna. 2017. "Role of H Distribution on Coherent Quantum Transport of Electrons in Hydrogenated Graphene" Condensed Matter 2, no. 4: 37. https://doi.org/10.3390/condmat2040037
APA StyleParisi, L., Angilella, G. G. N., Deretzis, I., Pucci, R., & La Magna, A. (2017). Role of H Distribution on Coherent Quantum Transport of Electrons in Hydrogenated Graphene. Condensed Matter, 2(4), 37. https://doi.org/10.3390/condmat2040037







