Time-Correlated Vortex Tunneling in Layered Superconductors
Abstract
:1. Introduction
2. Results
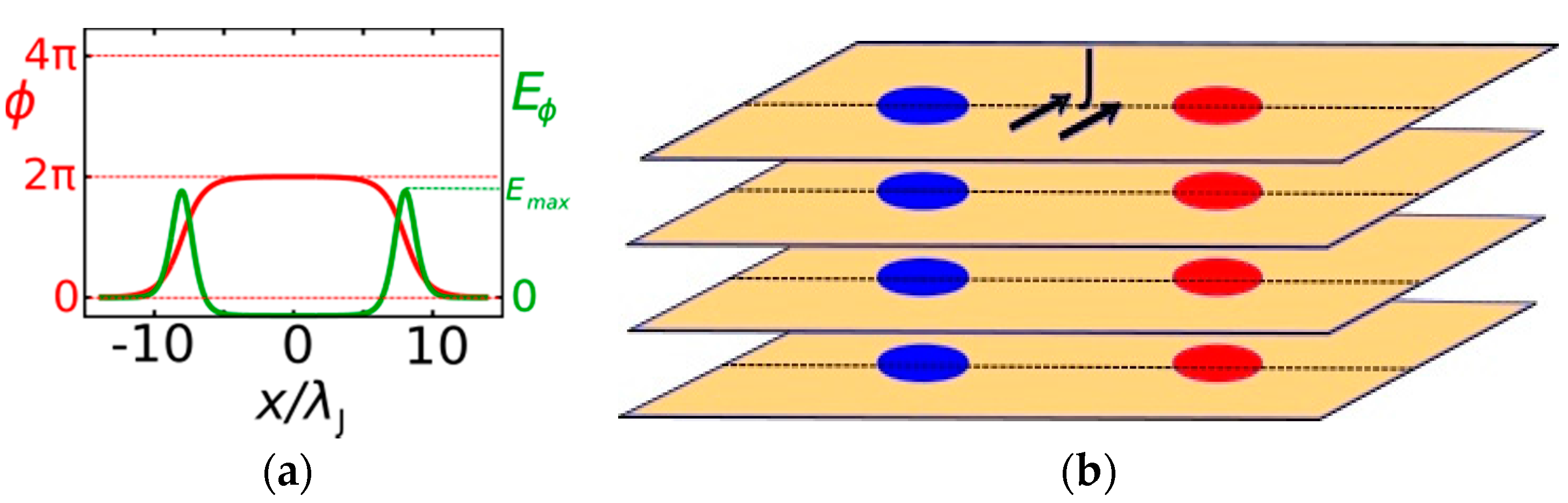
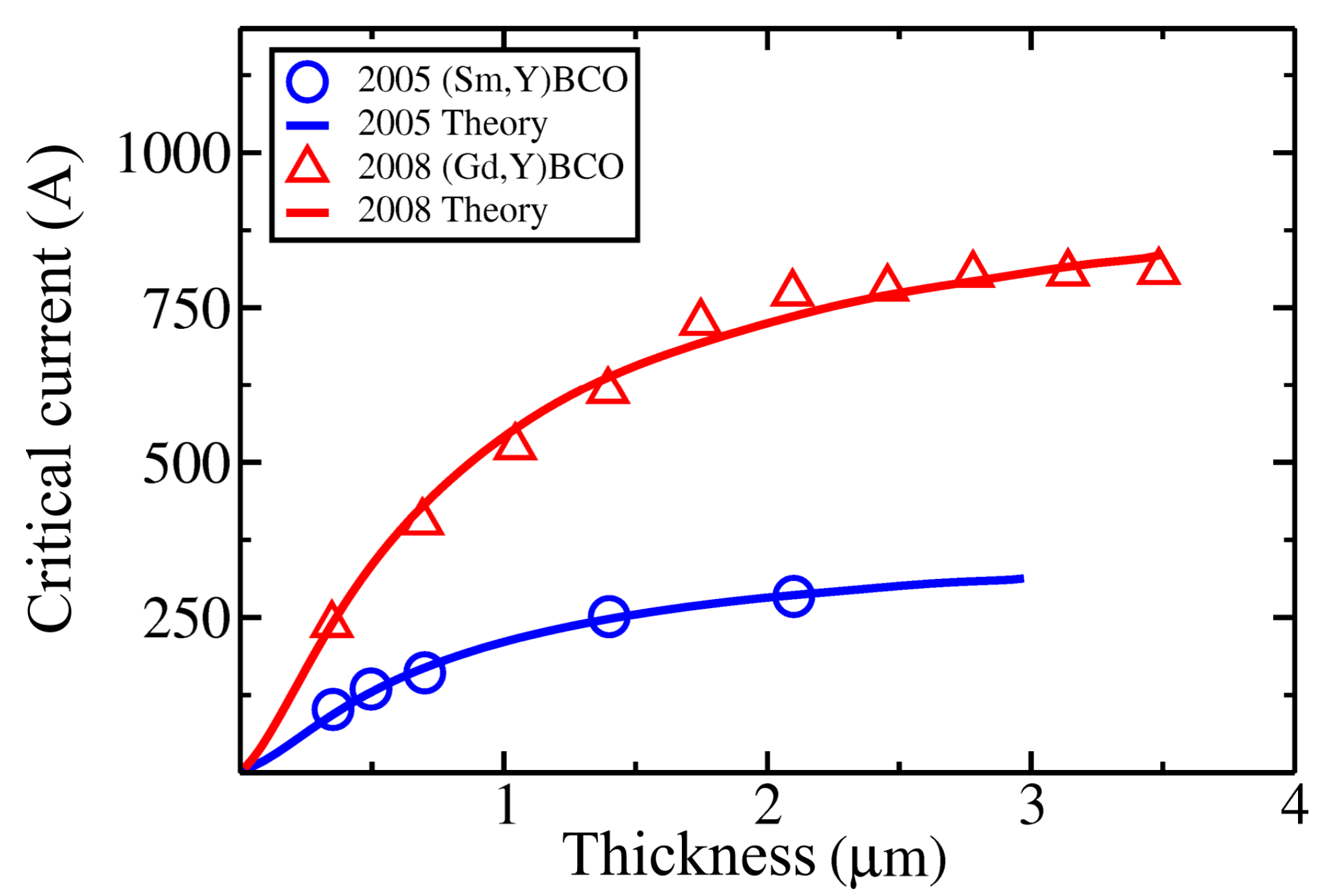
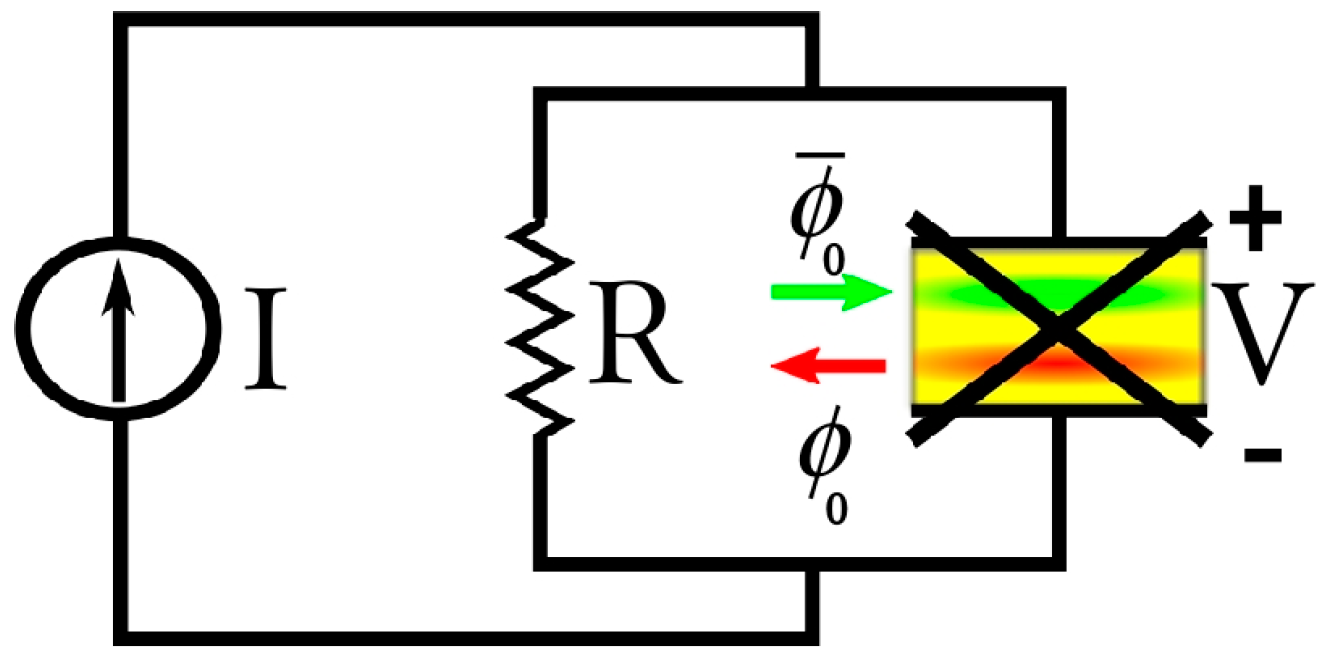
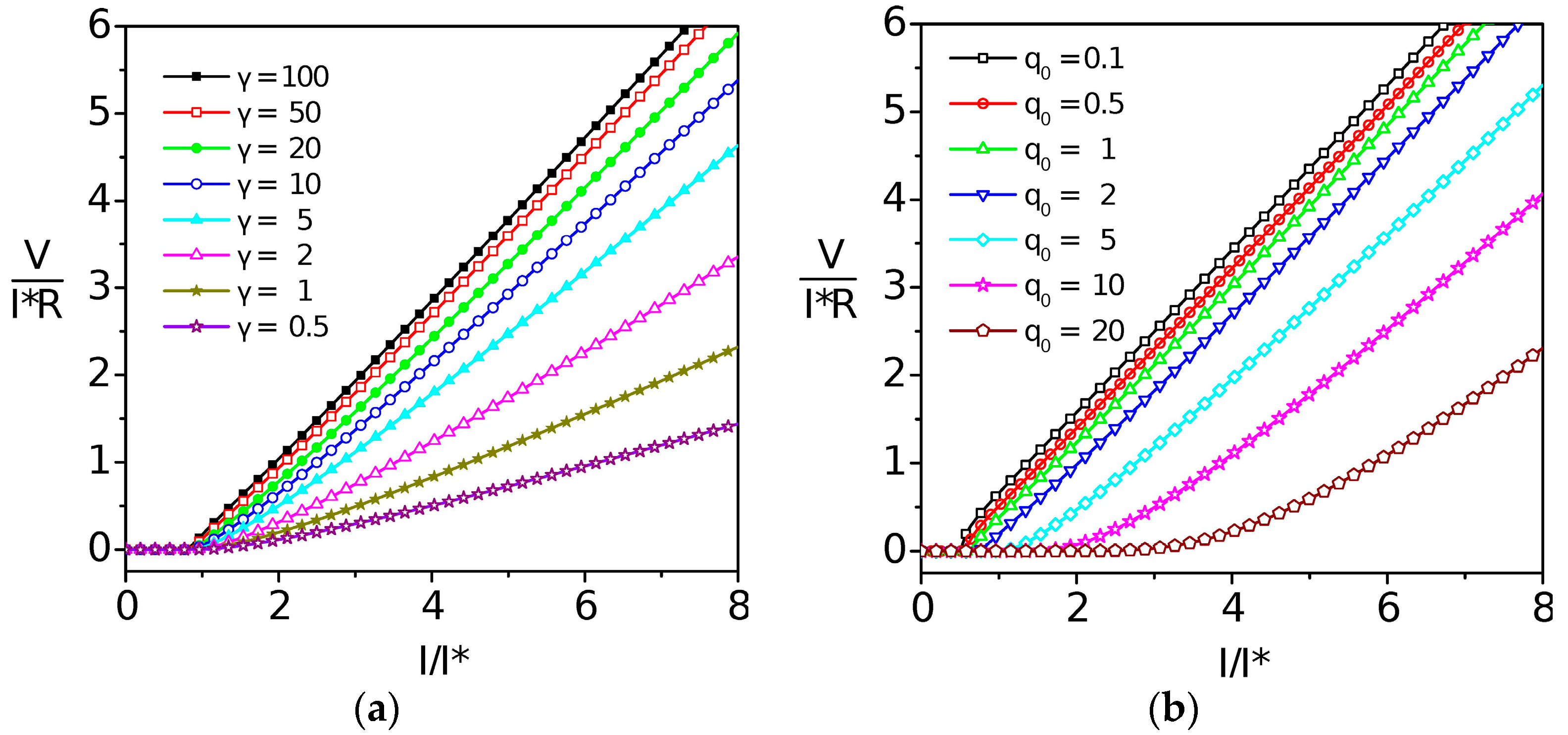
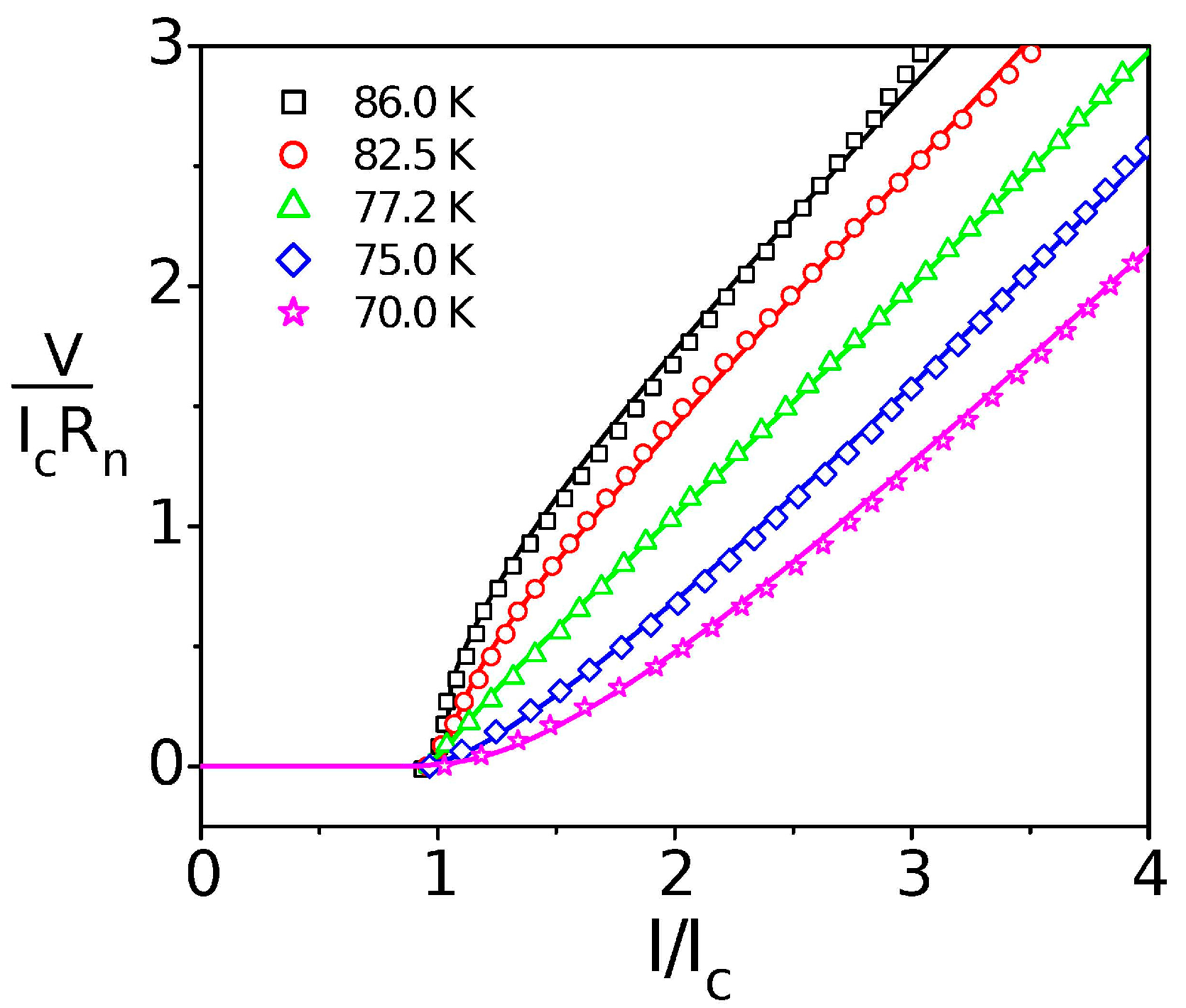
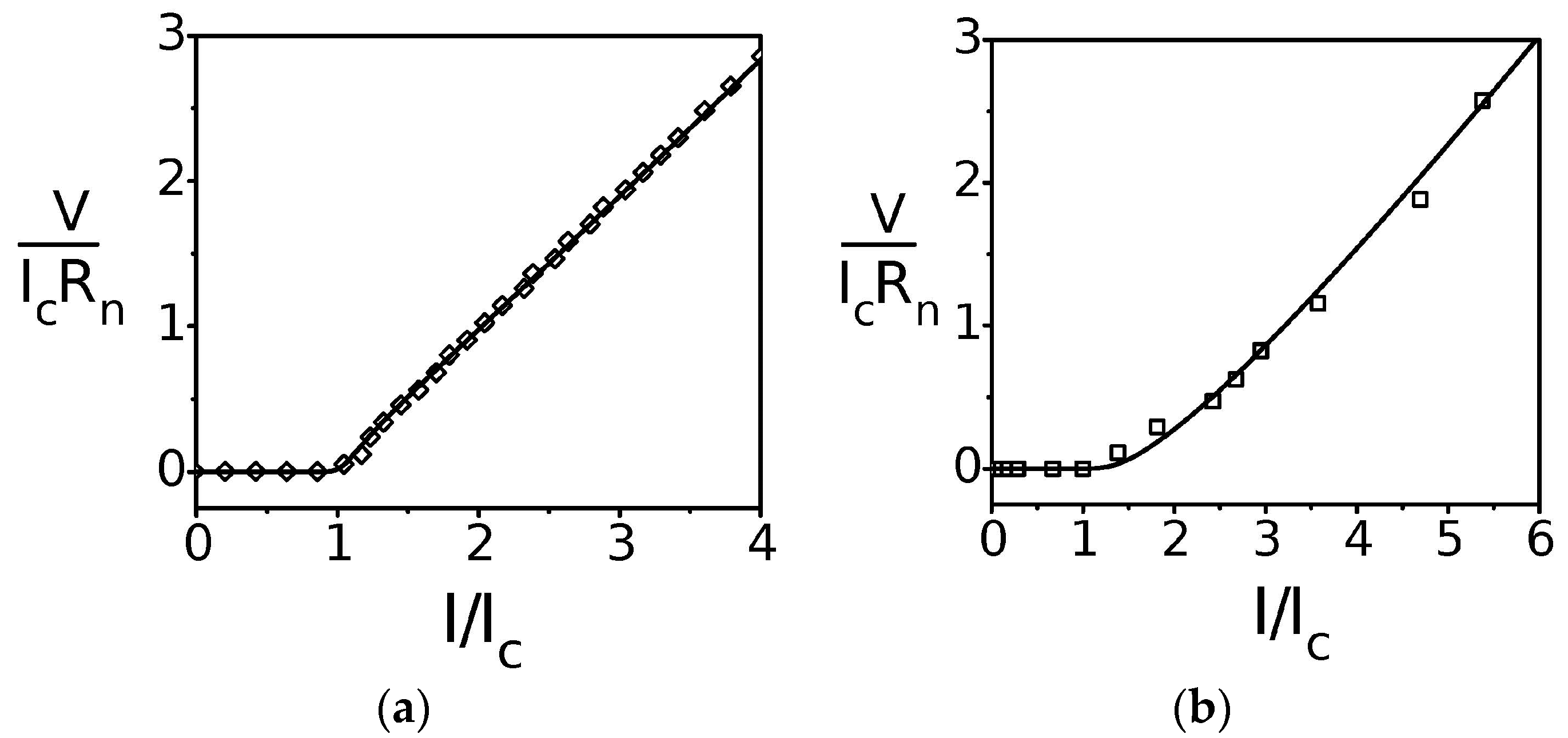
2.1. Weber Blockade Threshold Current for Vortex Pair Creation
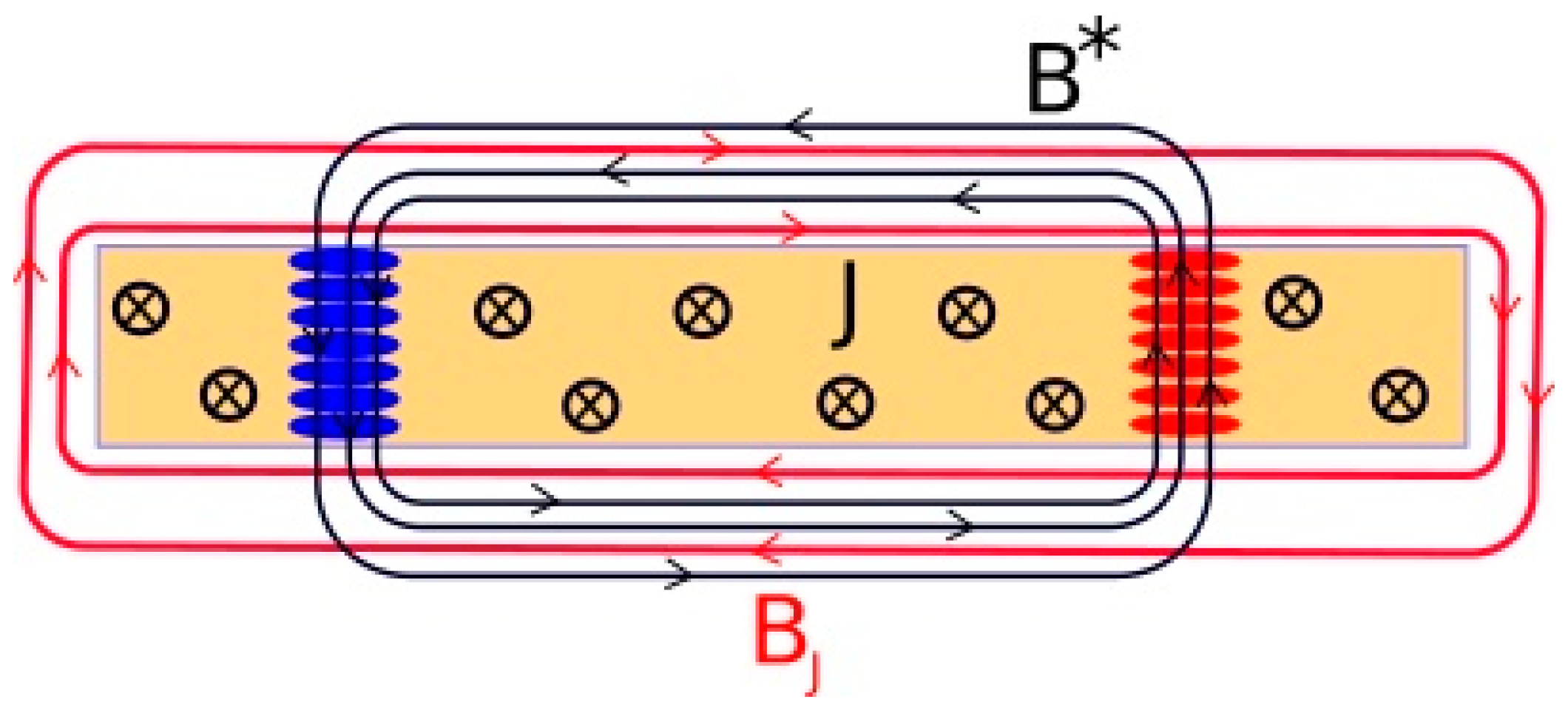
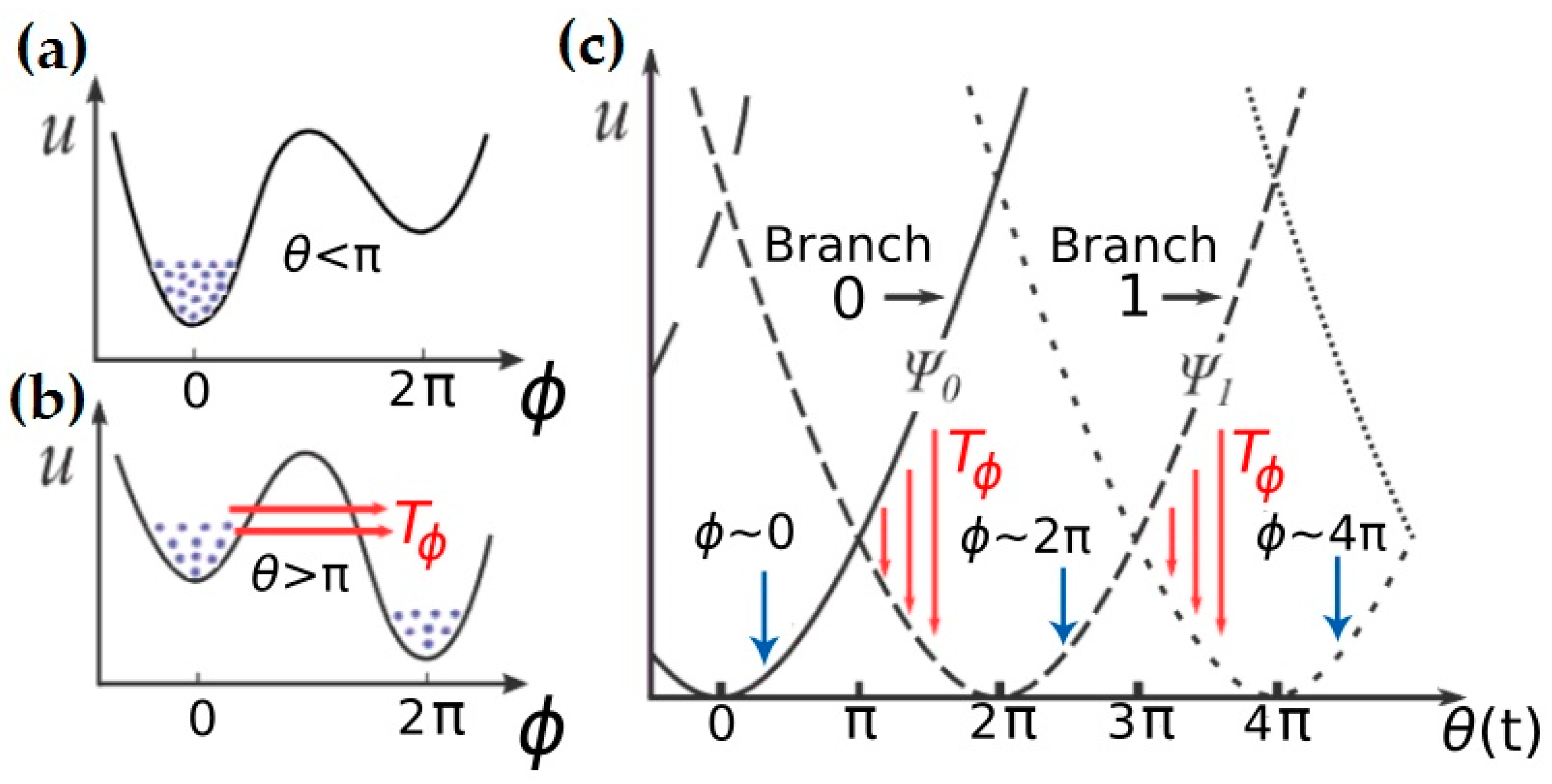
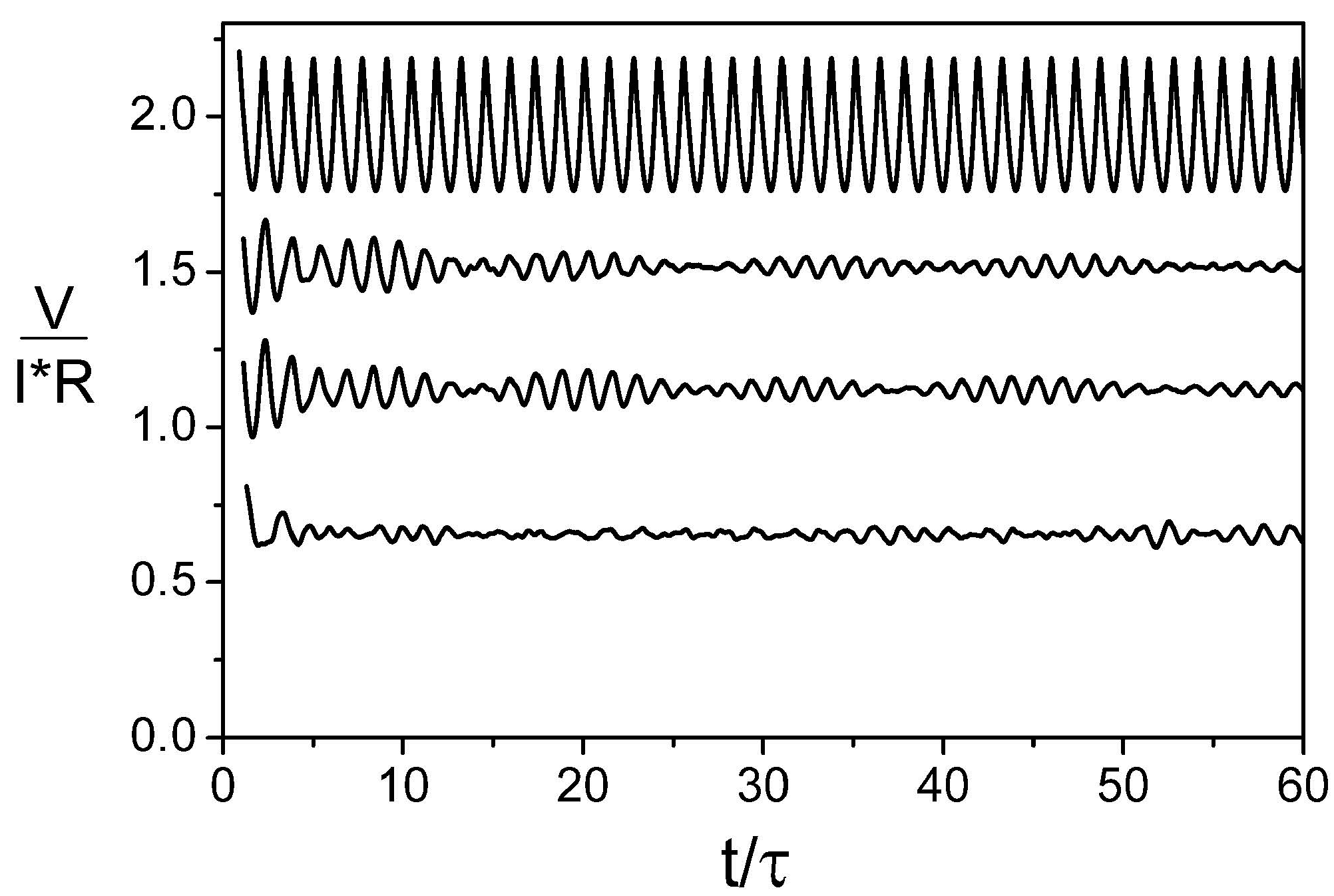
2.2. Time-Correlated, Coherent Tunneling of Josephson Vortices
3. Discussion and Conclusions
4. Materials and Methods
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dimos, D.; Chaudhari, P.; Mannhart, J. Superconducting transport properties of grain boundaries in YBa2Cu3O7 bicrystals. Phys. Rev. B 1990, 41, 4038. [Google Scholar] [CrossRef]
- Graser, S.; Hirschfeld, P.J.; Kopp, T.; Gutser, R.; Andersen, B.M.; Mannhart, J. How grain boundaries limit supercurrents in high-temperature superconductors. Nat. Phys. 2010, 6, 609–614. [Google Scholar] [CrossRef]
- Held, R.; Schneider, C.W.; Mannhart, J.; Allard, L.F.; More, K.L.; Goyal, A. Low-angle grain boundaries in YBa2Cu3O7−δ with high critical current densities. Phys. Rev. B 2009, 79, 014515. [Google Scholar] [CrossRef]
- Hilgenkamp, H.; Mannhart, J. Grain boundaries in high-Tc superconductors. Rev. Mod. Phys. 2002, 74, 485. [Google Scholar] [CrossRef]
- Miller, J., Jr.; Ying, Q.; Zou, Z.; Fan, N.; Xu, J.; Davis, M.; Wolfe, J. Use of Tricrystal Junctions to Probe the Pairing State Symmetry of YBa2Cu3O7−δ. Phys. Rev. Lett. 1995, 74, 2347–2350. [Google Scholar] [CrossRef] [PubMed]
- Barone, A.; Paterno, G. Physics and Applications of Josephson Effect; John Wiley & Sons: Hoboken, NJ, USA, 1982; p. 529. [Google Scholar]
- Blatter, G.; Feigel’man, M.V.; Geshkenbein, V.B.; Larkin, A.I.; Vinokur, V.M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 1994, 66, 1125. [Google Scholar] [CrossRef]
- Roditchev, D.; Brun, C.; Serrier-Garcia, L.; Cuevas, J.C.; Bessa, V.H.L.; Milosevic, M.V.; Debontridder, F.; Stolyarov, V.; Cren, T. Direct observation of Josephson vortex cores. Nat. Phys. 2015, 11, 332–337. [Google Scholar] [CrossRef]
- Marken, K. Fundamental Issues in High Temperature Superconductor (HTS) Materials Science and Engineering; Woodhead Publishing Limited: Cambridge, UK, 2012; pp. 1–31. [Google Scholar]
- Shnirman, A.; Ben-Jacob, E.; Malomed, B. Tunneling and resonant tunneling of fluxons in a long Josephson junction. Phys. Rev. B 1997, 56, 14677. [Google Scholar] [CrossRef]
- Miller, J.H.; Ordóñez, C.; Prodan, E. Time-Correlated Soliton Tunneling in Charge and Spin Density Waves. Phys. Rev. Lett. 2000, 84, 1555. [Google Scholar] [CrossRef] [PubMed]
- Miller, J.H.; Wijesinghe, A.I.; Tang, Z.; Guloy, A.M. Correlated Quantum Transport of Density Wave Electrons. Phys. Rev. Lett. 2012, 108, 036404. [Google Scholar] [CrossRef] [PubMed]
- Miller, J.H.; Wijesinghe, A.I.; Tang, Z.; Guloy, A.M. Coherent quantum transport of charge density waves. Phys. Rev. B 2013, 87, 115127. [Google Scholar] [CrossRef]
- Miller, J.H.; Wijesinghe, A.I. The effects of electric and magnetic fields on charge density wave solitons: Possible collective quantum behavior. Eur. Phys. J. Spec. Top. 2013, 222, 1017–1034. [Google Scholar] [CrossRef]
- Blatter, G.; Geshkenbein, V.B.; Vinokur, V.M. Quantum collective creep. Phys. Rev. Lett. 1991, 66, 3297. [Google Scholar] [CrossRef] [PubMed]
- Ao, P.; Thouless, D.J. Tunneling of a quantized vortex: Roles of pinning and dissipation. Phys. Rev. Lett. 1994, 72, 132. [Google Scholar] [CrossRef] [PubMed]
- Wallraff, A.; Lukashenko, A.; Lisenfeld, J.; Kemp, A.; Fistul, M.V.; Koval, Y.; Ustinov, A.V. Quantum dynamics of a single vortex. Nature 2003, 425, 155–158. [Google Scholar] [CrossRef] [PubMed]
- Glazman, L.; Fogel, N.Y. Possibility of quantum tunneling of vortices in thin superconducting films. Sov. J. Low Temp. Phys. 1984, 10, 51–52. [Google Scholar]
- Chudnovsky, E.M.; Tejada, J. Macroscopic Quantum Tunneling of the Magnetic Moment; Cambridge University Press: Cambridge, NY, USA, 1998; p. 173. [Google Scholar]
- Mints, R.G.; Snapiro, I.B. Dynamics of Josephson pancakes in layered superconductors. Phys. Rev. B 1994, 49, 6188. [Google Scholar] [CrossRef]
- Xue, Y.Y.; Huang, Z.J.; Hor, P.H.; Chu, C.W. Evidence for collective pinning in high-temperature superconductors. Phys. Rev. B 1991, 43, 13598. [Google Scholar] [CrossRef]
- Widom, A.; Srivastava, Y. Electrical engineering implications of the quantized sine-Gordon model. Phys. Lett. A 1986, 114, 337–338. [Google Scholar] [CrossRef]
- Dias, O.J.C.; Lemos, J.P.S. False vacuum decay: Effective one-loop action for pair creation of domain walls. J. Math. Phys. 2001, 42, 3292–3298. [Google Scholar] [CrossRef]
- Cohen, T.D.; McGady, D.A. Schwinger mechanism revisited. Phys. Rev. D 2008, 78, 036008. [Google Scholar] [CrossRef]
- Miller, J.H., Jr.; Cardenas, G.; Garcia-Perez, A.; More, W.; Beckwith, A.W. Quantum pair creation of soliton domain walls. J. Phys. A Math. Gen. 2003, 36, 9209–9221. [Google Scholar] [CrossRef]
- Krive, I.V.; Rozhavsky, A.S. On the nature of threshold electric field in quasi-one-dimensional commensurate charge-density-waves. Solid State Commun. 1985, 55, 691–694. [Google Scholar] [CrossRef]
- Grosfeld, E.; Stern, A. Observing Majorana bound states of Josephson vortices in topological superconductors. Proc. Natl. Acad. Sci. USA 2011, 108, 11810–11814. [Google Scholar] [CrossRef] [PubMed]
- Averin, D.V.; Likharev, K.K. Coulomb blockade of single-electron tunneling, and coherent oscillations in small tunnel junctions. J. Low Temp. Phys. 1986, 62, 345–373. [Google Scholar] [CrossRef]
- Morgan-Wall, T.; Leith, B.; Hartman, N.; Rahman, A.; Marković, N. Measurement of Critical Currents of Superconducting Aluminum Nanowires in External Magnetic Fields: Evidence for a Weber Blockade. Phys. Rev. Lett. 2015, 114, 077002. [Google Scholar] [CrossRef] [PubMed]
- Kogan, V.G.; Dobrovitski, V.V. Magnetic field of Josephson vortices outside superconductors. Phys. Rev. B 2008, 77, 132504. [Google Scholar] [CrossRef]
- Abrikosov, A.A. Fundamentals of the Theory of Metals; North-Holland, Elsevier Science Publishers: Amsterdam, The Netherlands, 1988; p. 630. [Google Scholar]
- Foltyn, S.R.; Civale, L.; MacManus-Driscoll, J.L.; Jia, Q.X.; Maiorov, B.; Wang, H.; Maley, M. Materials science challenges for high-temperature superconducting wire. Nat. Mater. 2007, 6, 631–642. [Google Scholar] [CrossRef] [PubMed]
- Foltyn, S.R.; Jia, Q.X.; Arendt, P.N.; Kinder, L.; Fan, Y.; Smith, J.F. Relationship between film thickness and the critical current of YBa2Cu3O7−δ-coated conductors. Appl. Phys. Lett. 1999, 75, 3692–3694. [Google Scholar] [CrossRef]
- Selvamanickam, V.; Yimin, C.; Xuming, X.; Xie, Y.Y.; Martchevski, M.; Rar, A.; Yunfei, Q.; Schmidt, R.M.; Knoll, A.; Lenseth, K.P.; et al. High Performance 2G Wires: From R&D to Pilot-Scale Manufacturing. IEEE Trans. Appl. Supercond. 2009, 19, 3225–3230. [Google Scholar] [CrossRef]
- Pearl, J. Current Distribution in Superconducting Films Carrying Quantized Fluxoids. Appl. Phys. Lett. 1964, 5, 65–66. [Google Scholar] [CrossRef]
- Tafuri, F.; Kirtley, J.R.; Medaglia, P.G.; Orgiani, P.; Balestrino, G. Magnetic Imaging of Pearl Vortices in Artificially Layered (Ba0.9Nd0.1CuO2+x)m/(CaCuO2)n Systems. Phys. Rev. Lett. 2004, 92, 157006. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wu, J.Z. Effect of interlayer magnetic coupling on the Jc of YBa2Cu3O7 insulator/YBa2Cu3O7 trilayers. Appl. Phys. Lett. 2006, 88, 062513. [Google Scholar] [CrossRef]
- Coleman, S. More about the massive Schwinger model. Ann. Phys. 1976, 101, 239–267. [Google Scholar] [CrossRef]
- Maiti, A.; Miller, J.H. Theory of charge-density-wave tunneling. Phys. Rev. B 1991, 43, 12205. [Google Scholar] [CrossRef]
- Hermon, Z.; Shnirman, A.; Ben-Jacob, E. Dephasing Length and Coherence of a Quantum Soliton in an Ideal Long Josephson Junction. Phys. Rev. Lett. 1995, 74, 4915–4918. [Google Scholar] [CrossRef] [PubMed]
- Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman Lectures on Physics; Addison-Wesley: Boston, MA, USA, 1965. [Google Scholar]
- Grigorenko, A.; Bending, S.; Tamegai, T.; Ooi, S.; Henini, M. A one-dimensional chain state of vortex matter. Nature 2001, 414, 728–731. [Google Scholar] [CrossRef] [PubMed]
- Redwing, R.D.; Hinaus, B.M.; Rzchowski, M.S.; Heinig, N.F.; Davidson, B.A.; Nordman, J.E. Observation of strong to Josephson-coupled crossover in 10° YBa2Cu3Ox bicrystal junctions. Appl. Phys. Lett. 1999, 75, 3171–3173. [Google Scholar] [CrossRef]
- Zhang, X.; Saha, S.R.; Butch, N.P.; Kirshenbaum, K.; Paglione, J.; Greene, R.L.; Liu, Y.; Yan, L.; Oh, Y.S.; Kim, K.H.; et al. Josephson effect between electron-doped and hole-doped iron pnictide single crystals. Appl. Phys. Lett. 2009, 95, 062510. [Google Scholar] [CrossRef]
- Lombardi, F.; Ivanov, Z.G.; Komissinski, P.; Fischer, G.M.; Larsson, P.; Claeson, T. The influence of the top and the bottom grain boundaries on the current transport in YBa2Cu3O7-δ step-edge Josephson junction. Appl. Supercond. 1998, 6, 437–443. [Google Scholar] [CrossRef]
- Dark, C.; Speller, S.; Wu, H.; Sundaresan, A.; Tanaka, Y.; Burnell, G.; Grovenor, C.R.M. Grain boundary properties of Tl-2212 and Tl-1223 thin films. IEEE Trans. Appl. Supercond. 2005, 15, 2931–2934. [Google Scholar] [CrossRef]
- Terpstra, D.; IJsselsteijn, R.P.J.; Rogalla, H. Subharmonic Shapiro steps in high-Tc Josephson junctions. Appl. Phys. Lett. 1995, 66, 2286–2288. [Google Scholar] [CrossRef]
- Chui, S.T. Depinning, defect creation and quantum tunnelling. Phys. Lett. A 1993, 180, 149–153. [Google Scholar] [CrossRef]
- Leggett, A.J. Macroscopic Quantum Systems and the Quantum Theory of Measurement. Progress Theor. Phys. Suppl. 1980, 69, 80–100. [Google Scholar] [CrossRef]
- Schrieffer, J.R. Theory of Superconductivity; Benjamin Cummings: San Francisco, CA, USA, 1964. [Google Scholar]
- Cahill, K.E.; Glauber, R.J. Density operators for fermions. Phys. Rev. A 1999, 59, 1538–1555. [Google Scholar] [CrossRef]
- Atkatz, D.; Pagels, H. Origin of the Universe as a quantum tunneling event. Phys. Rev. D 1982, 25, 2065–2073. [Google Scholar] [CrossRef]
- Linde, A. Quantum creation of an open inflationary universe. Phys. Rev. D 1998, 58, 083514. [Google Scholar] [CrossRef]
- Cordero, R.; Rojas, E. Nucleation of (4)R brane universes. Class. Quantum Gravity 2004, 21, 4231. [Google Scholar] [CrossRef]
- Laughlin, R.B. A Different Universe: Reinventing Physics from the Bottom Down; Basic Books, Perseus Books Group: New York, NY, USA, 2005. [Google Scholar]
- Tytgat, M.H.G. QCD at theta ~ pi reexamined: Domain walls and spontaneous CP violation. Phys. Rev. D 2000, 61, 114009. [Google Scholar] [CrossRef]
- Martin, A.D.; Ruostekoski, J. Quantum dynamics of atomic bright solitons under splitting and recollision, and implications for interferometry. New J. Phys. 2012, 14, 043040. [Google Scholar] [CrossRef]
- Elion, W.J.; Wachters, J.J.; Sohn, L.L.; Mooij, J.E. Observation of the Aharonov-Casher effect for vortices in Josephson-junction arrays. Phys. Rev. Lett. 1993, 71, 2311–2314. [Google Scholar] [CrossRef] [PubMed]
- Bardeen, J. Tunnelling from a Many-Particle Point of View. Phys. Rev. Lett. 1961, 6, 57–59. [Google Scholar] [CrossRef]
- Duke, C.B. Tunneling in Solids; Academic Press: New York, NY, USA, 1969. [Google Scholar]
- Swihart, J. Field Solution for a Thin-Film Superconducting Strip Transmission Line. J. Appl. Phys. 1961, 32, 461–469. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miller, J.H., Jr.; Villagrán, M.Y.S. Time-Correlated Vortex Tunneling in Layered Superconductors. Condens. Matter 2017, 2, 21. https://doi.org/10.3390/condmat2020021
Miller JH Jr., Villagrán MYS. Time-Correlated Vortex Tunneling in Layered Superconductors. Condensed Matter. 2017; 2(2):21. https://doi.org/10.3390/condmat2020021
Chicago/Turabian StyleMiller, John H., Jr., and Martha Y. S. Villagrán. 2017. "Time-Correlated Vortex Tunneling in Layered Superconductors" Condensed Matter 2, no. 2: 21. https://doi.org/10.3390/condmat2020021
APA StyleMiller, J. H., Jr., & Villagrán, M. Y. S. (2017). Time-Correlated Vortex Tunneling in Layered Superconductors. Condensed Matter, 2(2), 21. https://doi.org/10.3390/condmat2020021





