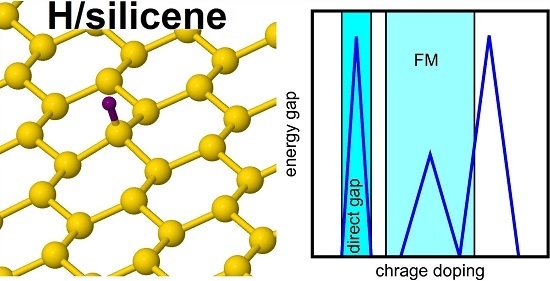
Tuning the Electronic Structure of Hydrogen-Decorated Silicene
Abstract
:1. Introduction
2. Details of Calculations
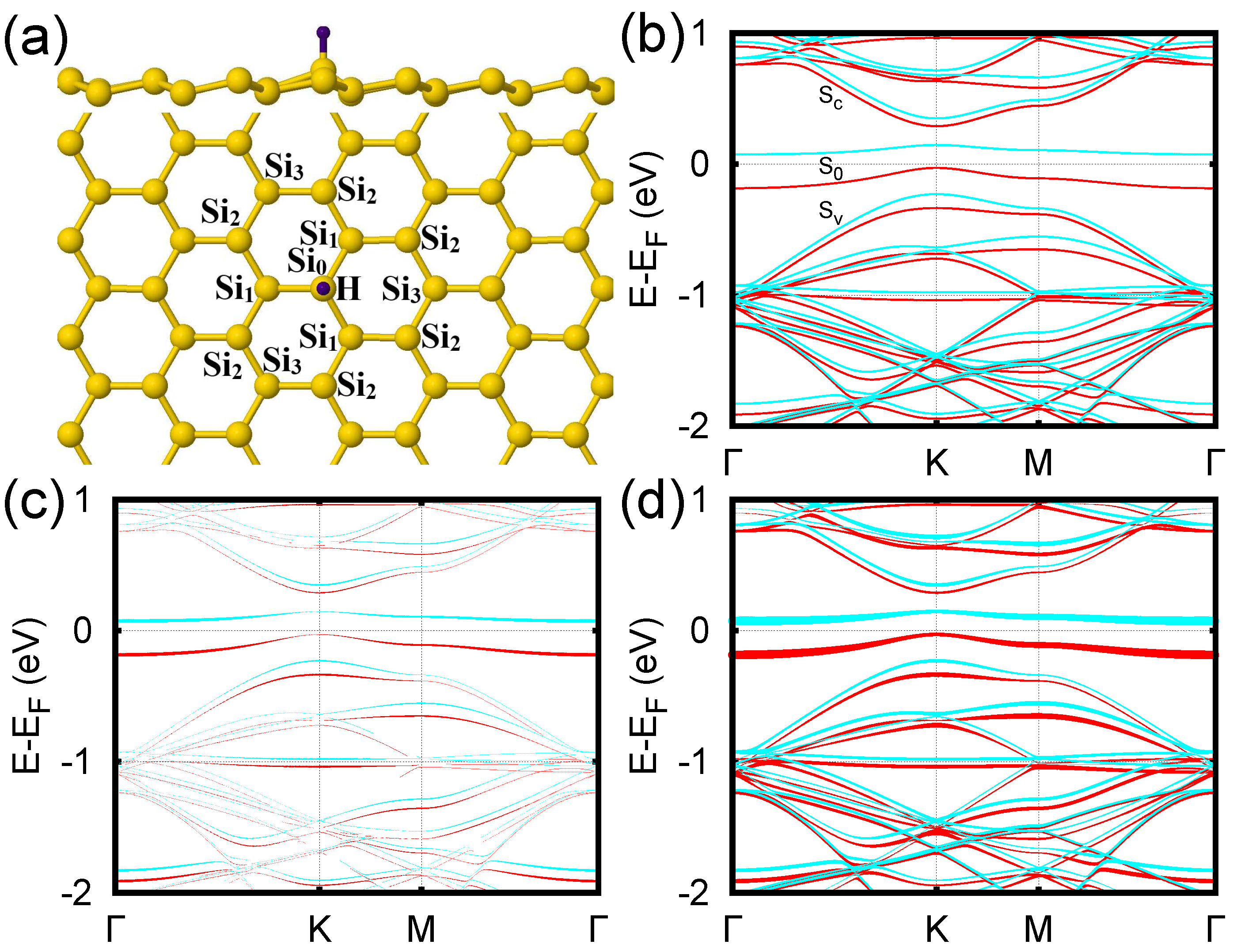
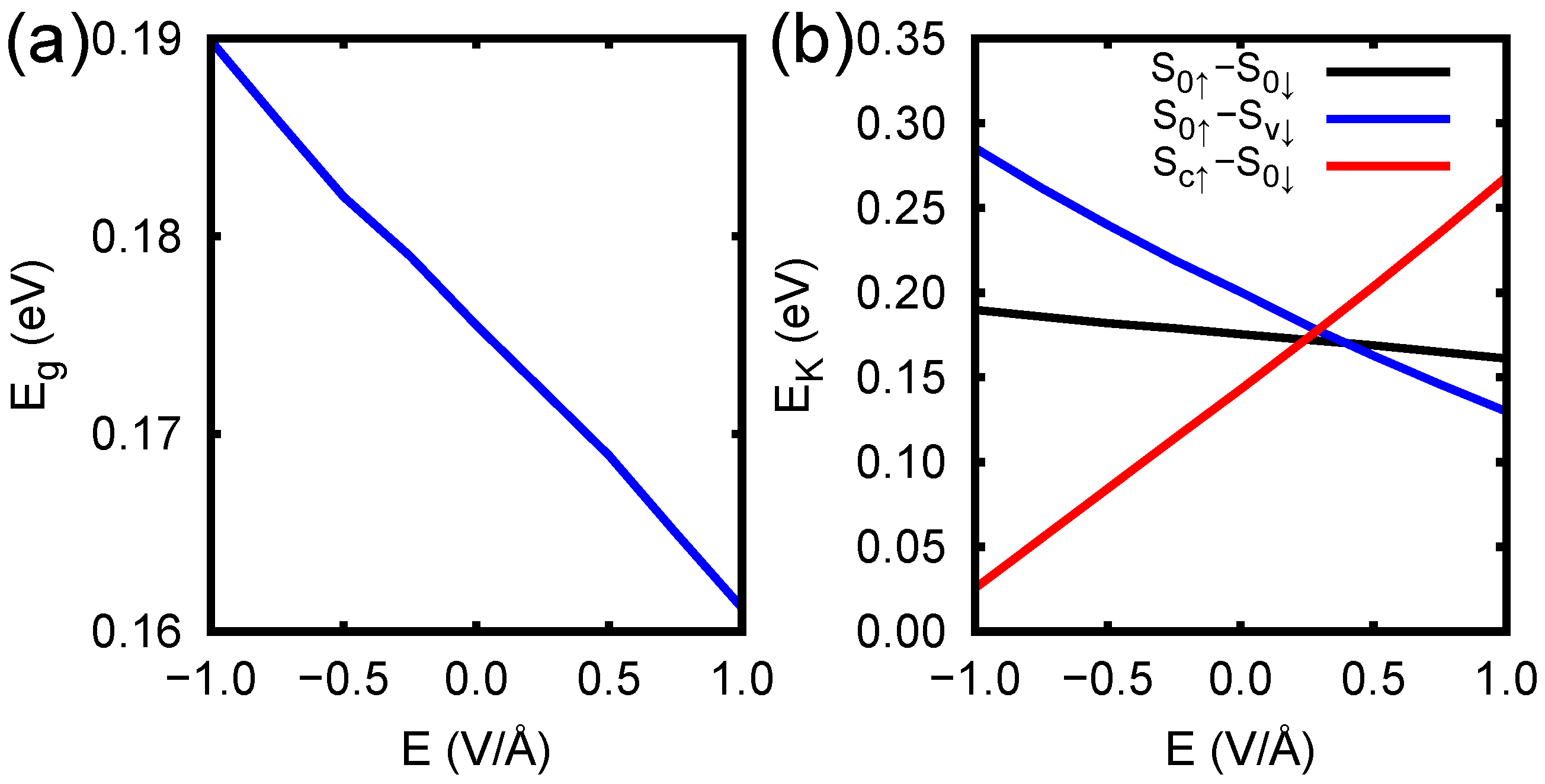
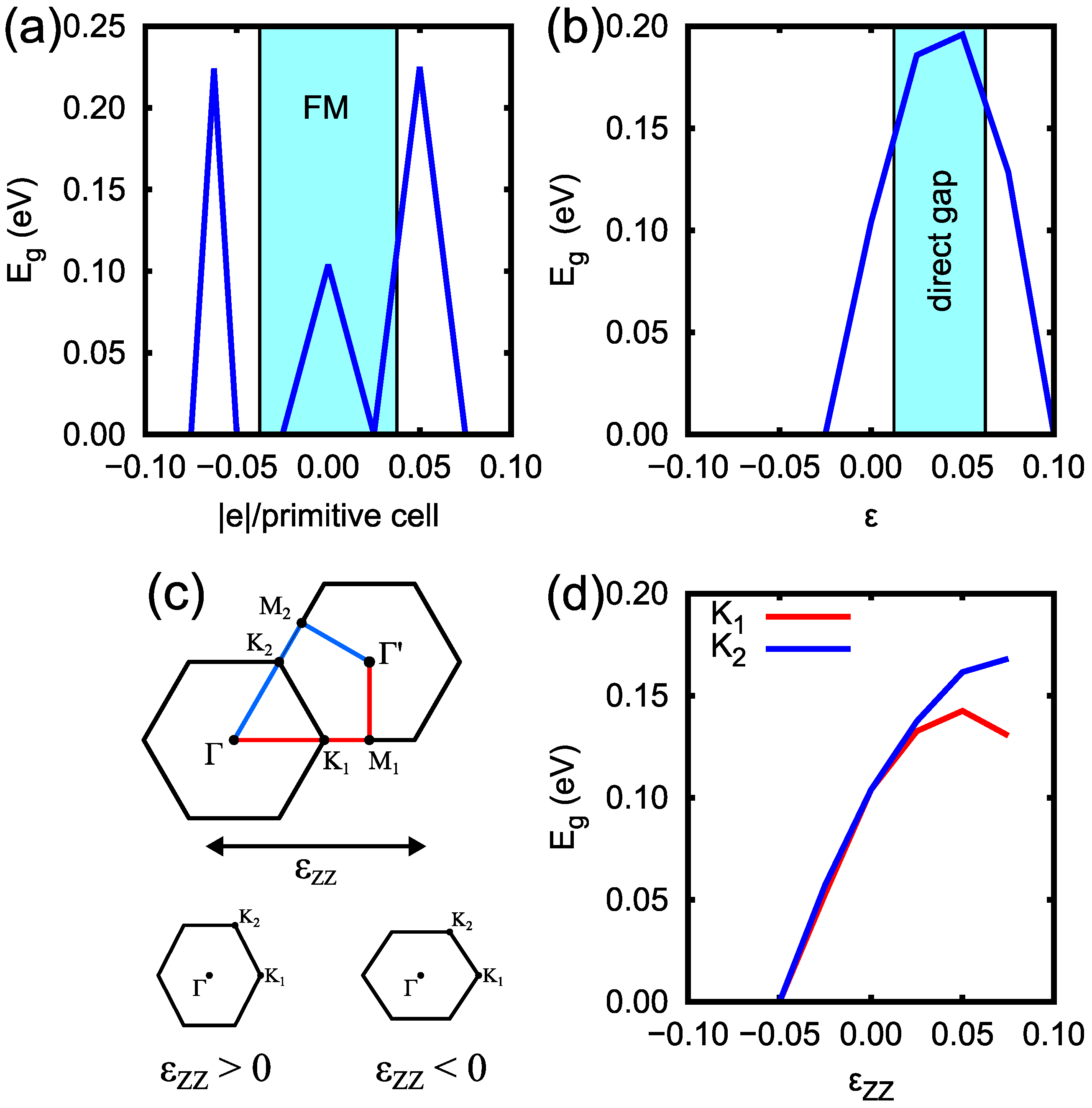
3. Results and Discussion
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Butler, S.Z.; Hollen, M.S.M.; Cao, L.; Cui, Y.; Gupta, J.A.; Gutierrez, H.R.; Heinz, T.F.; Hong, S.S.; Huang, J.; Ismach, A.F.; et al. Progress, challenges, and opportunities in two-dimensional materials beyond graphene. ACS Nano 2013, 7, 2898–2926. [Google Scholar] [CrossRef] [PubMed]
- Bhimanapati, G.R.; Lin, Z.; Meunier, V.; Jung, Y.; Cha, J.; Das, S.; Xiao, D.; Son, Y.; Strano, M.S.; Cooper, V.R.; et al. Recent advances in two-dimensional materials beyond graphene. ACS Nano 2015, 9, 11509–11539. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Sakthivel, T.; Seal, S. Recent development in 2D materials beyond graphene. Prog. Mater. Sci. 2015, 73, 44–126. [Google Scholar] [CrossRef]
- Houssa, M.; Scalise, E.; Sankaren, K.; Pourtois, G.; Afanasev, V.V.; Stesmans, A. Electronic properties of hydrogenated silicene and germanene. Appl. Phys. Lett. 2011, 98, 223107. [Google Scholar] [CrossRef]
- Zhong, H.; Quhe, R.; Wang, Y.; Shi, J.; Liu, J. Silicene on Substrates: A Theoretical Perspective. Chin. Phys. B 2015, 24, 087308. [Google Scholar] [CrossRef]
- Le Lay, G.; Salomon, E.; Angot, T. Silicene: Silicon conquers the 2D world. Europhys. News 2016, 47, 17–21. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, H.; Yu, Z.; Quhe, R.; Zhou, S.; Wang, Y.; Liu, C.C.; Zhong, H.; Han, N.; Lu, J.; et al. Rise of silicene: A competitive 2D material. Prog. Mater. Sci. 2016, 83, 24–151. [Google Scholar] [CrossRef]
- Takeda, K.; Shiraishi, K. Theoretical possibility of stage corrugation in Si and Ge analogs of graphite. Phys. Rev. B 1994, 50, 14916–14922. [Google Scholar] [CrossRef]
- Cahangirov, S.; Topsakal, M.; Aktürk, E.; Sahin, H.; Ciraci, S. Two- and One-Dimensional Honeycomb Structures of Silicon and Germanium. Phys. Rev. Lett. 2009, 102, 236804. [Google Scholar] [CrossRef] [PubMed]
- Sahin, H.; Cahangirov, S.; Topsakal, M.; Bekaroglu, E.; Aktürk, E.; Senger, R.T.; Ciraci, S. Monolayer honeycomb structures of group-IV elements and III-V binary compounds: First-principles calculations. Phys. Rev. B 2009, 80, 155453. [Google Scholar] [CrossRef]
- Vogt, P.; De Padova, P.; Quaresima, C.; Avila, J.; Frantzeskakis, E.; Asensio, M.C.; Resta, A.; Ealet, B.; Le Lay, G. Silicene: Compelling Experimental Evidence for Graphenelike Two-Dimensional Silicon. Phys. Rev. Lett. 2012, 108, 155501. [Google Scholar] [CrossRef] [PubMed]
- Fleurence, A.; Friedlein, R.; Ozaki, T.; Kawai, H.; Wang, Y.; Yamada-Takamura, Y. Experimental Evidence for Epitaxial Silicene on Diboride Thin Films. Phys. Rev. Lett. 2012, 108, 245501. [Google Scholar] [CrossRef] [PubMed]
- Jamgotchian, H.; Colington, Y.; Hamazaouri, N.; Ealet, B.; Hoarau, J.; Aufray, B.; Biberian, J.P. Growth of silicene layers on Ag(111): Unexpected effect of the substrate temperature. J. Phys. Condens. Matter 2012, 24, 172001. [Google Scholar] [CrossRef] [PubMed]
- Chiappe, D.; Granzietti, C.; Tallarida, G.; Fanciulli, M.; Molle, A. Local Electronic Properties of Corrugated Silicene Phases. Adv. Matter 2012, 24, 5088–5093. [Google Scholar] [CrossRef] [PubMed]
- Majzik, Z.; Tchalala, M.R.; Svec, M.; Hapala, P.; Enriquez, H.; Kara, A.; Mayne, A.J.; Dujardin, G.; Jelinek, P.; Oughaddou, H. Combined AFM and STM measurements of a silicene sheet grown on the Ag(111) surface. J. Phys. Condens. Matter 2013, 25, 225301. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Liu, C.C.; Feng, B.; He, X.; Cheng, P.; Ding, Z.; Meng, S.; Zao, Z.G.; Wu, K.H. Evidence for Dirac Fermions in a Honeycomb Lattice Based on Silicon. Phys. Rev. Lett. 2012, 109, 056804. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Cheng, H. Absence of a Dirac cone in silicene on Ag(111): First-principles density functional calculations with a modified effective band structure technique. Phys. Rev. B 2013, 87, 245430. [Google Scholar] [CrossRef]
- Guo, Z.; Furuya, S.; Iwata, J.I.; Oshiyama, A. Absence and presence of Dirac electrons in silicene on substrates. Phys. Rev. B 2013, 87, 235435. [Google Scholar] [CrossRef]
- Lin, C.; Arafune, R.; Kawahara, K.; Kanno, M.; Tsukahara, N.; Minamitani, E.; Kim, Y.; Kawai, M.; Takagi, N. Substrate-Induced Symmetry Breaking in Silicene. Phys. Rev. Lett. 2013, 110, 076801. [Google Scholar] [CrossRef] [PubMed]
- Feng, B.; Li, H.; Liu, C.; Shao, T.; Cheng, P.; Yao, Y.; Meng, S.; Chen, L.; Wu, K. Observation of Dirac Cone Warping and Chirality Effects in Silicene. ACS Nano 2013, 10, 9049–9054. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Liu, D.; Feng, B.; Liu, X.; Zhao, L.; Xie, Z.; Liu, Y.; Liang, A.; Hu, C.; Hu, Y.; et al. Direct Evidence of Interaction-Induced Dirac Cones in Monolayer Silicene/Ag(111) System. 2015; arXiv:1503.06278. [Google Scholar]
- Meng, L.; Wang, Y.; Zhang, L.; Du, S.; Wu, R.; Li, L.; Zhang, Y.; Li, G.; Zhou, H.; Hofer, W.A.; et al. Buckled Silicene Formation on Ir(111). Nano Lett. 2013, 13, 685–690. [Google Scholar] [CrossRef] [PubMed]
- Morishita, T.; Spencer, M.J.S.; Kawamoto, S.; Snook, I.K. A New Surface and Structure for Silicene: Polygonal Silicene Formation on the Al(111) Surface. J. Phys. Chem. C 2013, 117, 22142–22148. [Google Scholar] [CrossRef]
- Aizawa, T.; Suehara, S.; Otani, S. Silicene on Zirconium Carbide (111). J. Phys. Chem. C 2014, 118, 23049–23057. [Google Scholar] [CrossRef]
- Cai, Y.; Chuu, C.P.; Wei, C.; Chou, M.Y. Stability and electronic properties of two-dimensional silicene and germanene on graphene. Phys. Rev. B 2013, 88, 245408. [Google Scholar] [CrossRef]
- Liu, H.; Gao, J.; Zhao, J. Silicene on Substrates: A Way To Preserve or Tune Its Electronic Properties. J. Phys. Chem. C 2013, 117, 10353–10359. [Google Scholar] [CrossRef]
- Scalise, E.; Houssa, M.; Cinquanta, E.; Grazianetti, C.; Van den Broek, B.; Pourtois, G.; Stesmans, A.; Fanciulli, M.; Molle, A. Engineering the electronic properties of silicene by tuning the composition of MoX2 and GaX (X = S, Se, Te) chalchogenide templates. 2D Mater. 2014, 1, 011010. [Google Scholar] [CrossRef]
- Kanno, M.; Arafune, R.; Lin, C.L.; Minamitani, E.; Kawai, M.; Takagi, N. Electronic decoupling by h-BN layer between silicene and Cu(111): A DFT-based analysis. New J. Phys. 2014, 16, 105019. [Google Scholar] [CrossRef]
- Zhu, J.; Schwingenschlögl, U. Structural and Electronic Properties of Silicene on MgX2 (X = Cl, Br, and I). Appl. Mater. Interfaces 2014, 6, 11675–11681. [Google Scholar] [CrossRef] [PubMed]
- Podsiadły-Paszkowska, A.; Krawiec, M. Dirac fermions in silicene on Pb(111) surface. Phys. Chem. Chem. Phys. 2015, 17, 2246–2251. [Google Scholar] [CrossRef] [PubMed]
- Podsiadły-Paszkowska, A.; Krawiec, M. Silicene on metallic quantum wells: An efficient way of tuning silicene-substrate interaction. Phys. Rev. B 2015, 92, 165411. [Google Scholar] [CrossRef]
- Zhu, J.; Schwingenschlögl, U. Stability and electronic properties of silicene on WSe2. J. Mater. Chem. C 2015, 3, 3946–3953. [Google Scholar] [CrossRef]
- Johnson, N.W.; Muir, D.I.; Moewes, A. Oxidized Monolayer of Epitaxial Silicene on Ag(111). Sci. Rep. 2016, 6, 22510. [Google Scholar] [CrossRef] [PubMed]
- Cinquanta, L.T.E.; Chiappe, D.; Grazianetti, C.; Fanciulli, M.; Dubey, M.; Molle, A.; Akinwande, D. Silicene field-effect transistors operating at room temperature. Nat. Nanotech. 2015, 10, 227–231. [Google Scholar]
- Guzmán-Verri, G.G.; Voon, L.C.L.Y. Electronic structure of silicon-based nanostructures. Phys. Rev. B 2007, 76, 075131. [Google Scholar] [CrossRef]
- Zheng, F.B.; Zhang, C.W. The electronic and magnetic properties of functionalized silicene: A first-principles study. Nanoscale Res. Lett. 2012, 7, 422. [Google Scholar] [CrossRef] [PubMed]
- Sahin, H.; Peeters, F.M. Adsorption of alkali, alkaline-earth, and 3d transition metal atoms on silicene. Phys. Rev. B 2013, 87, 085423. [Google Scholar] [CrossRef]
- Sivek, J.; Sahin, H.; Partoens, B.; Peeters, F.M. Adsorption and absorption of boron, nitrogen, aluminum, and phosphorus on silicene: Stability and electronic and phonon properties. Phys. Rev. B 2013, 87, 085444. [Google Scholar] [CrossRef]
- Huang, S.M.; Lee, S.T.; Mou, C.Y. Ferromagnetism and quantum anomalous Hall effect in one-side-saturated buckled honeycomb lattices. Phys. Rev. Lett. 2013, 111, 145502. [Google Scholar] [CrossRef] [PubMed]
- Özcelik, V.O.; Ciraci, S. Local Reconstructions of Silicene Induced by Adatoms. J. Phys. Chem. C 2013, 117, 26305–26315. [Google Scholar] [CrossRef] [Green Version]
- Van den Broek, B.; Houssa, M.; Scalise, E.; Pourtois, G.; Afanas’ev, V.V.; Stesmans, A. First-principles electronic functionalization of silicene and germanene by adatom chemisorption. Appl. Surf. Sci. 2014, 291, 104–108. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Zhu, Z.Y.; Schwingenschlögl, U. Doped silicene: Evidence of a wide stability range. Europhys. Lett. 2011, 95, 17005. [Google Scholar] [CrossRef]
- Ni, Z.; Liu, Q.; Tang, K.; Zheng, J.; Zhou, J.; Qin, R.; Gao, Z.; Yu, D.; Lu, J. Tunable Bandgap in Silicene and Germanene. Nano Lett. 2012, 12, 113–118. [Google Scholar] [CrossRef] [PubMed]
- Drummond, N.D.; Zolyomi, V.; Falko, V.I. Electrically tunable band gap in silicene. Phys. Rev. B 2012, 85, 075423. [Google Scholar] [CrossRef]
- Kaloni, T.P.; Cheng, Y.C.; Schwingenschlögl, U. Hole doped Dirac states in silicene by biaxial tensile strain. J. Appl. Phys. 2013, 113, 104305. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, Y. Strain-induced self-doping in silicene and germanene from first-principles. Solid State Commun. 2013, 155, 6–11. [Google Scholar] [CrossRef]
- Liu, G.; Wu, M.S.; Ouyang, C.Y.; Xu, B. Strain-induced semimetal-metal transition in silicene. Europhys. Lett. 2012, 99, 17010. [Google Scholar] [CrossRef]
- Yan, J.A.; Gao, S.P.; Stein, R.; Coard, G. Tuning the electronic structure of silicene and germanene by biaxial strain and electric field. Phys. Rev. B 2015, 91, 245403. [Google Scholar] [CrossRef]
- Wu, W.; Ao, Z.; Wang, T.; Li, C.; Li, S. Electric field induced hydrogenation of silicene. Phys. Chem. Chem. Phys. 2014, 16, 16588–16594. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.C.; Ao, Z.M.; Yang, C.H.; Li, S.; Wang, G.X.; Li, C.M.; Li, S. Hydrogenation of silicene with tensile strains. J. Mater. Chem. C 2015, 3, 2593–2602. [Google Scholar] [CrossRef]
- Pulci, O.; Gori, P.; Marsili, M.; Garbuio, V.; Sole, R.D.; Bechstedt, F. Strong excitons in novel two-dimensional crystals: Silicane and germanane. Europhys. Lett. 2012, 98, 37004. [Google Scholar] [CrossRef]
- Wei, W.; Dai, Y.; Huang, B.; Jacob, T. Many-body effects in silicene, silicane, germanene and germanane. Phys. Chem. Chem. Phys. 2013, 15, 8789–8794. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H. Strain and chirality effects on the mechanical and electronic properties of silicene and silicane under uniaxial tension. Phys. Lett. A 2012, 376, 3546–3550. [Google Scholar] [CrossRef]
- Peng, Q.; De, S. Elastic limit of silicane. Nanoscale 2014, 6, 12071–12079. [Google Scholar] [CrossRef] [PubMed]
- Qiu, J.; Fu, H.; Xu, Y.; Zhou, Q.; Meng, S.; Li, H.; Chen, L.; Wu, K. From Silicene to Half-Silicane by Hydrogenation. ACS Nano 2015, 9, 11192–11199. [Google Scholar] [CrossRef] [PubMed]
- Prévot, G.; Bernard, R.; Cruguel, H.; Borensztein, Y. Monitoring Si growth on Ag(111) with scanning tunneling microscopy reveals that silicene structure involves silver atoms. Appl. Phys. Lett. 2014, 105, 213106. [Google Scholar] [CrossRef]
- Rahman, M.S.; Nakagawa, T.; Mizuno, S. Growth of Si on Ag(111) and determination of large commensurate unit cell of high-temperature phase. Jpn. J. App. Phys. 2015, 54, 015502. [Google Scholar] [CrossRef]
- Qiu, J.; Fu, H.; Xu, Y.; Oreshkin, A.I.; Shao, T.; Lii, H.; Meng, S.; Chen, L.; Wu, K. Ordered and Reversible Hydrogenation of Silicene. Phys. Rev. Lett. 2015, 114, 126101. [Google Scholar] [CrossRef] [PubMed]
- Podsiadły-Paszkowska, A.; Krawiec, M. Electrical and mechanical controlling of the kinetic and magnetic properties of hydrogen atoms on free-standing silicene. J. Phys. Condens. Matter 2016, 28, 284004. [Google Scholar] [CrossRef] [PubMed]
- Ordejon, P.; Artacho, E.; Soler, J. Self-consistent order-N density-functional calculations for very large systems. Phys. Rev. B 1996, 53, R10441–R10444. [Google Scholar] [CrossRef]
- Sánchez-Portal, D.; Ordejón, P.; Artacho, E.; Soler, J. Density-functional method for very large systems with LCAO basis sets. Int. J. Quantum Chem. 1997, 65, 453–461. [Google Scholar] [CrossRef]
- Artacho, E.; Sánchez-Portal, D.; Ordejón, P.; García, A.; Soler, J. Linear-scaling ab-initio calculations for large and complex systems. Phys. Status Solidi B 1999, 215, 809–817. [Google Scholar] [CrossRef]
- Soler, J.; Artacho, E.; Gale, J.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The Siesta method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Artacho, E.; Anglada, E.; Dieguez, O.; Gale, J.D.; García, A.; Junquera, J.; Martin, R.M.; Ordejón, P.; Pruneda, J.M.; Sánchez-Portal, D.; et al. The Siesta method; developments and applicability. J. Phys. Condens. Matter 2008, 20, 064208. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B Condens. Matter 1991, 43, 1993–2006. [Google Scholar] [CrossRef] [PubMed]
- Gao, N.; Li, J.C.; Jiang, Q. Bandgap opening in silicene: Effect of substrates. Chem. Phys. Lett. 2014, 592, 222–226. [Google Scholar] [CrossRef]
- Podsiadły-Paszkowska, A.; Krawiec, M. Spin-polarized gapped Dirac spectrum of unsupported silicene. Appl. Surf. Sci. 2016, 373, 45–50. [Google Scholar] [CrossRef]
- Houssa, M.; Dimoulas, A.; Molle, A. Silicene: A review of recent experiments and theoretical inverstigations. J. Phys. Condens. Matter 2015, 27, 253002. [Google Scholar] [CrossRef] [PubMed]
- Ju, W.; Li, T.; Su, X.; Cui, H.; Li, H. Engineering magnetism and electronic properties of silicene by changing adsorption coverage. Appl. Surf. Sci. 2016, 384, 65–72. [Google Scholar] [CrossRef]
- De Padova, P.; Quaresima, C.; Ottaviani, C.; Sheverdyaeva, P.M.; Moras, P.; Carbone, C.; Topwal, D.; Olivieri, B.; Kara, A.; Oughaddou, H.; et al. Evidence of graphene-like electronic signature in silicene nanoribbons. Appl. Phys. Lett. 2010, 96, 261905. [Google Scholar] [CrossRef]
- Lalmi, B.; Oughaddou, H.; Enriquez, H.; Kara, A.; Vizzini, S.; Ealet, B.; Aufray, B. Epitaxial growth of a silicene sheet. Appl. Phys. Lett. 2010, 97, 223109. [Google Scholar] [CrossRef]
- Lazzeri, M.; Mauri, F. Nonadiabatic Kohn Anomaly in a Doped Graphene Monolayer. Phys. Rev. Lett. 2006, 97, 266407. [Google Scholar] [CrossRef] [PubMed]
- Peng, Q.; Wen, X.; De, S. Mechanical stabilities of silicene. RSC Adv. 2013, 3, 13772–13781. [Google Scholar] [CrossRef]
- Restrepo, O.D.; Mishra, R.; Goldberger, J.E.; Windl, W. Tunable gaps and enhanced mobilities in strain-engineered silicane. J. Appl. Phys. 2014, 115, 033711. [Google Scholar] [CrossRef]
- Pereira, V.M.; Neto, A.H.C.; Peres, N.M.R. Tight-binding approach to uniaxial strain in graphene. Phys. Rev. B 2009, 80, 045401. [Google Scholar] [CrossRef]
- Mohan, B.; Kumar, A.; Ahluwalia, P.K. Electronic and dielectric properties of silicene functionalized with monomers, dimers and trimers of B, C and N atoms. RSC Adv. 2014, 4, 31700–31705. [Google Scholar] [CrossRef]
- Bianconi, A.; Marcelli, A. (Eds.) Atomically Controlled Surfaces Interfaces and Nanostructures; Superstripes Press: Rome, Italy, 2016; ISBN 9788866830597.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Podsiadły-Paszkowska, A.; Krawiec, M. Tuning the Electronic Structure of Hydrogen-Decorated Silicene. Condens. Matter 2017, 2, 1. https://doi.org/10.3390/condmat2010001
Podsiadły-Paszkowska A, Krawiec M. Tuning the Electronic Structure of Hydrogen-Decorated Silicene. Condensed Matter. 2017; 2(1):1. https://doi.org/10.3390/condmat2010001
Chicago/Turabian StylePodsiadły-Paszkowska, Agata, and Mariusz Krawiec. 2017. "Tuning the Electronic Structure of Hydrogen-Decorated Silicene" Condensed Matter 2, no. 1: 1. https://doi.org/10.3390/condmat2010001
APA StylePodsiadły-Paszkowska, A., & Krawiec, M. (2017). Tuning the Electronic Structure of Hydrogen-Decorated Silicene. Condensed Matter, 2(1), 1. https://doi.org/10.3390/condmat2010001