The Solution to Hardy’s Paradox

Abstract

By using both the weak-value formulation as well as the standard probabilistic approach, we analyze Hardy’s experiment introducing a complex and dimensionless parameter ($ϵ$), which eliminates the assumption of complete annihilation when both the electron and the positron departing from a common origin cross the intersection point P. We then find that the paradox does not exist for all the possible values taken by the parameter. The apparent paradox only appears when $ϵ=1$, which is just a singular value. In this paper we demonstrate that this particular value is forbidden inside the scenario proposed by the experiment.

1. Introduction

Hardy’s paradox is a gedanken experiment designed for demonstrating how different Quantum Mechanics is from classical approaches [1]. It is a proof of the non-local character of Quantum Mechanics [2]. The experiment analyzes how an electron and a positron, created initially as a pair (common origin), evolve through different paths. Both particles have then two possible trajectories (two possibilities for each particle) during their evolution. Among all the possible paths, two of them (one for each particle) intersect at a point P. In the original derivation of Hardy, total annihilation was assumed for the pair if both particles are able to simultaneously cross the intersection point P. The paradox consists precisely of the final detection of patterns, which are only possible if both particles travel through the point P. Any final detection of patterns is forbidden classically, but they occur at the Quantum level, challenging any common sense [1,2]. A weak-value interpretation [3] of Hardy’s paradox was subsequently performed in [4] by using the single- and two-particle interpretation of the problem. The single-particle approach suggested the necessity for the two particles to cross the intersection point P in order to develop the observed patterns in the instruments. The single-particle approach does not care at what time each particle crosses the intersection point. This means that in principle, the particles could cross the point P at different times. On the other hand, the two-particle approach showed an apparent contradiction with respect to the single-particle approximation, suggesting the impossibility for the two particles to simultaneously cross the point P. Within the two-particle approach, the results obtained in [4], from the perspective of the weak-value formulation, also suggested that the option for both of the particles to select a path where they do not cross the point P is related to a negative weak-value occupation number. This result was interpreted as a repulsive effect. Although interesting research in the subject was conducted [5,6,7,8], an explanation about the contradictory results between the single- and two-particle approximation and the possibility of having a reconciliation between both situations has not been found to date. In this paper, we propose the relevant arguments able to conciliate the single- and the two-particle approximations proposed in [4], as well as the apparent contradictions found within the probabilistic approximation. We analyze the paradox by introducing a complex and dimensionless parameter $ϵ$, which allows for the possibility of the two particles in the pair to cross the intersection point P without annihilation. In particular, for the singular point $ϵ=1$, we return back to Hardy’s case where both particles arrive at P and (in principle) annihilate. On the other hand, the case $ϵ=0$ corresponds to the one where the final desired pattern $D^{+-}$ is not detected due to the orthogonality of the initial state and the final desired state. Finally, we analyze the cases $ϵ=2,4$ and $ϵ\to \infty$, explaining within the text why they are so relevant for the analysis. In particular, $ϵ=4$ corresponds to the case where the detectors never register a $C^{+-}$ event. Interestingly, for this situation, combinations of detection in the form $C^{+}{D}^{-}$ are allowed. In the original Hardy argument, the possibility of first detecting the electron and then the positron in one frame of reference $F^{-}$, and then reversing the order of the events by detecting first the positron and then the electron in another frame $F^{+}$, means that in the laboratory frame of reference, the particle detectors are separated by spacelike intervals. Hardy then assumes that the particles really meet at the point P in all the frames of reference. This is a valid statement, consistent with Special Relativity. However, it is still very restrictive in the sense that there is no guarantee that the particles will really meet at P when they depart from their corresponding origins, even if they travel equal distances. The reason for this is the intrinsic uncertainty of the time arrivals, consistent with the uncertainty principle $\Delta E\Delta t\ge \hslash$. If we take into account the energy–time uncertainty relation, there is no reason for the particles to arrive at the same point P simultaneously and instead they might be slightly separated at the time of arrival at P. This also suggests that the particles still have some degree of uncertainty in their location at the moment when they are supposed to be at P. From Special Relativity, we know that if two particles do not meet at P in one frame of reference, then they will never meet in all the frames of reference. Additionally, the causal order of the events is maintained and then the first particle crossing the point P will always be the first particle to do so in all the frames of references $F^{+}$. The frames of reference describing a different sequence of events, here dubbed $F^{-}$, are causally disconnected from $F^{+}$. Then, in general, assuming that the particles really meet at P for all the events is a very high restriction, removed in this paper due to the introduction of the parameter $ϵ$. Another way to explain the same situation is by understanding that when relativistic effects are involved in Quantum Mechanics, the multiparticle approach of Quantum Field Theory (QFT) is necessary and then the particle number is not conserved in such a case [9]. The non-conservation of the particle number is a natural consequence of the fact that in QFT, there is a permanent creation and annihilation of particles over the vacuum state. This process of creation and annihilation is also related to the energy–time uncertainty principle [10,11]. In this paper, the necessity of a multiparticle approach is demonstrated by using the weak-value approach. In such a case, it is proved that the two-particle approximation disagrees with the single-particle approximation, in connection with the previous explanations. In this paper, the inclusion of the parameter $ϵ$ helps to conciliate the single-particle and the two-particle approximations. The paper is organized as follows: In Section 2, we explain the standard Hardy formulation and we propose an improvement to Hardy’s approach. In Section 3, we explain the weak-value approach to the problem. In Section 4, we make the same improvements to Hardy’s approach from the perspective of the weak-value. Finally, in Section 6 we conclude.

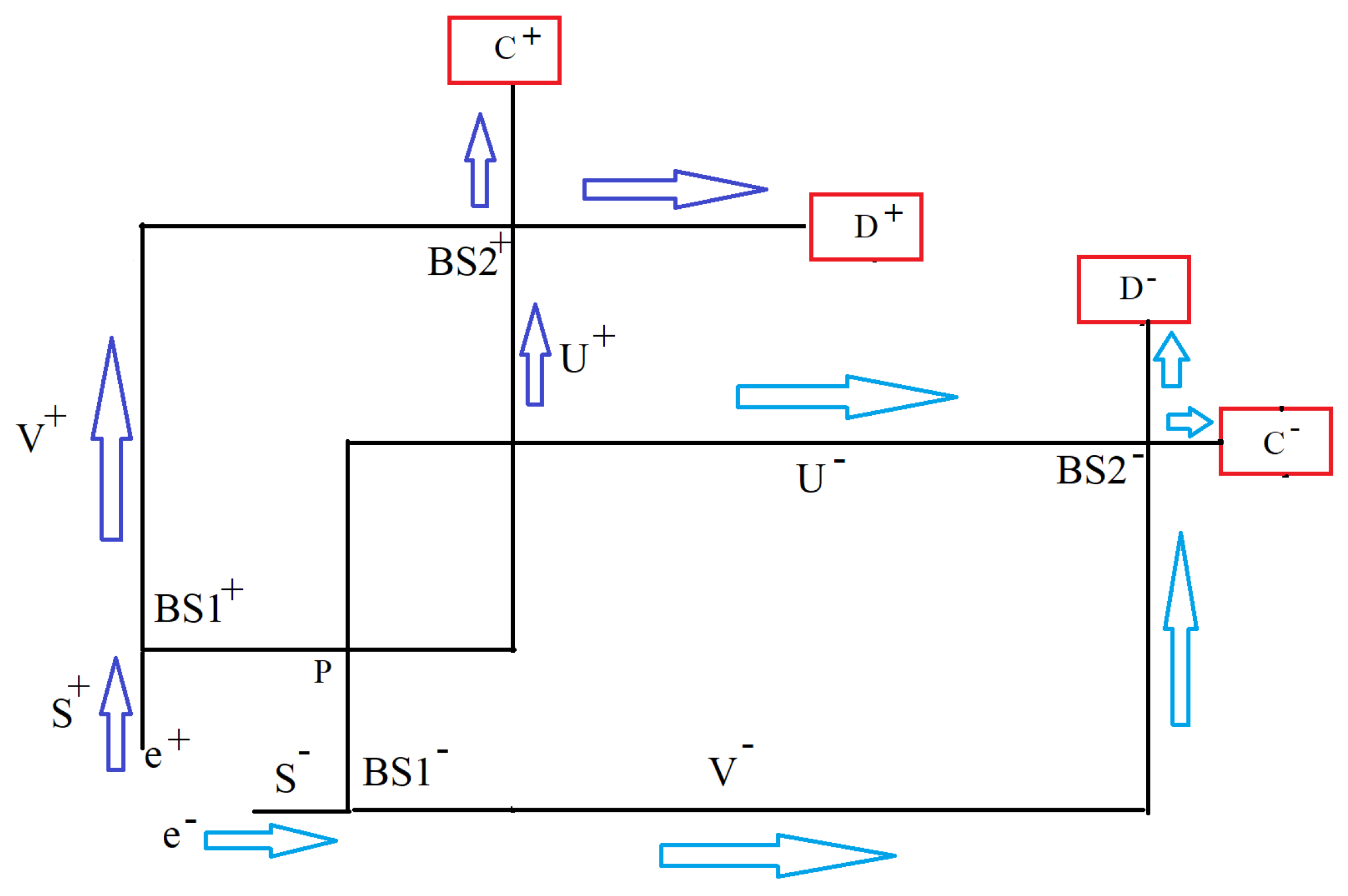
2. Hardy’s Paradox: Formulation of the Problem

The standard formulation of Hardy’s analysis starts with the definition of an electron–positron pair emerging from a common point as it is illustrated in Figure 1. There are two possible paths for each particle. Then, we have a total of four possibilities. Among all of them, only two have a common intersection point. Hardy’s key assumption consists of the complete annihilation of the pairs if they meet at the intersection point P. The electron and the positron emerging from the initial common point are represented by the function

$$|\psi {>}_i=|s^{+}>|s^{-}>.$$

(1)

Subsequently, the electron and the positron take different paths. Once the particles cross the beam splitters defined as $B{S}_1^{\pm }$ in Figure 1, the functions for the electron and the positron become equivalent to [1]

$$|s^{\pm }>\to {\displaystyle \frac{1}{\sqrt{2}}}\left(i|u^{\pm }>+|v^{\pm }>\right).$$

(2)

The effect of the second beam splitter $B{S}_2^{\pm }$ can be summarized as

$$\begin{array}{c}\hfill |u^{\pm }>\to {\displaystyle \frac{1}{\sqrt{2}}}\left(|c^{\pm }>+i|d^{\pm }>\right),\\ \hfill |v^{\pm }>\to {\displaystyle \frac{1}{\sqrt{2}}}\left(i|c^{\pm }>+|d^{\pm }>\right).\end{array}$$

(3)

In [1], different options related to whether or not the beam splitters are removed are analyzed, finding then a contradiction for different cases. The contradiction appears when the final detection of the electron and the positron obey some specific patterns defined as $D^{\pm }$ in Figure 1. When both beam splitters are in place, these patterns can only occur if there is interference between the two particles during their journey. However, such interference is only possible if both of the particles are able to cross the point P, resulting in complete annihilation in agreement with Hardy’s assumption. Although the paradox is valid, the formulation of Hardy is quite restrictive and there are some points to analyze in deeper detail. Hardy’s assumption of relative simultaneity for the detection at $D^{\pm }$ is correct because the interval between the detectors is spacelike. However, assuming that the particles always meet at P for every event is incorrect and restrictive and in disagreement with the uncertainty principle of Quantum Mechanics.

Then, in general, both particles can cross the intersection point P and still survive the event because in most of the cases one particle will cross first at an instant $t_0$ and the other particle will cross next at an instant $t_0+\Delta t$, with $\Delta t\ge \hslash /\Delta E$. In this letter we will see how we can generalize Hardy’s arguments, solving any apparent paradox.

2.1. Improvements in Hardy’s Formulation

The first assumption, which we will change with respect to Hardy’s case, is the condition

$$|u^{+}>|u^{-}>=\gamma ,$$

(4)

which is the statement suggesting that, when the electron and the positron meet at P, they annihilate. In our case, considering the possibility of no-annihilation at P, we will take

$$|u^{+}>|u^{-}>\to (1-ϵ)|u^{+}>|u^{-}>,nearP.$$

(5)

Here, $ϵ=\left|ϵ\right|e^{i\alpha }$ is a complex number. The limit $ϵ\to 1$ gives us back Hardy’s result since the photons generated by the annihilation process are assumed not to reproduce pair creation processes [12]. Changing (4) into (5) modifies the scenario such that the paradox disappears. Here, we will show how.

The definition (5) excludes absolute annihilation at P. A singular case is $ϵ=1$ where the term $|u^{+}>|u^{-}>$ disappears from the scene because, in principle, it represents the simultaneous arrival and subsequent annihilation of the electron and the positron when they meet at P in all the frames of reference. After crossing the first beam splitters $B{S}^{\pm }1$, the state (1) becomes

$$\begin{array}{c}\hfill |s^{+}>|s^{-}>\to A(-(1-ϵ)|u^{+}>|u^{-}>+i|u^{+}>|v^{-}>\\ \hfill +i|v^{+}>|u^{-}>+|v^{+}>|v^{-}>).\end{array}$$

(6)

Here, we have used Equation (2) inside Equation (1) and we have also used the condition (5). The normalization factor A depends on $ϵ$ and it is given by

$$A={\displaystyle \frac{1}{\sqrt{4-(ϵ+{ϵ}^{*})+{\left|ϵ\right|}^2}}}.$$

(7)

If we take a frame of reference where the positron has crossed $BS{2}^{+}$ but where the electron has not yet arrived at $BS{2}^{-}$, then the previous state becomes

$$\begin{array}{c}\hfill {\displaystyle \frac{A}{\sqrt{2}}}(-[1-ϵ]\left[|c^{+}>+i|d^{+}>\right]|u^{-}>-|c^{+}>|u^{-}>\\ \hfill +2i|c^{+}>|v^{-}>+i|d^{+}>|u^{-}>).\end{array}$$

(8)

If the positron is detected at $D^{+}$, then we project the state (8) on $|d^{+}>$, and the state of the electron is projected to ${\displaystyle \frac{Aϵ}{\sqrt{2}}}|u^{-}>$ (depending on $ϵ$). Then, we can normalize the event projecting the state (8) toward $|u^{-}>$. Then, we obtain

$$\left[U^{-}\right],ifdetectionat{D}^{+},$$

(9)

with probability

$$P_{u^{-}{d}^{+}}=P_{u^{+}{d}^{-}}={\displaystyle \frac{A^2}{2}}{\left|ϵ\right|}^2.$$

(10)

If instead of $F^{+}$ we now consider the conjugate frame $F^{-}$, where the electron is detected at $D^{-}$ before the positron crosses $BS{2}^{+}$, by performing an analogous analysis, we get

$$\left[U^{+}\right],ifdetectionat{D}^{-},$$

(11)

with the same probability defined in Equation (10). For this reason we have expressed the equality $P_{u^{-}{d}^{+}}=P_{u^{+}{d}^{-}}$. Note that the probability (10) depends on $ϵ$ in the same way for both cases, namely, (9) and (11). This only means that due to the symmetry of the experiment, we can take the frames $F^{+}$ and $F^{-}$ to have the same velocity but moving in opposite directions. Then, both results must share the same probability. The experiments with an outcome $D^{\pm }$ occur with a probability

$$P_{d^{+}{d}^{-}}={\displaystyle \frac{A^2}{4}}{\left|ϵ\right|}^2.$$

(12)

This result can be obtained if we introduce Equation (3) inside Equation (6) and after projecting over the state $|d^{+}>|d^{-}>$, respecting the corresponding normalization factor. Note that the probability of occurrence depends on $ϵ$. On the other hand, the projection of the state (6) over $|u^{-}>|u^{+}>$ gives us

$$\left[U^{+}{U}^{-}\right],$$

(13)

with probability

$$P_{u^{+}{u}^{-}}=A^2(1-(ϵ+{ϵ}^{*})+{\left|ϵ\right|}^2).$$

(14)

In [1,2], a reality condition of the form

$$\left[U^{+}{U}^{-}\right]=\left[U^{+}\right]\left[U^{-}\right],$$

(15)

was defined, no matter how we normalize the result $\left[U^{+}\right]$. This relation is defined through Equations (9), (11) and (13). This condition is not completely accurate because the left-hand side in Equation (15) says that both the electron and the positron arrive simultaneously at P. However, although the right-hand side of the same expression suggests that both the electron and the positron arrive at P, this portion of the equation does not specify if the arrival is simultaneous. Then, Equation (15) is not a precise equality because it does not consider the correction due to the uncertainty on the arrival times on the right-hand side of the expression. This uncertainty is considered by the parameter $ϵ$. Then, in Hardy’s original formulation, the paradox appears from the fact that apparently $\left[U^{+}{U}^{-}\right]=0$ during the experiments. This is the case because the right-hand side of Equation (15) corresponds to the case where the particles cross P but not necessarily at the same instant due to the energy–time uncertainty principle $\Delta E\Delta t\ge \hslash$. Mathematically, we can say that while the left-hand side of Equation (15) is true when $ϵ=1$, the right-hand side corresponds in general to situations where $ϵ\ne 1$, invalidating then the expression (15) in general. It is for this reason that we have to revise Hardy’s experiment with the parameter $ϵ$ included. We could then conclude a connection between $ϵ$ and the uncertainty in the arrival times at the point P.

2.2. Relations Between Probabilities and Probability Invariants

At this point we can find some relations between probabilities. From Equations (10) and (12), it is evident that the following relations are valid:

$$P_{u^{+}{d}^{-}}=P_{u^{-}{d}^{+}}=2P_{d^{+}{d}^{-}}=2P_{d^{+}{c}^{-}}=2P_{c^{+}{d}^{-}}.$$

(16)

From Equation (14), it is clear that $P_{u^{+}{u}^{-}}$ has a dependence not only on the norm $\left|ϵ\right|$ but also on the phase $\alpha$, appearing if we explicitly expand the expression as

$$P_{u^{+}{u}^{-}}=A^2{(1-2|ϵ|cos\alpha +|ϵ|}^2).$$

(17)

Then, by only knowing the results in Equations (10) and (16), we cannot fix any reliable relation with $P_{u^{+}{u}^{-}}$. In order to find some useful relations between probabilities, we have to evaluate all the other probabilities for the different paths, by using Equations (6) and (8), with the corresponding exchanges considering the symmetry of the experiment in Equation (8). The relevant probabilities are

$$\begin{array}{c}\hfill P_{u^{+}{v}^{-}}=P_{v^{+}{v}^{-}}=P_{v^{+}{u}^{-}}=A^2,\\ \hfill P_{c^{+}{v}^{-}}=P_{v^{+}{c}^{-}}=2A^2,\\ \hfill P_{c^{+}{u}^{-}}=P_{u^{+}{c}^{-}}={\displaystyle \frac{A^2}{2}}{(4-4|ϵ|cos\alpha +|ϵ|}^2),\\ \hfill P_{c^{+}{c}^{-}}=A^2\left(4-2\left|ϵ\right|cos\alpha +{\displaystyle \frac{{\left|ϵ\right|}^2}{4}}\right).\end{array}$$

(18)

We can know define the following invariant expressions of probability (independent of $ϵ$)

$$\begin{array}{c}\hfill P_{v^{+}{v}^{-}}+P_{v^{+}{u}^{-}}+P_{u^{+}{v}^{-}}+P_{u^{+}{u}^{-}}=1,\\ \hfill P_{d^{+}{d}^{-}}+P_{c^{+}{d}^{-}}+P_{d^{+}{c}^{-}}+P_{c^{+}{c}^{-}}=1,\\ \hfill P_{u^{+}{d}^{-}}+P_{u^{+}{c}^{-}}+P_{v^{+}{c}^{-}}=1,\\ \hfill P_{d^{+}{u}^{-}}+P_{c^{+}{u}^{-}}+P_{c^{+}{v}^{-}}=1,\end{array}$$

(19)

with the additional condition $P_{v^{+}{d}^{-}}=P_{d^{+}{v}^{-}}=0$. This condition complements the last two equations in (19), which correspond to equations where one particle arrives at the detector before the other one. The consistency of Equation (19) can be proved with Equations (6) and (8) and other expressions that can be obtained from them and the transformations (3). Other two general conditions are

$$\begin{array}{c}\hfill P_{u^{+}{v}^{-}}+P_{u^{+}{u}^{-}}=P_{c^{+}{u}^{-}}+P_{u^{+}{d}^{-}}=\\ \hfill P_{c^{+}{c}^{-}}+P_{c^{+}{d}^{-}}+P_{u^{+}{d}^{-}}+P_{c^{+}{v}^{-}}.\end{array}$$

(20)

The previous expressions cannot constraint the parameter $ϵ$. However, they mark general invariants that the system must respect. One additional expression, this time being able to constrain $ϵ$, could be derived if we consider Figure 2.

From this figure, we can write the following relations:

$$P_{u^{+}{u}^{-}}+P_{d^{+}{d}^{-}}=P_{u^{+}{d}^{-}}+P_{u^{-}{d}^{+}}.$$

(21)

If we replace Equations (10), (12) and (14), then we get the following quadratic equation:

$${\left|ϵ\right|}^2-8\left|ϵ\right|cos\alpha +4=0.$$

(22)

If we solve this equation, then we get

$$\left|ϵ\right|=4cos\alpha \left(1\pm \sqrt{1-{\displaystyle \frac{1}{4co{s}^2\alpha }}}\right).$$

(23)

It is clear that given the restriction for $\left|ϵ\right|$ to be real and positive, then the phase $\alpha$ is restricted to take the range of values

$${\displaystyle \frac{\pi }{3}}\ge \alpha \ge -{\displaystyle \frac{\pi }{3}}.$$

(24)

For the extreme cases where $\alpha =\pm \pi /3$, then we get $\left|ϵ\right|=2$. On the other hand, when $\alpha =0$, we get

$$\left|ϵ\right|=4\pm 2\sqrt{3}.$$

(25)

This result suggests that there are two possible values for $\left|ϵ\right|$ when $\alpha =0$. Then, we can say that the allowed values of $\left|ϵ\right|$ are

$$4-2\sqrt{3}\le \left|ϵ\right|\le 4+2\sqrt{3}.$$

(26)

Equations (24) and (26) represent the allowed values that the phase $\alpha$ and $\left|ϵ\right|$ can take, respectively, in each experiment. Note that although the value $\left|ϵ\right|=1$ appears inside the possible range of values, this value would still correspond to the phase $\alpha$ = 51.3 deg. Then, evidently, the value $ϵ=1$ is not allowed inside Hardy’s arrangement. If the value $ϵ=1$ is forbidden, then the paradox is solved.

2.3. The Solution to Hardy’s Paradox: Probabilistic Approach

The

Table 1. Key probability values for some key values of the parameter $ϵ$. The asterisk * is put over the values excluded by the allowed ranges defined in Equations (24) and (26). Hardy’s paradox corresponds to the value $ϵ=1$, which is physically excluded. Note that when $ϵ\to \infty$, all the events cross the intersection point P. However, this value is also physically excluded from the allowed ranges.

$\mathit{ϵ}$	${\mathit{P}}_{{\mathit{d}}^{+}{\mathit{d}}^{-}}$	${\mathit{P}}_{{\mathit{u}}^{+}{\mathit{u}}^{-}}$	${\mathit{P}}_{{\mathit{v}}^{+}{\mathit{v}}^{-}}$	${\mathit{P}}_{{\mathit{c}}^{+}{\mathit{u}}^{-}}$	${\mathit{P}}_{{\mathit{c}}^{+}{\mathit{c}}^{-}}$
0 *	0	1/4	1/4	1/2	1
1 *	1/12	0	1/3	1/6	3/4
2	1/4	1/4	1/4	0	1/4
4	1/3	3/4	1/12	1/6	0
∞ *	1/4	1	0	1/2	1/4

summarizes the results obtained from Hardy’s experiment for the different values taken by the parameter $ϵ$. In agreement with the range of values defined in Equations (24) and (26), the values $ϵ=0$ as well as $ϵ=1$ and $ϵ=\infty$ are not allowed; still, it is interesting to mention them.

From the values obtained in the Table 1, it is clear that what is known as Hardy’s paradox in the literature corresponds to the not-allowed value $ϵ=1$. Note that the Table 1 deals with the values of $ϵ$ for which some of the probability values vanish. The remaining probability values can be found from the relations (16) and (18)–(20). The range of possible values allowed for $ϵ=\left|ϵ\right|e^{i\alpha }$ is obtained from the allowed values defined in Equations (24) and (26). The allowed values emerged from the constraint defined in Equation (21). Hardy’s paradox is then solved because we have demonstrated that the value $ϵ=1$ is excluded from the possible values taken by the parameter in agreement with the constraint defined in Equation (21). Evidently, without the constraint (21), $ϵ=1$ would just be one among the infinite possibilities taken by the parameter $ϵ$. Even in such a case, suggesting that $ϵ$ is exact would be a huge assumption.

3. The Weak-Value Explanation

In [4], an alternative explanation to Hardy’s paradox was performed from the perspective of the weak-value. The weak-value is a complex number defined as [3,13]

$$X_w={\displaystyle \frac{<\Phi \left|X\right|\psi >}{<\Phi |\psi >}},$$

(27)

where X can be any operator defining an observable. An interesting property of the weak-value is the fact that even if two observables are not compatible, their weak-values can still commute. This is the case because the measurements related to $X_w$ are supposed to be weak enough in order to avoid the limitations related to the uncertainty principle. In Equation (27), $|\psi >$ corresponds to an initial state (pre-selection) and $|\Phi >$ corresponds to a final state (post-selection).

In [4], the wave-functions related to the paths crossing the intersection point P were defined as (Overlapping) $|O{>}_{e,p}$ for the electron and the positron, respectively. In the same way, (Non-overlapping) $|NO{>}_{e,p}$ represents the wave-functions corresponding to the paths that never cross the point P for both the electron and the positron, respectively. These states appear after the initial wave-function departing from the lines $s^{+}$ and $s^{-}$ in Figure 1 cross through the initial beam splitters $B{S}_1^{\pm }$. The second beam splitter defines the post-selected state in [4]. When the initial state crosses $B{S}_1^{\pm }$, the state of the electron–positron pair is defined as

$$|\varphi >={\displaystyle \frac{1}{2}}\left(|O{>}_p+|NO{>}_p\right)\left(|O{>}_e+|NO{>}_e\right).$$

(28)

In [4], the pre-selected state is chosen such that it ignores the contribution $|O{>}_e|O{>}_p$, corresponding to the simultaneous arrival of the electron and the positron to the point P. Ignoring this contribution agrees with Hardy’s assumption suggesting that any meeting of the electron and the positron at P is a secure annihilation. Following this argument, we get the following pre-selected state:

$$\begin{array}{c}\hfill |\psi >={\displaystyle \frac{1}{\sqrt{3}}}\left(\right|NO{>}_p|O{>}_e+\left|O{>}_p\right|NO{>}_e\\ \hfill +|NO{>}_p\left|NO{>}_e\right).\end{array}$$

(29)

In the same way as we did before, we will consider later the possibility of including a fraction of the states $(1-ϵ)|O{>}_e|O{>}_p$ corresponding to the events where both the electron and the positron can cross the intersection point P. The parameter $ϵ$ will then appear in the analysis when we consider the two-particle cases inside the weak-value formulation. The post-selected state in [4] is the one corresponding to the case where there is a click for the detectors at $D^{+}$ and $D^{-}$ over Figure 1. The post-selected state is then defined as

$$|\Phi >={\displaystyle \frac{1}{2}}\left(|NO{>}_p-|O{>}_p\right)\left(|NO{>}_e-|O{>}_e\right).$$

(30)

By looking at the single-particle approach, we define the number operators for the electron and positron as

$$\begin{array}{c}\hfill {\widehat{N}}_{NO}^p=|NO{>}_p{<NO|}_p,{\widehat{N}}_O^p={|O{>}_p<O|}_p,\\ \hfill {\widehat{N}}_{NO}^e=|NO{>}_e{<NO|}_e,{\widehat{N}}_O^e={|O{>}_e<O|}_e.\end{array}$$

(31)

By introducing these definitions inside Equation (27), and by taking the pre-selected state as (29) and the post-selected state as (30), then we can calculate the weak-value version of the occupation numbers for the single-particle approach as

$$\begin{array}{c}\hfill {\widehat{N}}_{Ow}^e=1,{\widehat{N}}_{Ow}^p=1,\\ \hfill {\widehat{N}}_{NOw}^e=0,{\widehat{N}}_{NOw}^p=0.\end{array}$$

(32)

These numbers will be independent of $ϵ$ even after including the possibility $(1-ϵ)|O{>}_p|O{>}_e$ inside the pre-selected state (29). The result (32) is telling us that for the system to obtain the final desired patterns, both particles (the electron and the positron) must cross the intersection point P. The result (32), however, does not specify at what time each particle crosses the intersection point P. If we look at the pairs, then we have to work inside a two-particle formalism by defining the weak-value occupation numbers as

$$\begin{array}{c}\hfill {\widehat{N}}_{NO,Ow}^{p,e}={\widehat{N}}_{NOw}^p{\widehat{N}}_{Ow}^e,{\widehat{N}}_{O,NOw}^{p,e}={\widehat{N}}_{Ow}^p{\widehat{N}}_{NOw}^e,\\ \hfill {\widehat{N}}_{O,Ow}^{p,e}={\widehat{N}}_{Ow}^p{\widehat{N}}_{Ow}^e,{\widehat{N}}_{NO,NOw}^{p,e}={\widehat{N}}_{NOw}^p{\widehat{N}}_{NOw}^e.\end{array}$$

(33)

By using the same pre-selected and post-selected states, the explicit result for the weak-value version of the pair occupation number is obtained as

$$\begin{array}{c}\hfill {\widehat{N}}_{NO,Ow}^{p,e}=1,{\widehat{N}}_{O,NOw}^{p,e}=1,\\ \hfill {\widehat{N}}_{O,Ow}^{p,e}=0,{\widehat{N}}_{NO,NOw}^{p,e}=-1.\end{array}$$

(34)

These results will have a dependence on $ϵ$ after introducing this parameter in this formulation. For the moment, we can say that the results obtained in Equation (34) suggest that in order to get the desired post-selected state $D^{\pm }$, the electron and the positron must cross the intersection point P (results ${\widehat{N}}_{NO,Ow}^{p,e}=1$ and ${\widehat{N}}_{O,NOw}^{p,e}=1$). However, they cannot cross P simultaneously as the result ${\widehat{N}}_{O,Ow}^{p,e}=0$ suggests. Indeed, the weak-value number ${\widehat{N}}_{O,Ow}^{p,e}$ is a number able to specify if the particles simultaneously cross the point P or not. Basically, if ${\widehat{N}}_{O,Ow}^{p,e}$ vanishes, the number is telling us that no particle can appear at the same time at P and then survive the event. In other words, the role of ${\widehat{N}}_{O,Ow}^{p,e}$ is to measure the differences on the arrival times at P between the electron and the positron.

We must remark once again that the single-particle approach of the weak-value formulation cannot specify whether or not the particles arrive at the same time (simultaneous) at P or at different times. What Equation (32) says is that the particles must cross the point P if we want to get $D^{\pm }$ on the detectors. For this reason, the two-particle approach formulated in Equation (34) is very important.

At this point we can see that from the perspective of the weak-value approximation, the apparent paradox can be interpreted as an apparent disagreement between the single- and the two-particle approximation related to the events happening at P during the evolution of the pair (electron–positron) inside the system. This apparent disagreement comes from the standard interpretation of the results related to the two-particles number in Equation (34) in the original approaches of Hardy and in [4]. In this paper we reinterpret these results by introducing the parameter $ϵ$.

Note that there is an intriguing result connected to the event related to the evolution of the particles through paths not crossing P. In Equation (34), ${\widehat{N}}_{NO,NOw}^{p,e}=-1$ suggests that these events are related to a negative weak-value occupation number. In [4] this is interpreted as a repulsive effect. This can be also interpreted as a shift of the phases of the particles moving through the system. This means that a negative weak occupation number can be expressed as ${\widehat{N}}_{NO,NOw}^{p,e}=-1=e^{i\pi }$, with a phase difference of $\pi$ between the electron and the positron moving through the system. ${\widehat{N}}_{NO,NOw}^{p,e}$ is interpreted in general as a number measuring the events where the particles do not cross the intersection point P simultaneously.

4. Improvements in the Weak-Value Approximation: The Inclusion of the States $(\mathbf{1}-\mathit{ϵ})|\mathit{O}{>}_{\mathit{p}}|\mathit{O}{>}_{\mathit{e}}$

We can introduce the parameter $ϵ$ inside the weak-value formalism. The only change will appear in the pre-selected state defined initially in Equation (29). Note that if we include the term $|O{>}_p|O{>}_e$ in Equation (29), all the relevant weak-values would diverge since the pre-selected state would be orthogonal to the post-selected state defined in Equation (30). The divergence disappears if we introduce the parameter $ϵ$ in the form $(1-ϵ)|O{>}_p|O{>}_e$, with $ϵ\ne 0$ in the pre-selected state (29). This variation in the pre-selected state is equivalent to the change performed in Equation (5) when we analyzed the probabilities. In this way we obtain

$$\begin{array}{c}\hfill |\psi >=A(\left|NO{>}_p\right|O{>}_e+\left|O{>}_p\right|NO{>}_e\\ \hfill +|NO{>}_p|NO{>}_e+(1-ϵ)|O{>}_p\left|O{>}_e\right).\end{array}$$

(35)

Here, A is the same normalization factor used in Equations (6) and (8) when we analyzed the original probability formulation. The redefinition of the pre-selected state does not affect the single-particle results obtained in Equation (32). However, it will affect the two-particle results obtained in Equation (34). The modifications for the two-particle weak-value numbers are

$$\begin{array}{c}\hfill N_{NO,Ow}^{p,e}={\displaystyle \frac{e^{-i\alpha }}{\left|ϵ\right|}},N_{O,NOw}^{p,e}={\displaystyle \frac{e^{-i\alpha }}{\left|ϵ\right|}},\\ \hfill N_{O,Ow}^{p,e}=1-{\displaystyle \frac{e^{-i\alpha }}{\left|ϵ\right|}},N_{NO,NOw}^{p,e}=-{\displaystyle \frac{e^{-i\alpha }}{\left|ϵ\right|}},\end{array}$$

(36)

where we have used $ϵ=\left|ϵ\right|e^{i\alpha }$. The probability for the detection of the patterns $D^{\pm }$ can be obtained by projecting the post-selected state over the pre-selected state. We obtain in this way

$${|<\Phi |\psi >|}^2={\displaystyle \frac{A^2{\left|ϵ\right|}^2}{4}}={\displaystyle \frac{{\left|ϵ\right|}^2}{4(4-(ϵ+{ϵ}^{*})+|ϵ{|}^2)}},$$

(37)

consistent with the result obtained in Equation (12). Note that in general, $P_{d^{+}{d}^{-}}$ depends on $ϵ$. If we choose $ϵ=1$, then we get $P_{d^{+}{d}^{-}}=1/12$, consistent with the results obtained in [4]. This makes sense because for $ϵ=1$, we return to the pre-selected state (29), which avoids the inclusion of the option $|O{>}_p|O{>}_e$. It can be proved from Equation (37) that more generally $P_{d^{+}{d}^{-}}=1/12$ if

$$\left|ϵ\right|=-{\displaystyle \frac{cos\alpha }{2}}\left(1-{\displaystyle \frac{1}{\left|cos\alpha \right|}}\sqrt{co{s}^2\alpha +8}\right).$$

(38)

Then, there is a full family of parameters $ϵ$ for which $P_{d^{+}{d}^{-}}=1/12$. This means that there is nothing special about the value $ϵ=1$ after all because there are plenty of possibilities such that we can still get the same outputs from Hardy’s experiment and then get a detection pattern $D^{\pm }$. For these mentioned possibilities, the particles can still cross the intersection point P.

Finally, it is important to remark that the following condition over the pair of particles

$$N_{NO,Ow}^{p,e}+N_{O,NOw}^{p,e}+N_{O,Ow}^{p,e}+N_{NO,NOw}^{p,e}=1,$$

(39)

is just equivalent to the equation $P_{v^{+}{v}^{-}}+P_{v^{+}{u}^{-}}+P_{u^{+}{v}^{-}}+P_{u^{+}{u}^{-}}=1$, showed in Equation (19). Then, the weak-value approach is consistent with the probabilistic method developed in Section 2. The

Table 2. Key values for the weak-value occupation number for the electron-positron pair. They correspond to some key values of the parameter $ϵ$. The asterisk * over some of the values means that they are excluded from the range of possible values in agreement in Equations (24) and (26). Hardy’s paradox corresponds to the value $ϵ=1$, which is one of the mentioned forbidden values in the system. Note that when $ϵ\to \infty$ all the events cross the intersection point P and then $N_{O,Ow}^{p,e}\to 1$. However, this is also another forbidden value.

$\mathit{ϵ}$	${\mathit{N}}_{\mathit{O},\mathit{O}\mathit{w}}^{\mathit{e},\mathit{p}}$	${\mathit{N}}_{\mathit{NO},\mathit{O}\mathit{w}}^{\mathit{e},\mathit{p}}$	${\mathit{N}}_{\mathit{O},\mathit{NO}\mathit{w}}^{\mathit{e},\mathit{p}}$	${\mathit{N}}_{\mathit{NO},\mathit{NO}\mathit{w}}^{\mathit{e},\mathit{p}}$
0 *	$-\infty$	∞	∞	$-\infty$
1 *	0	1	1	−1
2	1/2	1/2	1/2	−1/2
4	1/4	1/4	1/4	−1/4
∞ *	1	0	0	0

illustrates the possible values taken by $ϵ$ in agreement with the weak-value approach. The method developed in this section illustrates the discrepancies between the single- and the two-particle approaches when we analyze Hardy’s experiment. This suggests that the paradox is solved when we consider a multiparticle approach like Quantum Field Theory (QFT), for example. This is expected because Hardy’s arguments involve Special Relativity (SR) and Quantum Mechanics (QM) and it is well-known that QFT is precisely the unification of QM and SR. In QFT, there is no conservation of the particle number because particles are permanently created and destroyed over the vacuum state of the theory. Then, among the proposed solutions of Hardy’s paradox, the non-conservation of the particle number was proposed in [9], which is consistent with the conclusions of this paper because this phenomena is related to the energy–time uncertainty relation [10,11]. A generalization of Hardy’s arguments was considered in [14], which is also consistent with the arguments presented in this paper.

5. Experimental Test

The results proposed in this paper can be verified experimentally. This is possible if we find ways to measure the values taken by the parameter $ϵ$. A possibility is to measure the effective probability for the final detectors to click $D^{+}$ and $D^{-}$, namely, the probability $P_{d^{+}{d}^{-}}$. Then, we compare the findings with the result (12). Deviations from $ϵ=1$ can then be measured. In advance there are claims of experimental detection of Hardy’s paradox events in [15,16,17]. If these observations could be adapted to the measurements of the values of $ϵ$, then an experimental verification of the content of this paper is possible. Then, if all the experiments suggest $epsilon=1$ or, equivalently, $P_{d^{+}{d}^{-}}={\displaystyle \frac{1}{12}}$ from Equation (12), we then would conclude that Hardy’s arguments are completely accurate and then there is no way to conciliate the two-particle approach, proposed via the weak-value through the results (36), with the single-particle approach defined through the expressions (32). In this way, although measurements of the weak-value are possible, the easiest way to test the results proposed in this paper is by using the probabilistic approach directly. If the experiments suggest a significant deviation from $ϵ=1$, we can then conclude that the single- and two-particle approaches just mentioned can be conciliated and that Hardy’s arguments require a correction via the dimensionless parameter $ϵ$.

6. Conclusions

In Hardy’s paper we have found a novel formulation to analyze Hardy’s paradox. We have found that there are many different ways for the electron and the positron to cross the intersection point P without annihilation. We have introduced a complex parameter $ϵ$, which in general allows for the possibility of the particles in the pair to cross P without annihilation. The same parameter conciliates the single- and two-particle approaches for the weak-value formulation as it has been analyzed within this paper. This conciliation suggests that the reality condition (15) is wrong because it corresponds to the equality of a quantity that suggests that the particles arrive at the same time at P (left-hand side), with a quantity that does not care at what time both particles arrive (right-hand side). In fact, the inclusion of the parameter $ϵ$ allows both particles to cross P but not necessarily at the same time. The fact that both particles do not necessarily cross the point P at the same time is a natural consequence of the energy–time uncertainty principle $\Delta E\Delta t\ge \hslash$. Then, even if the two particles depart at the same time, with the same energy, at the moment of measuring the arrival time at P, one particle will register the travel interval t, while the other will register $t\pm \Delta t$, where $\Delta t$ is consistent with the uncertainty principle. In the scenario of QFT, the energy–time uncertainty relation is connected with the permanent creation and annihilation of particles over the vacuum state of the theory and then the particle number is not necessarily conserved [10,11]. Then, another way to visualize the solution of Hardy’s paradox is through the non-conservation of the particle number as it was proposed in [9]. However, this paper offers a unique way to analyze the problem by not only using the standard probability approaches but in addition by using the weak-value formulation, which clarifies the origin of the paradox. The weak-value formulation, in particular, helps us to understand the necessity of a multiparticle approach in order to explain and solve the paradox. Finally, we must remark that in this paper we demonstrated that the value $ϵ=1$, which corresponds to Hardy’s paradox value, is forbidden due to the constraint defined in Equation (21). This constraint gave us all the possible values taken by $\left|ϵ\right|$ and $\alpha$ in the experiment. Those ranges of values can be found in Equations (24) and (26). The present formulation of Hardy’s paradox offers a unique scenario for carrying out future experiments in order to verify the values taken by the parameter $ϵ$ and then it offers the chance of testing the results behind the paradox. In future papers we will be exploring real experimental set-ups and the possibility of testing the proposed results with some experimental collaboration. The key value to measure is the probability $P_{d^{+}{d}^{-}}$.