Effect of Surface Passivation on the Quasi-Two-Dimensional Perovskite X2Cs(n−1) PbnI(3n+1)
Abstract
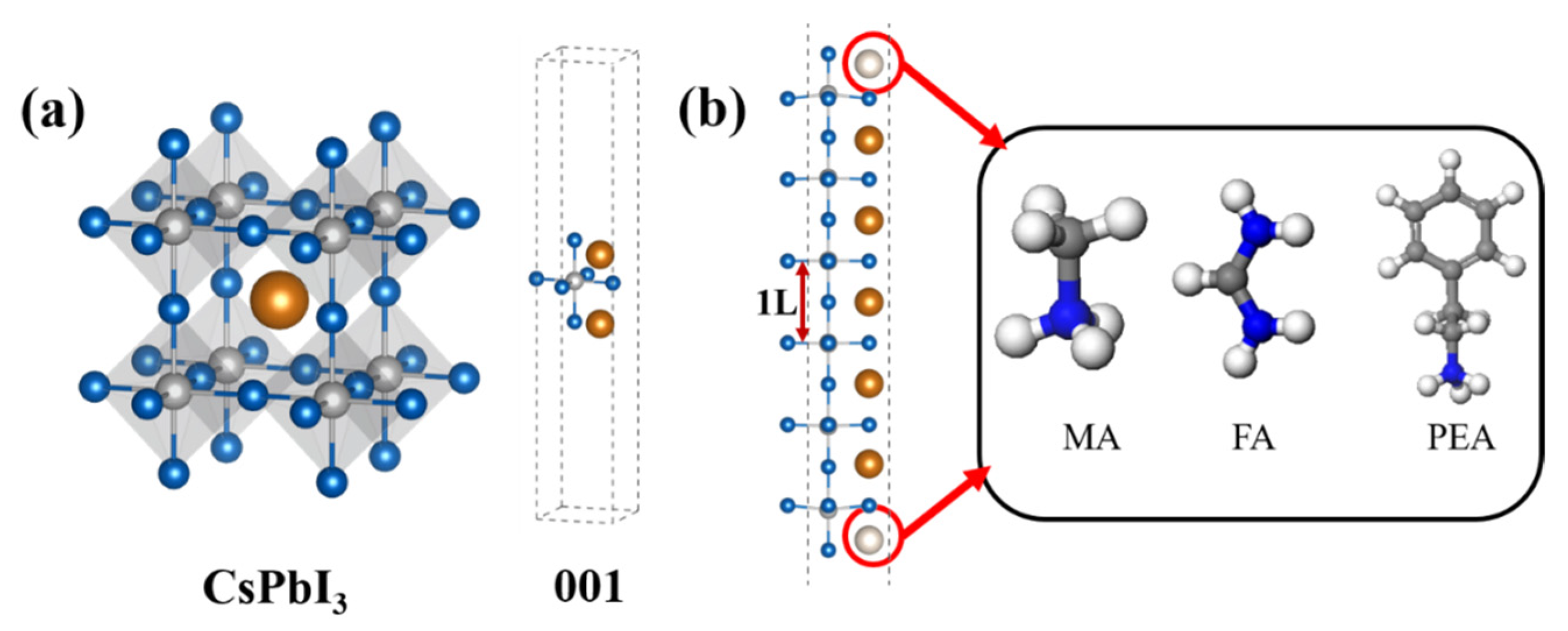
1. Introduction
2. Computational Details
3. Results and Discussion
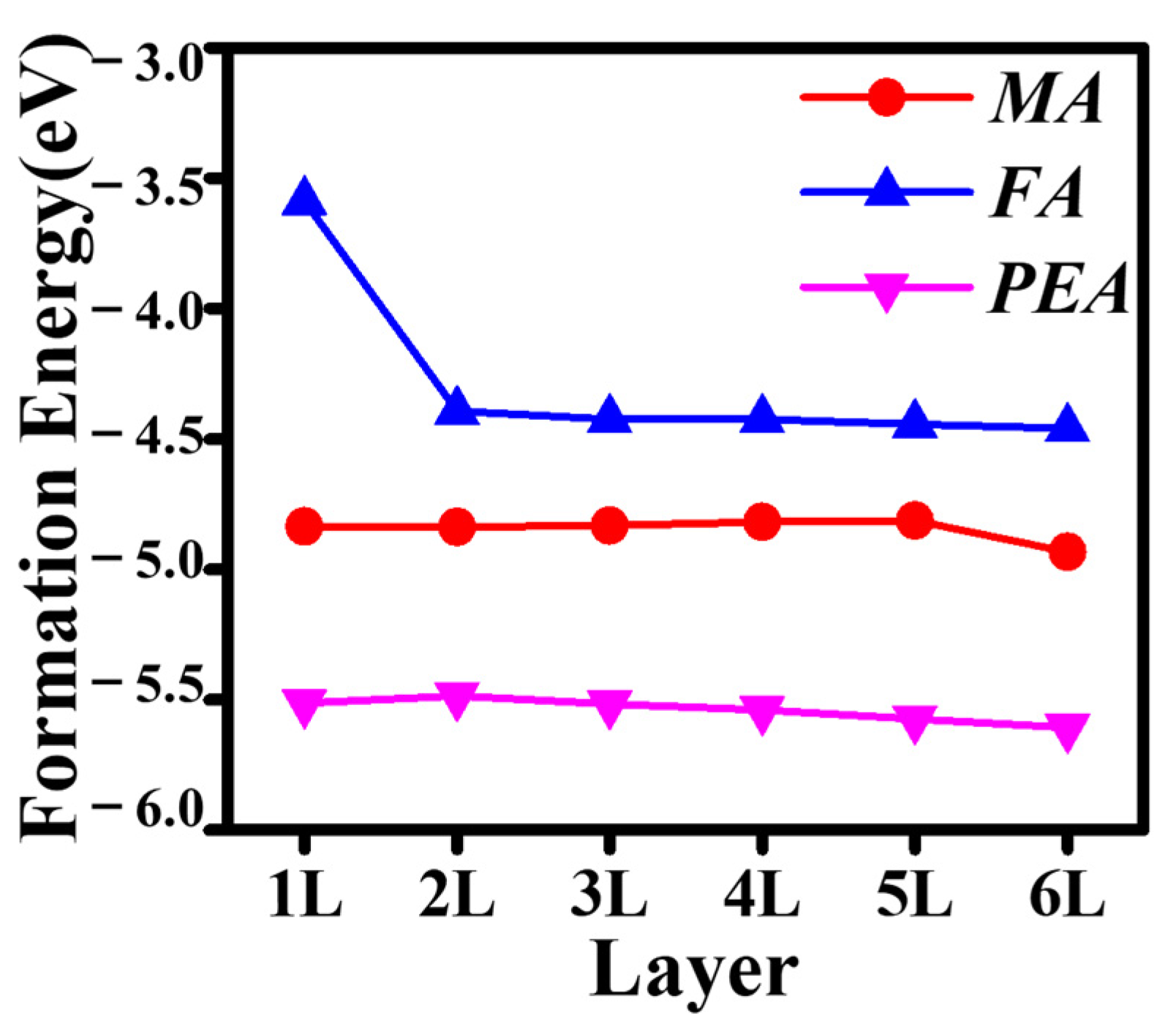
3.1. Thermodynamic Stability
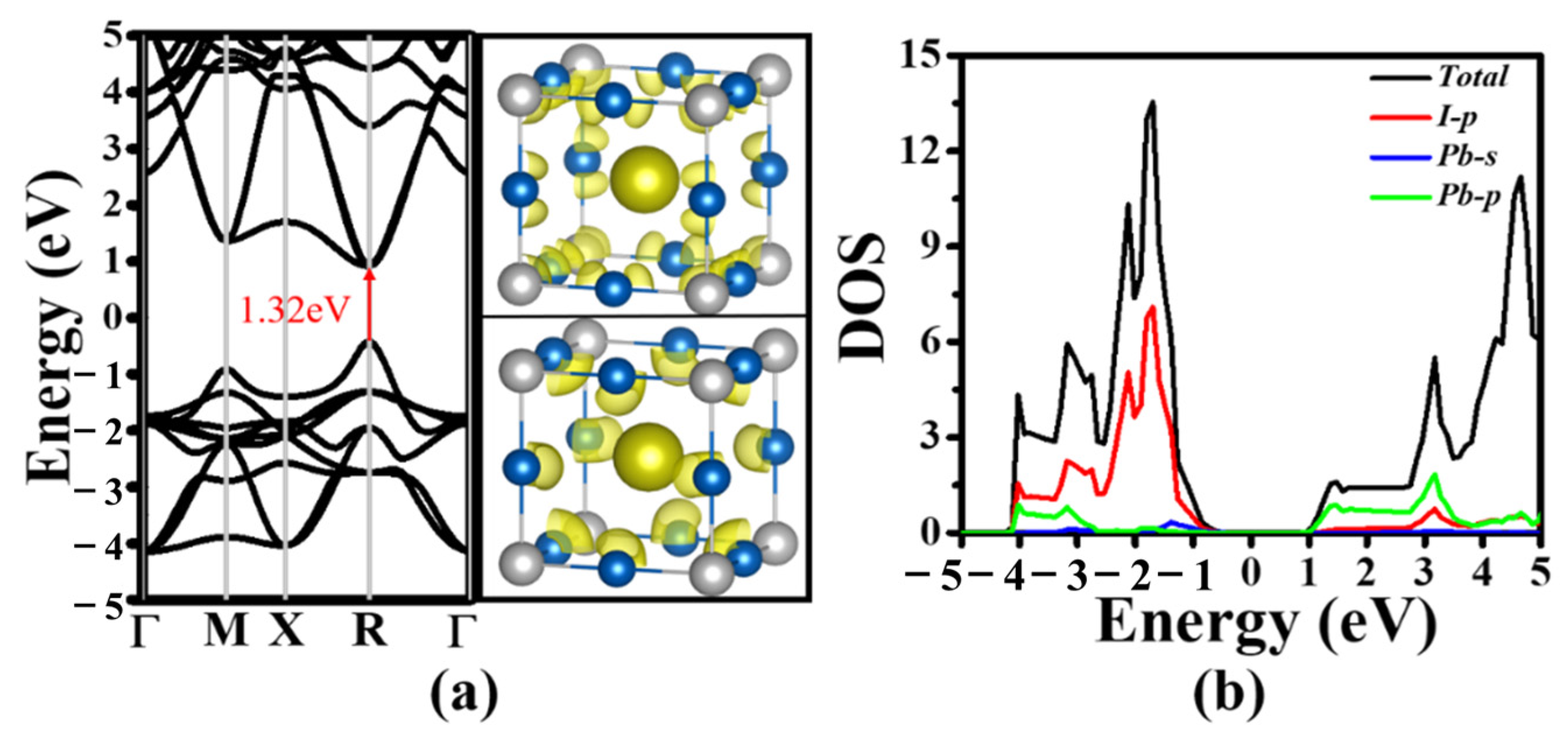
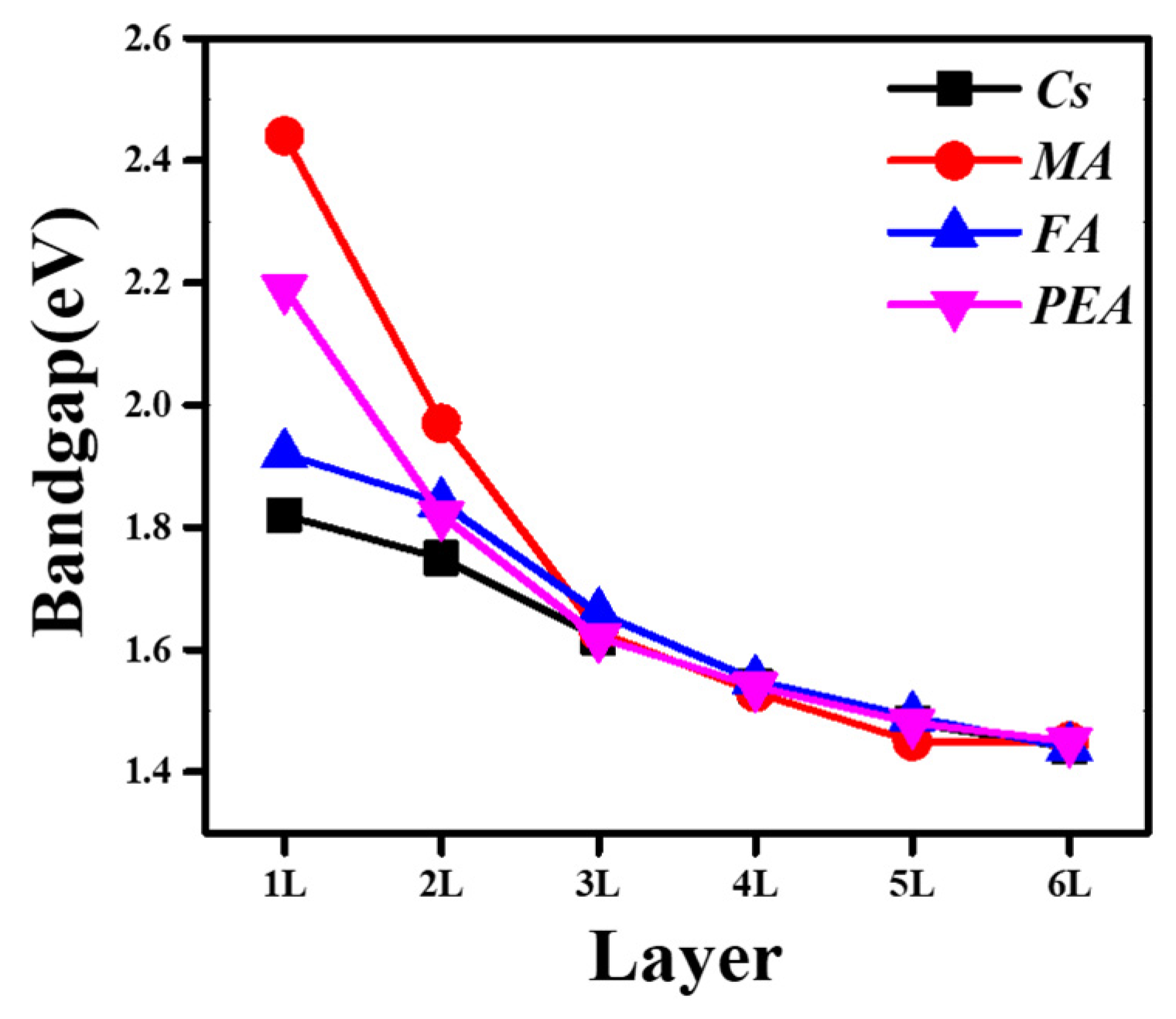
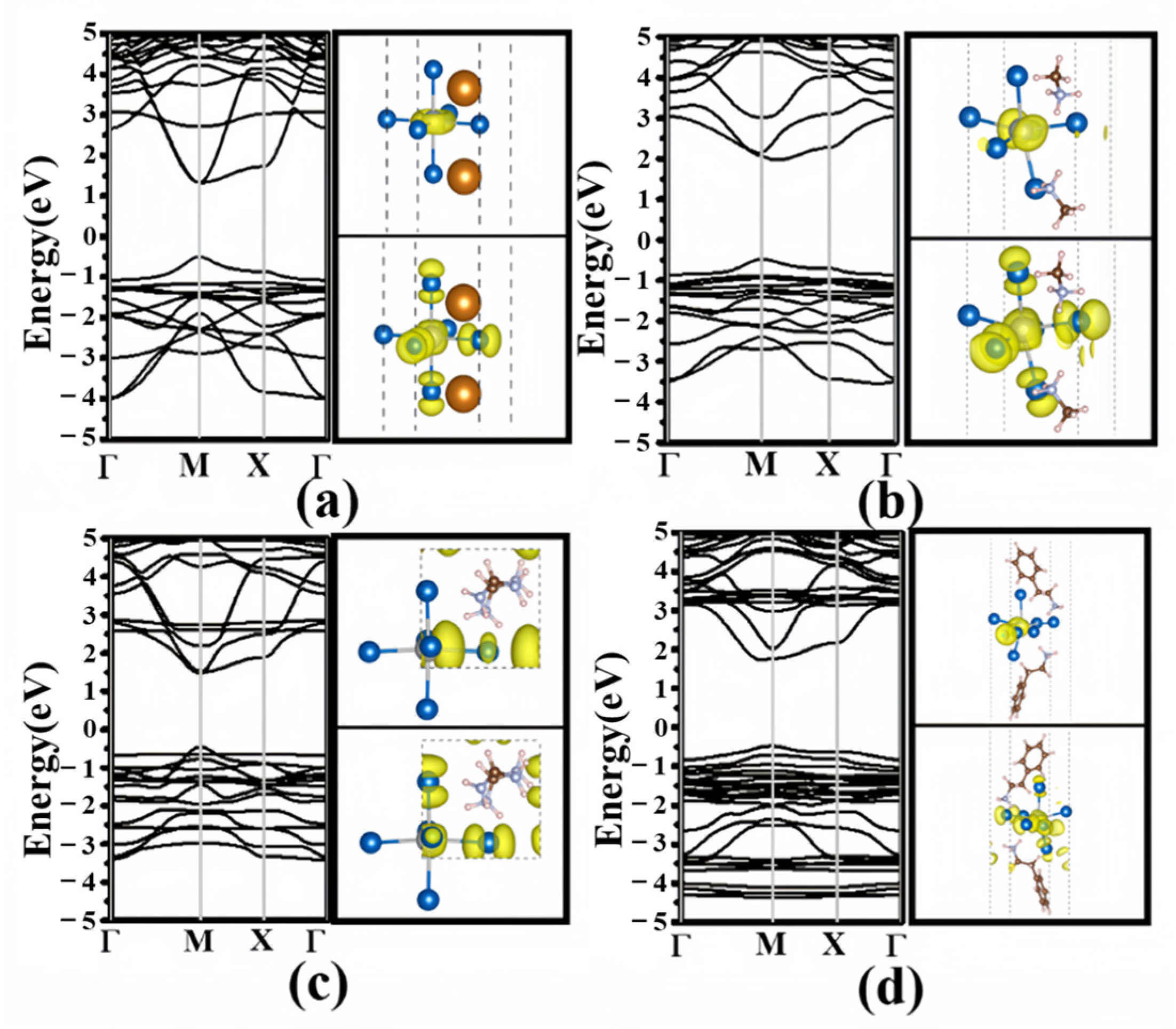
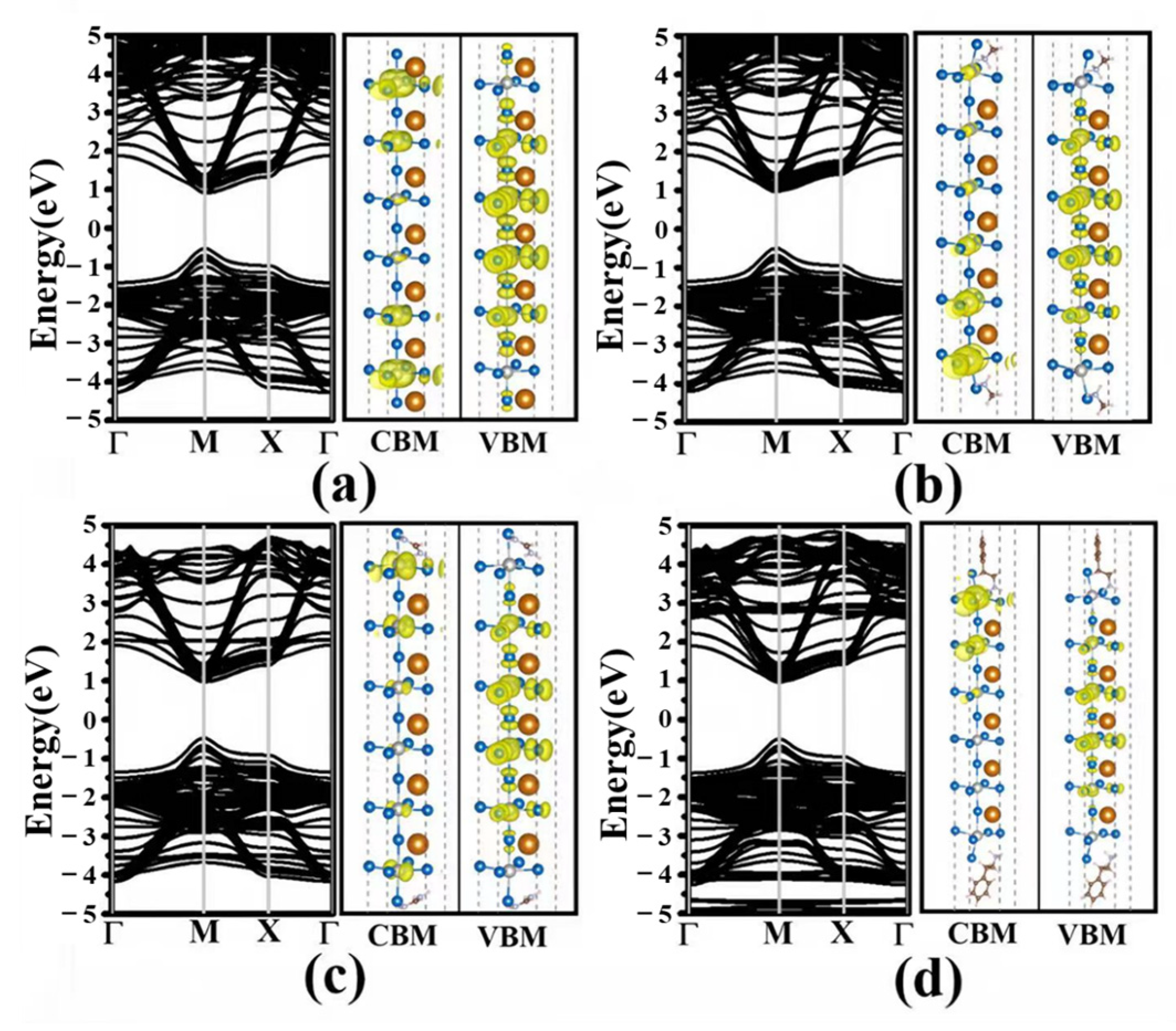
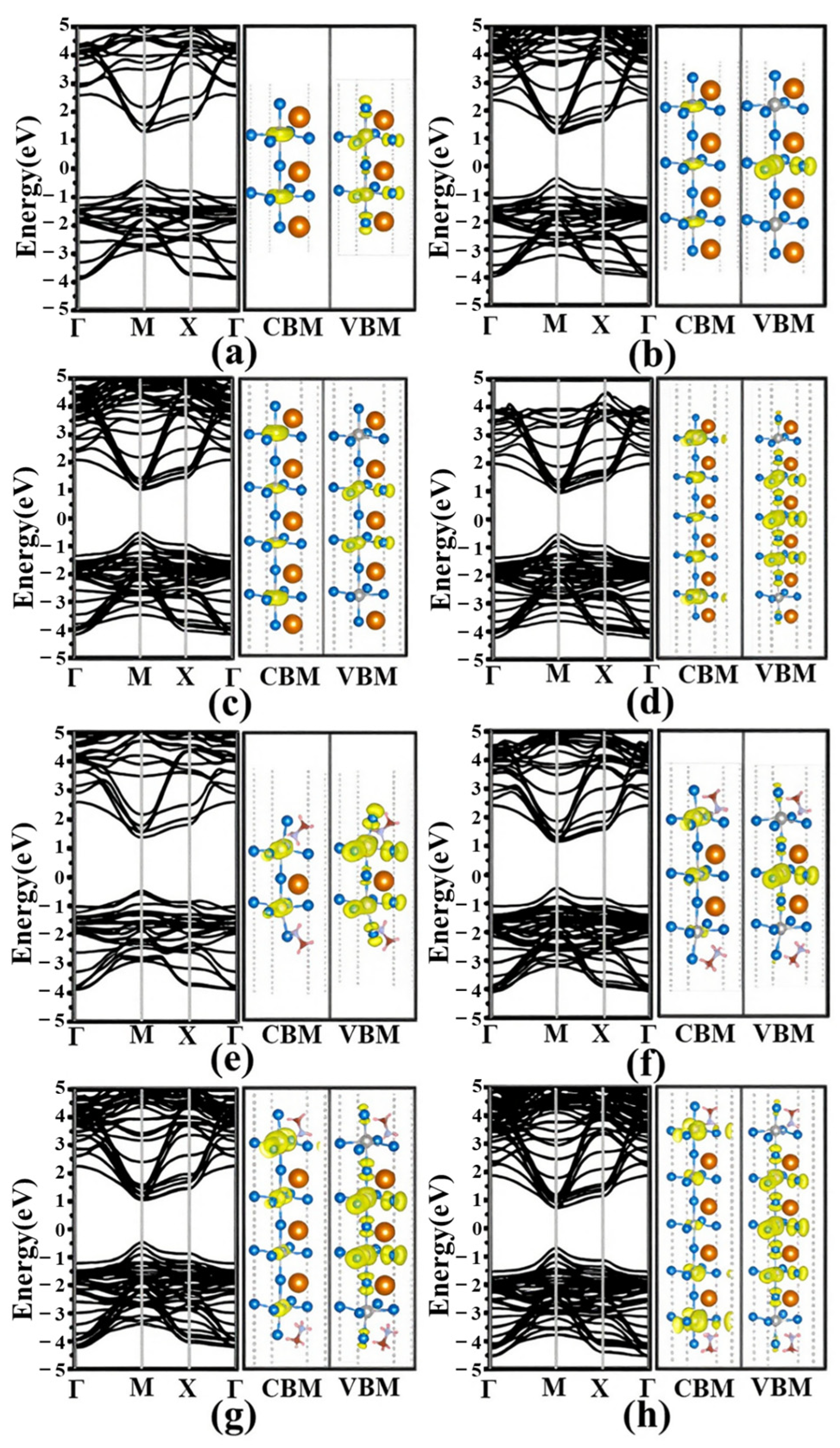
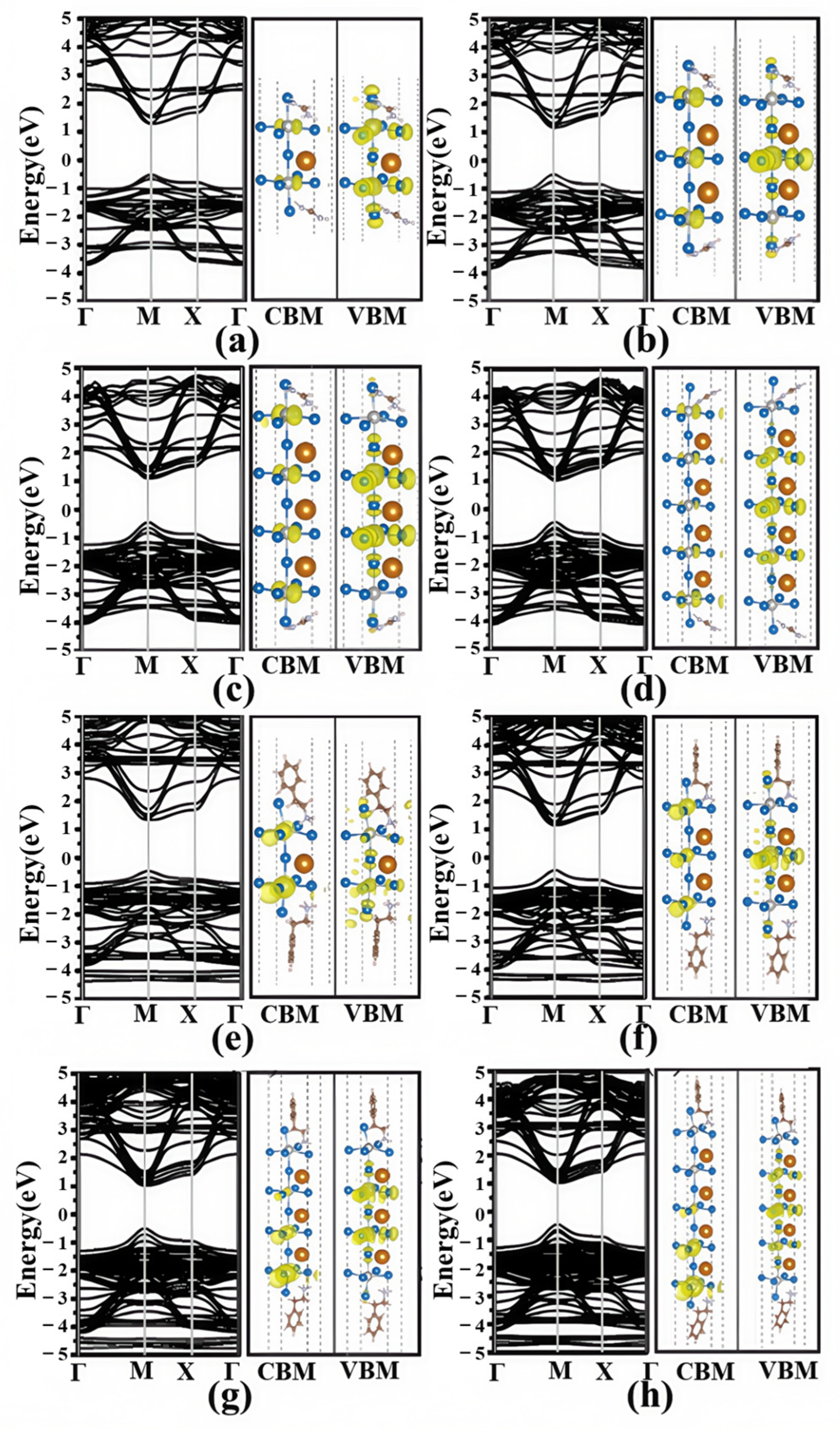
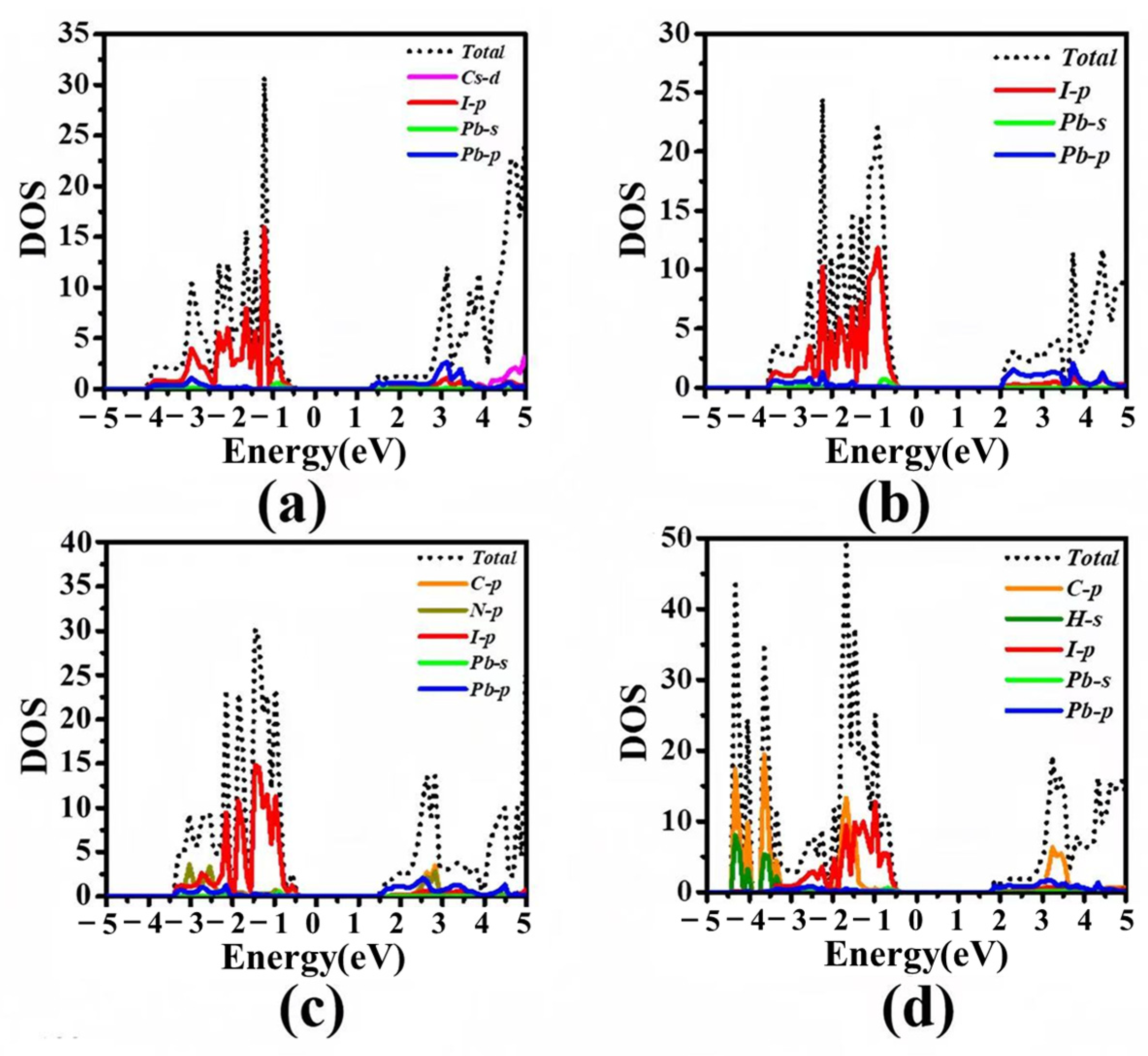
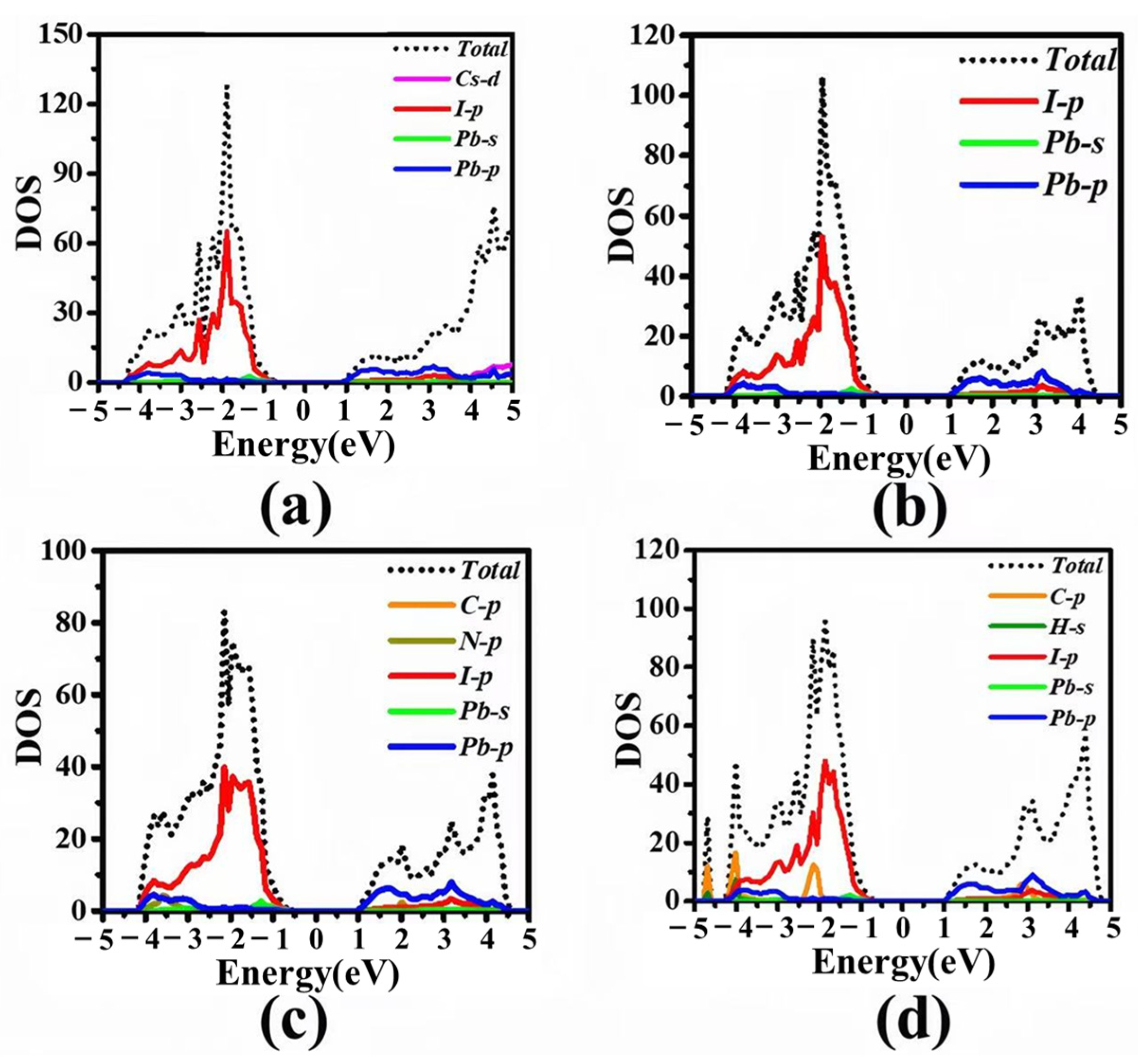
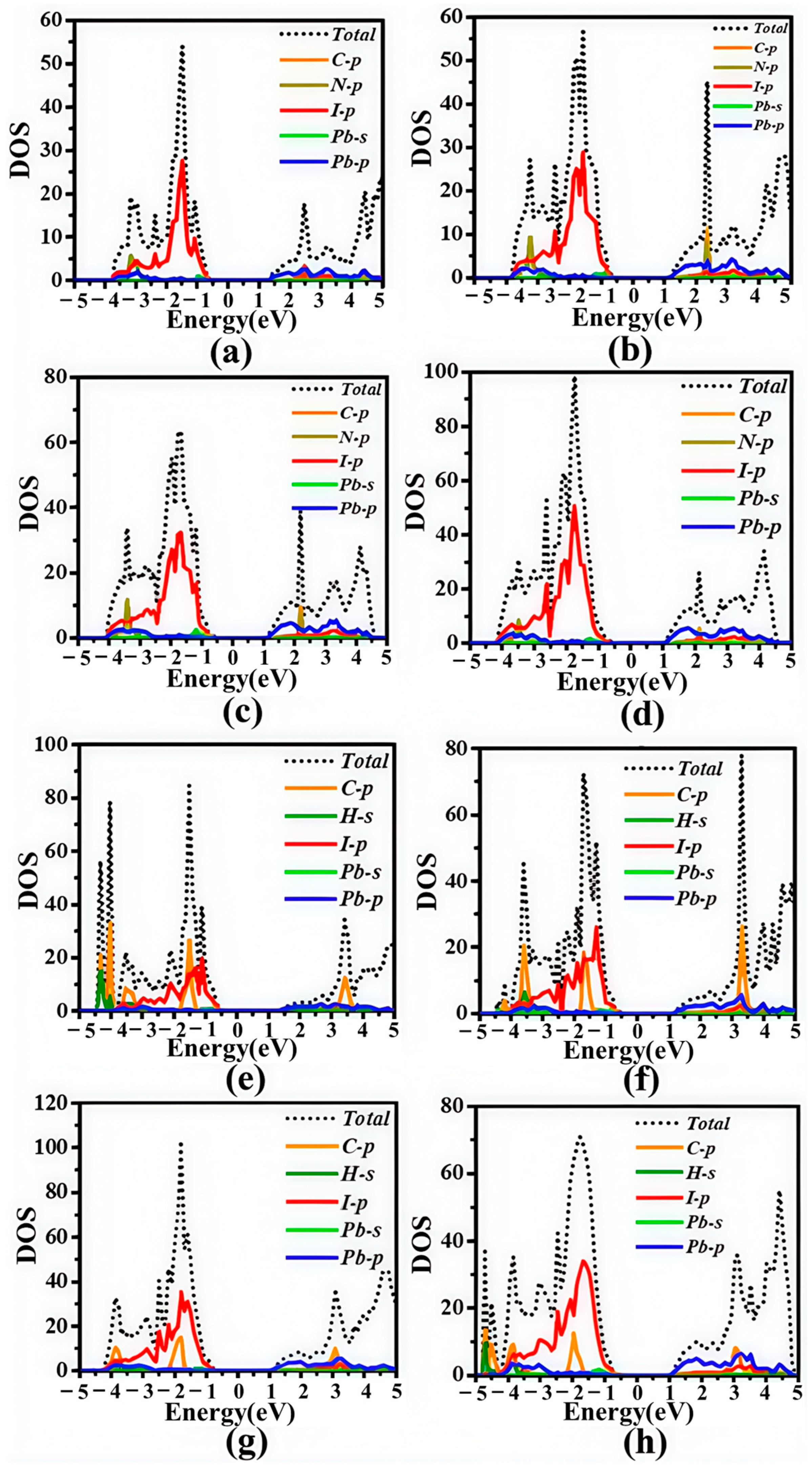
3.2. Electronic Structures
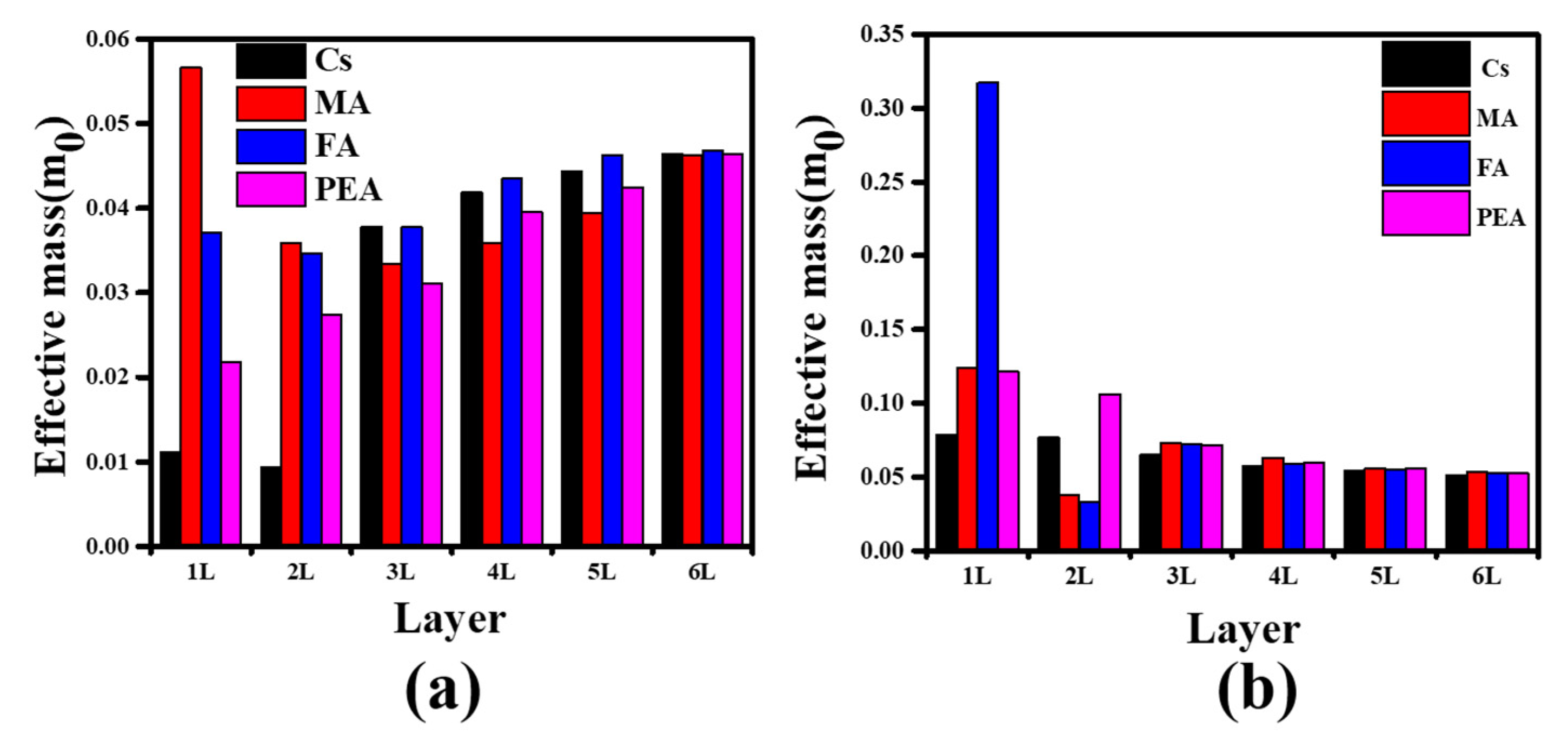
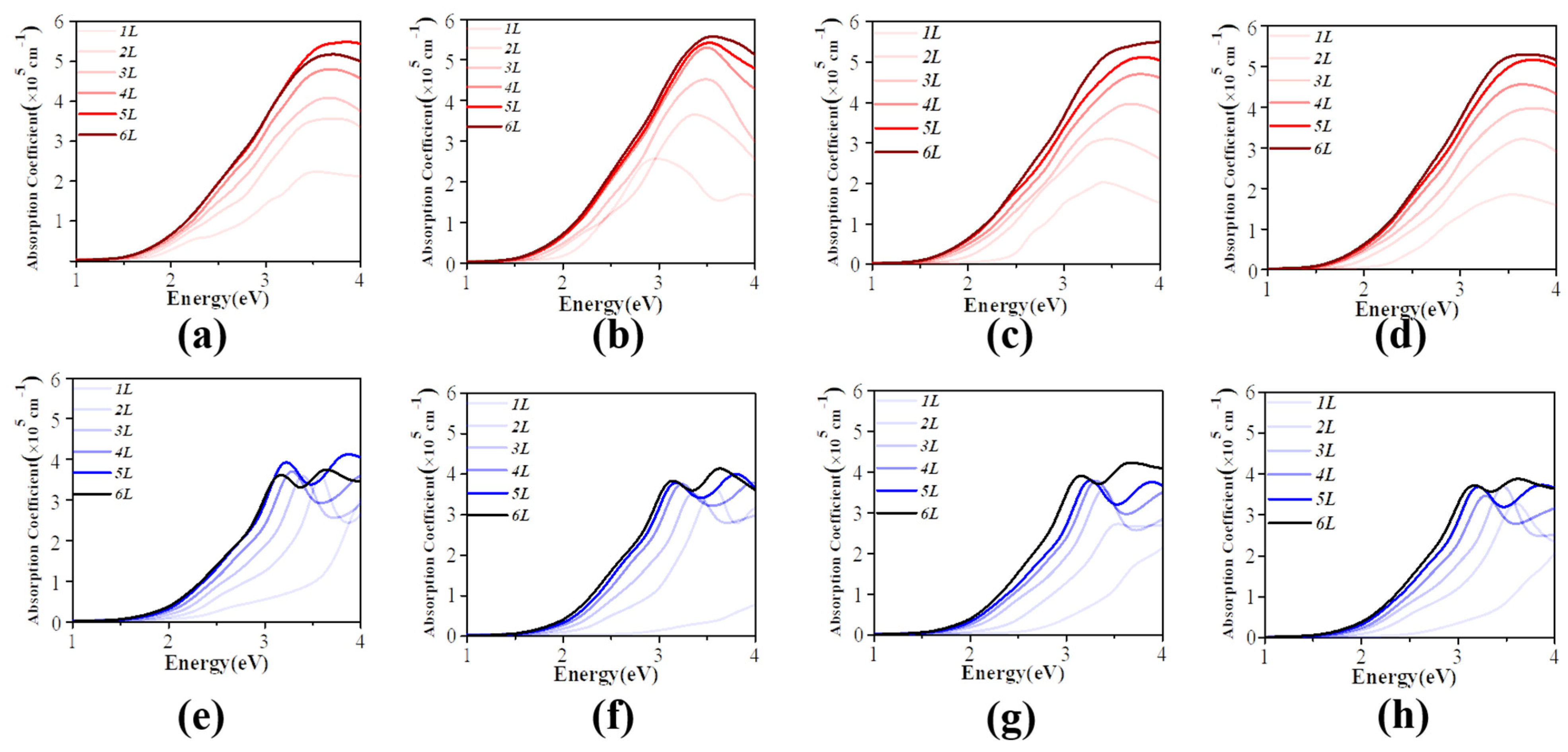
3.3. Effective Mass and Optical Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jung, E.H.; Jeon, N.J.; Park, E.Y.; Moon, C.S.; Shin, T.J.; Yang, T.-Y.; Noh, J.H.; Seo, J. Efficient, stable and scalable perovskite solar cells using poly(3-hexylthiophene). Nature 2019, 567, 511–515. [Google Scholar] [CrossRef]
- Kim, M.; Jeong, J.; Lu, H.; Lee, T.K. Conformal quantum dot–SnO2 layers as electron transporters for efficient perovskite solar cells. Science 2022, 375, 302–306. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, L.; Deng, Y.; Xiao, X.; Ni, Z.; Xu, S.; Huang, J. Perovskite-filled membranes for flexible and large-area direct-conversion X-ray detector arrays. Nat. Photonics 2020, 14, 612–617. [Google Scholar] [CrossRef]
- Veldhuis, S.A.; Boix, P.P.; Yantara, N.; Li, M.; Sum, T.C.; Mathews, N.; Mhaisalkar, S.G. Perovskite Materials for Light-Emitting Diodes and Lasers. Adv. Mater. 2016, 28, 6804–6834. [Google Scholar] [CrossRef]
- Turren-Cruz, S.-H.; Saliba, M.; Mayer, M.T.; Juárez-Santiesteban, H.; Mathew, X.; Nienhaus, L.; Tress, W.; Erodici, M.P.; Sher, M.-J.; Bawendi, M.G.; et al. Enhanced charge carrier mobility and lifetime suppress hysteresis and improve efficiency in planar perovskite solar cells. Energy Environ. Sci. 2018, 11, 78–86. [Google Scholar] [CrossRef]
- Stranks, S.D.; Eperon, G.E.; Grancini, G.; Menelaou, C.; Alcocer, M.J.P.; Leijtens, T.; Herz, L.M.; Petrozza, A.; Snaith, H.J. Electron-Hole Diffusion Lengths Exceeding 1 Micrometer in an Organometal Trihalide Perovskite Absorber. Science 2013, 342, 341–344. [Google Scholar] [CrossRef]
- Protesescu, L.; Yakunin, S.; Bodnarchuk, M.I.; Krieg, F.; Caputo, R.; Hendon, C.H.; Yang, R.X.; Walsh, A.; Kovalenko, M.V. Nanocrystals of Cesium Lead Halide Perovskites (CsPbX3, X = Cl, Br, and I): Novel Optoelectronic Materials Showing Bright Emission with Wide Color Gamut. Nano Lett. 2015, 15, 3692–3696. [Google Scholar] [CrossRef]
- Lin, K.; Xing, J.; Quan, L.N.; de Arquer, F.P.G.; Gong, X.; Lu, J.; Xie, L.; Zhao, W.; Zhang, D.; Yan, C.; et al. Perovskite light-emitting diodes with external quantum efficiency exceeding 20 per cent. Nature 2018, 562, 245–248. [Google Scholar] [CrossRef]
- Best-Research-Cell-Efficiencies.pdf. (n.d.). Available online: https://www.nrel.gov/pv/assets/pdfs/best-research-cell-efficiencies.pdf (accessed on 8 November 2024).
- Kwak, K.; Lim, E.; Ahn, N.; Heo, J.; Bang, K.; Kim, S.K.; Choi, M. An atomistic mechanism for the degradation of perovskite solar cells by trapped charge. Nanoscale 2019, 11, 11369–11378. [Google Scholar] [CrossRef]
- Chowdhury, T.A.; Bin Zafar, M.A.; Sajjad-Ul Islam, M.; Shahinuzzaman, M.; Islam, M.A.; Khandaker, M.U. Stability of perovskite solar cells: Issues and prospects. RSC Adv. 2023, 13, 1787–1810. [Google Scholar] [CrossRef]
- Wolff, C.M.; Caprioglio, P.; Stolterfoht, M.; Neher, D. Nonradiative Recombination in Perovskite Solar Cells: The Role of Interfaces. Adv. Mater. 2019, 31, 1902762. [Google Scholar] [CrossRef]
- Gong, J.; Hao, M.; Zhang, Y.; Liu, M.; Zhou, Y. Layered 2D Halide Perovskites beyond the Ruddlesden–Popper Phase: Tailored Interlayer Chemistries for High-Performance Solar Cells. Angew. Chem. 2022, 134, e202112022. [Google Scholar] [CrossRef]
- Ke, W.; Kanatzidis, M.G. Prospects for low-toxicity lead-free perovskite solar cells. Nat. Commun. 2019, 10, 965. [Google Scholar] [CrossRef]
- Stoumpos, C.C.; Cao, D.H.; Clark, D.J.; Young, J.; Rondinelli, J.M.; Jang, J.I.; Hupp, J.T.; Kanatzidis, M.G. Ruddlesden–Popper Hybrid Lead Iodide Perovskite 2D Homologous Semiconductors. Chem. Mater. 2016, 28, 2852–2867. [Google Scholar] [CrossRef]
- Gao, L.; Spanopoulos, I.; Ke, W.; Huang, S.; Hadar, I.; Chen, L.; Li, X.; Yang, G.; Kanatzidis, M.G. Improved Environmental Stability and Solar Cell Efficiency of (MA,FA)PbI3 Perovskite Using a Wide-Band-Gap 1D Thiazolium Lead Iodide Capping Layer Strategy. ACS Energy Lett. 2019, 4, 1763–1769. [Google Scholar] [CrossRef]
- Umeyama, D.; Lin, Y.; Karunadasa, H.I. Red-to-Black Piezochromism in a Compressible Pb–I–SCN Layered Perovskite. Chem. Mater. 2016, 28, 3241–3244. [Google Scholar] [CrossRef]
- Shi, W.; Ye, H. Efficient and Stable Perovskite Solar Cells with a Superhydrophobic Two-Dimensional Capping Layer. J. Phys. Chem. Lett. 2021, 12, 4052–4058. [Google Scholar] [CrossRef]
- Wang, Y.; Song, Q.; Hu, W.; Wang, D.; Peng, L.; Shi, T.; Liu, X.; Zhu, Y.; Lin, J. Temperature-driven phase transition and transition dipole moment of two-dimensional (BA)2CsPb2Br7 perovskite. Phys. Chem. Chem. Phys. 2021, 23, 16341–16348. [Google Scholar] [CrossRef]
- Feng, Z.; Xia, Z.; Wu, Z.; Hua, Y.; Zhu, G.; Chen, X.; Huang, S. Efficient and stable perovskite solar cells via organic surfactant interfacial passivation. Sol. Energy 2021, 227, 438–446. [Google Scholar] [CrossRef]
- Wang, D.; Liang, P.; Dong, Y.; Shu, H.; Liu, Z. Electronic and optical properties of layered Ruddlesden Popper hybrid X2(MA)n-1SnnI3n+1 perovskite insight by first principles. J. Phys. Chem. Solids 2020, 144, 109510. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Körbel, S.; Marques, M.A.L.; Botti, S. Stability and electronic properties of new inorganic perovskites from high-throughput ab initio calculations. J. Mater. Chem. C 2016, 4, 3157–3167. [Google Scholar] [CrossRef]
- Quan, L.N.; Yuan, M.; Comin, R.; Voznyy, O.; Beauregard, E.M.; Hoogland, S.; Buin, A.; Kirmani, A.R.; Zhao, K.; Amassian, A.; et al. Ligand-stabilized reduced-dimensionality perovskites. J. Am. Chem. Soc. 2016, 138, 2649–2655. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M.; Rehman, G.; Ali, L.; Shafiq, M.; Iqbal, R.; Ahmad, R.; Khan, T.; Jalali-Asadabadi, S.; Maqbool, M.; Ahmad, I. Structural, electronic and optical properties of CsPbX3 (X = Cl, Br, I) for energy storage and hybrid solar cell applications. J. Alloys Compd. 2017, 705, 828–839. [Google Scholar] [CrossRef]
- Fang, Z.; Shang, M.; Hou, X.; Zheng, Y.; Du, Z.; Yang, Z.; Chou, K.-C.; Yang, W.; Wang, Z.L.; Yang, Y. Bandgap alignment of α-CsPbI3 perovskites with synergistically enhanced stability and optical performance via B-site minor doping. Nano Energy 2019, 61, 389–396. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ernzerhof, M.; Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]

| Parameter | MA-Based | FA-Based | PEA-Based |
|---|---|---|---|
| Lattice param (Å) | 6.29 | 6.35 | 6.42 |
| Bandgap (eV) | 1.45 | 1.44 | 1.45 |
| ΔH_form (eV) | −0.82 | −0.91 | −0.76 |
| me/m0 | 0.046 | 0.043 | 0.048 |
| Method | PBE | PBE | PBE |
| Property | Calculated Value | Experimental Value |
|---|---|---|
| (This Work) | (Literature) | |
| Bulk CsPbI3 Bandgap | 1.32 V | 1.73 eV |
| Quasi-2D PEA-Passivated | 1.45 eV | ~1.55 eV |
| Bandgap (n = 3) | ||
| 2D(BA)2CsPb2Br7 Bandgap | 2.5 eV | 2.9 eV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Zheng, H.; Ke, X.; Zhang, D.; Huang, J. Effect of Surface Passivation on the Quasi-Two-Dimensional Perovskite X2Cs(n−1) PbnI(3n+1). Condens. Matter 2025, 10, 44. https://doi.org/10.3390/condmat10030044
Li M, Zheng H, Ke X, Zhang D, Huang J. Effect of Surface Passivation on the Quasi-Two-Dimensional Perovskite X2Cs(n−1) PbnI(3n+1). Condensed Matter. 2025; 10(3):44. https://doi.org/10.3390/condmat10030044
Chicago/Turabian StyleLi, Min, Haoyan Zheng, Xianliang Ke, Dawei Zhang, and Jie Huang. 2025. "Effect of Surface Passivation on the Quasi-Two-Dimensional Perovskite X2Cs(n−1) PbnI(3n+1)" Condensed Matter 10, no. 3: 44. https://doi.org/10.3390/condmat10030044
APA StyleLi, M., Zheng, H., Ke, X., Zhang, D., & Huang, J. (2025). Effect of Surface Passivation on the Quasi-Two-Dimensional Perovskite X2Cs(n−1) PbnI(3n+1). Condensed Matter, 10(3), 44. https://doi.org/10.3390/condmat10030044





