The Solution to Hardy’s Paradox
Abstract
1. Introduction
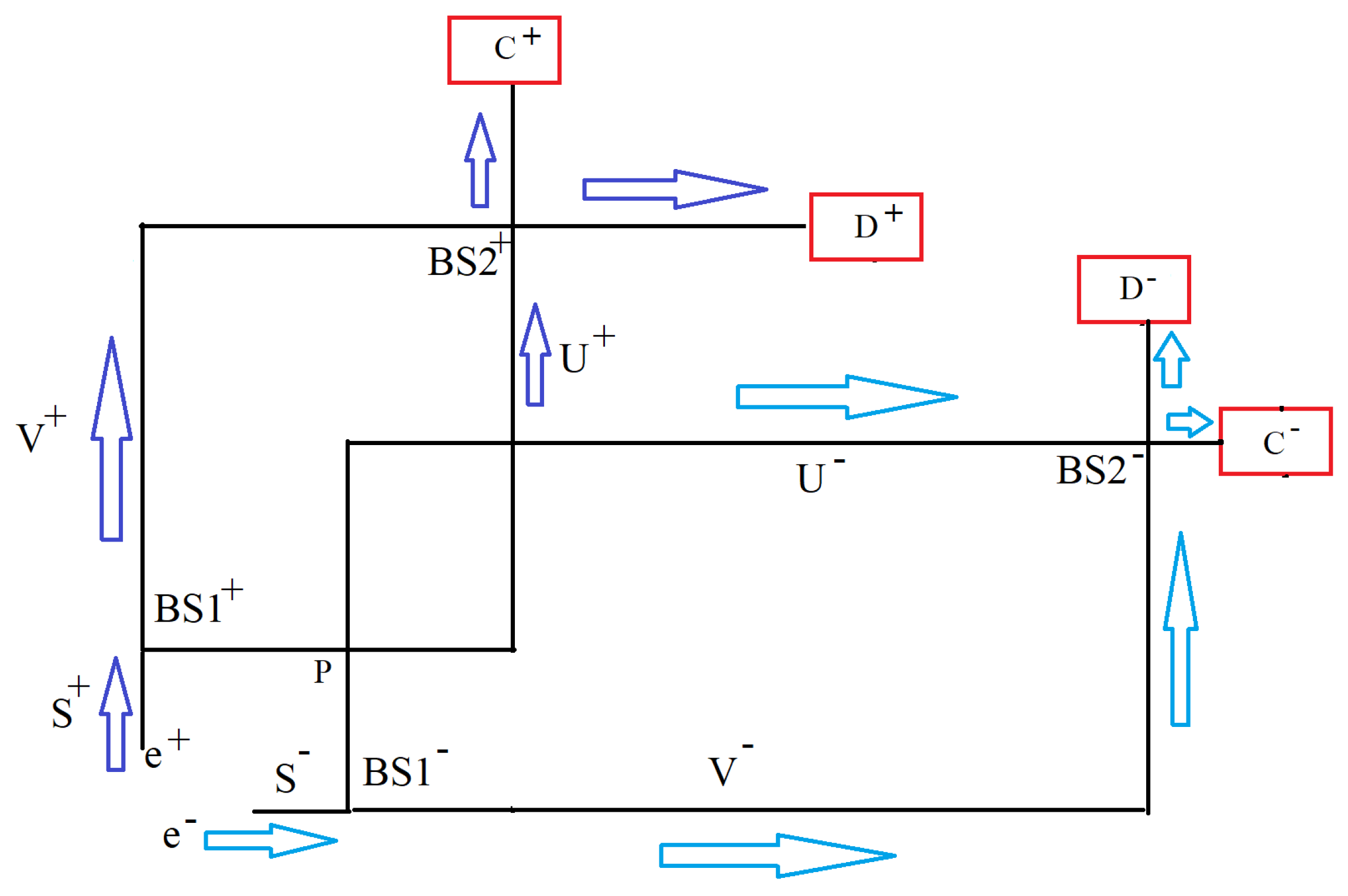
2. Hardy’s Paradox: Formulation of the Problem
2.1. Improvements in Hardy’s Formulation
2.2. Relations Between Probabilities and Probability Invariants
2.3. The Solution to Hardy’s Paradox: Probabilistic Approach
3. The Weak-Value Explanation
4. Improvements in the Weak-Value Approximation: The Inclusion of the States
5. Experimental Test
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hardy, L. Quantum mechanics, local realistic theories, and Lorentz-invariant realistic theories. Phys. Rev. Lett. 1992, 68, 2981. [Google Scholar] [CrossRef]
- Hardy, L. Nonlocality for two particles without inequalities for almost all entangled states. Phys. Rev. Lett. 1993, 71, 1665. [Google Scholar] [CrossRef]
- Aharonov, Y.; Albert, D.Z.; Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2particle can turn out to be 100. Phys. Rev. Lett. 1988, 60, 1351–1354. [Google Scholar] [CrossRef]
- Aharonov, Y.; Botero, A.; Popescu, S.; Reznik, B.; Tollaksen, J. Revisiting Hardy’s paradox: Counterfactual statements, real measurements, entanglement and weak values. Phys. Lett. A 2002, 301, 130–138. [Google Scholar] [CrossRef]
- Vaidman, L. The analycis of Hardy’s experiment revisited. arXiv 1997, arXiv:quant-ph/9703018. [Google Scholar]
- Vaidman, L. Lorentz-Invariant “Elements of Reality” and the Question of Joint Measurability of Commuting Observables. Phys. Rev. Lett. 1993, 70, 3369. [Google Scholar] [CrossRef] [PubMed]
- Marchildon, L. Hardy’s setup and elements of reality. Physica E 2010, 42, 323–326. [Google Scholar] [CrossRef][Green Version]
- Sahin, I. Can parallel lives provide a solution to Hardy’s paradox? Found. Phys. 2021, 51, 9. [Google Scholar] [CrossRef]
- Peres, A. Nonlocal effects in Fock space. Phys. Rev. Lett. 1995, 74, 4571, Erratum in 1996, 76, 2205. [Google Scholar] [CrossRef] [PubMed]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; Westview Press: Boulder, CO, USA, 1995; p. 80. ISBN 0-201-50397-2. [Google Scholar]
- Jaffe, R.L. Casimir effect and the quantum vacuum. Phys. Rev. D 2005, 72, 021301. [Google Scholar] [CrossRef]
- Griffiths, D. Introduction to Elementary Particles, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2008; ISBN-10:9783527406012/ISBN-13:978-3527406012. [Google Scholar]
- Mori, T.; Tsutsui, I. Quantum Trajectories based on the Weak Value. Prog. Theor. Exp. Phys. 2015, 2015, 043A01. [Google Scholar] [CrossRef]
- Goldstein, S. Nonlocality without inequalities for almost all entangled states for two particles. Phys. Rev. Lett. 1951, 72, 1665. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.R.; Zhao, S.; Dong, H.H.; Liu, W.Z.; Chen, J.L.; Chen, K.; Zhang, Q.; Pan, J.W. Loophole-Free Test of Local Realism via Hardy’s Violation. Phys. Rev. Lett. 2024, 133, 060201. [Google Scholar] [CrossRef] [PubMed]
- Lundeen, J.S.; Steinberg, A.M. Experimental Joint Weak Measurement on a Photon Pair as a Probe of Hardy’s Paradox. Phys. Rev. Lett. 2009, 102, 020404. [Google Scholar] [CrossRef] [PubMed]
- Yokota, K.; Yamamoto, T.; Koashi, M.; Imoto, N. Direct observation of Hardy’s paradox by joint weak measurement with an entangled photon pair. New J. Phys. 2009, 11, 033011. [Google Scholar] [CrossRef]

| 0 * | 0 | 1/4 | 1/4 | 1/2 | 1 |
| 1 * | 1/12 | 0 | 1/3 | 1/6 | 3/4 |
| 2 | 1/4 | 1/4 | 1/4 | 0 | 1/4 |
| 4 | 1/3 | 3/4 | 1/12 | 1/6 | 0 |
| ∞ * | 1/4 | 1 | 0 | 1/2 | 1/4 |
| 0 * | ∞ | ∞ | ||
| 1 * | 0 | 1 | 1 | −1 |
| 2 | 1/2 | 1/2 | 1/2 | −1/2 |
| 4 | 1/4 | 1/4 | 1/4 | −1/4 |
| ∞ * | 1 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arraut, I. The Solution to Hardy’s Paradox. Condens. Matter 2025, 10, 45. https://doi.org/10.3390/condmat10030045
Arraut I. The Solution to Hardy’s Paradox. Condensed Matter. 2025; 10(3):45. https://doi.org/10.3390/condmat10030045
Chicago/Turabian StyleArraut, Ivan. 2025. "The Solution to Hardy’s Paradox" Condensed Matter 10, no. 3: 45. https://doi.org/10.3390/condmat10030045
APA StyleArraut, I. (2025). The Solution to Hardy’s Paradox. Condensed Matter, 10(3), 45. https://doi.org/10.3390/condmat10030045






