Field-Induced Ferroaxiality in Antiferromagnets with Magnetic Toroidal Quadrupole
Abstract
1. Introduction
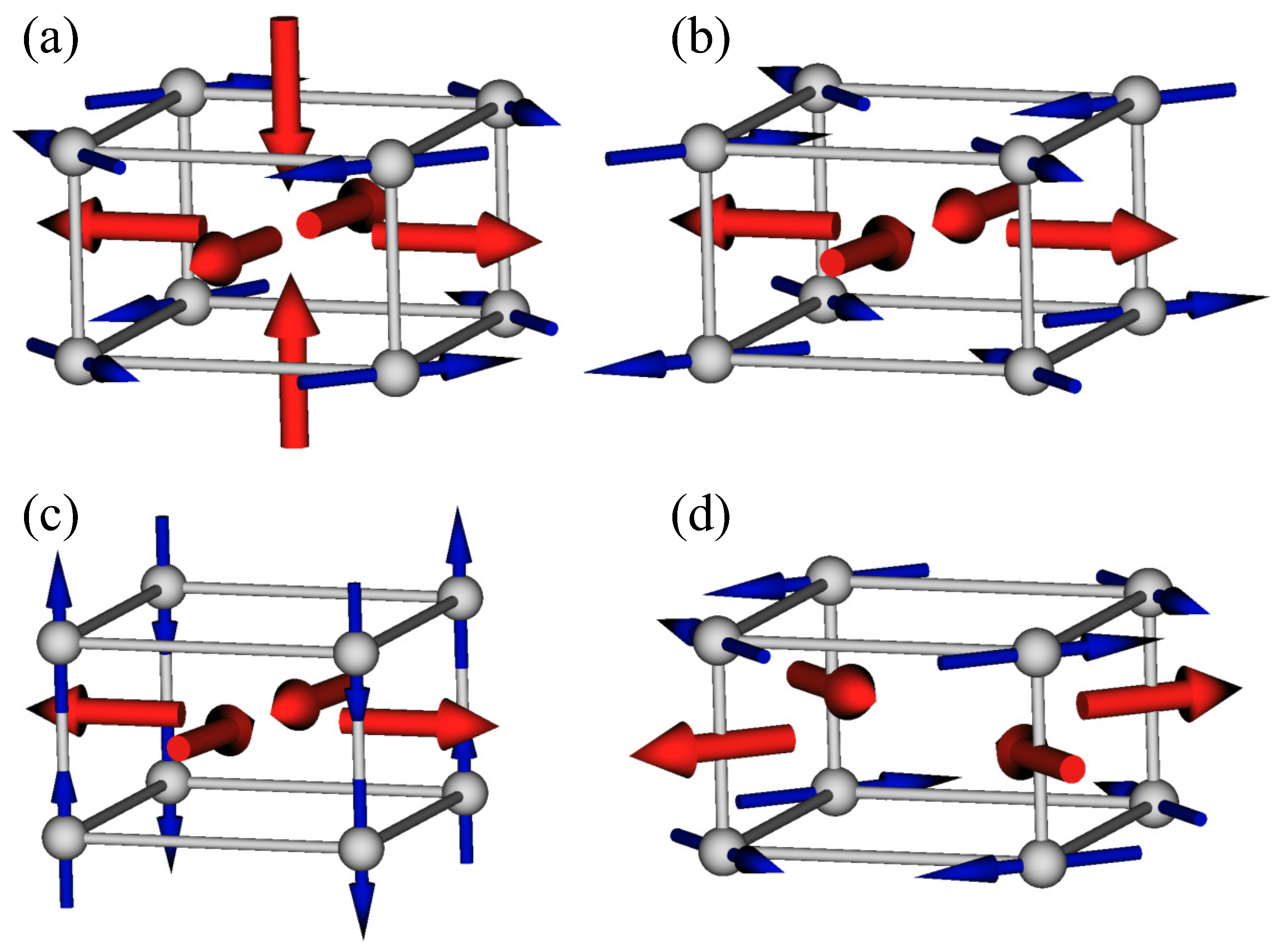
2. Magnetic Toroidal Quadrupole
3. Field-Induced Axiality
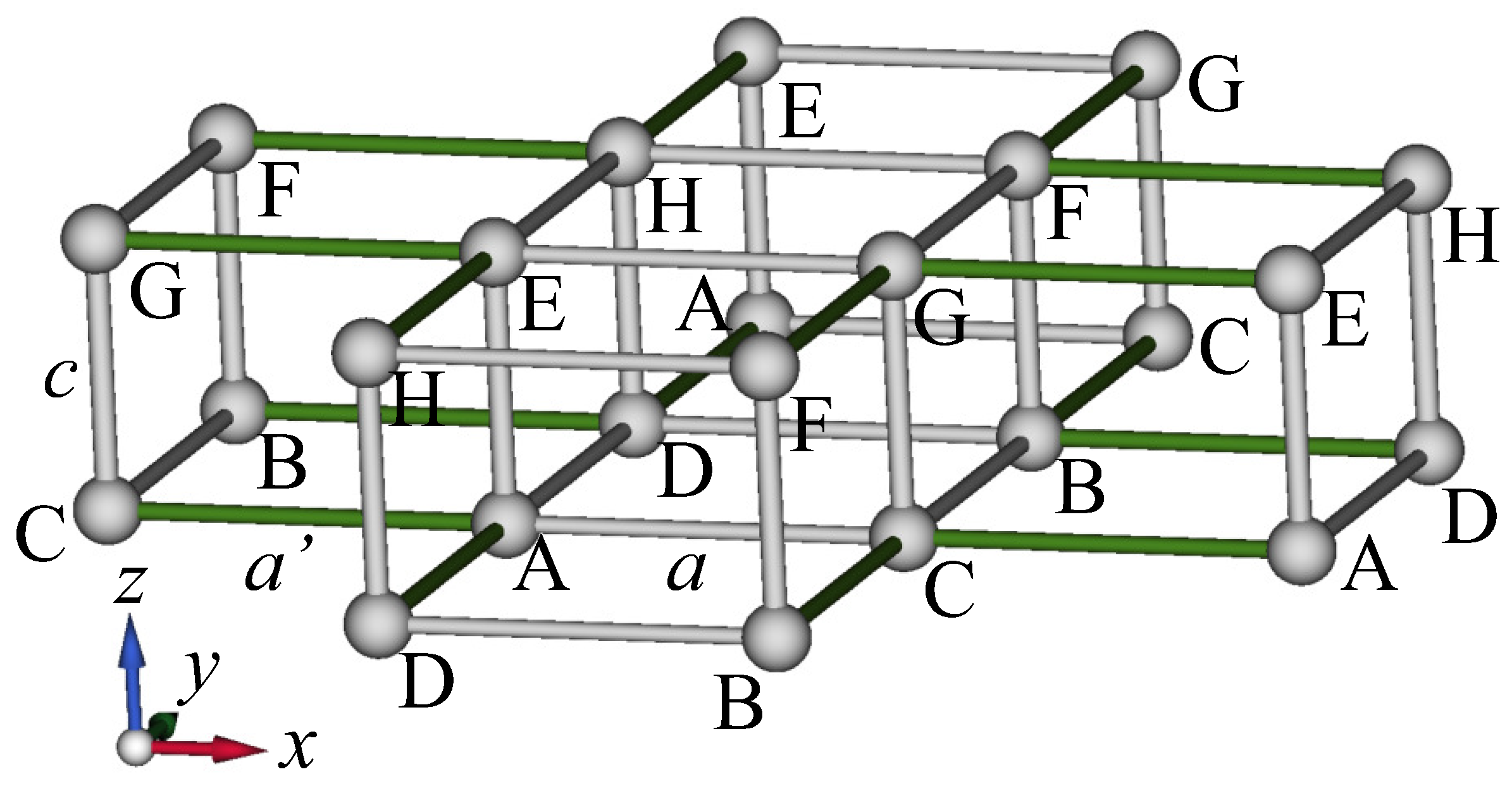
4. Model Analyses
5. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dubovik, V.; Cheshkov, A. Multipole expansion in classical and quantum field theory and radiation. Sov. J. Part. Nucl. 1975, 5, 318–337. [Google Scholar]
- Dubovik, V.; Tugushev, V. Toroid moments in electrodynamics and solid-state physics. Phys. Rep. 1990, 187, 145–202. [Google Scholar] [CrossRef]
- Gorbatsevich, A.; Kopaev, Y.V. Toroidal order in crystals. Ferroelectrics 1994, 161, 321–334. [Google Scholar] [CrossRef]
- Kopaev, Y.V. Toroidal ordering in crystals. Physics-Uspekhi 2009, 52, 1111–1125. [Google Scholar] [CrossRef]
- Spaldin, N.A.; Fiebig, M.; Mostovoy, M. The toroidal moment in condensed-matter physics and its relation to the magnetoelectric effect. J. Phys. Condens. Matter 2008, 20, 434203. [Google Scholar] [CrossRef]
- Kusunose, H.; Hayami, S. Generalization of microscopic multipoles and cross-correlated phenomena by their orderings. J. Phys. Condens. Matter 2022, 34, 464002. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Unified description of electronic orderings and cross correlations by complete multipole representation. J. Phys. Soc. Jpn. 2024, 93, 072001. [Google Scholar] [CrossRef]
- Popov, Y.F.; Kadomtseva, A.; Belov, D.; Vorob’ev, G.; Zvezdin, A. Magnetic-field-induced toroidal moment in the magnetoelectric Cr2O3. J. Exp. Theor. Phys. Lett. 1999, 69, 330–335. [Google Scholar] [CrossRef]
- Schmid, H. On ferrotoroidics and electrotoroidic, magnetotoroidic and piezotoroidic effects. Ferroelectrics 2001, 252, 41–50. [Google Scholar] [CrossRef]
- Ederer, C.; Spaldin, N.A. Towards a microscopic theory of toroidal moments in bulk periodic crystals. Phys. Rev. B 2007, 76, 214404. [Google Scholar] [CrossRef]
- Yanase, Y. Magneto-Electric Effect in Three-Dimensional Coupled Zigzag Chains. J. Phys. Soc. Jpn. 2014, 83, 014703. [Google Scholar] [CrossRef]
- Thöle, F.; Spaldin, N.A. Magnetoelectric multipoles in metals. Philos. Trans. R. Soc. A 2018, 376, 20170450. [Google Scholar] [CrossRef] [PubMed]
- Yanagi, Y.; Hayami, S.; Kusunose, H. Manipulating the magnetoelectric effect: Essence learned from Co4Nb2O9. Phys. Rev. B 2018, 97, 020404. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent odd-parity multipoles and magnetoelectric effects on a diamond structure: Implication for the 5d transition metal oxides AOsO4 (A = K, Rb, and Cs). Phys. Rev. B 2018, 97, 024414. [Google Scholar] [CrossRef]
- Miyahara, S.; Furukawa, N. Nonreciprocal Directional Dichroism and Toroidalmagnons in Helical Magnets. J. Phys. Soc. Jpn. 2012, 81, 023712. [Google Scholar] [CrossRef]
- Miyahara, S.; Furukawa, N. Theory of magneto-optical effects in helical multiferroic materials via toroidal magnon excitation. Phys. Rev. B 2014, 89, 195145. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Asymmetric Magnon Excitation by Spontaneous Toroidal Ordering. J. Phys. Soc. Jpn. 2016, 85, 053705. [Google Scholar] [CrossRef]
- Okuma, N. Nonreciprocal superposition state in antiferromagnetic optospintronics. Phys. Rev. B 2019, 99, 094401. [Google Scholar] [CrossRef]
- Matsumoto, T.; Hayami, S. Nonreciprocal magnons due to symmetric anisotropic exchange interaction in honeycomb antiferromagnets. Phys. Rev. B 2020, 101, 224419. [Google Scholar] [CrossRef]
- Sawada, K.; Nagaosa, N. Optical Magnetoelectric Effect in Multiferroic Materials: Evidence for a Lorentz Force Acting on a Ray of Light. Phys. Rev. Lett. 2005, 95, 237402. [Google Scholar] [CrossRef]
- Kawaguchi, H.; Tatara, G. Effective Hamiltonian theory for nonreciprocal light propagation in magnetic Rashba conductor. Phys. Rev. B 2016, 94, 235148. [Google Scholar] [CrossRef]
- Watanabe, H.; Yanase, Y. Nonlinear electric transport in odd-parity magnetic multipole systems: Application to Mn-based compounds. Phys. Rev. Res. 2020, 2, 043081. [Google Scholar] [CrossRef]
- Watanabe, H.; Yanase, Y. Photocurrent response in parity-time symmetric current-ordered states. Phys. Rev. B 2021, 104, 024416. [Google Scholar] [CrossRef]
- Suzuki, Y. Tunneling spin current in systems with spin degeneracy. Phys. Rev. B 2022, 105, 075201. [Google Scholar] [CrossRef]
- Yatsushiro, M.; Oiwa, R.; Kusunose, H.; Hayami, S. Analysis of model-parameter dependences on the second-order nonlinear conductivity in -symmetric collinear antiferromagnetic metals with magnetic toroidal moment on zigzag chains. Phys. Rev. B 2022, 105, 155157. [Google Scholar] [CrossRef]
- Kondo, H.; Akagi, Y. Nonlinear magnon spin Nernst effect in antiferromagnets and strain-tunable pure spin current. Phys. Rev. Res. 2022, 4, 013186. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M.; Kusunose, H. Nonlinear spin Hall effect in -symmetric collinear magnets. Phys. Rev. B 2022, 106, 024405. [Google Scholar] [CrossRef]
- Wang, C.; Gao, Y.; Xiao, D. Intrinsic Nonlinear Hall Effect in Antiferromagnetic Tetragonal CuMnAs. Phys. Rev. Lett. 2021, 127, 277201. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, J.; Huang, Y.X.; Wu, W.; Sheng, X.L.; Xiao, C.; Yang, S.A. Intrinsic Second-Order Anomalous Hall Effect and Its Application in Compensated Antiferromagnets. Phys. Rev. Lett. 2021, 127, 277202. [Google Scholar] [CrossRef]
- Kirikoshi, A.; Hayami, S. Microscopic mechanism for intrinsic nonlinear anomalous Hall conductivity in noncollinear antiferromagnetic metals. Phys. Rev. B 2023, 107, 155109. [Google Scholar] [CrossRef]
- Folen, V.J.; Rado, G.T.; Stalder, E.W. Anisotropy of the Magnetoelectric Effect in Cr2O3. Phys. Rev. Lett. 1961, 6, 607–608. [Google Scholar] [CrossRef]
- Krotov, S.; Kadomtseva, A.; Popov, Y.F.; Zvezdin, A.; Vorob’ev, G.; Belov, D. Magnetoelectric interactions and induced toroidal ordering in Cr2O3. J. Magn. Magn. Mater. 2001, 226, 963–964. [Google Scholar] [CrossRef]
- Arima, T.; Jung, J.H.; Matsubara, M.; Kubota, M.; He, J.P.; Kaneko, Y.; Tokura, Y. Resonant magnetoelectric X-ray scattering in GaFeO3: Observation of ordering of toroidal moments. J. Phys. Soc. Jpn. 2005, 74, 1419–1422. [Google Scholar] [CrossRef]
- Staub, U.; Bodenthin, Y.; Piamonteze, C.; García-Fernández, M.; Scagnoli, V.; Garganourakis, M.; Koohpayeh, S.; Fort, D.; Lovesey, S.W. Parity- and time-odd atomic multipoles in magnetoelectric GaFeO3 as seen via soft x-ray Bragg diffraction. Phys. Rev. B 2009, 80, 140410. [Google Scholar] [CrossRef]
- Staub, U.; Piamonteze, C.; Garganourakis, M.; Collins, S.P.; Koohpayeh, S.M.; Fort, D.; Lovesey, S.W. Ferromagnetic-type order of atomic multipoles in the polar ferrimagnetic GaFeO3. Phys. Rev. B 2012, 85, 144421. [Google Scholar] [CrossRef]
- Nie, Y.m. First-principles approach to investigate toroidal property of magnetoelectric multiferroic GaFeO3. J. Appl. Phys. 2016, 119. [Google Scholar] [CrossRef]
- Van Aken, B.B.; Rivera, J.P.; Schmid, H.; Fiebig, M. Observation of ferrotoroidic domains. Nature 2007, 449, 702–705. [Google Scholar] [CrossRef]
- Zimmermann, A.S.; Meier, D.; Fiebig, M. Ferroic nature of magnetic toroidal order. Nat. Commun. 2014, 5, 4796. [Google Scholar] [CrossRef]
- Fogh, E.; Zaharko, O.; Schefer, J.; Niedermayer, C.; Holm-Dahlin, S.; Sørensen, M.K.; Kristensen, A.B.; Andersen, N.H.; Vaknin, D.; Christensen, N.B.; et al. Dzyaloshinskii-Moriya interaction and the magnetic ground state in magnetoelectric LiCoPO4. Phys. Rev. B 2019, 99, 104421. [Google Scholar] [CrossRef]
- Tóth, B.; Kocsis, V.; Tokunaga, Y.; Taguchi, Y.; Tokura, Y.; Bordács, S. Imaging antiferromagnetic domains in LiCoPO4 via the optical magnetoelectric effect. Phys. Rev. B 2024, 110, L100405. [Google Scholar] [CrossRef]
- Wadley, P.; Novák, V.; Campion, R.; Rinaldi, C.; Martí, X.; Reichlová, H.; Železnỳ, J.; Gazquez, J.; Roldan, M.; Varela, M.; et al. Tetragonal phase of epitaxial room-temperature antiferromagnet CuMnAs. Nat. Commun. 2013, 4, 2322. [Google Scholar] [CrossRef] [PubMed]
- Wadley, P.; Howells, B.; Železnỳ, J.; Andrews, C.; Hills, V.; Campion, R.P.; Novák, V.; Olejník, K.; Maccherozzi, F.; Dhesi, S.; et al. Electrical switching of an antiferromagnet. Science 2016, 351, 587–590. [Google Scholar] [CrossRef] [PubMed]
- Godinho, J.; Reichlová, H.; Kriegner, D.; Novák, V.; Olejník, K.; Kašpar, Z.; Šobáň, Z.; Wadley, P.; Campion, R.; Otxoa, R.; et al. Electrically induced and detected Néel vector reversal in a collinear antiferromagnet. Nat. Commun. 2018, 9, 4686. [Google Scholar] [CrossRef]
- Manchon, A.; Železný, J.; Miron, I.M.; Jungwirth, T.; Sinova, J.; Thiaville, A.; Garello, K.; Gambardella, P. Current-induced spin-orbit torques in ferromagnetic and antiferromagnetic systems. Rev. Mod. Phys. 2019, 91, 035004. [Google Scholar] [CrossRef]
- Mentink, S.A.M.; Drost, A.; Nieuwenhuys, G.J.; Frikkee, E.; Menovsky, A.A.; Mydosh, J.A. Magnetic Ordering and Frustration in Hexagonal UNi4B. Phys. Rev. Lett. 1994, 73, 1031–1034. [Google Scholar] [CrossRef]
- Oyamada, A.; Kondo, M.; Fukuoka, K.; Itou, T.; Maegawa, S.; Li, D.X.; Haga, Y. NMR studies of the partially disordered state in a triangular antiferromagnet UNi4B. J. Phys. Condens. Matter 2007, 19, 145246. [Google Scholar] [CrossRef]
- Saito, H.; Uenishi, K.; Miura, N.; Tabata, C.; Hidaka, H.; Yanagisawa, T.; Amitsuka, H. Evidence of a New Current-Induced Magnetoelectric Effect in a Toroidal Magnetic Ordered State of UNi4B. J. Phys. Soc. Jpn. 2018, 87, 033702. [Google Scholar] [CrossRef]
- Ota, K.; Shimozawa, M.; Muroya, T.; Miyamoto, T.; Hosoi, S.; Nakamura, A.; Homma, Y.; Honda, F.; Aoki, D.; Izawa, K. Zero-field current-induced Hall effect in ferrotoroidic metal. arXiv 2022, arXiv:2205.05555. [Google Scholar]
- Zhao, K.; Deng, H.; Chen, H.; Ross, K.A.; Petříček, V.; Günther, G.; Russina, M.; Hutanu, V.; Gegenwart, P. Realization of the kagome spin ice state in a frustrated intermetallic compound. Science 2020, 367, 1218–1223. [Google Scholar] [CrossRef]
- Li, N.; Huang, Q.; Yue, X.Y.; Guang, S.K.; Xia, K.; Wang, Y.Y.; Li, Q.J.; Zhao, X.; Zhou, H.D.; Sun, X.F. Low-temperature transport properties of the intermetallic compound HoAgGe with a kagome spin-ice state. Phys. Rev. B 2022, 106, 014416. [Google Scholar] [CrossRef]
- Zhao, K.; Tokiwa, Y.; Chen, H.; Gegenwart, P. Discrete degeneracies distinguished by the anomalous Hall effect in a metallic kagome ice compound. Nat. Phys. 2024, 20, 442–449. [Google Scholar] [CrossRef]
- Kirikoshi, A.; Hayami, S. Finite-q antiferrotoroidal and ferritoroidal order in a distorted kagome structure. Phys. Rev. B 2025, 111, L201112. [Google Scholar] [CrossRef]
- Schmid, H. Some symmetry aspects of ferroics and single phasemultiferroics. J. Phys. Condens. Matter 2008, 20, 434201. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Time-reversal switching responses in antiferromagnets. Phys. Rev. B 2023, 108, L140409. [Google Scholar] [CrossRef]
- Mook, A.; Neumann, R.R.; Johansson, A.; Henk, J.; Mertig, I. Origin of the magnetic spin Hall effect: Spin current vorticity in the Fermi sea. Phys. Rev. Res. 2020, 2, 023065. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M. Spin Conductivity Based on Magnetic Toroidal Quadrupole Hidden in Antiferromagnets. J. Phys. Soc. Jpn. 2022, 91, 063702. [Google Scholar] [CrossRef]
- Koizumi, H.; Yamasaki, Y.; Yanagihara, H. Quadrupole anomalous Hall effect in magnetically induced electron nematic state. Nat. Commun. 2023, 14, 8074. [Google Scholar] [CrossRef] [PubMed]
- Hayashida, T.; Matsumoto, K.; Kimura, T. Electric Field-Induced Nonreciprocal Directional Dichroism in a Time-Reversal-Odd Antiferromagnet. Adv. Mater. 2024, 37, 2414876. [Google Scholar] [CrossRef]
- Knight, K.S.; Khalyavin, D.D.; Manuel, P.; Bull, C.L.; McIntyre, P. Nuclear and magnetic structures of KMnF3 perovskite in the temperature interval 10 K–105 K. J. Alloy. Compd. 2020, 842, 155935. [Google Scholar] [CrossRef]
- Porter, D.G.; Granata, V.; Forte, F.; Di Matteo, S.; Cuoco, M.; Fittipaldi, R.; Vecchione, A.; Bombardi, A. Magnetic anisotropy and orbital ordering in Ca2RuO4. Phys. Rev. B 2018, 98, 125142. [Google Scholar] [CrossRef]
- Karigerasi, M.H.; Lam, B.H.; Avdeev, M.; Shoemaker, D.P. Two-step magnetic ordering into a canted state in ferrimagnetic monoclinic Mn3As2. J. Solid State Chem. 2021, 294, 121901. [Google Scholar] [CrossRef]
- Eriksson, T.; Bergqvist, L.; Nordblad, P.; Eriksson, O.; Andersson, Y. Structural and magnetic characterization of Mn3IrGe and Mn3Ir (Si1−xGex): Experiments and theory. J. Solid State Chem. 2004, 177, 4058–4066. [Google Scholar] [CrossRef]
- Li, M.R.; Retuerto, M.; Walker, D.; Sarkar, T.; Stephens, P.W.; Mukherjee, S.; Dasgupta, T.S.; Hodges, J.P.; Croft, M.; Grams, C.P.; et al. Magnetic-Structure-Stabilized Polarization in an Above-Room-Temperature Ferrimagnet. Angew. Chem. Int. Ed. 2014, 53, 10774. [Google Scholar] [CrossRef]
- Donnay, G.; Corliss, L.M.; Donnay, J.D.H.; Elliott, N.; Hastings, J.M. Symmetry of Magnetic Structures: Magnetic Structure of Chalcopyrite. Phys. Rev. 1958, 112, 1917–1923. [Google Scholar] [CrossRef]
- Oleksyn, O.; Schobinger-Papamantellos, P.; Ritter, C.; De Groot, C.; Buschow, K. Structure and magnetic ordering in the defect compound ErGe1.83. J. Alloys Compd. 1997, 252, 53–58. [Google Scholar] [CrossRef]
- Nirmala, R.; Morozkin, A.; Isnard, O.; Nigam, A. Understanding the magnetic ground state of rare-earth intermetallic compound Ce4Sb3: Magnetization and neutron diffraction studies. J. Magn. Magn. Mater. 2009, 321, 188–191. [Google Scholar] [CrossRef]
- Hlinka, J. Eight Types of Symmetrically Distinct Vectorlike Physical Quantities. Phys. Rev. Lett. 2014, 113, 165502. [Google Scholar] [CrossRef]
- Hlinka, J.; Privratska, J.; Ondrejkovic, P.; Janovec, V. Symmetry Guide to Ferroaxial Transitions. Phys. Rev. Lett. 2016, 116, 177602. [Google Scholar] [CrossRef]
- Jin, W.; Drueke, E.; Li, S.; Admasu, A.; Owen, R.; Day, M.; Sun, K.; Cheong, S.W.; Zhao, L. Observation of a ferro-rotational order coupled with second-order nonlinear optical fields. Nat. Phys. 2020, 16, 42–46. [Google Scholar] [CrossRef]
- Hayashida, T.; Uemura, Y.; Kimura, K.; Matsuoka, S.; Hagihala, M.; Hirose, S.; Morioka, H.; Hasegawa, T.; Kimura, T. Phase transition and domain formation in ferroaxial crystals. Phys. Rev. Mater. 2021, 5, 124409. [Google Scholar] [CrossRef]
- Hayashida, T.; Uemura, Y.; Kimura, K.; Matsuoka, S.; Morikawa, D.; Hirose, S.; Tsuda, K.; Hasegawa, T.; Kimura, T. Visualization of ferroaxial domains in an order-disorder type ferroaxial crystal. Nat. Commun. 2020, 11, 4582. [Google Scholar] [CrossRef] [PubMed]
- Yokota, H.; Hayashida, T.; Kitahara, D.; Kimura, T. Three-dimensional imaging of ferroaxial domains using circularly polarized second harmonic generation microscopy. Npj Quantum Mater. 2022, 7, 106. [Google Scholar] [CrossRef]
- Hasegawa, T.; Yoshida, W.; Nakamura, K.; Ogita, N.; Matsuhira, K. Raman Scattering Investigation of Structural Transition in Ca5Ir3O12. J. Phys. Soc. Jpn. 2020, 89, 054602. [Google Scholar] [CrossRef]
- Hanate, H.; Hasegawa, T.; Hayami, S.; Tsutsui, S.; Kawano, S.; Matsuhira, K. First Observation of Superlattice Reflections in the Hidden Order at 105 K of Spin–Orbit Coupled Iridium Oxide Ca5Ir3O12. J. Phys. Soc. Jpn. 2021, 90, 063702. [Google Scholar] [CrossRef]
- Hayami, S.; Tsutsui, S.; Hanate, H.; Nagasawa, N.; Yoda, Y.; Matsuhira, K. Cluster Toroidal Multipoles Formed by Electric-Quadrupole and Magnetic-Octupole Trimers: A Possible Scenario for Hidden Orders in Ca5Ir3O12. J. Phys. Soc. Jpn. 2023, 92, 033702. [Google Scholar] [CrossRef]
- Hanate, H.; Tsutsui, S.; Yajima, T.; Nakao, H.; Sagayama, H.; Hasegawa, T.; Matsuhira, K. Space-Group Determination of Superlattice Structure Due to Electric Toroidal Ordering in Ca5Ir3O12. J. Phys. Soc. Jpn. 2023, 92, 063601. [Google Scholar] [CrossRef]
- Xu, X.; Huang, F.T.; Admasu, A.S.; Kratochvílová, M.; Chu, M.W.; Park, J.G.; Cheong, S.W. Multiple ferroic orders and toroidal magnetoelectricity in the chiral magnet BaCoSiO4. Phys. Rev. B 2022, 105, 184407. [Google Scholar] [CrossRef]
- Cheong, S.W.; Lim, S.; Du, K.; Huang, F.T. Permutable SOS (symmetry operational similarity). Npj Quantum Mater. 2021, 6, 58. [Google Scholar] [CrossRef]
- Hayami, S.; Oiwa, R.; Kusunose, H. Electric Ferro-Axial Moment as Nanometric Rotator and Source of Longitudinal Spin Current. J. Phys. Soc. Jpn. 2022, 91, 113702. [Google Scholar] [CrossRef]
- Cheong, S.W.; Huang, F.T.; Kim, M. Linking emergent phenomena and broken symmetries through one-dimensional objects and their dot/cross products. Rep. Prog. Phys. 2022, 85, 124501. [Google Scholar] [CrossRef]
- Nasu, J.; Hayami, S. Antisymmetric thermopolarization by electric toroidicity. Phys. Rev. B 2022, 105, 245125. [Google Scholar] [CrossRef]
- Roy, A.; Guimarães, M.H.D.; Sławińska, J. Unconventional spin Hall effects in nonmagnetic solids. Phys. Rev. Mater. 2022, 6, 045004. [Google Scholar] [CrossRef]
- Inda, A.; Hayami, S. Nonlinear Transverse Magnetic Susceptibility under Electric Toroidal Dipole Ordering. J. Phys. Soc. Jpn. 2023, 92, 043701. [Google Scholar] [CrossRef]
- Gallego, S.V.; Perez-Mato, J.M.; Elcoro, L.; Tasci, E.S.; Hanson, R.M.; Momma, K.; Aroyo, M.I.; Madariaga, G. MAGNDATA: Towards a database of magnetic structures. I. The commensurate case. J. Appl. Crystallogr. 2016, 49, 1750–1776. [Google Scholar] [CrossRef]
- Kusunose, H.; Oiwa, R.; Hayami, S. Complete Multipole Basis Set for Single-Centered Electron Systems. J. Phys. Soc. Jpn. 2020, 89, 104704. [Google Scholar] [CrossRef]
- Yatsushiro, M.; Kusunose, H.; Hayami, S. Multipole classification in 122 magnetic point groups for unified understanding of multiferroic responses and transport phenomena. Phys. Rev. B 2021, 104, 054412. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous parity breaking in spin-orbital coupled systems. Phys. Rev. B 2014, 90, 081115. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent spin-valley-orbital physics by spontaneous parity breaking. J. Phys. Condens. Matter 2016, 28, 395601. [Google Scholar] [CrossRef]
- Suzuki, M.T.; Koretsune, T.; Ochi, M.; Arita, R. Cluster multipole theory for anomalous Hall effect in antiferromagnets. Phys. Rev. B 2017, 95, 094406. [Google Scholar] [CrossRef]
- Suzuki, M.T.; Ikeda, H.; Oppeneer, P.M. First-principles theory of magnetic multipoles in condensed matter systems. J. Phys. Soc. Jpn. 2018, 87, 041008. [Google Scholar] [CrossRef]
- Kusunose, H.; Oiwa, R.; Hayami, S. Symmetry-adapted modeling for molecules and crystals. Phys. Rev. B 2023, 107, 195118. [Google Scholar] [CrossRef]
- Solana-Madruga, E.; Dos santos García, A.; Arévalo-López, A.; Ávila-Brande, D.; Ritter, C.; Attfield, J.; Sáez-Puche, R. High pressure synthesis of polar and non-polar cation-ordered polymorphs of Mn2ScSbO6. Dalton Trans. 2015, 44, 20441–20448. [Google Scholar] [CrossRef]
- Boehm, M.; Roessli, B.; Schefer, J.; Wills, A.S.; Ouladdiaf, B.; Lelièvre-Berna, E.; Staub, U.; Petrakovskii, G.A. Complex magnetic ground state of CuB2O4. Phys. Rev. B 2003, 68, 024405. [Google Scholar] [CrossRef]
- Moron, M.C.; Palacio, F.; Rodríguez-Carvajal, J. Crystal and magnetic structures of RbMnF4 and KMnF4 investigated by neutron powder diffraction: The relationship between structure and magnetic properties in the Mn3+ layered perovskites AMnF4 (A= Na, K, Rb, Cs). J. Phys. Condens. Matter 1993, 5, 4909. [Google Scholar] [CrossRef]
- Reehuis, M.; Ulrich, C.; Pattison, P.; Ouladdiaf, B.; Rheinstädter, M.C.; Ohl, M.; Regnault, L.P.; Miyasaka, M.; Tokura, Y.; Keimer, B. Neutron diffraction study of YVO3, NdVO3, and TbVO3. Phys. Rev. B 2006, 73, 094440. [Google Scholar] [CrossRef]
- Rousse, G.; Rodríguez-Carvajal, J.; Wurm, C.; Masquelier, C. A neutron diffraction study of the antiferromagnetic diphosphate LiFeP2O7. Solid State Sci. 2002, 4, 973–978. [Google Scholar] [CrossRef]
- Fernández-Díaz, M.T.; Alonso, J.A.; Martínez-Lope, M.J.; Casais, M.T.; García-Muñoz, J.L. Magnetic structure of the HoNiO3 perovskite. Phys. Rev. B 2001, 64, 144417. [Google Scholar] [CrossRef]
- Khalyavin, D.D.; Manuel, P.; Hatnean, M.C.; Petrenko, O.A. Fragile ground state and rigid field-induced structures in the zigzag ladder compound BaDy2O4. Phys. Rev. B 2021, 103, 134434. [Google Scholar] [CrossRef]
- Liu, X.; Taddei, K.M.; Li, S.; Liu, W.; Dhale, N.; Kadado, R.; Berman, D.; Cruz, C.D.; Lv, B. Canted antiferromagnetism in the quasi-one-dimensional iron chalcogenide BaFe2Se4. Phys. Rev. B 2020, 102, 180403. [Google Scholar] [CrossRef]
- Solana-Madruga, E.; Ritter, C.; Aguilar-Maldonado, C.; Mentré, O.; Attfield, J.P.; Arévalo-López, Á.M. Mn3MnNb2O9: High-pressure triple perovskite with 1: 2 B-site order and modulated spins. Chem. Commun. 2021, 57, 8441–8444. [Google Scholar] [CrossRef]
- Li, M.R.; Adem, U.; McMitchell, S.R.; Xu, Z.; Thomas, C.I.; Warren, J.E.; Giap, D.V.; Niu, H.; Wan, X.; Palgrave, R.G.; et al. A polar corundum oxide displaying weak ferromagnetism at room temperature. J. Am. Chem. Soc. 2012, 134, 3737–3747. [Google Scholar] [CrossRef] [PubMed]
- Kautzsch, L.; Georgescu, A.B.; Puggioni, D.; Kent, G.; Taddei, K.M.; Reilly, A.; Seshadri, R.; Rondinelli, J.M.; Wilson, S.D. Canted antiferromagnetism in polar MnSiN2 with high Néel temperature. Phys. Rev. Mater. 2023, 7, 104406. [Google Scholar] [CrossRef]
- Favre, V.Y.; Tucker, G.S.; Ritter, C.; Sibille, R.; Manuel, P.; Frontzek, M.D.; Kriener, M.; Yang, L.; Berger, H.; Magrez, A.; et al. Ferrimagnetic 120∘ magnetic structure in Cu2OSO4. Phys. Rev. B 2020, 102, 094422. [Google Scholar] [CrossRef]
- Plumier, R.; Sougi, M.; Saint-James, R. Neutron-diffraction reinvestigation of NiCO3. Phys. Rev. B 1983, 28, 4016–4020. [Google Scholar] [CrossRef]
- May, A.F.; Liu, Y.; Calder, S.; Parker, D.S.; Pandey, T.; Cakmak, E.; Cao, H.; Yan, J.; McGuire, M.A. Magnetic order and interactions in ferrimagnetic Mn3Si2Te6. Phys. Rev. B 2017, 95, 174440. [Google Scholar] [CrossRef]
- Markkula, M.; Arévalo-López, A.M.; Attfield, J.P. Field-induced spin orders in monoclinic CoV2O6. Phys. Rev. B 2012, 86, 134401. [Google Scholar] [CrossRef]
- Rousse, G.; Rodriguez-Carvajal, J.; Patoux, S.; Masquelier, C. Magnetic structures of the triphylite LiFePO4 and of its delithiated form FePO4. Chem. Mater. 2003, 15, 4082–4090. [Google Scholar] [CrossRef]
- Lu, K.; Sapkota, D.; DeBeer-Schmitt, L.; Wu, Y.; Cao, H.B.; Mannella, N.; Mandrus, D.; Aczel, A.A.; MacDougall, G.J. Canted antiferromagnetic order in the monoaxial chiral magnets V1/3TaS2 and V1/3NbS2. Phys. Rev. Mater. 2020, 4, 054416. [Google Scholar] [CrossRef]
- Yelon, W.B.; Cox, D.E. Magnetic Transitions in CsNiCl3. Phys. Rev. B 1973, 7, 2024–2027. [Google Scholar] [CrossRef]
- Gonzalo, J.A.; Cox, D.E.; Shirane, G. The Magnetic Structure of FeSb2O4. Phys. Rev. 1966, 147, 415–418. [Google Scholar] [CrossRef]
- Garca-Muoz, J.L.; Rodrguez-Carvajal, J.; Obradors, X.; Vallet-Reg, M.; González-Calbet, J.; Parras, M. Complex magnetic structures of the rare-earth cuprates R2Cu2O5 (R = Y,Ho,Er,Yb,Tm). Phys. Rev. B 1991, 44, 4716–4719. [Google Scholar] [CrossRef] [PubMed]
- Caignaert, V.; Pralong, V.; Hardy, V.; Ritter, C.; Raveau, B. Magnetic structure of CaBaCo4O7: Lifting of geometrical frustration towards ferrimagnetism. Phys. Rev. B 2010, 81, 094417. [Google Scholar] [CrossRef]
- Hutanu, V.; Sazonov, A.; Meven, M.; Murakawa, H.; Tokura, Y.; Bordács, S.; Kézsmárki, I.; Náfrádi, B. Determination of the magnetic order and the crystal symmetry in the multiferroic ground state of Ba2CoGe2O7. Phys. Rev. B 2012, 86, 104401. [Google Scholar] [CrossRef]
- Gitgeatpong, G.; Zhao, Y.; Avdeev, M.; Piltz, R.O.; Sato, T.J.; Matan, K. Magnetic structure and Dzyaloshinskii-Moriya interaction in the S = helical-honeycomb antiferromagnet α-Cu2V2O7. Phys. Rev. B 2015, 92, 024423. [Google Scholar] [CrossRef]
- Garcia-Castro, A.C.; Ibarra-Hernandez, W.; Bousquet, E.; Romero, A.H. Direct Magnetization-Polarization Coupling in BaCuF4. Phys. Rev. Lett. 2018, 121, 117601. [Google Scholar] [CrossRef] [PubMed]
- Cockayne, E.; Levin, I.; Wu, H.; Llobet, A. Magnetic structure of bixbyite α-Mn2O3: A combined DFT+U and neutron diffraction study. Phys. Rev. B 2013, 87, 184413. [Google Scholar] [CrossRef]
- Lee, J.H.; Kratochvílová, M.; Cao, H.; Yamani, Z.; Kim, J.S.; Park, J.G.; Stewart, G.R.; Oh, Y.S. Unconventional critical behavior in the quasi-one-dimensional S = 1 chain NiTe2O5. Phys. Rev. B 2019, 100, 144441. [Google Scholar] [CrossRef]
- Warner, J.K.; Cheetham, A.K.; Cox, D.E.; Von Dreele, R.B. Valence contrast between iron sites in. alpha.-Fe2PO5: A comparative study by magnetic neutron and resonant x-ray powder diffraction. J. Am. Chem. Soc. 1992, 114, 6074–6080. [Google Scholar] [CrossRef]
- Brown, P.; Forsyth, J. A neutron diffraction study of weak ferromagnetism in nickel fluoride. J. Phys. C Solid State Phys. 1981, 14, 5171. [Google Scholar] [CrossRef]
- Calder, S.; Garlea, V.O.; McMorrow, D.F.; Lumsden, M.D.; Stone, M.B.; Lang, J.C.; Kim, J.W.; Schlueter, J.A.; Shi, Y.G.; Yamaura, K.; et al. Magnetically Driven Metal-Insulator Transition in NaOsO3. Phys. Rev. Lett. 2012, 108, 257209. [Google Scholar] [CrossRef]
- Plaza, I.; Palacios, E.; Bartolomé, J.; Rosenkranz, S.; Ritter, C.; Furrer, A. Neutron diffraction study of the magnetic ordered Nd3+ in NdCoO3 and NdInO3 below 1 K. Phys. B Condens. Matter 1997, 234, 632–634. [Google Scholar] [CrossRef]
- Ritter, C.; Ceretti, M.; Paulus, W. Determination of the magnetic structures in orthoferrite CeFeO3 by neutron powder diffraction: First order spin reorientation and appearance of an ordered Ce-moment. J. Phys. Condens. Matter 2021, 33, 215802. [Google Scholar] [CrossRef]
- Ritter, C.; Vilarinho, R.; Moreira, J.A.; Mihalik, M.; Mihalik, M.; Savvin, S. The magnetic structure of DyFeO3 revisited: Fe spin reorientation and Dy incommensurate magnetic order. J. Phys. Condens. Matter 2022, 34, 265801. [Google Scholar] [CrossRef] [PubMed]
- Podchezertsev, S.; Barrier, N.; Pautrat, A.; Suard, E.; Retuerto, M.; Alonso, J.A.; Fernandez-Diaz, M.T.; Rodríguez-Carvajal, J. Influence of Polymorphism on the Magnetic Properties of Co5TeO8 Spinel. Inorg. Chem. 2021, 60, 13990–14001. [Google Scholar] [CrossRef] [PubMed]
- Lacorre, P.; Pannetier, J.; Fleischer, T.; Hoppe, R.; Ferey, G. Ordered magnetic frustration: XVI. Magnetic structure of CsCoF4 at 1.5 K. J. Solid State Chem. 1991, 93, 37–45. [Google Scholar] [CrossRef]
- Fruchart, D.; Bertaut, E.F. Magnetic studies of the metallic perovskite-type compounds of manganese. J. Phys. Soc. Jpn. 1978, 44, 781–791. [Google Scholar] [CrossRef]
- Garlea, V.O.; Jin, R.; Mandrus, D.; Roessli, B.; Huang, Q.; Miller, M.; Schultz, A.J.; Nagler, S.E. Magnetic and Orbital Ordering in the Spinel MnV2O4. Phys. Rev. Lett. 2008, 100, 066404. [Google Scholar] [CrossRef]
- Morosan, E.; Fleitman, J.A.; Huang, Q.; Lynn, J.W.; Chen, Y.; Ke, X.; Dahlberg, M.L.; Schiffer, P.; Craley, C.R.; Cava, R.J. Structure and magnetic properties of the Ho2Ge2O7 pyrogermanate. Phys. Rev. B 2008, 77, 224423. [Google Scholar] [CrossRef]
- Taddei, K.M.; Sanjeewa, L.; Kolis, J.W.; Sefat, A.S.; de la Cruz, C.; Pajerowski, D.M. Local-Ising-type magnetic order and metamagnetism in the rare-earth pyrogermanate Er2Ge2O7. Phys. Rev. Mater. 2019, 3, 014405. [Google Scholar] [CrossRef]
- Pajerowski, D.M.; Taddei, K.M.; Sanjeewa, L.D.; Savici, A.T.; Stone, M.B.; Kolis, J.W. Quantification of local Ising magnetism in rare-earth pyrogermanates Er2Ge2O7 and Yb2Ge2O7. Phys. Rev. B 2020, 101, 014420. [Google Scholar] [CrossRef]
- Lappas, A.; Alexandrakis, V.; Giapintzakis, J.; Pomjakushin, V.; Prassides, K.; Schenck, A. Impurity-induced antiferromagnetic order in the Haldane-gap compound PbNi2-xMgxV2O8(x = 0.24). Phys. Rev. B 2002, 66, 014428. [Google Scholar] [CrossRef]
- Sale, M.; Xia, Q.; Avdeev, M.; Ling, C.D. Crystal and Magnetic Structures of Melilite-Type Ba2MnSi2O7. Inorg. Chem. 2019, 58, 4164–4172. [Google Scholar] [CrossRef] [PubMed]
- Dalmas de Réotier, P.; Marin, C.; Yaouanc, A.; Ritter, C.; Maisuradze, A.; Roessli, B.; Bertin, A.; Baker, P.J.; Amato, A. Long-range dynamical magnetic order and spin tunneling in the cooperative paramagnetic states of the pyrochlore analogous spinel antiferromagnets CdYb2X4 (X = S or Se). Phys. Rev. B 2017, 96, 134403. [Google Scholar] [CrossRef]
- Jauch, W.; Reehuis, M.; Schultz, A. γ-ray and neutron diffraction studies of CoF2: Magnetostriction, electron density and magnetic moments. Acta Crystallogr. A 2004, 60, 51–57. [Google Scholar] [CrossRef]
- Petit, S.; Lhotel, E.; Damay, F.; Boutrouille, P.; Forget, A.; Colson, D. Long-Range Order in the Dipolar XY Antiferromagnet Er2Sn2O7. Phys. Rev. Lett. 2017, 119, 187202. [Google Scholar] [CrossRef]
- Bos, J.W.G.; Colin, C.V.; Palstra, T.T.M. Magnetoelectric coupling in the cubic ferrimagnet Cu2OSeO3. Phys. Rev. B 2008, 78, 094416. [Google Scholar] [CrossRef]
- Kurbakov, A.I.; Susloparova, A.E.; Pomjakushin, V.Y.; Skourski, Y.; Vavilova, E.L.; Vasilchikova, T.M.; Raganyan, G.V.; Vasiliev, A.N. Commensurate helicoidal order in the triangular layered magnet Na2MnTeO6. Phys. Rev. B 2022, 105, 064416. [Google Scholar] [CrossRef]
- Volkova, O.S.; Mazurenko, V.V.; Solovyev, I.V.; Deeva, E.B.; Morozov, I.V.; Lin, J.Y.; Wen, C.K.; Chen, J.M.; Abdel-Hafiez, M.; Vasiliev, A.N. Noncollinear ferrimagnetic ground state in Ni(NO3)2. Phys. Rev. B 2014, 90, 134407. [Google Scholar] [CrossRef]
- Amano Patino, M.; Denis Romero, F.; Goto, M.; Saito, T.; Orlandi, F.; Manuel, P.; Szabó, A.; Kayser, P.; Hong, K.H.; Alharbi, K.N.; et al. Multi-k spin ordering in CaFe3Ti4O12 stabilized by spin-orbit coupling and further-neighbor exchange. Phys. Rev. Res. 2021, 3, 043208. [Google Scholar] [CrossRef]
- Li, F.; Pomjakushin, V.; Mazet, T.; Sibille, R.; Malaman, B.; Yadav, R.; Keller, L.; Medarde, M.; Conder, K.; Pomjakushina, E. Revisiting the magnetic structure and charge ordering in La1/3Sr2/3FeO3 by neutron powder diffraction and Mössbauer spectroscopy. Phys. Rev. B 2018, 97, 174417. [Google Scholar] [CrossRef]
- Hao, X.F.; Stroppa, A.; Picozzi, S.; Filippetti, A.; Franchini, C. Exceptionally large room-temperature ferroelectric polarization in the PbNiO3 multiferroic nickelate: First-principles study. Phys. Rev. B 2012, 86, 014116. [Google Scholar] [CrossRef]
- Lee, M.; Choi, E.S.; Huang, X.; Ma, J.; Dela Cruz, C.R.; Matsuda, M.; Tian, W.; Dun, Z.L.; Dong, S.; Zhou, H.D. Magnetic phase diagram and multiferroicity of Ba3MnNb2O9: A spin-52 triangular lattice antiferromagnet with weak easy-axis anisotropy. Phys. Rev. B 2014, 90, 224402. [Google Scholar] [CrossRef]
- Zvereva, E.A.; Raganyan, G.V.; Vasilchikova, T.M.; Nalbandyan, V.B.; Gafurov, D.A.; Vavilova, E.L.; Zakharov, K.V.; Koo, H.J.; Pomjakushin, V.Y.; Susloparova, A.E.; et al. Hidden magnetic order in the triangular-lattice magnet Li2MnTeO6. Phys. Rev. B 2020, 102, 094433. [Google Scholar] [CrossRef]
- Zhou, J.S.; Alonso, J.A.; Muoñz, A.; Fernández-Díaz, M.T.; Goodenough, J.B. Magnetic Structure of LaCrO3 Perovskite under High Pressure from In Situ Neutron Diffraction. Phys. Rev. Lett. 2011, 106, 057201. [Google Scholar] [CrossRef] [PubMed]
- Ding, L.; Xu, X.; Jeschke, H.O.; Bai, X.; Feng, E.; Alemayehu, A.S.; Kim, J.; Huang, F.T.; Zhang, Q.; Ding, X.; et al. Field-tunable toroidal moment in a chiral-lattice magnet. Nat. Commun. 2021, 12, 5339. [Google Scholar] [CrossRef]
- Muñoz, A.; Alonso, J.A.; Martínez-Lope, M.J.; Casáis, M.T.; Martínez, J.L.; Fernández-Díaz, M.T. Magnetic structure of hexagonal RMnO3(R = Y, Sc): Thermal evolution from neutron powder diffraction data. Phys. Rev. B 2000, 62, 9498–9510. [Google Scholar] [CrossRef]
- Leblanc, M.; De Pape, R.; Ferey, G.; Pannetier, J. Ordered magnetic frustration–V. Antiferromagnetic structure of the hexagonal bronzoid HTB FeF3; Comparison with the non frustrated rhombohedral form. Solid State Commun. 1986, 58, 171–176. [Google Scholar] [CrossRef]
- Munoz, A.; Alonso, J.; Martínez-Lope, M.; Casáis, M.; Martínez, J.; Fernandez-Diaz, M. Evolution of the magnetic structure of hexagonal HoMnO3 from neutron powder diffraction data. Chem. Mater. 2001, 13, 1497–1505. [Google Scholar] [CrossRef]
- Ma, J.; Kamiya, Y.; Hong, T.; Cao, H.B.; Ehlers, G.; Tian, W.; Batista, C.D.; Dun, Z.L.; Zhou, H.D.; Matsuda, M. Static and Dynamical Properties of the Spin-1/2 Equilateral Triangular-Lattice Antiferromagnet Ba3CoSb2O9. Phys. Rev. Lett. 2016, 116, 087201. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Essential role of the anisotropic magnetic dipole in the anomalous Hall effect. Phys. Rev. B 2021, 103, L180407. [Google Scholar] [CrossRef]
- Inda, A.; Hayami, S. Emergent cross-product-type spin-orbit coupling under ferroaxial ordering. Phys. Rev. B 2025, 111, L041104. [Google Scholar] [CrossRef]
- Sekine, D.; Sato, T.; Tokunaga, Y.; Arima, T.h.; Matsubara, M. Second harmonic imaging of antiferromagnetic domains and confirmation of absence of ferroaxial twins in MnTiO3. Phys. Rev. Mater. 2024, 8, 064406. [Google Scholar] [CrossRef]


| MPG | MTQ | ETD | Materials | |
|---|---|---|---|---|
| #1 | 1 | , , , , | , , | Mn2ScSbO6 [92], CuB2O4 [93] |
| #3 | , , , , | , , | RbMnF4 [94], YVO3 [95] | |
| #6 | 2 | , , | LiFeP2O7 [96], HoNiO3 [97] | |
| #8 | , | BaDy2O4 [98], BaFe2Se4 [99] | ||
| #9 | m | , , | Mn4Nb2O9 [100] | |
| #11 | , | ScFeO3 [101], MnSiN2 [102] | ||
| #12 | , , | Cu2OSO4 [103], NiCO3 [104] | ||
| #16 | , | Mn3Ti2Te6 [105], CoV2O6 [106] | ||
| #17 | 222 | , | FePO4 [107] | |
| #19 | VNb3S6 [108], CsNiCl3 [109] | |||
| #20 | , | FeSb2O4 [110], Er2Cu2O5 [111] | ||
| #22 | CaBaCo4O7 [112], Ba2CoGe2O7 [113] | |||
| #23 | -Cu2V2O7 [114], BaCuF4 [115] | |||
| #24 | , | -Mn2O3 [116], NiTe2O5 [117], Fe2PO5 [118] | ||
| #27 | NiF2 [119], NaOsO3 [120], YFeO3 ( Ce, Nd, Dy) [121,122,123] | |||
| #29 | 4 | Ce5TeO8 [124] | ||
| #31 | , | |||
| #32 | ||||
| #34 | , | CsCoF4 † [125] | ||
| #35 | Mn3CuN [126], MnV2O4 [127] | |||
| #37 | , | |||
| #40 | 422 | Ho2Ge2O7 † [128] | ||
| #42 | Er2Ge2O7 [129,130] | |||
| #44 | ||||
| #46 | PbNi1.76Mg0.24V2O8 [131] | |||
| #48 | Ba2MnSi2O7 [132], CuFeS2 † [64] | |||
| #50 | ||||
| #51 | Ce4Sb3 † [66] | |||
| #53 | CdYb2S4 † [133], KMnF3 [59] | |||
| #56 | CoF2 † [134], Er2Sn2O7 [135] | |||
| #60 | 3 | Cu2OSeO3 [136], Na2MnTeO6 [137] | ||
| #62 | NiN2O6 [138], CaFe3Ti4O12 [139] | |||
| #65 | 32 | La0.33Sr0.67FeO3 [140] | ||
| #68 | PbNiO3 [141], Ba3MnNb2O9 † [142] | |||
| #71 | Li2MnTeO6 [143], LaCrO3 [144] | |||
| #76 | 6 | BaCoSiO4 [145], ScMnO3 [146] | ||
| #79 | ||||
| #82 | FeF3 [147] | |||
| #87 | 622 | |||
| #91 | HoMnO3 [148], YMnO3 [146] | |||
| #95 | Ba3CoSb2O9 [149] | |||
| #100 |
| MTQ | |||
|---|---|---|---|
| – | |||
| – | |||
| – | |||
| – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayami, S. Field-Induced Ferroaxiality in Antiferromagnets with Magnetic Toroidal Quadrupole. Condens. Matter 2025, 10, 35. https://doi.org/10.3390/condmat10020035
Hayami S. Field-Induced Ferroaxiality in Antiferromagnets with Magnetic Toroidal Quadrupole. Condensed Matter. 2025; 10(2):35. https://doi.org/10.3390/condmat10020035
Chicago/Turabian StyleHayami, Satoru. 2025. "Field-Induced Ferroaxiality in Antiferromagnets with Magnetic Toroidal Quadrupole" Condensed Matter 10, no. 2: 35. https://doi.org/10.3390/condmat10020035
APA StyleHayami, S. (2025). Field-Induced Ferroaxiality in Antiferromagnets with Magnetic Toroidal Quadrupole. Condensed Matter, 10(2), 35. https://doi.org/10.3390/condmat10020035






