Abstract
We studied relaxation processes in heavily doped two-dimensional Dirac systems associated with electron scattering by acoustic and optical phonons and by static disorder. The frequency dependence of the real and imaginary parts of the relaxation function is calculated for different temperatures. The two-component low-frequency dynamical conductivity is found to be strongly dependent on temperature. At low temperatures, the imaginary part of the zero-frequency relaxation function and the DC resistivity are characterized by the scaling law with the exponent x between 2.5 and 3.
1. Introduction
The Bethe–Salpether equations represent the most accurate way to describe properties of electron-hole pairs created in solids by external electromagnetic fields [1,2]. It is well-known that the intraband Bethe–Salpether equation can be easily transformed into a finite-temperature quantum transport equation (QTE) [3]. In this finite-temperature diagrammatic approach, the electron–hole pair self-energy is a function of two Matsubara frequencies and two wave vectors. The dependence on the external wave vector can be neglected, and, in the leading approximation, the internal Matsubara frequency can be replaced by an appropriate energy scale. After the usual analytical continuation procedure [1,4], this leads to a wave-vector- and frequency-dependent electron–hole pair self-energy , which is usually called the intraband memory function.
In the present analysis, we use an alternative approach to determine the structure of the intraband memory function and the related intraband dynamical and DC conductivity. This approach is a simple generalization of the self-consistent random phase approximation (RPA) equation of motion [5,6] to the case where conduction electrons are scattered by static disorder and/or by phonons [7]. In such an RPA-based quantum transport equation, plays a role of relaxation function, which is a complex function of frequency. The most important advantage of this approach is that, in any order of perturbation theory for , this approach treats single-electron self-energy contributions and the corresponding vertex corrections on an equal footing. Therefore, this equation can help us to better understand the role of vertex corrections and to emphasize the differences between the results obtained by using gauge-invariant approximations and the results obtained by widely used gauge-noninvariant methods [8,9,10,11] in which vertex corrections are neglected.
The present electron–phonon system consists of conduction electrons in the heavily doped upper band of the two-dimensional (2D) massless Dirac model, in-plane Debye acoustic phonons, and in-plane Einstein optical phonons. The electrons are assumed to be scattered by static disorder as well. The electronic system is in interaction with external transverse electromagnetic fields. At that doping level, the effective number of conduction electrons is temperature-independent and consists only of intraband contributions [12]. As a result, the temperature dependence of the dynamical and DC conductivity originates from the temperature dependence of the relaxation function in question, the intraband memory function .
2. Intraband Quantum Transport Equation and Intraband Conductivity Formula
In the RPA-based intraband quantum transport equation [3,5,6,7], the starting point is the equation of motion for the expectation value of the density operator , . This equation can be shown in the following form:
Here, is the electron creation operator in the band labeled by the band index L, is the momentum distribution function, is the intraband dipole vertex function, is the intraband current vertex function, and is the Fourier transform of the macroscopic electric field . Finally, and are useful abbreviations.
For longitudinal external fields, it is common to take into consideration only the long-range part of nonretarded electron–electron interactions through the RPA series of diagrams and neglect all scattering processes. In this case, we obtain , in Equation (1), with replaced by . This form of the self-consistent equation for is the well-known textbook result [5,6]. The most singular RPA contributions in powers of are present here through the screened scalar potential .
The first important advantage of this approach is that it is gauge-invariant. This means that the longitudinal macroscopic electric field in Equation (1) can be shown either in terms of the screened scalar potential or in terms of the screened vector potential , . It is also easily seen that the coupling of external transverse electromagnetic fields to conduction electrons leads to the same self-consistent equation for the expectation value . In this case, is described in terms of the transverse vector potential , . The gauge invariance also means that the induced intraband charge and current densities obtained in this way satisfy the charge continuity equation, at least on average. The second advantage is that at least two single-electron self-energy contributions to are treated on an equal footing with the corresponding vertex corrections in a way consistent with the Ward identity relations [13]. Two single-electron self-energy contributions can be illustrated by the and Feynman diagrams in Figure 1 and the corresponding vertex corrections by the diagram. They are given, respectively, by the contributions in Equation (2) associated with the term 1 and the term in the brackets .
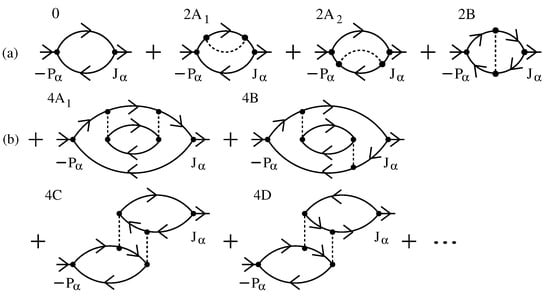
Figure 1.
The expansion of the current–dipole correlation function in powers of [3,13]. The solid/dashed lines illustrate the bare electron–phonon propagators. (a) The first two contributions ( and ) represent two self-energy contributions and the last one () the corresponding vertex correction. (b) The first quartet of contributions consists of one self-energy term and three terms with vertex corrections.
In most cases of interest, the low-energy physics is completely described in terms of the induced intraband charge and/or current densities (heavily doped 2D Dirac systems being an example). In the leading approximation, it is convenient to retain in the scattering Hamiltonian only processes in which the electron does not change the band when it is scattered by phonons, , or by static disorder, (as usual in perturbation theory, the parameter is introduced to keep track of the number of times the single-particle perturbation enters). For the electron–phonon coupling functions, we assume that , . We use a similar assumption for the scattering by static disorder, .
The contributions to that are second order in the perturbation parameter are given by
with replaced by . Here, is the electron dispersion, is the electron group velocity, is the phonon frequency, is the Bose–Einstein distribution function, and is the Fermi–Dirac distribution function. In order to make the numerical calculations easier, the damping parameter will be taken to be of the order of 5 meV. It is easily seen that is nothing but the electron lifetime from the Hartree–Fock expression for , which includes electron scattering by static disorder in powers of to infinity [7]. This electron lifetime is present in the momentum distribution functions in Equation (1) as well. Therefore, in the present model for dynamical conductivity, the scattering by static disorder is presented by two phenomenological parameters, and .
For simplicity, in numerical calculations, we consider the electron scattering either by in-plane acoustic or in-plane optical phonons from a single phonon branch. We use the Debye and Einstein models for the dispersions of acoustic and optical phonons, respectively, , . Similarly, the corresponding electron–phonon coupling functions are assumed to be and (a is the length of the primitive vector in the 2D hexagonal Bravais lattice, is the averaged sound velocity, and is the sound velocity given in units of eV). The specific values of and used below are in agreement with the ab-initio results in graphene [11]. The values of and are chosen in such a way to give the intraband relaxation rate meV at room temperature, found in the heavily doped Dirac semimetal TlBiSSe [12].
In the QTE approach, the intraband dynamical conductivity is given by the current–dipole conductivity formula [3]
When the vertex corrections in are neglected [14], this expression reduces to the result of the widely used current–current Kubo approach [8,9,10,11].
It is important also to recall that the intraband conductivity tensor is, by definition, a complex function of both wave vector and frequency. In the current–dipole Kubo aprroach, the result for is given by Equation (3) with replaced by [13]. The Drude limit, used in the present analysis, corresponds to in . On the other hand, for , we obtain the Thomas–Fermi expression for in the leading approximation. However, to obtain a more detailed description of the latter limit, one usually uses the approach presented in Ref. [15].
In systems with isotropic or nearly isotropic Fermi surfaces, the relaxation function can be replaced by its average over the Fermi surface . The result is the well-known generalized Drude formula [16]
with
representing the effective number of charge carriers. In the isotropic single-band case, the memory function is given by Equation (2), calculated at an arbitrary point on the Fermi surface (, hereafter).
3. Comparison with Other Work
The right-hand-side expression in Equation (4) represents the high-energy expansion of the generalized Drude formula in powers of . The and contributions to can be represented by the Feynman diagrams shown in Figure 1a. They can be calculated either by using the usual finite-temperature perturbation theory [1,4] or by using the self-consistent RPA approach. In the Hartree–Fock scheme, the recollection of higher-order contributions to corresponds to the replacement of the bare electron propagators in the contributions by the renormalized propagators. This leads to
Here, and are the electron spectral function and the bare phonon spectral function, respectively. This approximation is also known as the approximation. Alternatively, it is possible to replace the bare phonon propagators in the contributions with the renormalized phonon propagators leading to the expression for ( diagrams in the figure).
Both of these two approximate expressions for are evidently incomplete. The and diagrams in Figure 1b are the two diagrams taken into account in the approach. According to the Ward identity relations, these two diagrams have to be treated together with the other two diagrams shown in the figure. For nonretarded electron–electron interactions, for example, this leads to the complete cancelation of the normal electron–electron scattering contributions to . This is the well-known result from semiclassical transport theory [5,13,17].
In the widely used current–current Kubo approach, the diagram is the only diagram taken into account. In this approach, the relaxation processes are described by Equation (6) with the term neglected. In the approximation, the product from Equation (6) is replaced by . All this means that the phenomenological parameter used in the numerical calculations below is related to the half-width of the electron (in the approximation) or phonon (in the approximation) spectral functions. In the approach, for electron scattering by static disorder, is expected to be nearly independent of both and T.
4. Intraband Memory Function in 2D Massless Dirac Systems
The memory function in Equation (4) is a complex function of frequency and temperature, with its real and imaginary parts, and , connected by the Kramers–Kronig relations. Before we present and in 2D massless Dirac systems for typical values of the model parameters, it is useful to show the zero-temperature result obtained in a closely related toy model, the weakly doped 2D Holstein model with a free-electron-like dispersion, where and . In this case, the contributions to and can be easily evaluated and shown in a closed analytical form [18].
It is important first to recall that in this model the vertex contributions to vanish for symmetry reasons. The result for at is represented in Figure 2a by the unit step function. The threshold energy for the absorption of energy of external electromagnetic fields is associated with the creation of one optical phonon and one zero-energy electron–hole pair (see Figure 1a). The real part , obtained by the Kramers–Kronig transformation, is characterized by the singular behavior in the vicinity of the threshold energy, and it is linear in for frequencies well below .
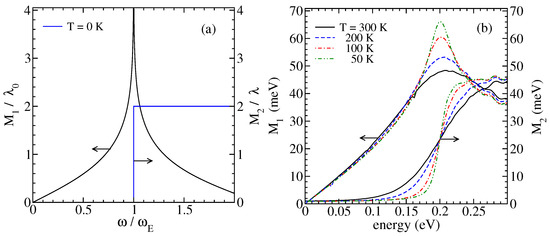
Figure 2.
The real and imaginary parts of the memory function as a function of temperature. (a) The 2D Holstein model with the parabolic electron dispersion ( is a convenient energy scale from Ref. [18]). (b) Heavily electron-doped 2D massless Dirac system, the electron scattering by optical phonons, for eV, eV, eV2, eV, and meV.
Figure 2b illustrates the temperature effects in and in a heavily electron-doped 2D Dirac system described by the electron dispersion
for the damping energies meV and , and for . The thermal energy and the damping energy have similar effects on both and at energies close to . The imaginary part is characterized by the isosbestic point at . For , increases with increasing (not shown in the figure), while it is nearly unaffected by the change in temperature. A similar dependence on temperature and on the interband relaxation rate is found for the interband dynamical conductivity of 2D Dirac systems. In this case, the vertex contributions to are negligible as well.
The electron scattering by acoustic phonons is much more interesting because it is responsible for the scaling laws for small- and small-T regimes of observed in optical and transport experiments. Figure 3a illustrates and in the temperature region between 50 K and room temperature, calculated again for a relatively large value of and for . The real part has the maximum at . This frequency is directly related with the Debye frequency and, consequently, with the sound velocity and the corresponding acoustic phonon bandwidth. The main difference with respect to Figure 2b is that the imaginary part possesses strong temperature dependence for .
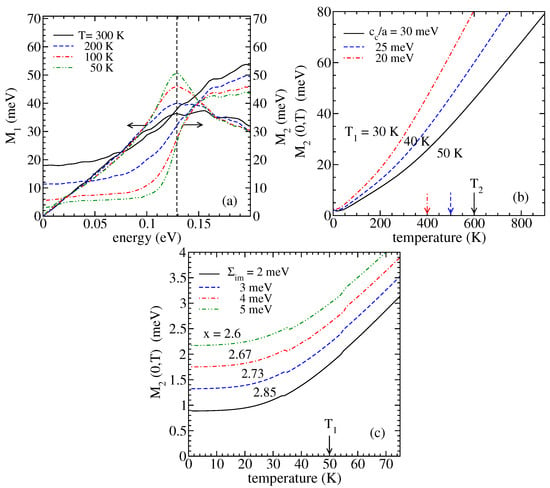
Figure 3.
(a) The real and imaginary parts of the memory function as a function of temperature in heavily electron-doped 2D Dirac systems for the electron scattering by acoustic phonons, for eV, eV, eV2, meV, and meV. (b) The temperature dependence of for three different values of , and 20 meV), and meV. (c) The temperature dependence of for four different values of (, and 5 meV), and meV. The other parameters in (b,c) are the same as in (a). The temperature is illustrated in (b) by arrows. At low temperatures, follows the scaling law . In (b), the exponent x is approximately equal to 2.7 for all three curves. The characteristic temperatures and are introduced in the text.
Figure 3b,c show the zero-frequency imaginary part as a function of temperature for different values of the sound velocity and the damping energy . For the relation between and T is linear, while for , can be shown in the following form: . The values of the fitting parameters a, b and x are summarized in Table 1 and Table 2. As shown in these figures, is characterized by the nonuniversal low-temperature scaling law. For example, for meV, the exponent is almost unaffected by the change in , while decreases with decreasing . Figure 3c illustrates the dependence of on for meV. In this case, the exponent x decreases with increasing (here K).


In order to understand the dependence of on temperature, it is important to notice that the expression (2) comprises two types of contributions. The contributions proportional to the Bose–Einstein distribution function represent the generalization of the intraband relaxation rate from the semiclassical transport theory [5,6] to the case where is replaced by . These contributions are responsible for the temperature dependence of . The contributions proportional to the Fermi–Dirac distribution function are absent in the semiclassical transport theory. In the present analysis, they lead to the redistribution of the intraband conductivity spectral weight. The intraband relaxation rate is affected by these processes in the way discussed below (see Equation (9)).
According to the semiclassical transport theory, at temperatures above , all acoustic phonons can be understood as classical lattice vibrations. In the 2D Dirac systems characterized by two Dirac cones (at the K and points in the band ), the value of , as well the value of , is very sensitive to the details in the acoustic phonon dispersions. This is a consequence of the fact that is proportional to q. Therefore, the main contribution to is expected to originate from the inter-cone scattering by the large-momentum acoustic phonons. The replacement of the Debye dispersion by that obtained by ab initio calculations is expected to shift the values of both and downwards. The resulting is expected to be close to the value K found in experiments performed on weakly doped graphene [19]. The presence of two Dirac cones in , with , leads here to finite values of the vertex corrections. However, these corrections are very small in comparison with the dominant single-electron self-energy contribution. The vertex corrections are expected to be significant in 3D and quasi-2D Dirac semimetals with a single Dirac cone, for both acoustic phonons and infrared-active optical phonons.
5. Intraband Dynamical Conductivity and DC Resistivity
It is well known [9,14] that the interband contribution to the dynamical conductivity plays an important role in understanding anomalies seen in experiments in weakly doped graphene [19,20] not only in low-frequency conductivity but also in DC conductivity. In weakly doped Dirac systems, the temperature effects originate from the temperature dependence of both the effective number of charge carriers and the relaxation rate [12]. In heavily doped Dirac systems, on the other hand, the interband contribution is well separated from the intraband contribution, and the redistribution of the total spectral weight between these two channels can be easily understood by using the relaxation-time approximation [3,14]. The present analysis is focused on an additional redistribution of the low-energy spectral weight in the intraband channel associated with the intraband electron scattering by acoustic and/or optical phonons.
The frequency dependence of is responsible for the redistribution of the intraband conductivity spectral weight over a large frequency range. At low temperatures and for the large enough coupling function , this leads to a two-component structure of the intraband conductivity. The first contribution is an effective ordinary Drude term and the second one is the corresponding mid-infrared term. The real part is usually expressed in terms of the dimensionless electron–phonon coupling function . In this notation, the effective ordinary Drude contribution reads as [7,16]
Here,
are, respectively, the reduced effective number of charge carriers and the corresponding intraband relaxation rate.
Figure 4 shows the intraband conductivity (4) in the heavily electron-doped 2D Dirac case calculated by using the memory function from Figure 3a. In this case, the mass enhancement factor is approximately equal to 1.33, leading to the reduction in the Drude spectral weight by a factor of . Lowering the temperature increases the low-frequency conductivity, and simultaneously the two-component structure is better seen in the mid-infrared part of the spectrum. This effect is clearly seen in different Dirac systems (the quasi-2D Dirac semimetal BaNiS2 is an example) [21].
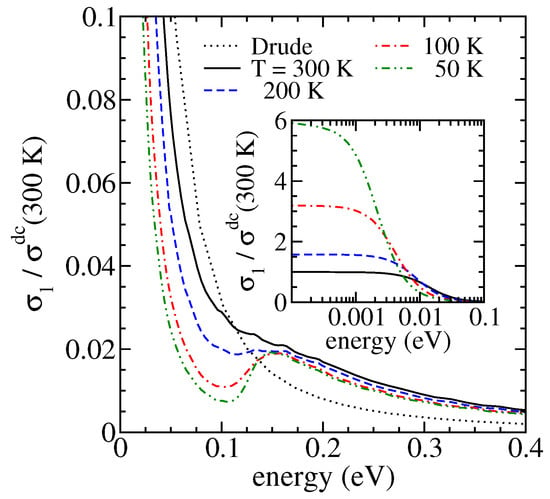
Figure 4.
The real part of the intraband dynamical conductivity as a function of temperature calculated by using from Figure 3a. The dotted line is the ordinary Drude conductivity for meV.
Finally, it should be recalled that the DC conductivity is given by
The effective mass enhancement factor cancels out in this expression. As a consequence, the imaginary part shown in Figure 3b,c also illustrates the DC resistivity multiplied by .
6. Discussion and Conclusions
Detailed ab initio studies of electron–phonon coupling in 2D Dirac systems revealed that electronic and lattice degrees of freedom can be described well by using the massive 2D Dirac model for conduction electrons and the Debye model for in-plane acoustic phonons [11,22]. The Dirac mass is zero in graphene, leading to linear dependence of the electron dispersion on k. In other systems (MgS2 is an example), it is quite large, resulting in a nearly parabolic dispersion [23]. The acoustic phonon bandwidth is found to be in the range between 20 meV (arsenene) and 100 meV (graphene) [11]. Similar ab initio studies show that the electron dispersions in the three-dimensional (3D) Dirac semimetals can be fitted well by the massive 3D Dirac model [24].
The RPA-based quantum transport equations can be used to study the dependence of the intraband dynamical conductivity and the DC resistivity on the model parameters in such 2D and 3D electron–phonon systems. The main advantage of the present approach over the widely used current–current approach is that all general requirements from the semiclassical transport equations [5] can be easily incorporated in the quantum transport equations (the complete cancelation of the normal contributions to the intraband relaxation rate originating from nonretarded electron–electron interactions being an example).
In this article, we show how the DC resistivity and the low-frequency dynamical conductivity depend on the acoustic phonon bandwidth in the case where the 2D electron dispersion is given beyond the Dirac-cone approximation. It is shown that the intraband relaxation rate depends on both the imaginary and real part of the memory function . The imaginary part, taken at , is responsible for the temperature dependence of through the contributions to that are proportional to . On the other hand, the slope of the real part, , related with the contributions proportional to , leads to the renormalization of both and the corresponding effective number of charge carriers . For example, for the Debye frequency of the order of 100 meV, the DC resistivity is linear for K, and it is characterized by the scaling law , , at K.
Author Contributions
Conceptualization, methodology and writing—original draft preparation, I.K.; investigation, formal analysis and writing—review and editing, I.K. and P.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the University of Zagreb Grant No. 20286570.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fetter, A.L.; Walecka, J.D. Quantum Theory of Many-Particle Systems; McGraw–Hill: London, UK, 1971. [Google Scholar]
- Ziman, J.M. Elements of Advanced Quantum Theory; Cambridge University Press: London, UK, 1988. [Google Scholar]
- Kupčić, I. General theory of intraband relaxation processes in heavily doped graphene. Phys. Rev. B 2015, 91, 205428. [Google Scholar] [CrossRef]
- Mahan, G.D. Many-Particle Physics; Plenum Press: New York, NY, USA, 1990. [Google Scholar]
- Pines, D.; Noziéres, P. The Theory of Quantum Liquids I; Addison-Wesley: New York, NY, USA, 1989. [Google Scholar]
- Platzman, P.M.; Wolff, P.A. Waves and Interactions in Solid State Plasmas; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Kupčić, I. Intraband memory function and memory-function conductivity formula in doped graphene. Phys. Rev. B 2017, 95, 035403. [Google Scholar] [CrossRef]
- Shon, N.H.; Ando, T. Quantum Transport in Two-Dimensional Graphite System. J. Phys. Soc. Jpn. 1998, 67, 2421. [Google Scholar] [CrossRef]
- Carbotte, J.P.; Nicol, E.J.; Sharapov, S.G. Effect of electron-phonon interaction on spectroscopies in graphene. Phys. Rev. B 2010, 81, 045419. [Google Scholar] [CrossRef]
- Tabert, C.J.; Carbotte, J.P.; Nicol, E.J. Optical and transport properties in three-dimensional Dirac and Weyl semimetals. Phys. Rev. B 2016, 93, 085426. [Google Scholar] [CrossRef]
- Girotto, N.; Novko, D. Dynamical renormalization of electron-phonon coupling in conventional superconductors. Phys. Rev. B 2023, 107, 064310. [Google Scholar] [CrossRef]
- Kupčić, I.; Kordić, J. Optical conductivity of anisotropic Dirac semimetals: The relaxation-time approximation. Phys. Rev. B 2024, 109, 045426. [Google Scholar] [CrossRef]
- Kupčić, I. Damping effects in doped graphene: The relaxation-time approximation. Phys. Rev. B 2014, 90, 205426. [Google Scholar] [CrossRef]
- Kupčić, I.; Nikšić, G.; Rukelj, Z.; Pelc, D. Effective numbers of charge carriers in doped graphene: Generalized Fermi liquid approach. Phys. Rev. B 2016, 94, 075434. [Google Scholar] [CrossRef]
- Dolgov, O.V.; Kirzhnits, D.A.; Maksimov, E.G. On an admissible sign of the static dielectric function of matter. Rev. Mod. Phys. 1981, 53, 81. [Google Scholar] [CrossRef]
- Götze, W.; Wölfle, P. Homogeneous Dynamical Conductivity of Simple Metals. Phys. Rev. B 1972, 6, 1226. [Google Scholar] [CrossRef]
- Ziman, J.M. Principles of the Theory of Solids; Cambridge University Press: London, UK, 1979. [Google Scholar]
- Rukelj, Z.; Radić, D.; Krsnik, J.; Barišić, O.S.; Mishchenko, A.S.; Kupčić, I. Dynamical conductivity of a two-dimensional weakly doped Holstein system. Phys. Rev. B 2023, 108, 155151. [Google Scholar] [CrossRef]
- Bolotin, K.I.; Sikes, K.J.; Hone, J.; Stormer, H.L.; Kim, P. Temperature-Dependent Transport in Suspended Graphene. Phys. Rev. Lett. 2008, 101, 096802. [Google Scholar] [CrossRef]
- Li, Z.Q.; Henriksen, E.A.; Jiang, Z.; Hao, Z.; Martin, M.C.; Kim, P.; Stormer, H.L.; Basov, D.N. Dirac charge dynamics in graphene by infrared spectroscopy. Nat. Phys. 2008, 4, 532. [Google Scholar] [CrossRef]
- Santos-Cottin, D.; Casula, M.; de’Medici, L.; Le Mardelé, F.; Wyzula, J.; Orlita, M.; Klein, Y.; Gauzzi, A.; Akrap, A.; Lobo, R.P.S.M. Optical conductivity signatures of open Dirac nodal lines. Phys. Rev. B 2021, 104, L201115. [Google Scholar] [CrossRef]
- Despoja, V.; Novko, D.; Dekanić, K.; Šunjić, M.; Marušić, L. Two-dimensional and π plasmon spectra in pristine and doped graphene. Phys. Rev. B 2013, 87, 075447. [Google Scholar] [CrossRef]
- Rukelj, Z.; Štrkalj, A.; Despoja, V. Optical absorption and transmission in a molybdenum disulfide monolayer. Phys. Rev. B 2016, 94, 115428. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, C.-X.; Qi, X.-L.; Fang, Z.; Zhang, S.-C. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 438. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).