Abstract
We propose a new way to establish the existence of a superfluid phase in an exciton bilayer system by exploiting the properties of its collective modes. We focus on the density collective modes and treat them within Random Phase Approximation. By comparing results for the normal and superfluid states, we are able to identify unambiguous fingerprints of the exciton superfluid phase. We compare the collective modes of the exciton system and cold atom systems, and we discuss the collective modes of the exciton superfluid order parameter.
1. Introduction
Recent reports of the probable observation of superfluidity in exciton semiconductor bilayer systems in zero magnetic fields are currently attracting a lot of interest [1,2,3,4,5,6,7]. The excitons are in the interlayer: bound electron–hole pairs that form across the spatially separate electron and hole conducting layers. The spatial separation suppresses electron–hole recombination, thus opening the way to stable exciton superfluids in equilibrium [8,9]. The strong binding energy of the excitons leads to predictions of high superfluid transition temperatures.
The long-range pairing interaction makes this system [10] very different from familiar superconductors and superfluids in which the pairing interaction is contact or short-range. Changing the charge-carrier density with top and bottom metal gates tunes the strength of the screening of the electron–hole pairing attraction [11]. This allows a continuous scan of the BEC-BCS crossover from strongly bound pairs forming an exciton Bose–Einstein condensate (BEC) to weakly bound electron–hole pairs in the crossover regime [12,13].
In the last decade, with the discovery of new materials and the rapid advances in experimental techniques, there has been a huge effort to search for and identify the existence of stable exciton normal liquid and superfluid phases in these bilayer systems. Techniques include interlayer tunneling [1], electroluminescence [2], counterflow measurements [3], and Coulomb drag [6]. However, to date, while these works have been able to establish the existence of a strongly correlated excitonic phase, a definitive claim for the existence of a superfluid state is still missing. Observation of dissipationless currents and measurements of phase coherence are particularly challenging because, even though excitons contain charged electrons and holes, they are overall neutral particles.
Here, we establish that collective modes are a powerful tool to unambiguously identify exciton superfluidity in these systems. Collective modes describe the macroscopic response to an external perturbation acting on a many-body system. We propose a complete description of the density collective modes using a superfluid model without any restriction on the localization of electrons and holes. Previously, Ref. [14] has treated these modes within a “quasi-localized approximation” where the electrons and holes are assumed to be highly localized. This is valid only at low densities and large interlayer separations. We present results for the superfluid and normal states, searching for fingerprints of exciton superfluidity.
2. Materials and Methods
The response functions that describe the collective modes of macroscopic observables can be measured by externally perturbing the system at a given wavenumber q and frequency [15]. We explore the response of the system to particle density perturbations using Random Phase Approximation (RPA) in the normal liquid and superfluid exciton phases. RPA has proved to be a quantitatively good approximation to treat density fluctuations in the zero temperature exciton bilayer system [16,17].
Within RPA, the Dyson equation gives the density response function [15,18]:
is the zero-order polarization function matrix in the superfluid state [19]. is the bare Coulomb interaction matrix:
where and are the bare intralayer repulsive and interlayer attractive interactions, respectively. is the dielectric constant of the insulating barrier between the conducting layers, and d is the interlayer separation.
We consider only equal electron and hole effective masses and densities, making the symmetric:
is the density response in a layer from a density perturbation in the same layer, while is the density response in one layer due to a density perturbation in the opposite layer.
The zero-order polarization matrix can be written as
The and are the normal and anomalous zero-order polarizations [20]:
where , S is the layer surface area, and and are the Bogoliubov amplitudes:
The superfluid energy dispersion relation is
with the electronic parabolic dispersion relation, and is the intralayer correlation energy term evaluated within the Hartree–Fock approximation [17]. The superfluid gap and the single-particle chemical potential are evaluated as a function of the density n by solving the energy gap and number equations:
and are the spin and valley degeneracies. In Equations (8) and (9), is the static screened repulsive intralayer interaction [11,21] and the static screened attractive interlayer interaction [19,22]:
where and .
We solve Equations (9) and (10) self-consistently as a function of the density [10,17]. Then, we calculate the density response functions (Equation (3)):
The energy spectra of the density collective modes correspond to the which satisfies
The collective modes are stable only if Equation (15) gives a real solution . When the solution is complex, , the collective modes have a lifetime defined by the damping parameter . The solution is complex if and only if and have poles for real [23]. This occurs in the so-called pair-breaking continuum region. Equation (15) is invariant under the transformation to so we need consider only .
Here, we examine the stable collective modes that lie outside the pair-breaking continuum region. The branch cut in which and diverge in the superfluid phase is given by , originating from the denominator in the zero-order polarization functions. To locate the branch cut and hence the lower boundary of the pair-breaking continuum region, we must minimize as a function of k. The dispersion relation , and thus the position of the pair-breaking continuum in the (-q) space, depends on the density.
3. Results
We consider a system with and interlayer distance , where is the effective Bohr radius. For the BEC regime, we set the average interparticle distance [17], for the crossover regime , and for the normal state . The particle density in each layer is .
3.1. Density Collective Modes in the BEC Regime
Figure 1 shows the pair-breaking continuum region for the exciton superfluid state at a low density in the deep BEC and for the normal state. Appendix A presents the calculation and results for the collective modes in the normal state.
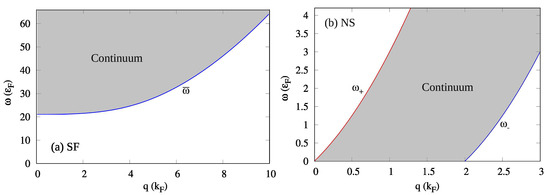
Figure 1.
(a) The continuum region (gray area) in the BEC superfluid state (SF) for interparticle distance . (b) The continuum region in the normal state (NS) for interparticle distance . The interlayer distance .
Remarkably, in the superfluid phase, Figure 1a, the pair-breaking region with has no upper boundary for the following reason. In the numerators of the superfluid polarization functions, Equations (5) and (6), the Bogoliubov amplitudes smoothly approach zero for large momenta. There is no cutoff to the sum in k, and thus for any q and for there is always a value of k for which the denominators of the polarization functions are zero. Thus, there is no upper bound of the continuum region in the superfluid phase.
In contrast, in the normal liquid state, Figure 1b, the continuum has an upper boundary. This is because the zero temperature Fermi step functions in Equation (A3) impose a cutoff to the sum in k, so for a fixed q and for , as well as for the lower boundary , there exists no k-value for which the denominator of vanishes.
In the superfluid state outside the continuum, Equation (15) has stable solutions only when is real and positive. Figure 2a shows for . The imaginary part is zero for , the boundary of the pair-breaking excitation region, while the real part is negative. At the boundary, the imaginary part is a maximum and the real part becomes positive. With increasing , the imaginary part remains non-zero. Thus, outside the continuum for , Equation (15) has no real solutions (Figure 3), and we conclude here that there are no stable density collective modes in the BEC regime of exciton bilayer superfluidity. In the superfluid BEC regime, the effect of density fluctuations is negligible because the excitons are well spaced (very large ) so they interact minimally with each other [11]. For this reason, density fluctuations do not induce any stable collective response in the system in the BEC regime.
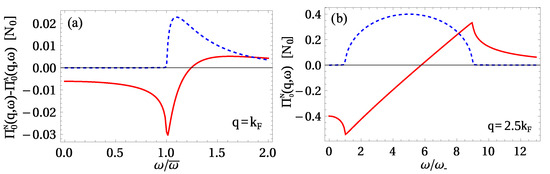
Figure 2.
(a) Real (red solid line) and imaginary (blue dashed line) in the exciton superfluid state for as a function of in units of , the 2D density of states per unit area at the Fermi surface. is the energy boundary of the superfluid continuum. (b) Real (red solid line) and imaginary (blue dashed line) in the liquid normal state for . is the lower energy boundary of the normal state continuum.
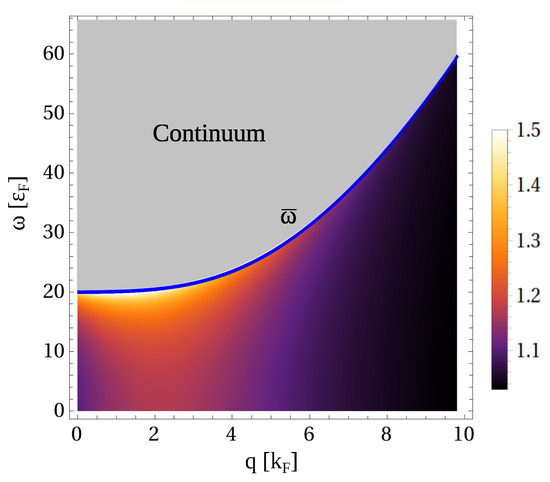
Figure 3.
Modulus of the denominator of the normal and anomalous polarization functions, Equation (15), as a function of momentum q and energy outside the continuum, , in the deep BEC regime, . Gray area shows the continuum region. .
This is in sharp contrast with the collective mode properties in the normal liquid state for which we recall that above the continuum, , the real part of the polarization function is positive and the imaginary part is zero (Figure 2b). For , Equation (A4) has two real solutions, the acoustic and optic density collective modes (Figure A2) [16,24].
3.2. Density Collective Modes in the Crossover Regime
As the density is increased, the system passes from the BEC regime into the BCS-BEC crossover regime. In this regime, the interlayer and intralayer interactions become significantly affected by density fluctuations and by screening [17]. We find that, as in the BEC regime, in the crossover regime there are no real solutions for Equation (15) lying outside the continuum since the denominator of the polarization functions is always greater than zero (Figure 4). Figure 4 shows that the intralayer correlations lower the boundary of the continuum, from the dashed blue line down to the solid blue line. This is because the gap energy is significantly suppressed by the correlations [17]. The small peak in reflects the maximum in the gap energy that appears near in the crossover regime. As in the BEC regime, outside the continuum is always negative. This again means Equation (15) has no real solutions.
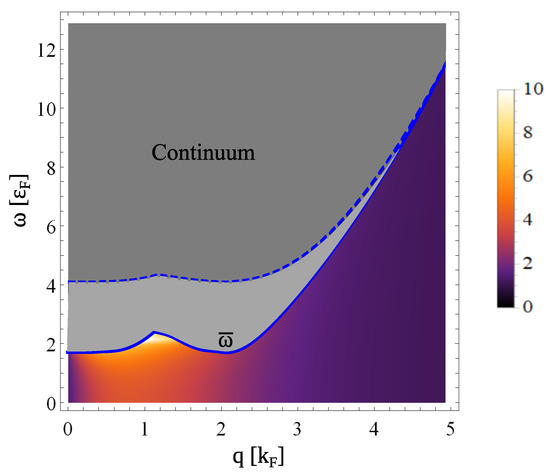
Figure 4.
Dark gray area is the continuum region for the system in the crossover regime, . When intralayer correlations are neglected it is bounded from below by the dashed blue line. Light gray area is the additional continuum region when intralayer correlations are included, bounded from below by the solid blue line . For , the modulus of the denominator of the normal and anomalous polarization functions is shown with intralayer correlations included. .
References [11,25] have shown that very strong screening blocks the exciton superfluid from entering the weakly interacting BCS regime. Reference [11] found that, as a result, the gap energy in this system is always larger than the Fermi energy.
We consider only density fluctuations and we find that the optic and acoustic modes in the normal state disappear at the superfluid transition by tuning the density at temperature zero. An optic out of phase mode in the exciton superfluid state is not possible because of the large binding energy and rigidity of the excitons in the superfluid state [26]. For the acoustic mode, its energy in the normal liquid state is found to lie below the Fermi energy. Consequently, in the superfluid state it would lie within the forbidden region inside the energy gap of the excitation spectrum. The disappearance of the acoustic and optic branches at the normal liquid to superfluid transition is a striking characteristic of the transition.
4. Superfluid Collective Modes in Ultracold Atoms and Exciton Bilayers Compared
We recall features of the collective modes in ultracold atoms. Since experimentally it is not possible to isolate one perturbation channel, perturbations of the three fields (density, amplitude, and phase of the order parameter) are generally simultaneously included [27]. Thus a perturbation of the density will couple with the amplitude and phase response of the order parameter [28,29].
In zero temperature ultracold atoms, there is a stable acoustic Anderson–Bogoliubov (AB) mode lying outside the continuum [30] throughout the entire BCS-BEC crossover. This mode is driven by both density and phase modulations but it is not coupled to amplitude of the order parameter. In neutral systems, the AB mode is gapless [31]. We recall that in 3D charged systems, due to the repulsive Coulomb interactions, the AB mode acquires a gap of the order of the plasmon frequency [32]. In the BCS regime of 3D cold atoms systems, the AB mode has been shown to appear in the density and phase response functions outside the continuum [33]. Moving toward the crossover and BEC regimes, the AB mode disappears from the density response function but remains in the phase response function [32].
In 2D charged systems there is as yet no investigation of the AB mode. The plasmon frequency in 2D goes to zero at (Figure A2), so it is reasonable to expect that the AB mode for a 2D charged system will be gapless too.
In the exciton bilayer system, strong screening prevents the system from entering the BCS regime. The absence of a BCS regime in the exciton superfluid implies that the AB modes are governed solely by phase fluctuations of the order parameter. Here, we investigate modes that couple only to density fluctuations, and we indeed find no stable collective modes outside the continuum in the crossover and BEC regimes of the exciton superfluid system.
By incorporating phase fluctuations, acoustic AB modes are expected to emerge in the exciton superfluid outside the continuum, analogous to those observed in ultracold atoms, where the transition from normal to BCS superfluidity (small energy gap) leads to a smooth behavior of the AB modes [34,35,36]. A non-smooth transition of the AB modes may be expected from the normal liquid to the exciton superfluid phase, reflecting the sudden shift in the collective mode’s nature: density-driven in the normal state and phase-driven in the superfluid state.
Inside the continuum, in the BCS-Crossover regime of ultracold atoms, a pair-breaking mode related to fluctuations of the amplitude of the order parameter has been reported [27,37]. This pair-breaking mode does not couple with density fluctuations. In the exciton bilayer system, we have noted that the long-range interactions have a strong dependence on screening and particle density. The density fluctuations can significantly affect the amplitude of the order parameter in the crossover regime. This should generate additional and relatively long-lived density collective mode branches inside the continuum.
There have been as yet no experimental investigations of the collective modes in exciton bilayer superfluids. Exciton bilayers in Transition Metal Dichalcogenides (TMDs) would be particularly attractive in this regard. The binding energies of excitons in these systems are large [38] and the expected transition temperatures to the superfluid state are high [39]. Reference [40] has investigated phonon propagation in the normal state in a TMD exciton bilayer system using different spectroscopic techniques including Raman. Raman spectroscopy has been successfully used to study collective modes in superconductors [41] and could be adapted for the collective modes in the exciton bilayer superfluid phase.
5. Conclusions
In the liquid normal state of the bilayer system, the response of the system to small external density perturbations is through the low-energy optic and acoustic density collective modes. When the system enters the exciton superfluid phase, the response changes significantly. Due to the strong screening associated with the long-range Coulomb interactions, the exciton superfluid always features a large energy gap and this prevents the propagation of stable acoustic and optic density collective modes. Unlike with ultracold atoms, the long-range attractive interaction in exciton bilayers will cause an order parameter amplitude response from density fluctuations. It is likely that this will result in additional long-lived unstable collective modes in the amplitude channel appearing in the continuum at the normal to superfluid transition. At the transition, the disappearance of the optic mode, the probable change in behavior of the acoustic mode outside the continuum, and the likely appearance of amplitude-density modes in the continuum are all experimentally detectable. These should act as signatures of the superfluid phase in the exciton bilayer system.
Author Contributions
Conceptualization, F.P., J.T. and A.P.; methodology, F.P. and J.T.; software, F.P.; validation, F.P., J.T. and D.N.; formal analysis, S.C. and F.P.; investigation, S.C., F.P., D.N. and J.T.; resources, F.P. and S.C.; data curation, F.P. and S.C.; writing—original draft preparation, F.P. and S.C.; writing—review and editing, S.C., A.P., F.P., J.T. and D.N.; visualization, F.P.; supervision, A.P., J.T. and D.N.; project administration, A.P. and J.T.; funding acquisition, F.P. and S.C. All authors have read and agreed to the published version of the manuscript.
Funding
S.C. and F.P. are supported by the FWO-Vl (Fonds Wetenschappelijk Onderzoek-Vlaanderen).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the data in this study are available within this paper.
Acknowledgments
We thank S. De Palo and G. Senatore and H. Kurkjian for useful discussions.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| BCS | Bardeen–Cooper–Schrieffer |
| BEC | Bose–Einstein Condensation |
| RPA | Random Phase Approximation |
| AB | Anderson–Bogoliubov |
| TMD | Transition Metal Dichalcogenide |
Appendix A. Normal State Collective Modes
In the liquid normal state, the RPA electron–electron and electron–hole response functions of a bilayer system are obtained by setting the anomalous zero-order polarization to zero in Equations (13) and (14):
where the zero-order normal polarization function in the normal state is the 2D dynamic Lindhard function [42]:
, where the Hartree–Fock with the screened interaction calculated in RPA for the normal liquid state, and is the Fermi step function. The energy spectra of the density collective modes in the normal liquid bilayer are obtained by solving the following:
In the region of (-q) space in which has poles, it is impossible to solve Equation (A4). The polarization function diverges in the interval on the real axis for . The limits of the branch cut are given by [23]:
is the Fermi velocity.
Figure A1 shows the real and imaginary parts of the polarization function for the normal liquid as a function of for different q. For (Figure A1a), the imaginary part of the polarization is non-zero for , and it is characterized by the “shark tail” shape [23]. For (Figure A1b), the lower boundary of the continuum region has moved up to , and there is a small interval close to zero frequency in which the imaginary part of the polarization is zero.
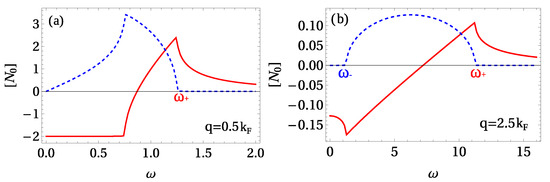
Figure A1.
The real (red solid line) and imaginary parts (blue dashed line) of the zero-order normal liquid polarization function in units of the 2D density of states , as a function of in units of the Fermi energy for (a) and (b) . , .
It is possible to prove that Equation (A4) has real solutions only if is real and positive. We solve Equation (A4) outside the continuum for as a function of q.
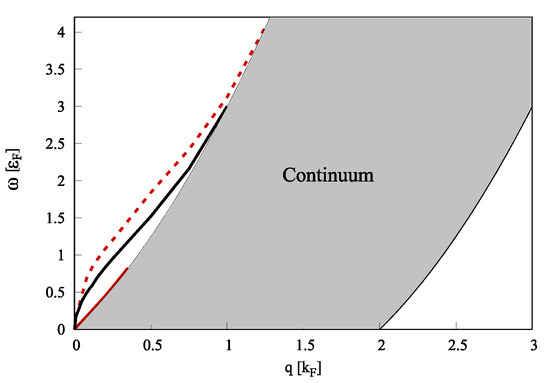
Figure A2.
Energy spectra of the acoustic (red solid line) and optic (red dashed line) collective modes for normal liquid as a function of momentum q. Interlayer distance , interparticle spacing . Plasma mode energy spectrum for an isolated electron layer (black solid line) is shown for comparison.
We recall that there are two distinct branches of solutions for Equation (A4) as a function of the momentum q: the acoustic and optic density collective modes. In the acoustic branch, the relative electron and hole motion is in phase while in the optic mode it is out of phase. In both cases, at a certain q the modes approach the continuum and disappear [24], like plasma collective modes in an isolated 2D electron layer [23].
References
- Burg, G.W.; Prasad, N.; Kim, K.; Taniguchi, T.; Watanabe, K.; MacDonald, A.H.; Register, L.F.; Tutuc, E. Strongly Enhanced Tunneling at Total Charge Neutrality in Double-Bilayer Graphene-WSe2 Heterostructures. Phys. Rev. Lett. 2018, 120, 177702. [Google Scholar] [CrossRef]
- Wang, Z.; Rhodes, D.A.; Watanabe, K.; Taniguchi, T.; Hone, J.C.; Shan, J.; Mak, K.F. Evidence of high-temperature exciton condensation in two-dimensional atomic double layers. Nature 2019, 574, 76–80. [Google Scholar] [CrossRef]
- Ma, L.; Nguyen, P.X.; Wang, Z.; Zeng, Y.; Watanabe, K.; Taniguchi, T.; MacDonald, A.H.; Mak, K.F.; Shan, J. Strongly correlated excitonic insulator in atomic double layers. Nature 2021, 598, 585–589. [Google Scholar] [CrossRef]
- Gamucci, A.; Spirito, D.; Carrega, M.; Karmakar, B.; Lombardo, A.; Bruna, M.; Pfeiffer, L.; West, K.; Ferrari, A.; Polini, M.; et al. Anomalous low-temperature Coulomb drag in graphene-GaAs heterostructures. Nat. Commun. 2014, 5, 5824. [Google Scholar] [CrossRef]
- Gu, J.; Ma, L.; Liu, S.; Watanabe, K.; Taniguchi, T.; Hone, J.C.; Shan, J.; Mak, K.F. Dipolar excitonic insulator in a moiré lattice. Nat. Phys. 2022, 18, 395–400. [Google Scholar] [CrossRef]
- Nguyen, P.X.; Ma, L.; Chaturvedi, R.; Watanabe, K.; Taniguchi, T.; Shan, J.; Mak, K.F. Perfect Coulomb drag in a dipolar excitonic insulator. arXiv 2023, arXiv:2309.14940. [Google Scholar]
- Conti, S.; Perali, A.; Hamilton, A.R.; Milošević, M.V.; Peeters, F.M.; Neilson, D. Chester Supersolid of Spatially Indirect Excitons in Double-Layer Semiconductor Heterostructures. Phys. Rev. Lett. 2023, 130, 057001. [Google Scholar] [CrossRef]
- Kogan, V.G.; Tavger, B.A. Possibility of Pair Correlation of Electrons and Holes in a Sandwich Consisting of n- and p-Type Semiconductor Films. In Physics of p-n Junctions and Semiconductor Devices; Springer: Boston, MA, USA, 1971; pp. 39–45. [Google Scholar] [CrossRef]
- Lozovik, Y.E.; Yudson, V.I. A new mechanism for superconductivity: Pairing between spatially separated electrons and holes. Sov. Phys. JETP 1976, 44, 389–397. [Google Scholar]
- Perali, A.; Neilson, D.; Hamilton, A.R. High-temperature superfluidity in double-bilayer graphene. Phys. Rev. Lett. 2013, 110, 146803. [Google Scholar] [CrossRef]
- Neilson, D.; Perali, A.; Hamilton, A.R. Excitonic superfluidity and screening in electron-hole bilayer systems. Phys. Rev. B 2014, 89, 060502. [Google Scholar] [CrossRef]
- Nilsson, F.; Aryasetiawan, F. Effects of dynamical screening on the BCS-BEC crossover in double bilayer graphene: Density functional theory for exciton bilayers. Phys. Rev. Mater. 2021, 5, L050801. [Google Scholar] [CrossRef]
- De Palo, S.; Tramonto, F.; Moroni, S.; Senatore, G. Quadriexcitons and excitonic condensate in a symmetric electron-hole bilayer with valley degeneracy. Phys. Rev. B 2023, 107, L041409. [Google Scholar] [CrossRef]
- De Palo, S.; Trevisanutto, P.E.; Senatore, G.; Vignale, G. Collective excitations and quantum incompressibility in electron-hole bilayers. Phys. Rev. B 2021, 104, 115165. [Google Scholar] [CrossRef]
- Fetter, A.L. Electrodynamics of a layered electron gas. II. Periodic array. Ann. Phys. 1974, 88, 1–25. [Google Scholar] [CrossRef]
- Neilson, D.; Świerkowski, L.; Szymański, J.; Liu, L. Excitations of the strongly correlated electron liquid in coupled layers. Phys. Rev. Lett. 1993, 71, 4035–4038. [Google Scholar] [CrossRef] [PubMed]
- Pascucci, F.; Conti, S.; Perali, A.; Tempere, J.; Neilson, D. Effects of intralayer correlations on electron-hole double-layer superfluidity. Phys. Rev. B 2024, 109, 094512. [Google Scholar] [CrossRef]
- Altland, A.; Simons, B.D. Condensed Matter Field Theory; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Sodemann, I.; Pesin, D.A.; MacDonald, A.H. Interaction-enhanced coherence between two-dimensional Dirac layers. Phys. Rev. B 2012, 85, 195136. [Google Scholar] [CrossRef]
- Lozovik, Y.E.; Ogarkov, S.L.; Sokolik, A.A. Condensation of electron-hole pairs in a two-layer graphene system: Correlation effects. Phys. Rev. B 2012, 86, 045429. [Google Scholar] [CrossRef]
- Lozovik, Y.E.; Sokolik, A.A. Multi-band pairing of ultrarelativistic electrons and holes in graphene bilayer. Phys. Lett. A 2009, 374, 326. [Google Scholar] [CrossRef]
- Mazloom, A.; Abedinpour, S.H. Interplay of interlayer pairing and many-body screening in a bilayer of dipolar fermions. Phys. Rev. B 2018, 98, 014513. [Google Scholar] [CrossRef]
- Giuliani, G.; Vignale, G. Quantum Theory of the Electron Liquid; Masters Series in Physics and Astronomy; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Liu, L.; Świerkowski, L.; Neilson, D.; Szymański, J. Static and dynamic properties of coupled electron-electron and electron–hole layers. Phys. Rev. B 1996, 53, 7923–7931. [Google Scholar] [CrossRef]
- Maezono, R.; López Ríos, P.; Ogawa, T.; Needs, R.J. Excitons and biexcitons in symmetric electron-hole bilayers. Phys. Rev. Lett. 2013, 110, 216407. [Google Scholar] [CrossRef]
- Nikolaev, V.V.; Portnoi, M.E. Mott transition of spatially indirect excitons. In Proceedings of the Optical Science and Technology, the SPIE 49th Annual Meeting, Denver, CO, USA, 2 August 2004; SPIE: Denver, CO, USA, 2004; Volume 5509, pp. 187–193. [Google Scholar] [CrossRef]
- Kurkjian, H.; Tempere, J.; Klimin, S.N. Linear response of a superfluid Fermi gas inside its pair-breaking continuum. Sci. Rep. 2020, 10, 11591. [Google Scholar] [CrossRef]
- Hoinka, S.; Dyke, P.; Lingham, M.G.; Kinnunen, J.J.; Bruun, G.M.; Vale, C.J. Goldstone mode and pair-breaking excitations in atomic Fermi superfluids. Nat. Phys. 2017, 13, 943–946. [Google Scholar] [CrossRef]
- Djadaojee, L.; Douillet, A.; Grucker, J. Stimulated Brillouin Gain Spectroscopy of Superfluid Helium-4. J. Low Temp. Phys. 2021, 203, 234–243. [Google Scholar] [CrossRef]
- Anderson, P.W. Random–Phase Approximation in the Theory of Superconductivity. Phys. Rev. 1958, 112, 1900–1916. [Google Scholar] [CrossRef]
- Van Loon, S.; Sá de Melo, C.A.R. Effects of Quantum Fluctuations on the Low-Energy Collective Modes of Two-Dimensional Superfluid Fermi Gases from the BCS to the Bose Limit. Phys. Rev. Lett. 2023, 131, 113001. [Google Scholar] [CrossRef]
- Klimin, S.N.; Tempere, J.; Repplinger, T.; Kurkjian, H. Collective excitations of a charged Fermi superfluid in the BCS-BEC crossover. New J. Phys. 2023, 25, 063011. [Google Scholar] [CrossRef]
- Ohashi, Y.; Griffin, A. Superfluidity and collective modes in a uniform gas of Fermi atoms with a Feshbach resonance. Phys. Rev. A 2003, 67, 063612. [Google Scholar] [CrossRef]
- Donnelly, R.J. The two-fluid theory and second sound in liquid helium. Phys. Today 2009, 62, 34–39. [Google Scholar] [CrossRef]
- Ville, J.L.; Saint-Jalm, R.; Le Cerf, E.; Aidelsburger, M.; Nascimbène, S.; Dalibard, J.; Beugnon, J. Sound Propagation in a Uniform Superfluid Two-Dimensional Bose Gas. Phys. Rev. Lett. 2018, 121, 145301. [Google Scholar] [CrossRef] [PubMed]
- Singh, G.; Jouan, A.; Herranz, G.; Scigaj, M.; Sánchez, F.; Benfatto, L.; Caprara, S.; Grilli, M.; Saiz, G.; Couëdo, F.; et al. Gap suppression at a Lifshitz transition in a multi-condensate superconductor. Nat. Mater. 2019, 18, 948. [Google Scholar] [CrossRef]
- Pekker, D.; Varma, C. Amplitude/Higgs Modes in Condensed Matter Physics. Annu. Rev. Condens. Matter Phys. 2015, 6, 269–297. [Google Scholar] [CrossRef]
- Fogler, M.M.; Butov, L.V.; Novoselov, K.S. High-temperature superfluidity with indirect excitons in van der Waals heterostructures. Nat. Commun. 2014, 5, 4555. [Google Scholar] [CrossRef]
- Conti, S.; Neilson, D.; Peeters, F.M.; Perali, A. Transition metal dichalcogenides as strategy for high temperature electron-hole superfluidity. Condens. Matter 2020, 5, 22. [Google Scholar] [CrossRef]
- Ng, R.C.; El Sachat, A.; Cespedes, F.; Poblet, M.; Madiot, G.; Jaramillo-Fernandez, J.; Florez, O.; Xiao, P.; Sledzinska, M.; Sotomayor-Torres, C.M.; et al. Excitation and detection of acoustic phonons in nanoscale systems. Nanoscale 2022, 14, 13428–13451. [Google Scholar] [CrossRef]
- Monien, H.; Zawadowski, A. Theory of Raman scattering with final-state interaction in high-Tc BCS superconductors: Collective modes. Phys. Rev. B 1990, 41, 8798–8810. [Google Scholar] [CrossRef] [PubMed]
- Lindhard, J. On the properties of a gas of charged particles. Kgl. Dan. Videnskab. Selsk. Mat. Fys. Medd. 1954, 28, 8. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).