Modelling Early Growth of Totoaba macdonaldi (Teleostei: Sciaenidae) under Laboratory Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Ethical Statements
2.2. Obtaining the Stock and Culture Conditions
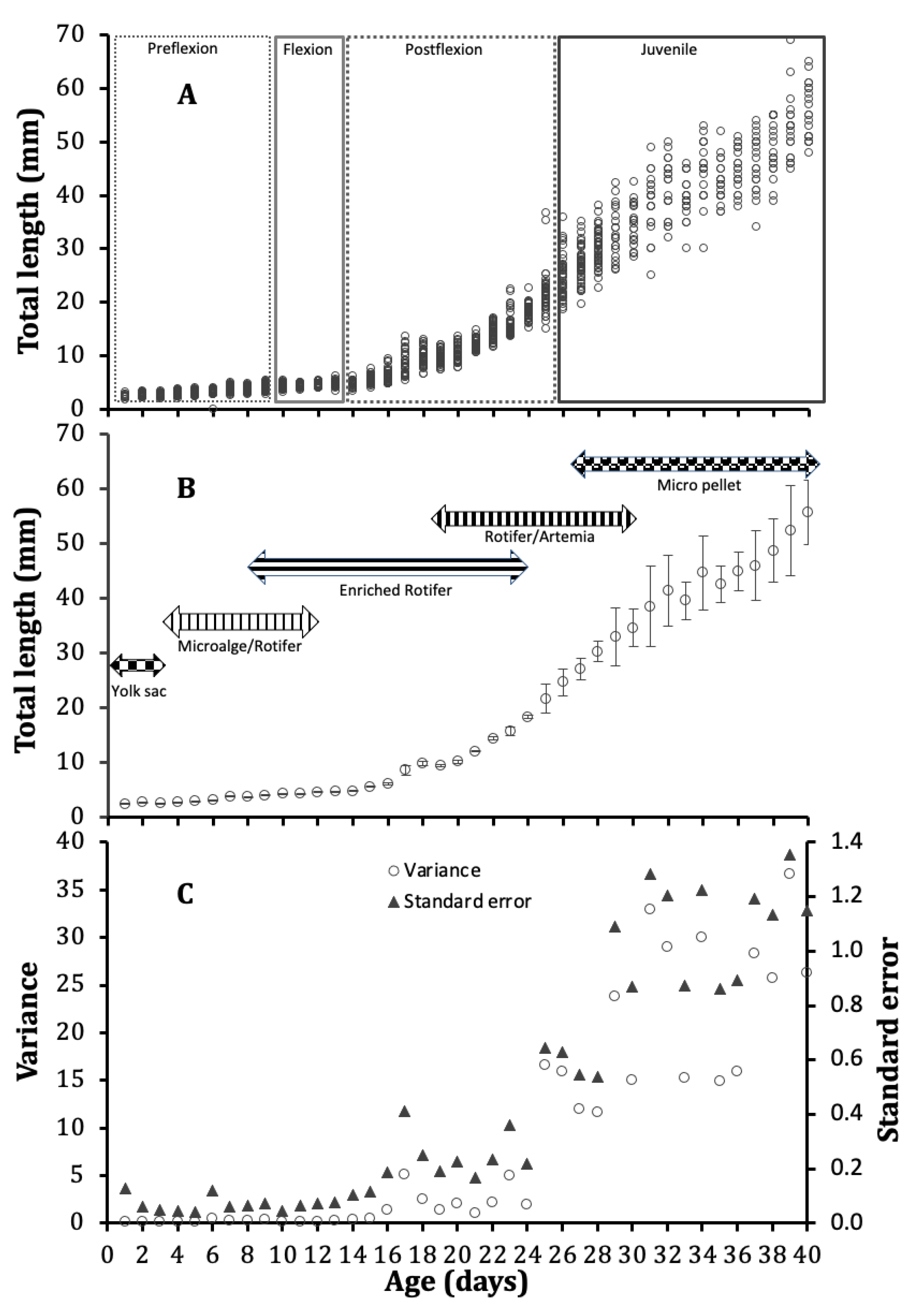
2.3. Growth
2.4. Database
2.5. Modelling
2.6. Model Selection
3. Results
3.1. Growth
3.2. Model Selection
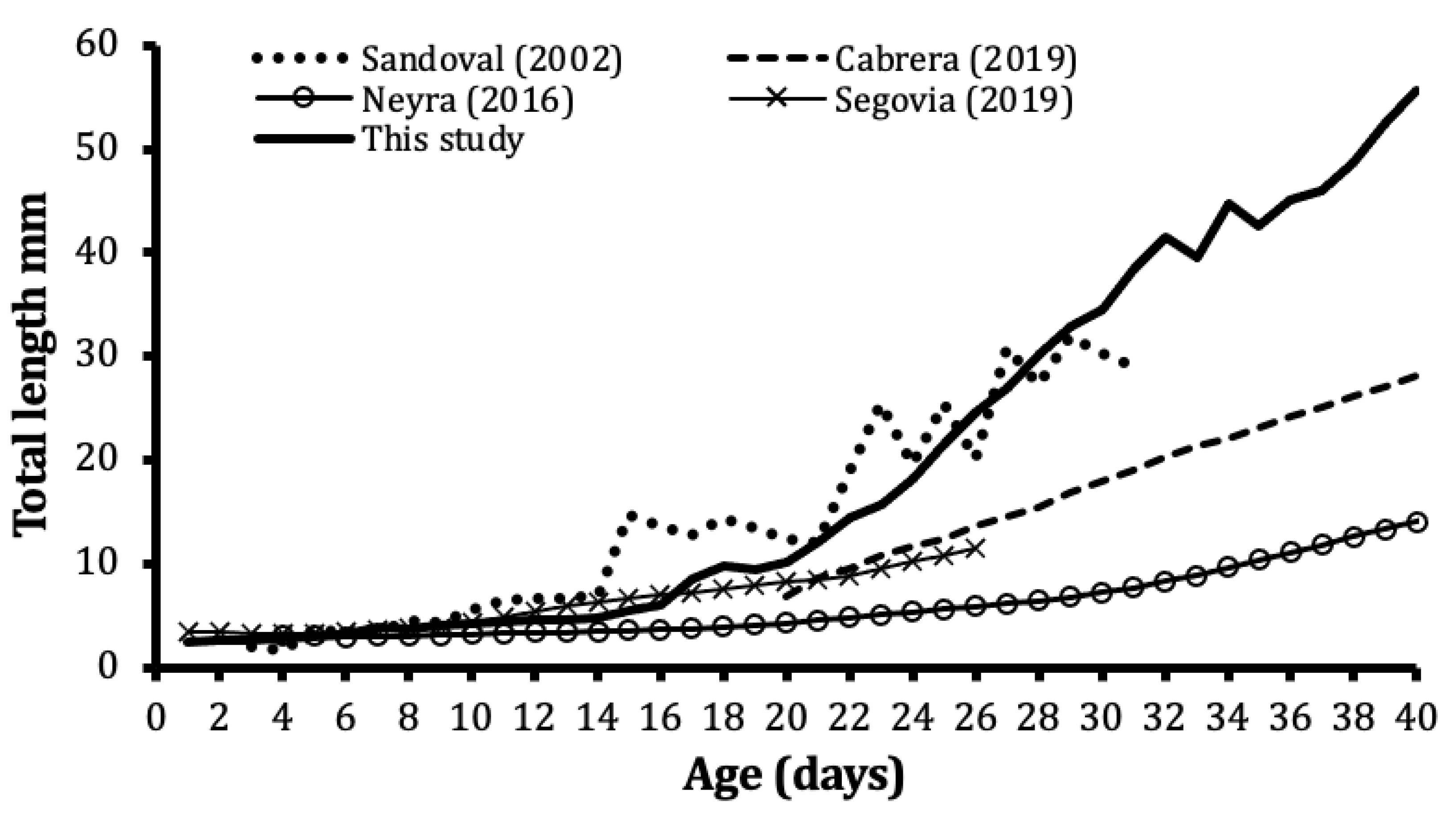
3.3. Growth from Literature
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gilbert, C.H. A preliminary report on the fishes collected by the streamer “Albatross” on the Pacific coast of North America during the year 1889, with descriptions of twelve new genera and ninety-two new species. Proc. US Natl. Mus. 1890, 13, 49–126. [Google Scholar] [CrossRef]
- De Anda-Montañez, J.A.; García-de León, F.J.; Zenteno-Savín, T.; Balart-Páez, E.; Méndez-Rodríguez, L.C.; Bocanegra-Castillo, N.; Martínez-Delgado, M.E. Estado de Salud y Estatus de Conservación de La(s) Población(es) de Totoaba (Totoaba Macdonaldi) en el Golfo de California: Una Especie en Peligro de Extinción; Informe Final, SNIB-CONABIO. Proyecto Núm. hK050. Centro de Investigaciones Biológicas del Noroeste, S.C., Baja California Sur. 2013. Available online: http://www.conabio.gob.mx/institucion/proyectos/resultados/InfHK050.pdf (accessed on 1 February 2023).
- Barrera-Guevara, J.C. The conservation of Totoaba macdonaldi (Gilbert), (Pisces: Sciaenidae), in the Gulf of California, Mexico. J. Fish Biol. 1990, 37, 201–202. [Google Scholar] [CrossRef]
- Cisneros-Mata, M.A.; True, C.; Enriquez-Paredes, L.M.; Savody, Y.; Liu, M. Totoaba macdonaldi. The IUCN Red List Threatened Species 2021: e.T22003A2780880. Available online: https://dx.doi.org/10.2305/IUCN.UK.2021-2.RLTS.T22003A2780880.en (accessed on 1 February 2023).
- Giffard-Mena, I.; Hernández-Montiel, A.H.; Pérez-Robles, J.; True, C.D. Effects of salinity on survival and plasma osmolarity of Totoaba macdonaldi eggs, larvae, and juveniles. J. Exp. Mar. Biol. Ecol. 2020, 526, 151339. [Google Scholar] [CrossRef]
- True, D.C. Desarrollo de la Biotecnología de Totoaba macdonaldi. Ph.D. Thesis, Universidad Autónoma de Baja California, Ensenada, Mexico, 2012. [Google Scholar]
- Chen, Y.; Fournier, D. Impacts of atypical data on Bayesian inference and robust Bayesian approach in fisheries. Can. J. Fish. Aquat. Sci. 1999, 56, 1525–1533. [Google Scholar] [CrossRef]
- Curiel-Bernal, M.V.; Aragón-Noriega, E.A.; Cisneros-Mata, M.Á.; Sánchez-Velasco, L.; Jiménez-Rosenberg, S.P.A.; Parés-Sierra, A. Using Observed residual error structure yields the best estimates of individual growth parameters. Fishes 2021, 6, 35. [Google Scholar] [CrossRef]
- Castillo-Vargasmachuca, S.G.; Aragón-Noriega, E.A.; Rodríguez-Domínguez, G.; Martínez-Cárdenas, L.; Arámbul-Muñoz, E.; Burgos Arcos, Á.J. The standard deviation structure as a new approach to growth analysis in weight and length data of farmed Lutjanus guttatus. Fishes 2021, 6, 60. [Google Scholar] [CrossRef]
- Abdo-de la Parra, M.I.; Rodríguez-Ibarra, E.; Rodríguez-Montes de Oca, G.; Velasco-Blanco, G.; Ibarra-Casto, L. Estado actual del cultivo de larvas del pargo flamenco (Lutjanus guttatus). Lat. Am. J. Aquat. Res. 2015, 43, 415–423. [Google Scholar] [CrossRef]
- Ibarra-Castro, L.; Ochoa-Bojórquez, M.O.; Sánchez-Téllez, J.L.; Rojo-Cebreros, A.H.; Alvarez-Lajonchere, L. A new efficient method for the mass production of juvenile spotted rose snapper. Lutjanus Guttatus. Aquac. Rep. 2020, 18, 100550. [Google Scholar] [CrossRef]
- Restrepo, V.R.; Diaz, G.A.; Walter, J.F.; Neilson, J.D.; Campana, S.E.; Secor, D.; Wingate, R.L. Updated estimate of the growth curve of western Atlantic bluefin tuna. Aquat. Living Resour. 2010, 23, 335–342. [Google Scholar] [CrossRef]
- Keast, A.; Eadie, J.M. Growth Depensation in Year-0 Largemouth Bass: The Influence of Diet. Trans. Am. Fish. Soc. 1985, 114, 204–213. [Google Scholar] [CrossRef]
- Smith, M.E.; Fuiman, L.A. Causes of Growth Depensation in Red Drum, Sciaenops Ocellatus, Larvae. Environ. Biol. Fishes 2003, 66, 49–60. [Google Scholar] [CrossRef]
- Ratkowsky, D.A. Handbook of Nonlinear Regression Models, 1st ed.; Marcel Dekker Inc: New York, NY, USA, 1990; pp. 1–241. [Google Scholar]
- Katsanevakis, S. Modelling fish growth: Model selection, multi-model inference and model selection uncertainty. Fish. Res. 2006, 81, 229–235. [Google Scholar] [CrossRef]
- Baer, A.; Schulz, C.; Traulsen, I.; Krieter, J. Analysing the growth of turbot (Psetta maxima) in a commercial recirculation system with the use of three different growth models. Aquacult. Int. 2010, 19, 497–511. [Google Scholar] [CrossRef]
- Aragón-Noriega, E.A.; Alcántara-Razo, E.; Valenzuela-Quiñonez, W.; Rodríguez-Quiroz, G. Multi-model inference for growth parameter estimation of the Bigeye Croaker Micropogonias megalops in the Upper Gulf of California. Rev. Biol. Mar. Ocean. 2015, 50, 25–38. [Google Scholar] [CrossRef]
- Zhu, L.; Li, L.; Liang, Z. Comparison of six statistical approaches in the selection of appropriate fish growth models. Chin. J. Oceanol. Limnol. 2009, 27, 457–467. [Google Scholar] [CrossRef]
- Aragón-Noriega, E.A. Model selection to describe the growth of the squalid callista (Megapitaria squalida) from the eastern Gulf of California. J. Shellfish Res. 2016, 35, 747–755. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-theoretic Approach, 2nd ed.; Springer: New York, NY, USA, 2002; pp. 1–488. [Google Scholar]
- Alvarez-Lajonchere, L. Determinación de la edad y el crecimiento de Mugil liza, M. curema, M.hospes y M. trichodon (PISCES, MUGILIDAE) en aguas cubanas. Rev. Inves. Mar. 1981, 2, 142–162. [Google Scholar]
- Morales-Ortiz, C. Descripción del Desarrollo Embrionario de Totoaba (Totoaba macdonaldi) Bajo Condiciones de Laboratorio. Master’s Thesis, Universidad Autónoma de Baja California, Ensenada, Mexico, 1999. [Google Scholar]
- Ansah, Y.B.; Frimpong, E.A. Using model-based inference to select a predictive growth curve for farmed Tilapia. N. Am. J. Aquac. 2015, 77, 281–288. [Google Scholar] [CrossRef]
- Tanaka, M. A new growth curve which expresses infinite increase. Publ. Amakusa Mar. Biol. Lab. 1982, 6, 166–177. [Google Scholar]
- Tjorve, E. Shapes and functions of species-area curves (II): A review of new models and parameterizations. J. Biogeogr. 2009, 36, 1435–1445. [Google Scholar] [CrossRef]
- Mercier, L.; Panfili, J.; Paillon, C.; N’diaye, A.; Mouillot, D.; Darnaude, A.M. Otolith reading and multi-model inference for improved estimation of age and growth in the gilthead seabream Sparus aurata (L.). Estuar. Coast. Shelf Sci. 2011, 92, 534–545. [Google Scholar] [CrossRef]
- Schnute, J. A versatile growth model with statistically stable parameters. Can. J. Fish. Aquat. Res. 1981, 38, 1128–1140. [Google Scholar] [CrossRef]
- Castillo-Vargasmachuca, S.G.; Ponce-Palafox, J.T.; Arambul-Muñoz, E.; Rodríguez-Domínguez, G.; Aragón-Noriega, E.A. The spotted rose snapper (Lutjanus guttatus Steindachner 1869) farmed in marine cages: Review of growth models. Rev. Aquac. 2018, 10, 376–384. [Google Scholar] [CrossRef]
- Neter, J.; Kutner, M.H.; Nachtsheim, C.J.; Wasserman, W. Applied Linear Statistical Models, 4th ed.; McGraw-Hill: New York, NY, USA, 1996; pp. 1–720. [Google Scholar]
- Neyra-Flores, A.E. Evaluación del desempeño de la progenie de familias de totoaba silvestre y F1 bajo crianza comunal. Master’s Thesis, Universidad Autónoma de Baja California Repositorio Institucional (CRIS), Ensenada, Mexico, 2016. Available online: https://repositorioinstitucional.uabc.mx/handle/20.500.12930/912 (accessed on 12 December 2022).
- Cabrera-Lozano, R. Efecto de la Temperatura en la Proporción de Sexos de Totoaba macdonaldi. Master’s Thesis, Centro de Investigación Científica y de Educación Superior de Ensenada, Baja California, Ensenada, Mexico, 2019. Available online: http://cicese.repositorioinstitucional.mx/jspui/handle/1007/2827 (accessed on 12 December 2022).
- Sandoval-Garibaldi, G. Desarrollo morfológico de Totoaba macdonaldi (Gilbert, 1890) durante su estadio larval. Master’s Thesis, Facultad de Ciencias Marinas, UABC, Ensenada, Mexico, 2002. Available online: https://repositorioinstitucional.uabc.mx/bitstream/20.500.12930/8676/1/ENS031207.pdf (accessed on 12 December 2022).
- Segovia-Salas, J.C. Efecto del enriquecimiento de rotíferos (Brachionus plicatilis) y Artemia sp. con taurina sobre el crecimiento y sobrevivencia de larvas de Totoaba macdonaldi. Master’s Thesis, Repositorio Institucional (CRIS) Universidad Autónoma de Baja California, Ensenada, Mexico, 2019. Available online: https://repositorioinstitucional.uabc.mx/handle/20.500.12930/886 (accessed on 12 December 2022).
- Mata-Sotres, J.A.; Lazo, J.P.; Baron-Sevilla, B. Effect of age on weaning success in totoaba (Totoaba macdonaldi) larval culture. Aquac. 2015, 437, 292–296. [Google Scholar] [CrossRef]
- Galaviz, M.A.; López, L.M.; García-Gasca, A.; Álvarez-González, C.A.; True, C.D.; Gisbert, E. Digestive system development and study of acid and alkaline protease digestive capacities using biochemical and molecular approaches in totoaba (Totoaba macdonaldi) larvae. Fish Physiol Biochem. 2015, 41, 1117–1130. [Google Scholar] [CrossRef] [PubMed]
- Papadakis, I.E.; Kentouri, M.; Divanach, P.; Mylonas, C.C. Ontogeny of the eye of meagre (Argyrosomus regius) from hatching to juvenile and implications to commercial larval rearing. Aquaculture 2018, 484, 32–43. [Google Scholar] [CrossRef]
- Diken, G.; Demir, O.; Naz, M. The inhibitory situational analysis of some feed ingredients for meagre, Argyrosomus regius (Asso 1801) larvae and evaluation for diet formulations. Aquat. Res. 2019, 2, 41–52. [Google Scholar] [CrossRef]
- Schnute, J.; Fournier, D. A new approach to length-frequency analysis: Growth structure. Can. J. Fish. Aquat. Res. 1980, 37, 1337–1351. [Google Scholar] [CrossRef]


| Models | Function | Parameter Description |
|---|---|---|
| EXP-Schnute 1 | is the youngest age in the data set, is the oldest age in the data set | |
| Schnute 1 | a: is the constant of the relative growth rate (units in time) | |
| Schnute 3 | b: is the incremental relative rate of relative growth rate (dimensionless) | |
| Schnute 4 | Y1 is the size at age | |
| Logistic | Y2 is the size at age | |
| Bertalanffy | Parameters a and b can be positive, negative or zero. | |
| Power | a: is a proportionality constant and b is the power exponent | |
| Extended power | a, b, c: are constants determined by X | |
| Persistence | a, b, c: are constants determined by X | |
| Tanaka | a: maximum growth rate, c: age at which the growth rate is maximum, d: the body size at which the growth rate reaches a maximum f: rate of change o growth rate. |
| Models | Parameters | BIC | Δi | Wi | Y1 | Y2 | A | b | c | d | F |
|---|---|---|---|---|---|---|---|---|---|---|---|
| EXP-Schnute 1 | 44 | 5052 | 0 | 1 | 0.88 | 3.88 | 0.37 | −7.01 | 0 | 0 | 0 |
| Persistence | 43 | 5814 | 762 | 0 | 0 | 0 | 2.89 | 1.53 | 24.22 | 0 | 0 |
| Tanaka | 44 | 5837 | 785 | 0 | 0 | 0 | 0.02 | 0 | 25.08 | 37.95 | 0.04 |
| Schnute 1 | 44 | 6487 | 1435 | 0 | 2.62 | 70.04 | −0.42 | 4.40 | 0 | 0 | 0 |
| Logistic | 43 | 6707 | 1655 | 0 | 0.10 | −1.00 | 1.82 | 62.49 | 0 | 0 | 0 |
| Bertalanffy | 43 | 6724 | 1672 | 0 | 2.14 | 69.61 | −0.10 | 1.00 | 0 | 0 | 0 |
| Schnute 4 | 42 | 6783 | 1753 | 0 | 1.94 | 67.06 | 0 | 0 | 0 | 0 | 0 |
| Schnute 3 | 43 | 6790 | 1760 | 0 | 1.93 | 66.95 | 0 | 1.78 × 10−3 | 0 | 0 | 0 |
| Extended power | 43 | 10,056 | 5003 | 0 | 0 | 0 | 2.63 | 0.53 | −22.51 | 0 | 0 |
| Power | 42 | 16,743 | 11,691 | 0 | 0 | 0 | 0.13 | 1.52 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Curiel-Bernal, M.V.; Cisneros-Mata, M.Á.; Rodríguez-Domínguez, G.; Sánchez-Velasco, L.; Jiménez-Rosenberg, S.P.A.; Parés-Sierra, A.; Aragón-Noriega, E.A. Modelling Early Growth of Totoaba macdonaldi (Teleostei: Sciaenidae) under Laboratory Conditions. Fishes 2023, 8, 155. https://doi.org/10.3390/fishes8030155
Curiel-Bernal MV, Cisneros-Mata MÁ, Rodríguez-Domínguez G, Sánchez-Velasco L, Jiménez-Rosenberg SPA, Parés-Sierra A, Aragón-Noriega EA. Modelling Early Growth of Totoaba macdonaldi (Teleostei: Sciaenidae) under Laboratory Conditions. Fishes. 2023; 8(3):155. https://doi.org/10.3390/fishes8030155
Chicago/Turabian StyleCuriel-Bernal, Marcelo V., Miguel Á. Cisneros-Mata, Guillermo Rodríguez-Domínguez, Laura Sánchez-Velasco, S. Patricia A. Jiménez-Rosenberg, Alejandro Parés-Sierra, and E. Alberto Aragón-Noriega. 2023. "Modelling Early Growth of Totoaba macdonaldi (Teleostei: Sciaenidae) under Laboratory Conditions" Fishes 8, no. 3: 155. https://doi.org/10.3390/fishes8030155
APA StyleCuriel-Bernal, M. V., Cisneros-Mata, M. Á., Rodríguez-Domínguez, G., Sánchez-Velasco, L., Jiménez-Rosenberg, S. P. A., Parés-Sierra, A., & Aragón-Noriega, E. A. (2023). Modelling Early Growth of Totoaba macdonaldi (Teleostei: Sciaenidae) under Laboratory Conditions. Fishes, 8(3), 155. https://doi.org/10.3390/fishes8030155






