Modeling the Individual Growth of the Bonnethead Shark Sphyrna tiburo of the Western Gulf of Mexico Using the Multimodel Approach
Abstract
1. Introduction
2. Materials and Methods
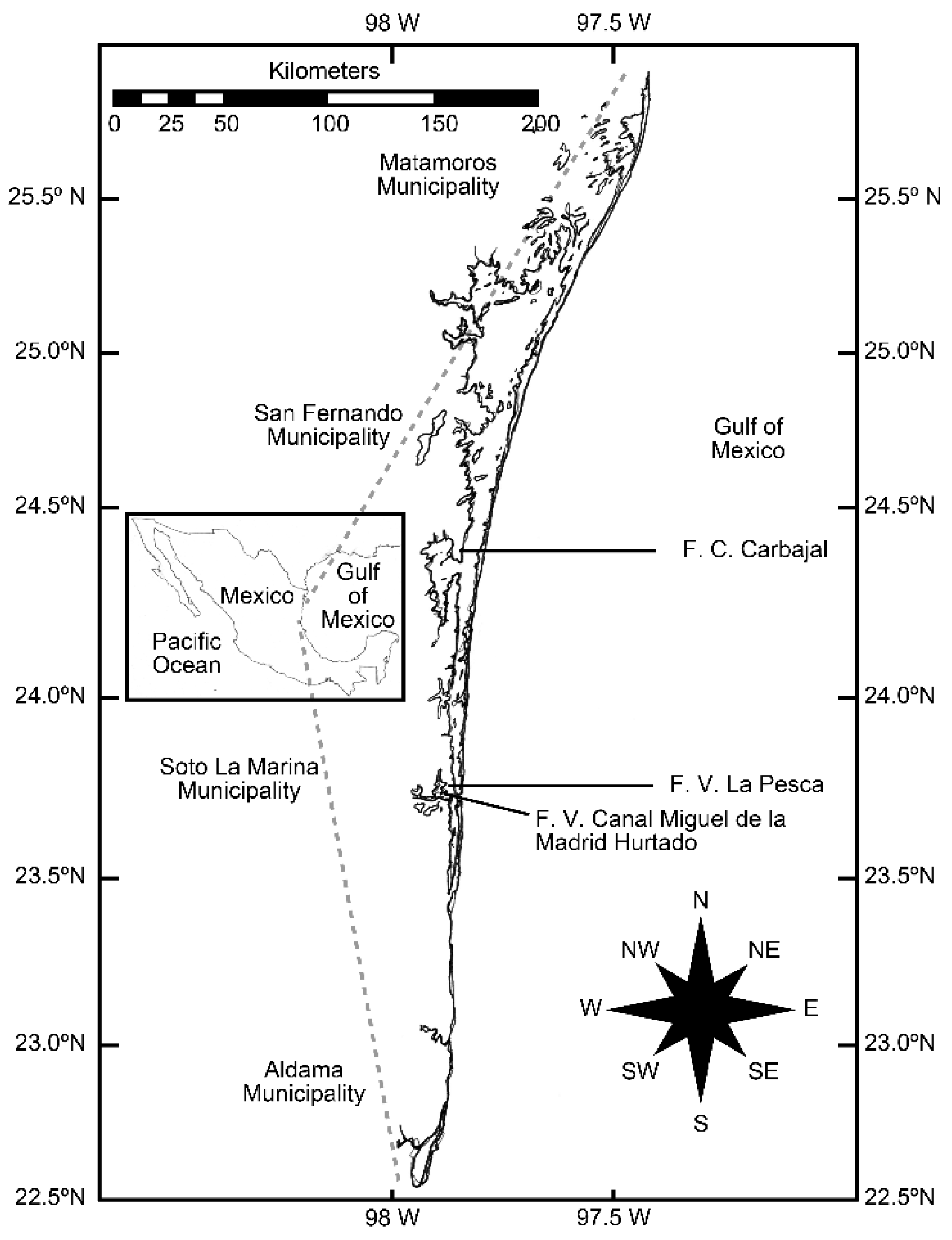
2.1. Study Area
2.2. Multinomial Analysis
2.3. Age Determination
2.4. Candidate Models
2.5. Model Fitting
2.6. Selection of Models
2.7. Differences and Plausibility of the Models
2.8. Multimodel Inference
2.9. Uncertainty in the Average Model
2.10. Statistical Tests
3. Results
3.1. Structure of Total Lengths and Gutted Weights
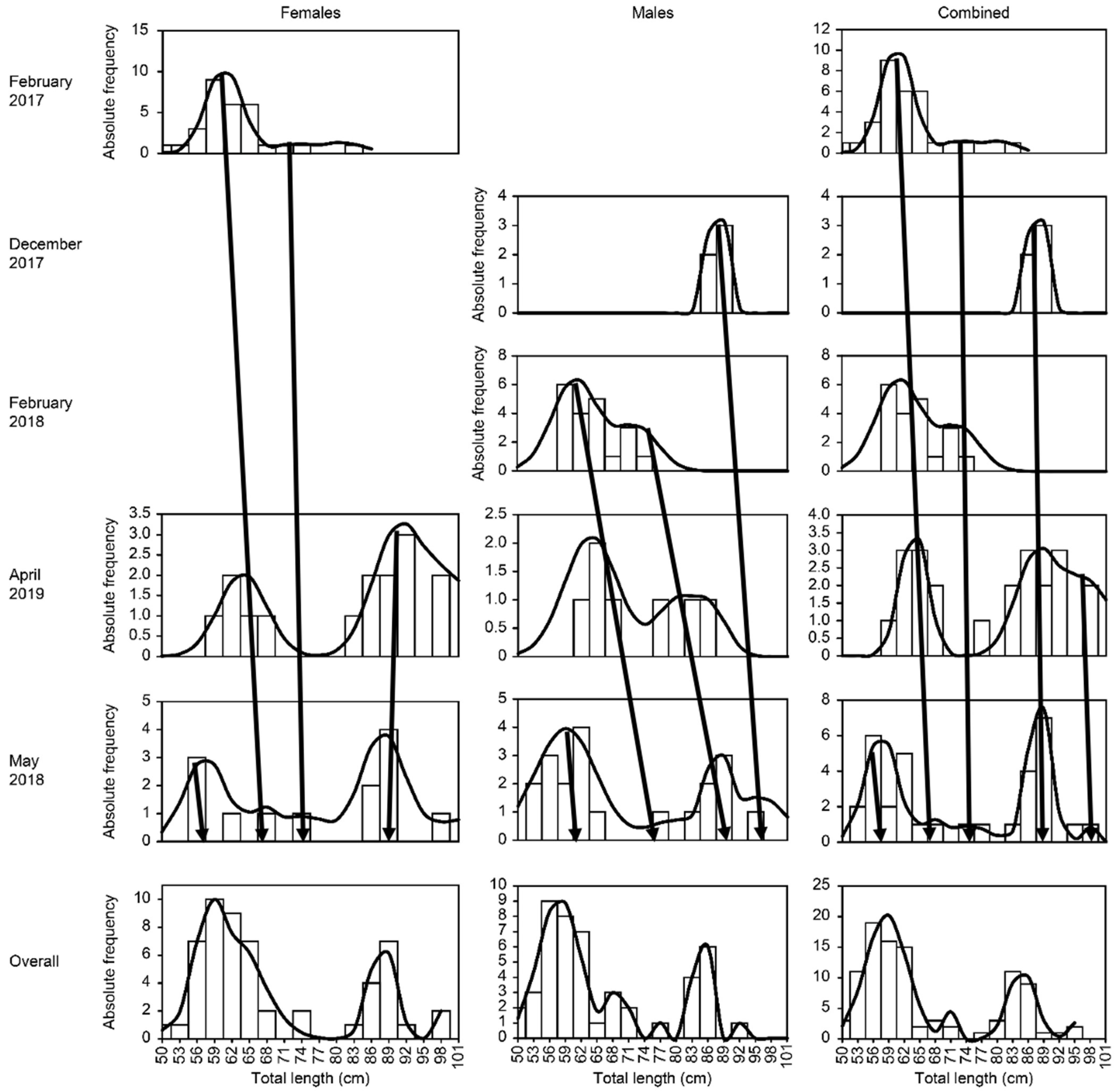
3.2. Identification of Modes in the Size Frequency Distributions
3.3. Fit of Growth Models
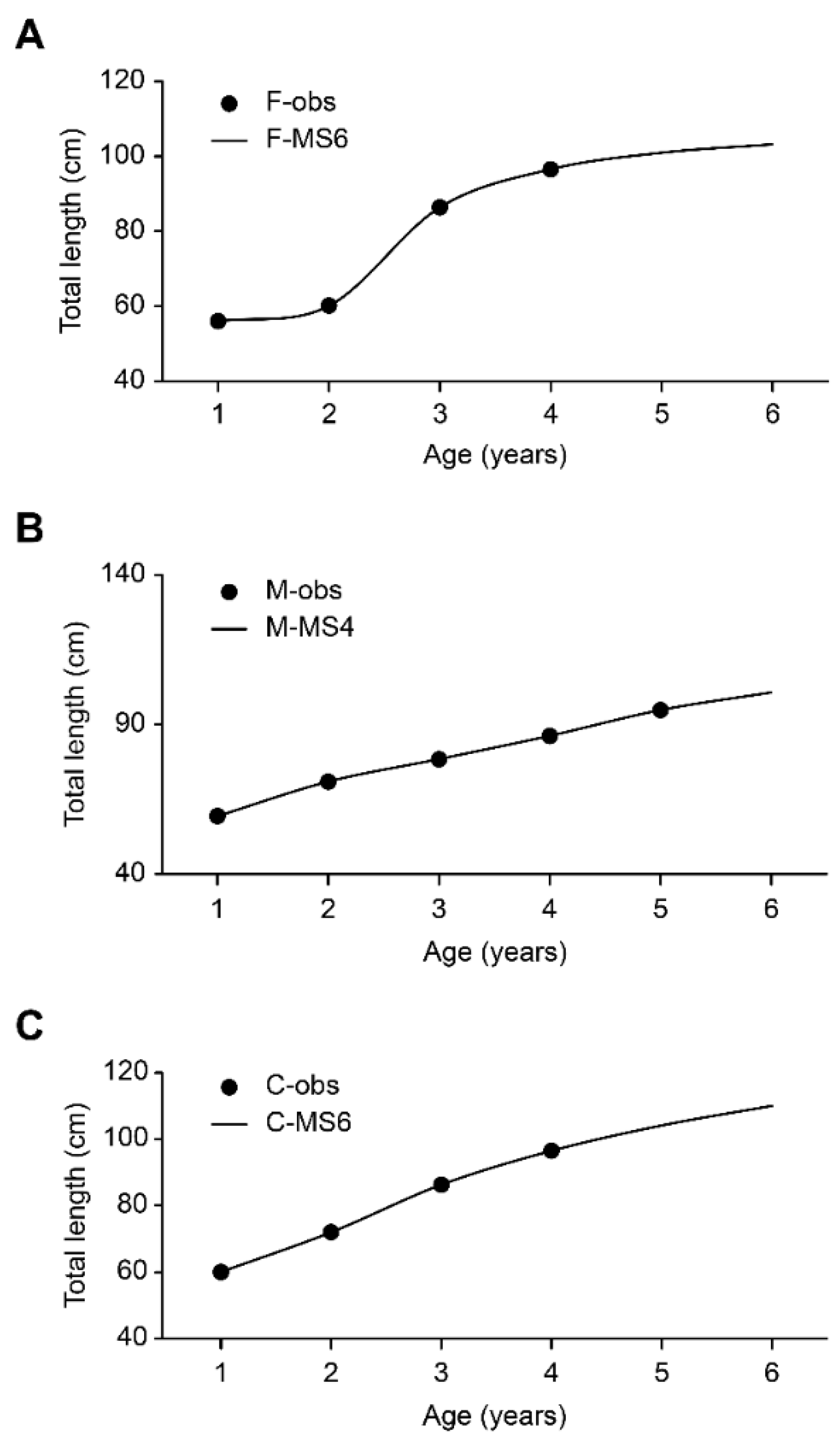
3.4. Differences in Total Lengths and Growth Curves
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Richardson, J. The Fish. In Fauna Boreali-Americana; or the Zoology of the Northern Parts of British America; J. Murray: London, UK, 1836; Volume 3, pp. 74–97. [Google Scholar]
- Rodríguez−Castro, J.H.; Adame−Garza, J.A.; Olmeda-de la Fuente, S.E. La actividad pesquera en Tamaulipas, ejemplo nacional. CienciaUAT 2010, 4, 28–35. [Google Scholar]
- Linnaeus, C. Systema Naturae per Regna tria Naturae, Secundum Classes, Ordinus, Genera, Species, cum Characteribus, Differentiis, Synonymis, Locis, 10th ed.; Laurentii Salvii: Holmiae, Sweden, 1758; 824p. [Google Scholar]
- Cortés, E.; Neer, J. Updated Catches of Atlantic Sharks. SEDAR 11 LCS05/06−DW−16; National Marine Fisheries Service, Southeast Fisheries Science Center: Panama, FL, USA, 2005.
- Pérez−Jiménez, J.C.; Mendez−Loeza, I. The small−scale shark fisheries in the Southern Gulf of Mexico: Understanding their heterogeneity to improve their management. Fish. Res. 2015, 172, 96–104. [Google Scholar] [CrossRef]
- Poey, F. Memorias Sobre la Historia Natural de la isla de Cuba, Acompañadas de Sumarios Latinos y Extractos en Francés; Imprenta de Barcina: Habana, Cuba, 1860; Volume 2. [Google Scholar]
- Ranzani, C. Dispositio familiae Molarum in genera et in species. Novi Comment. Acad. Sci. Inst. Bononiensis 1839, 3, 63–82. [Google Scholar]
- Castillo−Géniz, J.L. Aspectos Biológico−Pesqueros de los Tiburones Que Habitan las Aguas del Golfo de México; Tesis de Maestría, Facultad de Ciencias, Universidad Nacional Autónoma de México: México City, México, 2001. [Google Scholar]
- Márquez−Farias, F.; Castillo−Géniz, J.L.; de la Cruz, M.C.R. Demography of the bonnethead shark, Sphyrna tiburo (Linnaeus, 1758), in the Southeastern Gulf of Mexico. Cienc. Mar. 1998, 24, 13–34. [Google Scholar] [CrossRef][Green Version]
- DOF. NORMA Oficial Mexicana NOM−029−PESC−2006, Pesca Responsable de Tiburones y Rayas. Especificaciones para su Aprovechamiento; Diario Oficial de la Federación: México City, México, 2007.
- Müller, J.; Henle, F.G.J. Systematische Beschreibung der Plagiostomen; Veit und Comp.: Berlín, Germany, 1839; pp. 1–200. [Google Scholar]
- SEDAR. Stock Assessment Report Small Coastal Shark Complex, Atlantic Sharpnose, Blacknose, Bonnethead, and Finetooth Shark. In SEDAR 13 Stock Assessment Report; SEDAR: Calgary, Alberta, 2013. [Google Scholar]
- Cortés, E.; Parsons, G.R. Comparative demography of two populations of the bonnethead shark (Sphyrna tiburo). Can. J. Fish. Aquat. Sci. 1996, 53, 709–718. [Google Scholar] [CrossRef]
- Parsons, G.R.; Hoffmayer, E.R. Seasonal changes in the distribution and relative abundance of the Atlantic sharpnose shark rhizoprionodon terraenovaein the North Central Gulf of Mexico. Copeia 2005, 914–920. [Google Scholar] [CrossRef]
- Arkhipkin, A.I.; Roa−Ureta, R. Identification of ontogenetic growth models for squid. Mar. Freshw. Res. 2005, 56, 371–386. [Google Scholar] [CrossRef]
- Katsanevakis, S.; Maravelias, C.D. Modelling fish growth: Multi−model inference as a better alternative to a priori using von Bertalanffy equation. Fish Fish. 2008, 9, 178–187. [Google Scholar] [CrossRef]
- Araya, M.; Cubillos, L.A. Evidence of two−phase growth in elasmobranchs. Environ. Biol. Fishes 2006, 77, 293–300. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information−Theoretic Approach; Springer: New York, NY, USA, 2002. [Google Scholar]
- Cailliet, G.M.; Smith, W.D.; Mollet, H.F.; Goldman, K.J. Age and growth studies of chondrichthyan fishes: The need for consistency in terminology, verification, validation, and growth function fitting. Environ. Biol. Fishes 2006, 77, 211–228. [Google Scholar] [CrossRef]
- Paine, C.E.T.; Marthews, T.R.; Vogt, D.R.; Purves, D.; Rees, M.; Hector, A.; Turnbull, L.A. How to fit nonlinear plant growth models and calculate growth rates: An update for ecologists. Methods Ecol. Evolut. 2012, 3, 245–256. [Google Scholar] [CrossRef]
- Wilson, K.L.; Honsey, A.E.; Moe, B.; Venturelli, P. Growing the biphasic framework: Techniques and recommendations for fitting emerging growth models. Methods Ecol. Evol. 2017, 9, 822–833. [Google Scholar] [CrossRef]
- Day, T.; Taylor, P.D. Von Bertalanffy’s growth equation should not be used to model age and size at maturity. Am. Nat. 1997, 149, 381–393. [Google Scholar] [CrossRef]
- Lester, N.P.; Shuter, B.J.; Abrams, P.A. Interpreting the von Bertalanffy model of somatic growth in fishes: The cost of reproduction. Proc. Biol. Sci. 2004, 271, 1625–1631. [Google Scholar] [CrossRef]
- Paloheimo, J.E.; Dickie, L.M. Food and growth of fishes: I. A growth curve derived from experimental data. J. Fish. Res. Board Can. 1965, 22, 521–542. [Google Scholar] [CrossRef]
- Parker, R.R.; Larkin, P.A. A concept of growth in fishes. J. Fish. Res. Board Can. 1959, 16, 721–745. [Google Scholar] [CrossRef]
- Contreras−Reyes, J.E.; Wiff, R.; Soto, J.; Donovan, C.R.; Araya, M. Biphasic growth modelling in elasmobranchs based on asymmetric and heavy-tailed errors. Environ. Biol. Fish 2021, 104, 615–628. [Google Scholar] [CrossRef]
- Beverton, R.J.H.; Holt, S.J. On the Dynamics of Exploited Fish Populations; Fisheries Investment Series; U.K. Ministry of Agriculture and Fisheries: London, UK, 1957; Volume 19.
- Thompson, W.F.; Bell, F.H. Biological statistics of the Pacific halibut fishery. 2. Effect of changes in intensity upon total yield and yield per unit of gear. Rep. Int. Fish. Commn. 1934, 8, 49. [Google Scholar]
- Parsons, G.R. Geographic variation in reproduction between two populations of the bonnethead shark, Sphyrna tiburo. Environ. Biol. Fishes 1993, 38, 25–35. [Google Scholar] [CrossRef]
- Carlson, J.K.; Parsons, G.R. Age and growth of the bonnethead shark, Sphyrna tiburo, from Northwest Florida, with comments on clinal variation. Environ. Biol. Fishes 1997, 50, 331–341. [Google Scholar] [CrossRef]
- Lombardi−Carlson, L.A.; Cortés, E.; Parsons, G.R.; Manire, C.A. Latitudinal variation in life−history traits of bonnethead sharks, Sphyrna tiburo, (Carcharhiniformes: Sphyrnidae) from the Eastern Gulf of Mexico. Mar. Freshw. Res. 2003, 54, 875–883. [Google Scholar] [CrossRef]
- Frazier, B.S.; Driggers, W.B.; Adams, D.H.; Jones, C.M.; Loefer, J.K. Validated age, growth and maturity of the bonnethead Sphyrna tiburo in the Western North Atlantic ocean. J. Fish Biol. 2014, 85, 688–712. [Google Scholar] [CrossRef] [PubMed]
- Haddon, M. Modelling and Quantitative Methods in Fisheries; Chapman and Hall: New York, NY, USA, 2001. [Google Scholar]
- Montgomery, S.S.; Walsh, C.T.; Kesby, C.L.; Johnson, D.D. Studies on the Growth and Mortality of School Prawns; FRDC Project No 2001(/029); Industry and Investment NSW–Fisheries Final Report Series No. 119; Cronulla Fisheries Research Centre of Excellence: Cronulla, Australia, 2010. [Google Scholar]
- Aguirre−Villasenor, H.; Morales-Bojórquez, E.; Morán-Angulo, R.E.; Madrid-Vera, J.; Valdez-Pineda, M.C. Biological indicators for the Pacific sierra (Scomberomorus sierra) fishery in the southern Gulf of California, Mexico. Cienc. Mar. 2006, 32, 471–484. [Google Scholar] [CrossRef][Green Version]
- Neter, J.; Kutner, M.H.; Nachtschien, J.; Wasserman, W. Applied Linear Statistical Models; McGraw−Hill: New York, NY, USA, 1996. [Google Scholar]
- Sparre, P.; Venema, S.C. Introduction to Tropical Fish Stock Assessment, Part 1: Manual. In FAO Fisheries and Aquaculture Technical Paper 306/1, Rev. 2; FAO: Rome, Italy, 1998. [Google Scholar]
- Parsons, G.R. Age determination and growth of the bonnethead shark Sphyrna tiburo: A comparison of two populations. Mar. Biol. 1993, 117, 23–31. [Google Scholar] [CrossRef]
- von Bertalanffy, L. A Quantitative theory of organic growth (inquiries on growth laws. II). Hum. Biol. 1938, 10, 181–213. [Google Scholar]
- Soriano, M.; Moreau, J.; Hoenig, J.M.; Pauly, D. New functions for the analysis of two−phase growth of juvenile and adult fishes, with application to nile perch. Trans. Am. Fish. Soc. 1992, 121, 486–493. [Google Scholar] [CrossRef]
- Ricker, W.E. Growth rates and models. In Fish Physiology: Bioenergetics and Growth; Hoar, W.S., Randall, D.J., Brett, J.R., Eds.; Academic Press: New York, NY, USA, 1979; pp. 677–743. [Google Scholar]
- Grosjean, P. Growth Model of the Reared Sea Urchin Paracentrotus Lividus (Lamarck, 1816). Ph.D. Thesis, Faculte des Sciences Laboratoire de Biologie Marine, Universite Libre de Bruxelles, Bruxelles, Belgium, 2001. [Google Scholar]
- Ricker, W.E. Computation and interpretation of biological statistics of fish populations. Bull. Fish. Res. Board Can. 1975, 191, 1–382. [Google Scholar]
- Mollet, H.F.; Ezcurra, J.M.; O’Sullivan, J.B. Captive biology of the pelagic stingray, Dasyatis violacea (Bonaparte, 1832). Mar. Freshw. Res. 2002, 53, 531–541. [Google Scholar] [CrossRef]
- Akaike, H. Information theory as an extension of the maximum likelihood principle. In Proceedings of the 2nd International Symposium on Information Theory, Tsahkadsor, Armenia, 2–8 September 1971; Petrov, B.N., Csaki, F., Eds.; pp. 267–281. [Google Scholar]
- Zar, J. Biostatistical Analysis; Prentice Hall: Hoboken, NJ, USA, 2009. [Google Scholar]
- Lombardi−Carlson, L.A. Life History Traits of Bonnethead Sharks, Sphyrna tiburo, from the Eastern Gulf of Mexico; SEDAR 13−DW−24; SEDAR: North Charleston, SC, USA, 2007. [Google Scholar]
- Thorson, J.T.; Simpfendorfer, C.A. Gear selectivity and sample size effects on growth curve selection in shark age and growth studies. Fish. Res. 2009, 98, 75–84. [Google Scholar] [CrossRef]
- Braccini, J.M.; Gillanders, B.M.; Walker, T.I.; Tovar−Avila, J. Comparison of deterministic growth models fitted to length−at−age data of the piked spurdog (Squalus megalops) in South−Eastern Australia. Mar. Freshw. Res. 2007, 58, 24–33. [Google Scholar] [CrossRef]
- Tribuzio, C.; Kruse, G.; Fujioka, J. Age and growth of spiny dogfish (Squalus acanthias) in the Gulf of Alaska: Analysis of alternative growth models. Fish. Bull. 2010, 108, 119–135. [Google Scholar]
- Mejía−Falla, P.A.; Cortés, E.; Navia, A.F.; Zapata, F.A. Age and growth of the round stingray Urotrygon rogersi, a particularly fast−growing and short−lived elasmobranch. PLoS ONE 2014, 9, e96077. [Google Scholar] [CrossRef] [PubMed]
- Aversa, M.I.; Dans, S.L.; GarcÍA, N.A.; Crespo, E.A. Growth models fitted to Dipturus chilensis length−at−age−data support a two phase growth. Rev. Chil. Hist. Nat. 2011, 84, 33–49. [Google Scholar] [CrossRef]
- Hernández−Betancourt, S.; Serrano−Flores, F.; Chumba−Segura, L.; Sélem−Salas, C.I. Los Tiburones en la Costa Norte de Yucatán: Poblaciones Amenazadas por la Sobrepesca? 2020. Available online: chrome-extension://efaidnbmnnnibpcajpcglclefindmkaj/viewer.html?pdfurl=https%3A%2F%2Fwww.ccba.uady.mx%2Fbioagro%2FV4N2%2FV4N2.pdf&clen=1738846&chunk=true (accessed on 11 February 2022).
- González−de Acevedo, M. Reproductive Biology of the Bonnethead (Sphyrna tiburo) from the Southeastern U.S. Atlantic Coast. Master’s Thesis, University of North Florida, Jacksonville, FL, USA, 2014. [Google Scholar]
- García−Alvarez, M.A. Uso de Recursos Tróficos por Rhizoprionodon terraenovae y Sphyrna tiburo, en el Sureste del Golfo de México. Master´s Thesis, Universidad Veracruzana, Veracrúz, México, 2014. [Google Scholar]
- Palacios−Hernández, D.; Castillo−Géniz, J.L.; Méndez−Loeza, I.; Pérez−Jiménez, J.C. Temporal and latitudinal comparisons of reproductive parameters in a heavily exploited shark, the bonnethead, Sphyrna tiburo (L. 1758), in the Southern Gulf of Mexico. J. Fish Biol. 2020, 97, 100–112. [Google Scholar] [CrossRef] [PubMed]
- Froese, R.; Binohlan, C. Empirical relationships to estimate asymptotic length, length at first maturity and length at maximum yield per recruit in fishes, with a simple method to evaluate length frequency data. J. Fish Biol. 2000, 56, 758–773. [Google Scholar] [CrossRef]
- Munro, J.L.; Pauly, D. A simple method for comparing the growth of fishes and invertebrates. Fishbyte 1983, 1, 5–6. [Google Scholar]
- Moreau, J.; Bambino, C.; Pauly, D. Indices of overall fish growth performance of 100 Tilapia (Cichlidae) populations. In The First Asian Fisheries Forum; Maclean, J.L., Dizon, L.B., Hosillos, L.V., Eds.; Asian Fisheries Society: Manilla, Philippines, 1986; pp. 201–206. [Google Scholar]
- Minte-Vera, C.V.; Maunder, M.N.; Casselman, J.M.; Campana, S.E. Growth functions that incorporate the cost of reproduction. Fish. Res. 2016, 180, 31–44. [Google Scholar] [CrossRef]
- Kroetz, A.M.; Drymon, J.M.; Powers, S.P. Comparative dietary diversity and trophic ecology of two estuarine mesopredators. Estuaries Coasts 2017, 40, 1171–1182. [Google Scholar] [CrossRef]
- Bethea, D.M.; Hale, L.; Carlson, J.K.; Cortés, E.; Manire, C.A.; Gelsleichter, J. Geographic and ontogenetic variation in the diet and daily ration of the bonnethead shark, Sphyrna tiburo, from the eastern Gulf of Mexico. Mar. Biol. 2007, 152, 1009–1020. [Google Scholar] [CrossRef]
- Ulrich, G.; Jones, C.; Driggers, W.B.I.; Drymon, M.; Oakley, D.; Riley, C. Habitat utilization, relative abundance and seasonality of sharks in the estuarine and near shore waters of South Carolina. Am. Fish. Soc. Symp. 2007, 50, 125–139. [Google Scholar]
- Cortés, E. Life history patterns and correlations in sharks. Rev. Fish. Sci. 2000, 8, 299–344. [Google Scholar] [CrossRef]
- Branstetter, S. Early life-history implications of selected carcharhinid and lamnoid sharks of the Northwest Atlantic. In Elasmobranchs as Living Resources: Advances in the Biology, Ecology, Systematics, and the Status of the Fisheries; Pratt, H.L., Gruber, S.H., Taniuchi, T., Eds.; NMFS: Maryland, MA, USA, 1990; pp. 17–28. [Google Scholar]
- Katsanevakis, S. Multi−model inference and model selection in Mexican fisheries. Cienc. Pesq. 2014, 22, 6–7. [Google Scholar]
- Fabens, A.J. Properties and fitting of the Von Bertalanffy growth curve. Growth 1965, 29, 265–289. [Google Scholar] [PubMed]
- Kenchington, T.J. Natural mortality estimators for information−limited fisheries. Fish Fish. 2013, 15, 533–562. [Google Scholar] [CrossRef]
- Zhou, S.; Yin, S.; Thorson, J.T.; Smith, A.D.M.; Fuller, M. Linking fishing mortality reference points to life history traits: An empirical study. Can. J. Fish. Aquat. Sci. 2012, 69, 1292–1301. [Google Scholar] [CrossRef]
| Model | Type | Function | Parameters to Be Estimated | Reference |
|---|---|---|---|---|
| VB1 (3 parameters) | S | L∞; k; t0 | von Bertalanffy [26] | |
| VB2 (3 parameters) | S | L∞; k; L0; | Fabens [32] | |
| S1 (5 parameters) | B | L∞; k; t0; th; h | Soriano et al. [27] | |
| S2 (5 parameters) | B | L∞; k; t0; th; h | Soriano et al. [27] | |
| S3 (5 parameters) | B | L∞S1; k S1; t0S1 Lth; L∞S2; k S2; th S1 | Soriano et al. [27] | |
| S4 (5 parameters) | B | L∞; L0; k; h; th; | Soriano et al. [27] | |
| S5 (4 parameters) | B | L∞; L0VB2; k; h; th; | Soriano et al. [27] | |
| S6 (4 parameters) | B | L∞; L0G2; k; h; th; | Soriano et al. [27] | |
| G1 (3 parameters) | S | L∞; k; t0 | Ricker [30] | |
| G2 (3 parameters) | S | L∞; k; L0 | Mollet et al. [31] | |
| J1 (3 parameters) | S | L∞; k; t0 | Grosjean [29] | |
| L1 (3 parameters) | S | L∞; k; t0 | Ricker [30] | |
| L2 (3 parameters) | S | L∞; k; L0 | Ricker [28] |
| Month/Year | Ngm | n | Mean (cm) | CI (cm) | SI |
|---|---|---|---|---|---|
| Females | |||||
| September 2016 | 1 | 54.40 | |||
| February 2017 | 1 | 20 | 59.09 | 56.11, 62.07 | 3.98 |
| 2 | 5 | 71.02 | 68.00, 74.04 | 2.65 | |
| 3 | 4 | 79.12 | 76.03, 82.21 | ||
| September 2017 | 1 | 81.00 | |||
| February 2018 | 2 | 85.50 | |||
| May 2018 | 1 | 5 | 56.02 | 52.52, 59.52 | 3.40 |
| 2 | 1 | 65.72 | 63.51, 67.93 | 2.41 | |
| 3 | 2 | 73.12 | 69.20, 77.04 | 3.53 | |
| 4 | 6 | 86.45 | 82.81, 90.09 | ||
| April 2019 | 1 | 6 | 62.41 | 58.41, 66.41 | 6.49 |
| 2 | 9 | 89.03 | 84.83, 93.23 | 2.19 | |
| 3 | 2 | 98.21 | 94.01, 102.41 | ||
| Males | |||||
| February 2017 | 1 | 57 | |||
| December 2017 | 1 | 6 | 86.13 | 85.89, 86.37 | 2.35 |
| February 2018 | 1 | 14 | 59.43 | 55.2, 63.66 | 2.89 |
| 2 | 6 | 71.12 | 67.25, 74.99 | ||
| May 2018 | 1 | 11 | 59.34 | 54.34, 64.34 | 3.81 |
| 2 | 3 | 78.37 | 73.37, 83.37 | 2.24 | |
| 3 | 4 | 86.21 | 84.21, 88.21 | 2.84 | |
| 4 | 2 | 94.73 | 90.73, 98.73 | ||
| April 2019 | 1 | 6 | 62.34 | 57.34, 67.34 | 3.70 |
| 2 | 1 | 78.37 | 74.7, 82.04 | 2.02 | |
| 3 | 1 | 85.11 | 82.11, 88.11 | ||
| Combined | |||||
| September 2016 | 1 | 54.40 | |||
| February 2017 | 1 | 20 | 59.09 | 56.11, 62.07 | 3.98 |
| 2 | 6 | 71.02 | 68.00, 74.04 | 2.65 | |
| 3 | 4 | 79.12 | 76.03, 82.21 | ||
| September 2017 | 1 | 81.00 | |||
| December 2017 | 1 | 6 | 86.13 | 84.67, 87.59 | |
| February 2018 | 1 | 21 | 59.43 | 55.20, 63.66 | 2.89 |
| 2 | 1 | 71.12 | 67.25, 74.99 | ||
| May 2018 | 1 | 13 | 56.02 | 53.02, 59.02 | 3.88 |
| 2 | 1 | 65.72 | 63.72, 67.72 | 2.50 | |
| 3 | 2 | 73.12 | 69.20, 77.04 | 4.54 | |
| 4 | 17 | 86.56 | 84.56, 88.56 | 6.31 | |
| 5 | 1 | 96.02 | 95.02, 97.02 | ||
| April 2019 | 1 | 7 | 62.34 | 59.84, 64.84 | 7.37 |
| 2 | 10 | 86.21 | 82.23, 90.19 | 2.42 | |
| 3 | 7 | 95.87 | 91.85, 99.89 | 2.14 | |
| 4 | 1 | 101.23 | 100.25, 102.21 |
| Model | Additive Error | Multiplicative Error | ||||||
|---|---|---|---|---|---|---|---|---|
| ML | AICc | Δi | wi | ML | AICc | Δi | wi | |
| Females | ||||||||
| VB1 | −13.859 | 33.719 | 99.212 | 0.000 | −14.116 | 34.231 | 101.123 | 0.000 |
| VB2 | −11.726 | 27.453 | 95.742 | 0.000 | −11.794 | 29.588 | 96.480 | 0.000 |
| S1 | 33.022 | −56.044 | 8.052 | 0.017 | 33.064 | −56.128 | 7.968 | 0.018 |
| S2 | 26.168 | −42.336 | 21.759 | 0.000 | 26.168 | −42.336 | 21.759 | 0.000 |
| S3 | −20.084 | 54.168 | 111.253 | 0.000 | −20.084 | 40.168 | 111.253 | 0.000 |
| S4 | 18.355 | −26.711 | 37.385 | 0.000 | 18.420 | −26.841 | 37.255 | 0.000 |
| S5 | 32.286 | −56.572 | 8.922 | 0.011 | 32.286 | −56.572 | 8.922 | 0.011 |
| S6 | 36.747 | −65.494 | 0.000 | 0.971 | 36.747 | −65.494 | 0.000 | 0.971 |
| G1 | −11.518 | 29.036 | 95.927 | 0.000 | −11.530 | 29.060 | 95.952 | 0.000 |
| G2 | −11.514 | 27.027 | 95.317 | 0.000 | −11.514 | 27.027 | 95.317 | 0.000 |
| J | −20.484 | 46.969 | 113.860 | 0.000 | −26.296 | 58.592 | 125.484 | 0.000 |
| L1 | −11.492 | 28.985 | 95.877 | 0.000 | −11.536 | 29.072 | 95.964 | 0.000 |
| L2 | −14.292 | 32.583 | 100.873 | 0.000 | −14.418 | 32.836 | 101.126 | 0.000 |
| Males | ||||||||
| VB1 | −15.009 | 36.019 | 101.928 | 0.000 | −15.009 | 36.019 | 102.099 | 0.000 |
| VB2 | −5.215 | 16.430 | 82.340 | 0.000 | −5.341 | 14.682 | 82.063 | 0.000 |
| S1 | −9.224 | 28.447 | 91.755 | 0.000 | −9.224 | 28.447 | 91.925 | 0.000 |
| S2 | −11.192 | 32.383 | 95.691 | 0.000 | −11.192 | 32.383 | 95.861 | 0.000 |
| S3 | −27.127 | 54.254 | 124.067 | 0.000 | −26.923 | 53.845 | 123.829 | 0.000 |
| S4 | 36.654 | −63.308 | 0.000 | 1.000 | 36.739 | −63.478 | 0.000 | 1.000 |
| S5 | −3.403 | 14.807 | 79.416 | 0.000 | −3.403 | 14.807 | 79.586 | 0.000 |
| S6 | −4.402 | 16.803 | 81.412 | 0.000 | −4.391 | 16.782 | 81.561 | 0.000 |
| G1 | −5.615 | 17.230 | 83.140 | 0.000 | −5.615 | 17.230 | 83.310 | 0.000 |
| G2 | −5.607 | 15.214 | 82.424 | 0.000 | −5.607 | 15.214 | 82.595 | 0.000 |
| J | −13.890 | 33.781 | 99.690 | 0.000 | −13.994 | 33.988 | 100.068 | 0.000 |
| L1 | −5.959 | 17.918 | 83.828 | 0.000 | −5.959 | 17.918 | 83.998 | 0.000 |
| L2 | −10.645 | 25.290 | 92.501 | 0.000 | −10.817 | 25.633 | 93.015 | 0.000 |
| Combined sexes | ||||||||
| VB1 | −11.839 | 29.677 | 77.981 | 0.000 | −11978 | 29.955 | 79.638 | 0.000 |
| VB2 | −4.379 | 12.758 | 63.858 | 0.000 | −4461 | 14.923 | 64.605 | 0.000 |
| S1 | 23.151 | −36.302 | 10.604 | 0.004 | 23679 | −37.357 | 9.529 | 0.007 |
| S2 | 26.402 | −42.804 | 4.103 | 0.113 | 26402 | −42.804 | 4.082 | 0.114 |
| S3 | −19.365 | 52.731 | 96.841 | 0.000 | −21140 | 42.279 | 96.156 | 0.000 |
| S4 | −10.987 | 31.974 | 78.881 | 0.000 | −8074 | 26.148 | 73.035 | 0.000 |
| S5 | 21.978 | −35.956 | 12.348 | 0.002 | 21978 | −35.956 | 12.328 | 0.002 |
| S6 | 28.152 | −48.304 | 0.000 | 0.881 | 28142 | −48.284 | 0.000 | 0.877 |
| G1 | −4.091 | 14.182 | 63.885 | 0.000 | −4176 | 14.351 | 64.034 | 0.000 |
| G2 | −4.091 | 14.182 | 63.885 | 0.000 | −4091 | 12.182 | 63.262 | 0.000 |
| J | −49.778 | 105.556 | 155.258 | 0.000 | −49778 | 105.556 | 155.238 | 0.000 |
| L1 | −3.773 | 13.546 | 63.249 | 0.000 | −3863 | 13.725 | 63.408 | 0.000 |
| L2 | −11.189 | 26.378 | 77.478 | 0.000 | −11189 | 26.378 | 77.458 | 0.000 |
| Model | Φ | L∞ (Annual) | k (Annual) | t0 (Annual) | L0 | th | h | Lth | Condition |
|---|---|---|---|---|---|---|---|---|---|
| Females | |||||||||
| VB1 | 3 | 102.51 | 0.60 | 0.000 | |||||
| VB2 | 3 | 2.153.65 | 0.00 | 37.672 | |||||
| S1 | 5 | 103.76 | 1.38 | 0.000 | 1.699 | 0.416 | 54.806 | ||
| S2 | 5 | 98.76 | 1.11 | 0.000 | 2.220 | 0.603 | 61.457 | ||
| S3 | 3 | 103.76 | 1.38 | 0.000 | If t < th | ||||
| 4 | 98.76 | 1.11 | 2.220 | 61.46 | If t > th | ||||
| S4 | 5 | 111.86 | 0.31 | 74.034 | 1.237 | 2.377 | 47.561 | ||
| S5 | 4 | 104.99 | 0.58 | 37.672 * | 1.732 | 0.700 | 55.319 | ||
| S6 | 4 | 105.96 | 0.54 | 42.628 ** | 1.641 | 0.791 | 53.342 | ||
| G1 | 3 | 1.101.29 | 0.07 | 15.994 | |||||
| G2 | 3 | 1.878.97 | 0.06 | 42.628 | |||||
| J | 3 | 1.042.01 | 0.12 | 0.000 | |||||
| L1 | 3 | 258.86 | 0.28 | 5.753 | |||||
| L2 | 2 | 98.66 | 0.51 | ||||||
| Males | |||||||||
| VB1 | 3 | 89.23 | 0.93 | 0.000 | |||||
| VB2 | 3 | 165.02 | 0.10 | 48.837 | |||||
| S1 | 5 | 95.84 | 1.08 | 0.000 | 2.476 | 0.199 | 71.444 | ||
| S2 | 5 | 91.84 | 1.19 | 0.000 | 2.641 | 0.527 | 71.061 | ||
| S3 | 3 | 95.84 | 1.08 | 0.000 | If t < th | ||||
| 4 | 91.84 | 1.19 | 2.641 | 71.061 | If t > th | ||||
| S4 | 5 | 122.18 | 0.2184 | 44.368 | 3.479 | 0.151 | 81.355 | ||
| S5 | 4 | 165.63 | 0.10 | 48.837 * | 3.695 | 0.070 | 83.552 | ||
| S6 | 4 | 216.14 | 0.07 | 49.735 ** | 4.160 | 0.061 | 87.288 | ||
| G1 | 3 | 135.61 | 0.20 | 0.000 | |||||
| G2 | 3 | 133.44 | 0.21 | 49.735 | |||||
| J | 3 | 99.89 | 1.74 | 0.000 | |||||
| L1 | 3 | 121.12 | 0.32 | 1.060 | |||||
| L2 | 2 | 101.90 | 0.43 | ||||||
| Combined sexes | |||||||||
| VB1 | 3 | 108.79 | 0.54 | 0.000 | |||||
| VB2 | 3 | 263.38 | 0.07 | 45.610 | |||||
| S1 | 5 | 102.90 | 2.42 | 0.546 | 2.120 | 0.283 | 72.11 | ||
| S2 | 5 | 98.05 | 1.25 | 0.085 | 2.460 | 0.542 | 72.90 | ||
| S3 | 3 | 102.90 | 2.42 | 0.55 | If t < th | ||||
| 4 | 98.05 | 1.25 | 2.460 | 72.90 | If t > th | ||||
| S4 | 5 | 140.87 | 0.16 | 60.016 | 1.653 | 0.575 | 68.82 | ||
| S5 | 4 | 102.83 | 0.69 | 45.610 * | 2.337 | 0.368 | 65.12 | ||
| S6 | 4 | 132.63 | 0.23 | 46.457 ** | 1.449 | 0.290 | 64.31 | ||
| G1 | 3 | 156.65 | 0.23 | 0.844 | |||||
| G2 | 3 | 156.81 | 0.23 | 46.457 | |||||
| J | 3 | 156.65 | 0.23 | 0.844 | |||||
| L1 | 3 | 132.67 | 0.40 | 1.506 | |||||
| L2 | 2 | 102.31 | 0.53 | ||||||
| Parameter | Estimates | Selected Model | Average Model | ||||
|---|---|---|---|---|---|---|---|
| Females (S6) | Males (S4) | Combined | Females | Males | Combined | ||
| L0 | Ep | 105.957 | 122.182 | 132.628 | 106.453 | 122.182 | 128.581 |
| Linf | 105.099 | 122.158 | 125.643 | 105.605 | 122.158 | 121.662 | |
| Lsup | 106.815 | 122.207 | 139.612 | 107.300 | 122.207 | 135.499 | |
| k | Ep | 0.541 | 0.218 | 0.226 | 0.537 | 0.218 | 0.275 |
| Linf | 0.530 | 0.194 | 0.137 | 0.526 | 0.194 | 0.191 | |
| Lsup | 0.552 | 0.243 | 0.314 | 0.549 | 0.243 | 0.359 | |
| th | Ep | 1.641 | 3.479 | 1.449 | 1.606 | 3.479 | 1.566 |
| Linf | 1.580 | 3.455 | 1.245 | 1.545 | 3.455 | 1.364 | |
| Lsup | 1.703 | 3.504 | 1.653 | 1.666 | 3.504 | 1.769 | |
| h | Ep | 0.791 | 0.151 | 0.290 | 0.930 | 0.151 | 0.318 |
| Linf | 0.551 | 0.126 | 0.234 | 0.694 | 0.126 | 0.264 | |
| Lsup | 1.032 | 0.176 | 0.345 | 1.166 | 0.176 | 0.373 | |
| L0 | Ep | 42.628 | 44.368 | 46.457 | 45.511 | 45.996 | 46.455 |
| Linf | 37.566 | 42.273 | 46.428 | 40.484 | 44.208 | 46.427 | |
| Lsup | 47.691 | 46.462 | 46.486 | 50.537 | 47.783 | 46.484 | |
| Lt | Ep | 53.342 | 81.355 | 64.314 | 52.853 | 81.355 | 65.322 |
| Linf | 52.497 | 81.330 | 62.574 | 52.019 | 81.330 | 63.599 | |
| Lsup | 54.186 | 81.379 | 66.053 | 53.687 | 81.379 | 67.044 | |
| Author | Year | Place | Method | L∞ | k | L0 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F | M | C | F | M | C | F | M | C | ||||
| This study | 2021 | Tamaulipas (Mexico) | sfd | 105.96 | 122.18 | 132.63 | 0.54 | 0.22 | 0.23 | 42.63 | 44.37 | 46.46 |
| Palacios−Hernández et al. [51] | 2020 | Tabasco and Campeche (Mexico) | nmu | 97.48 * | 123.06 * | 0.24 *** | 0.21 *** | 31.5 | ||||
| 124.07 * | 125.08 * | 0.21 *** | 0.21 *** | 33 | ||||||||
| García−Álvarez [50] | 2014 | Campeche (Mexico) | 115.99 * | 107.91 * | 0.22 *** | 0.23 *** | 37.8 | |||||
| González de Acevedo [49] | 2014 | Atlantic coast | 30.2 | |||||||||
| Frazier et al. [19] | 2014 | East Coast of Florida (Atlantic Ocean) | 128.02 ** | 97.59 ** | 0.18 | 0.29 | 38.77 ** | 37.57 ** | ||||
| Hernández−Betancourt et al. [48] | 2011 | Yucatan (Mexico) | 112.96 * | 0.22 *** | 40 | |||||||
| Lombardi−Carlson [35] | 2007 | West Coast of Florida GM | hs | 89.40 | 70.30 | 0.28 | 0.54 | 52.31 ** | 52.55 ** | |||
| Lombardi−Carlson et al. [18] | 2003 | North−West Florida | 139.80 | 100.70 | 0.18 | 0.35 | ||||||
| Tampa Bay | 127.70 | 86.80 | 0.16 | 0.44 | 23.7 | |||||||
| Florida Bay | 93.90 | 85.80 | 0.29 | 0.25 | 21.5 | |||||||
| Castillo−Géniz [47] | 2001 | Tamaulipas (Mexico) | nmu | 127.10 * | 0.20 *** | 35−40 | ||||||
| Veracruz (Mexico) | 100.32 * | 0.24 *** | ||||||||||
| Tabasco (Mexico) | 124.07 * | 0.21 *** | ||||||||||
| Campeche (Mexico) | 124.58 * | 0.21 *** | ||||||||||
| Yucatan (Mexico) | 121.04 * | 0.21 *** | ||||||||||
| Márquez−Farías et al. [46] | 1998 | Southeastern Gulf of Mexico | 30−35 | |||||||||
| Carlson and Parsons [17] | 1997 | North−West Florida | hs | 122.6 | 89.7 | 0.28 | 0.69 | |||||
| Parsons [25] | 1993b | Tampa Bay | 115 | 88.8 | 0.34 | 0.58 | 34.7 | |||||
| Florida Bay | 103.3 | 81.5 | 0.37 | 0.53 | 27.2 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olmeda-de la Fuente, S.E.; Rodríguez-Castro, J.H.; Ramírez-de León, J.A.; Caballero-Rico, F.C.; Rodríguez-Olmeda, J.A.; Toledano-Toledano, F. Modeling the Individual Growth of the Bonnethead Shark Sphyrna tiburo of the Western Gulf of Mexico Using the Multimodel Approach. Fishes 2022, 7, 157. https://doi.org/10.3390/fishes7040157
Olmeda-de la Fuente SE, Rodríguez-Castro JH, Ramírez-de León JA, Caballero-Rico FC, Rodríguez-Olmeda JA, Toledano-Toledano F. Modeling the Individual Growth of the Bonnethead Shark Sphyrna tiburo of the Western Gulf of Mexico Using the Multimodel Approach. Fishes. 2022; 7(4):157. https://doi.org/10.3390/fishes7040157
Chicago/Turabian StyleOlmeda-de la Fuente, Sandra Edith, Jorge Homero Rodríguez-Castro, Jose Alberto Ramírez-de León, Frida Carmina Caballero-Rico, Jorge Alejandro Rodríguez-Olmeda, and Filiberto Toledano-Toledano. 2022. "Modeling the Individual Growth of the Bonnethead Shark Sphyrna tiburo of the Western Gulf of Mexico Using the Multimodel Approach" Fishes 7, no. 4: 157. https://doi.org/10.3390/fishes7040157
APA StyleOlmeda-de la Fuente, S. E., Rodríguez-Castro, J. H., Ramírez-de León, J. A., Caballero-Rico, F. C., Rodríguez-Olmeda, J. A., & Toledano-Toledano, F. (2022). Modeling the Individual Growth of the Bonnethead Shark Sphyrna tiburo of the Western Gulf of Mexico Using the Multimodel Approach. Fishes, 7(4), 157. https://doi.org/10.3390/fishes7040157






