Abstract
Linear mixed-effects modeling has been used to characterize fish growth changes over time, but early studies did not fully consider the implicit relationship among the three major factors of fish age, year-class, and sampling year in model development. Our objective is to resolve this issue and develop a linear mixed-effects model to clearly assess how lake trout (Salvelinus namaycush) growth has responded to the ecosystem regime shift in Lake Huron. We found that, from the late 1970s through the early 2000s, lake trout weight-at-age in northern Lake Huron had large variation with no apparent temporal trend, whereas the weight-at-age in southern Lake Huron steadily declined but remained larger than that in northern Lake Huron. The difference between northern and southern Lake Huron almost disappeared prior to the 2003 collapse of alewives, which accelerated the weight-at-age declines during the 2000s in both regions. By 2010, lake trout growth had a modest recovery and then stabilized. Our model fitted and explained variation in lake trout weight-at-age between years, regions, and recruitment origins, with the fixed age effect representing the general growth trajectory, the fixed year effect as the year-specific growth index, and the random year-class effect as the cohort-specific growth index.
Keywords:
growth comparison across years; cohort-specific and size-dependent growth; ecosystem regime shift; size-at-age data; linear mixed-effects model; model comparison and selection; Akaike information criterion; Bayesian information criterion; lake trout; Lake Huron Key Contribution:
With a wide age range and long lifespan, fish size-at-age variation under an ecosystem regime shift is assessed clearly between years, regions, and recruitment origins by selecting the best linear mixed-effects model to separate the three major effects of fish age, year-class, and sampling years.
1. Introduction
An important issue in studying fish population dynamics is the assessment of fish growth in response to environmental changes. Problems often arise because fish growth is partly influenced by cohort and size-dependent effects. To evaluate the effects of environmental changes on fish growth, the cohort and size-dependent effects must be separated from the year effect. For a sound growth comparison based on either body size, size increment, or relative growth rate, individual fish size should be the same or similar at the beginning of a time interval [1]. In reality, however, the environmental conditions for juvenile and adult growth are typically not the same within a year and across years [2,3]. Young juvenile growth and its carryover effect on subsequent body growth of a fish cohort need to be considered when fish growth is used as the indicator to understand the impact of environmental changes on fish population dynamics [4].
Commonly used statistical comparisons of fish growth consist of growth curve comparisons or growth parameter comparisons, typically based on the von Bertalanffy growth function [5,6,7,8]. Very little progress, however, has been made to resolve the long-standing concerns of whether or not and in what circumstances the growth parameter comparisons are compatible with direct size-at-age comparisons [9,10,11,12,13]. Direct size-at-age comparison is important for understanding fish population dynamics associated with decadal ecosystem changes, and the comparison appears to be straightforward [14,15]. The unsolved concern is that for comparative size-at-age descriptions through a continued process of environmental changes, particularly for fish species of a long lifespan with many age groups, the method is messy and not very effective.
Lake trout (Salvelinus namaycush) size-at-age and body condition in the main basin of Lake Huron, one of the Laurentian Great Lakes of North America, have shown declines with decreasing abundance of pelagic prey fish, including alewives (Alosa pseudoharengus) and rainbow smelt (Osmerus mordax), and further dropped sharply after the alewife population collapse in 2003 [16,17,18,19,20,21]. Meanwhile, the collapse of alewives signaled the removal of a long-standing impediment to lake trout natural reproduction, and the recruitment of wild lake trout has occurred every consecutive year since the alewife population collapsed [22,23,24]. Given the tradeoff between more rapid body growth and the success of natural reproduction, a clear understanding of how lake trout body growth has responded to the abundance decline and eventually population collapse of alewives is critical for the current and future management of lake trout rehabilitation and lake trout fisheries.
Lake trout is the native top predator in the Great Lakes but has experienced population collapses in the middle of the 20th century due to excessive mortality of sea lamprey (Petromyzon marinus) predation and commercial harvests [25,26]. Consequently, the non-native pelagic prey fish alewife proliferated in four of the five Great Lakes. Due to alewife predation on lake trout fry and thiamine deficiency associated with lake trout consumption of alewives, the presence of abundant alewives became an impediment to lake trout natural reproduction [27,28,29,30]. Coordinated efforts of lake trout rehabilitation started from the early 1970s, including lake trout stocking from hatcheries, sea lamprey abundance control, and harvest regulation [31,32,33,34]. Stocked lake trout reached their peak abundance during the early 2000s, after the strong year-classes of the 1990s and the reduction in adult mortality since the end of the 1990s [35]. The increased predation pressure on alewives became unsustainable [36], as the total piscivore biomass was dominated by lake trout along with other species such as Chinook salmon (Oncorhynchus tshawytscha) and walleye (Sander vitreus). Pelagic productivity also declined [37] due to decreases in nutrient loading and benthic-oriented new invasive species, such as dreissenid mussels (Dreissenia spp.) and round goby (Neogobius melanostomus). Eventually, the alewife population collapsed in 2003 [16,17]. All those historical and recent benchmarks are characterized by the status of lake trout as the keystone species and alewives as the dominant but non-native pelagic prey fish. The management challenge is to understand how lake trout growth has responded to the continued environmental changes under the most recent ecosystem regime shift, as indicated by the 2003 alewife population collapse.
Weisberg [38] and Weisberg et al. [39] introduced using the linear and linear mixed-effects models as an alternative modeling approach to the von Bertalanffy growth function. Under the approach of commonly used growth models, including the von Bertalanffy growth function [40,41,42,43], random effects based on explicit assumptions can be evaluated and incorporated into the growth model, such as random effects on size and age measures of individual fish [44,45] and random effects on growth parameters and model prediction [45,46,47,48]. In contrast, the linear mixed-effects models do not use any explicit assumptions about the growth process but are structured to separate the age and year effects on fish growth, where the age effects represent the average growth trajectory for a fish species in a given environment, and the year effects represent environmental variation across years. The model structure has been expanded recently because the environmental effect should include both year and year-class effects [13,19].
The three factors of fish age, year-class, and sampling year can be incorporated into linear mixed-effects models via a variety of model structures. It can be difficult to interpret effects separately, as both the year-class and year effects represent growth variation over time and are both ecological effects [19]. Using only the relevant data, by excluding irrelevant samples and data, may facilitate model development such that the best model with a clear interpretation of model estimates is selected. For example, to compare size-at-age between stocked and wild lake trout, a previous study only used data for 2003 and more recent year-classes [13]. All lake trout samples collected before the 2003 sampling year were excluded, and many lake trout samples collected since the 2003 sampling year were also excluded. These kinds of options, however, do not ensure that all potential issues affecting fish growth are explored and investigated.
Our objective in this paper is to re-evaluate the procedure of model development for using the linear mixed-effects models to conduct direct size-at-age comparisons and thereby to clearly assess how lake trout growth has responded to the ecosystem regime shift in the main basin of Lake Huron. Previous studies fully relied on an exploration process for model development, in which the fixed effects were first evaluated one by one through comparisons with other factors, and a factor could be further considered as a random effect, particularly when it was not included as a fixed effect at previous steps of model development [13,19]. In analyzing age-structured fish data, however, the most critical consideration is not necessarily about a factor being estimated and interpreted as a fixed or random effect [49], but to effectively separate the three major effects in model estimates, as these three factors of fish age, year-class (Yc), and sampling year (Yr) are connected by their implicit relationship: . In addition to the three factors of fish age, year-class, and sampling year, other key factors, such as spatial region and recruitment origin, i.e., stocked vs wild, should all be included in the model development. The complexity embodied in fish size-at-age data must be fully explored and incorporated in the model to separate and understand the age, year-class, and year effects on fish growth.
2. Materials and Methods
We analyzed 45,814 lake trout samples, with the age range of 2–34 years, collected from northern and southern Lake Huron during 1975–2024 by the Michigan Department of Natural Resources (MDNR), including 3550 wild lake trout and 42,264 lake trout that were stocked from hatcheries at age1 or age0 (Table 1). Northern and southern Lake Huron are delineated by the 45th parallel, which is consistent with the boundary between the statistical districts of OH2 and OH3 in Ontario waters, stretching across the international boundary to the North Point of Thunder Bay in the north of the boundary between the statistical districts of MH2 and MH3 in Michigan waters [50]. All lake trout samples were collected during the annual spring benthic gillnet surveys by MDNR [51]. The annual survey was typically conducted in late April through early June before the water column became thermally stratified. Lake trout were captured from nearshore waters between 10 and 60 m depth using multifilament nylon gillnets set overnight on the lake bottom. Individual gillnet panel was 30.5 m long and 1.83 m tall, with stretched mesh size ranging from 50.8 to 152.4 mm, in 12.7 mm increments. Nine panels, each of a different mesh size, were attached together to form a single gang of gill net. All hatchery-stocked lake trout captured during the survey were identified based upon the presence of a fin clip, and lake trout without a fin clip were considered wild [23,24]. Total length (mm) and body mass (g) of all individual lake trout samples were measured on the boat. Age assignments for stocked lake trout were based on coded-wire tags, fin clips, or the combination of a fin clip with the reading of maxilla or otolith section [52,53]. Age assignments to wild lake trout were all based on the reading of maxilla or otolith sections.

Table 1.
Numbers of stocked and wild lake trout (Salvelinus namaycush) samples collected during the annual spring gillnetting surveys in 1975–2024 by the Michigan Department of Natural Resources from northern Lake Huron (NLH) and southern Lake Huron (SLH).
To fit lake trout size-at-age data, we used the Akaike information criterion (AIC) and the Bayesian information criterion (BIC) to compare models [54,55]. Our model selection was mostly based on BIC comparisons. For comparative purposes, we also presented AIC comparisons because the two criteria have both been widely used for model comparison and selection in ecological studies [56,57]. The model with a smaller AIC or BIC value was considered to be the better model. When the difference in AIC or BIC was less than 2.0 between two models, the two models were considered not to be different from each other, and the more complex model was considered to be unsupported.
We compared 12 model structures listed below, in which all explanatory variables were used as categorical variables, including fish Age. Equation (1) with only the age effect was used to describe the weight-at-age trajectory that is asymptotic and has embedded size dependence of body growth. The weight-at-age trajectory could be altered by other factors, and the relative importance of each of the other five factors was evaluated through AIC and BIC comparisons of models 1–6 (Table 2).
Here, represents the body mass of individual fish with age assignment (weight-at-age), and is the residual error of model prediction. We assumed lognormal distribution of body mass at a given age, which is the most widely used assumption in studying fish size at a given age. Based on comprehensive reviews and investigations, violations of this kind of assumption will not substantially alter the performance and prediction of the linear mixed-effects models [58]. We followed the convention of using a Greek letter (e.g., α, β, and γ) to represent a fixed effect in the model and a Roman letter (e.g., e) to represent a random effect [59] in the model. The subscripts are mostly used to indicate factors such as fish Age, Sex, recruitment origin (wild or not, Wd), year (Yr), year-class (Yc), and region of the lake (Rg), as well as interactions between region and year (R.Yr), and between recruitment origin and year-class (W.Yc). The interaction between recruitment origin and year-class may enter further interaction with fish age (W.Yc.A). The subscript AR1 in Equation (12) stands for the first-order autoregressive process, such that the residual errors () of model prediction were allowed to have region-specific residual variance and first-order autocorrelation across years.

Table 2.
Using the Akaike information criterion (AIC) and Bayesian information criterion (BIC) to compare and select linear mixed-effects models for size-at-age comparison of lake trout (Salvelinus namaycush) through a time-series of 1975–2024 from the main basin of Lake Huron based on the annual spring gillnetting surveys conducted by the Michigan Department of Natural Resources. Model structures include major factors, such as fish Age, Sex, recruitment origin (wild or not, Wd), sampling year (Yr), year-class (Yc), and region of the lake (Rg), as well as the interaction between region and year (R.Yr), and the interaction between recruitment origin and year-class (W.Yc). The interaction of recruitment origin with year-class may also enter further interaction with fish age (W.Yc.A). The factors in parentheses indicate random effects. The sequence of the 12 models represented the steps of model development from the simplest to the best through AIC and BIC comparisons. Provided are the degrees of freedom (df) of each model and the difference in AIC (∆AIC) and in BIC (∆BIC) between a model and the best model, with the best model having ∆AIC = 0 and ∆BIC = 0. The negative log-likelihood (-logLik) value for each model is also provided to compare data fits.
Recall that both the year and year-class effects were used as ecological effects. The year effect represents growth variation across years, and the year-class effect represents growth variation among year-classes. Both the year and year-class effects are additive to the general growth trajectory as the year-specific and cohort-specific growth indices, respectively. The year-class effect is determined by, or primarily reflects, the growth and body size of young juveniles and is carried out subsequently through all ages in a cohort-specific growth history [13,19].
It is impossible to include both year (Yr) and year-class (Yc) as fixed effects along with the age effect in a model because one level of those three factors cannot be estimated as coming from an independent distribution, given the relationship: . Models 7 and 8 represent the following two alternatives: using the year-class as a fixed effect and the year as a random effect, and vice versa, where the year effect was allowed to be different between regions of the lake and the year-class effect was allowed to be different between recruitment origins (wild or not). Recruitment origin was added in model 9 as a fixed effect and was evaluated through the comparison between models 8 and 9. The interaction of year-class with recruitment origin may enter further interaction with fish age, which was evaluated via the comparison between models 9 and 10.
In models 1 through 10, residual errors (ε) were modeled as independent and identically distributed with a zero mean from a normal distribution. The comparison of Equation (10) with Equation (11) evaluated the error structure () such that residual errors were allowed to have region-specific variance. Further comparison with Equation (12) evaluated the error structure () that residual errors for individual lake trout from a given region were allowed to have first-order autocorrelation across years.
The above 12 models were also implemented with the length-at-age data of the same lake trout time series. The results of model comparisons were generally the same or similar to using weight-at-age data and thus were not reported in the results section of this paper. All model implementations and comparisons in this study were using the base package of “nlme” in R with the maximum likelihood option [60,61].
3. Results
The AIC and BIC comparisons of all 12 models yielded compatible results, except for model 2 with the sex effect that was supported by the AIC comparison but not by the BIC comparison (Table 2). Through the model comparisons and selections (Table 2), the final and best model indicated the growth difference between the stocked and wild lake trout, although the growth trajectory of wild lake trout was within the 95% confidence intervals for the growth trajectory of stocked lake trout (Figure 1). From the final and best model, the lake trout growth has involved fixed year effects and systematic changes across years that were not the same between northern and southern Lake Huron, and the lake trout growth has also involved cohort-specific random variation that was not the same between stocked and wild lake trout (Table 2).
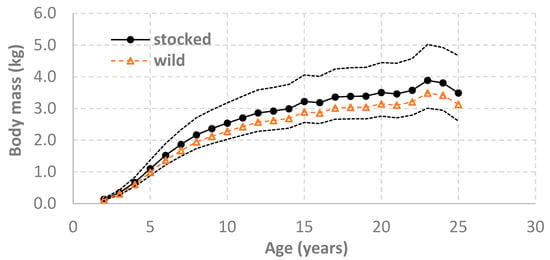
Figure 1.
Comparison of lake trout (Salvelinus namaycush) body mass growth trajectory (weight-at-age) between stocked lake trout (black dot and solid line) and wild lake trout (open triangles and dashed line), based on the best linear mixed-effects model (Equation (12) and Table 2) and lake trout samples collected from the annual spring gillnetting surveys during 1975–2024 by Michigan Department of Natural Resources. Dot lines present the 95% confidence intervals for weight-at-age of stocked lake trout. Data and model estimates for age 26–32 lake trout are available (Table 1) but are not included in this figure because of small sample sizes and large confidence intervals.
Observed average weight-at-age showed temporal trends and differences between northern and southern Lake Huron (Figure 2 and Figure 3). In the early part of the time series, lake trout weight-at-age was substantially larger in southern Lake Huron than in northern Lake Huron, but this difference between the two regions gradually decreased and almost disappeared by the end of the 1990s because lake trout weight-at-age in southern Lake Huron showed a steady decline, whereas in northern Lake Huron only showed large variation with no apparent temporal trend. During the 2000s, weight-at-age declines in southern Lake Huron accelerated, and the declines in northern Lake Huron also became apparent and similar to those in southern Lake Huron. By the late 2000s or early 2010s, lake trout weight-at-age showed a modest recovery and then stabilized.
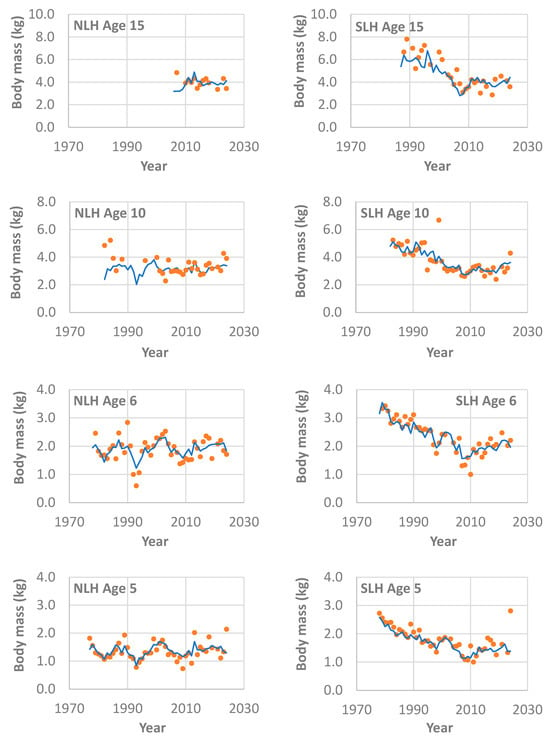
Figure 2.
Comparisons between the estimated (lines) and observed (dots) body mass at ages 5, 6, 10, and 15 with variation across years for stocked lake trout (Salvelinus namaycush) in northern Lake Huron (NLH) and southern Lake Huron (SLH), based on the best linear mixed-effects model (Table 2) and lake trout samples collected from the annual spring gillnetting surveys during 1975–2024 by Michigan Department of Natural Resources. Note that the Y-axis scale differs among the panels. Also note that the model estimate for the interaction between year-class and fish age was not used for the prediction of size-at-age.
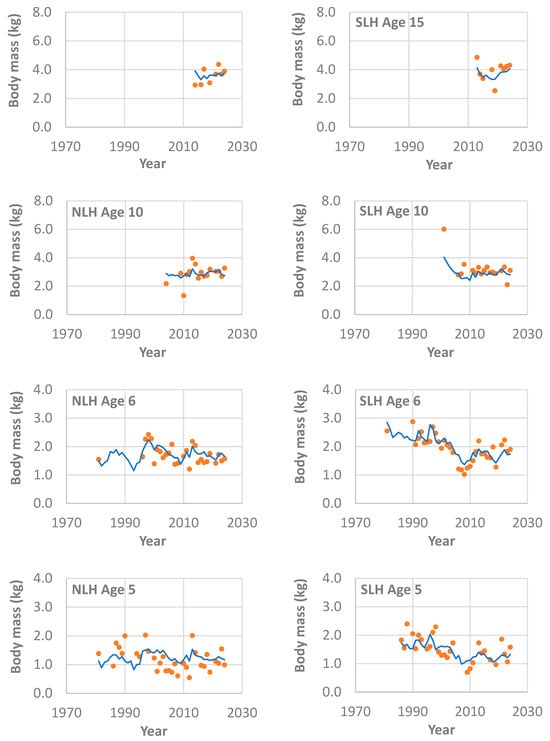
Figure 3.
Comparisons between the estimated (lines) and observed (dots) body mass at ages 5, 6, 10, and 15 with variation across years for wild lake trout (Salvelinus namaycush) in northern Lake Huron (NLH) and southern Lake Huron (SLH), based on the best linear mixed-effects model (Table 2) and lake trout samples collected from the annual spring gillnetting surveys during 1975–2024 by Michigan Department of Natural Resources. Note that the Y-axis scale differs among the panels. Also note that the model estimate for the interaction between year-class and fish age was not used in the prediction of size-at-age.
From the final and best model (Table 2), the model estimates included (1) the age effect over all ages that represents a log-scale growth trajectory (Figure 4a); (2) the year effect representing a year-specific growth index (Figure 4b); and (3) the year-class effect representing a cohort-specific growth index (Figure 4c). For many combinations of the year, region, fish age and origin, the weight-at-age observations were either absent or very sparse, particularly during those early years of population recovery (Figure 2 and Figure 3). Nonetheless, the available data were fitted well in general, although the modeling fit was better for the southern region compared with the northern region (Figure 2 and Figure 3). Back transformation of the age effect represented the general growth trajectory for lake trout in the US waters of Lake Huron (Figure 1).
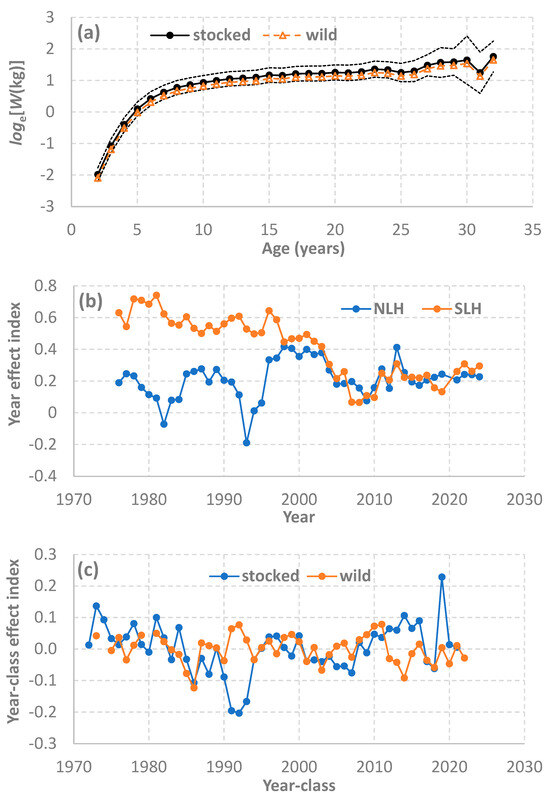
Figure 4.
Lake trout (Salvelinus namaycush) body mass decomposed as the age, year, and year-class effects, based on the best linear mixed-effects model (Equation (12) and Table 2), and lake trout samples collected from the annual spring gillnetting surveys during 1975–2024 by the Michigan Department of Natural Resources. (a) The age effect represents the average trajectories of log-scale weight-at-age that are compared between stocked and wild lake trout, with 95% confidence intervals (dot lines) for stocked lake trout. (b) The year effect represents the additive year-specific growth index that differed between northern Lake Huron (NLH) and southern Lake Huron (SLH). (c) The year-class effect represents the additive cohort-specific growth index that differed between stocked and wild lake trout.
The estimated year effect showed differences between northern and southern Lake Huron. For southern Lake Huron, the year-specific growth index showed a decreasing trend during 1976–2003, followed by a relatively steeper decline during 2003–2007, and then a modest recovery was followed by relatively stable index values from the early 2010s through 2024 (Figure 4b). In contrast, for northern Lake Huron, the year-specific growth index exhibited wide year-to-year variation with no apparent temporal trend during 1976–2003 but then also underwent a sharp decline during 2003–2009, as was observed for the southern region (Figure 4b). The year-specific growth index for the northern region began to converge with that for the southern region by the end of the 1990s, and the difference between the two indices was minimal during 2009–2024.
The estimated year-class effect showed differences between stocked and wild lake trout, although for both stocked and wild lake trout, the random variation showed no general trends (Figure 4c). For stocked lake trout, however, the index suggested that the young juvenile growth steadily declined during the 1980s and reached the lowest point in the early 1990s, and then the recovery during the middle and late 1990s was followed by declines again during the 2000s. For wild lake trout, the index suggested that the young juvenile growth increased during the 2000s, while the increase did not happen for stocked lake trout until nearly the end of the 2000s. Since 2010, young juvenile growth for stocked lake trout has appeared to be faster but more variable than wild lake trout.
4. Discussion
Like the von Bertalanffy and other growth functions, the linear mixed-effects models can be broadly used to describe organismal growth [39,40,62,63]. We compared linear mixed-effects models and selected the best model to fit size-at-age data of lake trout from the US waters of Lake Huron. Lake trout is the indicator species in the ecosystems of the Great Lakes [64]. Understanding the systematic changes and random variations in lake trout growth is essential for us to better understand the ecosystem regime shift in the main basin of Lake Huron [16,17]. We used the linear mixed-effects models in this paper to emphasize direct size-at-age comparisons across a time series of 50 years with a wide age range of lake trout, rather than growth parameter comparison based on the von Bertalanffy growth function.
Our findings characterized the Lake Huron ecosystem before and after the 2003 collapse of alewives. In the late 1970s, lake trout had attained a much larger size-at-age in southern Lake Huron than in northern Lake Huron, indicating that the availability of pelagic prey fish such as alewives and rainbow smelt was higher in southern Lake Huron than in northern Lake Huron. Lake trout size-at-age continuously declined in southern Lake Huron from the late 1970s through the early 2000s, likely due to declines in the abundance of pelagic prey fish, especially alewives [65]. By the end of the 1990s, the difference in lake trout growth between northern and southern Lake Huron had almost disappeared, and the complete alewife population collapse in 2003 led to an acceleration of lake trout growth declines during the 2000s in both regions. By the early 2010s, while the alewife population had no sign of recovering from its complete collapse, the lake trout diet was dominated by round goby (Neogobius melanostomus) and rainbow smelt [36,66], lake trout growth showed a modest recovery and then stabilized.
Unlike commonly used growth curve and growth parameter comparisons, for which data fitting is mostly about fitting the growth curves, our data fitting is not presented to emphasize potential alteration of the growth curve for fitting one or another subset of data, e.g., to fit a year-specific or cohort-specific growth curve for lake trout in northern or southern Lake Huron. Rather, our data fitting is focused on explanation for the direct comparison of average size-at-age between years, regions, and recruitment origins, even though the multiple age groups for the fish of a long lifespan typically involve some possible situations of absent, sparse, and even biased data. From our model, in addition to the age effect representing the general growth trajectory, the year and year-class effects are the year-specific and cohort-specific growth indices that reveal and summarize the responses of fish growth to environmental changes.
The best model structure from this study was the same between the AIC and BIC comparisons (Table 2), but it was different from a recent study that analyzed the same lake trout time series [19]. In the recent previous study, the year-class was selected over year as the fixed effect because many year-classes were distinctly characterized as either before or after the ecosystem regime shift, as indicated by the 2003 collapse of alewives, while other year-classes crossed the two time periods at various ages. Consequently, year-class accounted for more variation in size-at-age than sampling year and, therefore, year-class appeared to be more important than year when these two factors were evaluated in comparison with each other. In our current study, we did not fully rely on the relative importance of a single factor. Given the relationship , we compared alternative model structures for including all three major effects of fish age, year-class, and sampling year. The early study also did not consider potential differences between spatial regions and between recruitment origins. In our current study, the year effect was allowed to be different between regions, and the year-class effect was allowed to be different between recruitment origins.
In the recent previous study [19], model estimates failed to reflect a clear distinction between the year-class and year effects. The fixed year-class effect appeared to have a step decline beginning with the 1986 year-class, the fixed age effect indicated nearly zero growth in body length after age 12, and the random year effect showed an increasing pattern prior to 1998 and a decreasing pattern after 1998. A combination of the fixed age and year-class effects appeared to be consistent with the random year effect for indicating the change point in lake trout growth occurred in 1998, which in turn was consistent with the finding from a time-varying von Bertalanffy growth function that lake trout growth potential (the asymptotic body length) declined between the pre-1998 and post-1997 time periods [19,21]. Overall, however, it appeared difficult to separately interpret the model estimates of the year-class and year effects.
In our current study, the model estimates of the three major effects of fish age, year-class, and sampling year were clearly interpretable. The age effect represented the asymptotic growth trajectory that embodied size-dependent fish growth. The fixed year effect represented the year-specific growth index and environmental changes across years, with a spatial difference between two regions of the lake. The random year-class effect represented the cohort-specific growth index, primarily reflecting random growth variation in young juveniles that differed between recruitment origins.
The final model structure selected in the current study was also slightly different from another recent study that focused on the comparison of body growth between wild and stocked lake trout [13]. That early study only used the data for the more recent year-classes since 2003, and, thus, fish age entered a two-way interaction with recruitment origin in the selected model [13]. Our current study has used the full time series of lake trout weight-at-age since 1975 with consideration of all major factors of fish age, year-class, and sampling year, as well as spatial region and recruitment origin. Thus, via objective model comparisons, fish age and recruitment origin were treated separately as the main effects in the final selected model.
Overall, our linear mixed-effects model has provided insights into lake trout growth changes in the main basin of Lake Huron over the past 50 years. The year effects estimated from our model reflected changes in environmental conditions influencing the growth of older juveniles and adults, whereas the estimated year-class effects primarily reflected changes in environmental conditions influencing growth of young juveniles. Several environmental factors can affect lake trout growth, including prey availability, density-dependent effects, and water temperature [2,19,67]. Our model and modeling results provided a new platform to explore the mechanisms behind lake trout growth changes and to assess the relative importance of each of these environmental factors in future modeling exercises.
5. Conclusions
The approach of linear mixed-effects model could be broadly applied for studying fish growth, including other lake trout populations and other fish species, particularly for studying fish growth variation across years with major changes in environmental conditions and fish population dynamics. Using the approach of linear mixed-effects model, year-specific and cohort-specific growth indices can be summarized from direct size-at-age comparisons with a wide age range and a long lifespan. In comparison with single-age measures and the use of growth parameters based on the von Bertalanffy or other growth functions, the year-specific and cohort-specific growth indices provide more direct and unbiased bases for studying potential density-dependent effects on fish growth and relationships between changes in fish growth and environmental conditions. Clearly separating the year and year-class effects in model estimates may also provide insights for studying fish recruitment dynamics, because the year-class effect or cohort-specific growth index is determined at the beginning of a cohort-specific growth history, and young juvenile growth often has a direct connection to recruitment success [68,69].
Author Contributions
Conceptualization: J.X.H. and C.P.M.; methodology: J.X.H.; validation: C.P.M.; formal analysis: J.X.H. and C.P.M.; investigation: J.X.H. and C.P.M.; data curation: J.X.H.; writing—original draft preparation: J.X.H.; writing—review and editing: C.P.M.; visualization: J.X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data analyzed and generated by this study are available upon a reasonable request to the corresponding author.
Acknowledgments
This study was funded with financial support from the Federal Aid in Sport Fish Restoration Program F-61 to the Michigan Department of Natural Resources, Fishery Division, Studies 230451 and 230522, at Lake Huron Research Station. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government. The authors thank Shawn Sitar for providing a USGS in-house review of the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MDNR | Michigan Department of Natural Resources |
| NLH | Northern Lake Huron |
| SLH | Southern Lake Huron |
| AIC | Akaike Information Criterion |
| BIC | Bayesian Information Criterion |
References
- Ricker, W.E. Growth rate and models. In Fish Physiology; Hoar, W.S., Randall, D.J., Brett, J.R., Eds.; Academic Press: New York, NY, USA, 1979; Volume 8, pp. 677–743. [Google Scholar]
- Walters, C.J.; Post, J.R. Density-dependent growth and competitive asymmetries in size-structured fish populations: A theoretical model and recommendations for field experiments. Trans. Am. Fish. Soc. 1993, 122, 34–45. [Google Scholar] [CrossRef]
- He, J.X.; Stewart, D.J. A stage-explicit expression of the von Bertalanffy growth model for understanding age at first reproduction of Great Lakes fishes. Can. J. Fish. Aquat. Sci. 2002, 59, 250–261. [Google Scholar] [CrossRef]
- He, J.X.; Rudstam, L.G.; Forney, J.L.; VanDeValk, A.J.; Stewart, D.J. Long-term patterns in growth of Oneida Lake walleye: A multivariate and stage-explicit approach for applying the von Bertalanffy growth function. J. Fish Biol. 2005, 66, 1459–1470. [Google Scholar] [CrossRef]
- von Bertalanffy, L. A quantitative theory of organic growth (inquiries on growth laws. II). Hum. Biol. 1938, 10, 181–213. [Google Scholar]
- Gallucci, V.F.; Quinn, T.J., II. Reparameterizing, fitting and testing a simple growth model. Trans. Am. Fish. Soc. 1979, 108, 14–25. [Google Scholar] [CrossRef]
- Chen, Y.; Jackson, B.A.; Harvey, H.H. A comparison of von Bertalanffy and polynomial functions in modelling fish growth data. Can. J. Fish. Aquat. Sci. 1992, 49, 1228–1235. [Google Scholar] [CrossRef]
- Wang, Y.; Milton, D.A. On comparison of growth curves: How do we test whether growth rates differ? Fish. Bull. 2000, 98, 874–880. [Google Scholar]
- Knight, W. Asymptotic growth: An example of nonsense disguised as mathematics. J. Fish. Res. Board Can. 1968, 25, 1303–1306. [Google Scholar] [CrossRef]
- Knight, W. A formulation of the von Bertalanffy growth curve when the growth rate is roughly constant. J. Fish. Res. Board Can. 1969, 26, 3069–3072. [Google Scholar] [CrossRef]
- Roff, D.A. A motion for the retirement of the von Bertalanffy function. Can. J. Fish. Aquat. Sci. 1980, 37, 127–129. [Google Scholar] [CrossRef]
- Živkov, M.T.; Trichkova, T.A.; Raikova-Petrova, G.N. Biological reasons for the unsuitability of growth parameters and indices for comparing fish growth. Environ. Biol. Fish. 1999, 54, 67–76. [Google Scholar] [CrossRef]
- He, J.X. Growth stability after the collapse of alewives in Lake Huron and direct size-at-age comparisons between stocked and wild lake trout. J. Gt. Lakes Res. 2024, 50, 102315. [Google Scholar] [CrossRef]
- Clark, W.G.; Hare, S.R.; Parma, A.M.; Sullivan, P.J.; Trumble, R.J. Decadal changes in growth and recruitment of Pacific halibut (Hippoglossus stenolepis). Can. J. Fish. Aquat. Sci. 1999, 56, 242–252. [Google Scholar] [CrossRef]
- Han, P.; Li, J.; Dan, Y.; Liu, B.; Chen, X.; Fang, Z. Decadal Changes in the Annual Growth of Two Commercial Ommastrephid Species in the Pacific Ocean. Fishes 2022, 7, 280. [Google Scholar] [CrossRef]
- Riley, S.C.; Roseman, E.F.; Nichols, S.J.; O’Brien, T.P.; Kiley, C.S.; Schaeffer, J.S. Deepwater demersal fish community collapse in Lake Huron. Trans. Am. Fish. Soc. 2008, 137, 1879–1890. [Google Scholar] [CrossRef]
- Madenjian, C.P.; Rutherford, E.S.; Stow, C.A.; Roseman, E.F.; He, J.X. Trophic shift, not collapse. Environ. Sci. Technol. 2013, 47, 11915–11916. [Google Scholar] [CrossRef] [PubMed]
- He, J.X.; Bence, J.R. Modeling annual growth variation using a hierarchical Bayesian approach and the von Bertalanffy growth function, with application to lake trout in southern Lake Huron. Trans. Am. Fish. Soc. 2007, 136, 318–330. [Google Scholar] [CrossRef]
- He, J.X.; Bence, J.R. Systematic changes and random variations: Understanding lake trout (Salvelinus namaycush) growth dynamics in US waters of Lake Huron. J. Gt. Lakes Res. 2023, 49, 737–745. [Google Scholar] [CrossRef]
- He, J.X.; Bence, J.R.; Johnson, J.E.; Clapp, D.F.; Ebener, M.P. Modeling variation in mass-length relations and condition indices of lake trout and Chinook salmon in Lake Huron: A hierarchical Bayesian approach. Trans. Am. Fish. Soc. 2008, 137, 801–817. [Google Scholar] [CrossRef]
- He, J.X.; Bence, J.R.; Roseman, E.F.; Fielder, D.G.; Ebener, M.P. Using time-varying asymptotic length and body condition of top piscivores to indicate ecosystem regime shift in the main basin of Lake Huron: A Bayesian hierarchical modeling approach. Can. J. Fish. Aquat. Sci. 2016, 73, 1092–1103. [Google Scholar] [CrossRef]
- Riley, S.C.; He, J.X.; Johnson, J.E.; O’Brien, T.P.; Schaeffer, J.S. Evidence of widespread natural reproduction by lake trout Salvelinus namaycush in the Michigan Waters of Lake Huron. J. Gt. Lakes Res. 2007, 33, 917–921. [Google Scholar] [CrossRef]
- He, J.X.; Ebener, M.P.; Riley, S.C.; Cottrill, A.; Kowalski, A.; Koproski, S.; Mohr, L.; Johnson, J.E. Lake Trout Status in the Main Basin of Lake Huron, 1973–2010. N. Am. J. Fish. Manag. 2012, 32, 402–412. [Google Scholar] [CrossRef]
- Johnson, J.E.; He, J.X.; Fielder, D.G. Rehabilitation stocking of walleyes and lake trout: Restoration of reproducing stocks in Michigan waters of Lake Huron. N. Am. J. Fish. Aquac. 2015, 77, 396–408. [Google Scholar] [CrossRef]
- Hile, R. 1949. Trends in the lake trout fishery of Lake Huron through 1946. Trans. Am. Fish. Soc. 1949, 76, 121–147. [Google Scholar] [CrossRef]
- Walters, C.J.; Steer, G.; Spangler, G. Responses of lake trout (Salvelinus namaycush) to harvesting, stocking, and lamprey reduction. Can. J. Fish. Aquat. Sci. 1980, 37, 2133–2145. [Google Scholar] [CrossRef]
- Smith, S.H. Species succession and fishery exploitation in the Great Lakes. J. Fish. Res. Board Can. 1968, 25, 667–693. [Google Scholar] [CrossRef]
- Walters, C.; Kitchell, J.F. Cultivation/depensation effects on juvenile survival and recruitment: Implications for the theory of fishing. Can. J. Fish. Aquat. Sci. 2001, 58, 39–50. [Google Scholar] [CrossRef]
- Madenjian, C.P.; O’Gorman, R.; Bunnell, D.B.; Argyle, R.L.; Roseman, E.F.; Warner, D.M.; Stockwell, J.D.; Stapanian, M.A. Adverse effects of alewives on Laurentian Great Lakes fish communities. N. Am. J. Fish. Manag. 2008, 28, 263–282. [Google Scholar] [CrossRef]
- Fitzsimons, J.D.; Brown, S.; Brown, L.; Honeyfield, D.; He, J.; Johnson, J.E. Increase in lake trout reproduction in Lake Huron following the collapse of alewife: Relief from thiamine deficiency or larval predation? Aquat. Ecosyst. Health Manag. 2010, 13, 73–81. [Google Scholar] [CrossRef]
- DesJardine, R.L.; Gorenflo, T.K.; Payne, R.N.; Schrouder, J.D. Fish-Community Objectives for Lake Huron; Great Lakes Fishery Commission: Ann Arbor, MI, USA, 1995; Special Publication 95-1; 38p, Available online: https://www.glfc.org/pubs/SpecialPubs/Sp95_1.pdf (accessed on 5 October 2025).
- Eshenroder, R.L.; Payne, N.R.; Johnson, J.E.; Bowen, C.; Ebener, M.P. Lake trout rehabilitation in Lake Huron. J. Gt. Lakes Res. 1995, 21 (Suppl. 1), 108–127. [Google Scholar] [CrossRef]
- Ebener, M.P. A Lake Trout Rehabilitation Guide for Lake Huron; Great Lakes Fishery Commission: Ann Arbor, MI, USA, 1998; 48p, Available online: https://www.glfc.org/pubs/lake_committees/huron/LkTroutRepHuron.pdf (accessed on 5 October 2025).
- Nowicki, S.M.; Criger, L.A.; Hrodey, P.J.; Sullivan, W.P.; Neave, F.B.; He, J.X.; Gorenflo, T.K. A case history of sea lamprey (Petromyzon marinus) abundance and control in Lake Huron: 2000–2019. J. Gt. Lakes Res. 2021, 47 (Suppl. 1), 455–478. [Google Scholar] [CrossRef]
- He, J.X. Adult mortality and year-class strength of lake trout before and after alewife collapse in the main basin of Lake Huron. J. Gt. Lakes Res. 2024, 50, 102315. [Google Scholar] [CrossRef]
- He, J.X.; Bence, J.R.; Madenjian, C.P.; Pothoven, S.A.; Dobiesz, N.E.; Fielder, D.G.; Johnson, J.E.; Ebener, M.P.; Cottrill, A.R.; Mohr, L.C.; et al. Coupling age-structured stock assessment and fish bioenergetics models: A system of time-varying models for quantifying piscivory patterns during the rapid trophic shift in the main basin of Lake Huron. Can. J. Fish. Aquat. Sci. 2015, 72, 7–23. [Google Scholar] [CrossRef]
- Barbiero, R.P.; Lesht, B.M.; Warren, G.J.; Rudstam, L.G.; Watkins, J.M.; Reavie, E.D.; Kovalenko, K.E.; Karatayev, A.Y. A comparative examination of recent changes in nutrients and lower food web structure in Lake Michigan and Lake Huron. J. Gt. Lakes Res. 2018, 44, 573–589. [Google Scholar] [CrossRef] [PubMed]
- Weisberg, S. Using hard-part increment data to estimate age and environmental effects. Can. J. Fish. Aquat. Sci. 1993, 50, 1229–1237. [Google Scholar] [CrossRef]
- Weisberg, S.; Spangler, G.; Richmond, L.S. Mixed effects models for fish growth. Can. J. Fish. Aquat. Sci. 2010, 67, 269–277. [Google Scholar] [CrossRef]
- Richards, F.J. A flexible growth function for empirical use. J. Exp. Bot. 1959, 10, 290–300. [Google Scholar] [CrossRef]
- Schnute, J. A versatile growth model with statistically stable parameters. Can. J. Fish. Aquat. Sci. 1981, 38, 1128–1140. [Google Scholar] [CrossRef]
- Lorenzen, K. Toward a new paradigm for growth modeling in fisheries stock assessments: Embracing plasticity and its consequences. Fish. Res. 2016, 180, 4–22. [Google Scholar] [CrossRef]
- Flinn, S.A.; Midway, S.R. Trends in Growth Modeling in Fisheries Science. Fishes 2021, 6, 1. [Google Scholar] [CrossRef]
- Cope, J.M.; Punt, A.E. Admitting ageing error when fitting growth curves: An example using the von Bertalanffy growth function with random effects. Can. J. Fish. Aquat. Sci. 2007, 64, 205–218. [Google Scholar] [CrossRef]
- Cadigan, N.G.; Campana, S.E. Hierarchical model-based estimation of population growth curves for redfish (Sebastes mentella and Sebastes fasciatus) off the Eastern coast of Canada. ICES J. Mar. Sci. 2016, 74, 687–697. [Google Scholar] [CrossRef]
- Shelton, A.O.; Mangel, M. Estimating von Bertalanffy parameters with individual and environmental variations in growth. J. Biol. Dyn. 2012, 6 (Suppl. 2), 3–30. [Google Scholar] [CrossRef]
- Vincenzi, S.; Jesensek, D.; Crivelli, A.J. Biological and statistical interpretation of size-at-age, mixed-effects models of growth. R. Soc. Open Sci. 2020, 7, 192146. [Google Scholar] [CrossRef]
- Correa, G.M.; Monnahan, C.C.; Sullivan, J.Y.; Thorson, J.T.; Punt, A.E. Modelling time-varying growth in state-space stock assessments. ICES J. Mar. Sci. 2023, 80, 2036–2049. [Google Scholar] [CrossRef]
- He, J.X.; Madenjian, C.P. Comparing Year-Class Strength Indices from Longitudinal Analysis of Catch-at-Age Data with Those from Catch-Curve Regression: Application to Lake Huron Lake Trout. Fishes 2025, 10, 332. [Google Scholar] [CrossRef]
- Smith, S.H.; Buettner, H.J.; Hile, R. Fishery Statistical Districts of the Great Lakes; Great Lakes Fishery Commission: Ann Arbor, MI, USA, 1961; Technical Report No. 2; 24p, Available online: https://www.glfc.org/pubs/TechReports/Tr02.pdf (accessed on 5 October 2025).
- He, J.X.; Madenjian, C.P.; Wills, T.C. A generalized application of the catch-curve regression with comparisons of adult mortality and year-class strength between hatchery-stocked and wild-reared lake trout in US waters of Lake Huron. Can. J. Fish. Aquat. Sci. 2023, 80, 1714–1722. [Google Scholar] [CrossRef]
- Wellenkamp, W.; He, J.X.; Vercnocke, D. Using maxillae to estimate ages of Lake Trout. N. Am. J. Fish. Manag. 2015, 35, 296–301. [Google Scholar] [CrossRef]
- Murphy, E.W.; Smith, M.L.; He, J.X.; Wellenkamp, W.; Barr, E.; Downey, P.C.; Miller, K.M.; Meyer, K.A. Revised fish aging techniques improve fish contaminant trend analyses in the face of changing Great Lakes food webs. J. Gt. Lakes Res. 2018, 44, 725–734. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the Second International Symposium on Information Theory; Petrov, B.N., Csáki, F., Eds.; Akadémiai Kiadó: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multi-Model Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Aho, K.; Derryberry, D.; Peterson, T. Model selection for ecologists: The worldviews of AIC and BIC. Ecology 2014, 95, 631–636. [Google Scholar] [CrossRef]
- Schielzeth, H.; Dingemanse, N.J.; Nakagawa, S.; Westneat, D.F.; Allegue, H.; Teplitsky, C.; Réale, D.; Dochtermann, N.A.; Garamszegi, L.Z.; Araya-Ajoy, Y.G. Robustness of linear mixed-effects models to violations of distributional assumptions. Methods Ecol. Evol. 2020, 11, 1141–1152. [Google Scholar] [CrossRef]
- McCulloch, C.M.; Searle, S.R.; Neuhaus, J.M. Generalized, Linear, and Mixed Models, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NY, USA, 2008; 424p. [Google Scholar]
- Pinheiro, J.C.; Bates, D.M. Mixed-Effects Models in S and S-PLUS; Springer: New York, NY, USA, 2000; 528p. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2025; Available online: https://www.R-project.org/ (accessed on 5 October 2025).
- Zhang, L. Cross-validation of non-linear growth functions for modelling tree height–diameter relationships. Ann. Bot. 1997, 79, 251–257. [Google Scholar] [CrossRef]
- Hao, X.; Yujun, S.; Xinjie, W.; Jin, W.; Yao, F. Linear Mixed-Effects Models to Describe Individual Tree Crown Width for China-Fir in Fujian Province, Southeast China. PLoS ONE 2015, 10, e0122257. [Google Scholar] [CrossRef] [PubMed]
- Muir, A.M.; Krueger, C.C.; Hansen, M.J. Re-establishing lake trout in the Laurentian Great Lakes: Past, present, and future. In Great Lakes Fisheries Policy and Management: A Binational Perspective, 2nd ed.; Taylor, W.W., Lynch, A.J., Leonard, N.J., Eds.; Michigan State University Press: East Lansing, MI, USA, 2012; pp. 533–588. [Google Scholar]
- Hondorp, D.W.; DeBruyne, R.; Brant, C.O.; Esselman, P.C.; O’Brien, T.P. Status and Trends of the Lake Huron Prey Fish Community, 1976–2024; Great Lakes Fishery Commission: Ann Arbor, MI, USA, 2025; 24p, Available online: https://www.glfc.org/pubs/lake_committees/common_docs/Status_Trends_LakeHuron_PreyFish_2024_FINAL_20250505.pdf (accessed on 20 September 2025).
- Roseman, E.F.; Schaeffer, J.S.; Bright, E.; Fielder, D.G. Angler-caught piscivore diets reflect fish community changes in Lake Huron. Trans. Am. Fish. Soc. 2014, 143, 1419–1433. [Google Scholar] [CrossRef]
- Stewart, D.J.; Weininger, D.; Rottiers, D.V.; Edsall, T.A. An Energetics Model for Lake Trout, Salvelinus namaycush: Application to the Lake Michigan Population. Can. J. Fish. Aquat. Sci. 1983, 40, 681–698. [Google Scholar] [CrossRef]
- Fontes, J.; Santos, R.S.; Afonso, P.; Caselle, J.E. Larval growth, size, stage duration and recruitment success of a temperate reef fish. J. Sea Res. 2011, 65, 1–7. [Google Scholar] [CrossRef]
- Dub, J.D.; Redman, R.A.; Wahl, D.H.; Czesny, S.J. Size-specific growth and mortality of juvenile yellow perch in southwestern Lake Michigan. J. Gt. Lakes Res. 2014, 40, 179–186. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).