Mutual Effects of Carassius carassius and Microcystis aeruginosa on Growth Dynamics and Water Quality
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Materials
2.2. Experimental Methods
2.3. Measurement of Monitoring Indicators
2.4. Statistical Analysis
2.5. Theoretical Basis
3. Results
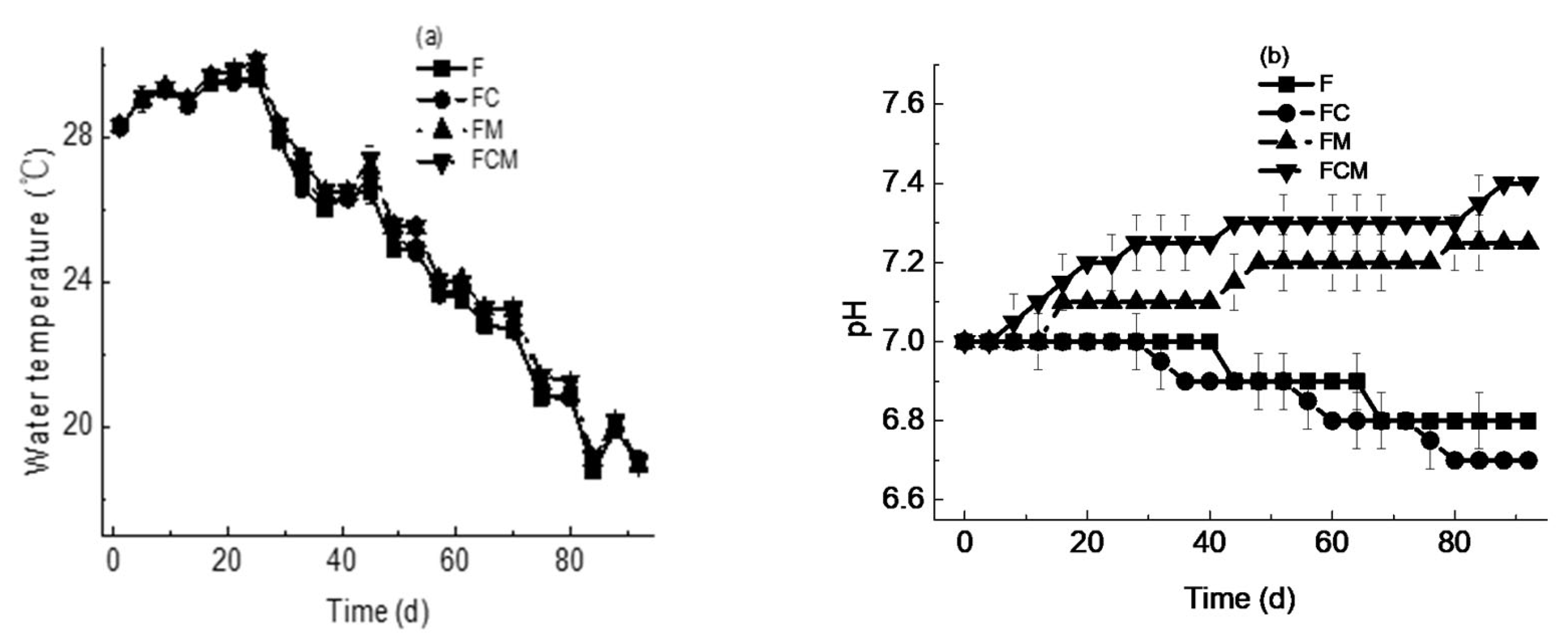
3.1. Water Temperature
3.2. pH
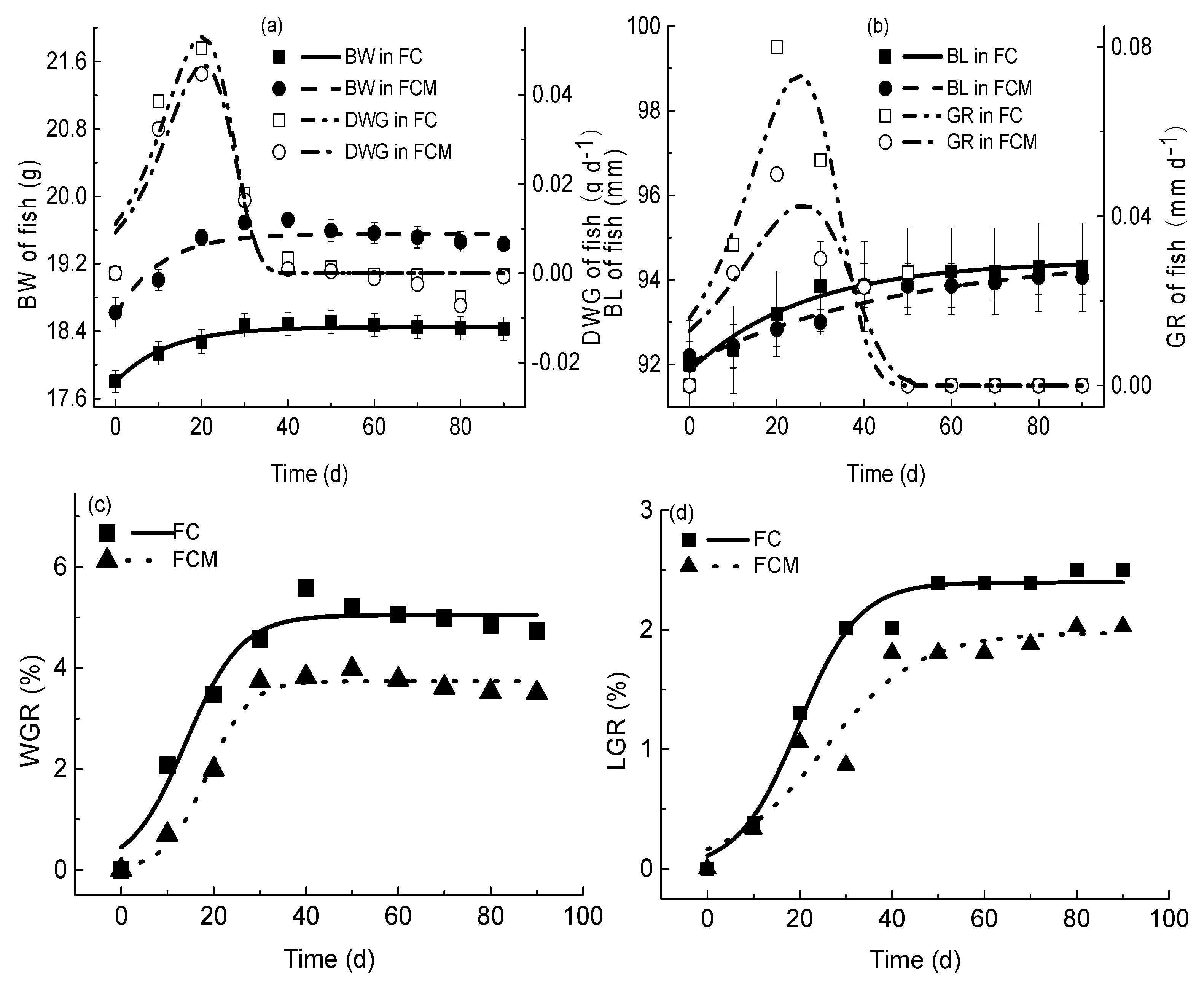
3.3. Effects of M. aeruginosa on Crucian Carp Growth
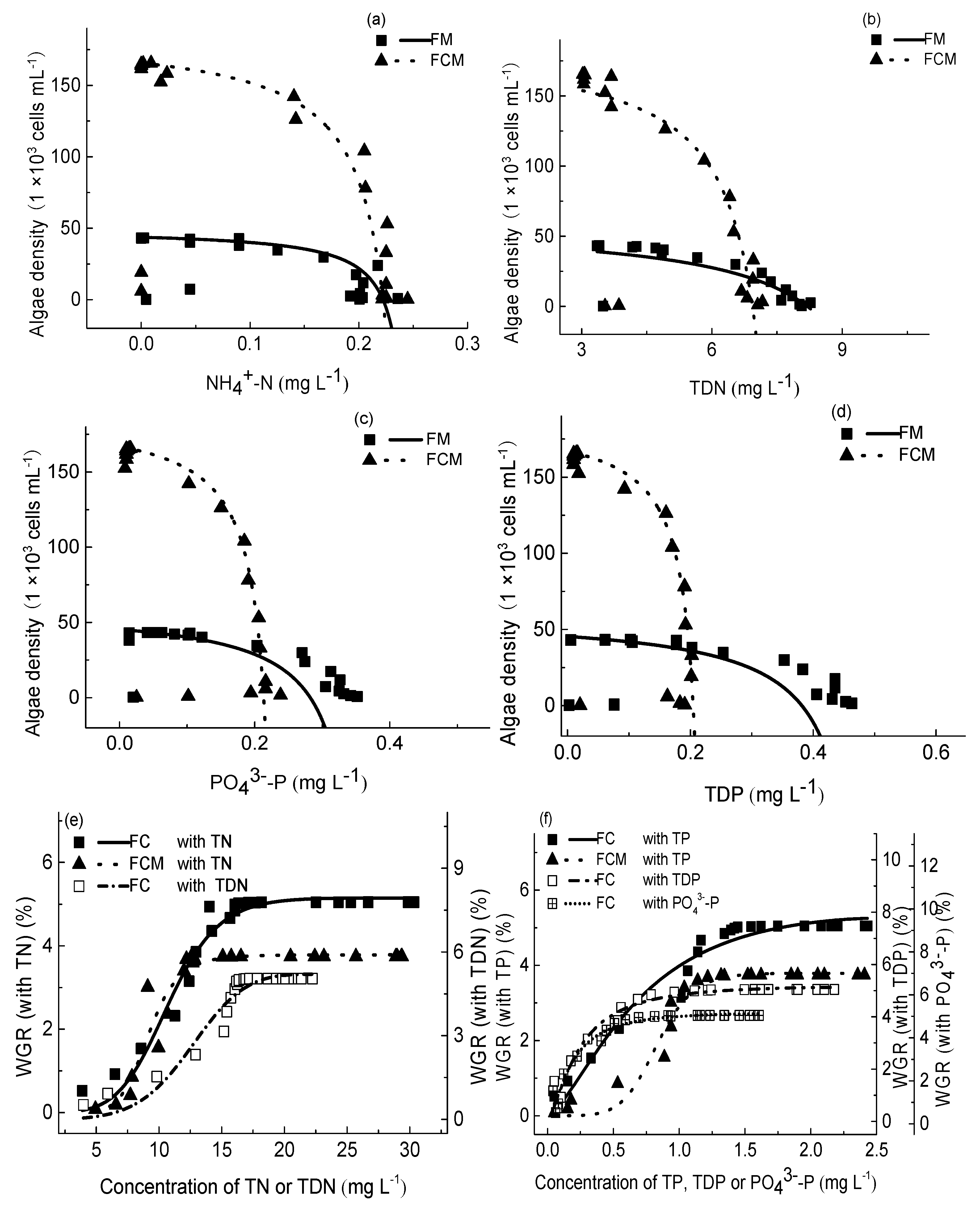
3.4. Effects of Crucian Carp on M. aeruginosa Growth
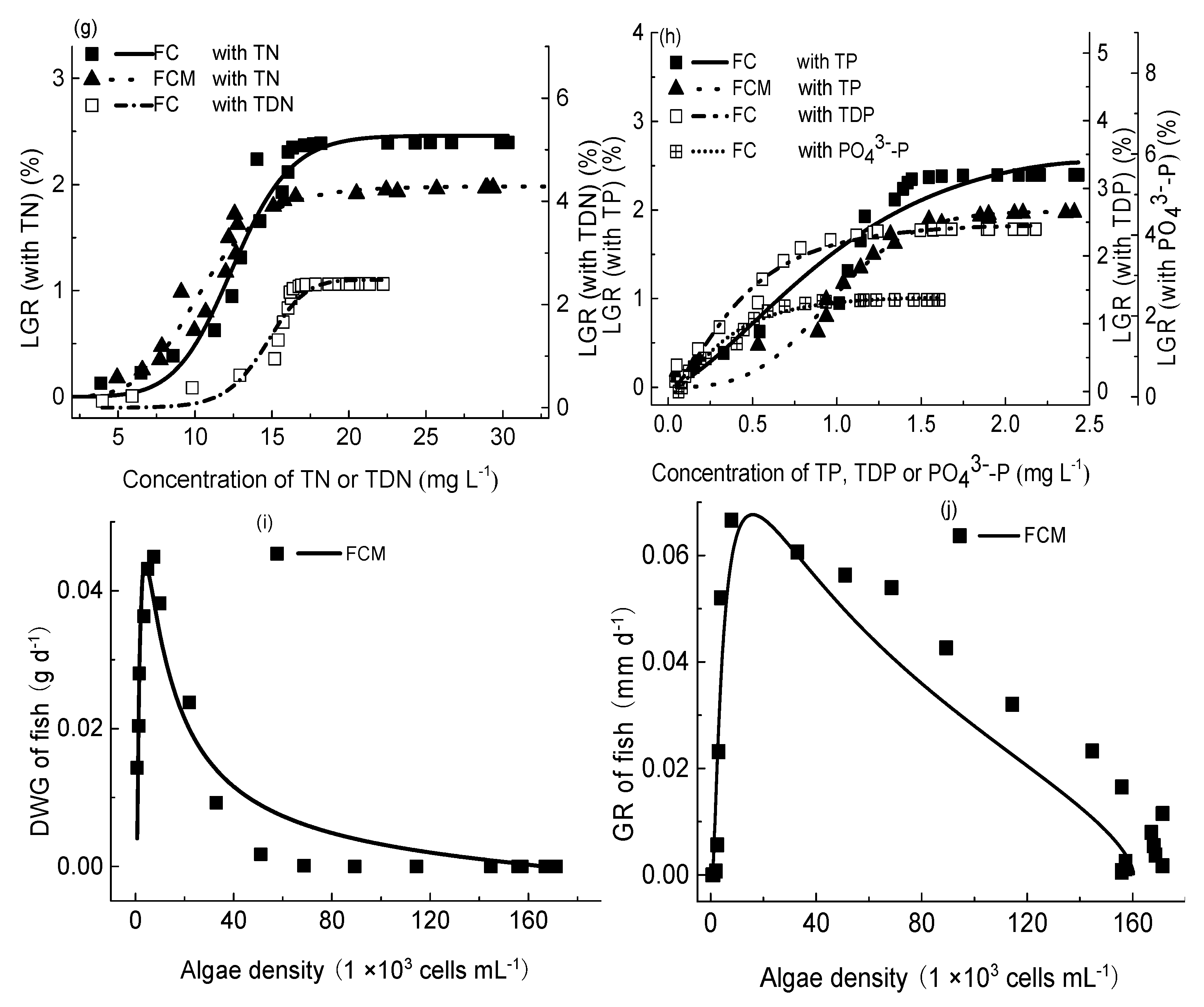
3.5. Nutrients Kinetics
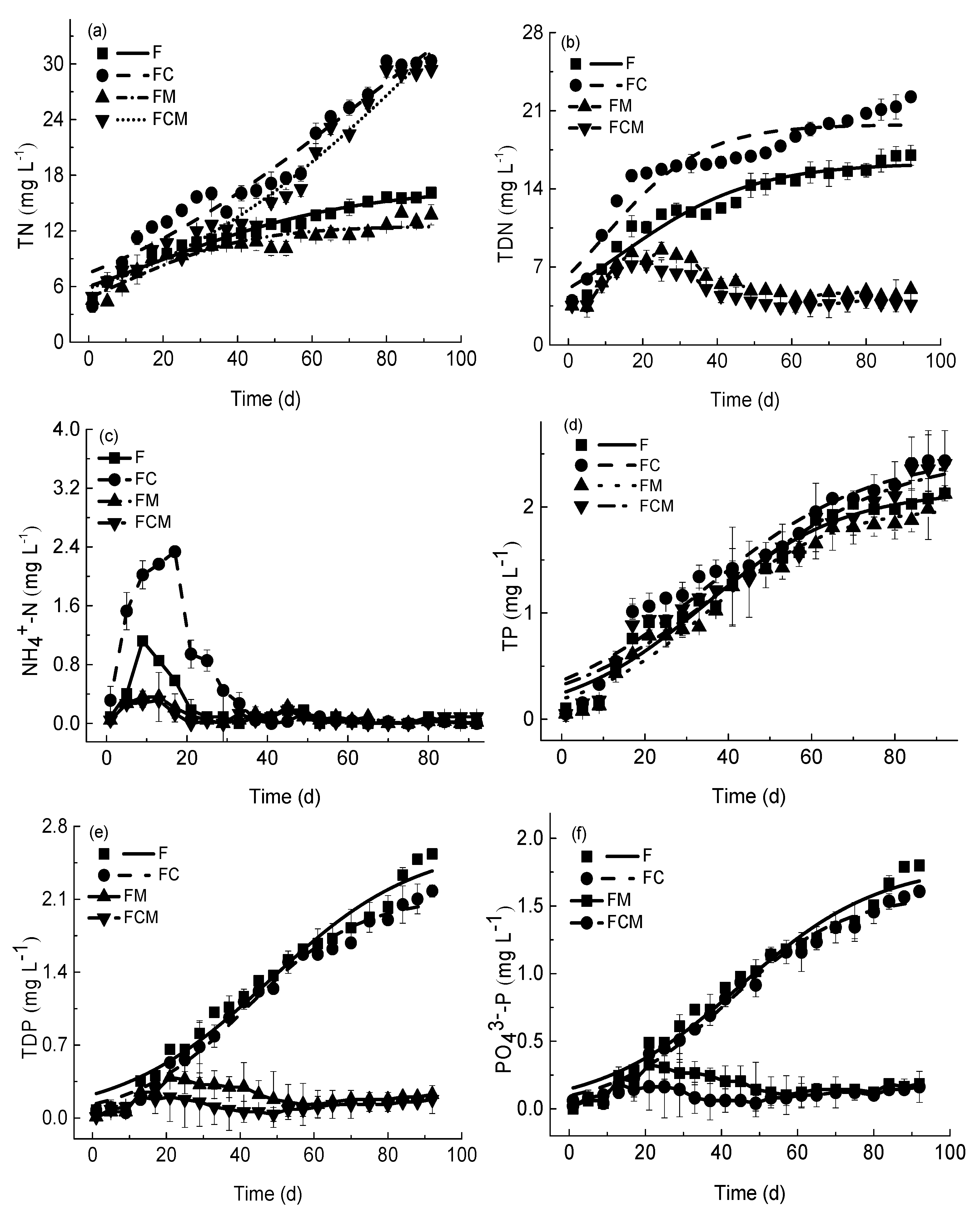
3.5.1. Temporal Changes in Nutrient Concentrations
3.5.2. The Impact of M. aeruginosa and Crucian Carp on Nutrient Concentrations
3.6. Nutrients’ Proportions
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Degefu, F.; Mengistu, S.; Schagerl, M. Influence of fish cage farming on water quality and plankton in fish ponds: A case study in the rift valley and north shoa reservoirs, Ethiopia. Aquaculture 2011, 316, 129–135. [Google Scholar] [CrossRef]
- Chen, L.; Yang, X.; Sun, C.; Wang, Y.; Xu, D.; Zhou, C. Feed intake prediction model for group fish using the MEA-BP neural network in intensive aquaculture. Inf. Process. Agric. 2020, 7, 261–271. [Google Scholar] [CrossRef]
- Han, Y.; Gu, J.; Li, Q.; Zhang, Y.; He, H.; Shen, R.; Li, K. Effects of juvenile crucian carp (Carassius carassius) removal on submerged macrophyte growth-implications for subtropical shallow lake restoration. Environ. Sci. Pollut. Res. 2019, 27, 42198–42209. [Google Scholar] [CrossRef] [PubMed]
- Lopes, I.G.; Lalander, C.H.; Vidotti, R.M.; Vinners, B. Using Hermetia illucens larvae to process biowaste from aquaculture production. J. Clean. Prod. 2020, 251, 119753. [Google Scholar] [CrossRef]
- Rahman, M.M.; Verdegem, M.; Nagelkerke, L.; Wahab, M.D.; Milstein, A.; Verreth, J. Effects of common carp Cyprinus carpio (L.) and feed addition in rohu Labeo rohita (Hamilton) ponds on nutrient partitioning among fish, plankton and benthos. Aquac. Res. 2008, 39, 85–95. [Google Scholar] [CrossRef]
- Anderson, D.M.; Glibert, P.M.; Burholder, J.M. Harmful algal blooms and eutrophication: Nutrient sources, composition, and consequences. Estuaries 2002, 25, 704–726. [Google Scholar] [CrossRef]
- Huang, S.L.; Wu, M.; Zang, C.J.; Du, S.L.; Domagalski, J.; Gajewska, M.; Gao, F.; Lin, C.; Guo, Y.; Liu, B.; et al. Dynamics of algae growth and nutrients in experimental enclosures culturing bighead carp and common carp: Phosphorus dynamics. Int. J. Sediment Res. 2016, 31, 173–180. [Google Scholar] [CrossRef]
- Tsai, K.P.; Uzun, H.; Chen, H.; Karanfil, T.; Chow, A.T. Control wildfire-induced Microcystis aeruginosa blooms by copper sulfate: Trade-offs between reducing algal organic matter and promoting disinfection byproduct formation. Water Res. 2019, 158, 227–236. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, J.; Ou, M.; Wang, Y.; Jia, J. Study of Microcystis aeruginosa inhibition by electrochemical method. Biochem. Eng. J. 2007, 36, 215–220. [Google Scholar] [CrossRef]
- Yang, M.; Wang, X. Interactions between Microcystis aeruginosa and coexisting bisphenol A at different phosphorus levels. Sci. Total Environ. 2019, 658, 439–448. [Google Scholar] [CrossRef]
- Miao, Y.; Zheng, S.; Lu, X.; Zhang, K.; Fan, J. Investigation on lanthanum modified kaolinite for control of cyanobacterial growth and microcystin production. Water 2025, 17, 428. [Google Scholar] [CrossRef]
- Kong, W.W.; Huang, S.L.; Shi, F.F.; Zhou, J.G.; Feng, Y.B.; Xiao, Y. Study on Microcystis aeruginosa growth in incubator experiments by combination of Logistic and Monod functions. Algal Res. 2018, 35, 602–612. [Google Scholar] [CrossRef]
- Aleynik, D.; Dale, A.C.; Porter, M.; Davidson, K. A high resolution hydrodynamic model system suitable for novel harmful algal bloom modelling in areas of complex coastline and topography. Harmful Algae 2016, 53, 102–117. [Google Scholar] [CrossRef] [PubMed]
- Lv, Q.; Pitchford, J.W. Stochastic von Bertalanffy models, with applications to fish recruitment. J. Theor. Biol. 2007, 244, 640–655. [Google Scholar] [CrossRef]
- Neori, A.; Chopin, T.; Troell, M.; Buschmann, A.H.; Kraemer, G.P.; Halling, C.; Shpigel, M.; Yarish, C. Integrated aquaculture: Rationale, evolution and state of the art emphasizing seaweed biofiltration in modern mariculture. Aquaculture 2004, 231, 361–391. [Google Scholar] [CrossRef]
- Thompson, F.L.; Abreu, P.C.; Wasielesky, W. Importance of biofilm for water quality and nourishment in intensive shrimp culture. Aquaculture 2002, 203, 263–278. [Google Scholar] [CrossRef]
- Carbis, C.R.; Rawlin, G.T.; Mitchell, G.F.; Anderson, J.W.; McCauley, I. The histopathology of carp, Cyprinus carpio L. exposed to microcystins by gavage, immersion and intraperitoneal administration. J. Fish Dis. 1996, 19, 199–207. [Google Scholar] [CrossRef]
- Wu, Q.; Yan, W.; Liu, C.; Li, L.; Yu, L.; Zhao, S.; Li, G. Microcystin-LR exposure induces developmental neurotoxicity in zebrafish embryo. Environ. Pollut. 2016, 213, 793–800. [Google Scholar] [CrossRef]
- Liu, J.; Sun, Z.; Lavoie, M.; Fan, X.; Bai, X.; Qian, H. Ammonium reduces chromium toxicity in the freshwater alga Chlorella vulgaris. Appl. Microbiol. Biotechnol. 2016, 99, 3249–3258. [Google Scholar] [CrossRef]
- Ramcharan, C.W.; France, R.L.; Mcqueen, D.J. Multiple effects of planktivorous fish on algae through a pelagic trophic cascade. Can. J. Fish. Aqua. Sci. 1996, 53, 2819–2828. [Google Scholar] [CrossRef]
- Wang, J.; Wu, R.; Wang, J.; Guo, J.; Zhang, Y.; Shi, N.; Gu, J.; Han, Y.; Guo, X.; Yu, Z.; et al. Investigation of feeding effects and environmental impact of fish-feed quality: Evidence from crucian carp feeding experiments. Fishes 2025, 10, 50. [Google Scholar] [CrossRef]
- Yang, Z.J.; Huang, S.L.; Kong, W.W.; Chen, L.; Ekaterina, P.; Khatoon, Z.; Ashraf, M.; Akram, W. Effects of fish feed addition scenarios with prometryn on Microcystis aeruginosa growth and water qualities. Ecotoxicol. Environ. Saf. 2021, 209, 111810. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Huang, S.L.; Zang, C.J.; Du, S.L. Release of nutrient from fish feed and effects on Microcystis aeruginosa growth. Aquac. Res. 2012, 43, 1460–1470. [Google Scholar] [CrossRef]
- Zhou, X.; Li, Y.; Li, H.; Yang, Z.; Zuo, C. Responses in the crucian carp (Carassius auratus) exposed to environmentally relevant concentration of 17α-Ethinylestradiol based on metabolomics. Ecotoxicol. Environ. Saf. 2019, 183, 109501. [Google Scholar] [CrossRef]
- Yang, Z.; Zhao, D.; Gu, J.; Wu, R.; Liu, B.; Yu, G.; Dong, P.; H, X.; Li, M.; Li, G. Investigation of biotoxicity and environmental impact of prometryn on fish and algae coexistent system. Water 2024, 16, 2531. [Google Scholar] [CrossRef]
- Daendee, S.; Thongsong, B.; Kalandakanond-Thongsong, S. Effects of time of estrogen deprivation on anxiety-like behavior and GABAA receptor plasticity in ovariectomized rats. Behav. Brain Res. 2013, 246, 86–93. [Google Scholar] [CrossRef]
- Lim, S.J.; Lee, K.J. Partial replacement of fish meal by cottonseed meal and soybean meal with iron and phytase supplementation for parrot fish Oplegnathus fasciatus. Aquaculture 2009, 290, 283–289. [Google Scholar] [CrossRef]
- Hamre, K.; Yúfera, M.; Rønnestad, I.; Boglione, C.; Conceição, L.E.C.; Izquierdo, M. Fish larval nutrition and feed formulation: Knowledge gaps and bottlenecks for advances in larval rearing. Rev. Aquac. 2013, 5, S26–S58. [Google Scholar] [CrossRef]
- Rountos, K.J.; Kim, J.J.; Hattenrath-Lehmann, T.K.; Gobler, C.J. Effects of the harmful algae, Alexandrium catenella and Dinophysis acuminata, on the survival, growth, and swimming activity of early life stages of forage fish. Mar. Environ. Res. 2019, 148, 46–56. [Google Scholar] [CrossRef]
- Wang, C.Y.; Wang, X.L.; Su, R.G.; Liang, S.K. No detected toxic concentrations in in situ algal growth inhibition tests-A convenient approach to aquatic ecotoxicology. Ecotoxicol. Environ. Saf. 2011, 74, 225–229. [Google Scholar] [CrossRef]
- Fussmann, G.F.; Ellner, S.P.; Shertzer, K.W.; Hairston, N.G. Crossing the Hopf bifurcation in a live predator-preysystem. Science 2000, 290, 1358–1360. [Google Scholar] [CrossRef]
- Huang, S.L.; Kong, W.W.; Yang, Z.J.; Yu, H.; Li, F.Y. Combination of Logistic and modified Monod functions to study Microcystis aeruginosa growth stimulated by fish feed. Ecotoxicol. Environ. Saf. 2019, 167, 146–160. [Google Scholar] [CrossRef]
- Yang, Z.J.; Huang, S.L.; Kong, W.W.; Yu, H.; Li, F.Y.; Khatoon, Z.; Ashraf, M.N.; Akram, W. Effect of different fish feeds on water quality and growth of crucian carp (Carassius carassius) in the presence and absence of prometryn. Ecotoxicol. Environ. Saf. 2021, 227, 112914. [Google Scholar] [CrossRef]
- Hargreaves, J.A. Nitrogen biogeochemistry of aquaculture ponds. Aquaculture 1998, 166, 181–212. [Google Scholar] [CrossRef]
- Haug, R.T.; McCarty, P.L. Nitrification with the submerged filter. Tech. Rep. Dep. Civ. Eng. 1971, 149, 206. [Google Scholar]
- Eze, V.C.; Velasquez-Orta, S.B.; Hernández-García, A.; Monje-Ramírez, I.; Orta-Ledesma, M.T. Kinetic modelling of microalgae cultivation for wastewater group and carbon dioxide sequestration. Algal Res. 2018, 32, 131–141. [Google Scholar] [CrossRef]
- Yogev, U.; Gross, A. Reducing environmental impact of recirculating aquaculture systems by introducing a novel microaerophilic assimilation reactor: Modeling and proof of concept. J. Clean. Prod. 2019, 226, 1042–1050. [Google Scholar] [CrossRef]
- Cancemi, G.; Falco, G.D.; Pergent, G. Effects of organic matter input from a fish farming facility on a Posidonia oceanica meadow. Estuar. Coast. Shelf Sci. 2003, 56, 961–968. [Google Scholar] [CrossRef]
- Burford, M.A.; Williams, K.C. The fate of nitrogenous waste from shrimp feeding. Aquaculture 2001, 198, 79–93. [Google Scholar] [CrossRef]
- Yone, Y.; Toshima, N. The utilization of phosphorus in fish meal by carp and black sea bream. Bull. Jap. Soc. Sci. Fish 1979, 45, 753–756. [Google Scholar] [CrossRef]
- Yang, S.D.; Lin, T.S.; Liu, F.G.; Liou, C.H. Influence of dietary phosphorus levels on growth, metabolic response and body composition of juvenile silver perch (Bidyanus bidyanus). Aquaculture 2006, 253, 592–601. [Google Scholar] [CrossRef]
- Wang, X.; Andresen, K.; Handa, A.; Jensen, B.; Olsen, Y. Chemical composition and release rate of waste discharge from an Atlantic salmon farm with an evaluation of IMTA feasibility. Aquac. Environ. Interact. 2013, 4, 147–162. [Google Scholar] [CrossRef]
- Chu-Koo, F.; Stewart, P.M.; Babilonia, J.L.; Garcia-Davilia, C. Water temperature effects on growth, feed utilization and survival of black pacu (Colossoma macropomum) fingerlings. Folia Amaz. 2011, 20, 15–21. [Google Scholar] [CrossRef]
- Zucchi, M.R.; Necchi, O. Effects of temperature, irradiance and photoperiod on growth and pigment content in some freshwater red algae in culture. Phycol. Res. 2001, 49, 103–114. [Google Scholar] [CrossRef]
- Swingle, H.S. Relationships of pH of pond waters to their suitability for fish culture. Proc. Pac. Sci. Congr. 1961, 10, 72–75. [Google Scholar]
- Prairie, Y.T.; Duarte, C.M.; Kalff, J. Unifying nutrient-Chlorophyll Relationship in Lakes. Can. J. Fish. Aquat. Sci. 1989, 46, 1176–1182. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, J.; Ding, L.; Li, Y.; Liu, H.; Zhao, Y.; Fu, G. Eutrophication evolution trajectory influenced by human activities and climate in the shallow Lake Gehu, China. Ecol. Indic. 2022, 138, 108821. [Google Scholar] [CrossRef]
- Downing, J.A. The nitrogen: Phosphorus relationship in lakes. Limnol. Oceanogr. 1992, 37, 936–945. [Google Scholar] [CrossRef]
- Islam, M.S. Nitrogen and phosphorus budget in coastal and marine cage aquaculture and impacts of effluent loading on ecosystem: Review and analysis towards model development. Mar. Pollut. Bull. 2005, 50, 48–61. [Google Scholar] [CrossRef]
- Krom, M.D.; Neori, A. A total nutrient budget for an experimental intensive fishpond with circularly moving seawater. Aquaculture 1989, 88, 345–358. [Google Scholar] [CrossRef]
- Sikorska, J.; Kondera, E.; Kaminski, R.; Lugowska, K.; Witeska, M.; Wolnicki, J. Effect of four rearing water temperatures on some performance parameters of larval and juvenile crucian carp, Carassius carassius, under controlled conditions. Aquac. Res. 2018, 49, 3874–3880. [Google Scholar] [CrossRef]

| Parameter | F | FC | FM | FCM |
|---|---|---|---|---|
| Growth-related parameters of crucian carp | ||||
| aW | - | −3.32 | - | −2.97 |
| rW | - | 0.09 | - | 0.08 |
| BWmax | - | 18.45 | - | 19.56 |
| R2 | - | 0.876 | - | 0.775 |
| aL | - | −3.58 | - | −3.60 |
| rL | - | 0.04 | - | 0.02 |
| BLmax | - | 94.45 | - | 94.59 |
| R2 | - | 0.958 | - | 0.894 |
| DWGmax | - | 0.61 | - | 0.57 |
| GRmax | - | 1.39 | - | 0.70 |
| FCE | - | 9.70 | - | 8.50 |
| WGRmax | - | 5.04 | - | 3.74 |
| LGRmax | - | 2.40 | - | 1.97 |
| PER | - | 32.34 | - | 28.35 |
| Parameters of equations describing M. aeruginosa growth | ||||
| a | - | - | 5.29 | 6.66 |
| r/d−1 | - | - | 0.15 | 0.16 |
| Nmax | - | - | 43.28 | 165.68 |
| Nave | - | - | 26.52 | 90.86 |
| R2 | - | - | 0.987 | 0.992 |
| μ′cmax | - | - | 1.62 | 6.63 |
| μ′cave | - | - | 0.44 | 1.81 |
| μcmax | - | - | 0.15 | 0.16 |
| μcave | - | - | 0.04 | 0.05 |
| Nutrients’ proportions in different groups | ||||
| NH4+-N/TN (%) | 1.39 | 4.46 | 1.91 | 1.53 |
| TDN/TN (%) | 72.13 | 90.54 | 39.95 | 30.35 |
| PO43−-P/TP (%) | 63.94 | 56.16 | 16.64 | 14.37 |
| TDP/TP (%) | 88.15 | 73.68 | 23.77 | 18.46 |
| TN/TP | 12.40 | 12.98 | 13.77 | 11.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Li, G.; Wang, J.; Zhou, J.; Wang, W.; Guo, J. Mutual Effects of Carassius carassius and Microcystis aeruginosa on Growth Dynamics and Water Quality. Fishes 2025, 10, 486. https://doi.org/10.3390/fishes10100486
Yang Z, Li G, Wang J, Zhou J, Wang W, Guo J. Mutual Effects of Carassius carassius and Microcystis aeruginosa on Growth Dynamics and Water Quality. Fishes. 2025; 10(10):486. https://doi.org/10.3390/fishes10100486
Chicago/Turabian StyleYang, Zhenjiang, Guoxi Li, Jianhua Wang, Jianshe Zhou, Wanliang Wang, and Jiangtao Guo. 2025. "Mutual Effects of Carassius carassius and Microcystis aeruginosa on Growth Dynamics and Water Quality" Fishes 10, no. 10: 486. https://doi.org/10.3390/fishes10100486
APA StyleYang, Z., Li, G., Wang, J., Zhou, J., Wang, W., & Guo, J. (2025). Mutual Effects of Carassius carassius and Microcystis aeruginosa on Growth Dynamics and Water Quality. Fishes, 10(10), 486. https://doi.org/10.3390/fishes10100486






