1. Introduction
With the rapid development of blockchain [
1] and technology, the scale of cryptocurrency transactions has experienced exponential growth. While cryptocurrencies are also utilized in certain illegal activities, it is important to note that their primary value lies in providing decentralized and efficient digital transaction mechanisms. Cryptocurrencies, exemplified by Bitcoin [
2], are characterized by decentralization and anonymity. Although users can transact without revealing real-world identities, most blockchain transactions are publicly recorded and traceable, making them fundamentally different from cash in terms of privacy. These properties, including global accessibility and transaction efficiency, have also led to their misuse in various illegal activities [
3], including but not limited to (1) crimes utilizing cryptocurrency as a payment tool, (2) money laundering and terrorist financing facilitated by cryptocurrency, (3) crimes directly targeting cryptocurrency assets, and (4) fraudulent schemes and pyramid selling disguised as cryptocurrency investment opportunities. According to their underlying concept, cryptocurrencies can also be referred to as decentralized digital currencies. While the degree of anonymity remains a topic of academic debate [
4,
5,
6,
7,
8,
9], it is widely acknowledged that most cryptocurrencies offer a level of traceability not present in cash transactions, due to their public and immutable ledger systems. The transfer of cryptocurrency occurs between addresses. A cryptocurrency address is analogous to a bank card number without real-life identity information and is represented by a string of characters and numbers. Up until now, a large number of public chains have been issued, among which Bitcoin (BTC) and Ethereum (ETH) are dominant in terms of market capitalization, while Tron has emerged as a major platform in terms of transaction volume, particularly for USDT transfers. The market price of cryptocurrencies fluctuates wildly, especially for Bitcoin. Since its creation, Bitcoin has achieved a million-fold increase in price. Violent price fluctuations bring many risks, which are not conducive to the development of the digital currency market. USDT has been issued by Tether to minimize the volatility of the digital currencies and provide a relatively stable medium for digital asset trading. It is a digital token pegged to the US dollar (USD), that is, one USD is equal to one USDT. Nowadays, USDT is one of the most widely used stablecoins [
10] in the digital currency market. As a stablecoin, USDT was originally issued on Bitcoin’s Omni protocol and was later issued on the Ethereum network using the ERC20 token standard. With the development of different blockchain networks, USDT has successively existed in different token standards on other public chains, such as in the form of TRC20 token standard on the Tron blockchain. Tron has become particularly significant in the USDT ecosystem due to its high transaction throughput and low fees, making it an important blockchain despite a relatively lower market capitalization ranking. Users can choose which blockchain network to transact on using USDT based on their needs and preferences. In digital currency trading, stablecoins are often used as a low-cost exit from the digital currency market. Currently, the global landscape of virtual currency-related crimes has become increasingly severe. Virtual currencies have become a primary channel for illicit funds in emerging cybercrimes, such as telecommunications network fraud and online gambling. In 2024, the global virtual currency market exhibited heightened activity compared to 2023, with the price of Bitcoin surpassing USD 100,000 and the total market capitalization of cryptocurrencies having doubled. Notably, USDT remains the most commonly involved currency in digital currency-related illegal activities.
With the increasing prevalence of criminal activities involving digital currency transactions, it is imperative to enhance the regulatory oversight of digital currencies, investigate the correlations between virtual currency addresses, and identify clusters of addresses associated with the same user or group. Existing studies on USDT tracing mainly focus on single-network analysis (e.g., only analyzing USDT transaction records) and lack consideration of the correlation between USDT-TRC20 and its underlying TRX transaction network. Thus, the objective of this paper is to enhance regulatory oversight of digital currencies by investigating correlations between virtual currency addresses and identifying clusters associated with the same user or group.
As an increasing number of cybercrimes involve virtual currency transactions, and one of the most commonly used digital currencies by suspects is USDT. The market capitalization of USDT has surged to a record high, from about USD 94.9 billion at the beginning of 2024 to USD 160 billion in July 2025. Nowdays, most of the newly issued USDT is on the Tron blockchain. Indeed, the majority of USDT transactions occur through centralized exchanges (CEX), where user-level addresses are generally not publicly accessible on-chain, and effective tracing often requires judicial cooperation with the exchange or the use of integrated cross-chain analysis tools. In this paper, we focus on USDT and propose a two-layer transaction network-based approach for identifying hidden relationships and encrypted assets in on-chain transaction scenarios. This method is particularly suited for analyzing direct on-chain interactions between publicly accessible addresses, rather than off-chain or CEX-internal transfers. Specifically, Layer A describes the flow of USDT-TRC20 between on-chain addresses over time, while Layer B represents the flow of TRX between on-chain addresses over time. TRX is a digital currency based on Tron, and its full name is Tronix, the basic unit of Tron. TRX is the native digital currency of Tron, which can be used to pay for various costs in the network, such as transaction fees, bandwidth points, energy, and so on. It can be seen from the existing practical cases that the flow of TRX is crucial for identifying suspects’ hidden on-chain address, while existing transaction data analysis methods primarily concentrate on the flow of USDT-TRC20 and often overlook TRX.
The remainder of this paper is organized as follows. In
Section 2, we review and synthesize the related work on blockchain transaction analysis and address tracing. In
Section 3, we elaborate on the characteristics of USDT-TRC20 transactions and the construction of a two-layer network (i.e., the USDT-TRC20 transaction network and the TRX transaction network), using publicly available transaction records queried from OKlink, a blockchain explorer. In
Section 4, an identity metric is introduced to identify hidden on-chain relationships and distinguish addresses belonging to the same user or group. Furthermore, a methodology for calculating the effective transfer amount between any two addresses is presented for tracing encrypted assets in this section. In
Section 5, the validity of the proposed tracing method is verified. The conclusions are given in
Section 6.
2. Related Work
Currently, research on the traceability of digital currency transactions remains relatively limited both domestically and internationally. Existing studies can be broadly categorized into two primary areas: network-layer traceability technologies [
11,
12,
13] and transaction data analysis methodologies [
6,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23]. Using Bitcoin as an example, network-layer traceability technology entails the collection of information transmitted over the Bitcoin network layer, the analysis of propagation paths of Bitcoin transactions within the network, and the tracking of IP information associated with servers that generate these transactions. This approach directly associates anonymous transactions with the IP addresses of the originating nodes or the nodes initiating the transactions, thereby achieving traceability [
12]. In 2014, Koshy et al. [
13] examined the propagation characteristics of broadcast messages observed over a specific timeframe and put forward four models describing how messages propagate within blockchain networks. This tracing approach monitors the patterns of message dissemination, analyzes the actual initiating nodes, and establishes correlations between IP addresses and on-chain addresses embedded in the messages, posing significant risks to communication privacy and user anonymity. To avoid such tracking, many users now employ proxy servers or virtual private networks (VPNs) to obscure their real IP addresses. Consequently, existing network-layer traceability technologies suffer from limited accuracy, high computational and storage resource demands, and poor practical applicability. To address these limitations, Gao et al. [
12] proposed an innovative Bitcoin transaction traceability mechanism using neighbor node identification through the deployment of probe nodes. The probe nodes collect the transaction information with different timestamps from the neighbor nodes and predict the propagation path of the transaction information according to the time order in the network. Then, this traceability mechanism is used to find the IP address of the first server node of the Bitcoin network where the transaction information enters, and the inbound traffic of the server node is analyzed to find the IP address of the client node. In fact, the network delay between different nodes and probe nodes is different. This may cause the order in which the transaction information reaches the probe node to be different from the time order of the node forwarding the transaction information, thus affecting the accuracy of traceability. Bitcoin transactions are not considered truly anonymous because private user information (e.g., IP addresses) can be uncovered through transaction tracking, combined with the ongoing development of cryptanalysis techniques [
24]. Xiao et al. [
25] proposed a mixing mechanism integrated with a decentralized signature protocol to safeguard privacy within the Bitcoin blockchain, in which the direct associations between original input addresses and output addresses are disconnected.
Transaction data analysis technology, grounded in the examination of transaction records, aims to infer the relationships and transfer pathways between distinct transaction addresses by analyzing trading patterns and fund flows. According to Bitcoin’s public transaction records, Reid and Harrigan [
6] established topological structures corresponding to transaction and user networks, respectively, and combined these structures with external identifying information and techniques such as context discovery and flow analysis to investigate Bitcoin transaction traceability. Meiklejohn et al. [
7] developed a new clustering heuristic based on change addresses, which can be used to cluster Bitcoin addresses belonging to the same user. By conducting a comprehensive analysis of ransom payment timestamps, both longitudinally across CryptoLocker’s operating period and transversely across times of day, Liao et al. [
14] systematically investigated the ransom process of CryptoLocker. Their study identified 795 ransom payments totalling 1128.40 BTC, based on a cluster of 968 Bitcoin addresses associated with CryptoLocker. In 2017, Chen et al. [
15] proposed a new method for de-anonymizing transaction systems by using information including the number of transactions and timestamps of sending and receiving. Yousaf et al. [
16] explored the tracing of transactions across cryptocurrency ledgers, differentiating between diverse patterns of cross-currency transactions and the general utilization of these platforms to determine whether such activities serve criminal groups or other profit-oriented entities. Chen et al. (2020) [
17] pioneered a graph-based approach to model token creator-holder-transfer relationships, constructing multi-layered graphs to uncover ecosystem dynamics. Their algorithm identified “whale” accounts and token manipulation strategies, such as wash trading, by analyzing subgraph motifs. This work laid the groundwork for detecting collusive behaviors in decentralized finance (DeFi).
Li et al. [
18] introduced a traceable Monero system and elaborated on the detailed construction of such a traceable version by superimposing Monero with two categories of tracing mechanisms. To characterize key participants in the cryptocurrency economy, Liu et al. conducted an analysis of Ethereum token transactions and assessed their identifiability through the application of interpretable machine learning models [
19]. Song et al. [
20] summarized and analyzed the literature on cryptocurrency transaction data from the perspective of complex networks, establishing a systematic framework for blockchain data analysis. They emphasized the role of complex network metrics (e.g., average path length, clustering coefficient) in identifying transaction patterns and detecting anomalies. Their work highlights how network modeling can reveal hidden relationships between addresses, such as money laundering circuits and pseudonymous account clusters. Faced with the computational complexity and excessive memory consumption of traditional graph traversal methods when applied to massive blockchain datasets, Wu et al. (2022) [
21] proposed TRacer, a subgraph search framework optimized for account-based blockchains like Ethereum. TRacer integrates temporal and token-flow attributes into a weighted multigraph, enabling efficient tracing of fund flows through ranking-guided expansion. By prioritizing nodes with high pollution scores (e.g., addresses linked to known illicit activities), the system achieves sublinear time complexity, making it feasible for real-time analysis of terabyte-scale datasets. In 2023, Dearden et al. [
22] developed a structured approach for quantitatively examining the Bitcoin blockchain ledger. Their findings indicate that cryptocurrency transactions, including both legal and illegal activities as well as attempts to obfuscate transactions, are generally identifiable with 90%. These studies have demonstrated that the analysis and mining of transaction-related information from transaction records can facilitate the tracking of cryptocurrency transactions and the detection of illegal activities.
While the aforementioned studies can assist in tracing virtual currency, tracking virtual currency transactions from the perspectives of network-layer traceability or blockchain supervision is not feasible in the practical cases examined by public security agencies. Once a criminal incident occurs, collecting information transmitted through the cryptocurrency network layer by deploying probe nodes, or tracking operations and users by designing new blockchain-based proof methods, becomes too late. Consequently, transaction data analysis technology based on transaction records has emerged as a crucial approach for tracing transaction paths, uncovering hidden encrypted assets and suspects, and preventing digital currency-related crimes.
3. Two-Layer Transaction Network
In actual transfer processes, users transferring USDT via virtual currency wallet software are required to consume a certain amount of TRX, rendering the source of TRX (i.e., TRX transfers between users) significant. However, not every USDT transfer necessitates TRX, as this specifically depends on the blockchain network where the USDT resides. In
Table 1, there is an USDT-TRC20 transaction at 13:32:48 on 22 September 2023 showing a transfer of 5 USDT from the output address (TDhXA…) to the input address (TGgzC…). The transaction fee of 27.2559 TRX simultaneously deducted from the output address (TDhXA…). In fact, the transaction fee for this output address comes from a transfer of 100 TRX at 16:25:39 on 21 September 2023, which can also be seen in
Table 1. Therefore, the transaction data analysis method proposed in this paper not only focuses on the flow of USDT-TRC20 but also examines the transfer of TRX.
The digital token transaction data encompass records of both USDT-TRC20 and TRX transfers. The transaction network formed by USDT-TRC20 and TRX transactions can be abstracted into a complex two-layer network [
23], where virtual currency addresses act as nodes, and TRC20 or TRX transactions between addresses serve as edges. This two-layer network is illustrated in
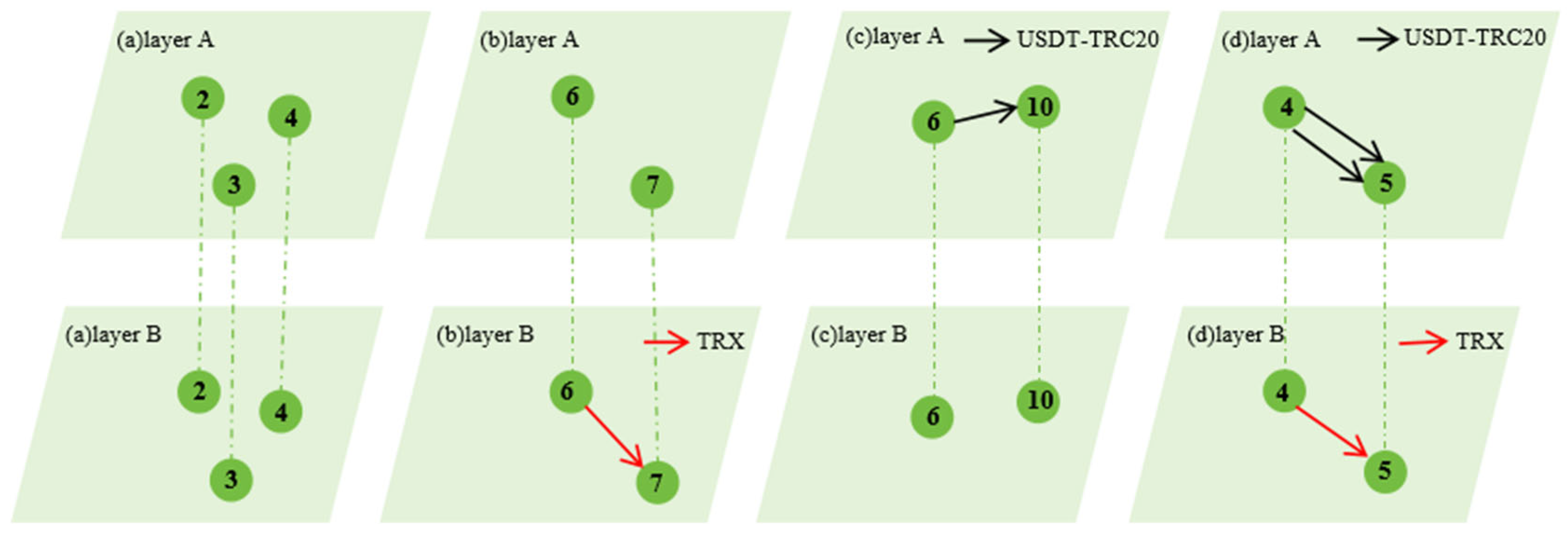
Figure 1, which depicts an example with 11 nodes numbered 1 through 11, where each node in Layer A has a one-to-one correspondence with a node in Layer B.
Layer A represents the USDT-TRC20 transaction network, while Layer B represents the TRX transaction network. Within Layer A, there are
nodes and
directed edges, corresponding to
on-chain addresses and
USDT-TRC20 transactions between these addresses. In lower Layer B, there are
nodes and
directed edges, corresponding to
addresses and
TRX transfers between these addresses, respectively. In each layer, every directed edge between a source and a target node represents a single transaction, containing the transaction amount and timestamp from the output address to the input address. Given that the number of USDT-TRC20 transactions typically exceeds that of TRX transactions,
Figure 1 shows that the number of inter-node links in Layer A is greater than that in Layer B. Within this two-layer network, nodes representing virtual currency addresses are shared consistently across both Layer A and Layer B, with each node in one layer having a strict one-to-one correspondence in the other. These addresses correspond to those used in the Tron blockchain, where TRX addresses are typically 34-character alphanumeric strings starting with the letter “T”.
Next, we abstract the two-layer network into a directed graph
to characterize the coupled relationship between the USDT-TRC20 and TRX transaction networks, where
represents the set of nodes denoting virtual currency addresses started with capital “T”, and
denotes the set of edges in layer
. For example,
denotes the set of edges corresponding to USDT-TRC20 transactions in Layer A, and
denotes the set of edges corresponding to TRX transactions in Layer B. Consider two nodes,
and
, in the transaction graph of Layer A, where
represents a source (output) address and
represents a destination (input) address (i.e.,
). If there are
transactions from node
to node
in Layer A,
, otherwise
. Similarly, if there is one or more transaction from the source node (output address,
) to the destination node (input address,
) in Layer B,
, otherwise
, where
denotes the number of transactions from node
to node
in Layer B. If
, no USDT-TRC20 or TRX transaction exists from node
to node
in layer
. If
, no transaction exists from node
to node
neither USDT-TRC20 nor TRX in layer
. It can be observed that the coupled relationship between the USDT-TRC20 and TRX transaction networks is characterized by a pair of values consisting of
and
. For the connected node pair
, there are four possible value pairs of
, which are listed below,
where
and
represent the number of transactions from node
to node
in layers A and B, respectively.
Figure 2a–d illustrate that these four groups of values correspond to four distinct node connection patterns in the two-layer network.
Because the transactions between two nodes may occur in opposite directions,
differs fundamentally from
, meaning that the connected node pairs
and
represent opposite directions. Similarly, the connected node pair
corresponds to four different kinds of node connections within the two-layer network, where the only difference from
Figure 2a–d lies in the opposite direction of node connections.
Since there may be multiple transactions in any pair of addresses, there are multiple one-way or bidirectional edges between the same two nodes, which can be characterized by labeled property graph. This graph has the following characteristics: (1) The labeled property graph consists of nodes and connections, where nodes correspond to on-chain addresses, and connections correspond to transaction relationship between addresses. (2) The node has properties described by key-value pairs. For example, create (n1:address {addr:‘TDhXAE4’}) represents the creation of a node with a label “address” and an attribute “addr”. In this attribute, the key-value pair is “addr: TDhXAE4”, where “TDhXAE4” is the actual on-chain address. (3) The connection can have one or more attributes, and always has a start node and an end node. For example, create (n1:address {addr:‘TDhXAE4’})-[r:usdt_trans_to{time:[‘2023-09-22 13:32:48’],amount:[‘5 USDT’]}]->(n2: address {addr:‘TGgzCJL’}) represents the creation of a relationship between two nodes with a label “usdt_trans_to” and two attributes “time” and “amounttrx_”, resulting in the graph as shown in
Figure 3. Because different transaction types can exist between two addresses, such as USDT and TRX, two different labeled relationships exist between two nodes, such as “usdt_trans_to” and “trx_trans_to”, in the graph as shown in
Figure 4. Similarly, multiple transaction relationships recorded in the transaction records between addresses can be inserted between nodes to form a labeled property graph characterizing digital currency transaction relationships.
At this stage, the multi-relationship network graph has been constructed. To facilitate subsequent topological structure analysis, the graph will be abstracted into a two-layer network: Layer A characterizes USDT transaction relationships between addresses, while Layer B characterizes TRX transaction relationships between addresses.
4. Method for Determining Address Identity
Traditional methods for cryptocurrency tracing based on transaction data analysis primarily rely on tracking the upstream and downstream addresses according to the transaction data recorded in the blockchain ledger. The analysis of transaction data includes summarizing the incoming and outgoing amounts and number of transactions for specific addresses, as well as summarizing the amounts and number of transactions between address pairs. Currently, the complexity of crimes and the efficacy of evidence pose significant challenges in combating crimes involving virtual currencies. Therefore, tracing the origins and destinations of virtual currency transactions, and digging out hidden encrypted assets and suspects, have become a crucial measure in investigating cases related to virtual currencies, such as money laundering, cyber fraud, terrorism financing, etc.
Next, focusing on the USDT-TRC20 token on the Tron blockchain, we propose an identity consistency determination method. This method aims to uncover underlying relationships between addresses and compute effective transaction pathways of encrypted assets among them. Specifically, the proposed method accomplishes two main tasks. First, starting from a given address, it identifies other addresses controlled by the same entity or affiliated with the same controlling party. Then, it computes both the effective transaction paths and the corresponding amounts between those addresses. Since transaction paths may involve multiple intermediate addresses, the method draws on the max-flow problem from network flow theory to identify all valid paths and compute the maximum transferable amount between the source and target addresses.
The detail steps of the proposed method are summarized as follows:
Step 1: Transaction data acquisition. Transaction data, including both USDT-TRC20 and TRX records, were collected through the following procedure. Starting from a suspect’s USDT-TRC20 address involved in a virtual currency money laundering case, we recursively retrieved all transaction records using OKLink, a blockchain explorer. For each transaction, counterparty addresses were extracted, and their transaction histories were further downloaded iteratively. The retrieval process terminated when a counterparty address was identified as belonging to a known exchange or platform. This procedure was repeated for all USDT-TRC20 addresses associated with the suspects. After acquisition, all non-filtered records were cleaned and summarized by removing invalid records, such as non-USDT or non-TRX transactions and those with amounts less than 0.01. The final output is a structured table containing the transaction hash, block height, timestamp, output address (from), input address (to), token type, and transaction amount.
Step 2: Two-layer network construction. Based on the summarized transaction table obtained in the first step and the two-layer network construction method outlined in
Section 3, the two-layer direction graph
can be represented using USDT-TRC20 and TRX transaction data. We denote the set of nodes in Layer A as
, where
is the number of on-chain addresses involved in USDT-TRC20 transactions within Layer A. The set of nodes in Layer B is denoted as
, where
represents the number of on-chain addresses involved in TRX transactions within Layer B. The graph
can also be denoted as
, where
is the union of the node sets from layers A and B, and
is the number of nodes in this union. Similarly,
and
denote the set of USDT-TRC20 transactions (edges) in Layer A and the set of TRX transactions (edges) in Layer B, respectively. When there are one or more transactions from the source node (output address)
to the destination node (input address)
in layer
(i.e.,
), we set
and
otherwise, where
denotes the number of transactions from node
to node
in layer
. Among these
transactions, each transaction amount is represented by
with the transaction timestamp
. If no transaction exists from node
to node
, we set
and
corresponds to no transaction from node
to node
.
Step 3: uncovering relationships between addresses. We introduce a new metric for evaluating strong relationships between addresses, in addition to traditional statistical metrics of transaction amounts and counts. The traditional statistical metrics comprise the total amount and number of both outgoing and incoming transactions for a given address, as detailed below.
By summing the elements in the rows and columns of the
matrix, the total amount and number of outgoing and incoming transactions for a given address can be calculated. The total amount of outgoing and incoming transactions for node
in layer
can be denoted as
where
denotes the number of transactions from node
to node
in
or from node
to node
in
,
is the total number of unique nodes after aggregation from nodes in layers A and B.
The number of outgoing and incoming transactions for node in layer can be denoted as and , where and denote the number of transactions from node to node and from node to node in layer respectively, and is as defined above.
Given that transactions between addresses primarily involve USDT-TRC20, we introduce a metric
based on the revised harmonic mean to quantify the number of round-trip transactions between on-chain addresses in Layer A.
is denoted as
where
and
are as defined above. It should be noted here why the harmonic mean was selected for parameter design. This choice is based on the characteristic that the harmonic mean is sensitive to extreme values, with a greater susceptibility to extremely small values than to extremely large ones. For instance, consider two node pairs, one with
and
, and the other with
and
. The corresponding values of
are 46.15 and 5.22, respectively. In cases where no round-trip transfers occur between node
and node
(i.e.,
or
), the condition
is not satisfied, and thus there is no need to calculate the value of
. As evident from Equation (4), the larger the value of
, the greater the probability of mutual transfer of USDT-TRC20 between node
and node
.
Metric. Based on the inter-transfer parameter and incorporating both USDT-TRC20 and TRX transactions, a metric noted as the identity metric is proposed to quantify the shared ownership relationships between addresses. The identity metric is denoted as
where
denotes the round-trip transfer indicator for USDT-TRC20 transactions between addresses in Layer A. From Equation (5), it can be observed that when both
and
take zero simultaneously, The identity metric degenerates into
(i.e.,
). In such cases where both
and
are zero, it indicates there is no TRX transfer between nodes
and
, and the strength of their common social relationship is still measured by
. In contrast to
,
not only considers the mutual transfer of USDT-TRC20 but also incorporates TRX transfers, allowing for more effective quantification of the shared ownership relationship between two addresses. Specifically, a relatively large value of
may imply a strong correlation between the pair of addresses in Layer A, while a higher value of
may suggest an increased likelihood that the pair of addresses is associated with the same user or accomplices.
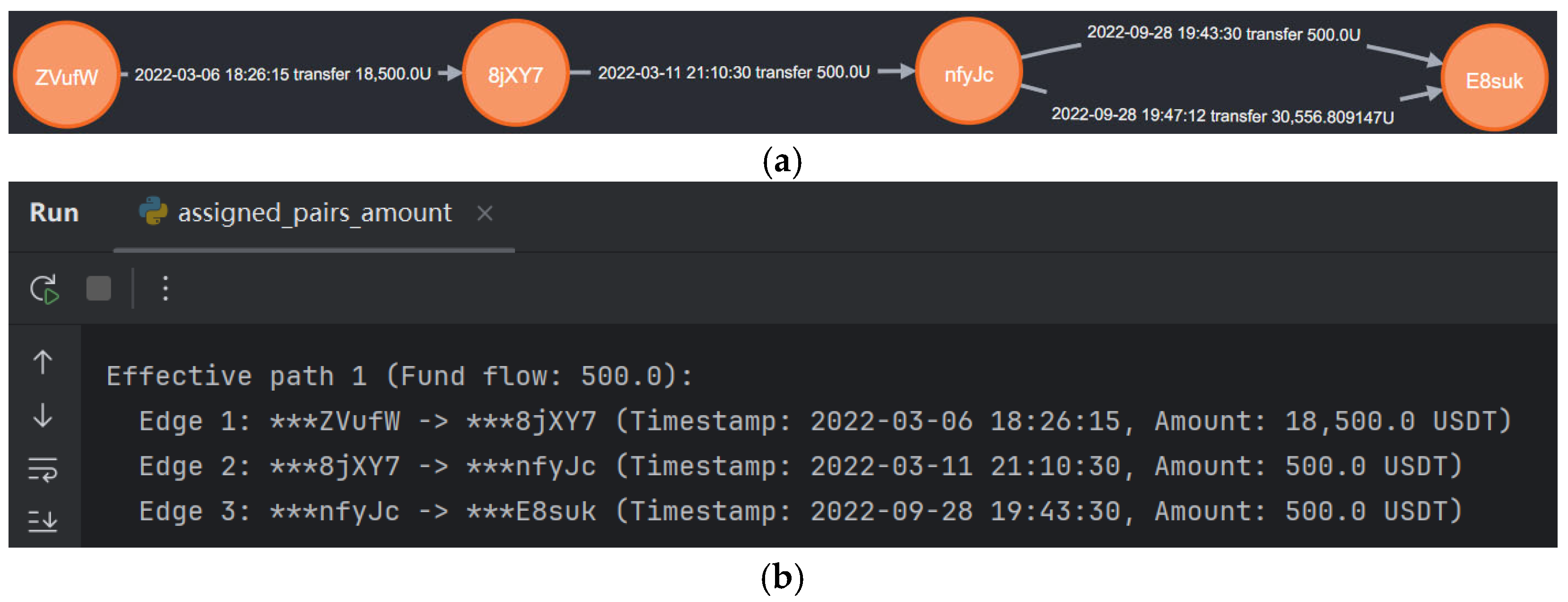
In this step, we calculate the values of using Equation (5), sort them in descending order based on these values, and output the corresponding addresses and , along with the values of and . Notably, if round-trip USDT-TRC20 transfers and TRX transfers coexist in the two-layer transaction network, a larger value of indicates a closer relationship between addresses and .
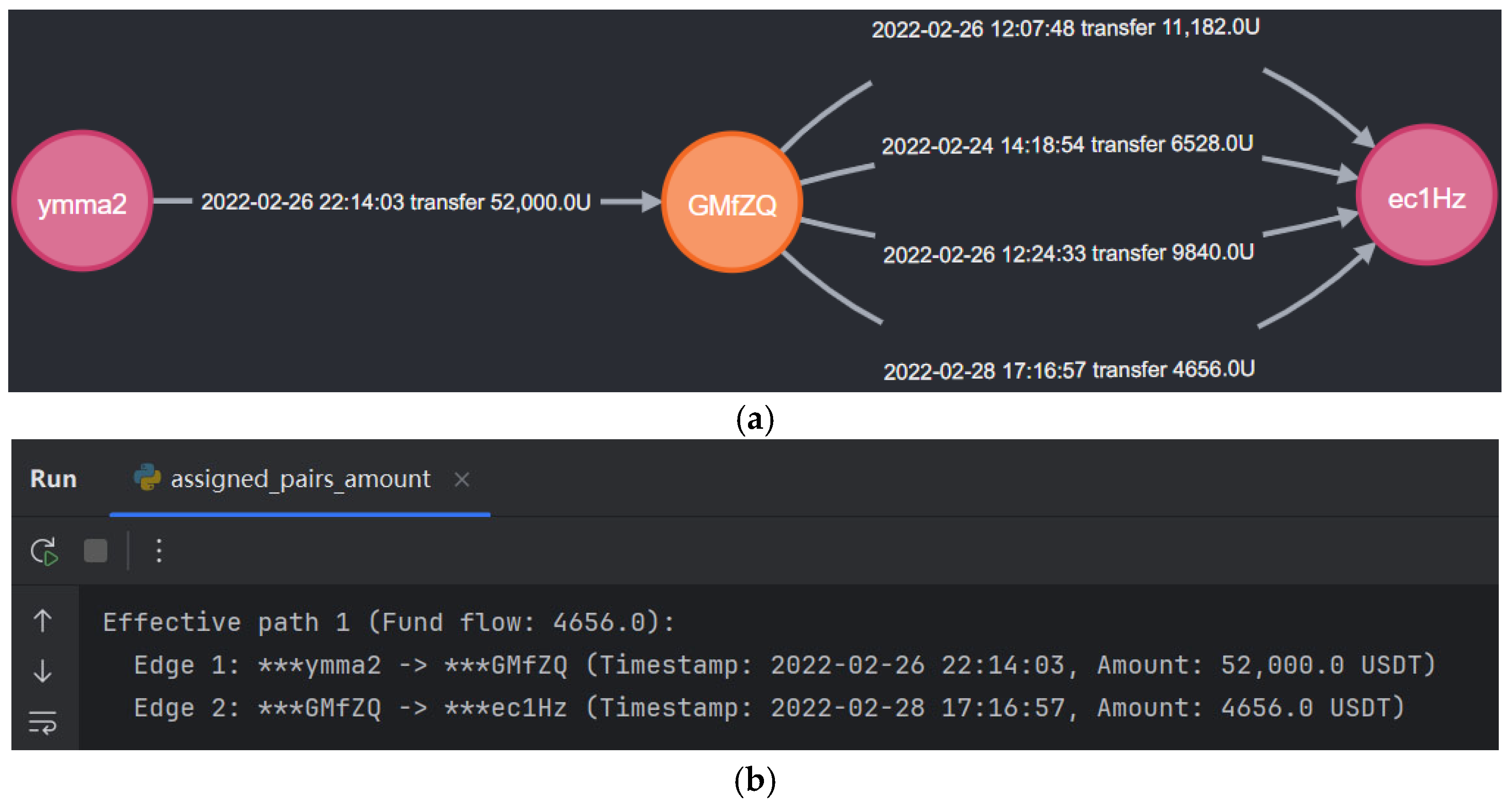
Step 4: Calculation of effective transfer amount. To identify suspicious addresses and trace the primary transaction flow paths between them, we analyze USDT-TRC20 transaction flows to detect concealed fund movements. For example, Address C → (transfer 200 USDT) → Address D → (transfer 50 USDT) → Address E → (transfer 150 USDT) → Address F. After filtering valid transaction paths under temporal constraints, the actual transfer amount from C to F corresponds to the minimum value along the path, which is 50 USDT in this example.
By enforcing temporal order constraints on the transaction sequence, we screen for valid transaction paths. Since each transaction in the flow has a specific timestamp, we first examine each path from the source node
to the sink node
, as illustrated in Equation (6), to verify whether the timestamps satisfy the monotonic increase condition along the path. A path
is considered valid if
where
denotes the timestamp of the direct transaction from node
to node
,
forms a path from source node
to sink node
, with
being the number of intermediate nodes. If a path satisfies the temporal order constraint, it is retained as a valid transaction path for further analysis.
Then compute the maximum feasible flow for each valid transaction path. For each valid path
, the effective transaction amount
is defined as the minimum transaction amount along the path:
where
denotes the amount of the direct transaction from node
to node
, and
is the number of intermediate nodes.
Finally, calculate the effective transfer amount from source to sink. The total effective transfer amount
from source node
to sink node
is the sum of the effective amounts over all valid paths:
where
is the set of all valid transaction paths from
to
, and
is the effective amount for path
.
Through the above steps, the effective transfer amount between any two addresses can be calculated.
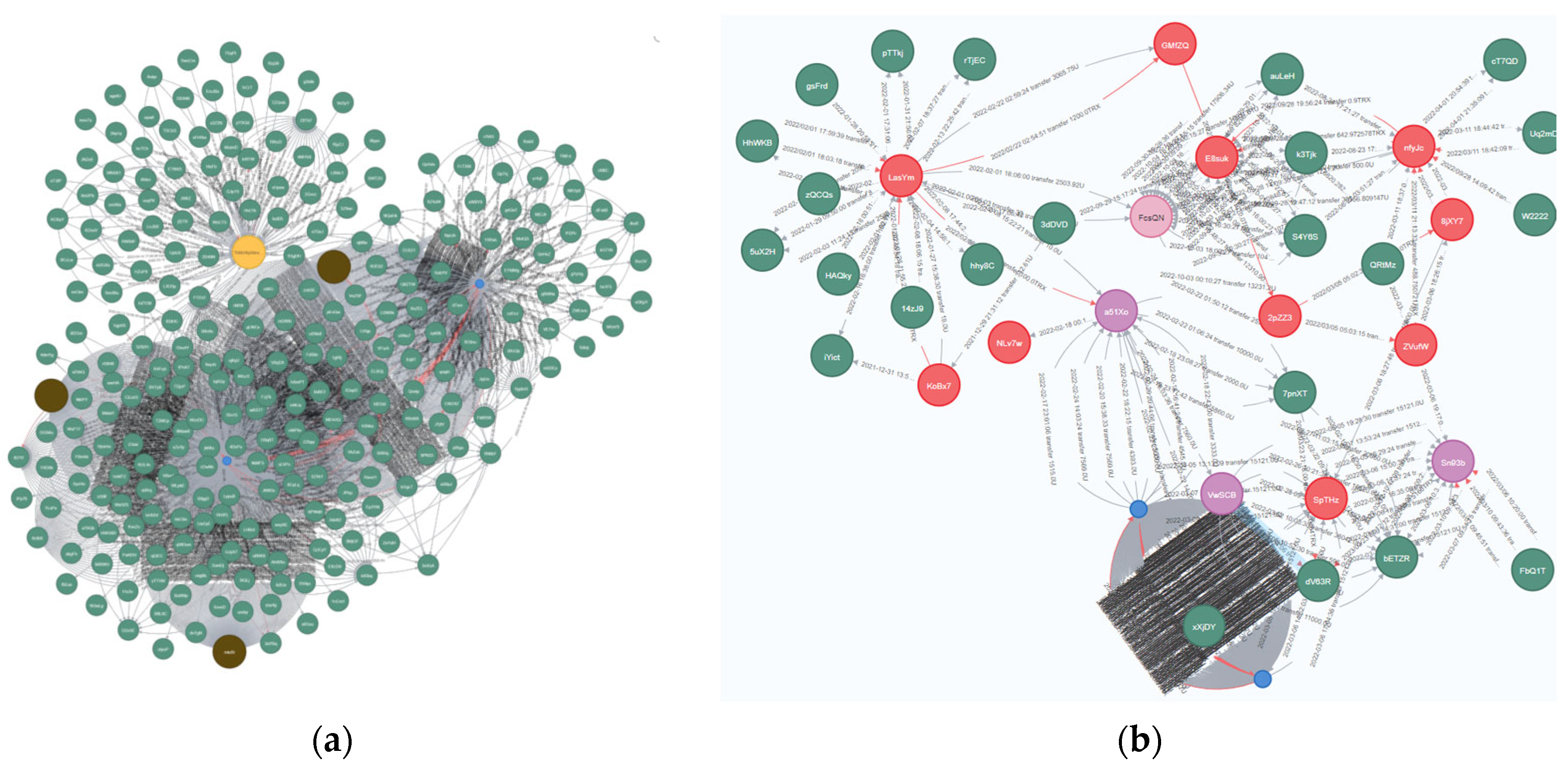
Step 5: Visualization of transaction data. To depict the transaction relationships between addresses using a labeled property graph, we utilize the py2neo package in Python to bulk import virtual currency transaction data into the Neo4j database, which stores the complex transaction network topology between addresses. Transaction paths between addresses and basic statistical analyses can be generated using Cypher, a declarative graph query language.
Following the aforementioned steps, we can identify address pairs with common social relationships in transaction records and visualize the transaction topology between addresses using Neo4j.