Abstract
Modern distributed computing systems and applications with strict privacy requirements demand robust data confidentiality. A primary challenge involves enabling parties to exchange data or perform joint computations. These interactions must avoid revealing private information about the data. Protocols with the obliviousness property, known as oblivious protocols, address this issue. They ensure that no party learns more than necessary. This survey analyzes the security and performance of post-quantum oblivious protocols, with a focus on oblivious transfer and oblivious pseudorandom functions. The evaluation assesses resilience against malicious adversaries in the Universal Composability framework. Efficiency is quantified through communication and computational overhead. It identifies optimal scenarios for these protocols. This paper also surveys related primitives, such as oblivious signatures and data structures, along with their applications. Key findings highlight the inherent trade-offs between computational cost and communication complexity in post-quantum oblivious constructions. Open challenges and future research directions are outlined. Emphasis is placed on quantum-resistant designs and formal security proofs in stronger adversarial models.
1. Introduction
Modern distributed computing systems and privacy-sensitive applications continue to show a strong demand for methods and protocols that ensure data confidentiality. A core challenge in this field is to enable parties to securely exchange data or perform joint computations. Critically, these interactions must prevent the disclosure of private information, whether about the participants themselves or the transmitted data. Protocols achieving obliviousness (called oblivious protocols) provide the foundation for solving this challenge.
Rabin’s 1981 paper introduced the first formal oblivious protocol, known as oblivious transfer (OT) [1]. The protocol allows a message to be received with probability . The sender transmits one message. The sender remains unaware if the receiver obtained it. Subsequently, in [2], Even, Goldreich, and Lempel proposed the 1-out-of-2 OT protocol, where the sender transmits two messages and the receiver obtains exactly one chosen message. In this protocol, the receiver gains no information about the unselected message while preserving the sender’s obliviousness to the receiver’s choice.
Notably, several years before Rabin’s work, the same idea had been proposed by Stephen Wiesner in a now-famous but initially unpublished manuscript [3]. Wiesner described how information could be stored and transmitted via polarized photons—by sending two messages over a quantum channel encoded in conjugate bases, the receiver could measure and learn only one message since quantum mechanics forbids extracting both simultaneously.
Rabin’s protocol [1] did not gain widespread adoption due to its limited applicability. However, the version of the protocol by Even, Goldreich, and Lempel [2] proved to be more practical and applicable in numerous other protocols, such as private set intersection (PSI) protocols [4,5,6,7] and Yao’s garbled circuits [8], which are further used in privacy-preserving biometric identification [9] and in federated machine learning [10].
Following the OT protocol, other protocols that allow confidential queries were proposed. Many of these are based on the following constructs:
- Cryptographic primitives: OT [11], oblivious signature (OS) [12];
- Data structures: oblivious random access memory (ORAM) [13], oblivious key–value store (OKVS) [14];
- Polynomial and Boolean functions: oblivious pseudorandom function (OPRF) [15], oblivious polynomial evaluation (OPE) [11], oblivious linear evaluation (OLE) [16], and vector oblivious linear evaluation (VOLE) [17].
Private information retrieval (PIR) protocols [18] address a similar issue by ensuring confidential client interactions with data stored on a potentially untrusted server. PIR lets a client query a database so that the server does not learn which item was requested. Although PIR and some oblivious protocols (OT, ORAM) may seem deceptively similar at first glance, they are distinct.
Many oblivious primitives (OT, ORAM) differ from PIR by offering stronger security guarantees. They ensure complete privacy for both inputs and outputs, preventing access to the server’s data. In PIR, unlike in OT, there is typically no restriction preventing the client from learning other data; the focus is solely on hiding the query index.
In general, oblivious protocols and PIR serve related but distinct purposes. Each class has many variants and is often interreducible [19] or can be combined [20]. This further boosts the appeal of the protocols and widens their practical adoption.
The practical demand for oblivious protocols is undeniable. OPRFs are used in PSI protocols [4,21,22], oblivious dictionary search [4,23], updatable cloud key management [24], privacy pass protocols [25], and password-authenticated key exchange (PAKE) protocols [26] (e.g., WhatsApp [27]).
Oblivious signatures are applied in electronic voting protocols [28], for online shopping [29], and in PIR protocols [12].
Oblivious data structures play a key role in the construction of PIR protocols [30], ensuring data protection in untrusted environments [31], in searchable encryption [32], and in the construction of PSI protocols [14]. Furthermore, the oblivious polynomial evaluation protocol is one of the building blocks for secure computation protocols [33] and PAKE protocols [11].
Table 1 offers a comparative overview of oblivious protocols and their applications. All protocols ensure the confidentiality of inputs and outputs. They function as components in secure computation frameworks or as primitives for complex cryptographic protocols.

Table 1.
Comparison of oblivious protocols.
Broad adoption of oblivious protocols imposes strict security and efficiency demands. Quantum computing threats necessitate post-quantum designs.
Post-quantum analysis is crucial for two reasons. First, security against isolated quantum algorithms (Shor [34] and Grover [35]) does not extend to nested protocols in complex systems, necessitating formal composability proofs. Second, many post-quantum designs impose high computational and communication costs, restricting their applicability in constrained environments.
Therefore, research on post-quantum oblivious protocols requires cryptographic security and performance comparisons. Bandwidth and latency must be measured under realistic parameters. Such evaluations yield secure and practical protocols.
Prior surveys advance understanding but remain limited. Santos et al. [36] provide a concise review of quantum OT but focus on quantum-native constructions rather than on post-quantum schemes. The systematization in [37] classifies oblivious PRF constructions into PRF families and characterizes their functional properties and applications. However, it predominantly addresses classical instantiations and gives limited attention to post-quantum OPRF protocols. Yadav et al. [38] offer a comprehensive overview of OT variants (1-out-of-2, 1-out-of-n, k-out-of-n) and OT extensions, including security analyses in semi-honest and malicious models within the universal composability (UC) framework. The protocols examined here are not included. This survey reviews post-quantum oblivious protocols from the past decade. Recent contributions receive emphasis. Recommendations on recent post-quantum protocol usage are provided.
Contributions
This survey presents a systematic study of post-quantum oblivious protocols. Emphasis falls on oblivious transfer and oblivious pseudorandom functions. These primitives support applications like PSI and PAKE. They represent the primary focus of recent post-quantum research. In contrast, oblivious signatures, ORAM, and OPE have fewer post-quantum realizations. This study includes a detailed comparison of OT and OPRF protocols (separately) instantiated under various cryptographic assumptions, such as lattice-based, code-based, and isogeny-based constructions, with performance benchmarks under the 128-bit post-quantum security level.
The key contributions are as follows:
- A systematic evaluation of recent post-quantum oblivious transfer and pseudorandom function constructions, using unified metrics (communication rounds, data size, and CPU cycles for the sender and receiver).
- The security of OT and OPRF protocols is examined within the universal composability framework, with adversaries considered in the malicious model. The evaluation encompasses both the random oracle model (ROM) and the quantum random oracle model (QROM).
- Based on the conducted analysis, recommendations are formulated regarding the selection of specific OT and OPRF protocols according to the requirements of the target system. Particular attention is given to scenarios in which protocol efficiency, communication overhead, or a combination thereof constitute critical performance factors.
- An illustrative, detailed comparative analysis of the considered oblivious protocols is presented, highlighting their respective application domains and clarifying distinctions from related primitives, such as PIR.
This paper is organized as follows. In Section 2, the methodology for selecting the analyzed articles and evaluating the performance of the examined protocols is presented. Section 3 provides a formal description of the oblivious protocol. The overview of post-quantum OT and OPRF protocols is provided in Section 4 and Section 5, respectively. Section 6 analyzes additional oblivious protocols, including post-quantum constructions, and outlines their key differences. Finally, Section 7 discusses open challenges and outlines future research directions for the development of practical and quantum-secure oblivious protocols.
2. Methodology
A systematic, keyword-based search was performed to identify literature on post-quantum oblivious protocols. Queries were executed in IEEE Xplore, Google Scholar, and the OpenAlex catalog using combinations of terms describing post-quantum security and oblivious primitives, including common synonyms. The searches were restricted to titles and abstracts and limited to works published or made available as preprints from 2015 through 2025 to capture recent developments.
During the catalog search, the terms “post-quantum”, “quantum-resistant”, and protocol names were used. For instance, some of the queries were conducted with the following keywords: “post-quantum oblivious transfer”, “quantum-resistant oblivious transfer”, “lattice-based oblivious transfer”, “isogeny-based oblivious transfer”, “code-based oblivious transfer”; “post-quantum OPRF”, “quantum-resistant OPRF”, “lattice-based OPRF”, “isogeny-based OPRF”, “code-based OPRF”; “post-quantum oblivious signature”, “post-quantum ORAM”, “post-quantum oblivious polynomial evaluation”, “post-quantum oblivious linear evaluation”, “post-quantum vector oblivious linear evaluation”, “post-quantum oblivious key–value store”.
Search results were merged and de-duplicated manually. Titles and abstracts were screened to exclude clearly irrelevant items; full texts were retrieved for candidate papers and examined in detail.
Only papers meeting all of the following criteria were included:
- The work must explicitly address oblivious primitives designed to resist quantum adversaries and malicious adversaries. Studies on non-post-quantum constructions or unrelated primitives were excluded.
- The paper must provide either a formal security proof in a standard model with malicious adversaries or a rigorous empirical performance evaluation. Papers lacking provable security guarantees or substantive empirical data were excluded. Also, protocols with known successful attacks were excluded from the list.
- The paper must have been published or made available as a pre-print from 2015 onward.
To ensure completeness beyond the database queries, backward and forward snowballing were performed. Reference lists of included papers were examined to locate earlier relevant works (backward snowballing), and citations of included papers were checked to identify subsequent relevant publications (forward snowballing).
All steps were carried out manually via the databases’ web interfaces. Records were maintained in spreadsheets and written notes. Screening was performed by one author and independently checked by a second to reduce bias. Full texts were examined when either reviewer considered a paper potentially relevant.
The article selection was performed in several stages. First, titles and abstracts were screened, and studies unrelated to post-quantum cryptography or oblivious protocols were excluded. Next, a full-text review was conducted to eliminate works that did not meet the inclusion criteria. Finally, backward and forward snowballing were applied, which identified additional relevant studies.
In summary, the methodology combined structured database queries, manual de-duplication and screening, and backward/forward snowballing with explicit inclusion criteria to compile a comprehensive, up-to-date bibliography of post-quantum oblivious protocols.
All protocols were analyzed within a strong security model. The UC framework under a malicious-adversary model served as the baseline. Each scheme’s security proof was inspected to determine whether it achieves UC security against malicious adversaries or a weaker notion (semi-honest security). Proofs were furthermore classified according to the model in which they are given, ROM or QROM. The QROM, which permits quantum oracle queries, models adversaries with quantum access to hash functions and is therefore essential for post-quantum security analysis.
To ensure transparency, Table 2 and Table 3 list all reviewed papers on OT and OPRF protocols, which constitute the foundation of this study. This enables readers to assess the scope of the review and identify potential inaccuracies. In the “Assumption” column, “framework” means that any post-quantum public-key encryption scheme can be integrated into the protocol. In the “UC” column, the “+” and “—” signs indicate the presence or absence of security proof within the UC framework.

Table 2.
List of considered post-quantum OT protocols.

Table 3.
List of considered post-quantum OPRF protocols.
Table 2 and Table 3 compile the 12 core protocols reviewed in Section 4 and Section 5. Additional protocols from Section 6 were screened, but not the primary focus, as they have fewer post-quantum realizations.
Protocols were compared according to three principal efficiency metrics: round complexity, communication requirements, and computational cost. For each protocol, the following quantities were recorded:
- Number of communication rounds: a round is defined as either one-way data transfer or simultaneous two-way transfer, where messages are independent.
- Communication overhead: this assesses the data overhead required for protocol operation, excluding the size of transmitted messages.
- Computational complexity for the sender and the receiver: this metric captures the computational cost of the protocol’s execution on both sides, accounting for the most expensive operations as well as the estimated runtime in terms of CPU cycles.
Data collection followed a two-pronged approach. Published performance figures (message sizes, cycle counts for core routines, etc.) were extracted where available. When a software implementation was provided by the authors or could be reproduced, implementations were executed on contemporary hardware to obtain empirical cycle counts. For OT protocols, measurements referenced implementations on an x86-64 Linux machine with an Intel Core i7 processor; for OPRF protocols, measurements referenced an x86-64 Linux machine with an AMD Ryzen 7 processor. Cycle counts for OT protocols were estimated from operation complexity reported in the literature (expressed in cycles). For the OPRF protocols, cycle counts were obtained from available software implementations using the processor timestamp counter.
Reported computational complexity values should be interpreted as lower-bound estimates focused on the dominant cryptographic operations. The following components were excluded from the cycle measurements:
- Arithmetic (addition, subtraction) and logical operations;
- Sampling of random elements from a given set;
- Random oracle calls.
These components were excluded because their runtime contribution is negligible (e.g., arithmetic operations) or highly implementation-dependent (e.g., random sampling and oracle calls). Thus, actual runtimes may exceed estimates due to overhead.
Performance figures are drawn from published tables or from the measurements described above. When only theoretical operation counts were available, these counts were converted to cycle estimates using standard cost assumptions. All results are normalized with respect to the security parameter (128-bit security) to enable fair comparison. The methodology thus combines structured literature extraction, empirical measurement where feasible, and explicit normalization to produce a meta-analytic comparison of post-quantum OT and OPRF protocols.
3. Preliminaries
Let be a function computable in polynomial time, defined over sets , such that the family of functions , where is one-way. Consider the following functionality:
which realizes the computation of the function f. Let S and R be two parties in a communication protocol, where S is referred to as the sender and R as the receiver. Let be a secure two-party protocol implementing the functionality , where
- is the input of S, and the output of S is ⊥.
- is the input of R, and the output of R is .
The protocol , called an oblivious protocol, is secure if it satisfies the following properties:
- Correctness: For any , the value is correctly computed.
- Receiver security: The sender S learns nothing about the receiver’s input y and output z. That is, for any adversary S, there exists a probabilistic polynomial time (PPT) simulator such that for all , the following computational indistinguishability holds:
- Sender security: The receiver R learns nothing about the sender’s input x. That is, for any adversary R, there exists a PPT simulator such that for all and , the following computational indistinguishability holds:
The transcript of protocol for party P on inputs and is denoted by . The simulator is a probabilistic algorithm that, given the private input p of party P, queries the ideal functionality to obtain an output v. Based on , the simulator emulates the interaction of P with the other party. If the distribution of the real protocol transcript and the simulated transcript is computationally indistinguishable, denoted by , then the protocol is considered secure against adversaries corrupting party P.
An oblivious protocol is a special case of a secure two-party computation protocol where only one party (the receiver) learns the function’s output. This formulation imposes fewer restrictions on the choice of function f, since f only needs to be one-way in its first argument x (i.e., given y and , finding x should be hard).
The following metrics can be used to evaluate the security and efficiency of the protocols.
Adversary model. The model(s) within which the cryptographic security of the protocol is proven. It is crucial to consider the type of adversary (semi-honest or malicious) and its computational capabilities assumed during the security analysis. Proof of security against active (malicious) adversaries increases confidence in the protocol’s safety.
Security model. The foundational assumptions underlying the security proof. The more assumptions used in proving a protocol, the less robust the proof becomes, as practical implementation necessitates additional analysis to verify that these assumptions hold under specific parameter sets or cryptographic algorithms. Classical assumptions prevalent in proofs for many protocols include the hardness assumption of mathematical problems and modeling cryptographic hash functions as random oracles.
Universal composability. A security proof within the UC framework [53] provides guarantees about the protocol’s security in diverse execution environments and when composed with arbitrary other protocols. Without such a proof, security is only guaranteed when the protocol is used in isolation.
Performance metrics. Typically considered metrics include the number of communication rounds between participants, the volume of data transmitted over the network, and the computational complexity of the algorithms—evaluated both theoretically (relative to the security level) and empirically (execution time). While developers aim to minimize all these metrics, priorities may shift towards optimizing specific parameters depending on the application scenario.
Each of these security metrics has its own limitations that are imposed on the protocol’s performance or security. Let us briefly compare ROM, QROM, and the UC framework.
ROM simplifies security proofs by modeling hash functions as ideal random oracles, though it lacks quantum resistance. This makes it suitable for classical or transitional cryptographic settings, where it often yields efficient proofs with tight security reductions.
QROM extends the ROM to adversaries making quantum superposition queries, offering a more realistic security model in the post-quantum setting. However, QROM-based proofs typically incur non-tight bounds and greater computational overhead.
UC framework provides composable security, enabling modular protocol design and integration. Its strict requirements often lead to hybrid constructions using ROM or QROM, which can result in complex and less efficient schemes. In post-quantum OT and OPRF, QROM balances quantum security and practicality, while ROM prioritizes efficiency, and UC ensures robustness in concurrent executions.
The adversary model also imposes limitations on the performance and security of the protocol, depending on the type of adversary against which it is secure. In cryptographic protocols, adversaries are modeled based on their behavior:
- Semi-honest adversary (also known as honest-but-curious): This adversary follows the protocol exactly as specified but attempts to extract additional information from the messages it receives or the protocol transcript. Strengths include a simpler defense strategy, particularly in scenarios involving trusted or cooperative parties where correct execution is assured. However, a key weakness is that this model fails to capture realistic threat scenarios where participants may exhibit actively malicious behavior.
- Malicious (active) adversary: This adversary can arbitrarily deviate from the protocol, including sending invalid messages, aborting early, or injecting faults to compromise security or privacy. It is “active” and more powerful, requiring robust mechanisms like zero-knowledge proofs or verifiable computations for security. This model provides robust security guarantees against malicious behavior, making it suitable for adversarial environments such as untrusted networks. However, these stronger assurances often result in increased protocol complexity and reduced efficiency due to the overhead of additional cryptographic checks and verifications.
4. Oblivious Transfer
4.1. Oblivious Transfer Construction
The oblivious transfer protocol is a two-party cryptographic protocol that enables one party (the sender) to transmit data to another party (the receiver) so that the sender does not learn which piece of data was received, and the receiver gains no information about the data that was not requested.
The sender has two messages, , and the receiver wishes to obtain one of them, denoted , where . The receiver’s goal is to keep the choice bit b hidden, while the sender must ensure that only the selected message is revealed.
To achieve this, the receiver sends the selection bit b to a trusted third party (TTP), and the sender provides both messages to the TTP. In response, the TTP delivers the selected message to the receiver. The sender learns nothing in return. Figure 1 illustrates the oblivious transfer of messages between the sender and receiver by TTP.
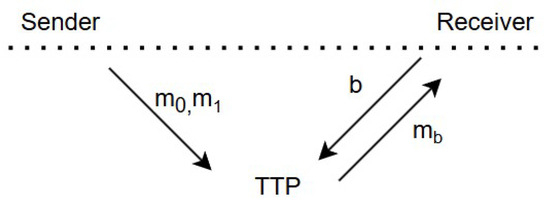
Figure 1.
OT with TTP.
While the use of a TTP simplifies the execution of the protocol, it significantly weakens its security guarantees, thereby undermining the fundamental principles of OT. Consequently, practical constructions of OT protocols are designed to operate without reliance on a TTP. Nevertheless, in the context of security analysis, the TTP-based version of the protocol is regarded as an ideal functionality and serves as a reference point for evaluating the security of the proposed OT constructions. Figure 2 exemplifies the general structure of an OT protocol. This construction eliminates the requirement for a TTP.
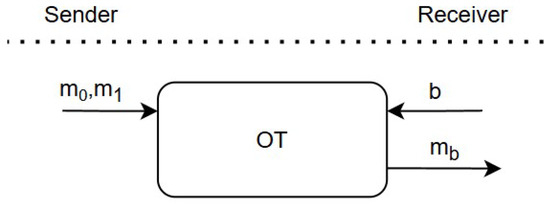
Figure 2.
OT without TTP.
The absence of a trusted third party imposes a fundamental limitation on oblivious transfer protocols. As shown in [54], two parties cannot construct a protocol with perfect security. Perfect security is possible only with a third party, yet such a model fails if two of the three parties are controlled by an adversary. Therefore, two-party oblivious transfer must rely on computational hardness assumptions, either on one-way functions or on the underlying mathematical problems to which they reduce.
Depending on the amount of information held by the sender and the amount requested by the receiver, various variants of OT protocols have been proposed. The example described above corresponds to the Basic 1-out-of-2 OT, where the receiver selects a single message from two available options. Other generalizations include the following:
- 1-out-of-n oblivious transfer [11]: the sender holds n messages , and the receiver is allowed to obtain only one of them, namely ;
- k-out-of-n OT [11]: the sender holds n messages , and the receiver is allowed to obtain a subset of k messages , where are the indices chosen by the receiver, and .
In the context of defining an oblivious protocol, the oblivious transfer can be formalized as follows:
- Let the sets be defined as , where denotes the message space,
- Define the function , where , , for all and . The function f is one-way with respect to its first argument.
This work highlights several foundational works that initiated the study and practical application of OT. In the seminal work by Bellare and Micali [55], the authors proposed a non-interactive OT protocol. The receiver selects a bit b and, based on it, computes and publishes a corresponding public key. Any party may assume the role of the sender and transmit encrypted messages, of which the receiver can decrypt only one, according to the selected bit. The authors demonstrated the applicability of non-interactive OT as a building block in non-interactive zero-knowledge proof systems. The security of the protocol relies on the hardness of the discrete logarithm problem.
M. Naor and B. Pinkas, in their work [11], introduced the 1-out-of-n and k-out-of-n OT protocols, significantly broadening the applicability of OT. In subsequent work, the same authors addressed the question of practical deployment of OT protocols and proposed several optimizations [44]. Notably, they reduced the number of communication rounds in the 1-out-of-n OT protocol from to .
In addition, they introduced techniques for reducing communication overhead and minimizing the number of computational operations required. This work laid the foundation for the widespread practical adoption of OT protocols.
OT protocols rely on computational hardness assumptions rooted in mathematical problems. Public-key encryption (PKE) serves as a key primitive, enabling general OT designs without tying to specific problems. This approach provides flexibility, as OT can derive from any PKE scheme. However, it often sacrifices efficiency for generality. To address this, certain OT protocols instead employ specialized mathematical primitives, achieving improved performance. At the same time, this strategy entails additional risk, as future advances may diminish the hardness of the underlying problem, thereby weakening security.
Given that OT employs public-key cryptography, it is impractical to use messages of arbitrary length. In such cases, it is preferable to use OT to transfer keys, which can subsequently be employed for encrypting messages using symmetric encryption algorithms.
OT vs. PIR
Based on the definition of the 1-out-of-n OT protocol, a clear similarity with PIR can be observed. However, there is an important distinction between them—in OT, it is crucial that the client obtains only a part of the server’s data, meaning that some information must remain hidden. In contrast, PIR protocols do not impose such a requirement. PIR is designed solely to protect the privacy of the receiver, while the server’s data is not required to remain secret, and the client may access the same data element multiple times.
4.2. Variants of Oblivious Transfer
The Oblivious Transfer protocol is typically employed as a building block within more complex cryptographic protocols. The specific requirements for the security, efficiency, and design of OT are determined by the characteristics of the overarching protocol in which it is used.
The main approaches to the construction and optimization of OT protocols in cryptography can be classified according to the following criteria:
- 1.
- Cryptographic primitives. This category is defined by the fundamental building blocks on which an OT protocol is constructed. It focuses on the types of cryptographic primitives that provide the security guarantees and computational foundation. This can include constructions based on public-key cryptography or quantum computing.
- 2.
- Functional variants. This group encompasses variations in the protocol’s behavior and capabilities, particularly how OT adapts to different use cases. The classification highlights differences in operational logic, regardless of implementation details. For example, random OT or correlated OT.
- 3.
- OT optimization techniques. This category groups methods aimed at improving the efficiency of the protocol, such as reducing computational or communication costs. The focus is on strategies that extend or simplify the basic OT without altering its core properties (e.g., OT extension, silent OT).
Notably, these protocols can be combined. For example, one may construct a random OT extension or a silent correlated OT via appropriate combinations. The above classification captures the main approaches to constructing OT protocols, but is not exhaustive.
4.2.1. Random Oblivious Transfer Protocol
The Random Oblivious Transfer protocol (ROT) does not take any inputs from either the sender or the receiver. Instead, it outputs values to the sender, and a choice bit along with the corresponding value to the receiver. These values are generated uniformly at random.
Once the parties obtain their respective values, they proceed to execute a basic OT protocol, where the receiver aims to retrieve the message .
During the OT execution, the sender holds the random values generated by ROT, as well as the actual messages . The sender computes the masked messages , and sends both to the receiver. The receiver, using the previously obtained value , recovers the intended message as follows:
ROT improves efficiency compared to basic OT while providing the necessary randomness. It can be executed in a single step (transmitting two random values to the receiver) or in two steps (if the receiver does not use the provided message bit). ROT is widely used in PSI protocols [6,56], simplifying the generation of random values and reducing both communication and computational overhead.
4.2.2. Correlated Oblivious Transfer
In addition to ROT, there is a correlated variant known as correlated-oblivious transfer (COT). In this setting, the messages are not only random but also related through a predetermined correlation.
Consider an example where the correlation is defined via bitwise XOR with a fixed string . The sender inputs the correlation into the COT protocol, while the receiver provides a choice bit . The protocol returns two values to the sender such that , and the receiver learns using a basic OT.
With COT, the sender transmits not two independent values but one value and its correlated counterpart, which reduces communication compared to basic OT. It can be observed that COT can be constructed from ROT and a correlation function, implying that the COT protocol can be reduced to ROT, which itself reduces to basic OT.
COT is especially useful when transferring correlated data, as it lowers communication costs [17,57]. ROT, on the other hand, is preferred in scenarios where speed and low overhead are critical.
4.2.3. Adaptive Oblivious Transfer
Adaptive OT (AOT) generalizes the classical k-out-of-n OT protocols by enabling the receiver to adaptively choose the message indices subsequent to the receipt of the initial message. In traditional k-out-of-n OT, the receiver must choose all k indices simultaneously before any data is transmitted. In contrast, AOT allows the receiver to first choose an index and receive the corresponding message from the sender. Based on the received information, the receiver can then choose the next index to obtain , and so on, up to k queries.
As in basic OT, the sender remains oblivious to the receiver’s choices, and the receiver gains no information about the messages not requested.
AOT is particularly useful in applications involving private computation and private data access. For example, the authors of [58] propose using AOT for private database search, such as querying patent or medical records, where queries are constructed based on the results of previous queries. Further research [59,60] has explored additional use cases and adaptations of AOT to meet the specific requirements of different systems.
4.2.4. Oblivious Transfer Extension
One of the key approaches to transferring large volumes of data using OT is OT extension (OTE). Since OT protocols require key agreement, they are typically built using public-key cryptography, which becomes computationally expensive when transmitting large amounts of data. OT Extension addresses this by running a small number of basic OT instances to establish keys and then using symmetric cryptography to transmit the actual data. This makes OT significantly more efficient in practical implementations.
The idea of extending OT was first proposed by Beaver [61] using one-way functions. However, this approach proved to be inefficient, with a computational complexity of , where n is the number of messages being transferred, making it impractical for large-scale data transmission.
The limitations of earlier approaches were overcome by Ishai et al. [62], whose protocol is commonly referred to as IKNP, named after the authors’ initials. Their work introduced an OTE protocol, offering a more efficient way to scale OT.
This approach reduces the number of basic OT invocations from n to k, where , with n being the number of data pairs to be transferred and k representing the security parameter of the protocol. The proposed protocol achieves linear complexity, making it significantly more efficient than the earlier construction by Beaver [61]. The IKNP protocol now constitutes a canonical OT primitive, with later optimizations exemplified by Kolesnikov and Kumaresan [63] who developed an efficient variant for short-secret applications.
4.2.5. Silent Oblivious Transfer
Silent OT (SOT) is an OT protocol that operates with minimal interaction between parties, enhancing efficiency and scalability. The primary advantage of SOT lies in its significant reduction of network communication. Classical OT protocols are characterized by high communication complexity due to intensive message exchange between the parties. In contrast, the SOT protocol is based on the concept of precomputation, after which the actual data transfer phase can be executed with virtually no additional communication. This level of efficiency makes SOT a preferred solution for applications in large-scale networks and cloud environments.
In [64], Boyle et al. introduced SOT as a protocol that reduces both communication and computational overhead. It employs a two-phase structure: during the offline phase, the sender and receiver perform precomputations that allow the sender to predefine messages and the receiver to select the desired index. The online phase then completes the OT in a single round with the exchange of only bits, where the sender transmits precomputed data and the receiver locally reconstructs the message. The communication cost of the offline phase is bits, where n is the number of OT instances and is the security parameter.
However, the protocol relies on LDPC code constructions, incurs high precomputation costs, and becomes inefficient when n is small, thus losing its performance advantages. This limitation, namely the inefficiency for small values of n, is inherent to all SOT protocols.
Following this work, increasingly optimized silent OT protocols have been proposed, surpassing the original construction in terms of efficiency [65,66,67,68].
4.2.6. Summary
Basic OT is foundational for more efficient OT variants. ROT simplifies it by using random values instead of messages, suiting randomization scenarios.
COT also operates on random inputs, but enforces a predefined correlation between the sender’s messages. This makes COT well-suited for cryptographic protocols that rely on structured or interdependent data.
SOT is designed for settings where communication latency is critical. By significantly reducing the number of interactions between the sender and receiver, SOT minimizes communication overhead and is therefore ideal for low-latency environments.
OTE enables the generation of a large number of OT instances using a small number of basic OTs, thereby drastically improving scalability and efficiency. Notably, OTE can be instantiated using ROT or COT as building blocks.
In summary, depending on the requirements of the target cryptographic protocol, the appropriate variant of OT can be selected to optimize performance, communication, or structural properties.
4.3. Post-Quantum Oblivious Transfer Protocols
The construction of OT protocols inherently requires the use of public-key cryptographic algorithms [54], as it is generally infeasible to rely solely on symmetric-key primitives. Consequently, the choice of the underlying hard problem for the public-key cryptographic primitive depends not only on performance evaluation but also on resistance against both classical and quantum attacks. It is well known that cryptographic algorithms based on discrete logarithm and integer factorization problems are vulnerable to quantum attacks (efficiently solvable via Shor’s algorithm [34]).
To achieve post-quantum security, two main approaches can be considered: (1) constructing protocols based on problems for which no efficient algorithms are currently known, either classical or quantum, or (2) utilizing quantum computation.
The analysis begins with an examination of the quantum-based approach. This method relies on the use of the quantum oblivious key (QOK) distribution protocol [69], which replaces conventional public-key mechanisms within classical OT frameworks. The QOK protocol requires the establishment of a quantum communication channel between the two parties. Presently, this necessitates specialized infrastructure, including optical fiber cables capable of transmitting single photons, as well as dedicated hardware for photon generation, detection, and signal amplification. Such technological requirements represent a significant barrier to practical deployment. Nonetheless, quantum OT protocols offer notable advantages: their security is grounded not in unproven computational hardness assumptions but in the fundamental principles of quantum mechanics. Additionally, they are highly efficient with respect to communication complexity, requiring only transmitted bits for an l-bit message, and incur a low computational overhead in terms of arithmetic operations [36,70].
A more general and practically viable approach to constructing OT protocols involves the use of cryptographic mechanisms based on computational assumptions believed to be hard for both classical and quantum adversaries. Such cryptographic algorithms are referred to as post-quantum algorithms.
One class of OT constructions relies on public-key encryption schemes or key encapsulation mechanisms (KEMs) [39]. These primitives can be instantiated using post-quantum algorithms. For example, Barreto et al. [39] propose OT protocols built upon encryption schemes based on error-correcting codes and lattice-based assumptions. However, other post-quantum approaches may also be employed. A significant advantage of the framework presented in [39] is the presence of a security proof in the UC model, which ensures the protocol’s secure integration into larger cryptographic systems. The total communication overhead of this approach primarily depends on the underlying public-key scheme, as the protocol transmits two public keys, two ciphertexts, and three binary strings of length equal to the message size. Therefore, the choice of encryption scheme directly impacts the overall communication cost.
To improve protocol efficiency, the work of Mansy et al. [42] introduces a security model with relaxed assumptions, referred to by the authors as the endemic model. Within this model, the adversary is allowed to influence both the sender’s message selection, i.e., , and the receiver’s choice bit b. By weakening the security guarantees, the protocol reduces communication overhead, as stricter models typically require additional sub-protocols to ensure the randomness of the messages .
The protocol is built upon public-key encryption schemes, with a critical requirement that the public key space possesses a group structure. In particular, the authors propose a lattice-based instantiation using the CRYSTALS-Kyber KEM [71], the winner of the NIST Post-Quantum Cryptography Standardization [72].
In a related line of work, Branco et al. [73] present a construction based on a one-round key agreement scheme. Their implementation utilizes a key exchange protocol based on the ring-learning-with-errors (RLWE) problem. However, alternative instantiations based on similar hardness assumptions may also be employed. A notable drawback of this approach is the relatively high communication cost, involving four rounds of interaction and a substantial amount of transmitted data.
A relatively recent contribution is presented in [43], where the authors propose a protocol that combines the classical Naor–Pinkas OT construction [44] with the Saber KEM [74]. The security of the scheme is based on the hardness of the module learning with rounding (MLWR) problem. In terms of performance, the proposed protocol outperforms the scheme of [42] when instantiated with the CRYSTALS-Kyber KEM.
The analysis now turns to OT protocols based on isogenies of elliptic curves. Early constructions, such as [75], were built upon the Supersingular Isogeny Diffie–Hellman (SIDH) protocol. However, SIDH was recently broken by Castryck and Decru [76], prompting the shift toward more secure alternatives. Thus, modern works adopt the commutative supersingular isogeny Diffie–Hellman (CSIDH) protocol [77], which is based on the group action inverse problem (GAIP). Since isogeny computations on elliptic curves are computationally intensive, a primary design goal in recent protocols is to minimize the number of such operations while maintaining equivalent levels of security.
In [40], the authors propose an isogeny-based OT protocol in which the number of isogeny computations remains fixed and does not scale with the security level. Two protocol variants are presented—one secure against a semi-honest adversary, and another secure against a malicious adversary. Both constructions are accompanied by formal security proofs in the UC model. The security of the protocol is based on a newly defined reciprocal CSIDH (RecCSIDH) problem, for which the authors establish computational hardness by proving its equivalence to the well-known computational CSIDH problem.
An alternative isogeny-based OT protocol is introduced in [78]. Unlike the approach in [40], the number of isogeny computations in this construction scales linearly with the security parameter. This design trades computational efficiency at elevated security levels for reduced round complexity, constituting a deliberate balance between computational and communication efficiency.
Orsini and Zanotto’s isogeny-based OT protocol [41] optimizes both computational and round complexity, maintaining constant-time isogeny evaluations (improving upon [40]) while reducing rounds by one. These improvements, however, come at the cost of increased communication overhead due to larger message sizes.
Table 4 illustrates the evolution of post-quantum OT protocols by organizing them chronologically (based on publication years derived from references and web sources), highlighting the shift from early constructions to more optimized ones.

Table 4.
Research landscape in post-quantum OT.
Despite progress in post-quantum OT protocols, several open challenges remain. Efficient lattice-based constructions with UC security and optimized isogeny-based designs with constant-time computations mark significant advancements. However, the field still lacks round-optimal protocols to resist quantum adversaries. Broader instantiations under alternative assumptions, such as code-based or multivariate cryptography, are needed to reduce the dependence on lattices and isogenies. In [39], the authors employ existing code-based KEMs [79,80].
Lightweight variants must be developed for resource-constrained IoT devices. In addition, empirical benchmarks on real hardware are required to assess scalability and integration with larger systems, including MPC and PSI.
4.4. Analysis of Post-Quantum Oblivious Transfer Protocols
4.4.1. Qualitative Analysis
For the qualitative evaluation of the protocols, the security models are analyzed, as well as the presence of a proof in the UC framework. From the perspective of the adversary model, only those protocols claiming resilience against an active adversary are selected for analysis. The analysis is presented in Table 5.

Table 5.
Post-quantum OT protocols: design perspective.
As shown in Table 5, all considered protocols are UC-secure and offer security guarantees against malicious adversaries. This ensures that each protocol can be securely deployed either in isolation or as part of a larger system, such as OTE protocols.
All protocols rely on the ROM in their security proofs. While the potential reduction in security guarantees due to the use of ROM remains an open research question, there are currently no known examples where the adoption of ROM has resulted in broken or weakened cryptographic protocols. Nonetheless, careful consideration must be given to the design of algorithms used to instantiate or simulate random oracle behavior in practice, as improper choices may undermine the protocol’s intended security properties.
In addition to relying on the ROM, the protocols in [40,43] also make use of the common reference string (CRS) and trusted setup curve (TSC) models, respectively. These models assume the presence of publicly known parameters that are randomly generated by a trusted third party. In the case of [43], the public parameter is a matrix , while in [40], it is the public elliptic curve E. The security of these protocols relies on the assumption that these parameters were honestly generated and were not influenced or computed in advance by the adversary. Consequently, any practical deployment of such protocols must ensure the secure generation and integrity of these setup parameters.
It is important to highlight that the security of a cryptographic scheme against quantum adversaries is generally argued based on two main assumptions—the hardness of the underlying mathematical problem, even for quantum algorithms, and the consideration of an adversary equipped with quantum capabilities. The latter typically necessitates the use of the QROM, which allows the adversary to query the random oracle, often modeling a hash function, in quantum superposition.
However, the security proofs of all the discussed oblivious protocols are currently provided only in the classical ROM, which assumes a classical adversary. As a result, such proofs do not guarantee security against quantum adversaries. Therefore, the quantum resistance of these protocols relies solely on the presumed hardness of the underlying mathematical problem, even for quantum algorithms.
This gap raises potential concerns regarding the robustness of these protocols in the post-quantum setting. Nonetheless, it is worth noting that, to date, no practical attacks exploiting this limitation in ROM-based OT protocols have been demonstrated. This suggests that, while the lack of QROM-based proofs is a theoretical vulnerability, it has not yet translated into concrete cryptanalytic weaknesses.
4.4.2. Quantitative Analysis
Table 6 presents a comparison of the considered protocols with respect to the defined performance metrics. The evaluation of computational complexity focuses on the most resource-intensive operations of each protocol. Additionally, the number of calls to the random oracle is explicitly accounted for, where applicable. Both communication overhead and computational cost are evaluated under the 128-bit security level, corresponding to NIST security level I. For protocols originally designed as 1-out-of-n OT, the special case is considered.

Table 6.
Post-quantum 1-out-of-2 OT protocols: efficiency.
The computational cost in CPU cycles and communication overhead is estimated for protocols from [39,42,43]. This estimation relies on performance benchmarks of the underlying KEMs: Saber [74], CRYSTALS-Kyber [71], Classic McEliece [79], and HQC [80].
For the isogeny-based protocols [40,41], the main operation is group action computation. The estimates for isogeny computation cost and communication size are based on the analysis in [81]. The authors propose conservative and practically motivated parameters for cryptographic schemes based on the GAIP, taking into account recent quantum attacks on the CSIDH protocol. Specifically, the CSIDH-5120 parameter set is selected to achieve a 128-bit quantum security level. CPU cycle estimates are given for an Intel Core i7 processor.
The computational complexity values in Table 6 should be interpreted as lower-bound estimates, since the analysis considers only the most expensive operations. Actual runtimes may be slightly higher due to implementation details and additional overhead from omitted operations. The relative strengths and trade-offs of the evaluated schemes depend on whether performance or security characteristics are given priority.
A clear comparison of protocols in terms of performance and data transfer size can be observed in Figure 3. In terms of computational complexity, lattice-based schemes achieve the highest efficiency, while isogeny-based schemes are the least efficient. However, with respect to communication overhead, isogeny-based and lattice-based schemes rank among the most efficient. Code-based protocols exhibit the highest communication cost.
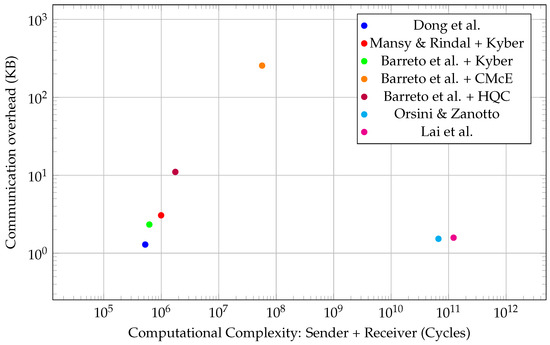
Figure 3.
Post-quantum OT protocol performance. The performance values are presented for the schemes Dong et al. [43], Mansy & Rindal [42], Barreto et.al. [39], Orsini & Zanotto [41] and Lai et al. [40].
Based on the performance metrics, the following observations can be made.
If minimizing communication overhead is the primary concern, the most efficient protocols in this regard are the isogeny-based schemes by Orsini and Zanotto [41] and Lai et al. [40], as well as the lattice-based protocol by Dong et al. [43]. In contrast, code-based protocols, specifically those of Barreto et al. [39] instantiated with Classic McEliece or HQC, are strongly discouraged due to their significantly higher communication costs.
If computational efficiency is prioritized, the best-performing protocols are those based on lattice-based KEMs—Barreto et al. [39] with CRYSTALS-Kyber and the protocol by Mansy and Rindal [42]. The protocol by Dong et al. [43] offers comparable computational performance, but it requires an additional round of communication, which may negatively impact overall runtime in latency-sensitive applications. Isogeny-based protocols [40,41] are the least favorable in this category due to the high cost of isogeny computations.
If a balanced trade-off between communication and computational efficiency is desired, the protocol by Dong et al. [43] stands out as the optimal choice. It achieves both relatively low communication overhead and high computational performance. If a two-round protocol is explicitly required, Barreto et al. [39] with Kyber or Mansy and Rindal [42] with Kyber may serve as practical alternatives.
5. Oblivious Pseudorandom Function
5.1. Oblivious Pseudorandom Function Construction
Let be a deterministic algorithm, referred to as a pseudorandom function (PRF), which takes as input a key and an input block , and outputs a value .
Pseudorandom functions are used to generate outputs that are computationally indistinguishable from truly random values. That is, for any fixed key , the function should behave as a random function to any efficient adversary without knowledge of k.
Assume that is a PRF defined over sets , such that the function family , where , is one-way.
Define the following functionality:
which represents the secure computation of the function f, where two parties, S (server) and C (client), participate in the protocol implementing such that we have the following:
- The input of S is , and its output is ⊥.
- The input of C is , and its output is .
The protocol is called an oblivious pseudorandom function (OPRF) if it satisfies the following properties:
- Correctness: For all , the output is computed correctly.
- Client security: The server S learns neither the client’s input v nor the output c. There exists a PPT simulator such that for all and , we have
- Server security: The client C learns nothing about the server’s key k. There exists a PPT simulator such that for all and , we have
OPRF can be instantiated using various families of pseudorandom functions. The most commonly employed PRF constructions include the following:
- Naor–Reingold PRF [82];
- Dodis–Yampolskiy PRF [83];
- Hashed Diffie–Hellman (HashDH) and 2HashDH PRFs [84].
The concept of OPRF was first introduced in [82] and later formalized in [15], where the authors proposed an OPRF-based protocol for private keyword search. In their construction, the server assigns indices to keywords using a PRF and then leverages OPRF in conjunction with OT to allow the client to retrieve information associated with selected keywords. This ensures that the server remains oblivious to the client’s query, while the client learns nothing beyond the specific result corresponding to the queried keyword.
The security of the protocol in [15] relies on the hardness of the decisional Diffie–Hellman (DDH) problem and the underlying security of the OT protocol. A notable drawback of this construction is that it requires m independent invocations of the OT protocol, which may become computationally expensive for large values of m.
5.2. Variants of Oblivious Pseudorandom Function
Modern constructions of OPRFs offer significant improvements over earlier designs. As outlined in the previous subsection, the initial OPRF protocol incurs high communication overhead, as it requires a large number of independent OT invocations. Additionally, the server must generate a new secret key for each session, which reduces the protocol’s adaptability and scalability.
Contemporary OPRF protocols can be realized not only via basic OT but also using OTE protocols, which substantially improve efficiency. For instance, Kolesnikov et al. [4] propose a batched, related-key OPRF protocol that enables multiple OPRF evaluations to be executed concurrently. This allows the client to obtain pseudorandom outputs on multiple distinct inputs in a single protocol execution. The improvement is achieved through the use of OTE. Notably, the efficiency of the protocol remains independent of the input length, making it suitable for applications involving large inputs. However, the security of this construction is proven only against semi-honest adversaries.
The following section examines OPRF constructions that incorporate additional properties to enhance both security and performance.
5.2.1. Verifiable Oblivious Pseudorandom Function
A verifiable OPRF (VOPRF) is an extension of the standard OPRF that enables the client to verify the correctness of the function output. The functionality is defined as follows:
- The input of S is , and its output is ⊥.
- The input of C is , and its output is along with a proof , which certifies that c was correctly computed using the key k.
VOPRF protocols are typically instantiated using zero-knowledge proofs (ZKPs) or cryptographic commitment schemes [45,84]. The verifiability property enhances security against malicious adversaries by enabling the client to detect deviations from the correct protocol execution. This property is particularly valuable in settings requiring robustness against malicious behavior. Another approach to improve OPRF security is to build a threshold OPRF.
5.2.2. Threshold Oblivious Pseudorandom Function
A threshold OPRF (TOPRF) distributes the evaluation of the pseudorandom function across multiple servers. Its functionality is defined as follows:
- Each server , for , holds a share of the master key k, such that a threshold is required to evaluate the function. All servers receive no output.
- The client C provides an input and obtains the output , where k is reconstructed jointly by the threshold set of servers.
TOPRF protocols are typically based on threshold secret-sharing schemes and aim to enhance both security and fault tolerance. By requiring the cooperation of multiple servers, TOPRF mitigates single points of failure and limits the risk posed by server compromise. Recent works, such as [46,47], propose verifiable variants of TOPRFs, combining threshold security with robustness against active adversaries.
This approach is further extended in a shuffled distributed OPRF. In this type of OPRF, outputs are permuted across multiple parties to hide the input–output correspondence and enhance privacy.
5.2.3. Shuffled Distributed Oblivious Pseudorandom Function
A shuffled distributed OPRF is a variant of the distributed OPRF that introduces output shuffling to hide the correspondence between the client’s input and output values. The functionality is defined as follows:
- Each server , for , holds a share of the master key k. All servers receive no output.
- The client C provides an input and obtains the output , where k is implicitly reconstructed from the server shares.
Unlike in threshold OPRF, the outputs are shuffled prior to being delivered to the client, thus obfuscating the linkage between the inputs and corresponding outputs.
A concrete instantiation of this primitive is proposed in [85], where the authors introduce a shuffled distributed OPRF based on a construction from [86] using the q-decisional Diffie–Hellman inversion (q-DHI) assumption. The protocol employs a homomorphic encryption scheme by Camenisch and Shoup [87] to share (and later reconstruct) the PRF key among multiple parties.
Prior to the evaluation phase, commitments are generated to bind the keys and PRF outputs. The outputs are then encrypted using ElGamal encryption and shuffled to hide the association between specific inputs and their results. This type of OPRF has important applications in privacy-preserving protocols such as PSI-cardinality [88] and private intersection-sum [89].
VOPRF, TOPRF, and shuffled distributed OPRF focus on improving the security of basic OPRF. In contrast, multi-point OPRF targets efficiency by allowing multiple inputs to be evaluated simultaneously within a single execution.
5.2.4. Multi-Point Oblivious Pseudorandom Function
In a multi-point protocol, the client evaluates the PRF at multiple input points in a single protocol execution. The functionality is defined as follows:
- The input of S is , and its output is ⊥.
- The input of C is a vector , and its output is a vector .
The idea of constructing a multi-point OPRF using OTE was further explored in several works. In [6], a protocol for multi-point evaluation is presented, which reduces the computational cost by approximately compared to [4], though it still falls short in efficiency compared to the construction in [21]. The protocol proposed in [21] leverages AES-based symmetric encryption and OTE to achieve linear computational complexity with respect to the number of inputs.
A distinct variant of OPRF is specifically tailored for PSI. In this case, the server can program outputs for intersecting inputs without disclosing additional information.
5.2.5. Oblivious Programmable Pseudorandom Function
Let be a programmable function. An oblivious programmable PRF (OPPRF) is an OPRF with the following functionality:
- The input of S is , and its output is ⊥.
- The client C provides an input and obtains the output:
The concept of an OPPRF was first introduced in [90] in the context of PSI. In this construction, the server is able to “program” the output of the PRF on a limited set of inputs , while keeping the rest of the PRF evaluations indistinguishable from truly random. The client receives the outputs of the PRF but cannot tell whether its query lies in the programmed domain, i.e., it cannot distinguish whether .
Since its introduction, the OPPRF has been actively studied and improved in terms of performance, security, and broader applicability [22,91,92].
Another OPRF variant partially reveals information about the client’s input. This controlled leakage increases the protocol’s resistance to dictionary attacks.
5.2.6. Partially Oblivious Pseudorandom Function
A partially oblivious PRF (POPRF) is a variant of OPRF where the PRF depends on both private and public inputs:
- The input of S is , and its output is ⊥.
- The client C provides an input and a public input shared with the server. The client receives the output .
The POPRF model allows PRF evaluations to be bound to a context or domain represented by the public input , which is known to both parties. This enables the server to enforce domain separation or to bind evaluations to specific identifiers. Notably, this structure ensures the uniqueness of PRF outputs for different public values .
The POPRF was first introduced in [93] to defend against precomputation and dictionary attacks in password-based systems. Later, Tyagi et al. [94] proposed using POPRF in the OPAQUE protocol [26] to allow a single master key k to support multiple users, instead of maintaining a separate key per user as in the original design.
Overall, these OPRF variants demonstrate different design choices among efficiency, trust distribution, and privacy in protocol design.
5.3. Post-Quantum Oblivious Pseudorandom Functions
One of the first approaches to constructing a post-quantum VOPRF was proposed in [45]. The security of the protocol relies on the ring learning with errors (RLWE) and one-dimensional short integer solution (1D-SIS) assumptions. As the underlying pseudorandom function, the authors employ the lattice-based PRF from [95]. To ensure verifiability, the construction incorporates a ZKP protocol, with one instantiation based on the classic Yao protocol [96].
A notable advantage of this scheme is that its security is proven in the QROM, which provides a strong argument for its quantum resistance. As will be shown later, none of the subsequent schemes provides a proof of security in this model. However, the construction in [45] remains primarily of theoretical interest, as its communication and computational costs are prohibitively high for practical deployment.
A more recent scheme presented in [46] addresses several limitations of the construction proposed in [45]. The primary focus of the new work is on reducing communication overhead, achieved through the following improvements:
- To prove security, the authors use Rényi divergence instead of statistical distance to analyze distribution indistinguishability. This approach allows for relaxing the bounds on the error vector, which in turn enables reducing the size of transmitted data.
- Instead of the classic ZKP scheme [96], a more efficient protocol from [97] is employed, which is further compressed using the LaBRADOR framework [98].
As a result, the communication cost is reduced to several hundred kilobytes. The paper also proposes a TOPRF, which increases fault tolerance and allows for distributed trust.
Albrecht et al. [48] propose a POPRF based on the fully homomorphic encryption scheme on the torus (TFHE) [99] and the “Crypto Dark Matter” PRF family [100]. The scheme uses a non-interactive ZK (NIZK) protocol [97] with LaBRADOR compression [98]. The security of the protocol, in the presence of a malicious client and a semi-honest server, is based on the MLWE problem and a matrix-based variant of the NTRU problem (matrix-NTRU). Additionally, the authors present a verifiable version of the POPRF, claiming security against both malicious clients and servers. However, the security analysis relies on the heuristic hardness of the problem described in [101], which concerns evaluating high-depth circuits using a homomorphic scheme designed for low-depth computations.
It is important to note that a successful cryptanalysis of the underlying verifiable homomorphic encryption scheme was recently published in [49]. This attack targets specific parameter settings. In response, the authors of [48] propose updated parameters for further analysis. Given these developments, it can be concluded that the security of the proposed scheme remains an open question and requires further scrutiny.
The authors of [47] propose a novel post-quantum verifiable POPRF scheme, referred to as LeOPaRd. This scheme can be naturally generalized to an n-out-of-n TOPRF construction.
The main innovation of LeOPaRd lies in the introduction of a modified MLWE problem tailored for interactive settings, formalized as interactive MLWE with re-use (iMLWE-RU). This interactive assumption enables the reuse of a single set of public parameters across multiple sessions.
The security analysis of LeOPaRd relies on reductions from the iMLWE-RU problem to newly formulated LWE-like assumptions. The authors present two variants of iMLWE-RU—one based on Gaussian noise (iMLWE-RU-G) and the other on rounding (iMLWE-RU-R). They prove that solving these problems is at least as hard as solving the MLWE-PRF problem, which in turn reduces to the standard MLWE/MLWR assumptions. Importantly, they emphasize the need for careful parameter selection, specifically regarding the ratio between the masking noise and the MLWE noise. If the masking noise is too small relative to , the construction becomes vulnerable to an averaging attack, in which an adversary can average multiple samples to nearly reconstruct the secret vector.
Verifiability and resilience against malicious adversaries on both the server and client sides are achieved through a commitment scheme based on the BDLOP construction [102], combined with an NIZK protocol [97,98].
In addition to lattice-based cryptographic primitives, isogeny-based OPRF protocols have been proposed. In [103], two OPRF protocols are introduced, relying on the SIDH [104] and GAIP [77] problems. Compared to the first lattice-based solution, these protocols, at a 128-bit security level, require substantial data transmission—over 11 MB across six rounds for SIDH, and 424 KB over three rounds for GAIP.
Subsequently, an efficient attack targeting the SIDH-based protocol was presented in [105], exploiting vulnerabilities inherent in the protocol itself. Later, an attack on the SIDH problem itself was proposed in [76].
Ref. [50] addresses the security weaknesses of the SIDH-based protocol introduced in [103]. The author proposes using irrational isogenies whose kernels are defined over the field . Although an adversary may recover partial information, the complete reconstruction of the server’s secret key remains infeasible. However, the use of high-degree isogenies (with requiring operations in the field ) incurs significant computational overhead. Thus, while the protocol enhances security, it remains resource-intensive both in terms of computation and communication cost.
Beullens et al. [51] propose a novel approach to constructing a quantum-secure 2Hash OPRF based on two-party computation and provide a formal proof of security in the UC model. Based on this approach, they introduce a post-quantum verifiable 2Hash OPRF based on the decisional shifted Legendre symbol (DSLS) problem. The scheme employs a Legendre-based PRF, OT, and ZKP constructed via vector oblivious linear evaluation (VOLE). An improved variant of this construction is presented in [52].
In [52], the authors describe a post-quantum OPRF protocol based on the decisional shifted power-residue symbol (DSPRS) problem. They introduce the Gold PRF, a generalization of the Legendre PRF, based on the power-residue PRF [106]. Unlike the Legendre PRF, which produces only a single-bit output, the Gold PRF can output bits, significantly improving efficiency. Here, e denotes the order of the root taken modulo a prime p, and the function is defined as , where is the secret key and is the input. The authors suggest using .
The hardness of the DSPRS problem lies in the computational indistinguishability of the Gold PRF output from a random e-th root of unity. The Gold PRF is considered cryptographically secure under the assumption that DSPRS cannot be solved in polynomial time. The construction is resistant to both classical and quantum adversaries—even after multiple queries to the PRF, an attacker learns nothing about the key and cannot predict for a new input x.
In [52], the OPRF protocol is constructed using VOLE, based on the scheme introduced in [51]. A notable advantage of the proposed construction is that VOLE is treated as a black-box component, which simplifies the implementation and enhances modularity. To ensure quantum resistance, VOLE is instantiated using an OT protocol based on the construction from [42].
The authors propose two versions of the OPRF protocol. The first variant offers security against a malicious client and a semi-honest server. The second variant provides protection against fully malicious adversaries on both sides. In the first variant, a one-bit leakage of the client input x may occur if . This vulnerability is mitigated in the second version through the use of a post-quantum VOLE-based ZKP [107], which prevents the server from learning any information about the client’s inputs.
Table 7 provides a chronological overview of the post-quantum OPRF protocols discussed in this paper. The timeline is based on the publication years of the relevant references and web sources. It highlights the transition from early lattice-based designs with high computational overhead to more efficient constructions.

Table 7.
Research landscape in post-quantum OPRF.
Notable progress in post-quantum OPRF protocols was achieved in 2024–2025. In particular, this is the 2Hash framework with efficient Legendre-based instantiations and Gold OPRF supporting multi-bit outputs. Despite these advances, key research gaps remain. Alternative instantiations beyond lattices, such as code-based or multivariate-based designs, are needed to reduce the reliance on current assumptions. Furthermore, hybrid quantum–post-quantum combiners must be explored to provide backward compatibility and long-term security.
5.4. Analysis of Post-Quantum Oblivious Pseudorandom Functions
5.4.1. Qualitative Analysis
To date, a considerable number of quantum-secure OPRF protocols have been proposed. However, this study focuses exclusively on schemes that include a formal security proof against malicious adversaries. Table 8 summarizes the design characteristics of the analyzed OPRF protocols.

Table 8.
Post-quantum OPRF protocols: design perspective.
As shown in Table 8, all considered protocols provide security proofs in the ROM, except for the scheme proposed by Albrecht et al. (2021) [45], which is proven secure in the QROM—a strictly stronger model.
However, the most significant observation is that only three protocols [50,51,52] are UC-secure. In other words, only these protocols retain their security guarantees when composed with other cryptographic protocols. For the remaining schemes, security is guaranteed only in the standalone setting.
5.4.2. Quantitative Analysis
Quantitative characteristics of the protocols at the 128-bit security level are summarized in Table 9.

Table 9.
Post-quantum OPRF protocols: efficiency.
It is important to highlight that implementations of the OPRF protocols are publicly available only for the constructions presented in [51,52]. As a result, CPU cycle-based performance measurements are provided exclusively for these implementations. All benchmarks were obtained using an AMD Ryzen 7 processor, assuming a 128-bit PRF output length.
From a practical deployment perspective, the protocol proposed by Albrecht et al. (2021) [45] can be excluded from further consideration, as it requires more than 140 GB of data transmission. The communication overhead of such magnitude imposes severe latency and bandwidth costs, rendering the protocol impractical both in terms of network efficiency and overall performance.
Among the remaining schemes, the LeOPaRd protocol [47] demonstrates the most favorable communication profile. The protocol requires a one-time transmission of the server’s public key, amounting to 34.11 KB, and each invocation of the protocol entails an additional 206 KB of data exchanged between the client and the server.
Analysis of the data in Table 8 and Table 9 identifies the protocols proposed by Beullens et al. [51] and Yang et al. [52] as the most promising post-quantum OPRF constructions currently available.
First, from a design perspective, both protocols offer the important advantage of UC security, which is essential for their integration into broader cryptographic constructions. Second, both works include publicly available software implementations, facilitating practical deployment and independent evaluation. Third, both protocols exhibit efficient performance due to the use of number-theoretic primitives combined with post-quantum OT techniques.
The two protocols differ in terms of communication cost and interaction complexity. If minimizing communication overhead is the priority, the scheme by Beullens et al. [51] is preferable. Conversely, if reducing the number of communication rounds is more important, the scheme by Yang et al. [52] is the better choice.
6. Additional Oblivious Protocols and Schemes
6.1. Oblivious Signature
The oblivious signature scheme is applicable in cases where the recipient of a signature does not want to reveal information about which message they need to sign or which key was used to create the signature. OS, like traditional cryptographic signatures, is composed of the following three algorithms: key generation, signing, and verification. However, the protocols involved may vary depending on the application context.
One variant of OS, described by Chen [12], involves a group of n signing parties and a signature recipient R. The recipient selects one of the n pairs of public and secret keys to obtain a signature on a message of their choice, in such a way that the key owner is unaware of which key pair was used. As a result, R obtains a valid signature from one of the n signers without revealing which one. This construction is applicable to systems where R has legitimate access to certain information but prefers to hide the specific content of their interest. In this context, the signer is obligated to respond, but cannot infer which piece of data was requested.
Another version of OS is the 1-out-of-n message variant, where the recipient R aims to obtain a signature on one message from a set without revealing which one. The recipient sends the full message set to the signer S, who returns the corresponding signature set . The recipient then selects a single valid signature for some index and may later publish it, revealing no further information. In this construction, the signer is aware of all messages being signed but cannot distinguish which one the recipient intends to use. The protocol ensures that R obtains only one valid signature and cannot derive signatures for any other messages.
A more formal definition of the 1-out-of-n OS scheme is provided in [109]. This work clearly outlines the roles of the parties involved in the protocol and formalizes their interaction:
- Signature recipient (R): Sends a set of messages to the signer S and obtains a valid signature on one of these messages.
- Signer (S): Signs a set of messages without learning which specific message was chosen by the recipient.
- Verifier (V): Verifies the validity of the signature without requiring any secret information.
This scheme can also be described using the general framework of oblivious protocols. In this case, the scheme is defined by the following sets and functions:
- Sets:is the set of signing keys, is the message space, and is the set of valid signatures.
- Function:represents the recipient’s choice, and k is the signer’s secret key.
The one-wayness of the function family is guaranteed by the obliviousness property of the underlying signature scheme. This formalization allows the 1-out-of-n OS scheme to be interpreted as a specific instance of a general oblivious computation protocol, emphasizing the core security properties of recipient privacy and signature obliviousness.
Most oblivious signature schemes are based on the discrete logarithm problem [12,109,110,111,112]. In contrast, only a limited number of quantum-resistant oblivious signature schemes have been proposed to date, including lattice-based constructions [113] and isogeny-based ones [114]. Recent research has focused primarily on the development of optimized frameworks for oblivious signature schemes [115,116], designed to minimize computational and memory overhead. These frameworks can subsequently be instantiated using concrete quantum-secure signature schemes.
6.2. Oblivious Data Structures
Oblivious data structures are defined as those that prevent leakage of information about the location of accessed data elements. In other words, if there exists an array a of size N, then accessing an element does not reveal the index i. The supported operations include reading and updating values.
Oblivious data structures can be formalized in terms of oblivious protocols. Let denote the set of key–value pairs. Then the corresponding domains are defined as . The function is given by , where , and denotes a specific operation (read or write) applied to the requested data.
The main security requirement is that the server should not be able to learn which particular element was requested by the receiver. Ensuring that the receiver learns nothing about the other elements is not always necessary. For instance, a trivial protocol may consist of the server transmitting the entire encrypted database to the receiver using a pre-shared key.
After a data access, the structure must be updated to prevent leakage of information during subsequent read operations and to ensure that the server cannot determine which element was modified during a write. In array-based structures, the key is typically an index, while in oblivious random-access memory constructions, the key corresponds to a memory address.
Examples of oblivious data structures include stacks and queues, as demonstrated in [117]. The fundamental building block underlying most oblivious data structures is ORAM.
6.2.1. Oblivious Random Access Memory
The concept of ORAM was first introduced in [13], where it is formalized as a memory abstraction enabling read and write operations without revealing which memory regions were accessed. The primary goal of ORAM is to hide the access patterns of a client interacting with a database or memory, ensuring that a server cannot determine which portions of the data were read or modified.
It is generally assumed that the data stored in memory is encrypted using symmetric encryption, and that the adversary (typically, the server) aims only to infer the access pattern. The ORAM protocol is usually executed within a Trusted Execution Environment (TEE), which prevents the adversary from accessing the internal cryptographic operations.
One of the most well-known approaches to implementing ORAM is the tree-based construction introduced in [118], where data blocks are stored in a binary tree, and each block is associated with a tree node. Further refinements of this approach have been presented in [32,119,120].
The idea of splitting the ORAM server’s role between two parties was proposed in [121].
This approach eliminates the need for a TEE, provided that at least one of the parties behaves honestly to preserve the ORAM security guarantees.
The application of ORAM in secure multiparty computation (SMPC) protocols was first explored in [122]. In this model, each party stores part of the ORAM structure and uses basic SMPC primitives to access memory. More recent protocols, such as [123,124], employ Yao’s garbled circuits with noisy tables [8] to implement memory accesses. The quantum security of such constructions depends on the underlying quantum resilience of the employed MPC protocols.
An alternative approach to ORAM design is based on fully homomorphic encryption [125,126,127]. This method offers two key advantages: reduced communication overhead and the use of quantum-resistant FHE schemes. The main drawback of FHE-based ORAM, however, lies in its high computational complexity and latency.
Regarding the current state of post-quantum security in ORAM protocols, the situation is as follows. The analysis of tree-based ORAM schemes in the presence of quantum adversaries is presented in [128]. This work introduces formal definitions of quantum-secure ORAM and a corresponding security model under quantum threats. It demonstrates that constructing post-quantum ORAM requires a quantum-secure symmetric encryption scheme and a cryptographically secure pseudorandom number generator. However, the paper does not provide concrete implementations based on known cryptographic primitives, offering instead only a theoretical construction.
The post-quantum security of ORAM protocols based on SMPC depends primarily on the quantum resistance of the underlying SMPC protocols. For example, the security of garbled circuits used in ORAM protocols [123,124] requires post-quantum secure OT protocols, since OT is essential for constructing Yao’s scheme.
The security of ORAM protocols built on FHE schemes depends on the chosen FHE construction. Most known FHE schemes are considered post-quantum secure. Thus, ORAM protocols based on them inherit a certain level of quantum resistance. For instance, the Panacea protocol [127] leverages RLWE-based FHE, ensuring robustness against quantum adversaries.
In general, the design of new ORAM protocols is often motivated by performance rather than security. The main goal is to reduce communication and computational overhead while hiding access patterns. Apart from [128], there is little comprehensive work analyzing ORAM protocols in terms of post-quantum security. Existing research either does not mention this property or discusses it only briefly. In particular, the threat model of an adversary with access to a quantum random oracle is rarely considered.
ORAM vs. PIR
The PIR protocol pursues the same objective as ORAM, namely, to conceal the client’s access patterns to a remote database. However, the two approaches differ significantly in terms of architecture and computational model.
In ORAM-based systems, the server functions as a passive storage provider—it merely stores and transmits data, while all computational operations are performed entirely on the client side. In contrast, PIR protocols require active participation from both client and server; the server must preprocess the database and compute responses to each query.
From the perspective of communication complexity, PIR protocols are generally more efficient than ORAM. However, ORAM schemes typically achieve faster execution times. Moreover, ORAM supports both read and secure update operations on the database, whereas PIR is mainly optimized for read-only access and is less suitable for dynamic updates.
6.2.2. Oblivious Key–Value Store
An oblivious dictionary, also known as an oblivious key–value store [14], is a data structure designed to encode key–value pairs in a way that hides access patterns. For each pair, an encoding structure is generated, and the value is retrieved by computing . Obliviousness ensures that the output distribution of reveals no information about the queried key and is statistically indistinguishable from random over the value space .
A simple instantiation of OKVS is based on polynomial interpolation, where a polynomial p is constructed such that , and its coefficients represent the encoded structure. The decoding algorithm then evaluates at the queried key. Other realizations of oblivious dictionaries include constructions based on random matrices, noisy Bloom filters [129], and the PaXoS scheme [130].
Key performance metrics for oblivious dictionaries are important. They include encoding size. This is the ratio of the structure’s size to the theoretical minimum . Next is encoding time. It measures the time to encode n key–value pairs. Finally, decoding time matters. It is time to retrieve one or all values from the structure.
OKVS is widely used in PSI protocols and serves as a fundamental building block in POPRF constructions. The cryptographic primitives used in OKVS include hash functions, symmetric encryption, and pseudorandom generators. These constructions are not highly vulnerable to quantum attacks. To strengthen security against a quantum adversary, the classical security level should be doubled. This ensures resistance against Grover’s algorithm. Thus, the quantum threat is not a critical issue for OKVS and can be addressed efficiently.
6.3. Oblivious Polynomial Evaluation
Oblivious polynomial evaluation is a cryptographic protocol that enables two parties to jointly evaluate a polynomial at a specific input without revealing their private inputs to each other. Let be a finite field. The server holds a polynomial of degree k, while the client provides an input and learns the value without revealing x or learning any additional information about the polynomial P.
This protocol can be expressed as an oblivious protocol where the domains are defined as follows: , , and . The evaluation function is , with and . The one-wayness of the function is based on the hardness of interpolating a degree-k polynomial from fewer than k points. Therefore, for a given polynomial P, the protocol is assumed to be executed at most times.
OPE protocols have practical applications such as privacy-preserving authentication. In this scenario, the server stores a polynomial P, and the client inputs a secret x (password). The server can verify whether matches the expected value without learning x, and the scheme is resistant to dictionary attacks. Another application is anonymous data aggregation, where x represents user behavior and is the value observed by the data collector.
The first OPE scheme was introduced by Naor and Pinkas in [11], based on the problem of noisy polynomial reconstruction, which is closely related to list decoding of Reed–Solomon codes. Their construction uses an OT protocol to hide the client’s input. The client cannot reconstruct the polynomial due to the noisy polynomial problem. However, subsequent works [131,132] demonstrated that the server’s polynomial could be recovered efficiently, rendering the original scheme insecure.
At present, several OPE schemes rely on problems that are not quantum secure. Examples include schemes based on the hardness of DDH [133] or the decisional composite residuosity (DCR) problem [134,135], which underlies the Paillier cryptosystem.
At present, only two works propose quantum secure implementations of OPE. The first [136] is based on post-quantum FHE, whose security relies on the hardness of Ring-LWE. The second [137] proposes a quantum-secure OPE built on principles of quantum cryptography.
In addition, several OPE protocols with unconditional (information-theoretic) security have since been proposed [137,138,139], in which adversaries are not restricted by computational power. These constructions generally require more than two parties to ensure security.
Oblivious Linear Evaluation
A special case of OPE is the Oblivious Linear Function Evaluation protocol, in which the evaluated polynomial is of degree at most one. OLE requires significantly fewer computational resources than general OPE protocols, making it particularly suitable for applications limited to linear computations.
Post-quantum OLE constructions based on lattice assumptions, such as the LWE and Ring-LWE problems, have been proposed in [16,140].
A natural generalization of OLE is Vector OLE, which allows multiple linear functions to be evaluated on a shared input x. VOLE can be seen as several parallel instances of OLE over the same input, and it is widely used in OPRF protocols. Post-quantum secure VOLE constructions have been introduced in [17,67,141,142], often leveraging lattice-based assumptions.
7. Discussion and Future Prospects
Analysis of existing approaches to the construction of oblivious protocols reveals several aspects that require consideration in the design of new protocols.
First, it’s a security model. Most post-quantum oblivious protocols establish security proofs in the ROM. Even when the reduction relies on problems for which no efficient quantum algorithms are known, the ROM still raises concerns. In particular, an adversary with a quantum computer can make quantum queries to hash functions, which is only captured in the QROM. To strengthen confidence in post-quantum security, proofs should ideally be given in either the QROM or the standard model. At the same time, as shown in [45], using QROM can lead to significant overhead in both communication and computation. Moreover, proving security in this model is technically more demanding.
Second, it’s a UC-security. Since oblivious protocols are rarely used in isolation and often serve as building blocks for larger protocols, it is important that their security is preserved under composition. Therefore, security in the UC model is a key property. However, not all post-quantum oblivious protocols provide such guarantees. For example, among OPRF constructions, only a few have been proven UC-secure against malicious adversaries.
Finally, it’s a performance. Post-quantum cryptographic primitives generally require more memory and computational resources than classical ones. This challenge applies not only to oblivious protocols, but also to post-quantum cryptography in general. Optimization of performance metrics remains a central problem in protocol design.
Notably, most proposed post-quantum oblivious protocols are theoretical. They frequently omit practical analyses, software implementations, and performance evaluations. Additionally, reliance on specially defined random oracles poses another obstacle for implementation. In practice, the realization of a random oracle may arise vulnerabilities not accounted for in the security proof.
Based on the above analysis, several research directions can be identified in the field of oblivious protocols:
- Stronger security analysis against quantum adversaries. Security proofs of post-quantum oblivious protocols should account for the full range of capabilities available to quantum adversaries. This can be achieved, for example, through the use of the QROM model. If QROM significantly reduces efficiency, then omitting it requires an additional risk assessment of potential quantum attacks on cryptographic hash functions and their consequences.
- Efficiency enhancement. Reducing runtime, communication rounds, and communication overhead remains a key objective in the design of post-quantum oblivious protocols.
- Practical design of new schemes. The construction of oblivious protocols should consider both qualitative and quantitative characteristics. Such evaluation is essential for their deployment in resource-constrained environments. A software implementation is a valuable addition to the description of a protocol. Implementation must also address randomness sources and resistance to side-channel attacks, including power analysis and timing attacks. Investigating the effect of side-channel attacks on oblivious protocols represents an important research direction.
- Synergy of quantum and post-quantum approaches. At present, quantum secure oblivious protocols, such as OT and OPRF, exist only in either quantum or post-quantum form. Exploring hybrid constructions that combine both approaches and exploit their advantages offers a promising research avenue.
- Framework-based protocol design. Future developments may render some post-quantum cryptographic assumptions insecure if novel efficient quantum algorithms are discovered. Designing oblivious protocols as flexible frameworks would enable the substitution of underlying cryptographic primitives. Such an approach enhances adaptability and resilience against potential advances in quantum algorithms.
Author Contributions
Conceptualization, A.K.; software, A.L.; validation, A.K., A.L. and S.B.; formal analysis, A.K. and A.L.; investigation, A.K. and A.L.; data curation, A.K.; writing—original draft preparation, A.K. and A.L.; writing—review and editing, S.B.; visualization, A.K.; supervision, S.B.; project administration, S.B. and A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the State Assignment grant number FSER-2025-0003.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank the anonymous reviewers and the editor for their constructive feedback, which substantially improved the clarity, structure, and comprehensiveness of the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| OLE | Oblivious Linear Evaluation |
| OPE | Oblivious Polynomial Evaluation |
| OPRF | Oblivious Pseudorandom Function |
| ORAM | Oblivious Random Access Memory |
| OS | Oblivious Signature |
| OT | Oblivious Transfer |
| OKVS | Oblivious Key–Value Store |
| QROM | Quantum Random Oracle Model |
| ROM | Random Oracle Model |
| TEE | Trusted Execution Environment |
| UC | Universal Composability |
| VOLE | Vector Oblivious Linear Evaluation |
References
- Rabin, M.O. How To Exchange Secrets with Oblivious Transfer. Available online: https://eprint.iacr.org/2005/187 (accessed on 8 February 2025).
- Even, S.; Goldreich, O.; Lempel, A. A randomized protocol for signing contracts. Commun. ACM 1985, 28, 637–647. [Google Scholar] [CrossRef]
- Wiesner, S. Conjugate coding. ACM Sigact News 1983, 15, 78–88. [Google Scholar] [CrossRef]
- Kolesnikov, V.; Kumaresan, R.; Rosulek, M.; Trieu, N. Efficient batched oblivious PRF with applications to private set intersection. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 818–829. [Google Scholar]
- Pinkas, B.; Schneider, T.; Zohner, M. Scalable private set intersection based on OT extension. ACM Trans. Priv. Secur. (TOPS) 2018, 21, 1–35. [Google Scholar] [CrossRef]
- Pinkas, B.; Rosulek, M.; Trieu, N.; Yanai, A. SpOT-light: Lightweight private set intersection from sparse OT extension. In Proceedings of the Advances in Cryptology–CRYPTO 2019: 39th Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2019; Proceedings, Part III 39. Springer: Cham, Switzerland, 2019; pp. 401–431. [Google Scholar]
- Burra, S.S.; Larraia, E.; Nielsen, J.B.; Nordholt, P.S.; Orlandi, C.; Orsini, E.; Scholl, P.; Smart, N.P. High-performance multi-party computation for binary circuits based on oblivious transfer. J. Cryptol. 2021, 34, 34. [Google Scholar] [CrossRef]
- Yao, A.C.C. How to generate and exchange secrets. In Proceedings of the 27th Annual Symposium on Foundations of Computer Science (FOCS), Toronto, ON, Canada, 27–29 October 1986; pp. 162–167. [Google Scholar]
- Bringer, J.; Chabanne, H.; Patey, A. Privacy-preserving biometric identification using secure multiparty computation: An overview and recent trends. IEEE Signal Process. Mag. 2013, 30, 42–52. [Google Scholar] [CrossRef]
- Xu, G.; Li, H.; Zhang, Y.; Xu, S.; Ning, J.; Deng, R.H. Privacy-preserving federated deep learning with irregular users. IEEE Trans. Dependable Secur. Comput. 2020, 19, 1364–1381. [Google Scholar] [CrossRef]
- Naor, M.; Pinkas, B. Oblivious transfer and polynomial evaluation. In Proceedings of the Thirty-First Annual ACM Symposium on Theory of Computing, Atlanta, GA, USA, 1–4 May 1999; Association for Computing Machinery: New York, NY, USA, 1999; pp. 245–254. [Google Scholar]
- Chen, L. Oblivious signatures. In Proceedings of the Computer Security-ESORICS 94: Third European Symposium on Research in Computer Security, Brighton, UK, 7–9 November 1994; Proceedings 3. Springer: Berlin/Heidelberg, Germany, 1994; pp. 161–172. [Google Scholar]
- Goldreich, O.; Ostrovsky, R. Software protection and simulation on oblivious RAMs. J. ACM 1996, 43, 431–473. [Google Scholar] [CrossRef]
- Garimella, G.; Pinkas, B.; Rosulek, M.; Trieu, N.; Yanai, A. Oblivious key-value stores and amplification for private set intersection. In Proceedings of the Advances in Cryptology–CRYPTO 2021: 41st Annual International Cryptology Conference, CRYPTO 2021, Virtual, 16–20 August 2021; Proceedings, Part II 41. Springer: Berlin/Heidelberg, Germany, 2021; pp. 395–425. [Google Scholar]
- Freedman, M.J.; Ishai, Y.; Pinkas, B.; Reingold, O. Keyword search and oblivious pseudorandom functions. In Proceedings of the Theory of Cryptography: Second Theory of Cryptography Conference, TCC 2005, Cambridge, MA, USA, 10–12 February 2005; Proceedings 2. Springer: Berlin/Heidelberg, Germany, 2005; pp. 303–324. [Google Scholar]
- Branco, P.; Döttling, N.; Mateus, P. Two-round oblivious linear evaluation from learning with errors. In Proceedings of the IACR International Conference on Public-Key Cryptography, Virtual, 8–11 March 2022; Springer: Cham, Switzerland, 2022; pp. 379–408. [Google Scholar]
- Boyle, E.; Couteau, G.; Gilboa, N.; Ishai, Y. Compressing vector OLE. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 896–912. [Google Scholar]
- Chor, B.; Kushilevitz, E.; Goldreich, O.; Sudan, M. Private information retrieval. J. ACM 1998, 45, 965–981. [Google Scholar] [CrossRef]
- Di Crescenzo, G.; Malkin, T.; Ostrovsky, R. Single database private information retrieval implies oblivious transfer. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques—EUROCRYPT 2000, Bruges, Belgium, 14–18 May 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 122–138. [Google Scholar]
- Mayberry, T.; Blass, E.O.; Chan, A.H. Efficient Private File Retrieval by Combining ORAM and PIR. Available online: https://eprint.iacr.org/2013/086 (accessed on 10 February 2025).
- Chase, M.; Miao, P. Private set intersection in the internet setting from lightweight oblivious PRF. In Proceedings of the Advances in Cryptology–CRYPTO 2020: 40th Annual International Cryptology Conference, CRYPTO 2020, Santa Barbara, CA, USA, 17–21 August 2020; Proceedings, Part III 40. Springer: Berlin/Heidelberg, Germany, 2020; pp. 34–63. [Google Scholar]
- Nevo, O.; Trieu, N.; Yanai, A. Simple, fast malicious multiparty private set intersection. In Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security, Virtual, 15–19 November 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 1151–1165. [Google Scholar]
- Golle, P.; Staddon, J.; Waters, B. Secure conjunctive keyword search over encrypted data. In Proceedings of the International Conference on Applied Cryptography and Network Security: Second International Conference, ACNS 2004, Yellow Mountain, China, 8–11 June 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 31–45. [Google Scholar]
- Jarecki, S.; Krawczyk, H.; Resch, J. Updatable oblivious key management for storage systems. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 379–393. [Google Scholar]
- Davidson, A.; Goldberg, I.; Sullivan, N.; Tankersley, G.; Valsorda, F. Privacy pass: Bypassing internet challenges anonymously. Proc. Priv. Enhancing Technol. 2018, 2018, 164–180. [Google Scholar] [CrossRef]
- Jarecki, S.; Krawczyk, H.; Xu, J. OPAQUE: An asymmetric PAKE protocol secure against pre-computation attacks. In Proceedings of the Advances in Cryptology–EUROCRYPT 2018: 37th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Tel Aviv, Israel, 29 April–3 May 2018; Proceedings, Part III 37. Springer: Berlin/Heidelberg, Germany, 2018; pp. 456–486. [Google Scholar]
- Davies, G.T.; Faller, S.; Gellert, K.; Handirk, T.; Hesse, J.; Horváth, M.; Jager, T. Security analysis of the whatsapp end-to-end encrypted backup protocol. In Proceedings of the Advances in Cryptology—CRYPTO 2023: 43rd Annual International Cryptology Conference, Santa Barbara, CA, USA, 20–24 August 2023; Proceedings, Part VII. Springer: Cham, Switzerland, 2023; pp. 330–361. [Google Scholar]
- Chiou, S.Y.; Chen, J.M. Design and Implementation of a Multiple-Choice E-voting Scheme on Mobile System using Novel t-out-of-n Oblivious Signature. J. Inf. Sci. Eng. 2018, 34, 135. [Google Scholar]
- Chen, J.; Gong, L.; Ma, X.; Wang, D. E-commerce Scheme Based on Proxy t-out-of-n Oblivious Signature. Int. J. Netw. Secur. 2024, 26, 851–860. [Google Scholar]
- Huang, Y.; Goldberg, I. Outsourced private information retrieval. In Proceedings of the 12th ACM Workshop on Workshop on Privacy in the Electronic Society, Berlin, Germany, 4 November 2013; Association for Computing Machinery: New York, NY, USA, 2013; pp. 119–130. [Google Scholar]
- Eskandarian, S.; Zaharia, M. Oblidb: Oblivious query processing for secure databases. arXiv 2017, arXiv:1710.00458. [Google Scholar] [CrossRef]
- Garg, S.; Mohassel, P.; Papamanthou, C. TWORAM: Efficient oblivious RAM in two rounds with applications to searchable encryption. In Proceedings of the Advances in Cryptology—CRYPTO 2016: 36th Annual International Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2016; Proceedings, Part II. Springer: Berlin/Heidelberg, Germany, 2016; pp. 563–592. [Google Scholar]
- Döttling, N.; Ghosh, S.; Nielsen, J.B.; Nilges, T.; Trifiletti, R. TinyOLE: Efficient actively secure two-party computation from oblivious linear function evaluation. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 2263–2276. [Google Scholar]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; Association for Computing Machinery: New York, NY, USA, 1996; pp. 212–219. [Google Scholar]
- Santos, M.B.; Mateus, P.; Pinto, A.N. Quantum oblivious transfer: A short review. Entropy 2022, 24, 945. [Google Scholar] [CrossRef] [PubMed]
- Casacuberta, S.; Hesse, J.; Lehmann, A. SoK: Oblivious Pseudorandom Functions. In Proceedings of the 2022 IEEE European Symposium on Security and Privacy (EuroS&P), Genoa, Italy, 6–10 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 625–646. [Google Scholar]
- Yadav, V.K.; Andola, N.; Verma, S.; Venkatesan, S. A Survey of Oblivious Transfer Protocol; ACM: New York, NY, USA, 2022; pp. 1–37. [Google Scholar]
- Barreto, P.S.; David, B.; Dowsley, R.; Morozov, K.; Nascimento, A.C. A framework for efficient adaptively secure composable oblivious transfer in the ROM. arXiv 2017, arXiv:1710.08256. [Google Scholar] [CrossRef]
- Lai, Y.F.; Galbraith, S.D.; Delpech de Saint Guilhem, C. Compact, efficient and UC-secure isogeny-based oblivious transfer. In Proceedings of the Advances in Cryptology—EUROCRYPT 2021: 40th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 17–21 October 2021; Proceedings, Part I. Springer: Berlin/Heidelberg, Germany, 2021; pp. 213–241. [Google Scholar]
- Orsini, E.; Zanotto, R. Simple Two-Round OT in the Explicit Isogeny Model. Commun. Cryptol. 2024, 1, 1–34. [Google Scholar]
- Mansy, D.; Rindal, P. Endemic oblivious transfer. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 309–326. [Google Scholar]
- Dong, S.; Cui, H.; Zhang, K.; Yang, K.; Yu, Y. A Simple Post-Quantum Oblivious Transfer Protocol from Mod-LWR. Cryptology ePrint Archive, Report 2024/1116. 2024. Available online: https://eprint.iacr.org/2024/1116 (accessed on 12 March 2025).
- Naor, M.; Pinkas, B. Efficient oblivious transfer protocols. In Proceedings of the Twelfth Annual ACM-SIAM Symposium on Discrete Algorithms, Washington, DC, USA, 7–9 January 2001; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2001; Volume 1, pp. 448–457. [Google Scholar]
- Albrecht, M.R.; Davidson, A.; Deo, A.; Smart, N.P. Round-optimal Verifiable Oblivious Pseudorandom Functions From Ideal Lattices. In Proceedings of the IACR International Conference on Public-Key Cryptography, Virtual, 10–13 May 2021; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Albrecht, M.R.; Gur, K.D. Verifiable oblivious pseudorandom functions from lattices: Practical-ish and thresholdisable. In Proceedings of the Advances in Cryptology—ASIACRYPT 2024: 30th International Conference on the Theory and Application of Cryptology and Information Security, Kolkata, India, 15–19 December 2024; Proceedings, Part VIII. Springer: Berlin/Heidelberg, Germany, 2024; pp. 205–237. [Google Scholar]
- Esgin, M.F.; Steinfeld, R.; Tairi, E.; Xu, J. LeOPaRd: Towards Practical Post-Quantum Oblivious PRFs via Interactive Lattice Problems.Cryptology ePrint Archive, Report 2024/1615. 2024. Available online: https://eprint.iacr.org/2024/1615 (accessed on 3 April 2025).
- Albrecht, M.R.; Davidson, A.; Deo, A.; Gardham, D. Crypto Dark Matter on the Torus: Oblivious Prfs from Shallow Prfs and Tfhe. In Proceedings of theAdvances in Cryptology—EUROCRYPT 2024: 43rd Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zurich, Switzerland, 26–30 May 2024; Proceedings, Part I. Springer: Cham, Switzerland, 2024; pp. 447–476. [Google Scholar]
- Cheon, J.H.; Jang, D. Cryptanalysis on Lightweight Verifiable Homomorphic Encryption. arXiv 2025, arXiv:2502.12628. [Google Scholar]
- Basso, A. A post-quantum round-optimal oblivious PRF from isogenies. In Proceedings of the Selected Areas in Cryptography—SAC 2023: 29th International Conference, Saskatoon, SK, Canada, 15–16 August 2023; Revised Selected Papers. Springer: Cham, Switzerland, 2023; pp. 147–168. [Google Scholar]
- Beullens, W.; Dodgson, L.; Faller, S.; Hesse, J. The 2Hash OPRF framework and efficient post-quantum instantiations. In Proceedings of theAdvances in Cryptology—EUROCRYPT 2025: 44th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Ljubljana, Slovenia, 30 March–3 April 2025; Proceedings, Part I. Springer: Cham, Switzerland, 2025; pp. 332–362. [Google Scholar]
- Yang, Y.; Benhamouda, F.; Halevi, S.; Krawczyk, H.; Rabin, T. Gold OPRF: Post-quantum oblivious power-residue PRF. In Proceedings of the 2025 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 18–22 May 2025; IEEE: Piscataway, NJ, USA, 2025; pp. 259–278. [Google Scholar]
- Canetti, R. Universally composable security: A new paradigm for cryptographic protocols. In Proceedings of the 42nd Annual Symposium on Foundations of Computer Science, Las Vegas, NV, USA, 14–17 October 2001; IEEE: Piscataway, NJ, USA, 2001; pp. 136–145. [Google Scholar]
- Impagliazzo, R.; Rudich, S. Limits on the provable consequences of one-way permutations. In Proceedings of the Twenty-First Annual ACM Symposium on Theory of Computing, Seattle, WA, USA, 15–17 May 1989; Association for Computing Machinery: New York, NY, USA, 1989; pp. 44–61. [Google Scholar]
- Bellare, M.; Micali, S. Non-interactive oblivious transfer and applications. In Proceedings of the Advances in Cryptology—CRYPTO ’89: 9th Annual International Cryptology Conference, Santa Barbara, CA, USA, 20–24 August 1989; Proceedings. Springer: Berlin/Heidelberg, Germany, 1989; pp. 547–557. [Google Scholar]
- Branco, P.; Fiolhais, L.; Goulão, M.; Martins, P.; Mateus, P.; Sousa, L. Roted: Random oblivious transfer for embedded devices. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2021, 4, 215–238. [Google Scholar] [CrossRef]
- Yang, K.; Weng, C.; Lan, X.; Zhang, J.; Wang, X. Ferret: Fast extension for correlated OT with small communication. In Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security, Virtual, 9–13 November 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 1607–1626. [Google Scholar]
- Camenisch, J.; Neven, G.; Shelat, A. Simulatable adaptive oblivious transfer. In Proceedings of the Advances in Cryptology—EUROCRYPT 2007: 26th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Barcelona, Spain, 20–24 May 2007; Proceedings. Springer: Berlin/Heidelberg, Germany, 2007; pp. 573–590. [Google Scholar]
- Rial, A.; Kohlweiss, M.; Preneel, B. Universally composable adaptive priced oblivious transfer. In Proceedings of the Pairing-Based Cryptography–Pairing 2009: Third International Conference, Palo Alto, CA, USA, 12–14 August 2009; Proceedings 3. Springer: Berlin/Heidelberg, Germany, 2009; pp. 231–247. [Google Scholar]
- Coull, S.; Green, M.; Hohenberger, S. Controlling access to an oblivious database using stateful anonymous credentials. In Proceedings of the Public Key Cryptography–PKC 2009: 12th International Conference on Practice and Theory in Public Key Cryptography, Irvine, CA, USA, 18–20 March 2009; Proceedings 12. Springer: Berlin/Heidelberg, Germany, 2009; pp. 501–520. [Google Scholar]
- Beaver, D. Correlated pseudorandomness and the complexity of private computations. In Proceedings of theTwenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; Association for Computing Machinery: New York, NY, USA, 1996; pp. 479–488. [Google Scholar]
- Ishai, Y.; Kilian, J.; Nissim, K.; Petrank, E. Extending oblivious transfers efficiently. In Proceedings of the Advances in Cryptology—CRYPTO 2003: 23rd Annual International Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 2003; Proceedings. Springer: Berlin/Heidelberg, Germany, 2003; pp. 145–161. [Google Scholar]
- Kolesnikov, V.; Kumaresan, R. Improved OT extension for transferring short secrets. In Proceedings of the the Advances in Cryptology—ASIACRYPT 2013: 19th International Conference on the Theory and Application of Cryptology and Information Security, Bengaluru, India, 1–5 December 2013; Proceedings, Part II. Springer: Berlin/Heidelberg, Germany, 2013; pp. 54–70. [Google Scholar]
- Boyle, E.; Couteau, G.; Gilboa, N.; Ishai, Y.; Kohl, L.; Scholl, P. Efficient pseudorandom correlation generators: Silent OT extension and more. In Proceedings of the Advances in Cryptology–CRYPTO 2019: 39th Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2019; Proceedings, Part III 39. Springer: Cham, Switzerland, 2019; pp. 489–518. [Google Scholar]
- Boyle, E.; Couteau, G.; Gilboa, N.; Ishai, Y.; Kohl, L.; Rindal, P.; Scholl, P. Efficient two-round OT extension and silent non-interactive secure computation. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 291–308. [Google Scholar]
- Orlandi, C.; Scholl, P.; Yakoubov, S. The rise of paillier: Homomorphic secret sharing and public-key silent OT. In Proceedings of the Advances in Cryptology–EUROCRYPT 2021: 40th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 17–21 October 2021; Proceedings, Part I 40. Springer: Cham, Switzerland, 2021; pp. 678–708. [Google Scholar]
- Couteau, G.; Rindal, P.; Raghuraman, S. Silver: Silent VOLE and oblivious transfer from hardness of decoding structured LDPC codes. In Proceedings of the Advances in Cryptology—CRYPTO 2021: 41st Annual International Cryptology Conference, Virtual, 16–20 August 2021; Proceedings, Part I. Springer: Cham, Switzerland, 2021; pp. 502–534. [Google Scholar]
- Boyle, E.; Couteau, G.; Gilboa, N.; Ishai, Y.; Kohl, L.; Resch, N.; Scholl, P. Correlated pseudorandomness from expand-accumulate codes. In Proceedings of the Advances in Cryptology—CRYPTO 2022: 42nd Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 2022; Proceedings, Part II. Springer: Cham, Switzerland, 2022; pp. 603–633. [Google Scholar]
- Lemus, M.; Ramos, M.F.; Yadav, P.; Silva, N.A.; Muga, N.J.; Souto, A.; Paunković, N.; Mateus, P.; Pinto, A.N. Generation and distribution of quantum oblivious keys for secure multiparty computation. Appl. Sci. 2020, 10, 4080. [Google Scholar] [CrossRef]
- Santos, M.B.; Pinto, A.N.; Mateus, P. Quantum and classical oblivious transfer: A comparative analysis. IET Quantum Commun. 2021, 2, 42–53. [Google Scholar] [CrossRef]
- Avanzi, R.; Bos, J.; Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schanck, J.M.; Schwabe, P.; Seiler, G.; Stehlé, D.; et al. CRYSTALS-Kyber algorithm specifications and supporting documentation. NIST PQC Round 2019, 2, 1–43. [Google Scholar]
- Alagic, G.; Apon, D.; Cooper, D.; Dang, Q.; Dang, T.; Kelsey, J.; Lichtinger, J.; Miller, C.; Moody, D.; Peralta, R.; et al. Status Report on the Third Round of the NIST Post-Quantum Cryptography Standardization Process; Number NIST Internal or Interagency Report (NISTIR) 8413; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2022. [CrossRef]
- Branco, P.; Ding, J.; Goulão, M.; Mateus, P. A framework for universally composable oblivious transfer from one-round key-exchange. In Proceedings of the Cryptography and Coding: 17th IMA International Conference, IMACC 2019, Oxford, UK, 16–18 December 2019; Proceedings 17. Springer: Cham, Switzerland, 2019; pp. 78–101. [Google Scholar]
- D’Anvers, J.P.; Karmakar, A.; Sinha Roy, S.; Vercauteren, F. Saber: Module-LWR based key exchange, CPA-secure encryption and CCA-secure KEM. In Proceedings of the Progress in Cryptology—AFRICACRYPT 2018: 10th International Conference on Cryptology in Africa, Marrakesh, Morocco, 7–9 May 2018; Proceedings. Springer: Cham, Switzerland, 2018; pp. 282–305. [Google Scholar]
- Barreto, P.; Nascimento, A.; Oliveira, G.; Benits, W. Supersingular Isogeny Oblivious Transfer (SIOT). arXiv 2018, arXiv:1805.06589. [Google Scholar]
- Castryck, W.; Decru, T. An efficient key recovery attack on SIDH. In Proceedings of theAdvances in Cryptology—EUROCRYPT 2023: 42nd Annual International Conference on the Theory and Applications of Cryptographic Techniques, Lyon, France, 23–27 April 2023; Proceedings, Part III. Springer: Cham, Switzerland, 2023; pp. 423–447. [Google Scholar]
- Castryck, W.; Lange, T.; Martindale, C.; Panny, L.; Renes, J. CSIDH: An efficient post-quantum commutative group action. In Proceedings of the Advances in Cryptology–ASIACRYPT 2018: 24th International Conference on the Theory and Application of Cryptology and Information Security, Brisbane, QLD, Australia, 2–6 December 2018; Proceedings, Part III 24. Springer: Cham, Switzerland, 2018; pp. 395–427. [Google Scholar]
- Badrinarayanan, S.; Masny, D.; Mukherjee, P.; Patranabis, S.; Raghuraman, S.; Sarkar, P. Round-optimal oblivious transfer and MPC from computational CSIDH. In Proceedings of the Public-Key Cryptography—PKC 2023: 26th IACR International Conference on Public-Key Cryptography, Atlanta, GA, USA, 7–10 May 2023; Proceedings, Part I. Springer: Cham, Switzerland, 2023; pp. 376–405. [Google Scholar]
- Bernstein, D.J.; Chou, T.; Lange, T.; von Maurich, I.; Misoczki, R.; Niederhagen, R.; Persichetti, E.; Peters, C.; Schwabe, P.; Sendrier, N.; et al. Classic McEliece: Conservative code-based cryptography. NIST Submiss. 2017, 1, 1–25. [Google Scholar]
- Melchor, C.A.; Aragon, N.; Bettaieb, S.; Bidoux, L.; Blazy, O.; Deneuville, J.C.; Gaborit, P.; Persichetti, E.; Zémor, G.; Bos, J.; et al. HQC Supporting Documentation. 2025. Available online: http://pqc-hqc.org/resources.html (accessed on 4 June 2025).
- Campos, F.; Chavez-Saab, J.; Chi-Domínguez, J.-J.; Meyer, M.; Reijnders, K.; Rodríguez-Henríquez, F.; Schwabe, P.; Wiggers, T. Optimizations and Practicality of High-Security CSIDH. Cryptology ePrint Archive, Report 2023/793. 2023. Available online: https://eprint.iacr.org/2023/793 (accessed on 21 April 2025).
- Naor, M.; Reingold, O. Number-theoretic constructions of efficient pseudo-random functions. J. ACM 2004, 51, 231–262. [Google Scholar] [CrossRef]
- Dodis, Y.; Yampolskiy, A. A verifiable random function with short proofs and keys. In Proceedings of the Public Key Cryptography—PKC 2005: 8th International Workshop on Theory and Practice in Public Key Cryptography, Les Diablerets, Switzerland, 23–26 January 2005; Proceedings. Springer: Berlin/Heidelberg, Germany, 2005; pp. 416–431. [Google Scholar]
- Jarecki, S.; Kiayias, A.; Krawczyk, H. Round-optimal password-protected secret sharing and T-PAKE in the password-only model. In Proceedings of the Advances in Cryptology–ASIACRYPT 2014: 20th International Conference on the Theory and Application of Cryptology and Information Security, Kaoshiung, Taiwan, 7–11 December 2014; Proceedings, Part II 20. Springer: Berlin/Heidelberg, Germany, 2014; pp. 233–253. [Google Scholar]
- Miao, P.; Patel, S.; Raykova, M.; Seth, K.; Yung, M. Two-sided malicious security for private intersection-sum with cardinality. In Proceedings of theAdvances in Cryptology—CRYPTO 2020: 40th Annual International Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 2020; Proceedings, Part I. Springer: Cham, Switzerland, 2020; pp. 3–33. [Google Scholar]
- Jarecki, S.; Liu, X. Efficient oblivious pseudorandom function with applications to adaptive OT and secure computation of set intersection. In Proceedings of the Theory of Cryptography: 6th Theory of Cryptography Conference, TCC 2009, San Francisco, CA, USA, 15–17 March 2009; Proceedings 6. Springer: Berlin/Heidelberg, Germany, 2009; pp. 577–594. [Google Scholar]
- Camenisch, J.; Shoup, V. Practical verifiable encryption and decryption of discrete logarithms. In Proceedings of the Advances in Cryptology—CRYPTO 2003: 23rd Annual International Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 2003; Proceedings. Springer: Berlin/Heidelberg, Germany, 2003; pp. 126–144. [Google Scholar]
- Trieu, N.; Yanai, A.; Gao, J. Multiparty Private Set Intersection Cardinality and Its Applications. Available online: https://eprint.iacr.org/2022/735 (accessed on 2 May 2025).
- Ion, M.; Kreuter, B.; Nergiz, E.; Patel, S.; Saxena, S.; Seth, K.; Shanahan, D.; Yung, M. Private Intersection-Sum Protocol with Applications to Attributing Aggregate Ad Conversions. Cryptology ePrint Archive, Report 2017/738. 2017. Available online: https://eprint.iacr.org/2017/738 (accessed on 2 May 2025).
- Kolesnikov, V.; Matania, N.; Pinkas, B.; Rosulek, M.; Trieu, N. Practical multi-party private set intersection from symmetric-key techniques. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 1257–1272. [Google Scholar]
- Chandran, N.; Gupta, D.; Shah, A. Circuit-PSI with linear complexity via relaxed batch OPPRF. Proc. Priv. Enhancing Technol. 2022, 2022, 353–372. [Google Scholar] [CrossRef]
- Qin, S.; Xiao, Y.; Xin, Y.; Gao, B.; Zhang, R. Practical and veritable threshold multi-factor authentication for mobile devices. Comput. J. 2025, 7, 749–762. [Google Scholar] [CrossRef]
- Everspaugh, A.; Chaterjee, R.; Scott, S.; Juels, A.; Ristenpart, T. The pythia {PRF} service. In Proceedings of the 24th USENIX Security Symposium (USENIX Security 15), Washington, DC, USA, 12–14 August 2015; USENIX Association: Berkeley, CA, USA, 2015; pp. 547–562. [Google Scholar]
- Tyagi, N.; Celi, S.; Ristenpart, T.; Sullivan, N.; Tessaro, S.; Wood, C.A. A fast and simple partially oblivious PRF, with applications. In Proceedings of the Advances in Cryptology—EUROCRYPT 2022: 41st Annual International Conference on the Theory and Applications of Cryptographic Techniques, Trondheim, Norway, 30 May–3 June 2022; Proceedings, Part II. Springer: Cham, Switzerland, 2022; pp. 674–705. [Google Scholar]
- Banerjee, A.; Peikert, C. New and improved key-homomorphic pseudorandom functions. In Proceedings of the Advances in Cryptology–CRYPTO 2014: 34th Annual Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 2014; Proceedings, Part I 34. Springer: Berlin/Heidelberg, Germany, 2014; pp. 353–370. [Google Scholar]
- Yang, R.; Au, M.H.; Zhang, Z.; Xu, Q.; Yu, Z.; Whyte, W. Efficient lattice-based zero-knowledge arguments with standard soundness: Construction and applications. In Proceedings of the Advances in Cryptology–CRYPTO 2019: 39th Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2019; Proceedings, Part I 39. Springer: Cham, Switzerland, 2019; pp. 147–175. [Google Scholar]
- Lyubashevsky, V.; Nguyen, N.K.; Plançon, M. Lattice-based zero-knowledge proofs and applications: Shorter, simpler, and more general. In Proceedings of the Advances in Cryptology—CRYPTO 2022: 42nd Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 2022; Proceedings, Part II. Springer: Cham, Switzerland, 2022; pp. 71–101. [Google Scholar]
- Beullens, W.; Seiler, G. LaBRADOR: Compact proofs for R1CS from module-SIS. In Proceedings of the Advances in Cryptology—CRYPTO 2023: 43rd Annual International Cryptology Conference, Santa Barbara, CA, USA, 20–24 August 2023; Proceedings, Part VII. Springer: Cham, Switzerland, 2023; pp. 518–548. [Google Scholar]
- Chillotti, I.; Gama, N.; Georgieva, M.; Izabachène, M. TFHE: Fast fully homomorphic encryption over the torus. J. Cryptol. 2020, 33, 34–91. [Google Scholar] [CrossRef]
- Boneh, D.; Ishai, Y.; Passelègue, A.; Sahai, A.; Wu, D.J. Exploring crypto dark matter: New simple PRF candidates and their applications. In Proceedings of the Theory of Cryptography: 16th International Conference, TCC 2018, Panama City, Panama, 11–14 November 2018; Proceedings, Part II. Springer: Cham, Switzerland, 2018; pp. 699–729. [Google Scholar]
- Chen, H.; Huang, Z.; Laine, K.; Rindal, P. Labeled PSI from fully homomorphic encryption with malicious security. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 1223–1237. [Google Scholar]
- Baum, C.; Damgård, I.; Lyubashevsky, V.; Oechsner, S.; Peikert, C. More efficient commitments from structured lattice assumptions. In Proceedings of the Security and Cryptography for Networks: 11th International Conference, SCN 2018, Amalfi, Italy, 5–7 September 2018; Proceedings. Springer: Cham, Switzerland, 2018; pp. 368–385. [Google Scholar]
- Boneh, D.; Kogan, D.; Woo, K. Oblivious pseudorandom functions from isogenies. In Proceedings of the Advances in Cryptology–ASIACRYPT 2020: 26th International Conference on the Theory and Application of Cryptology and Information Security, Daejeon, Republic of Korea, 7–11 December 2020; Proceedings, Part II 26. Springer: Cham, Switzerland, 2020; pp. 520–550. [Google Scholar]
- Jao, D.; De Feo, L. Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies. In Proceedings of the Post-Quantum Cryptography: 4th International Workshop, PQCrypto 2011, Taipei, Taiwan, 29 November–2 December 2011; Proceedings 4. Springer: Berlin/Heidelberg, Germany, 2011; pp. 19–34. [Google Scholar]
- Basso, A.; Kutas, P.; Merz, S.P.; Petit, C.; Sanso, A. Cryptanalysis of an oblivious PRF from supersingular isogenies. In Proceedings of the Advances in Cryptology—ASIACRYPT 2021: 27th International Conference on the Theory and Application of Cryptology and Information Security, Singapore, 6–12 December 2021; Proceedings, Part IV 27. Springer: Cham, Switzerland, 2021; pp. 160–184. [Google Scholar]
- Damgård, I.B. On the randomness of Legendre and Jacobi sequences. In Proceedings of the Conference on the Theory and Application of Cryptography, Santa Barbara, CA, USA, 21–25 August 1988; Springer: Berlin/Heidelberg, Germany, 1988; pp. 163–172. [Google Scholar]
- Yang, K.; Sarkar, P.; Weng, C.; Wang, X. Quicksilver: Efficient and affordable zero-knowledge proofs for circuits and polynomials over any field. In Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security, Virtual, 15–19 November 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 2986–3001. [Google Scholar]
- Roy, L. SoftSpokenOT: Quieter OT extension from small-field silent VOLE in the minicrypt model. In Proceedings of the Advances in Cryptology—CRYPTO 2022: 42nd Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 2022; Proceedings, Part III. Springer: Cham, Switzerland, 2022; pp. 657–687. [Google Scholar]
- Tso, R.; Okamoto, T.; Okamoto, E. 1-out-of-n oblivious signatures. In Proceedings of the Information Security Practice and Experience: 4th International Conference, ISPEC 2008, Sydney, Australia, 21–23 April 2008; Proceedings 4. Springer: Berlin/Heidelberg, Germany, 2008; pp. 45–55. [Google Scholar]
- Song, C.; Yin, X.; Liu, Y. A practical electronic voting protocol based upon oblivious signature scheme. In Proceedings of the 2008 International Conference on Computational Intelligence and Security, Suzhou, China, 13–17 December 2008; IEEE: Piscataway, NJ, USA, 2008; Volume 1, pp. 381–384. [Google Scholar]
- Tso, R. Two-in-one oblivious signatures secure in the random oracle model. In Proceedings of the Network and System Security: 10th International Conference, NSS 2016, Taipei, Taiwan, 28–30 September 2016; Springer: Cham, Switzerland, 2016; pp. 143–155. [Google Scholar]
- Tso, R. Two-in-one oblivious signatures. Future Gener. Comput. Syst. 2019, 101, 467–475. [Google Scholar] [CrossRef]
- You, J.S.; Liu, Z.Y.; Tso, R.; Tseng, Y.F.; Mambo, M. Quantum-resistant 1-out-of-n oblivious signatures from lattices. In Proceedings of theInformation Security: 25th International Conference, ISC 2022, Bali, Indonesia, 18–20 December 2022; Springer: Cham, Switzerland, 2022; pp. 166–186. [Google Scholar]
- Khutsaeva, A.; Davydov, V.; Bezzateev, S. An Oblivious Signature Scheme Based on Isogenies of Supersingular Elliptic Curves. Probl. Informatsionnoy Bezop. Komp’yuternye Sist. 2023, 57, 116–121. (In Russian) [Google Scholar]
- Zhou, Y.; Liu, S.; Han, S. Generic Construction of 1-out-of-n Oblivious Signatures. IEICE Trans. Inf. Syst. 2022, 105, 1836–1844. [Google Scholar] [CrossRef]
- Tezuka, M.; Tanaka, K. 1-out-of-n Oblivious Signatures: Security Revisited and a Generic Construction with an Efficient Communication Cost. In Proceedings of the Information Security and Cryptology: 26th International Conference, ICISC 2023, Seoul, Republic of Korea, 29 November–1 December 2023; Springer: Cham, Switzerland, 2023; pp. 261–281. [Google Scholar]
- Zahur, S.; Evans, D. Circuit structures for improving efficiency of security and privacy tools. In Proceedings of the 2013 IEEE Symposium on Security and Privacy, San Francisco, CA, USA, 19–22 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 493–507. [Google Scholar]
- Stefanov, E.; Shi, E.; Song, D. Towards Practical Oblivious RAM. arXiv 2011, arXiv:1106.3652. Available online: https://arxiv.org/abs/1106.3652 (accessed on 17 May 2025).
- Stefanov, E.; Dijk, M.v.; Shi, E.; Chan, T.H.H.; Fletcher, C.; Ren, L.; Yu, X.; Devadas, S. Path ORAM: An extremely simple oblivious RAM protocol. J. ACM 2018, 65, 1–26. [Google Scholar] [CrossRef]
- Li, X.; Luo, Y.; Gao, M. BULKOR: Enabling Bulk Loading for Path ORAM. In Proceedings of the2024 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 20–23 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 4258–4276. [Google Scholar]
- Ostrovsky, R.; Shoup, V. Private information storage. In Proceedings of the Twenty-Ninth Annual ACM Symposium on Theory of Computing, El Paso, TX, USA, 4–6 May 1997; Association for Computing Machinery: New York, NY, USA, 1997; pp. 294–303. [Google Scholar]
- Gordon, S.D.; Katz, J.; Kolesnikov, V.; Krell, F.; Malkin, T.; Raykova, M.; Vahlis, Y. Secure two-party computation in sublinear (amortized) time. In Proceedings of the 2012 ACM Conference on Computer and Communications Security, Raleigh, NC, USA, 16–18 October 2012; Association for Computing Machinery: New York, NY, USA, 2012; pp. 513–524. [Google Scholar]
- Heath, D.; Kolesnikov, V.; Ostrovsky, R. Practical Garbled RAM: GRAM with O(log2n) Overhead. Cryptology ePrint Archive, Paper 2021/1519. 2021. Available online: https://eprint.iacr.org/2021/1519 (accessed on 12 July 2025).
- Park, A.; Lin, W.K.; Shi, E. NanoGRAM: Garbled RAM with O˜(logN) Overhead. Cryptology ePrint Archive, Paper 2022/191. 2022. Available online: https://eprint.iacr.org/2022/191 (accessed on 12 July 2025).
- Devadas, S.; Van Dijk, M.; Fletcher, C.W.; Ren, L.; Shi, E.; Wichs, D. Onion ORAM: A constant bandwidth blowup oblivious RAM. In Proceedings of the Theory of Cryptography: 12th Theory of Cryptography Conference, TCC 2015, Warsaw, Poland, 23–25 March 2015; Proceedings, Part I. Springer: Cham, Switzerland, 2015; pp. 145–174. [Google Scholar]
- Chen, H.; Chillotti, I.; Ren, L. Onion ring ORAM: Efficient constant bandwidth oblivious RAM from (leveled) TFHE. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 345–360. [Google Scholar]
- Cong, K.; Das, D.; Nicolas, G.; Park, J. Panacea: Non-Interactive and Stateless Oblivious RAM. In Proceedings of the 2024 IEEE 9th European Symposium on Security and Privacy (EuroS&P), Vienna, Austria, 8–12 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 790–809. [Google Scholar]
- Gagliardoni, T.; Karvelas, N.P.; Katzenbeisser, S. ORAMs in a Quantum World. In Proceedings of the Post-Quantum Cryptography: 8th International Workshop, PQCrypto 2017, Utrecht, The Netherlands, 26–28 June 2017; Springer: Cham, Switzerland, 2017; pp. 303–322. [Google Scholar]
- Dong, C.; Chen, L.; Wen, Z. When private set intersection meets big data: An efficient and scalable protocol. In Proceedings of the 2013 ACM SIGSAC Conference on Computer & Communications Security, Berlin, Germany, 4–8 November 2013; Association for Computing Machinery: New York, NY, USA, 2013; pp. 789–800. [Google Scholar]
- Pinkas, B.; Rosulek, M.; Trieu, N.; Yanai, A. PSI from PaXoS: Fast, malicious private set intersection. In Proceedings of the the Advances in Cryptology–EUROCRYPT 2020: 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 10–14 May 2020; Proceedings, Part II. Springer: Cham, Switzerland, 2020; pp. 739–767. [Google Scholar]
- Boneh, D. Finding smooth integers in short intervals using CRT decoding. In Proceedings of the Thirty-Second Annual ACM Symposium on Theory of Computing, Portland, OR, USA, 21–23 May 2000; Association for Computing Machinery: New York, NY, USA, 2000; pp. 265–272. [Google Scholar]
- Bleichenbacher, D.; Nguyen, P.Q. Noisy polynomial interpolation and noisy Chinese remaindering. In Proceedings of the Advances in Cryptology–EUROCRYPT 2000: International Conference on the Theory and Application of Cryptographic Techniques, Bruges, Belgium, 14–18 May 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 53–69. [Google Scholar]
- Hazay, C. Oblivious polynomial evaluation and secure set-intersection from algebraic PRFs. J. Cryptol. 2018, 31, 537–586. [Google Scholar] [CrossRef]
- Hazay, C.; Lindell, Y. Efficient Oblivious Polynomial Evaluation with Simulation-Based Security. Available online: https://eprint.iacr.org/2009/459 (accessed on 18 July 2025).
- Gajera, H.; Giraud, M.; Gérault, D.; Das, M.L.; Lafourcade, P. Verifiable and private oblivious polynomial evaluation. In Proceedings of the IFIP International Conference on Information Security Theory and Practice: 13th IFIP WG 11.2 International Conference, WISTP 2019, Paris, France, 11–12 December 2019; Springer: Cham, Switzerland, 2019; pp. 49–65. [Google Scholar]
- Izabachène, M.; Nitulescu, A.; de Perthuis, P.; Pointcheval, D. Myope: Malicious security for oblivious polynomial evaluation. In Proceedings of the Security and Cryptography for Networks: 13th International Conference, SCN 2022, Amalfi, Italy, 12–14 September 2022; Springer: Cham, Switzerland, 2022; pp. 663–686. [Google Scholar]
- Mohanty, T.; Srivastava, V.; Mesnager, S.; Debnath, S.K. A constant round quantum secure protocol for oblivious polynomial evaluation. J. Inf. Secur. Appl. 2023, 77, 103560. [Google Scholar] [CrossRef]
- Chang, Y.C.; Lu, C.J. Oblivious polynomial evaluation and oblivious neural learning. In Proceedings of the Advances in Cryptology-ASIACRYPT 2001: 7th International Conference on the Theory and Application of Cryptology and Information Security, Gold Coast, Australia, 9–13 December 2001; Proceedings 7. Springer: Berlin/Heidelberg, Germany, 2001; pp. 369–384. [Google Scholar]
- Cianciullo, L.; Ghodosi, H. Unconditionally secure oblivious polynomial evaluation: A survey and new results. J. Comput. Sci. Technol. 2022, 37, 443–458. [Google Scholar] [CrossRef]
- Baum, C.; Escudero, D.; Pedrouzo-Ulloa, A.; Scholl, P.; Troncoso-Pastoriza, J.R. Efficient protocols for oblivious linear function evaluation from ring-LWE. J. Comput. Secur. 2022, 30, 39–78. [Google Scholar] [CrossRef]
- de Castro, L.; Juvekar, C.; Vaikuntanathan, V. Fast vector oblivious linear evaluation from ring learning with errors. In Proceedings of the 9th Workshop on Encrypted Computing & Applied Homomorphic Cryptography, Seoul, Republic of Korea, 15 November 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 29–41. [Google Scholar]
- Sun, Y.; Liu, H.; Yang, K.; Yu, Y.; Wang, X.; Weng, C. Committed Vector Oblivious Linear Evaluation and Its Applications. Available online: https://eprint.iacr.org/2025/1037 (accessed on 18 July 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).