Abstract
Traceable ring signatures (TRSs) allow a signer to create a signature that maintains anonymity while enabling traceability if needed. It merges the characteristics of traditional ring signatures with the ability to trace signers, making it ideal for applications that demand both confidentiality and accountability. In a TRS scheme, a ring of potential signers generates a signature on a message without disclosing the actual signer’s identity. However, the identity can be traced if the signer uses the same tag for multiple signatures. This paper introduces a novel formal construction of TRS under universally composable (UC) security. We integrate verifiable random functions (VRFs) and zero-knowledge proofs for membership, employing Pedersen commitments. Our signature schemes maintain a logarithmic size while preserving the UC security guarantees. Additionally, we explore the potential to extend the property of one-time anonymity in TRS to K-time anonymity.
1. Introduction
In recent years, the field of traceable ring signatures (TRSs) has garnered significant attention due to its potential in the application of decentralized technologies, such as decentralized identifiers (DIDs) [1]. The functionality of TRS could expose the identities of malicious users while maintaining the anonymity of the other users. Despite the advancements made, there remains a critical gap in the understanding of the formulation under the security of universal composibility (UC) [2]. Existing literature, such as [3,4,5,6,7,8,9,10,11,12,13,14,15,16], predominantly focuses on different algorithms (some of which do not follow the typical security definitions of TRS) or different security models, yet overlooks the possibility of expanding TRS to support UC. This gap is particularly important because protocols that support UC security can operate under more realistic assumptions about the adversary’s capabilities, and UC security ensures that a protocol maintains its security properties even when composed with other protocols. Addressing this gap could improve the adaptability of the TRS scheme. Therefore, this study aims to design a UC functionality of TRS, propose one concrete construction with verifiable random function (VRF) and membership proof, and provide security proofs.
1.1. Background
- From Ring Signatures to Traceable Ring Signatures. Ring signatures have emerged as a significant cryptographic tool for ensuring anonymity while enabling verifiable signatures. Introduced by Rivest, Shamir and Tauman [17], a ring signature allows a member of a group to sign a message on behalf of the entire group without disclosing their identity. The signer remains anonymous as the system does not rely on a trusted manager or issuer; instead, a user can create a signature on behalf of a ring (a group that includes themselves), rendering the signer indistinguishable from the others. Consequently, no individual or group can exclusively control access to a signer’s identity. This feature has facilitated widespread adoption in various contexts, such as electronic voting [18], blockchain technologies, and cryptocurrencies [19,20].
However, the anonymity afforded by traditional ring signatures presents challenges, particularly in scenarios where accountability is paramount. For instance, in cases of misuse or fraudulent activities, such as double voting in e-voting systems, identifying the actual signer while preserving group privacy becomes essential. This necessity for both anonymity and traceability has driven the development of linkable ring signatures (LRSs) and traceable ring signatures (TRSs), variants specifically designed to address these challenges. While achieving different variants, the dominant anonymity is maintained, applicable primarily in standard scenarios, such as a single vote cast in a voting event.
LRS and TRS enhance the functionality of traditional ring signatures by incorporating mechanisms for accountability while preserving user anonymity. LRS, for example [21,22,23,24,25,26,27,28], enables the same signer to produce multiple signatures that can be linked, allowing for the detection of repeated signers across different messages without revealing their identities. This feature enhances tracking, proving advantageous in contexts like digital asset management [29,30,31,32,33]. Conversely, TRS introduces a mechanism that allows anyone in possession of the signatures to identify the signer in instances of misconduct while preserving the general anonymity of the group. This dual functionality renders TRS particularly appealing for applications requiring a balance between user privacy and oversight, such as in regulatory frameworks and secure communications. By integrating these features, TRS significantly broadens the potential applications of this cryptographic construct, paving the way for more robust privacy-preserving systems.
In the existing literature, numerous protocols with similar functionalities do not adhere to the TRS framework. We classify these protocols based on their alignment with the security definitions proposed by Fujisaki and Suzuki [3]. Several works [10,11,12,13,14,15,16] have proposed primitives that do not utilize the models outlined in [3]. These works ultimately achieve accountability by introducing additional mechanisms, such as the property of revokable-iff-linkable [10] and reporting mechanism [13,14], which we consider variants of TRS. In addition, existing research, such as [34,35], has examined different signature schemes within the framework of K-time anonymity as opposed to one-time anonymity. Generally, K-time anonymity stipulates that signers may sign for only K distinct messages associated with each issue (a unique identifier) to conceal their identities. However, this requirement requires more intricate security definitions.
- Significance of Traceability in Decentralized World. The advent of Web 3.0 (or Web3) has garnered public attention for its potential to revolutionize various industries and applications. This paradigm shift from the traditional centralized model (Web 2.0) to a more transparent and user-centric ecosystem is expected to facilitate new opportunities in value exchange, data ownership, and data management. A critical element of Web3 is DID [1], which can represent individuals, groups, or objects. By possessing a DID and its associated private key, users can disclose or withhold their credentials as desired in online interactions. Furthermore, a DID holder can use the private key to sign messages or conduct transactions. Maintaining traceability while ensuring the anonymity of users is a significant challenge in cryptography. Traceability enhances transparency, allowing users to track and verify transactions and interactions on the blockchain, thereby fostering trust and preventing fraud.
By combining TRS with the concept of DID, it may be possible to preserve anonymity while leveraging the decentralized identity features of DID. This integration could enable users to sign messages or transactions anonymously while linking their identity to a DID for verification purposes when necessary.
- VRFs Output Pseudorandom Values with Public Verifiability. Micali, Rabin, and Vadhan [36] introduced the concept of verifiable random functions (VRFs) and formalized their security properties. A VRF generates a random output that is both unpredictable and verifiable, allowing any party to confirm the output without needing access to the secret key used in its production. The significance of VRFs lies in their capacity to provide a reliable source of randomness in decentralized systems.
In studies such as [37,38,39], applications including cryptocurrency mining and randomized consensus mechanisms highlight the critical importance of the integrity of the random output for maintaining fairness and preventing manipulation. Furthermore, research efforts [40,41,42,43] have focused on optimizing the efficiency of VRFs while ensuring the preservation of their security properties. Additionally, [38] addressed VRFs within the framework of universally composable (UC) security, introducing additional security features such as unpredictability under malicious key generation (UMKG). However, the standard security definitions of VRF outlined in [36] do not account for the potential for malicious key generation.
- Ideal Functionalities versus Real-World Protocols in the UC Framework. Universally composable (UC) security [2] formalizes the intuition that a protocol remains secure even when executed concurrently with an arbitrary collection of other protocols. In the UC framework, a clear division is established between a functionality and a protocol. An ideal functionality is an abstract, interactive Turing machine that encapsulates the target task, such as coin tossing, under the assumption of a perfectly trustworthy execution environment. It exposes a well-defined interface to external parties while concealing all internal states from the adversary , thereby capturing the security objectives in their strongest possible form. By contrast, a protocol comprises concrete algorithms implemented by real-world participants. The protocol code specifies local computations, message formats, and timing, and is subject to active attacks by a probabilistic polynomial-time (PPT) adversary . The UC definition requires that, for every , there exists a simulator such that no environment can distinguish an execution of (or ) from an execution of (or ). Intuitively, the functionality serves as the ideal security benchmark, while the protocol must emulate that benchmark even when composed with arbitrary other protocols.
1.2. Literature Review on TRS Schemes and Their Variants
During the development in recent years, the typical existing TRS protocols, such as [3,4,5,6,7,8,9] and other variants, such as [10,11,12,13,14,15,16] do not consider the involvement of UC security. In this subsection, we introduce them and organize the information in Table 1. We denote the size of the ring as n and a security parameter .

Table 1.
Comparison of our TRS scheme with other existing schemes, considering a ring size of n and a security parameter of . Notably, our protocol is the first TRS to achieve UC security.
- Traceable Ring Signature. TRS is a variant of ring signature, providing flexibility on the maintenance of anonymity and accountability. Fujisaki and Suzuki (FS07) [3] proposed the first TRS with size . It formalized the security properties of TRS with correctness and public traceability, and the security definitions including exculpability, anonymity, and tag-linkability. Also, it proved that a traceable ring signature is unforgeable if it is tag-linkable and exculpable ([3], Theorem 2.6). Their scheme is under the DDH assumption and the random oracle model (ROM). In general, the signer’s identity will be disclosed if two signatures are signed for the same tag with different messages. The content of a tag usually includes a ring of signers and a identifier issue.
Since the idea from Fujisaki, many variants of TRS have been proposed, and we introduce some of them. Hu et al. (HL07) [4] introduced a version of TRS that offers forward security. The scheme ensures that even if the signer’s secret key is compromised, the generated signatures remain secure. This scheme is in the size of and is proven secure in the ROM. Fujisaki (Fujisaki11) [5] presented a version of TRS in size that is proven secure under the DDH assumption and employs Type-1 bilinear pairing within the common reference string (CRS) model. In this framework, a trusted setup phase creates a CRS that is available to all parties, which may complicate usage in decentralized settings. A recent work by Thanh Khuc et al. (TSD+25) [9] introduced the first generic construction of TRS with logarithmic signature size that is secure in the plain model. It assumes no trusted setup or idealized components.
For post-quantum resistant TRS, we highlight three recent contributions. Branco et al. (BM19) [6] developed the first code-based TRS scheme utilizing the Fiat–Shamir transformation and the Stern protocol. However, this scheme has some security proof flaws identified in [7]. Feng et al. (FLL+21) [7] introduced a general framework for TRS and provided two concrete, efficient TRS schemes based on lattices and symmetric-key primitives, both proven secure in the quantum random oracle model. Both schemes feature logarithmic signature sizes. Recently, Wei et al. (WLB+23) [8] constructed two TRS schemes based on group actions that can be instantiated using isogenies and lattices. These schemes also maintain a logarithmic signature size and are secure in ROM.
- Existing Ring Signature Schemes with Similarities. Apart from the existing work using the typical security formulation of TRS defined by Fujisaki and Suzuki (FS07) [3], we introduce some existing work which we consider to be variants of TRS from the functional perspective. Mostly, they adopt different security models with the considerations on different basis and applications.
Au et al. (ALS+13) [10] proposed a ID-based linkable and revocable-iff-linked ring signature. The linkable version only considered the linkage between signatures of the same event and same link tag, without considering disclosing the signer’s identity, while the revocable-iff-linked version considered disclosure when the signatures are linked. It proposed a scheme using a Type-2 bilinear pairing and the random oracle model. Since the revocable-iff-linked version was extended from a linkable signature, it does not follow the security definitions of TRS.
Bootle et al. (BCC+15) [11] proposed an improved accountable ring signature with size . The protocol is designed with an algorithm to open the signer’s identity of a specific signature, without considering the content of signature. In their construction, the Pedersen commitment [44] and a variant of membership proof considering ElGamal encryption [45] were adopted.
Zhang et al. (ZLS+19) [12] developed a revocable and linkable ring signature (RLRS) scheme with a size of . This scheme allows a revocation authority to disclose the identity of the real signer within a linkable ring signature context, ensuring both mandatory revocability and linkability. Additionally, the security of the scheme is proven in ROM.
Fraser and Quaglia (FQ21) [13] proposed a report and trace ring signature with the reporting mechanism using ElGamal encryption [45]. Here, in the reporting mechanism, the reporter is one of the ring members who generates a report. After receiving the report, a third-party tracer is able to reveal the identity of the signer being reported. However, the size of a signature is . Bultel et al. (BFQ21) [14] proposed an improvement in efficiency of [13] by introducing a new ElGamal variant based on bilinear pairing under the indistinguishability of a chosen-plaintext attack (IND-CPA).
Scafuro and Zhang (SZ21) [15] proposed a fast, key-oriented, post-quantum resistant scheme. It only requires the classic random oracle model, but it is of signature size , where is the security parameter. They introduced a one-time traceable ring signature, where all security properties hold assuming that a secret key is used at most once. Moreover, it described an approach to publishing “per-topic” keys under one main public key, in order to bootstrap signatures under different events with the same main key.
Kabaleeshwaran et al. (KK24) [16] introduce an efficient RLRS scheme, with security proven in the random oracle model. Compared to ZLS+19 [12], their scheme significantly enhances efficiency, reducing the time complexity of algorithms by a factor of four, while also halving the signature size. Nevertheless, the resultant size remains .
- Beyond One-Time Anonymity. One-time anonymity stipulates that signers are permitted to sign only one message for each identifier to conceal their identity. Several studies, including [3,4,5,6,7,8,9,10,11,12,13,14,15,16], have focused on this aspect of anonymity. However, in certain contexts, allowing signers to sign multiple messages can be more beneficial.
Research such as [34,35] has explored this topic, specifically considering the concept of K-time anonymity, which permits multiple signatures within a specified limit of K. For instance, Au et al. [34] proposed a group signature scheme that emphasizes both K-time anonymity and revocation linked to signatures. This scheme, however, relies on a group manager to oversee the K-time anonymity. Bultel et al. [35] demonstrated how K-time anonymity can be attained in delegation-supported signature schemes, particularly in proxy signatures and sanitizable signatures, which allow a delegate to modify certain components of signed messages. In general, a proxy signature allows a signer to authorize a delegate to sign messages on their behalf. Nonetheless, to the best of the author’s knowledge, there has been no direct study about K-time anonymity within the framework of traceable ring signatures.
1.3. Motivation
In this study, we explore the potential of extending the TRS security model to the UC framework [2], an area that has yet to be thoroughly investigated. Existing TRS protocols, such as those outlined in [3,4,5,6,7,8,9], along with various other variants [10,11,12,13,14,15,16], do not address the incorporation of UC security. Achieving TRS under the UC framework would ensure its compatibility with a wide range of cryptographic protocols. This leads to the central motivation of our investigation: is it feasible to construct a TRS scheme within the UC framework? We affirmatively answer this question and present our findings in this work. In this work, we concentrate on the construction that supports one-time anonymity. We also discuss the possibility of extending the schemes to accommodate K-time anonymity in Section 6.2.
To illustrate the significance of TRS, we consider two distinct scenarios.
- Decentralized Applications. Decentralization among tracers is crucial in certain contexts. The Web3 paradigm emphasizes the significance of decentralized identifiers (DIDs) [1] for enabling data ownership and management. The rapid development of decentralized protocols like blockchain and cryptocurrencies has led to an increased demand for a protocol that satisfies Web3 requirements. Cryptocurrencies like Monero [20,46] employ ring signatures to enhance privacy. However, traditional ring signatures cannot effectively trace abnormal transactions such as double-spending. Typically, third-party tracers are involved in achieving tracing objectives, such as [13,14], but this introduces potential risks, such as information leakage from a corrupted tracer or disruption of tracer availability due to DDoS attacks. Therefore, a scheme would be advantageous for protocols operating without any third parties, mitigating the associated risks and enhancing overall security.
- Publishing votes. In an e-voting scenario with a committee, the goal is to ensure the integrity of the voting process. The committee members form a ring and each member should ideally vote once. Signatures are used to verify the validity of the ballots on a bulletin board. However, if a member is corrupt or malicious, they may vote multiple times and compromise the results. Only achieving linkability is insufficient in this case. It becomes necessary to identify the signer for further actions like investigation or disqualification. Additionally, users may vote inadvertently more than once.
In such cases, the original and duplicate signatures should only be linked if the will expressed in the ballots is the same. It is important to note that in traditional voting, once a ballot is submitted, no changes to the will are allowed. To keep anonymity of the user and responsibility at the same time, a traceable ring signature scheme plays a significant role. The scheme allows a signer to keep her identity hidden while there exist some mechanisms to recover the identity of signers who violate the rules. For example, the existing e-voting application [47] was developed specifically to prevent double voting.
1.4. Our Contributions
We introduce a universally composable (UC) traceable ring signature (TRS) scheme that leverages verifiable random functions (VRFs) and incorporates a proposed related non-interactive zero-knowledge (NIZK) proof. Building on these foundational primitives, we present the ideal functionalities along with their corresponding security proofs. Our contributions can be summarized as follows:
- We propose a security definition for VRF within the UC framework, specifically designed to meet the security requirements of TRS. This definition includes an ideal functionality that captures the properties of uniqueness, provability, and pseudorandomness. We evaluate the security level of this proposed definition in the UC context and demonstrate its realization through the Dodis–Yampolskiy VRF (DY-VRF) [43], complete with a comprehensive security proof.
- We present a novel security definition for TRS within the UC framework. We define and prove the ideal functionality, which encompasses the properties of correctness, public traceability, tag-linkability, exculpability, and anonymity. Additionally, we realize this ideal TRS functionality through the integration of DY-VRF and a NIZK proof, along with a security proof in the UC setting. The size of the signature is .
These two UC primitives are noteworthy and may hold independent interest in the field.
1.5. Technical Overview and Technical Challenges
- Technical Overview. Generally, our proposed traceable ring signature scheme takes advantage of the 1-out-of-n proof proposed by Groth and Kohlweiss [48] as a membership proof for the ring. Moreover, our construction is constructed in a Type-3 bilinear curve with the Dodis–Yampolskiy VRF (DY-VRF) [43].
First, the signer who obtains the system parameter generates the key pair . After the signing algorithm, the signer generates the signature in the form of on , where , R is the ring, issue is a unique identifier, and m is the message. In the signature, is the instance of the zero-knowledge proof including the membership proof. Moreover, Z is the signature in , c is the hash of related information, and are the outputs of DY-VRF.
With sufficient information (including the system parameter param, the tag T and the message m), anyone is able to verify a particular signature . And, with the system parameter param, anyone is able to trace the origin of two signatures and signed with the same tag T, on messages , respectively. The trace algorithm may (1) output Accept if the input message–signature pairs are independent; (2) output Reject if either one of the signature fails to pass the verification algorithm; (3) output a key if ; and (4) output Linked if .
- Technical Challenges. The primary technical challenge of this research lies in the formal security functionalities and the proof of the proposed schemes.
In order to achieve UC security of DY-VRF and our TRS scheme, we first formalized the UC ideal functionalities. Next, we proceed to prove that our protocol achieves UC security based on the first step. The aim of a UC-security proof is to establish indistinguishability between the real world and the ideal world scenarios, rendering the requirement for the adversary impracticable, as it fails to simulate the dynamics of the real world accurately. To overcome this challenge, alternative strategies need to be employed in the UC-security proof. These strategies typically involve constructing simulations that capture the desired security properties while maintaining indistinguishability between the real and ideal worlds. By carefully designing and analyzing these simulations, it becomes possible to establish UC-security guarantees for the proposed schemes.
In this work, we utilize a membership proof [48] to maintain a signature size of . This proof achieves perfect -special soundness and perfect special honest verifier zero-knowledge (SHVZK), provided that the commitment scheme is both perfectly binding and hiding, with . However, the standard construction of the membership proof in [48] only verifies the possession of the secret key corresponding to one of the public keys in the ring. To prove membership while also establishing relationships between values in the signature tuple, a specialized design is necessary to satisfy both requirements. In general, we leverage the binding property to create a tailored approach to extend the proof of the relationship from possession. The additional values introduced in the proof will not reveal any extra information through potential calculations.
1.6. Organization
In this work, we first introduce the mathematical background in Section 2. We then recall the security requirements of VRF, propose our UC functionality of VRF, and present the realization with DY-VRF in Section 3, followed with security proofs. Then, we recall the security requirements of TRS, and propose our new UC functionality of TRS followed with security proof in Section 4. And, we present the realization and proof of TRS in UC, and the formulation of the zero-knowledge proof in Section 5. Finally, we present the discussion in Section 6. We present a roadmap of this work in Figure 1.
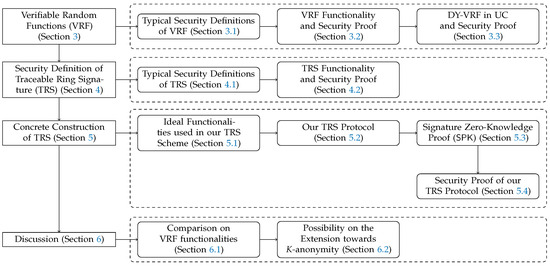
Figure 1.
Roadmap of this work. It is not exhaustive.
2. Preliminaries
2.1. Bilinear Pairing
According to the classification by Galbraith et al. [49], there are two generalized forms of pairings used in cryptographic literature: and , where , , are cyclic groups of prime order p. These pairings are further categorized into three basic types based on different instantiations.
- Type-1 pairing: In the form of ;
- Type-2 pairing: In the form of , but there is an efficiently computable homomorphism ;
- Type-3 pairing: In the form of , and there are no efficiently computable homomorphisms between and ,
In this work, we adopt Type-3 pairing, with the following details described below.
- Type-3 pairing. Consider , where , , are cyclic groups of prime order p. Assuming , and , the bilinear pairing function follows the properties (1) bilinearity: ; (2) non-degeneracy: ; (3) efficiency: is efficiently computable.
2.2. Security Assumptions
Definition 1 (Discrete logarithm Assumption (DLOG)).
If an algorithm runs in time at most and runs with a negligible probability such that
it -breaks the DLOG assumption. The DLOG assumption is -secure if there are no algorithm -solutions to the DLOG problem.
Definition 2
(q-co-Decisional Bilinear Diffie–Hellman Inversion Assumption (q-co-DBDHI) [50]). An algorithm -breaks the q-co-DBDHI assumption if runs with a negligible probability and in time at most such that
It is a variant of q-DBDHI assumption [50], which considers a Type-3 bilinear curve.
2.3. Homomorphic Commitment Scheme
A non-interactive commitment scheme (CS) consists of two polynomial-time algorithms , with specified a message space , a randomness space and a commitment space , defined below.
- : On input a security parameter , the setup algorithm outputs a commitment key ck.
- : On input of a message and a randomness , the commitment algorithm outputs a commitment , such that .
To open a commitment, one reveals m and r allowing anyone to verify that is indeed a commitment to m. Moreover, it achieves the homomorphic property such that
And, we require that the scheme is hiding and binding.
- Hiding. The hiding property ensures that the commitment itself does not reveal any information about the committed value. The adversary should not be able to guess the value or gain any partial knowledge about it from the commitment.
Definition 3
(Hiding). For all PPT stateful adversaries , the commitment scheme achieves the hiding property, and given a negligible function , such that
- Binding. The binding property ensures that once a commitment is made, the committer cannot change the value they committed to. They cannot open the commitment with a different value from the one they originally committed to.
Definition 4
(Binding). For all PPT stateful adversaries , the commitment scheme achieves binding property, and given a negligible function , such that
In this work, we adopt the typical Pedersen Commitment [44] schemes for the membership proof in [48], which achieves the homomorphic propery. We recall the definition below.
Definition 5
(Pedersen Commitment [44], ). Pedersen commitment is a homomorphic commitment scheme which consists of the algorithms below.
- : It constructs a cyclic group with prime order p and samples generators and . It outputs the commitment key .
- : The commit algorithm intakes the message and the randomness . It outputs the commitment .
2.4. Non-Interactive Zero-Knowledge (NIZK) Proofs and Sigma-Protocols
The NIZK for a relation is a tuple of PPT algorithms . The language is defined as , where is a statement, and w is the witness. The algorithms of NIZK are defined below.
- : On input of the security parameter , the setup algorithm returns a common reference string (CRS) .
- : On input of the CRS , the statement and the witness w, the prover algorithm outputs a proof .
- : On input of the CRS , the statement and the proof , the verification algorithm outputs 1 if is valid, and 0 otherwise.
The proof system should satisfy perfect completeness such that a prover with a witness w for can convince the verifier of this fact. Moreover, it should satisfy computational soundness and computational zero-knowledgeness, such that the following definitions stand.
Definition 6
(Perfect Completeness). For , a NIZK scheme achieves perfect completeness, such that , where .
Definition 7
(Computational Soundness). For any PPT adversary , NIZK achieves computational soundness, and given a negligible function , such that
Before we define the property of computational zero-knowledgeness, we first define two PPT algorithms for simulation below.
- 4.
- : It outputs a simulated CRS and a simulation trapdoor .
- 5.
- : It produces a simulated proof , without knowing the witness.
Moreover, the oracle is defined as: First, it returns ⊥ if , and continues otherwise. Then, it runs and receives and , where . Finally, it returns where b is a random bit.
Definition 8
(Computational Zero-Knowledgeness). For any adversary , NIZK achieves computational zero-knowledgeness, and given a negligible function , such that
- Sigma-protocols. A -protocol is a special type of three-move interactive proof system that allows a prover to convince a verifier that a statement is true. The prover sends an initial message to the verifier, the verifier picks a random public coin challenge , and the prover responds to the challenge. Finally, the verifier checks the transcript of the interaction and decides whether the proof should be accepted or rejected.
We will, in our instantiation, use NIZK proofs in the random oracle model obtained by applying the Fiat–Shamir transformation [51] to interactive -protocols. A -protocol is developed for a relation with respect to a tuple (.Setup, .Prove, .Verify), which is defined below.
- : On input of the security parameter , it outputs a common reference string crs.
- : On input of the reference string crs, a statement and a witness w, it generates an initial message .
- on input of the reference string crs, a statement , an initial message , a random challenge , and a response , it verifies the proof and outputs either 1 for acceptance or 0 for rejection.
In addition to completeness, we require -protocols to possess two key properties: Special Honest Verifier Zero-Knowledge (SHVZK) and n-Special Soundness. [48]:
- SHVZK: Given any statement and any verifier challenge , it is possible to simulate a transcript of the protocol.
- n-Special Soundness: For any statement , we can extract w, such that , from n accepting transcripts for where the challenges are distinct.
2.5. Membership Proof
Groth and Kohlweiss [48] proposed a zero-knowledge proof called membership proof (or one-out-of-many proof). It is an efficient logarithmic-size zero-knowledge proof for a list of commitments having at least one commitment that opens to 0. Since it is not required for the prover to know openings of the other commitments, it is instantiated as a variant of the ring signature. We recall the required mathematical background and the sigma-protocol for the membership proof in Appendix A.
3. UC-Security on Verifiable Random Function
Micali, Rabin and Vadhan [36] proposed the notion of verifiable random function (VRF), and formalized the security properties. In general, VRF is a pseudorandom function with non-interactive proof of correctness of its output. In this section, we first recall the security definitions of VRF in Section 3.1. We then propose our UC model on VRF and the realization of Dodis–Yampolskiy’s VRF (DY-VRF) [43] in Section 3.2 and Section 3.3, followed with security proofs.
3.1. Typical Definitions of Verifiable Random Function
The interface of VRF defined in [36] is recalled below.
Definition 9
(Verifiable Random Function [36]). The verifiable random function is defined with the interface such that
- 1.
- : With the security parameter λ, it generates a list of system parameters param.
- 2.
- : On input of the system parameters param, it generates a key pair .
- 3.
- : On input, a signing key vsk and a value , it outputs a value and a proof W. Denote and as polynomial bounded and efficiently computable functions in λ.
- 4.
- : On input a signing key vsk, a value α, a value Q, and a proof W, it outputs a bit .
Next, we recall that VRF follows properties including uniqueness, provability, and pseudorandomness from [36,43].
- Uniqueness. The property of uniqueness provides only one valid proof for each input.
Definition 10
(Uniqueness). For all and , the VRF scheme achieves the property of uniqueness, if , and , for any arbitrary value and any arbitrary proof such that and , it holds that
where is a negligible function.
- Provability. The property of provability ensures that outputs and proofs generated from consistent inputs will verify each other.
Definition 11
(Provability). For all and , the VRF scheme achieves the property of provability, if , and , it holds that
where is a negligible function.
- Pseudorandomness. The property of residual pseudorandomness ensures that the adversary cannot distinguish between outputs and random values.
Definition 12
(Pseudorandomness). We say that a VRF achieves the property of pseudorandomness if, for every PPT adversary , it holds that has a negligible advantage in the following experiment :
- 1.
- Generate .
- 2.
- Generate .
- 3.
- The experiment provides and to . The adversary is allowed to run the oracle for at most times (when the first input is ), where is the evaluation oracle with respect to .
- 4.
- outputs . The experiment generates and .
- 5.
- The experiment samples and provides to .
- 6.
- outputs a guess . The experiment outputs 1 if , , and α was not queried to by . It outputs 0 otherwise.
The probability of winning the game is in relation to its advantage as:
3.2. Security Model of VRF in the UC Framework
In this subsection, we present our version of UC framework of VRF in Functionality 1. It follows the standard VRF security definition in [43], as recalled above. Our definition of the UC framework for VRF simultaneously captures the properties of uniqueness and provability. We will subsequently demonstrate that the ideal functionality is equivalent to satisfying the security model of pseudorandomness, as stated in Theorem 1. We assume that this ideal functionality operates under fixed system parameters, thereby streamlining the VRF.Setup functionality interface. This approach eliminates the need for repetitive checks on the rationality of system parameters in subsequent interfaces, enhancing the overall efficiency.
Functionality 1 (The Verifiable Random Function Functionality ). The functionality is parameterized with a security parameter λ and a tuple of system parameter param.
|
Theorem 1.
If an arbitrary protocol can realize our , then it is secure in the pseudorandomness property of a verifiable random function.
Proof.
We first assume that does not satisfy the pseudorandomness property. Subsequently, we construct an environment such that for all simulators , it can distinguish the interaction with from the interaction with the ideal world adversary and .
- Pseudorandomness. If lacks pseudorandomness, a successful distinguisher D exists, which can break the pseudorandomness property of , with a non-negligible advantage. The distinguisher D can be viewed as a signer within . At first, invokes a party with and gives the returned verification key to D. Subsequently, relays all messages communicated between the distinguisher D and the parties . The distinguisher D is also allowed to call the evaluation oracle for at most times. With calls from D with the value , activates with . Next, if obtains a valid response from , samples and returns to D where . Finally, D returns as the guess of the random coin b chosen by . Here, returns .
Considering that D is a successful distinguisher for in the real world, D will then guess the coin b with a non-negligible advantage. However, in the ideal world, no matter how the simulator is implemented, we observe that the bit b remains secure in , and the ideal functionality does not communicate any information related to b to . It follows that the coins b are independent of D and , and even an unbounded D cannot guess such b with probability better than 1/2. It follows that there is a distinguisher between the real and the ideal worlds.
It is proven that holds the property of pseudorandomness, which contradicts the assumption. □
Remark 1.
The formulation of the UC functionality for VRF in Functionality 1 may hold independent interest. It is important to note that in this functionality we do not allow the adversary to generate any malicious keys. This limitation could be viewed as a weaker version of the UC functionality when considering a standalone VRF scheme. However, it aligns well with the security requirements of TRS. We will discuss this aspect in Section 6.1.
3.3. Realizing with Dodis-Yampolskiy VRF (DY-VRF)
In this work, we utilize the Dodis-Yampolskiy VRF (DY-VRF) within our TRS scheme. Dodis and Yampolskiy introduced this variant of VRF in [43], which operates on groups equipped with bilinear maps and is based on the q-DBDHI assumption [50]. The DY-VRF has been proven to achieve the properties of uniqueness, provability, and pseudorandomness. In this subsection, we revisit the construction of DY-VRF as detailed in Protocol 1 and demonstrate that it securely realizes the ideal functionality in Theorem 2.
Protocol 1 (Dodis-Yampolskiy VRF [43], ).
|
Theorem 2.
Protocol 1 () securely realizes under the q-co-DBDHI assumption.
Proof.
We prove that an ideal simulator can be constructed for any real-world adversary . It is indistinguishable between the ideal execution with and and the real execution with for all environments .
We build a black-box simulation of with simulator , relaying all communication between the simulated and the environment and acting on behalf of the honest parties.
Setup. We first describe the setup of the simulator . receives the q-co-DBDHI tuple from the experiment, where and for , and some unknown . Note that , and . Moreover, it samples distinct values such that the sets and have no mutual values. To simulate the items related to the outputs, it defines:
- for some coefficients ,
- for some coefficients .
However, may be calculated. For each user in , the simulator can set , for a value of issue different from . Note that we do not know the exact value of y since is a secret. However, may calculate from using the approach of [43] with the above polynomials.
For each , is able to calculate the required values during the simulation. First, may compute and . With the above settings, is able to compute . The simulator then calculates instances of the following items using for :
- ,
- , and
- .
Simulation. We describe a simulator that operates in the following manner.
- Upon receiving a message from , a new value is randomly selected. inserts in the internal registry of keys, where . In the case that the key exists already, returns fail and terminates. Otherwise, it returns to .
- Upon receiving a message from , retrieves the verification key vvk of and checks if has been queried before. If has been queried before, the value Q that corresponds to in the Table for is recovered. If has not been queried before, sets and . Subsequently, the tuple has been stored for future reference. Finally, returns to .
- Upon receiving from , check if the record exists to obtain a bit b. We set when the record exists; otherwise, . It returns to .
This gives a full description of the ideal-model simulator. Note that in the black-box simulation, we use fake values (the value of ), we claim that the differences are undetectable for the environment . This is proven through a sequence of games transforming an execution in the ideal-model scenario into one which is equal to the one of the actual protocol.
- Experiment describes the original attack of on the ideal-model simulation (including the black-box simulation of ).
- In , the simulator changes the computation of Q and W to and , where . Because of the q-co-DBDHI assumption, ’s output behavior will not change with a non-negligible probability when facing instead of .
All the steps in the final game now are exactly as in an attack on the real protocol with adversary , with the restriction that only queries could be made. Therefore, the environment’s output in the ideal-model simulation () and the real-world execution () are indistinguishable. □
4. Traceable Ring Signature and Its UC Functionality
In this section, we first recall the definition and security model for TRS in Section 4.1. Our design of the UC functionality of TRS is presented in Section 4.2.
4.1. Definitions
Fujisaki and Suzuki [3] introduced the concept of TRS and formalized its security properties. In this section, we will revisit the formal definitions established in their work, following the framework refined by Thanh Khuc et al. [9].
Definition 13
(Traceable Ring signature ). The traceable ring signature is defined with the interface such that
- 1.
- →: With the security parameter λ, it generates a list of system parameters param.
- 2.
- : On input of the system parameter param, it generates a key pair .
- 3.
- : On input a signing key sk, a tag and a message , it generates a signature σ.
- 4.
- : On input a tag , a signature σ and a message , it outputs a bit .
- 5.
- : On input a tag , and any message-signature pairs and , it outputs .
We first recall that TRS follows properties including correctness and public traceability.
- Correctness. Correctness ensures that a signature generated by honest users will be accepted by the verification algorithm with an overwhelming probability.
Definition 14
(Correctness). For all and all , all , all , the TRS scheme is correct, if , , and for some issue, , and it holds that
where is a negligible function.
- Public Traceability. The property of public traceability ensures that anyone can examine any two message-signature pairs along with their associated tags using the Trace algorithm. This algorithm allows for two signatures to be linked if they are signed by the same origin on the same message and bear the same tag. Conversely, the signatures can be traced if they originate from the same signer on distinct messages while still sharing the same tag.
The motivation of this property is to establish a message–tag–bound form of linkability that achieves a balance between anonymity and accountability. If the signer reuses only the tag, the resulting signatures become publicly linkable. Conversely, if the signer reuses both the tag and the message, the signer’s public key becomes publicly traceable. This straightforward deterrent discourages the malicious practice of issuing contradictory statements under anonymity, since equivocation becomes traceable. Furthermore, this property does not require a trusted tracing authority, a secret key, or an interactive protocol, thereby reducing the requisite trust assumptions and operational overhead relative to traditional group signature opening mechanisms.
Definition 15
(Public Traceability). For all , all , all , all issue, and all , the TRS scheme is public traceable, if , , and , and , it holds that:
- 1.
- If and ,
- 2.
- Otherwise (if at least one of the input message–signature pairs cannot pass TRS.Verify),
with overwhelming probability.
Next, we will revisit the formal definitions of the security requirements for TRS, which include exculpability, anonymity, and tag-traceability.
- Exculpability. The property of exculpability ensures that an honest ring user cannot be held accountable for signing the same tag more than once. Specifically, it guarantees that an adversary cannot generate a signature that would reveal the identity of the target signer when combined with a signature produced by that user using a publicly traceable algorithm. In the exculpability experiment, all user keys are generated internally within the experiment. Subsequently, the adversary may acquire knowledge of certain users’ secrets. However, the adversary is explicitly prohibited from adding their own key to the user’s ring.
Definition 16
(Exculpability). For every PPT adversary , we say that a TRS is exculpable if is a negligible advantage in the following experiment :
- 1.
- Generate .
- 2.
- For all , by using random coins , generate . The experiment sets .
- 3.
- A public key is chosen and provided to the experiment by the adversary.
- 4.
- Except for a random coin used to generate the pair of keys , the experiment provides all other random coins to the adversary .
- 5.
- is able to access the signing oracle with respect to param and sk to query signing any , where . Denote the output signature by .
- 6.
- In the end, outputs two pairs of message–signature pairs and , where and .
- 7.
- The experiment outputs 1 if the following conditions hold:
- (a)
- and ,
- (b)
- .
- (c)
- At least of and are not linked to any in the query / answer list between and .
Otherwise, the experiment outputs 0.
The probability of winning the game is in relation to its advantage as:
- Anonymity. The property of anonymity guarantees that a signer’s identity remains indistinguishable from that of any potential ring member, provided that the signer does not sign two different messages associated with the same tag. Moreover, signatures generated under distinct tags are unlinkable, ensuring that it is impossible to ascertain whether they were produced by the same signer. In the anonymity experiment, the adversary is constrained to querying the signing oracle for each tag T only once per message.
Definition 17
(Anonymity). For every PPT adversary , we say that a TRS is anonymous if is a negligible advantage in the following experiment :
- 1.
- Generate .
- 2.
- For all , generate .
- 3.
- Sample .
- 4.
- A public key is chosen and provided to the experiment by the adversary.
- 5.
- The experiment provides and to , and is able to append new keys to the global public key list R. The experiment requires both and must be collected in R. Moreover, can access three signing oracles , and , where
- is challenge signing oracle with respect to for signing . The experiment requires if and are two queries of to the challenge signing oracle then .
- (resp. ) is the signing oracle with respect to (resp. ) for signing . The experiment requires if ) is a query of to and is a query of to or then .
- 6.
- outputs a guess . The experiment outputs 1 if . Otherwise, it outputs 0.
The probability of winning the game is in relation to its advantage as:
- Tag-linkability. The property of tag-linkability guarantees that every pair of signatures generated by the same signer for the same tag is linked. If any two signatures are not linked, the maximum number of signatures associated with the same tag cannot exceed the total number of members in that tag. In the tag-linkability experiment, all user keys are generated internally within the experiment. Subsequently, the adversary may acquire knowledge of certain users’ secrets. However, the adversary is explicitly prohibited from adding their own key to the user’s ring.
Definition 18
(Tag-linkability). For every PPT adversary , we say that a TRS is tag-linkable if is a negligible advantage in the following experiment :
- 1.
- Generate .
- 2.
- For all , generate by using random coins . The experiment sets .
- 3.
- To generate the keys to the adversary , the experiment provides all random coins for all .
- 4.
- Adversary outputs and message-signature pairs, .
- 5.
- The experiment outputs 1 if the following conditions hold:
- (a)
- , .
- (b)
- , s.t. .
Otherwise, the experiment outputs 0.
The probability of winning the game is in relation to its advantage as:
If a traceable ring signature is tag-linkable and exculpable, it is unforgeable ([3], Theorem 2.6).
4.2. Security Model of TRS in the UC Framework
Considering the UC security model, we present the functionality of TRS in Functionality 2. We first introduce our definition of TRS within the UC framework, which captures both the properties of correctness and public traceability. Subsequently, we will prove that is equivalent to satisfy the security requirements of exculpability, anonymity, and tag-linkability, as stated in Theorem 3. We assume that this ideal functionality operates under fixed system parameters, which simplifies the TRS.Setup functionality interface.
In contrast to conventional ring signatures and linkable ring signatures, the TRS model does not adhere to the typical unforgeability requirement [3]. Instead, the security models of exculpability and tag-linkability inherently imply unforgeability, as shown in ([3], Theorem 2.6). Based on the security experiments outlined in Section 4.1, an adversary aiming to compromise exculpability and tag-linkability would need to produce two and message–signature pairs, respectively. All signatures generated by the adversary must successfully pass the signature verification algorithm and satisfy additional criteria to undermine the security framework. Thus, the signature verification component addresses only a subset of the security requirements associated with exculpability and tag-linkability, as indicated in Step 1(c) of the signature verification component of .
Functionality 2 (The ideal traceable ring signature functionality ).
The functionality is parameterized with a tuple of system parameter param. It interacts with n parties (the signatories), and a simulator . Moreover, it initializes an empty set . Denote , where is the verification key of and an arbitrary issue.
|
Theorem 3.
If an arbitrary protocol can realize our , then it is secure in the tag-linkability, exculpability and anonymity models of traceable ring signatures.
Proof.
We first assume that does not satisfy any one of the traceable ring signature security models. Subsequently, we construct an environment such that for all simulators , it can distinguish the interaction with from the interaction with the ideal world adversary and .
- Tag-linkability. First, if lacks tag-linkability, a successful forger exists, which can break the tag-linkability property of , with a non-negligible advantage. The environment internally runs an instance of . invokes parties , where , with , and gives the returned verification key to . When receives a signature query from the forger , where , activates each to obtain the signature results and forwards it to . uses to count the number of received from the party . When the simulated outputs forged message–signature pairs, runs , where . uses to count the number of 1’s from the verification process. If finds that it returns 0, it returns 1 otherwise. Moreover, runs , where and . uses to count the number of Accept received from the party . If finds that it returns 0 otherwise it returns 1.
In the real world, because is a successful forger, with a non-negligible probability, will observe , , and . It follows that when operates in the real world, it returns 1 with a non-negligible probability.
In the ideal world, when a verifier receives in the verification stage and in the trace stage, he will forward such messages to , and will check if the message–signature pair is a forgery using the information he possesses. Based on the definition of , is equal to the number of records with . By the definition of the signature generation stage, it is equal to the total number of messages obtained from the party . Hence, we have , and always returns 0 in the ideal world for the verification stage. Therefore, there is a distinguisher between the real and the ideal world for any implementation of .
- Exculpability. Second, if lacks exculpability, a successful forger exists, which can break the exculpability property of , with a non-negligible advantage. The environment internally runs an instance of . invokes parties , where , with , and gives the returned verification key to . The forger is allowed to call signature queries , where , for multiple times for a fixed verification key selected by itself. When receives a signature query from the forger , activates the party who owns to obtain the signature results and forwards it to . uses to count the number of received from the party . When the simulated outputs two message-signature pairs and , runs for . uses to count the number of 1’s from the verification process. If finds that it returns 0, continues otherwise. Next, runs , should be traced from the trace stage and continues, it returns 0 otherwise. Finally, runs and , where j are the indices of the total number of signature queries, except queries related to and . uses to count the number of Linked from the trace process. If finds that it returns 0, otherwise returns 1.
In the real world, because is a successful forger, with a non-negligible probability, will observe that . And, and could be verified successfully, i.e., . Moreover, will be traced from the trace stage, and at least one of the message-signature pairs from is not linked to any other message-signature pair in the query list, i.e., . It follows that when operates in the real world, it returns 1 with a non-negligible probability.
In the ideal world, when a verifier receives for in the verification stage, he will forward such messages to , and will check if the message-signature pair is a forgery using the information he possesses. Based on the definition of , is equal to the count of records with and . Hence, we have , and always returns 0 in the ideal world for the verification stage. Therefore, there is a distinguisher between the real and the ideal world for any implementation of .
- Anonymity. Third, if lacks anonymity, a successful distinguisher D exists, which can break the anonymity property of , with a non-negligible advantage. The distinguisher D can be viewed as a signer within . At first, invokes the parties and with , and gives the returned verification key and to D. Subsequently, relays all messages communicated between the distinguisher D and the parties and . The distinguisher D is also allowed to call additional key generation queries as other parties , and to append new keys to the ring R, thus generating new tags. With calls from D, activates and with and , where b is a random bit chosen by , and . Next, if obtains two valid responses from and , respectively, returns the two message–signature pairs and to D. Finally, D returns as the guess of the random coin b chosen by . Here, returns .
Consider that D is a successful distinguisher for in the real world, D will guess the coin b with a non-negligible advantage. However, in the ideal world, no matter how the simulator is implemented, we observe that the bit b remains secure in , and the ideal functionality does not communicate any information related to b to . It follows that the coins b are independent of D and , and even an unbounded D cannot guess such b with probability better than 1/2. It follows that there is a distinguisher between the real and the ideal worlds.
It is proven that holds the security of tag-linkability, exculpability and anonymity, which contradicts the assumption. □
5. A UC-Secure TRS Construction
In this section, we present the construction of our UC-secure TRS. We first define the functionalities of the building blocks involved in Section 5.1. Then, we present the construction of TRS in Section 5.2. Next, we propose and prove the actual protocol of the signature zero-knowledge (SPK) proof as the realization of the NIZK functionality in Section 5.3 as a building block of our TRS scheme. Finally, we present the security proof of our TRS scheme in Section 5.4.
5.1. Ideal Functionalities
- The Ideal UC Zero-Knowledge Functionality for a binary relation . We provide the ideal zero-knowledge functionality in Functionality 3. Denote as the statement, w as the witness, as the proof, and as an empty string. We follow the ideal functionality ([52], Section 5.2), which is defined by . Note that any zero-knowledge proof of knowledge fulfills the functionality [52], and the Fiat–Shamir paradigm [51] could be applied to switch the Sigma protocols to become non-interactive zero-knowledge (NIZK) in the random oracle model. As in [52], denote as the information leakage function.
Functionality 3 (The Ideal UC Zero-Knowledge Functionality for a binary relation ).
|
- Ideal UC NIZK Functionality for relation . We provide the ideal NIZK functionality in Functionality 4 following ([53], Figure 3). Denote at the statement, w at the witness, at the proof. We further recall that [54] proved that simulation-extractability is necessary for UC security of NIZK.
Functionality 4 (The Ideal UC NIZK Functionality for a NP relation ).
|
- Ideal UC Commitment Functionality . We provide a simple ideal commitment functionality in Functionality 5. The functionality is different from the multi-party version such as in [55], in which the functionality acts as a platform to transfer message. For the version of Functionality 5, it generally returns and records the commitments to the same party. Furthermore, it is evident that the Pedersen commitment scheme defined in Definition 5 securely realizes under the discrete logarithm (DLOG) assumption.
Functionality 5 (The Ideal UC Commitment Functionality ).
|
5.2. Construction of TRS
In this subsection, we present the concrete construction of TRS in Protocol 2. In our construction, the tag is defined as , where R is the ring and is the unique identifier in . The ring consists of n public keys such that , where , , and secret keys and for . Moreover, represents the index number of the public key of the signer in the ring R. For simplicity, we omit the session parameter sid. The formal proof will be presented in Theorem 5 in Section 5.4, after we present and prove the zero-knowledge proof building block in Section 5.3.
Our construction incorporates two values, and , as the public key vk of a ring member, while the membership proof in [48] considers only a single value. To address this issue, we broaden the scope of the membership proof by considering both the secret keys and the mathematical relationships among the elements in the signature tuple.
Protocol 2 (, securely computing with , and ).
: It calls and receives , where , and = are three cyclic groups of order p based on a bilinear-based elliptic curve with the bilinear pairing , and and are random generators. Moreover, it defines an additional generator , and hash functions . It outputs .: The key generation algorithm generates the key pair using the key generation algorithm. It
: The signing algorithm generates a signature σ on a message m and the tag . In this algorithm, we denote that the public key of a signer by with index ℓ, where , such that is the ring of the signers. Moreover, is a unique identifier. The signer
: The verify algorithm verifies the input signature tuple on . It verifies π by calling and checks if . It outputs 1 if the all verification passes, 0 otherwise.: It intakes the input of two signatures and , for , where and . It computes the following items.
|
5.3. Realizing
In this subsection, we present a building block of our TRS scheme, which is the zero-knowledge proof in Protocol 3. After that, we will present the formal proof in Theorem 4. For the sake of clarity, we omit the session parameter sid.
This construction primarily follows the membership proof outlined in [48], with some additional elements tailored to fit . Without loss of generality, we assume that , as per [48], which ensures that the size of the signature is . In Protocol 3, we consider the relation defined in Protocol 2.
We express i and ℓ as and in binary form, and define the Kronecker delta as , where when and otherwise (see Definition A1). The rationale behind the this proof is to reformulate the values to be proven as and . These expressions serve as a commitment to 0.
Before the proof, the prover obtains the ring such that , where and are Pedersen commitments.
In the sigma-protocols for , the prover reveals values of the form and . Let , , and . For each i, we have the product and . These products are polynomials of the form:
In this work, we present our proof in a non-interactive approach. In the proof, the prover will send commitments and that are used to cancel out the low-order coefficients corresponding to . Meanwhile, the high-order coefficient for ensures that the commitment and can be opened to 0. At the end, the verifier could check that
are commitments to 0 in a non-interactive approach. Therefore, according to the Schwartz–Zippel Lemma (see Definition A3), this has a negligible probability of being true unless and are indeed commitments to 0.
Moreover, we prove the mathematical relationship between values in the signature. This scheme randomly chooses additional parameters . It introduces the commitments with randomness involving and . This approach maintains -special soundness regarding the secret values of x and .
Protocol 3 (, securely computing on the relation with ).
: It parses and . It computes the following items:
: It parses and .
|
Theorem 4.
Protocol 3 () securely realizes in the -hybrid world with the random oracle model for a relation . That is, achieves completeness, special honest verifier zero-knowledge (SHVZK), and -special soundness, if the commitment scheme is (perfectly) hiding and binding, under the discrete logarithm (DLOG) assumption.
Proof.
In this proof, we demonstrate that the protocol in Protocol 3 achieves three key properties: completeness, special honest verifier zero-knowledge (SHVZK), and -special soundness. Since Protocol 3 mainly follows the idea of the membership proof with extra items, our approach aims to follow the proof from ([48], Theorem 3) and we present full proof below.
- Completeness. It is observed that and are polynomials in the challenge e of the form and , where is a Kronecker delta such that when and otherwise 0 (see Definition A1). If and are commitments to 0, we get and is a commitment to 0, while the other commitments and get raised to polynomials of degree in e as and in the verification equation. Moreover, it is observed thatandWith this in mind, straightforward verification shows that the protocol is perfectly complete.
- Special Honest Verifier Zero-Knowledge (SHVZK). Given the challenge , it starts by choosing the elements of the response uniformly at random as . It then chooses as random commitments to 0. It computes , , , for all . Moreover, it computeswhere , , , and . It returns the simulated transcript , , , .
We will now demonstrate that an adversary capable of distinguishing the simulation from a real argument with an advantage of can be transformed into an adversary that compromises the hiding property of the commitment scheme with an advantage of . First, we observe that in both real and simulated proofs, are uniformly random in . And, the verification equations uniquely determine conditioned on , both in real and simulated proofs. The adversary’s advantage of must therefore stem from its ability to differentiate between real and simulated commitments . A standard hybrid argument provides us with an advantage of in breaking the hiding property of the commitment scheme.
- -Special Soundness. We adopt the approach from ([48], Theorem 3) by illustrating how to transform an adversary with a probability of breaking -special soundness into another adversary with approximately the same runtime, which maintains a probability of violating the binding property of the commitment scheme.
With the original challenge , the extractor rewinds on to , and distinct accepting responses are generated as , on the same initial message .
The 2-special soundness of the protocol allows us to extract the openings of of the form and openings of of the form with . From the verification equations, we are able to get openings of and . Moreover, it must hold for all challenges that , and for all , unless the adversary successfully breaks the binding property of the commitment scheme.
From ’s and ’s, we get , , , and . For , we get that and are polynomials of the form and . we could express the verifications using and as
and
for some fixed that can be computed from the commitments in the statement and the initial messages.
Note that the vectors , where , can be interpreted as rows of a Vandermonde matrix (see Definition A2). Additionally, since are all distinct, the matrix is invertible, allowing us to find a linear combination of the rows that yields the vector . By combining the accepting verification equations, we get
and
This gives us the extracted openings of and to 0 with values and .
Next, we demonstrate that the extracted values align with the expressions in the bilinear verifications. Similarly, we can express the bilinear verifications using , , and as
and
for some fixed that can be computed from the initial messages. By combining the accepting verification equations, we get
and
This gives us the extracted openings of and to 0 with values and . □
5.4. Security Analysis of Our TRS
Theorem 5.
Protocol 2 () securely realizes in the -hybrid world with the random oracle model under the discrete logarithm (DLOG) assumption; if achieves (perfectly) hiding and binding, achieves pseudorandomness, and achieves the properties of special honest-verifier zero-knowledge and -special soundness.
Proof.
Setup. The setup of the simulator follows mainly the setup in Theorem 2, with the following additional items:
- .
Simulation. We describe a simulator that controls the random oracle H and operates in the following manner.
- Upon receiving from , calls to and receives . Moreover, it randomly selects and generates . In the case that the key exists already, returns fail and terminates. Otherwise, it returns to , where .
- Upon receiving from , calls and receives . Moreover, it calculates , where . In case has already been queried before, recover the the corresponding value c; otherwise, randomly select a unique c and record in the table of the random oracle H. In case this is not feasible and would make the table inconsistent, returns fail and terminates. After that, it sets and calls to , and receives . Finally, it outputs to , where .
- Upon receiving from , verify by calling to and receive such that is a bit b. If , it further verifies if . If so, returns . If but the check of fails, output fail and terminate. Otherwise, it returns . Note that will return the correct output to the verifier.
- Upon receiving from , it parses and . If , return . Otherwise, it calculates and outputs if . Otherwise, return . Note that the cases of Reject are handled by .
- Upon receiving a query from the random oracle H, select a distinct c at random, store and return c. In any other query with the same input , return the same c.
This gives a full description of the ideal-model simulator. Note that in the black-box simulation, we use fake values (the value of , and thus Z), and we claim that the differences are undetectable for the environment . This is proven through a sequence of games transforming an execution in the ideal-model scenario into one which is equal to the one of the actual protocol.
- Experiment describes the original attack of on the ideal-model simulation (including the black-box simulation of ).
- In , the simulator changes the computation of to where is random. Because of the DLOG assumption, ’s output behavior will not change with a non-negligible probability when facing instead of .
- In , the simulator changes the computation of Z to , where . Moreover, the simulator changes the computation of Q and W to and . Because of the DLOG assumption and the pseudorandomness of DY-VRF, ’s output behavior will not change with a non-negligible probability when facing instead of .
- In , the simulator changes the computation of to the actual proof using . By the special honest-verifier zero-knowledge (SHVZK) property, this substitution is indistinguishable for the environment .
All the steps in the final game now are exactly as in an attack on the real protocol with adversary , with the restriction that only queries could be made. Therefore, the environment’s output in the ideal-model simulation () and the real-world execution () are indistinguishable. □
6. Discussion
In this section, we examine several related topics pertinent to this work. Specifically, we provide a comparison of existing UC functionalities of VRF in Section 6.1. Additionally, we explore the potential for extending this research to accommodate K-time anonymity in Section 6.2.
6.1. UC Formulation of VRF
In Section 3.2, we formalized a VRF functionality, denoted , which mirrors the classic, stand-alone security definition of DY-VRF [43]. In this subsection, we compare with stronger UC–VRF models, explain why the absence of unpredictability under malicious key generation (UMKG) does not undermine our TRS construction, and support this claim through a comparative analysis of three multi-party deployment scenarios.
- Comparison between UC-VRF Functionalities. David et al. [38] introduced the functionality of the VRF in their work on Ouroboros Praos. It is a provably secure proof-of-stake protocol, and is the first to achieve security against adaptive adversaries while remaining scalable in a genuinely practical sense. This functionality was also adopted in the subsequent work Ouroboros Genesis [39]. However, their UC formulation cannot be derived from the standard VRF security definitions, as it includes additional security features, such as UMKG. This design was intended to meet extra security requirements specific to their scheme, making it not a pure or typical VRF.
In contrast, the DY-VRF protocol [43] fails to satisfy the property of UMKG [38]. If an adversary is allowed to generate its own key pair, the reliability of the VRF output distribution cannot be guaranteed. In particular, in the DY-VRF setting, a properly constructed malicious key can substantially distort the resulting output distribution.
In this work, we present a VRF functionality that adheres to the standard VRF security definition from [43]. Therefore, it can be viewed as a weaker version of the UC formulation of VRF, yet it is of independent interest. In the VRF functionality with UMKG [38] is able to act as a random oracle. However, the standard VRF in this work could not present a uniform distribution in the outputs; therefore, extra information may possibly be leaked from the distribution if malicious keys are injected.
Both VRF functionalities could be adopted to different protocols according to the security requirements, and we will discuss on this later in this subsection.
- Irrelevance of UMKG for TRS. In the context of existing security models for TRS, such as those in [3], malicious key generation is not permitted. The security definitions of TRS are revisited in Section 4.1. Therefore, a UC formulation of VRF with typical security features aligns well with the requirements of TRS.
TRS operate on a static ring, such that all public keys are fixed and publicly known before any signature is produced. It is impossible for a malicious signer to craft a malformed key prior to ring formation according to the definitions of security properties stated in Section 4.1. Moreover, the malicious signer is not allowed to swap in a fresh adversarial key after the ring is fixed. Since no adversary can inject a key once signatures start, the UMKG threat is absent. Incorporating UMKG into the ideal world would yield no extra real-world power and would unnecessarily complicate the simulation.
- Applying VRF Functionalities to Various Multi-party Settings. We consider different multi-party scenarios involving VRF functionalities. Since both the typical VRF functionality from this work and the VRF functionality with UMKG [38] could be adopted to different protocols according to the security requirements, we consider two use cases.
First, we consider late key registration of the TRS scheme. Typical security definitions of TRS do not consider malicious key generation, thus the standard VRF functionality in this work is suitable to use. However, if we consider a possible future extension on dynamic-membership TRS, the definition is no longer the same as the typical TRS. In this possible extension, new keys are allowed to be appended to the ring. The signer is able to generate signatures on the dynamic ring, and the identity of the signer could still be revoked if she signs on different messages. In the idea of dynamic-membership TRS, the security property of UMKG is necessary since adversaries are allowed to generate the secret and public key pair in the protocol.
Second, we consider possible key management, such as key revocation and key refresh in TRS. In the case of key revocation, we consider two approaches. If the method of key revocation is blacklisting, a blacklist of revoked public keys is published and the verifiers reject rings containing them, thus the property of UMKG remains irrelevant. If ring reconstitution is considered, a fresh ring is generated without the revoked keys, along with new tags. This refreshes the keys in the static ring. Similarly, in the case of key refresh, the keys in the static ring are refreshed after a specific condition. In most of the cases, new keys will be generated. Therefore, the property of UMKG is necessary.
6.2. Possibility on Allowing K-Time Anonymity
Apart from the applications mentioned in Section 1.3, considering a TRS scheme with K-time anonymity may offer significant advantages. This concept has been previously explored in various studies, including its application in group signature schemes such as [34], anonymous signature schemes such as [35], and anonymous authentication schemes such as [56,57].
- Modifying Security Definitions and UC Functionality. To extend our scheme to support K-time anonymity, we first need to modify the security definition of TRS as defined by Fujisaki and Suzuki [3]. Specifically, we must revisit the properties of public traceability and tag-linkability, and even introduce new security properties. (1) We need to specify conditions that allow for the tracing of signatures while accommodating the K-time anonymity, including limits on the number of signatures accepted; and (2) Modifications should clarify how to manage links between signatures, ensuring that they can be distinguished while still maintaining anonymity across multiple instances. Next, it is essential to update the definition of the UC functionality to incorporate the properties that support K-time anonymity. This involves creating a comprehensive security model that addresses the unique challenges posed by K-time anonymity.
- Construction Design. Once the new security definitions are established, the actual construction of the TRS scheme should be designed to align with these updated definitions, ensuring that it effectively supports K-time anonymity while maintaining the desired security properties.
The main technical challenge lies in formulating a comprehensive security model that adequately captures all necessary properties while remaining robust against potential adversarial strategies. Moreover, another technical challenge lies in constructing an actual protocol and proving the security.
7. Conclusions
In this work, we have formalized the functionality of TRS within the framework of UC security. Furthermore, we present a UC functionality of VRF that aligns with the security definition of TRS. Our construction of TRS is detailed, along with the corresponding zero-knowledge proof, which utilizes the Pedersen commitment [44], DY-VRF [43], and the membership proof from [48]. We demonstrate the security of our construction under the UC framework, supported by formal proofs.
Author Contributions
Conceptualization, K.Y.C. and T.H.Y.; methodology, K.Y.C.; formal analysis, K.Y.C.; writing—original draft preparation, K.Y.C.; writing—review and editing, K.Y.C. and T.H.Y.; supervision, T.H.Y. and S.M.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research is partly supported by HKU-SCF FinTech Academy, Shenzhen-Hong Kong-Macao Science and Technology Plan Project (Category C Project: SGDX20210823103537030), Theme-based Research Scheme of RGC, Hong Kong (T35-710/20-R).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We appreciate the insightful comments and feedback from the reviewers.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| Acc | Accountable Ring Signature |
| Com, CS | Commitment Scheme |
| CRS | Common Reference String |
| CSIDH | Commutative Supersingular Isogeny Diffie–Hellman |
| DID | Decentralized Identifier |
| DDH | Decisional Diffie–Hellman (Assumption) |
| DLOG | Discrete Logarithm (Assumption) |
| DY-VRF | Dodis–Yampolskiy Verifiable Random Function |
| IND-CPA | Indistinguishability under Chosen-plaintext Attack |
| LRS | Linkable Ring Signature |
| NIZK | Non-interactive Zero-knowledge (Proof) |
| NIWI | Non-interactive Witness-indistinguishable (Proof) |
| (M)LWE | (Module) Learning with Errors |
| (M)SIS | (Module) Short Integer Solution |
| Ped | Pedersen Commitment Scheme |
| q-co-DBDHI | q-co-Decisional Bilinear Diffie-Hellman Inversion (Assumption) |
| q-SDH | q-Strong Diffie-Hellman (Assumption) |
| ROM | Random Oracle Model |
| R&T | Report and Trace Ring Signature |
| RLRS | Revocable and Linkable Ring Signature |
| Rev-iff-Link | Revocable-iff-linked Ring Signature |
| SD | Syndrome Decoding |
| TRS | Traceable Ring Signature |
| UC | Universal Composibility |
| VRF | Verifiable Random Function |
Appendix A. Details of Membership Proof
In this Appendix, we provide detailed background of the membership proof proposed by Groth and Kohlweiss [48]. We recall the mathematical definitions and the protocol in Appendixes Appendix A.1 and Appendix A.2.
Appendix A.1. Mathematical Definitions
- Kronecker Delta. The Kronecker Delta [58] is used to express complex expressions.
Definition A1
(Kronecker Delta [58]). The Kronecker delta, denoted as , is a function of two variables, typically non-negative integers. It is defined as follows:
- Vandermonde Matrix. The Vandermonde matrix [59] is well-known for addressing the polynomial interpolation problem. In this problem, the goal is to find a polynomial that satisfies the conditions for given data points . This problem can be reformulated using linear algebra with the help of the Vandermonde matrix, which is defined in Definition A2.
Definition A2
(Vandermonde Matrix [59]). A Vandermonde matrix is an matrix characterized by the terms of a geometric progression in each row. It can be expressed as:
The Vandermonde matrix M computes the values of at the points through the matrix multiplication , where is the vector of coefficients and is the vector of values. Therefore, we could form the following mathematical expression.
If and are distinct, then M becomes a square matrix with a non-zero determinant, making it an invertible matrix. Consequently, with M and y, one can determine the required polynomial by solving for its coefficients a in the equation , leading to , thus the interpolation problem has a unique solution.
- Schwartz-Zippel Lemma. The Schwartz–Zippel Lemma (or Polynomial-Identity Lemma) [60,61,62] states that when evaluating a non-zero polynomial with inputs randomly selected from a sufficiently large set, it is likely to yield at least one input that results in a non-zero output.
Definition A3
(Schwartz–Zippel Lemma [60,61,62]). Let be a non-zero polynomial of total degree defined over an integral domain . Let S be a finite subset of , and let be chosen independently and uniformly at random from S. Then
Equivalently, for any finite subset S of , a set satisfies
where is the zero set of P.
Appendix A.2. Sigma-Protocol of Membership Proof
In this Appendix, we recall the typical definition of the membership proof in the form of a sigma-protocol.
Let the ring size be n, such that . We can express i and ℓ as and . We define the Kronecker delta as . The rationale behind the membership proof is to reformulate the values to be proven as . This expression serves as a commitment to 0.
Before the proof, the prover obtains the ring , where the public keys are Pedersen commitments. These public keys are then converted to bits .
In the sigma-protocols for , the prover reveals values of the form . Let and . For each i, we have the product . This product is a polynomial of the form:
In the initial message, the prover will send commitments that are used to cancel out the low-order coefficients corresponding to . Meanwhile, the high-order coefficient for ensures that the commitment can be opened to 0. In other words, at the end, the verifier will check that
is a commitment to 0. According to the Schwartz–Zippel Lemma (see Definition A3), this has a negligible probability of being true unless is indeed a commitment to 0.
In the membership proof, we consider the relation :
the sigma-protocol illustrates the interaction between and :
- For , samples , sets , and computes
- ,
- ,
- ,
- .
sends to . - sends the challenge to .
- For , sets and calculates
- ,
- ,
- ,
- .
sends to . - accepts with output 1 if all the following items are true:
- ,
- ,
- For all , ,
- For all , ,
- ,
where and . Otherwise, it outputs 0.
References
- W3C. Decentralized Identifiers (DIDs) v1.0. 2022. Available online: https://www.w3.org/TR/did-1.0/ (accessed on 9 September 2025).
- Canetti, R. Universally composable security: A new paradigm for cryptographic protocols. In Proceedings of the 42nd IEEE Symposium on Foundations of Computer Science, Las Vegas, NV, USA, 14–17 October 2001; pp. 136–145. [Google Scholar] [CrossRef]
- Fujisaki, E.; Suzuki, K. Traceable Ring Signature. In Proceedings of the PKC 2007, Beijing, China, 16–20 April 2007; Okamoto, T., Wang, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 181–200. [Google Scholar]
- Hu, C.; Li, D. Forward-Secure Traceable Ring Signature. In Proceedings of the Eighth ACIS International Conference on Software Engineering, Artificial Intelligence, Networking, and Parallel/Distributed Computing (SNPD 2007), Qingdao, China, 30 July–1 August 2007; Volume 3, pp. 200–204. [Google Scholar] [CrossRef]
- Fujisaki, E. Sub-linear Size Traceable Ring Signatures without Random Oracles. In Proceedings of the CT-RSA 2011, San Francisco, CA, USA, 14–18 February 2011; Kiayias, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 393–415. [Google Scholar]
- Branco, P.; Mateus, P. A Traceable Ring Signature Scheme Based on Coding Theory. In Proceedings of the Post-Quantum Cryptography, Chongqing, China, 8–10 May 2019; Ding, J., Steinwandt, R., Eds.; Springer: Cham, Switzerland, 2019; pp. 387–403. [Google Scholar]
- Feng, H.; Liu, J.; Li, D.; Li, Y.N.; Wu, Q. Traceable ring signatures: General framework and post-quantum security. Des. Codes Cryptogr. 2021, 89, 1111–1145. [Google Scholar] [CrossRef]
- Wei, W.; Luo, M.; Bao, Z.; Peng, C.; He, D. Traceable Ring Signatures from Group Actions: Logarithmic, Flexible, and Quantum Resistant. In Proceedings of the SAC 2023, Tallinn, Estonia, 27–31 March 2023; Carlet, C., Mandal, K., Rijmen, V., Eds.; Springer: Cham, Switzerland, 2024; pp. 169–188. [Google Scholar]
- Thanh Khuc, X.; Susilo, W.; Duong, D.H.; Guo, F.; Fukushima, K.; Kiyomoto, S. Traceable Ring Signatures: Logarithmic-Size, Without Any Setup, from Standard Assumptions. In Proceedings of the ProvSec 2024, Gold Coast, QLD, Australia, 25–27 September 2025; Liu, J.K., Chen, L., Sun, S.F., Liu, X., Eds.; Springer: Singapore; pp. 189–208. [Google Scholar]
- Au, M.H.; Liu, J.K.; Susilo, W.; Yuen, T.H. Secure ID-based linkable and revocable-iff-linked ring signature with constant-size construction. Theor. Comput. Sci. 2013, 469, 1–14. [Google Scholar] [CrossRef]
- Bootle, J.; Cerulli, A.; Chaidos, P.; Ghadafi, E.; Groth, J.; Petit, C. Short Accountable Ring Signatures Based on DDH. In Proceedings of the ESORICS 2015, Vienna, Austria, 21–25 September 2015; Pernul, G., Ryan, P.Y.A., Weippl, E., Eds.; Springer: Cham, Switzerland, 2015; pp. 243–265. [Google Scholar]
- Zhang, X.; Liu, J.K.; Steinfeld, R.; Kuchta, V.; Yu, J. Revocable and Linkable Ring Signature. In Proceedings of the Inscrypt 2019, Nanjing, China, 6–8 December 2019; Liu, Z., Yung, M., Eds.; Springer: Cham, Switzerland, 2020; pp. 3–27. [Google Scholar]
- Fraser, A.; Quaglia, E.A. Report and Trace Ring Signatures. In Proceedings of the CANS 2021, Vienna, Austria, 13–15 December 2021; Conti, M., Stevens, M., Krenn, S., Eds.; Springer: Cham, Switzerland, 2021; pp. 179–199. [Google Scholar]
- Bultel, X.; Fraser, A.; Quaglia, E. Improving the Efficiency of Report and Trace Ring Signatures. In Proceedings of the SSS 2022, Clermont-Ferrand, France, 15–17 November 2022; Devismes, S., Petit, F., Altisen, K., Di Luna, G.A., Fernandez Anta, A., Eds.; Springer: Cham, Switzerland, 2022; pp. 130–145. [Google Scholar]
- Scafuro, A.; Zhang, B. One-Time Traceable Ring Signatures. In Proceedings of the ESORICS 2021, Darmstadt, Germany, 4–8 October 2021; Bertino, E., Shulman, H., Waidner, M., Eds.; Springer: Cham, Switzerland, 2021; pp. 481–500. [Google Scholar]
- Kabaleeshwaran, R.; Kishan, B.K. Efficient Revocable Linkable Ring Signatures. In Proceedings of the INDOCRYPT 2024, Chennai, India, 18–21 December 2024; Mukhopadhyay, S., Stănică, P., Eds.; Springer: Cham, Switzerland, 2025; pp. 305–325. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Tauman, Y. How to Leak a Secret. In Proceedings of the ASIACRYPT 2001, Gold Coast, Australia, 9–13 December 2001; Boyd, C., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 552–565. [Google Scholar]
- Zhang, B.; Oliynykov, R.; Balogun, H. A Treasury System for Cryptocurrencies: Enabling Better Collaborative Intelligence. In Proceedings of the NDSS 2019, San Diego, CA, USA, 24–27 February 2019; The Internet Society. Available online: https://www.ndss-symposium.org/wp-content/uploads/2019/02/ndss2019_02A-2_Zhang_paper.pdf (accessed on 9 September 2025).
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2009. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 9 September 2025).
- Noether, S.; Mackenzie, A. The Monero Research Lab Ring Confidential Transactions. Ledger 2016, 1, 1–18. [Google Scholar] [CrossRef]
- Odoom, J.; Huang, X.; Zhou, Z.; Danso, S.; Zheng, J.; Xiang, Y. Linked or unlinked: A systematic review of linkable ring signature schemes. J. Syst. Archit. 2023, 134, 102786. [Google Scholar] [CrossRef]
- Liu, J.K.; Wong, D.S. Linkable ring signatures: Security models and new schemes. In Proceedings of the ICCSA 2005, Singapore, 9–12 May 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 614–623. [Google Scholar]
- Liu, J.K.; Wei, V.K.; Wong, D.S. Linkable Spontaneous Anonymous Group Signature for Ad Hoc Groups. In Proceedings of the ACISP 2004, Sydney, Australia, 13–15 July 2004; Wang, H., Pieprzyk, J., Varadharajan, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 325–335. [Google Scholar]
- Bultel, X.; Olivier-Anclin, C. On the Anonymity of Linkable Ring Signatures. In Proceedings of the CANS 2024, Cambridge, UK, 24–27 September 2024; Kohlweiss, M., Di Pietro, R., Beresford, A., Eds.; Springer: Singapore, 2024; pp. 212–235. [Google Scholar] [CrossRef]
- Hara, K. A linkable ring signature scheme with unconditional anonymity in the standard model. Theor. Comput. Sci. 2025, 1033, 115093. [Google Scholar] [CrossRef]
- Boyen, X.; Haines, T. Forward-Secure Linkable Ring Signatures from Bilinear Maps. Cryptography 2018, 2, 35. [Google Scholar] [CrossRef]
- Lin, H.; Sun, S.F.; Wang, M.; Liu, J.K.; Wang, W. Shorter Linkable Ring Signature Based on Middle-Product Learning with Errors Problem. Comput. J. 2022, 66, 2974–2989. [Google Scholar] [CrossRef]
- Chow, S.S.; Susilo, W.; Yuen, T.H. Escrowed linkability of ring signatures and its applications. In Proceedings of the VIETCRYPT 2006, Hanoi, Vietnam, 25–28 September 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 175–192. [Google Scholar]
- Wang, X.; Zhu, C.; Liu, Z. A Universally Composable Linkable Ring Signature Supporting Stealth Addresses. Mathematics 2024, 12, 491. [Google Scholar] [CrossRef]
- Wang, G.; Liu, Q.; Yu, Z.; Zhang, H.; Dong, A. BCE-PPDS: Blockchain-based cloud–edge collaborative privacy-preserving data sharing scheme for IoT. Future Gener. Comput. Syst. 2025, 174, 107922. [Google Scholar] [CrossRef]
- Noether, S. Ring Signature Confidential Transactions for Monero. 2015. Available online: https://eprint.iacr.org/2015/1098 (accessed on 9 September 2025).
- Sun, S.F.; Au, M.H.; Liu, J.K.; Yuen, T.H. RingCT 2.0: A Compact Accumulator-Based (Linkable Ring Signature) Protocol for Blockchain Cryptocurrency Monero. In Proceedings of the ESORICS 2017, Oslo, Norway, 11–15 September 2017; Foley, S.N., Gollmann, D., Snekkenes, E., Eds.; Springer: Cham, Switzerland, 2017; pp. 456–474. [Google Scholar]
- Yuen, T.H.; Sun, S.F.; Liu, J.K.; Au, M.H.; Esgin, M.F.; Zhang, Q.; Gu, D. RingCT 3.0 for Blockchain Confidential Transaction: Shorter Size and Stronger Security. In Proceedings of the FC 2020, Kota Kinabalu, Malaysia, 10–14 February 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 464–483. [Google Scholar] [CrossRef]
- Au, M.H.; Susilo, W.; Yiu, S.M. Event-oriented k-times revocable-iff-linked group signatures. In Proceedings of the ACISP 2006, Melbourne, Australia, 3–5 July 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 223–234. [Google Scholar]
- Bultel, X.; Olivier-Anclin, C. Taming Delegations in Anonymous Signatures: k-Times Anonymity for Proxy and Sanitizable Signature. In Proceedings of the CANS 2024, Cambridge, UK, 24–27 September 2024; Kohlweiss, M., Di Pietro, R., Beresford, A., Eds.; Springer: Singapore, 2024; pp. 165–186. [Google Scholar]
- Micali, S.; Rabin, M.; Vadhan, S. Verifiable random functions. In Proceedings of the 40th Annual Symposium on Foundations of Computer Science, New York, NY, USA, 17–18 October 1999; pp. 120–130. [Google Scholar] [CrossRef]
- Galindo, D.; Liu, J.; Ordean, M.; Wong, J.M. Fully Distributed Verifiable Random Functions and their Application to Decentralised Random Beacons. In Proceedings of the EuroS&P 2021, Vienna, Austria, 6–10 September 2021; pp. 88–102. [Google Scholar] [CrossRef]
- David, B.; Gaži, P.; Kiayias, A.; Russell, A. Ouroboros Praos: An Adaptively-Secure, Semi-synchronous Proof-of-Stake Blockchain. In Proceedings of the EUROCRYPT 2018, Tel Aviv, Israel, 29 April–3 May 2018; Nielsen, J.B., Rijmen, V., Eds.; Springer: Cham, Switzerland, 2018; pp. 66–98. [Google Scholar]
- Badertscher, C.; Gaži, P.; Kiayias, A.; Russell, A.; Zikas, V. Ouroboros Genesis: Composable Proof-of-Stake Blockchains with Dynamic Availability. In Proceedings of the ACM CCS 2018, CCS’18, New York, NY, USA, 9 May 2018; pp. 913–930. [Google Scholar] [CrossRef]
- Papadopoulos, D.; Wessels, D.; Huque, S.; Naor, M.; Včelák, J.; Reyzin, L.; Goldberg, S. Making NSEC5 Practical for DNSSEC. Available online: https://eprint.iacr.org/2017/099 (accessed on 9 September 2025).
- Jarecki, S.; Kiayias, A.; Krawczyk, H. Round-optimal password-protected secret sharing and T-PAKE in the password-only model. In Proceedings of the ASIACRYPT 2014, Kaoshiung, Taiwan, China, 7–11 December 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 233–253. [Google Scholar]
- Giunta, E.; Stewart, A. Unbiasable Verifiable Random Functions. In Proceedings of the EUROCRYPT 2024, Zurich, Switzerland, 26–30 May 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 142–167. [Google Scholar] [CrossRef]
- Dodis, Y.; Yampolskiy, A. A Verifiable Random Function with Short Proofs and Keys. In Proceedings of the PKC 2005, Les Diablerets, Switzerland, 23–26 January 2005; Vaudenay, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 416–431. [Google Scholar]
- Pedersen, T.P. Non-Interactive and Information-Theoretic Secure Verifiable Secret Sharing. In Proceedings of the CRYPTO 1991, Santa Barbara, CA, USA, 11–15 August 1991; Feigenbaum, J., Ed.; Springer: Berlin/Heidelberg, Germany, 1992; pp. 129–140. [Google Scholar]
- Elgamal, T. A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theory 1985, 31, 469–472. [Google Scholar] [CrossRef]
- Kumar, A.; Fischer, C.; Tople, S.; Saxena, P. A Traceability Analysis of Monero’s Blockchain. In Proceedings of the ESORICS 2017, Oslo, Norway, 11–15 September 2017; Foley, S.N., Gollmann, D., Snekkenes, E., Eds.; Springer: Cham, Switzerland, 2017; pp. 153–173. [Google Scholar]
- Tsang, P.P.; Wei, V.K. Short Linkable Ring Signatures for E-Voting, E-Cash and Attestation. In Proceedings of the ISPEC 2005, Singapore, 11–14 April 2005; Deng, R.H., Bao, F., Pang, H., Zhou, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 48–60. [Google Scholar]
- Groth, J.; Kohlweiss, M. One-Out-of-Many Proofs: Or How to Leak a Secret and Spend a Coin. In Proceedings of the EUROCRYPT 2015, Sofia, Bulgaria, 26–30 April 2015; Oswald, E., Fischlin, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 253–280. [Google Scholar]
- Galbraith, S.D.; Paterson, K.G.; Smart, N.P. Pairings for Cryptographers. Discret. Appl. Math. 2006, 156, 3113–3121. [Google Scholar] [CrossRef]
- Boneh, D.; Boyen, X. Efficient Selective-ID Secure Identity-Based Encryption Without Random Oracles. In Proceedings of the EUROCRYPT 2004, Interlaken, Switzerland, 2–6 May 2004; Cachin, C., Camenisch, J.L., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 223–238. [Google Scholar]
- Fiat, A.; Shamir, A. How To Prove Yourself: Practical Solutions to Identification and Signature Problems. In Proceedings of the CRYPTO 1986, Santa Barbara, CA, USA, 11–15 August 1986; Odlyzko, A.M., Ed.; Springer: Berlin/Heidelberg, Germany, 1987; pp. 186–194. [Google Scholar]
- Camenisch, J.; Casati, N.; Gross, T.; Shoup, V. Credential Authenticated Identification and Key Exchange. In Proceedings of the CRYPTO 2010, Santa Barbara, CA, USA, 15–19 August 2010; Rabin, T., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 255–276. [Google Scholar]
- Canetti, R.; Sarkar, P.; Wang, X. Triply Adaptive UC NIZK. In Proceedings of the ASIACRYPT 2022, Taipei, Taiwan, 5–9 December 2022; Agrawal, S., Lin, D., Eds.; Springer: Cham, Switzerland, 2022; pp. 466–495. [Google Scholar]
- Groth, J. Simulation-Sound NIZK Proofs for a Practical Language and Constant Size Group Signatures. In Proceedings of the ASIACRYPT 2006, Shanghai, China, 3–7 December 2006; Lai, X., Chen, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 444–459. [Google Scholar]
- Canetti, R.; Fischlin, M. Universally Composable Commitments. In Proceedings of the CRYPTO 2001, Santa Barbara, CA, USA, 19–23 August 2001; Kilian, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 19–40. [Google Scholar]
- Yang, Y.; Xue, W.; Sun, J.; Yang, G.; Li, Y.; Pang, H.H.; Deng, R.H. PkT-SIN: A secure communication protocol for space information networks with periodic k-time anonymous authentication. IEEE TIFS 2024, 19, 6097–6112. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, S.; Yang, G.; Mu, Y.; Yu, Y. Privacy-preserving k-time authenticated secret handshakes. In Proceedings of the ACISP 2017, Auckland, New Zealand, 3–5 July 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 281–300. [Google Scholar]
- Kronecker, L. Ueber bilineare Formen. J. FüR Reine Angew. Math. 1868, 68, 273–285. [Google Scholar]
- Kalman, D. The generalized Vandermonde matrix. Math. Mag. 1984, 57, 15–21. [Google Scholar] [CrossRef]
- Demillo, R.A.; Lipton, R.J. A probabilistic remark on algebraic program testing. Inf. Process. Lett. 1978, 7, 193–195. [Google Scholar] [CrossRef]
- Zippel, R. Probabilistic algorithms for sparse polynomials. In Proceedings of the International Symposium on Symbolic and Algebraic Computation, Marseille, France, 1 June 1979; Ng, E.W., Ed.; Springer: Berlin/Heidelberg, Germany, 1979; pp. 216–226. [Google Scholar]
- Schwartz, J.T. Fast Probabilistic Algorithms for Verification of Polynomial Identities. J. ACM 1980, 27, 701–717. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).