Non-Degenerate One-Time Pad and Unconditional Integrity of Perfectly Secret Messages

Abstract

We present a new construction of a one-time pad (OTP) with inherent diffusive properties and a redundancy injection mechanism that benefits from them. The construction is based on interpreting the plaintext and key as members of a permutation group in the Lehmer code representation after conversion to factoradic. The so-constructed OTP translates any perturbation of the ciphertext to an unpredictable, metrically large random perturbation of the plaintext. This allows us to provide unconditional integrity assurance without extra key material. The redundancy is injected using Foata’s “pun”: the reading of the one-line representation as the cyclic one; we call this Pseudo Foata Injection. We obtain algorithms of quadratic complexity that implement both mechanisms.

1. Introduction

Shannon’s concept of perfect secrecy [1] is an important theoretical yardstick by which any imperfect cryptographic solution can be measured. Let us recall what it implies. The scenario is one of Alice sending to Bob a message, which is a bit string of length L, enciphered under a key k. Alice requires the probability of Moriarty deciphering the message to be at most $2^{-L}$ provided that he has no information about the key (assuming that he has no information about the plaintext either). Formally, Alice needs the mutual information between the plaintext and the ciphertext to be equal to zero. Then, the only way Moriarty can learn the plaintext is by guessing, and the probability of guessing a string of L bits correctly in the absence of information about it is $2^{-L}$. The pigeonhole principle quickly leads to the assertion that the length of the key, no matter what cipher is used, cannot be less than L if the secrecy is to be perfect.

One-time pad (OTP), originally proposed by Vernam [2], is the standard method of achieving perfect secrecy: $c_i=k_i\oplus p_i$, $0\le i<L$, where $c_i$ is the ciphertex, $p_i$ the plaintext, and $k_i$ the secret key, all three drawn from a set of fixed-length bit strings with ⊕ being modulo-2 addition. The cipher function has to be injective with respect to the plain- and ciphertext, and this is usually strengthened to a bijection to minimise the size of the latter. For example, the OTP formula works in both directions due to the fact that $x\oplus x\oplus y=y$ for any $x,y\in \{0,1\}$. This means that for any values of $c_i$, there are some corresponding values of $p_i$. An unpleasant consequence of this is that any $c_i$ will decrypt and that Bob is left with no assurance (not even a probabilistic one) that the resulting plaintext has any relationship with what Alice actually sent.

So by itself perfect secrecy is perfectly useless unless messages are guaranteed to arrive untampered with. Without such a guarantee, the cipher only provides security for Alice, but not for Bob. Alice wants her secret not to be available to anyone but Bob, and that is guaranteed. Bob, on the other hand, wants to be sure that the message he has received is exactly the one from Alice, and that is not guaranteed at all.

A common solution is to add redundancy to the message so that not every ciphertext will decipher to a valid plaintext. This gives an integrity assurance but requires additional key material to maintain perfect secrecy for $2^L$ potential messages, since the redundancy makes the message longer than the amount of information in it requires. Normally, redundancy and encipherment are decoupled, and the scheme is their composition,

$$c=E_k\left(R_m\left(p\right)\right),$$

where $E:B^{n+m}\times B^{n+m}\to B^{n+m}$ is the encipherment, $R:B^n\to B^{n+m}$ is a redundancy injection, $p\in B^n$ is the plaintext, $c\in B^{n+m}$ is the ciphertext, and $B=\{0,1\}$. The integer $m\ge 0$ defines the amount of redundancy injected into the plaintext. If $m=0$, R is the identity function on $B^n$.

For a cipher $E_k:B^q\to B^q$ to be perfect, there are two requirements. Firstly, the key should be an evenly distributed random bit string of length at least q. This means that if Moriarty has not obtained a copy of the key, he has no information about it either. Secondly, the condition

$$(\forall x,y\in B^q)(\exists k\in B^q)E_k\left(x\right)=y$$

must hold. Indeed, a given ciphertext should decipher to any given plaintext with an appropriate choice of the key. If the condition is violated for some plaintext x, then Moriarty knows that this value is not possible, and so the amount of entropy in the plaintext is already less than q bits, which makes the cipher less than perfect. This applies just as much to the case when the key is longer than q. In that case there is an extra constraint since some of the plaintext/ciphertext pairs could have more associated key values than others, which leaks information about the plaintext under the random choice of the key.

We call the relation between the key, plaintext, and ciphertext defined by E trijective, or a trijection, when it is a bijection between any two of the three values x, y, and k, whenever the third one is fixed.

Since Moriarty has no information about the key, all key values are equally likely and so are all potential plaintexts. We will limit ourselves to minimally enciphered messages, i.e., those with $\left|k\right|=n+m$, as this is the smallest length possible for perfect encipherment, see [1]. Nor will we consider unprotected redundancy:

$$c=E_k\left(p\right)\left|\right|D_m\left(p\right)$$

with $E:B^n\times B^n\to B^n$ and $D_m:B^n\to B^m$, where $D_m$ is an m-bit digest of the plaintext, since $D_m$ leaks information about p, requiring the use of a nonce to compensate at the expense of the message length.

The function R is an injection, so the inverse relation is a bijection from the range of R, $V\subset B^{n+m}$ back to $B^n$, obviously with $\left|V\right|=2^n$. The integrity assurance of the scheme comes from the fact that if Moriarty alters the ciphertext c to some $c^{\prime }$, then the deciphered string $r^{\prime }=E_k^{-1}\left(c^{\prime }\right)$ will not necessarily belong to V. If the nature of the cipher is such that $r^{\prime }$ is a significant and random deviation from $r=E_k^{-1}\left(c\right)=R\left(p\right)$ even under the slightest alteration of c, then one hopes that the probability of $r^{\prime }\in V$ (i.e., Moriarty’s success probability) is just the cardinality ratio $\left|V\right|/|B^{n+m}|=2^{-m}$, irrespective of the nature of the redundancy injection R.

This is the general idea, but the issue is subtle and the details are more than capable of rendering the scheme ineffective. For example, if E is the classical Vernam cipher, and R extends the plaintext with m bits of a linear code, then Moriarty is able to produce a $c^{\prime }\ne c$ that belongs to V with probability 1 at first attempt. All he needs to do is flip a single bit in the data part of the ciphertext and flip the corresponding checksum bits in the enciphered extension according to the code matrix. One could say the difference between r and $r^{\prime }$ in this case is both small and insufficiently random, even though the idea of using a linear code for redundancy is sound. The problem with the Vernam cipher is that it is isometric with respect to the Hamming distance: $d_H(c,c^{\prime })=d_H(r,r^{\prime })$. Worse still, the bit flip operator commutes with the encryption, $k_i\oplus {\overline{p}}_i=\overline{k_i\oplus p_i}$, making it possible to flip specific bits under the cipher. The transparency of the Vernam cipher is a consequence of the fact that the trijection it is based on is degenerate: its application is position-wise for bit strings p, c, and k.

The purpose of the present paper is to establish an efficient integrity control scheme for a perfect cipher. The scheme we seek is one based purely on statistical considerations, without assumptions about the properties of the plaintext, but one which reduces the probability of a successful attack down to a value exponentially small in the size of the redundancy. The scheme is not based on the computational complexity of any algorithm, and so it belongs to the class of unconditional integrity control schemes, see the related work in Section 6.

The structure of this paper is as follows. Section 2 introduces a detailed threat model. Section 3 describes our novel non-degenerate one-time pad, where any alteration of a ciphertext component leads to mis-deciphering of not only the corresponding component of the plaintext but also all preceding components thereof, i.e., the cipher exhibits diffusive properties towards the front. In Section 4, we introduce two original bijections: the Pseudo-Hadamard Transform on Chinese remainders and the first derivative, which ensure that a ciphertext component alteration influences all plaintext components subsequent to the one being altered, i.e., they exhibit diffusion towards the back. Section 5 contains our original proposal of Pseudo Foata Injection, which is an effective redundancy mechanism available in the representation of the plaintext as a permutation of a finite sequence. We also provide some Monte Carlo results showing that the proposed injection is robust even on its own. Finally, there are sections on related work and some conclusions.

The main contribution of this paper is best described when our method is compared with widely accepted universal hashing (see related work in Section 6). The statistical guarantee of the latter comes from a physically random key that injects entropy into the tag. Our proposal, the Pseudo Foata Injection, does not rely on the entropy of the mapping parameter for its effect. Instead, by making the cipher non-degenerate, we deny Moriarty a chance to make localised (we call them low-dimensional) alterations to the redundant plaintext. As a result, any change in the intercepted ciphertext results in random (due to the OTP’s random key), unpredictable (due to the pad’s non-degeneracy) changes to both the “message” and its “tag”; these two are inseparable and well spread out in our injector’s output. As a result, the probability of Moriarty’s success is defined solely by the cardinality ratio of the injector’s range to codomain, just like the security of a universal hash family is determined by a similar cardinality ratio: the set of colliding hash functions to the full set.

The material gain of our approach is that we do without a random “tag key”, which could reach four times the amount of redundancy injected by the tag [3]. In our case, the only extra key material that we need is that for the lengthened OTP key to cover the longer message. However, the same would be required in the reference case of universal hashing, in addition to the integrity key of the aforementioned length.

2. Threat Model

Perfect ciphers already possess a weak integrity guarantee: clearly, a chosen plaintext attack is impossible when the cipher is perfect. We are interested in strong integrity, whereby Moriarty is deemed to have succeeded if Bob accepts a message that differs from the genuine message from Alice to any extent at all, down to a single bit. Moriarty is assumed to be able to intercept every copy of the genuine ciphertext message sent by Alice by various routes, modify it, and then send it on to Bob. Moriarty has unlimited resources to compute his forgery in a short enough time for Bob not to notice the delay. He can also produce an unlimited number of messages that Bob will never refuse to receive, decipher, and check the integrity of, until one message succeeds. The scheme is effective if no more than one in $2^m$ messages sent by Moriarty does.

So the integrity assurance cannot be based on the computational hardness of an algorithm, but solely on the information deficit created by the scheme.

Note that there is a drastic difference in practice between the confidentiality guarantee based on the security parameter n and the integrity assurance based on m. Confidentiality cannot be better than perfect, while m has no theoretical limit. However, whereas an attempt to decipher a message (if not perfectly secret) is invisible while Moriarty traverses the key domain on a super- or quantum computer, an attack on the message integrity involves sending to Bob masses of candidate messages that represent Moriarty’s attempt to modify the original in the hope to satisfy the redundancy constraint. For example, $2^{64}$ keys could be tested by Moriarty in secret and in a reasonable time if this helps to crack the key; by contrast, sending to Bob $2^{64}$ versions of a modified message from Alice to satisfy the redundancy with $m=64$ would necessitate the exchange of billions of terabytes, which is very noticeable and will take enough time for Alice and Bob to realise that their channel is under attack.

3. Non-Degenerate One-Time Pad

Let us switch to a representation where it will be easier to eliminate the degeneracy of the cipher and facilitate redundancy injection. This will be carried out in the following three steps. First, we represent the plaintext and the key as members of the symmetric group $S_{\nu }$, where $\nu !\gtrsim 2^n$. Since no power of two greater than 1 is exactly equal to a factorial, the message has to be padded; this does not alter security in a significant way. As far as the key is concerned, it does not have to be defined in binary but as an evenly distributed random permutation instead—and then converted to binary for ease of sharing.

The second step will be to propose a one-time pad that enciphers the message under the key in a non-degenerate manner. This results in a ciphertext that, if modified slightly (in the sense of some metric), still decrypts to a plaintext that differs from the original a great deal. The difference should be nonlocal, affecting a large proportion of the plaintext.

3.1. Lehmer Code and Factoradic Numbers

A member of $S_{\nu }$ is a permutation of a length-$\nu$ sequence of symbols, which can be assumed without loss of generality to be numbers taken from the same length range. In the following, we use the range $[0,\nu -1]$ rather than the more conventional $[1,\nu ]$ for our permutations as it simplifies some mappings. To define a specific permutation, we can just list the numbers as they appear in the sequence when the base range is permuted. For example, for $\nu =4$, the following is an identity permutation:

$$0123$$

and below is a cyclic one:

$$1230.$$

The above is called one-line notation. A well-formed permutation in this notation must use all numbers in the range $[0,\nu )$ exactly once, which is a nonlocal constraint, making it difficult to generate random, evenly distributed permutations. The permutation constraint can be made completely local by using the Lehmer code [4] as follows.

Let us arrange $\nu$ cells marked $0,1,\dots ,\nu -1$ left to right, and let us place symbols in them in ascending order according to the permutation. For the above example of a cyclic permutation 1 2 3 0, we place symbol “0” in position 3, symbol “1” in position 0, etc. In doing so, we will note as “distance” the number of empty cells on the left of the position we are placing the symbol in. So when we place symbol “0”, we note distance 3, and when we place symbol “1”, we note distance 0, etc. The result is

$$3000.$$

The above representation is the Lehmer code. Each of the four numbers is completely independent from the rest, and can vary from 0 to $\nu -1-P$, where P is the cell mark. So the first number must be in the interval from 0 to 3, inclusive; the second, 0 to 2, accounting for the fact that one cell is non-empty; the third one, from 0 to 1, since two cells have been used; and finally, the last one must be zero: when we have placed all symbols bar one, the last symbol goes in the last empty cell, which has distance 0 as there are no empty cells left. Note that for this reason the last element of any Lehmer codeword must be 0.

The mapping of permutations onto Lehmer codewords is obviously bijective, and the conversion from one-line notation to Lehmer is of no more than quadratic complexity. Clearly, there are exactly as many distinct Lehmer codewords as there are permutations:

$$\nu \times (\nu -1)\times \dots \times 1=\nu !$$

To generate evenly distributed random permutations, one only needs to place random numbers (evenly distributed within the appropriate intervals) in all positions of the codeword.

Next, to establish a linear order on permutations, we introduce factoradic numbers [5] as follows. Consider a positional number system where the jth digit from the right has a place value of $(j-1)!$ and ranges from 0 to $j-1$. Adding 1 to the maximum digit $j-1$ in position j would make the weighted contribution $(j-1+1)\times (j-1)!=j!$, which is the same as the contribution of digit 1 in the next position to the left, so factoradic numbers work in the same way as numbers in any other positional system.

Since elements of a Lehmer codeword satisfy the range constraint for factoradic digits, there are exactly as many codewords as there are factoradic numbers of the same length. Since two different factoradic numbers represent different quantities, the representation can be used to enumerate permutations. Moreover, it can be converted to/from binary to make it possible to represent a range (obviously not a power of 2 in length) of binary messages or keys.

3.1.1. Conversion to Factoradic and Back

To convert a number in the range $[0,\nu !-1]$ to factoradic, one cannot apply the conventional method of repeatedly dividing it by the base while keeping the remainders. The reason for it is that the place values are not powers of the base. However, a less convenient method of repeatedly dividing by the place value, while noting the quotient and replacing the dividend by the remainder for the next round, works just as well. In practice, one would precompute the binary strings for divisors for all positions in the factoradic number and use shifts and long subtraction, an algorithm of quadratic complexity. Conversion from factoradic is similar to the conversion to, the only difference being long addition instead of long subtraction, which has the same complexity.

Here is one complete example for $S_5$. We start with the conversion of a binary string 10101 (${21}_{10}$) to 5-digit factoradic. The place values are (left to right)

$$246211.$$

Here, 24 is too large, so the first digit is 0, the second is 3 (remainder 3), the third one is 1 (remainder 1), and the fourth one is also 1 (remainder 0). The Lehmer codeword is thus

$$03110.$$

Reversing the definition of the Lehmer code, we restore the permutation:

$$04231.$$

3.1.2. Differential Properties

Since conversion from one-line to Lehmer involves “skipping over” used cells as we determine distances, the effect of a perturbation of a Lehmer codeword is nonlocal: when we alter a component, we potentially affect the placement of all subsequent symbols. It is easier to understand such perturbations if we switch to an equivalent definition of the Lehmer code. Now, we start with the last symbol $\nu -1$ and we make a sequence of one element out of it and record the last component of the Lehmer code as 0. If the symbol $\nu -2$ occurs in the one-line representation before the symbol $\nu -1$, the Lehmer component indexed $\nu -2$ is 0, otherwise 1, and we assemble the corresponding sequence of the two symbols accordingly. Now, for any $0\le \nu -i<\nu -2$ as we progress towards the big end, take the sequence assembled so far of symbols $\nu -i+1,\dots ,\nu -1$ and insert the symbol $\nu -i$ in a place that agrees with the symbol precedence in the one-line representation. There will be i distinct insertion points since the sequence so far is of length $i-1$; insertion before the 0th element gives the Lehmer value 0, and insertion after the last element, i.

It is obvious that when the insertion process is finished, the result is the original one-line sequence and the original Lehmer code. The former is due to the invariant we maintained through the steps, and the latter to the fact that we only look at the symbols subsequent to position $\nu -i$, which means that we skip over all symbols from 0 to $\nu -i-1$. Here is an example of right-to-left conversion from one-line to Lehmer for the permutation

$$04231$$

that we used before:

Sequence	Code
4	0
4 3	1 0
4 2 3	1 1 0
4 2 3 1	3 1 1 0
0 4 2 3 1	0 3 1 1 0

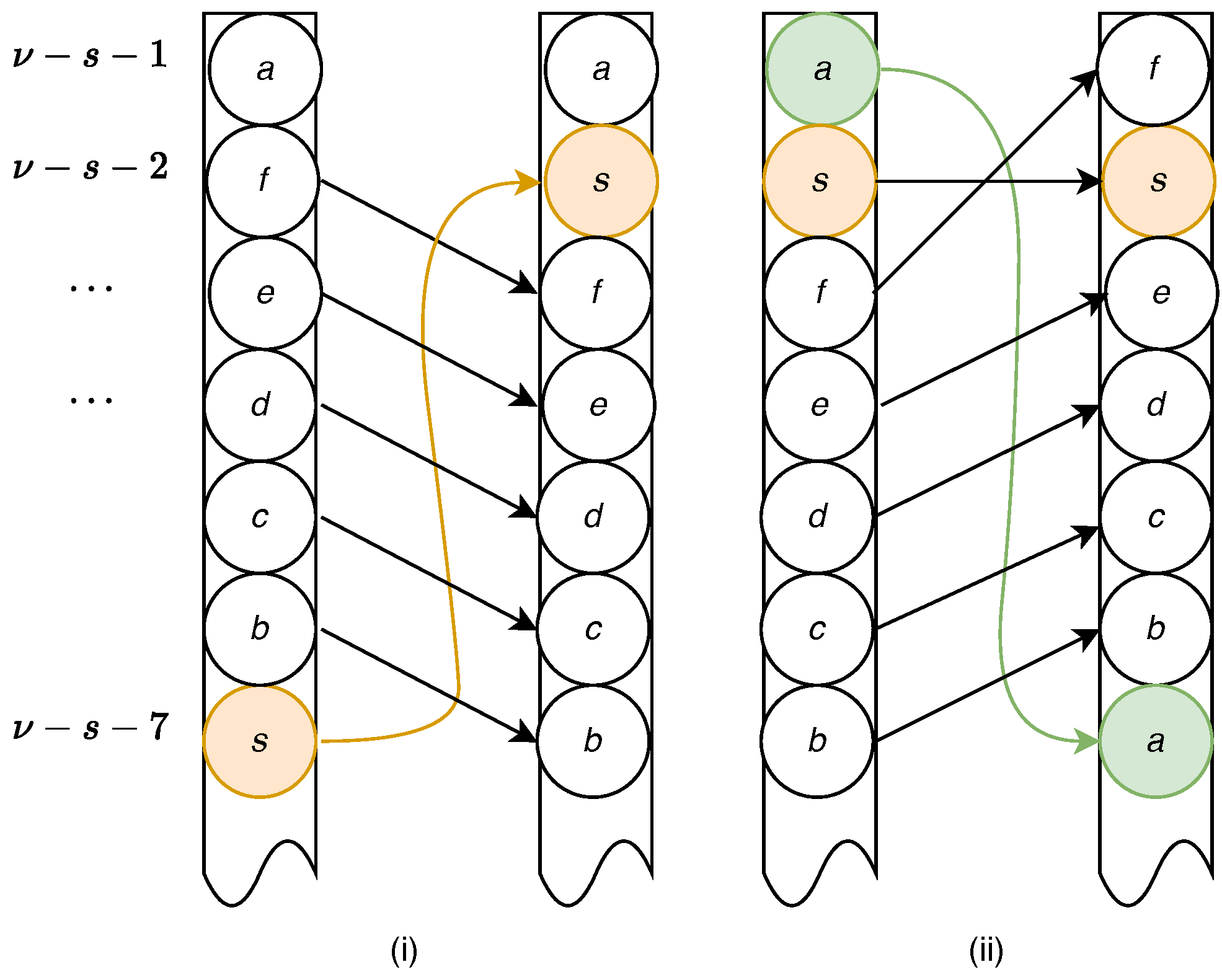
Now we have the necessary tools to discuss the differential properties, namely what happens to the sequence of symbols when a Lehmer component is altered. Consider the illustration shown in Figure 1 case (i). This is a snapshot of the sequence (arranged bottom-up) under right-to-left, one-line-to-Lehmer conversion when it reached a symbol s. The value of its corresponding Lehmer component is such that s is placed at $\nu -s-7$. We assume that

$$s<a<inf(b,c,d,e,f)$$

with the relationship between the last five symbols not being constrained. Now, increase the Lehmer component of s by 5. According to the right-to-left definition of the Lehmer code, s should be deleted at position $\nu -s-7$ and re-inserted at position $\nu -s-2$ in the one-line representation, as shown in the figure. The effect of this is equivalent to that of five transpositions: $(s,b)$, $(s,c)$, $(s,d)$, $(s,e)$, and $(s,f)$. Of course, symbols with values less than s will be inserted somewhere in this diagram, before the conversion is complete. However, these symbols will end up being inserted in the same positions before and after s is moved, and the effect of the movement will be the same. The minimum number of transpositions required to reach one permutation from another is a proper metric and is called the Cayley distance [6]. It easy to see that offsetting a Lehmer component $w_i$ by some integer $\Delta$, such that $0\le w_i+\Delta <\nu -i$, results in a permutation at a Cayley distance of $|\Delta |$ from the original.

Note that distances induced by subsequent offsets do not accumulate. Looking at diagram (ii) in Figure 1, we find what happens if, subsequent to the first alteration, a moves from position $\nu -s-1$ to position $\nu -s-7$, a jump over six places. Symbol s will not move, since it precedes a, and the rest of the symbols are pushed up by one place due to the insertion of a. The combined effect of two alterations (of s and of a) is that symbols from b to e are not moved, and the Cayley distance of the result from the original sequence is only 2, since the transposition $(f,s)$ followed by $(s,a)$ maps the final permutation onto the initial one. A distance of two is much shorter than either distance to the intermediate stage.

3.2. Non-Degenerate One-Time Pad (NDOTP)

We start with a trijection with a free parameter.

Proposition 1. 

Let r to be a positive integer, $a,b,c$ non-negative integers less than r, and π an arbitrary cyclic permutation from $S_r$. Then, the tripartite relation we use square brackets to index a cyclic permutation in one-line notation) $c={\pi }^b\left[a\right]$ is a trijection under any choice of π.

Proof. 

The bijective relation between c and b is due to the fact that any permutation is invertible.

The cyclic permutation $\pi$ can be visualised as a ring on which all unique non-negative integers less than r are placed according to the cycle. The value of the kth power of $\pi$ in a given position j along the ring is the number found k steps away from position j. Clearly, as k goes from 0 to $r-1$, all members will be encountered, and so for any a and c there exists a single b such that $c={\pi }^b\left[a\right]$.

We conclude that the relation is trijective. □

The next step is to define an encipherment that takes a plaintext p into a ciphertext c based on a key k, all three represented as Lehmer codes of the same length.

Proposition 2. 

Let $\nu \ge 2$ and let $0\le p_i,c_i,k_i<\nu -i$ for $1\le i<\nu$ be the Lehmer component of the plaintext, ciphertext, and key, respectively, with index $\nu -i-1$. The following recurrence relation in i,

$$\begin{array}{cc}\hfill {\pi }_i& =R_i({\pi }_{i-1},k_{i-1},p_{i-1})\hfill \\ \hfill c_i& ={\pi }_i^{k_i}\left[p_i\right]\hfill \end{array}$$

for $i=2,\dots ,\nu -1$ with the initial condition ${\pi }_1=10$(the only cyclic permutation of $S_2$), defines a non-degenerate trijection between p, c, and k. Here, $R_i:K_{i-1}\times {\mathbb{N}}_{i-1}^2\to K_i$, where $K_i$ is a set of all cyclic permutations from $S_{i+1}$ and ${\mathbb{N}}_i$ is the set of the first i non-negative integers, which is a family of arbitrary surjections that depend on all their arguments.

Proof. 

(by induction in $\nu$) The base case $\nu =2$ follows from Proposition 1 and the fact that a mapping of a single-component Lehmer codeword cannot be degenerate. For the inductive step, assume that the relation for $\nu ={\nu }_0$ is trijective and non-degenerate. According to Proposition 1, the relation between $c_{{\nu }_0}$, $p_{{\nu }_0}$, and $k_{{\nu }_0}$ is also trijective. Consequently, the combined $({\nu }_0+1)$-component plaintext, ciphertext, and key are in a trijective relation. Non-degeneracy follows from the fact that ${\pi }_{{\nu }_0}$ significantly depends on all preceding $p_i$. □

It should be noted that the encipherment introduced by Proposition 2 is constructive. The decryption process uses ${\pi }_1^{-k_1}$ and $c_1$ to obtain $p_1$, and for every $i>1$ it calculates ${\pi }_i$ based on the decrypted ps from the earlier steps. Decryption at step i is achieved by computing

$$p_i={\pi }_i^{-k_i}\left[c_i\right].$$

We call the cipher detailed in Proposition 2 a non-degenerate one-time pad (NDOTP).

The requirement that functions $\left\{R_i\right\}$ are surjective comes from the intention to maximise differential uncertainty. If $c_i$ is perturbed by a small amount (down to 1), the corresponding plaintext can take any legal value depending on the key. This is in contrast with, say, a fixed cyclic permutation, for example ${\widehat{\pi }}_i\left[l\right]=l+1modi$, which would result in

$$c_i=p_i+k_{i}modi.$$

Such a choice would be vulnerable to a differential attack whereby Moriarty increments or decrements some Lehmer components of the ciphertext to immediately obtain a plaintext within a short Manhattan distance from the original.

To eliminate such attacks, we should also even out the differential uncertainty by demanding that all ${\pi }_i$ are random and uncorrelated. This is, surprisingly, possible by utilising the true randomness of the key, which is required for perfect secrecy anyway. We can assume that all Lehmer components of the key are evenly distributed within their legal ranges (otherwise, the key’s entropy would be less than what Shannon’s model requires).

We conclude that the functions $\left\{R_i\right\}$ should build a random cyclic permutation ${\pi }_i$ from a smaller-sized one, ${\pi }_{i-1}$, according to the following:

• By a uniformly random expansion;
• In such a way that ${\pi }_i$ depends on the plaintext $p_{i-1}$ in a significant way;
• In such a way that ${\pi }_i$ is dissimilar to ${\pi }_{i-1}$.

Before we define and illustrate the construction of ${\pi }_i$, we would like to remind the reader of another standard notation for permutations, cyclic. In cyclic notation, a permutation is considered to be a collection of independent cycles. Symbols belonging to each cycle are listed between parentheses, in the order that they appear in the cycle, starting with an arbitrary member. For example, the following permutation from $S_5$,

$$42310$$

can be written in cyclic notation as

$$\left(04\right)\left(123\right)$$

A cyclic permutation will have only one bracketed list in cyclic notation, and its components can be indexed the same way as they are in one-line notation, except the origin is not the first symbol (there is no “first” in a cycle), but the symbol “0”. When we need to select a component of a cyclic permutation in cyclic notation, we use double brackets: $\pi \left[\right[0\left]\right]=0$.

Now, we address points 1–3 above. The first requirement is easy to achieve by utilising $k_{i-1}$. Permutation ${\pi }_{i-1}$ is a member of $S_i$, so its symbols run from 0 to $i-1$. Since it is cyclic, there are i distinct positions (after each symbol) in cyclic notation for insertion of the new symbol, i, in the cycle. We use $k_{i-1}$, which has the same range, to define this position:

$${\pi }_i\left[\left[j\right]\right]=\left\{\begin{array}{c}{\pi }_{i-1}\left[\left[j\right]\right],\mathrm{if}j<k_{i-1}\hfill \\ i,\mathrm{if}j=k_{i-1}\hfill \\ {\pi }_{i-1}\left[[j-1]\right]\mathrm{otherwise}.\hfill \end{array}\right.$$

(1)

Clearly, if all $k_i$ are uncorrelated random numbers uniformly distributed within their legal ranges, then all ${\pi }_i$ are random and evenly distributed cyclic permutations. We also note that this means that the function $R_i$ is a surjection. However, Equation (1) does not satisfy requirement 2. Consider the following modification:

$${\pi }_i\left[\left[j\right]\right]=\left\{\begin{array}{c}{\psi }_{i-1}\left[{\pi }_{i-1}\left[\left[j\right]\right]\right],\mathrm{if}j<k_{i-1}\hfill \\ i,\mathrm{if}j=k_{i-1}\hfill \\ {\psi }_{i-1}\left[{\pi }_{i-1}\left[[j-1]\right]\right],\mathrm{otherwise}.\hfill \end{array}\right.,$$

(2)

where for all $0\le j<i$

$${\psi }_i\left[j\right]={\rho }_i[j+p_{i}modi]$$

(3)

and

$${\rho }_i\left[j\right]=\left\{\begin{array}{c}j/2,\mathrm{if}j\mathrm{is}\mathrm{even}\hfill \\ (j-1)/2+\lceil i/2\rceil ,\mathrm{otherwise}.\hfill \end{array}\right.$$

(4)

Here, ${\rho }_i$ is the inverse riffle of a deck of size i, and ${\psi }_i$ is the same after a cut at the distance $p_i$.

Here are some examples. For $i=5$, the following is the cut at $p_i=2$ in one-line notation:

$$23401.$$

The inverse riffle of the same length is given as follows:

$$03142.$$

and the following is the combined permutation:

$$20314.$$

From elementary group theory, Equation (2) can be rewritten perhaps more elegantly using the group operation ∘ thus:

$${\pi }_i\left[\left[j\right]\right]=\left\{\begin{array}{c}({\psi }_{i-1}\circ {\pi }_{i-1}\circ {\psi }_{i-1}^{-1})\left[\left[j\right]\right],\mathrm{if}j<k_{i-1}\hfill \\ i,\mathrm{if}j=k_{i-1}\hfill \\ ({\psi }_{i-1}\circ {\pi }_{i-1}\circ {\psi }_{i-1}^{-1})\left[[j-1]\right]],\mathrm{otherwise}\hfill \end{array}\right.,$$

(5)

to emphasise the fact that the transformation of $\pi$ by $\psi$ is conjugation, but Equation (2) suggests a direct implementation in the cyclic representation.

Discussion

Recurrence 2 is well defined since ${\psi }_i$ is a bijection on its domain. Recurrence 1 already delivers a random cyclic permutation at each step. The cut and riffle together shuffle the codomain of this permutation pseudorandomly (like a deck of cards), and the result significantly depends on $p_{i-1}$. The reason why we include the riffle as well as the cut is that we wish to avoid dependency on the sum of ps as the permutations accumulate with each recurrence step. Without the riffle, at step $i+1$ we would observe the cut at the distance $p_i+p_{i+1}$ as the combined result of two steps for all but two components of the permutation cycle. On the other hand, there will be no consistent similarity between ${\pi }_i$ and ${\pi }_{i+1}$ with the riffle. The diffusion will be the greater the more steps have been taken with the recurrence relation, just as the deck of cards will be randomised as the deck is repeatedly cut and riffle-shuffled. This also ensures the satisfaction of requirement 3 above.

4. Preconditioning

Recall that the problem we are attempting to solve is that Moriarty’s attack strategy can be based on the valid ciphertext that he has intercepted. Even though the redundancy in the plaintext makes the acceptance of a random string sampled from the full domain and posing as the ciphertext to a valid plaintext exponentially unlikely, the probability distribution in close vicinity to the valid ciphertext can be uneven. Moriarty is in a position to mount a low-dimensional attack whereby only a few components of the intercepted ciphertext are altered. These close (in some metric sense) alterations may decipher to a valid plaintext with a higher probability, as the example of the Vernam cipher presented earlier suggests.

The template introduced with Proposition 2 ensures that, as we decrypt, alterations of the ciphertext propagate towards the “big end” in terms of the factoradic number system. This makes a low-dimensional attack on all but the greatest values of i very difficult. To achieve a perturbation confined to some area of the plaintext, Moriarty would have to go through all possible combinations of the ciphertext values in that area. The mapping of the ciphertext on the corresponding values of the plaintext in the affected area is random (if the key is unknown), so a full scan through the legal ranges of the Lehmer components is required. However, in the process of scanning, all values of ${\pi }_j$, $j>i$, will be affected as well. This means that the attack cannot be low-dimensional, unless the attack area is flush against the higher end of the interval of i, i.e., big-endian.

Indeed, if, say, three big-endian components, $\nu -3\le i<\nu$, are given all possible legal values, that is, $(\nu -1)(\nu -2)(\nu -3)$ combinations, we are guaranteed that $3!-1=5$ out of them will be deciphered as permutations of the original triplet of plaintext symbols 0, 1, and 2. In the process, none of the other plaintext components will be affected, since alterations propagate only towards the big end and since conversion from Lehmer to one-line representation, although proceeding towards the little end, depends only on the previously processed symbols but not on their relative order. So, for example, for $\nu =20$, the codewords

$$5117<\mathrm{tail}>$$

and

$$1285<\mathrm{tail}>$$

with the same tail, will produce the same one-line representation for the tail. Indeed, in both cases the first three symbols’ positions form the set $\{5,12,8\}$, and the tail components will skip over positions from this set.

This creates the possibility of a low-dimensional attack at a small polynomial cost, an entirely unsatisfactory situation. The attack would have to be on the big-end components of the Lehmer code, and so we require an additional diffusion mechanism that propagates towards the little end.

4.1. Big-Endian Pseudo-Hadamard Transform

Consider the first s Lehmer components of a size-$\nu$ codeword: $W_0,\dots ,W_{s-1}$. The number of combinations of their legal values is clearly

$$Z=\nu \times (\nu -1)\times \dots \times (\nu -s+1)={\displaystyle \frac{\nu !}{(\nu -s)!}}.$$

Now, represent Z as the product of its prime factors:

$$Z=\prod _{j=1}^t{f}_j^{e_j}$$

Proposition 3. 

Let j be a natural index and ν and s be such that

$$(\forall j\le t)f_j^{e_j}<\nu -s+1.$$

Then, there exists a bijective map of $W_0,\dots ,W_{s-1}$ on a sequence of non-negative $r_j$, $j\le t$, where all $r_j<f_j^{e_j}$.

Proof. 

Observe that for fixed $\nu$ and s, the map

$$W=\sum _{i=0}^{s-1}{\displaystyle \frac{(\nu -i)!}{(\nu -s)!}}{W}_i$$

is a bijection. Indeed, $W(\nu -s)!$ is the factoradic value of the truncated Lehmer codeword

$${\check{W}}_i=\left\{\begin{array}{c}{W}_i\mathrm{if}i<s\hfill \\ 0\mathrm{otherwise}\hfill \end{array}\right.$$

and as such is convertible to a sequence of factoradic digits (Lehmer code components) and back. Note that by construction $0\le W<Z$.

On the other hand, the Chinese Remainder Theorem (CRT, [7]) states that there exists a unique non-negative $R<Z$ such that $r_j=Rmod{f}_j^{e_j}$ for all $j\le t$. (This is because all $f_j^{e_j}$ are mutually coprime by construction. Given R, we immediately obtain all $r_j$, and the converse requires a known algorithm with linear complexity.) This means that there exists a bijection $W\to R$.

We conclude that the combined map $\left\{W_i\right\}\to W\to R\to \left\{r_j\right\}$ is bijective. □

Proposition 3 enables a transformation of the original codeword that entangles components $W_0,\dots ,W_{s-1}$ and components $W_{g_1},\dots ,W_{g_t}$, where $g_j=\nu -1-f_j^{e_j}$. Consider the following Pseudo-Hadamard Transform (PHT), introduced in [8] as a building block for a symmetric cipher:

$$\begin{array}{ccc}\hfill R^{*}& =& W+RmodZ\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill W^{*}& =& W+R^{*}modZ.\hfill \end{array}$$

(7)

The inverse transform is as follows:

$$\begin{array}{ccc}\hfill W& =& W^{*}-R^{*}modZ\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill R& =& R^{*}-WmodZ.\hfill \end{array}$$

(9)

This suggests the following enhanced variant of NDOTP. Assume that $\nu$ and s are fixed; we shall return to the choice of these parameters later. For encryption, the steps are as follows:

• Turn the plaintext into a Lehmer codeword using factoradic conversion;
• Turn $W_0,\dots ,W_{s-1}$ into W using truncated factoradic conversion (replacing factorial place values with numbers of permutations);
• Turn $W_{g_1},\dots ,W_{g_t}$ into R using the standard method associated with the CRT;
• Obtain $W^{*}$ and $R^{*}$ by PHT, Equations (6) and (7);
• Calculate new values $W_0^{*},\dots ,W_{s-1}^{*}$ from $W^{*}$ using truncated factoradic conversion and update the Lehmer codeword accordingly;
• Obtain new values $W_{g_1}^{*},\dots ,W_{g_t}^{*}$ from $R^{*}$ by calculating the Chinese remainders, and update the Lehmer codeword accordingly;
• Apply NDOTP encryption to the updated plaintext codeword and obtain the ciphertext codeword, then convert from factoradic to binary.

We call steps 2–6 preconditioning the plaintext. The purpose of preconditioning is to make big-end alterations impossible without altering Lehmer components from the lower-half of the codeword as well. A preconditioned plaintext contains the same information as the original one; it is only the representation that is different.

For decryption, the method is as follows:

• Convert the ciphertext from binary to factoradic. Apply NDOTP decryption to the ciphertext codeword. Obtain the preconditioned plaintext.
• Turn $W_0^{*},\dots ,W_{s-1}^{*}$ into $W^{*}$ using truncated factoradic conversion.
• Turn $W_{g_1}^{*},\dots ,W_{g_t}^{*}$ into $R^{*}$ using the CRT method.
• Obtain W and R by PHT, Equations (8) and (9).
• Calculate original values $W_0,\dots ,W_{s-1}$ from W using truncated factoradic conversion and update the Lehmer codeword accordingly.
• Obtain original values $W_{g_1},\dots ,W_{g_t}$ from R by calculating the Chinese remainders, and update the Lehmer codeword accordingly.
• Turn the resulting Lehmer codeword into the original plaintext by converting factoradic to binary.

4.2. Configuration

The choice of $\nu$ and s has been left out. We will discuss how this choice affects the non-degeneracy of the cipher in the next subsection. But first, let us focus on quantifying the parameters.

Recall that Proposition 3 has the following condition. For any choice of $\nu$ and s there exist a positive t and prime numbers $f_j$, $j=1,\dots ,t$ such that

$$\nu \times (\nu -1)\times \dots \times (\nu -s+1)=\prod _{j=1}^t{f}_j^{e_j},$$

(10)

where all $e_j$ are natural numbers. This factorisation is unique up to the ordering of $f_j$. The choice of $\nu$ and s is valid only when

$$(\forall j\le t)f_j^{e_j}<\nu -s+1.$$

(11)

Obviously, for every valid pair $(\nu ,s)$ there is the pair $(\nu ,s^{\prime })$, where $1<s^{\prime }<s$ is also valid, so we are interested in the greatest s for each given $\nu$. Also observe that if the interval $[\nu ,\nu -s+1]$ contains a power of a prime, then it must be one of the factors $f_j^{e_j}$, and so the condition in Equation (11) is broken. With this in mind, we have performed a direct search for suitable parameters for $\nu <200$ (message sizes up to, or around, 2 Kb), see

Table 1. Factorisation data for the lowest $\nu$ of a given $s_{\max }$. The first column shows the corresponding plaintext/ciphertext size in bits.

n	$\mathit{\nu }$	${\mathit{s}}_{\mathbf{max}}$	${\mathit{f}}_{\mathit{j}}^{{\mathit{e}}_{\mathit{j}}}\phantom{3^{3^{3^3}}}$
69	22	3	3, 5, 7, 8, 11
138	36	4	5, 7, 8, 11, 17, 27
382	78	5	7, 9, 11, 13, 16, 19, 25, 37
491	95	6	7, 13, 16, 19, 23, 25, 27, 31, 47
851	147	7	5, 11, 13, 29, 47, 49, 64, 71, 73, 81
1299	207	8	7, 17, 23, 29, 41, 67, 81, 101, 103, 125, 128
2066	303	9	7, 11, 13, 23, 37, 43, 59, 101, 125, 128, 149, 151, 243

, noting the first values of $\nu$ for which $s_{\max }$ leaps up.

4.3. Discussion

A preconditioned plaintext makes the big-endian attack infeasible even for a small s. The attacker would have to try all possible combinations of the first s components of the Lehmer codeword at the big end, since the mapping of the components of the ciphertext on the corresponding components of the preconditioned plaintext is, although bijective, still random thanks to the encipherment, according to Proposition 2. Since it is a bijection, if all combinations are attempted in the ciphertext, then after decryption all combinations of the preconditioned plaintext will be seen, too, albeit in a different order. As the preconditioning is reversed, all the original values of the first s Lehmer components will be covered, as follows from Equation (8). However, as evidenced by Equation (9), at the same time all values of the Chinese remainders will also be seen in some order. Since the positions $\left\{f_j^{e_j}\right\}$ are scattered over the little-end half of the Lehmer codeword, and they are not dense in it, the reconstruction of the original sequence of symbols will potentially affect all symbols from the left-most position of the set down. For example, as evidenced by Table 1, for $\nu =95$, scanning through the first six components of the ciphertext would potentially affect all components from 47 to 1, which is half of the Lehmer word size. To stop this happening, Moriarty could also scan through the values in the position set $\left\{f_j^{e_j}\right\}$ to try and find a combination that results in a close (in the metric sense) permutation of the original. This, however, would not work, since the cipher is left-propagating: a change in any values in the position set will affect the decryption of all the subsequent values towards the big end, thus destroying the local character of the attack.

For ease of reference, we provide the formula for step 3 of the encryption and decryption sequences, based on the Extended Euclid Method [7]. For encryption, the computation of R is as follows:

$$R=\sum _{i=1}^t{W}_{g_i}{b}_i{b}_i^{\prime }modZ$$

(12)

where

$$b_i=Z/f_i^{e_i}$$

and

$$b_i^{\prime }=b_i^{-1}mod{f}_i^{e_i},$$

and similarly for $R^{*}$ for decryption. Note that $b_i^{\prime }$ exists and is unique due to $b_i$ and $f_i^{e_i}$ being coprime by definition. Also note that all $b_i{b}_i^{\prime }$ in Equation (12) can be precomputed for the choice of $\nu$ and so Step 3 involves t modulo multiplications and $t-1$ additions and has a sublinear complexity in $\nu$.

Yet one question remains. The minimum alteration of a component that belongs to the position set is 1. This follows from the fact that by scanning through the s big-end components, all combinations of the Chinese remainders are enumerated. In particular, there will be a combination of big-endian values that results in the same remainders as those for the original plaintext, except the value in the position closest to the little end. In the case $\nu =95$, this would be position 7. In particular, the alteration in the value in this position from the original plaintext could result in any value less than 7, including 1, which leads to at most a single transposition of symbols (recall that the plaintext here is a Lehmer codeword). We conclude that the proposed scheme still leaves open the opportunity of an attack with no more than $s+1$ transpositions. Even though the statistical weight of such perturbations is small, we should seek a stronger diffusion mechanism that works toward the little end, which is our next step.

4.4. Differentiating the Lehmer Code

Definition 1. 

Let p be a permutation of $0,\dots ,\nu -1$ and let $\langle p_i\rangle$ be its Lehmer codeword. The first derivative $\langle p_i^{\prime }\rangle$ of the permutation is defined by the following recurrence relations:

$$p_{\nu -1}^{\prime }=p_{\nu -1}=0,p_{\nu -2}^{*}=p_{\nu -2};$$

(13)

for $i=2,\dots ,\nu -1$:

$$\begin{array}{ccc}\hfill p_{\nu -i}^{\prime }& =& p_{\nu -i}^{*}-p_{\nu -i-1}modi\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill p_{\nu -i-1}^{*}& =& p_{\nu -i-1}-p_{\nu -i}^{\prime }-1modi+1\hfill \end{array}$$

(15)

Finally,

$$p_0^{\prime }=p_0^{*}$$

(16)

Note that the first derivative satisfies the Lehmer code constraint:

$$0\le p_i^{\prime }<\nu -i\mathrm{for}\mathrm{all}0\le i<\nu -1,$$

and so it is a Lehmer codeword in its own right. This makes it possible to combine pre-differentiation with NDOTP.

Proposition 4. 

The mapping of a Lehmer codeword $\langle p_i\rangle$ onto its first derivative $\langle p_i^{\prime }\rangle =\mathcal{D}\left(\langle p_i\rangle \right)$ is bijective. The inverse mapping ${\mathcal{D}}^{-1}$ is given by the following recurrence relation:

$$p_0^{*}=p_0^{\prime };$$

(17)

for $i=0,\dots ,\nu -3$:

$$\begin{array}{ccc}\hfill p_i& =& p_i^{*}+p_{i+1}^{\prime }+1mod\nu -i\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill p_{i+1}^{*}& =& p_i+p_{i+1}^{\prime }mod\nu -i-1\hfill \end{array}$$

(19)

Finally,

$$p_{\nu -2}=p_{\nu -2}^{*}$$

(20)

$$p_{\nu -1}=0$$

(21)

Proof. 

Substitute j for i in Equation (14) and j for $\nu -i-1$ in Equation (19); they will become identical. Use the same substitutions with Equations (15) and (18), respectively, and they, too, will become identical. The boundary conditions Equations (13) and (16) are consistent with those given by Equations (17), (20) and (21). □

Discussion

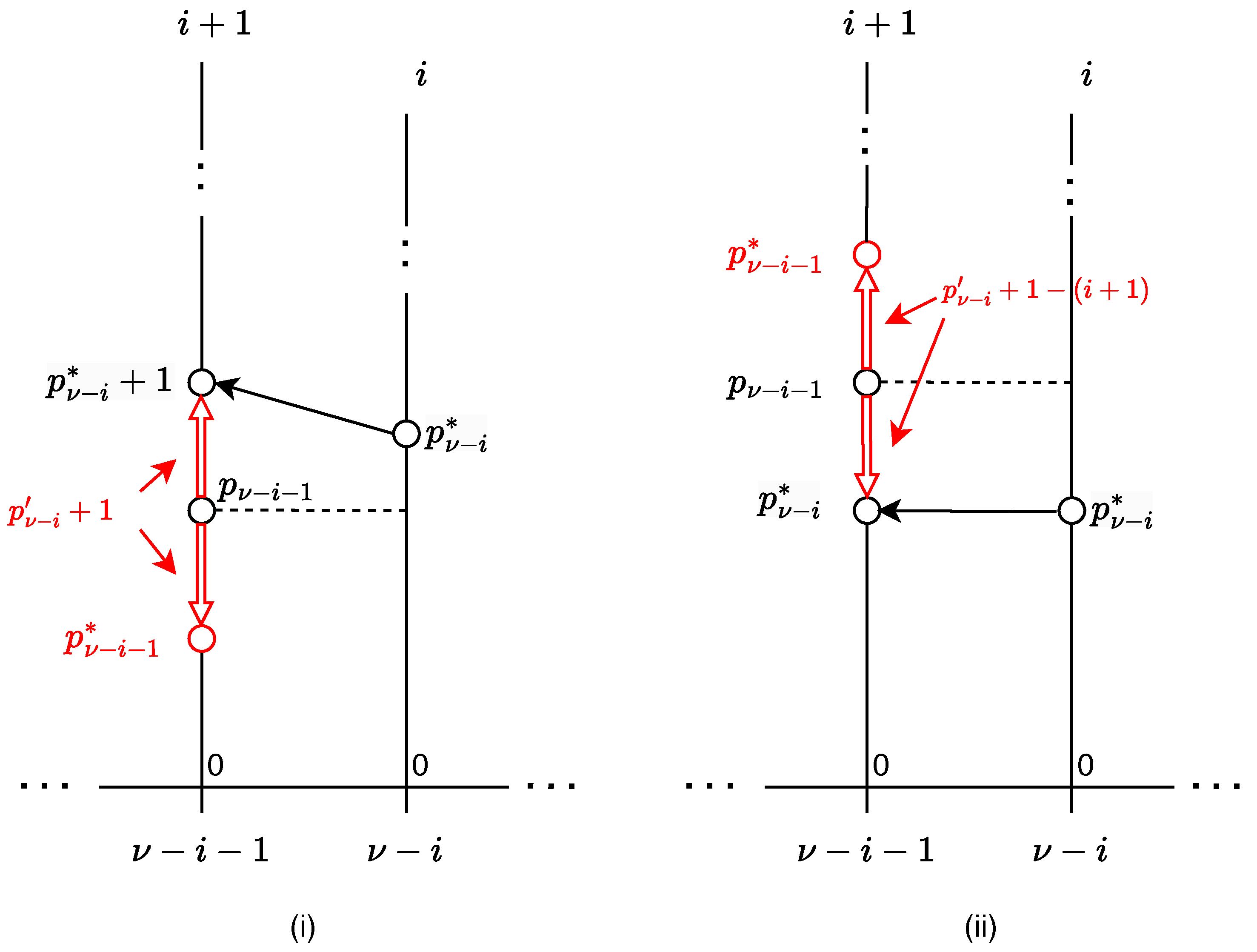
The diagram in Figure 2 illustrates the relationship between the current and next state of the recurrence relation defined by Equations (14) and (15) and helps to understand the properties of the proposed derivative. It is convenient to consider two separate cases, $p_{\nu -i}^{*}\ge p_{\nu -i-1}$ (case (i)), and $p_{\nu -i}^{*}<p_{\nu -i-1}$ (case (ii)), even though they are captured by the same pair of equations.

We start with the first case, and treat the Lehmer component for the symbol $\nu -i$ as a position of the symbol in the sequence taking into account the potential skip over the symbol $\nu -i-1$, which happens if $p_{\nu -i}^{*}\ge p_{\nu -i-1}$, as is the case here. To calculate the position difference, symbol $\nu -i$ should be placed in the domain of symbol $\nu -i-1$, which requires incrementing the Lehmer component of the former. Next, we determine the distance by travelling in the positive direction from the lesser symbol towards the greater one, as the red arrow indicates. Clearly, since the image of $p_{\nu -i}^{*}$ in the domain of $\nu -i-1$ never collides with $\nu -i-1$ and since there are $i+1$ positions in total (from 0 to i) available to the symbols, the distance between them is in the range $[1,i]$. If we subtract 1 from the distance, we can assign the result to the derivative component $p_{\nu -i}$, which takes values from the range $[0,i-1]$. The procedure is consistent with Equation (14). Finally, we reverse the direction of the distance vector and shift $p_{v-i-1}$ down, Equation (15). The value $p_{\nu -i}^{\prime }$ is the outcome of differentiation, and $p_{\nu -i-1}^{*}$ represents the next state of the recurrence.

Case (ii) is similar, except $p_{\nu -i}^{*}<p_{\nu -i-1}$, and so there is no skip. We do not increment $p_{\nu -1}^{*}$ when we map it on the domain of the symbol $\nu -i-1$. The distance is now negative and we must add $i+1$, the modulus for the symbol $\nu -i-1$, and only then, for reasons exposed with case (i), we also subtract one from the result. We arrive at the same equation, Equation (14). The shift that produces the next state now happens in the opposite direction as well, which is in accordance with Equation (15).

The above diagrams also help to understand the integration defined by Equations (18) and (19), but more importantly, they show the sensitivity of differentiation. Substituting Equation (18) in Equation (19), we obtain

$$p_{i+1}^{*}=(p_i^{*}+p_{i+1}^{\prime }+1mod\nu -i)+p_{i+1}^{\prime }mod\nu -i-1$$

(22)

from which we can see that $p_{i+1}^{*}$ depends on both $p_i^{*}$ and $p_{i+1}^{\prime }$. A change in $p_j^{\prime }$ will result in a change in $p_j^{*}$ for any given j: the red arrows on the diagram are of a length less than the modulus $i+1$ by construction. Furthermore, a change in $p_j^{*}$ will result in a change in $p_{j+1}^{*}$, even if $p_{j+1}^{\prime }$ remains the same. Changes in $p^{*}$ will propagate towards the little end (high indices), affecting all ps along the way. This may seem like a much stronger diffusion mechanism than the preconditioning, described in Section 4.1. However, many combinations of $p_i$ with $i<j$ for some j sufficiently greater than 0 will result in the same $p_j^{*}$, and then it follows from Equation (22) that all $p_{i>j}$ will remain the same for each of those combinations, thus enabling a low-dimensional attack. Only the combined effect of the differential plaintext and the Pseudo-Hadamard Transform on the big-endian components can make the big-endian attack impractical.

For example, for the case $\nu =95$, $s=5$, see Table 1, the attacker will have to try every combination of the first seven ciphertext components. Due to the left-propagation of the decryption process, no modification of the remainder positions 7, 13, 16, … or their vicinity is possible, since that would affect the decryption of all positions towards the big end, and the integration process will propagate to the little end the new values of the remainders changed as a result of the Pseudo-Hadamard Transform of the changed big-end values. This means that the last 47 positions will all be affected in addition to the directly affected seven (the six in the transform plus another one to stop the run-away integration process) at the big end.

To assess the diffusion properties of differentiation, recall from the metric theory of the symmetric group that the average Cayley distance between two random permutations of a length-$\nu$ sequence is $\nu -ln\nu$ [9]. Let us take the first derivative of an arbitrary permutation $a^{\prime }$, alter the first element of its sequence at random, and integrate the result to obtain some permutation A. We obtain an ensemble of A, in which we determine the Cayley distance (the minimum number of transpositions required to reach the destination) from each to a, $T(a,A)$. Now, we calculate the mean distance and average it over a. If the diffusion from differentiating is good, we should obtain the average distance in this ensemble close to the average distance in the whole group. 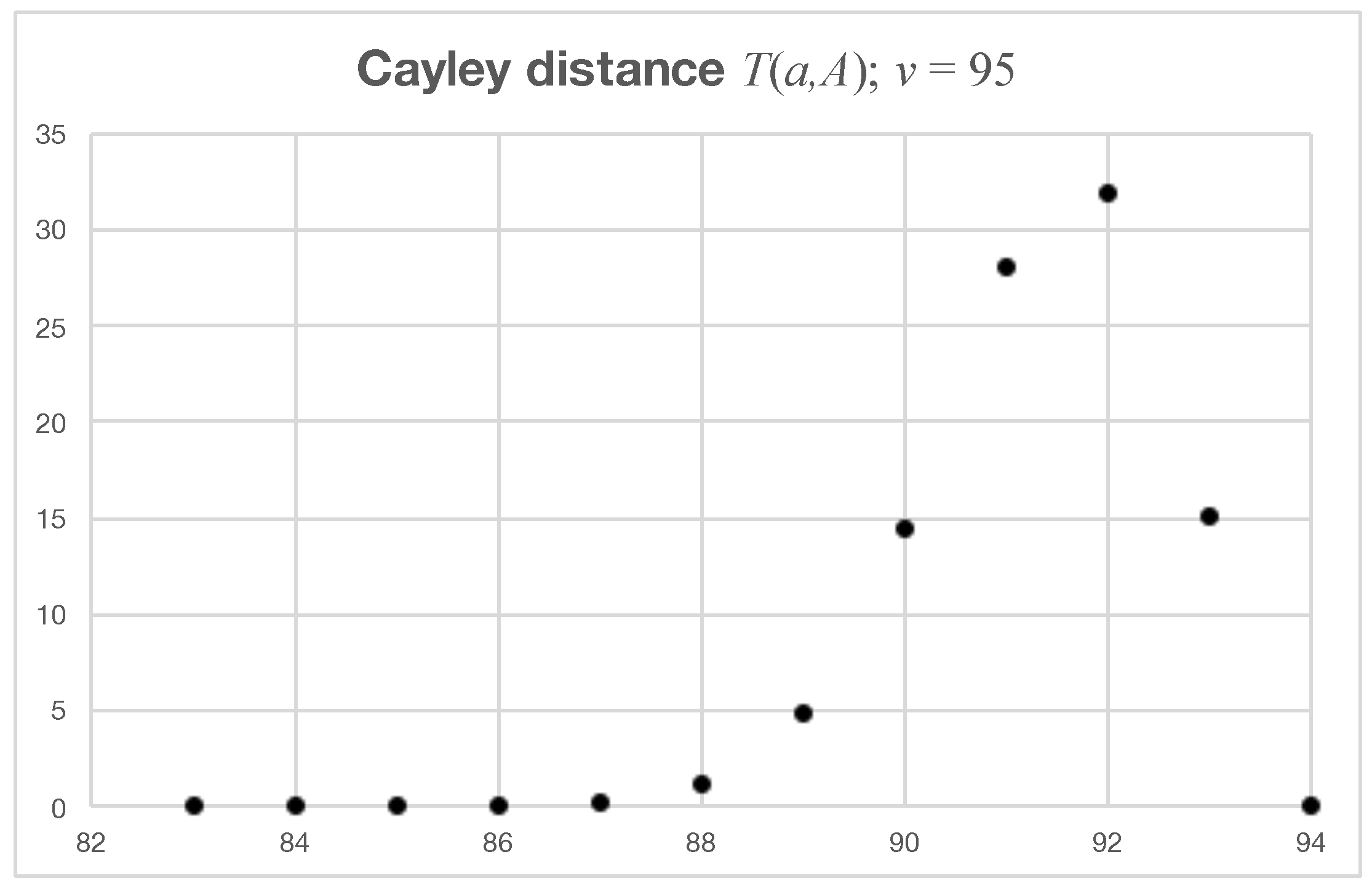Figure 3 shows the histogram of $T(a,A)$ that we obtained by Monte Carlo simulation for $\nu =95$. Although a crude measure, the mean distance is very close to that between a pair of permutations chosen at random, which suggests strong diffusion. The choice of metric (the Cayley distance) is not unique, since several others are available (the more familiar Hamming distance, widely used in cipher analysis, among them). However, our proposed method of redundancy injection (see the next section) is sensitive to transpositions, and so a transpositional distance seems the most pertinent.

5. Injecting Redundancy

In the previous sections, we developed an ND OTP with random diffusion towards the big end and a preconditioning that helps to diffuse towards the little end a big-endian attack on the ciphertext, especially if the plaintext is pre-differentiated. These measures should pave the way to the application of standard redundancy mechanisms within the plaintext that are robust enough with respect to an unlocalised random perturbation. Such redundancy could be introduced in the original binary message using a simple linear code. However, once the factoradic conversion has been performed, redundancy can also be injected into the target representation. As it turns out, a function exists that requires nothing more than a lookup table for its implementation, and whose mapping is robust enough to withstand even the most localised attack, albeit with a slightly increased redundancy overhead. We will define this function next.

5.1. Pseudo Foata Injection

Dominique Foata is known for his extensive contribution to combinatorics, among which there is the so-called Foata bijection [10]. This bijection is a map of the symmetric group onto itself based on a “pun”, i.e., deliberate misreading of the cyclic representation of a permutation as the one-line one. Foata takes credit for finding that under a particular ordering of the cycles, the pun is invertible and the map is a bijection. We use Foata’s pun to create an injection into the next order of the group, rather than a bijection.

Definition 2. 

For a natural n, the Pseudo Foata Injection (PFI) is a map ${\mathfrak{F}}_n:S_n\to S_{n+1}$ defined as follows. Let ${\langle p_i\rangle }_{0\le i<n}$ be the one-line representation of a permutation p from $S_n$. Then, ${\mathfrak{F}}_n\left(p\right)$ is the permutation q, whose cyclic representation consists of a single cycle.

$$(p_0,\dots ,p_{n-1},n).$$

The injective property of the PFI is obvious from its definition. The one-line representation of q, ${\langle q_i\rangle }_{0\le i<n+1}$ follows directly from Definition 2 as well:

$$q_i=\left\{\begin{array}{cc}{p}_{m+1}\hfill & \mathrm{if}(\exists m<n-1)p_m=i\hfill \\ n,\hfill & \mathrm{if}{p}_{n-1}=i,\hfill \\ p_0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Definition 3. 

A partial function ${\mathfrak{F}}_{n+1}^{-1}:S_{n+1}\to S_n$ is defined on the subset of $S_{n+1}$ that comprises all single-cycle permutations q. Since the cyclic representation of q, $(q_0,\dots ,q_n)$, is ambiguous, we can assume without loss of generality that $q_n=n$ (if not, rotate the cycle until the equation holds). Function ${\mathfrak{F}}_{n+1}^{-1}$ maps every q onto the p whose one-line representation is $q_0,\dots ,q_{n-1}$.

Proposition 5. 

For all $p\in S_n$, ${\mathfrak{F}}_{n+1}^{-1}\left({\mathfrak{F}}_n\left(p\right)\right)=p$.

Proof. 

Follows from Definitions 2 and 3. □

Corollary 1. 

For any $n,k>0$, $p\in S_n$, ${\mathfrak{F}}_{n+k}^{-k}\left({\mathfrak{F}}_n^k\left(p\right)\right)=p$.

Proposition 6. 

The density of the image of ${\mathfrak{F}}_n$ in its codomain is $1/(n+1)$.

Proof. 

The PFI is an injection, so the density is the domain-to-codomain ratio: $|S_n|/|S_{n+1}|=1/(n+1)$. □

The following are corollaries of the above for repeated application of the PFI.

Corollary 2. 

The density of the image of ${\mathfrak{F}}_n^k$ in its codomain is $n!/(n+k)!$

In the above corollaries,

$${\mathfrak{F}}_n^k\left(p\right)={\mathfrak{F}}_{n+k-1}(\dots {\mathfrak{F}}_{n+1}({\mathfrak{F}}_n\left(p\right)\dots ))$$

and

$${\mathfrak{F}}_{n+k}^{-k}\left(p\right)={\mathfrak{F}}_{n+1}^{-1}(\dots {\mathfrak{F}}_{n+k-1}^{-1}({\mathfrak{F}}_{n+k}^{-1}\left(p\right)\dots ))$$

denote repeated application of the function $\mathfrak{F}$ and its inverse, respectively. Let us set $\nu =85$ as an illustration and consider the redundancy injection by ${\mathfrak{F}}_{\nu }^{10}$ to obtain a plaintext for the NDOTP sized 95, which we use as a running example. Using Corollary 2 and assuming the attack results in a random deviation from the plaintext after deciphering (de-preconditioning, etc.), we conclude that the success probability of the attack is $85!/95!<2.8\times {10}^{-20}$, which is the probability expected from a 64-bit redundancy code.

As a concluding remark, we wish to mention that the complexity of the PFI is linear in n, and the implementation only uses table lookups and table storage, so it is probably the fastest way of injecting redundancy into a message if the message is already in the form of a permutation in the one-line representation. With NDODT, the binary message is turned into factoradic/Lehmer first; to utilise the PFI, the Lehmer code would have to be converted to one-line representation (at a quadratic cost) and then back (also at a quadratic cost) for the message with redundancy to be enciphered. Similar conversions would have to be made after deciphering.

5.2. Statistics of the PFI

We have discovered that despite its simplicity, the PFI is quite robust in resisting low-dimensional attacks, i.e., the type of attack that we introduced pre-conditioning and differentiation to thwart. To obtain a statistical illustration, we performed a Monte-Carlo experiment in which we performed the following:

(1)

Used 100,000 random 50-symbol plaintexts and injected them with 10 more symbols using ${\mathfrak{F}}_{50}^{10}$.

(2)

Each of the 100,000 60-symbol results was subjected to all possible perturbations with a Cayley distance of 2 using the transposition pattern $abc\to bca$ exhaustively.

(3)

Attempted an appropriate ${\mathfrak{F}}^{-1}$ on each transposition result repeatedly until the result became acyclic. The penetration depth, i.e., the number of successful applications of ${\mathfrak{F}}^{-1}$ before the result becomes acyclic, was histogrammed.

In point 2 above, the reason for using distance 2 is that a single transposition (Cayley distance 1) breaks a single cycle into two, which makes ${\mathfrak{F}}^{-1}$ undefined on the result. The chosen pattern is a smaller perturbation than the other one available at distance 2, i.e., $(ab\to ba,cd\to dc)$ in terms of another important metric, Hamming, and so represents the smallest possible perturbation of the sequence. More than $2\times {10}^{10}$ outcomes in total were collected. 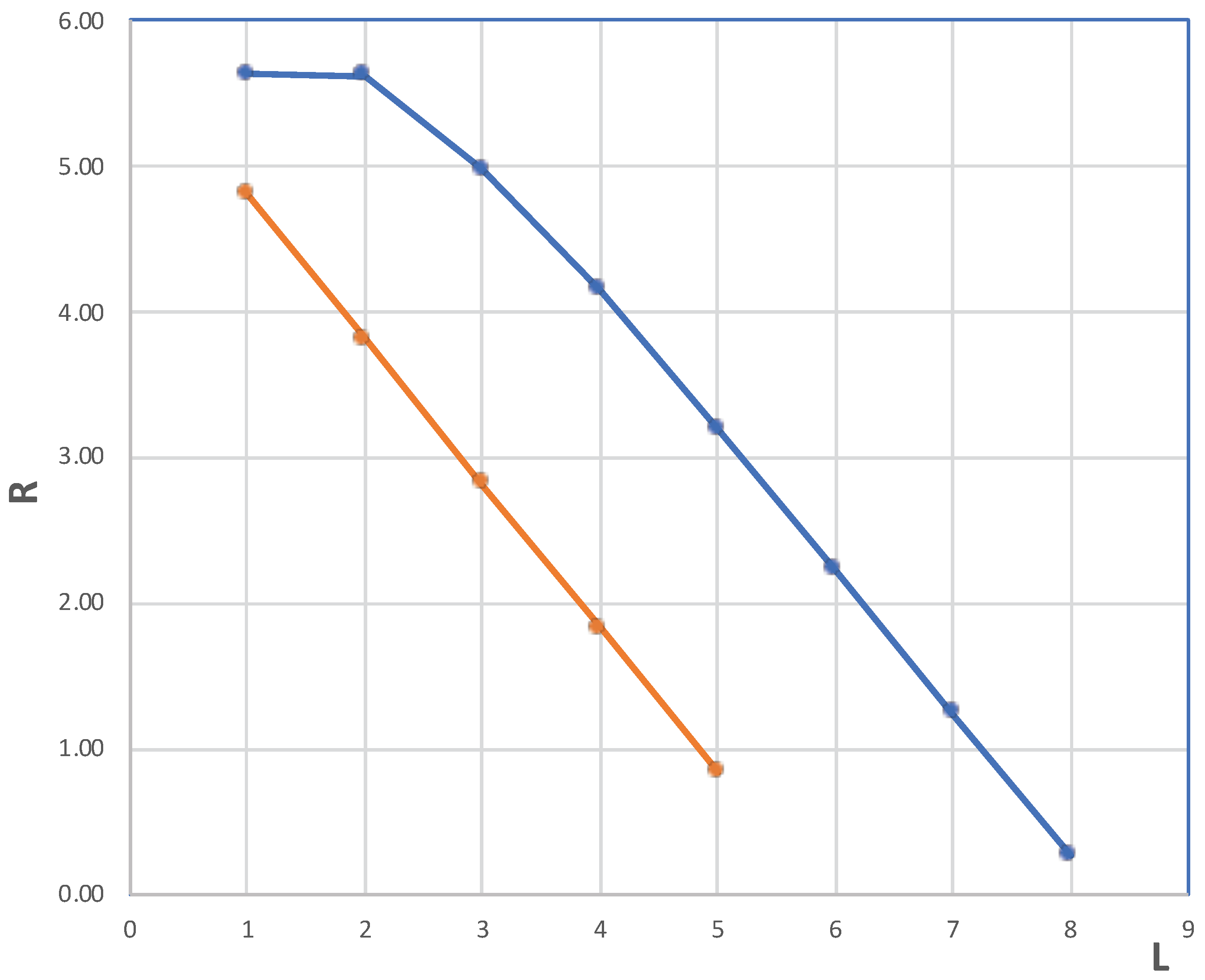The results are displayed in Figure 4.

The penetration statistics are placed on the logarithmic scale using base 60, so that the vertical drop of one unit represents the reduction by a factor of 60. If completely random permutations were presented to the inverse PFI, one would expect the curve to decline nearly linearly, in accordance with Corollary 2, see the orange curve. Since we deliberately tried the closest possible permutation to the one that actually satisfies the tenth power of ${\mathfrak{F}}^{-1}$, we observed a much higher penetration rate, a factor of ${60}^2$ higher. As shown from the plot, we increased the number of PFI applications by 3, i.e., going from 5- to 8-symbol redundancy levels off the difference in the worst-case scenario of the low-dimensional attack. To put things in perspective, after $2\times {10}^{10}$ attempts on behalf of Moriarty, we have not seen a single outcome at depth 9; we must have been two orders of magnitude away in the number of attempts for successful penetration.

6. Related Work

One of the earlier works where secrecy and integrity were approached as separate concerns even for a perfect cipher was by Desmedt [11]. However, the seminal work in the area of unconditional integrity was published by Carter and Wegman [12], where the method was proposed based on a family of so-called universal₂ hash functions. A message to be sent consists of the message proper $m\in M$ and its integrity tag $t\in T$. The family H is of functions $M\to T$, and it has the property that for any messages $m_1\ne m_2$,

$${\displaystyle \frac{\left|\right\{h\in H\mid h\left(m_1\right)=h\left(m_2\right)\left\}\right|}{\left|H\right|}}\le 1/\left|T\right|.$$

The family H is typically indexed by a key K, $H={\langle h_K\rangle }_{K\in {\{0,1\}}^L}$.

Later on [13], a more restrictive class of families was defined, called strongly universal_n. Such a family contains exactly $\left|H\right|/{\left|T\right|}^n$ functions that map any n pairwise distinct messages $a_1,\dots ,a_n$ onto any n (not necessarily pairwise distinct) tag values $t_1,\dots ,t_n$. Also, the fixed security parameter $1/\left|T\right|$ has been generalised to an arbitrary $ϵ$, giving rise to $ϵ$-Almost Strongly Universal₂ hash functions. But let us return to the integrity assurance.

The idea is that Alice and Bob share a secret K chosen at random. Alice then uses $h_K$ from a pre-agreed strongly universal family to produce an authentication tag $h_K\left(m\right)$, enciphers the tag using an OTP, and then sends it to Bob along with the message m. Bob produces his own tag value using the received message $m^{\prime }$, $t^{\prime }=h_K\left(m^{\prime }\right)$ and compares it with what Alice sent, after deciphering. Although Moriarty can intercept and alter m to $m^{*}$, he can only guess K, since t is perfectly secret (whereas m may not be secret at all). Moriarty is thus unable to compute the new tag $t^{*}$, but if he chooses it at random, strong universality₂ limits his success probability to $1/\left|T\right|$.

This avenue of research is still active, even though the early works were published more than 40 years ago. Various families of universal hash functions continue to be constructed and their applications to cybersecurity stretch as far as QKD protocols (e.g., see a recent paper [14]). Since universal hash families provide purely statistical guarantees (they are unconditional), they will work with standard binary OTPs.

Implementation of universal families generally follows two methods. One, which was proposed in the very first publications on the matter, is number-theoretical. The hash value is achieved as an affine product of the key and the message, both represented as vectors with components modulo a prime number. There are number-theoretical reasons why the result is well spread over the tag space, which makes the construction strongly universal. The other method was proposed in [15], and it is based on a random matrix, produced from a key with the help of a linear feedback shift register. Both methods originally required a key that was longer than the message itself. However, new structures were put forward, which reduced the key length to just over four times the tag length n, with the latter defining the probability of forgery as $2^{-n}$. For more details, see [3], where Table 3 summarises the known methods in terms of their security parameter and key length.

There is an important difference between integrity provided by universal hashing and our approach. The statistical guarantee of the former comes from a physically random key that injects entropy into the tag. Our proposal, the Pseudo Foata Injection, does not rely on the entropy of the mapping parameter for its effect. Instead, by making the cipher non-degenerate, we deny Moriarty a chance to make localised (we call them low-dimensional) alterations to the redundant plaintext. As a result, any change in the intercepted ciphertext results in random (due to the OTP’s random key), unpredictable (due to the Pad’s non-degeneracy) changes to both the “message” and its “tag”; these are inseparable and well spread out in the PFI output. As a result, the probability of Moriarty’s success is defined solely by the cardinality ratio of the PFI range to codomain, just like the security of the universal hash family is determined by a similar cardinality ratio: the set of colliding hash functions to the full set.

The material gain of our approach is that we do without a random “integrity key”, which, as we mentioned, could reach four times the amount of redundancy injected by the tag. In our case, the injected redundancy accords with Corollary 2, but the only extra key material that we need for it is that for the lengthened OTP key to cover the longer message. OTP protection of the tag would require the same in addition to the integrity key.

7. Conclusions

We have presented four tools from a toolkit that provides perfectly secret messages with an integrity assurance. The primary result of this work is the construction of a non-degenerate OTP, Section 3. The key advantage of the proposed ND OTP is the fact that it can use the encryption key without constraining it (and thus destroying the perfect secrecy) for a second purpose: to entangle the encipherment of units of the plaintext. Normally, the key cannot be used twice, since the trijection requirement would necessitate the consistency of both uses for any pair of plain- and ciphertexts. However, the ability of any cyclic subgroup of permutations to deliver a given symbol in any given position of a sequence decouples the two uses. The entanglement, however, works only in one direction (little to big end), and so the diffusion introduced by the non-degeneracy is not all-with-all. However, the nature of the entanglement is random, as it is based on the encryption key. The latter has to be physically random, i.e., have maximum entropy, to prevent information leakage from plain- to ciphertext, and we are able to utilise this entropy in the entanglement. Another key advantage is the favourable differential behaviour of NDOTP: even at the big end, where there is no diffusion to the left, it is impossible to predict the effect of a small change of the ciphertext on the plaintext: the cyclic subgroup that performs this mapping is dependent on the random key. As a result, a small deviation of the plaintext can only happen in the course of an exhaustive search through the ciphertext components of interest.

To address the unidirectional diffusion property of the proposed encryption, we introduced two further mappings. One is based on PHT/CRT, see Section 4.1, and it entangles a number of big-end components of the plaintext with some of its components in the little-end part. The latter components cannot be profitably altered by Moriarty by altering the corresponding components of the ciphertext: all plaintext components to the left of the affected area would be potentially altered in the process of deciphering the message. Yet, there is only a small number of little-end components affected by any alteration of the big-end ones, see Table 1. To make the diffusion to the right stronger, we proposed a further mapping: that of the plaintext on its first derivative, Section 4.4. Differentiating the Lehmer code has a useful side-effect of entangling the little-end components involved in the PHT/CRT, as well as any components in between and to the right of them. In our Monte-Carlo experiments, we found that differentiation makes the plaintext strongly dependent on its derivative: an alteration in the leftmost component of the derivative results in the change in the plaintext by a distance close to the average distance between members of the symmetric group. In other words, differentiation makes the plaintext extremely sensitive to alterations in even one of its components. The sensitivity is directional: the affected components are on the right of the affected area.

Finally, we proposed a method of injecting redundancy. Whereas all the above processing is performed in the Lehmer representation, the Pseudo Foata Injection requires the one-line representation, which can be obtained from the Lehmer one at a quadratic cost. This should not be a problem, since the factoradic conversion and the NDOTP encipherment/decipherment are also of quadratic complexity. Note that the conversion from the Lehmer to the one-line representation introduces useful diffusion to the right, see Section 3.1 and Figure 1.

The PFI is a linear-complexity procedure and it does not involve computation beyond table lookups. We have evaluated its statistical properties on the ensemble of perturbations that are extremely unlikely to be at Moriarty’s disposal in light of the properties of PHT/CRT and differentiation discussed above: minimum deviation from the valid redundancy-injected message. Yet, we discovered that even in these circumstances, the PFI is quite robust: it is capable of rejecting “near” alterations at the expense of just a few additional redundant components (three in our case).

Looking back at the above results, we believe we can make the following conclusions.

The four mappings, NDOTP, PHT/CRT, differentiation, and the PFI, constitute a toolkit for integrity assurance of perfectly secret messages. Used separately and in combination, they make it possible to find a solution with the right latency and resource footprint for individual circumstances:

• NDOTP can be combined with the PFI directly, but the redundancy parameter k should be increased to resist a big-endian attack. Our experiments show that a small increase is sufficient, but further data are needed to tighten the requirements.
• The PFI can be used with other forms of encryption to provide the benefit of distributed redundancy so that Moriarty is unable to attack the “tag” and the “message” separately.
• When the preconditioning, NDOTP and the PFI are combined, we enjoy the most economic form of perfectly secret communication: the length of the key is equal to the sum of the message length, and injected redundancy with all algorithms having no more than quadratic complexity; the result has perfect secrecy and unconditional integrity with a predictable probability of forgery.