Affine Cipher Encryption Technique Using Residue Number System
Abstract
1. Introduction
1.1. Contribution
- (1)
- A new efficient technique for the encryption of information flows based on a combination of affine ciphers and the RNS is developed, and its scheme and mathematical justification are proposed;
- (2)
- An example of affine encryption using RNS is given, in which the calculation of the basic parameters of the RNS, key generation, as well as the encryption and decryption features are considered;
- (3)
- It is determined that the cryptographic strength of the proposed system depends on the number of moduli and their bit size;
- (4)
- The parameters of the cryptographic system, which has the same resistance to cryptanalysis as the AES-256 symmetric encryption standard, are defined.
1.2. Organization
2. Related Work
3. Materials and Methods
3.1. Analysis of Affine Ciphers
3.2. Theoretical Foundations of the Residue Number System
- (1)
- All moduli are relatively prime;
- (2)
- The selected number N is less than the product of all moduli: , where k is a number of moduli.
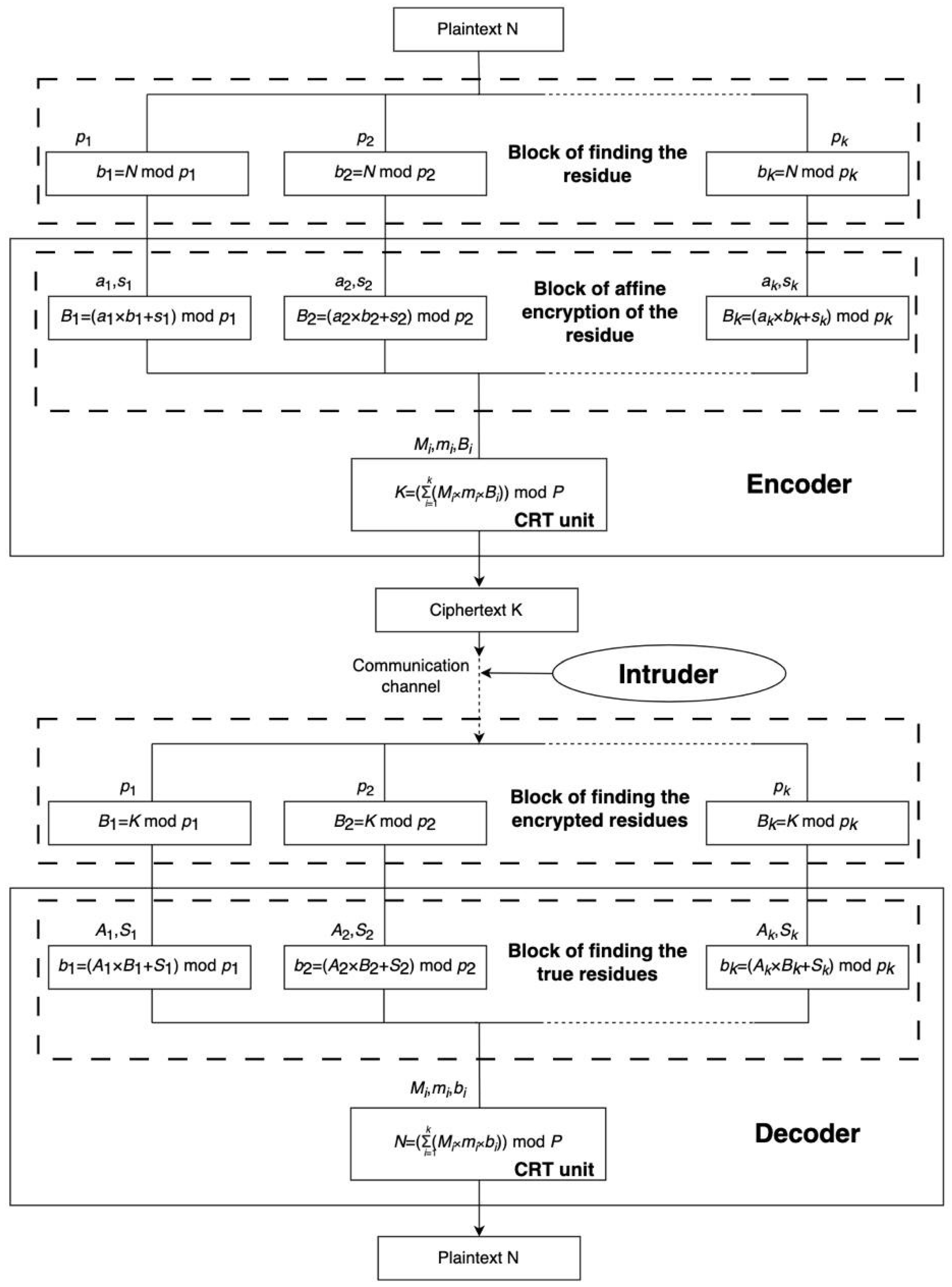
3.3. Affine Ciphers in the Residue Number System
| Algorithm 1: The ACRNS encryption algorithm |
| Input: N—number to be encrypted pi—list of pairwise coprime moduli [p1, p2, …, pk] ai, si—encryption keys, where 0 < ai < pi, 0 ≤ si < pi, GCD(ai, pi) = 1 Output: K—encrypted number function Encrypt(N, pi, ai, si): // Compute remainders of N modulo each modulus for x from 0 to k − 1: r = N mod pi[x] b.append(r) // Encrypt each remainder using the affine cipher: // B[x] = (ai[x] × b[x] + si[x]) mod pi[x] for x from 0 to k − 1: encrypted = (ai[x] × b[x] + si[x]) mod pi[x] B.append(encrypted) // Compute modular inverse using Extended Euclidean Algorithm function modular_inverse(a, m): t, newt = 0, 1 r, newr = m, a while newr ≠ 0: quotient = r // newr t, newt = newt, t − quotient × newt r, newr = newr, r − quotient × newr if r > 1: error “Inverse does not exist” if t < 0: t = t + m return t // CRT to reconstruct the encrypted number function CRT(residues, moduli): P = 1 for p in moduli: P = P × p result = 0 for i from 0 to length(moduli) − 1: pi = moduli[i] ri = residues[i] mi = P/pi mi_inv = modular_inverse(mi, pi) result = result + ri × mi × mi_inv return result mod P // 5. Build encrypted number K from wrong remainders K = CRT(B, pi) return K |
| Algorithm 2: The ACRNS decryption algorithm |
| Input: K—the encrypted number pi—list of moduli [p1, p2, …, pk] ai, si—encryption keys, where 0 < ai < pi, 0 ≤ si < pi, GCD(ai, pi) = 1 Output: N — decoded number function Decrypt(K, pi, ai, si): k = length(pi) B = [] // encrypted remainders extracted from K // Extract encrypted remainders by taking K mod each pi for x from 0 to k − 1: r = K mod pi[x] B.append(r) // Recover original remainders using inverse affine transformation b = [] # decrypted (correct) remainders for x from 0 to k − 1: ai_inv = modular_inverse(ai[x], pi[x]) b_x = (ai_inv × (B[x] − si[x])) mod pi[x] b.append(b_x) // Modular inverse function function modular_inverse(a, m): t, newt = 0, 1 r, newr = m, a while newr ≠ 0: quotient = r // newr t, newt = newt, t − quotient × newt r, newr = newr, r − quotient × newr if r > 1: error “Inverse does not exist” if t < 0: t = t + m return t // Use CRT to recover the original number from correct remainders function CRT(residues, moduli): P = 1 for p in moduli: P = P × p result = 0 for i from 0 to length(moduli) − 1: pi = moduli[i] ri = residues[i] mi = P/pi mi_inv = modular_inverse(mi, pi) result = result + ri × mi × mi_inv return result mod P // Recover the original number N N = CRT(b, pi) return N |
3.4. Special Cases of Affine Ciphers
4. Results
4.1. An Example of Affine Ciphers Using the Residue Number System
4.2. Example of the Use of Special Cases of Affine Ciphers
5. Discussion of the Results
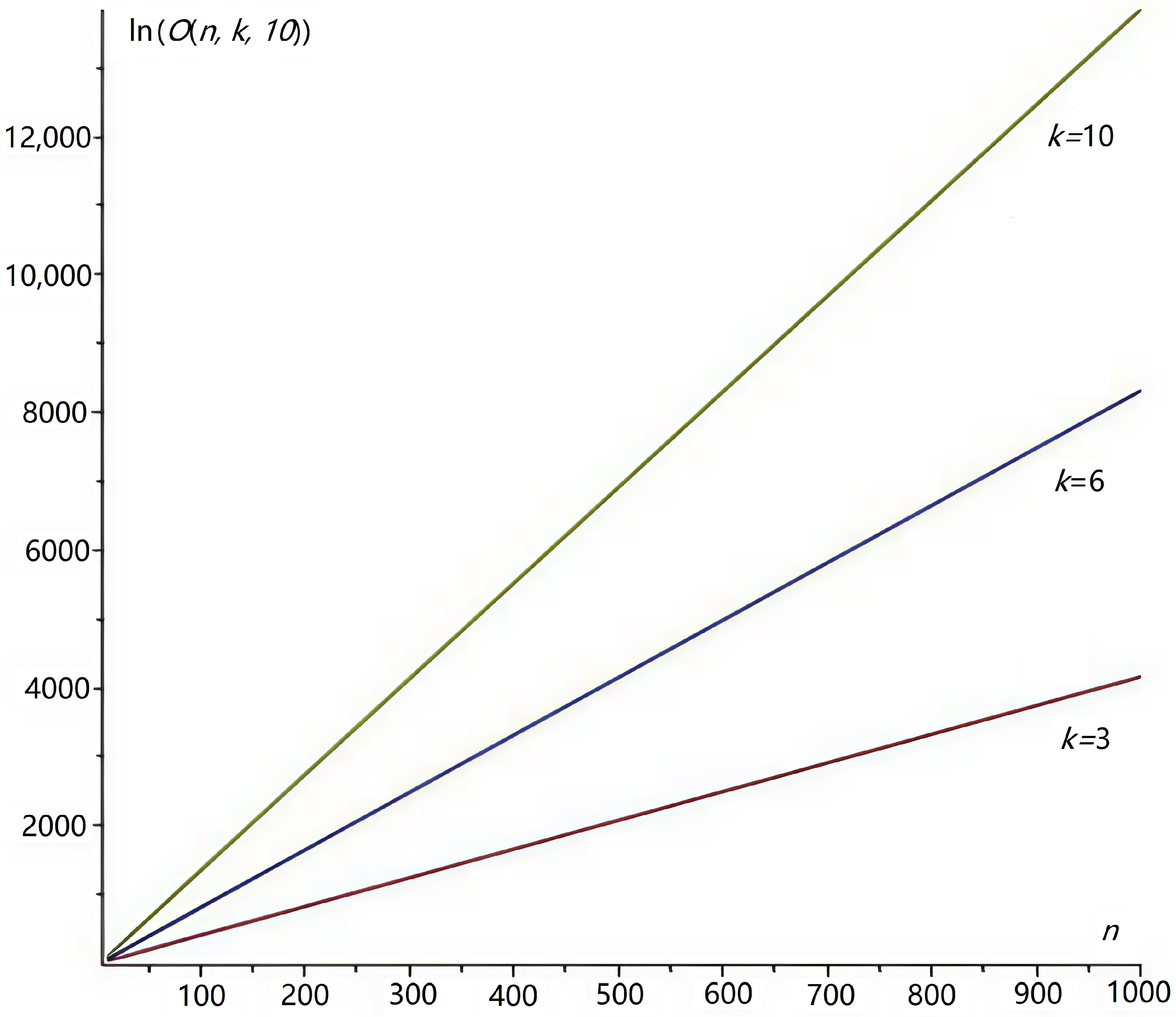
5.1. Cryptographic Strength of Affine Ciphers Using the Residue Number System
5.2. Comparison of the Cryptographic Strength of an Affine Cipher Using the Residue Number System with the AES Cryptographic Algorithm
6. Prospects and Directions for Further Research
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nieles, M.; Dempsey, K.; Pillitteri, V.Y. An Introduction to Information Security; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2017. [Google Scholar]
- Shirazi, S.-R.; Shah, S.A.; Anwar, A. Information Security. In Proceedings of the 27th International Conference, Arlington, VA, USA, 23–25 October 2024. [Google Scholar]
- Andrzejewski, K. Security Information Management Systems. Nauki Zarz. 2020, 24, 1–9. [Google Scholar] [CrossRef]
- Andrijchuk, V.A.; Kuritnyk, I.P.; Kasyanchuk, M.M.; Karpinski, M.P. Modern Algorithms and Methods of the Person Biometric Identification. In Proceedings of the 2005 IEEE Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications, Sofia, Bulgaria, 5–7 September 2005; pp. 403–406. [Google Scholar]
- Laybats, C.; Tredinnick, L. Information Security. Bus. Inf. Rev. 2016, 33, 76–80. [Google Scholar] [CrossRef]
- Hoffstein, J.; Pipher, J.; Silverman, J. An Introduction to Mathematical Cryptography; Springer New York: New York, NY, USA, 2008; ISBN 9780387779935. [Google Scholar]
- Jeffrey, H.; Jill, P.; Joseph, H. An Introduction to Cryptography; Springer: New York, NY, USA, 2008. [Google Scholar]
- Adki, V.; Hatkar, S. A Survey on Cryptography Techniques. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2015, 6, 469–475. [Google Scholar]
- Washington, L.C. Elliptic Curves; Chapman and Hall/CRC: London, UK, 2008; ISBN 9780429140808. [Google Scholar]
- Fadziso, T.; Thaduri, U.R.; Dekkati, S.; Ballamudi, V.-R.; Desamsetti, H. Evolution of the Cyber Security Threat: An Overview of the Scale of Cyber Threat. Digit. Sustain. Rev. 2023, 3, 1–12. [Google Scholar]
- Asaad, R.R.; Saeed, V.A. A Cyber Security Threats, Vulnerability, Challenges and Proposed Solution. Appl. Comput. J. 2022, 2, 227–244. [Google Scholar] [CrossRef]
- Wang, Z.; Adeyemo, D.; Akinsoto, A. Summary of Cyber Threat Intelligence. Int. J. Innov. Res. Multidiscip. Field 2022, 8, 32–42. [Google Scholar]
- Humayun, M.; Niazi, M.; Jhanjhi, N.Z.; Alshayeb, M.; Mahmood, S. Cyber Security Threats and Vulnerabilities: A Systematic Mapping Study. Arab. J. Sci. Eng. 2020, 45, 3171–3189. [Google Scholar] [CrossRef]
- Tarawneh, M. Perspective Chapter: Cryptography—Recent Advances and Research Perspectives. Biometrics and Cryptography; IntechOpen: London, UK, 2024; ISBN 9781837682621. [Google Scholar]
- Kumar, D.V.; Raheja, E.G.; Sareen, M.S. CRYPTOGRAPHY. Int. J. Comput. Technol. 2013, 4, 29–32. [Google Scholar] [CrossRef][Green Version]
- Onwutalobi, A.-C. Overview of Cryptography. SSRN Electron. J. 2011, 1, 1–10. [Google Scholar] [CrossRef][Green Version]
- Om, H.; Patwa, R. Affine Transformation in Cryptography. J. Discret. Math. Sci. Cryptogr. 2008, 11, 59–65. [Google Scholar] [CrossRef]
- Dhaief, Z.S. Encryption of Data Based on Triple Encryption and Affine Algorithm. Int. J. Adv. Sci. Res. Eng. 2021, 7, 25–34. [Google Scholar] [CrossRef]
- Rachmawati, D.; Budiman, M.A. New Approach toward Data Hiding by Using Affine Cipher and Least Significant Bit Algorithm. In Proceedings of the 2017 4th International Conference on Computer Applications and Information Processing Technology (CAIPT), Kuta Bali, Indonesia, 8–10 August 2017; pp. 1–6. [Google Scholar]
- Omondi, A.R.; Benjamin Premkumar, A. Residue Number Systems: Theory and Implementation; World Scientific: Singapore, 2007; ISBN 9781908979117. [Google Scholar]
- Mohan, P.-A. Residue Number Systems; Springer International Publishing: Cham, Switzerland, 2016; ISBN 9783319413839. [Google Scholar]
- Mezaal, Y.S.; Abdulkareem, S.F. Affine Cipher Cryptanalysis Using Genetic Algorithms. JP J. Algebra Number Theory Appl. 2017, 39, 785–802. [Google Scholar] [CrossRef]
- Mathews, M.M.; Panchami, V.; Ajith, V. Quantum Cryptanalysis of Affine Cipher. Res. Sq. 2022, 14, 507–519. [Google Scholar] [CrossRef]
- Lalitha, K.V.; Sailaja, V. High Performance Adder Using Residue Number System. J. Mater. Chem. A Mater. Energy Sustain. 2014, 5, 1323–1332. [Google Scholar]
- Nykolaychuk, Y.M.; Kasianchuk, M.M.; Yakymenko, I.Z. Theoretical Foundations for the Analytical Computation of Coefficients of Basic Numbers of Krestenson’s Transformation. Cybern. Syst. Anal. 2014, 50, 649–654. [Google Scholar] [CrossRef]
- Kasianchuk, M.M.; Yakymenko, I.Z.; Nykolaychuk, Y.M. Symmetric Cryptoalgorithms in the Residue Number System. Cybern. Syst. Anal. 2021, 57, 329–336. [Google Scholar] [CrossRef]
- Kazemi, M.; Naraghi, H.; Golshan, H.M. On the Affine Ciphers in Cryptography. Communications in Computer and Information Science; Springer Berlin Heidelberg: Berlin, Germany, 2011; pp. 185–199. ISBN 9783642253263. [Google Scholar]
- Hammood, D.A.; Maitham, A. Implementation and Enhancement Affine Cipher of Database. J. Eng. Sustain. Dev. 2016, 20, 264–276. [Google Scholar]
- Babu, S.A. Modification Affine Ciphers Algorithm for Cryptography Password. Int. J. Res. Sci. Eng. 2017, 3, 346–351. [Google Scholar]
- Al-Nuaimy, L. Internal Affine Stream Cipher. J. Appl. Eng. Technol. Sci. (JAETS) 2014, 1, 1–5. [Google Scholar]
- Carlo, J. A Keystream-Based Affine Cipher for Dynamic Encryption. Int. J. Emerg. Trends Eng. Res. 2020, 8, 2919–2922. [Google Scholar] [CrossRef]
- Putra, P.; Sari, C.A.; Isinkaye, F.O. Secure Text Encryption for IoT Communication Using Affine Cipher and Diffie-Hellman Key Distribution on Arduino Atmega2560 IoT Devices. J. Tek. Inform. (JUTIF) 2023, 4, 849–855. [Google Scholar] [CrossRef]
- Lone, M.A.; Qureshi, S. Encryption Scheme for RGB Images Using Chaos and Affine Hill Cipher Technique. Nonlinear Dyn. 2023, 111, 5919–5939. [Google Scholar] [CrossRef]
- Ke, Q.; Liao, Q.-N.; Li, A.-Q.; Gao, R. Digital Image Encryption Algorithm Based on Affine Cipher. In Advances in Intelligent Systems and Computing; Springer International Publishing: Cham, Switzerland, 2019; pp. 578–585. ISBN 9783319987750. [Google Scholar]
- Soekarta, R.; Sigit, M. Implementation of Affine Group Algebra on Digital Image Security. Mob. Forensics 2023, 4, 137–146. [Google Scholar] [CrossRef]
- Alhassan, M.J.; Hassan, A.; Sani, S.; Alhassan, Y. A Combine Technique of an Affine Cipher and Transposition Cipher. J. Res. Appl. Math. 2021, 7, 8–12. [Google Scholar]
- Budiman, M.A.; Handrizal; Azzahra, S. An Implementation of Rabin-p Cryptosystem and Affine Cipher in a Hybrid Scheme to Secure Text. J. Phys. Conf. Ser. 2021, 1898, 012042. [Google Scholar] [CrossRef]
- Maxrizal, M.; Aniska Prayanti, B.D. Application of Rectangular Matrices: Affine Cipher Using Asymmetric Keys. CAUCHY 2019, 5, 181–185. [Google Scholar] [CrossRef]
- Sundarayya, P.; Vara Prasad, G. A Public Key Cryptosystem Using Affine Hill Cipher under Modulation of Prime Number. J. Inf. Optim. Sci. 2019, 40, 919–930. [Google Scholar] [CrossRef]
- Arroyo, J.-T. An Improved Affine Cipher Using Blum Blum Shub Algorithm. Int. J. Adv. Trends Comput. Sci. Eng. 2020, 9, 3295–3298. [Google Scholar] [CrossRef]
- Shoup, V. A Computational Introduction to Number Theory and Algebra; Cambridge University Press: Cambridge, UK, 2009; ISBN 9780521516440. [Google Scholar]
- Laia, O.; Zamzami, E.M.; Sutarman; Larosa, F.-N.; Gea, A. Application of Linear Congruent Generator in Affine Cipher Algorithm to Produce Dynamic Encryption. J. Phys. Conf. Ser. 2019, 1361, 012001. [Google Scholar] [CrossRef]
- Stillwell, J. Elements of Number Theory; Springer New York: New York, NY, USA, 2003; ISBN 9781441930668. [Google Scholar]
- Hardy, G.H.; Wright, E.M.; Silverman, J. An Introduction to the Theory of Numbers, 6th ed.; Oxford University Press: London, UK, 2008; ISBN 9780199219865. [Google Scholar]
- Srivastava, A.; Mathur, A. The Rabin Cryptosystem & Analysis in Measure of Chinese Reminder Theorem. Int. J. Sci. Res. Publ. 2013, 3, 1–4. [Google Scholar]
- Venturi, D. Lecture Notes on Algorithmic Number Theory; Springer: New-York, NY, USA, 2009; 217p, ISSN 1433-8092. [Google Scholar]
- Karpinski, M.; Rajba, S.; Zawislak, S.; Warwas, K.; Kasianchuk, M.; Ivasiev, S.; Yakymenko, I. A Method for Decimal Number Recovery from Its Residues Based on the Addition of the Product Modules. In Proceedings of the 2019 10th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Metz, France, 18–21 September 2019; Volume 5, pp. 13–17. [Google Scholar]
- Nykolaychuk, Y.M.; Kasianchuk, M.M.; Yakymenko, I.Z. Theoretical Foundations of the Modified Perfect Form of Residue Number System. Cybern. Syst. Anal. 2016, 52, 219–223. [Google Scholar] [CrossRef]
- Bogdanov, A.; Khovratovich, D.; Rechberger, C. Biclique Cryptanalysis of the Full AES. In Lecture Notes in Computer Science; Springer Berlin Heidelberg: Berlin, Germany, 2011; pp. 344–371. ISBN 9783642253843. [Google Scholar]
- Tiessen, T. Polytopic Cryptanalysis. Lecture Notes in Computer Science; Springer Berlin Heidelberg: Berlin, Germany, 2016; pp. 214–239. ISBN 9783662498897. [Google Scholar]

| Letter | a | b | c | d | e | f | g | h | i | j | k | l | m |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number | 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 |
| Letter | n | o | p | q | r | s | t | u | v | w | x | y | z |
| Number | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| i | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| pi | 9 | 10 | 11 | 17 |
| Mi | 1870 | 1683 | 1530 | 990 |
| Mi mod pi | 7 | 3 | 1 | 4 |
| mi | 4 | 7 | 1 | 13 |
| i | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| pi | 9 | 10 | 11 | 17 |
| ai | 4 | 3 | 4 | 8 |
| N | 11,419 | |||
| bi = N mod pi | 7 | 9 | 1 | 12 |
| Bi = (aibi) mod pi | 1 | 7 | 4 | 11 |
| 2017 | ||||
| Ai | 7 | 7 | 3 | 15 |
| bi = (AiBi) mod pi | 7 | 9 | 1 | 12 |
| 11,419 | ||||
| i | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| pi | 9 | 10 | 11 | 17 |
| si | 4 | 6 | 5 | 10 |
| N | 11,419 | |||
| bi = N mod pi | 7 | 9 | 1 | 12 |
| Bi = (bi + si) mod pi | 2 | 5 | 6 | 5 |
| K | 12,755 | |||
| Si | 5 | 4 | 6 | 7 |
| bi = (AiBi) mod pi | 7 | 9 | 1 | 12 |
| 11,419 | ||||
| i | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| pi | 9 | 10 | 11 | 17 |
| ai | 4 | 3 | 4 | 8 |
| si | 4 | 6 | 5 | 10 |
| N | 11,419 | |||
| bi = N mod pi | 7 | 9 | 1 | 12 |
| Bi = (aibi + si) mod pi | 5 | 3 | 9 | 4 |
| 3353 | ||||
| i | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| pi | 9 | 10 | 11 | 17 |
| Ai | 7 | 7 | 3 | 15 |
| Si | 8 | 8 | 7 | 3 |
| K | 3353 | |||
| Bi = K mod pi | 5 | 3 | 9 | 4 |
| bi = (AiBi + Si) mod pi | 7 | 9 | 1 | 12 |
| 11,419 | ||||
| t | k | n | ||||||
|---|---|---|---|---|---|---|---|---|
| 16 | 32 | 64 | 128 | 256 | 512 | 1024 | ||
| 1 | 3 | 29 | 59 | 118 | 234 | 466 | 930 | 1855 |
| 6 | 57 | 117 | 234 | 467 | 931 | 1858 | 3709 | |
| 10 | 93 | 193 | 388 | 777 | 1550 | 3095 | 6180 | |
| 10 | 3 | 22 | 52 | 111 | 227 | 459 | 922 | 1848 |
| 6 | 43 | 102 | 220 | 453 | 917 | 1844 | 3695 | |
| 10 | 69 | 169 | 364 | 753 | 1526 | 3071 | 6156 | |
| Number of Moduli | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bit size when t = 1 | 63 | 42 | 32 | 26 | 22 | 19 | 17 | 16 | 14 | 13 | 12 | 11 | 11 | 10 |
| Bit size when t = 10 | 66 | 46 | 36 | 29 | 25 | 23 | 21 | 19 | 18 | 17 | 16 | 15 | 14 | 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kasianchuk, M.; Shevchuk, R.; Adamyk, B.; Benson, V.; Shylinska, I.; Holembiovskyi, M. Affine Cipher Encryption Technique Using Residue Number System. Cryptography 2025, 9, 26. https://doi.org/10.3390/cryptography9020026
Kasianchuk M, Shevchuk R, Adamyk B, Benson V, Shylinska I, Holembiovskyi M. Affine Cipher Encryption Technique Using Residue Number System. Cryptography. 2025; 9(2):26. https://doi.org/10.3390/cryptography9020026
Chicago/Turabian StyleKasianchuk, Mykhailo, Ruslan Shevchuk, Bogdan Adamyk, Vladlena Benson, Inna Shylinska, and Mykhailo Holembiovskyi. 2025. "Affine Cipher Encryption Technique Using Residue Number System" Cryptography 9, no. 2: 26. https://doi.org/10.3390/cryptography9020026
APA StyleKasianchuk, M., Shevchuk, R., Adamyk, B., Benson, V., Shylinska, I., & Holembiovskyi, M. (2025). Affine Cipher Encryption Technique Using Residue Number System. Cryptography, 9(2), 26. https://doi.org/10.3390/cryptography9020026







