A Quantum Key Distribution for Securing Smart Grids

Abstract

The development of Smart Grids (SGs) is a current trend and an indispensable essential living requirement. Due to economic development and improved quality of life, electricity demand has rapidly increased. However, the power grids in major cities have become outdated, leading to uneven power distribution and frequent power outages. SGs can adjust distribution strategies based on consumers’ real-time electricity demands, which requires continuous transmission of consumer electricity data within the grid. If the privacy and security of these data cannot be ensured, consumers’ habits will be exposed, and unnecessary waste may occur. In this article, we propose a key distribution process based on QKD, enabling entities within the SG to encrypt and authenticate each other’s data, ensuring the security and privacy of communication channels and transmitted data.

1. Introduction

The electric grid is a network system that connects power supply sources and demand centers to transmit electricity. It can also be referred to as the power system or power network. The electric grid is constructed from power plants, substations, transmission, and distribution systems [1]. Its purpose is to deliver electricity to commercial, governmental, medical, and residential equipment to meet societal electricity needs. The stable operation of these devices relies on the grid’s ability to deliver consistent power. However, the electric grids in most countries currently lack flexibility and the equipment is gradually aging. In recent years, increased electricity consumption and uneven distribution have led to frequent power outages.

The United Nations Climate Change Conference (COP29) [2], held on 11 November 2024, once again urged countries to adhere to the Paris Agreement’s commitments to reduce carbon emissions actively. In recent years, solar photovoltaic power has developed rapidly, providing a new avenue for power supply and reducing environmental burdens. However, insufficient feeder lines in power companies cannot be properly utilized even when power is available. Effectively utilizing feeder line capacity will significantly challenge promoting renewable energy generation.

Data security certification typically involves key exchange to provide the communicating parties with one or more keys for encryption and decryption, preventing unauthorized access or tampering with the data. Additionally, the agreed-upon keys are used for identity authentication to enhance the data’s integrity. Given the extensive scope of the SG, excessive data processing delays can slow down anomaly detection efficiency and lead to errors. Therefore, this article proposes a QKD security method to enable the communicating parties to agree on a key. Subsequently, this key is used for encryption and authentication. The design includes mechanisms to make the entire architecture’s transmission more secure.

The SG is the key to solving these problems. It comprises an Advanced Metering Infrastructure (AMI) composed of multiple SMs. It utilizes information and communication technology to control devices within the grid and monitor the grid’s status in real-time [3,4,5]. The essential features of the SG are enhancing overall system performance, improving Grid Resilience, and increasing self-healing capabilities. Grid Resilience refers to the grid’s ability to restore normal operations during power interruptions or outages quickly. It can be achieved by integrating additional decentralized power sources into the grid during power interruptions. Self-healing allows the system to quickly identify grid faults, reducing the duration of power outages and helping the grid to recover and continue operations more rapidly. Lastly, improving system performance is crucial; in traditional grids, energy loss can occur for various reasons, including station failures or transmission line damage. The SG enhances system performance by improving operations, reducing energy costs, and using more efficient methods to transmit power. To achieve this, many smart devices are distributed throughout the SG to effectively manage power generation, transmission, distribution, and consumption. Maintaining the security and stability of the SG is crucial for effectively managing these smart devices [6,7].

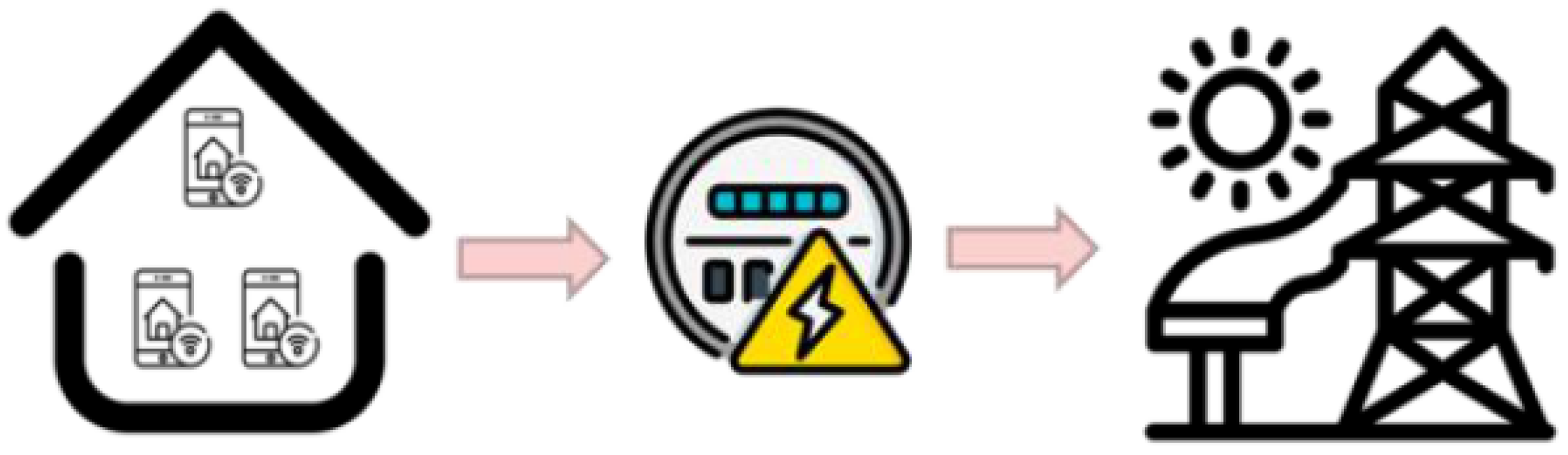
The SG can effectively utilize energy because it contains numerous sensors synchronizing their status with the control center (CC) for monitoring. The data transmitted include the status information of various nodes in the grid and, more importantly, the usage data of consumers. However, if the security of these data is not ensured, it can easily be tampered with by malicious users, leading to incorrect data within the grid. The SG determines its distribution strategy based on the current power usage level. The process of data transmission in the SG is illustrated in Figure 1. The usage data are measured by SMs that record consumers’ power consumption and transmit these data to the SG. Suppose the users’ data are tampered with or destroyed during transmission. In that case, it causes a mismatch between the meter and the grid data and introduces errors in the grid’s strategic decisions [8].

The SG needs to transmit a large amount of user electricity usage data. These data are continuously sent according to the measurement cycle of the power supplier, which could be every hour or even every 15 min. Many AMI devices simultaneously send statistical data to the power supplier for verification. Without an efficient verification mechanism, this can easily cause delays in the verification process [9]. For example, the SG comprises numerous Neighborhood Area Networks (NANs). Each NAN represents a floor, building, or community and is equipped with numerous SM and other devices to record users’ electricity usage data. Due to the large number of users, the amount of electricity usage data generated is enormous. Suppose the traditional one-by-one verification mechanism is still used—in that case, there will not be severe delays in the verification process, but it will not be easy to achieve real-time electricity monitoring and billing [10].

The structure of our paper is organized as follows: A review of related works on the smart grid’s data security and privacy protection is described in Section 2. Section 3 proposes a system model for securing the smart grid. Section 4 proposes a quantum key distribution scheme for securing the smart grid. In Section 5, we cryptanalyze the proposed scheme. Finally, Section 6 concludes the article.

2. Related Works

Multiple data generation and transmission nodes exist in the SG environment. If these nodes are not adequately protected, unauthorized access can leak user privacy. Akgün et al. [11] proposed a novel key initialization mechanism utilizing the Trusted Execution Environment (TTE) to inform users about consumption patterns. The projected energy consumption data can be transmitted through the SG and stored in an encrypted database.

The goal is to achieve remote electricity management, balance electricity demand, ensure the healthy operation of the grid, and maintain customer satisfaction. The main components of this model include the Distribution Management System (DMS), Computational Service Provider (CSP), Short Message Service (SMS) Gateway, SMs, and SAs. The DMS can centrally monitor and control the distribution network from a CC. The CSP offers storage and computational services to the DMS through the TEE and encrypted databases. SMs and SAs are deployed in consumer premises to record real-time electricity usage data and communicate with the DMS. The SMS Gateway allows the distribution company to communicate with customers via text.

Akgün et al. [11] proposed a solution where energy consumption data from SAs is encrypted and sent through the distributor’s network to a database with encryption mechanisms for storage. The TEE protects the database encryption keys, ensuring that no intermediate devices can access the content during data storage and transmission, achieving data confidentiality. In this architecture, SMs do not require any modifications to meet secure transmission requirements. The data encryption part uses a combination of asymmetric, symmetric, and keyed hash functions for key distribution and management. Additionally, symmetric block cipher algorithms with encryption authentication modes are used for actual data encryption, eliminating the need for additional integrity verification mechanisms.

The key distribution involves three phases: P1, P2, and P3. In the P1 phase, when an SA joins the system, the user inputs their phone number, PN, and a Verify Text VT through a configuration application. The application uses the public PK of the TEE to encrypt this information and then sends the ciphertext C to the CSP. The CSP forwards the ciphertext C along with the PN to the TEE. The TEE decrypts the information using its private key PrK and verifies the correctness of the PN. Then, the TEE generates a one-time password OTP and sends it to the consumer via SMS through the Short Message Service Gateway. Upon receiving the SMS, the consumer verifies the OTP and inputs the received OTP and other information into the SA management interface. Each SA must perform the above initialization process.

In the P2 phase, the TEE generates a distribution key KDist for encrypted communication based on the OTP and the consumer ID CustomerID. The TEE then uses KDist to encrypt each SA’s specific channel encryption key CKSA, producing ECKSA. It then sends this key to the CSP, which forwards it to the corresponding SA.

In the P3 phase, upon receiving the encrypted channel key ECKSA, each SA uses the OTP entered during initialization to verify the CustomerID and decrypt the ECKSA to obtain the channel encryption key CKSA. The SA then uses this key for subsequent secure communication. Finally, the TEE decrypts and verifies the information returned by each SA to complete the binding of the channel encryption key.

The key distribution process proposed by Akgün et al. [11] has the following two advantages:

• This solution does not affect the utility’s deployment model for SMs since the TEE performs the most important calculations.
• The communication between the utility and SAs uses the channel encryption key CKSA to ensure encrypted communication. Symmetric encryption ensures high encryption and decryption efficiency.

However, the key distribution process [11] also has two disadvantages:

• Since the TEE holds a copy of all keys and performs energy consumption data analysis queries, the security of the TEE becomes critically important.
• If there are too many users and the measurement frequency is once per hour, it takes almost three minutes to complete the data aggregation, which is relatively inefficient.

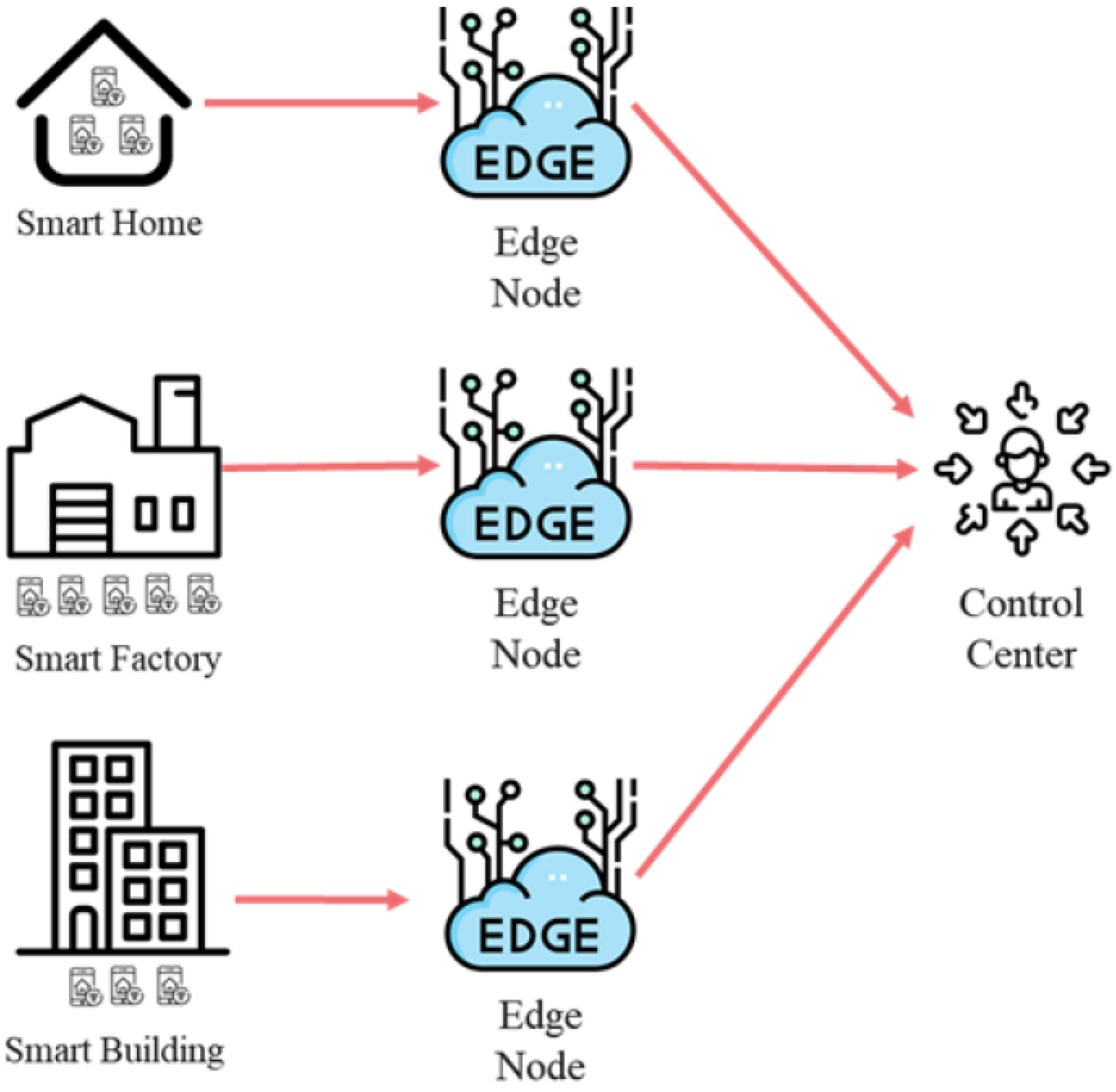
The SG’s metering data (MD) allow suppliers to accurately predict consumers’ electricity usage and generation conditions. However, when tasks are processed locally, the SG can only realize its full potential. Cloud computing can result in significant latency and bandwidth consumption, and terminal devices processing these computations might consume substantial power. Prateek et al. [12] proposed using fog computing to provide computational and storage functions between the cloud and terminal devices. They designed a privacy-preserving verification mechanism employing quantum communication protocols and identity authentication, enabling the SG to securely install and verify the authenticity of SMs and edge nodes. Figure 2 illustrates the system model proposed by Prateek et al. [12].

The designed privacy protection mechanism consists of the following steps: First, SMs and edge nodes must register at the CC to establish a trust relationship. After registration, these two entities obtain a shared secret through a quantum key exchange protocol. Next, the SM uses the shared secret to send an identity authentication request to the CC, simultaneously requesting the key materials needed to generate a session key and virtual identity. Upon successful verification, the CC provides the corresponding materials. Finally, the SM uses the obtained materials to generate the session key and virtual identity. The edge node also acquires the same materials to verify messages received from the SM.

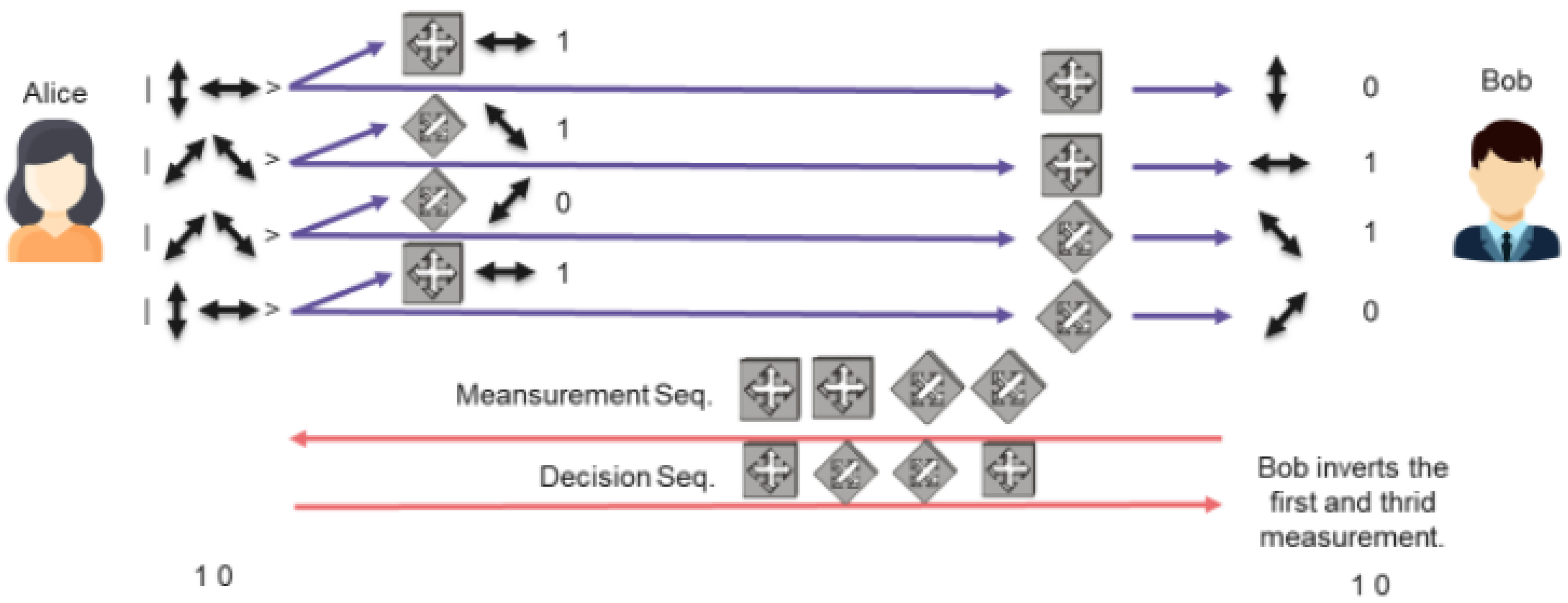
Prateek et al. [12] use qubits and quantum entanglement technology to exchange keys between different SG entities securely. Binary bits are converted into qubits through an inter-conversion rule IR and are represented by the photons’ polarization states. The decision sequence D and measurement sequence M consist of different types of polarizers: the former determines the transmitted qubits, while the latter is used for measurement and conversion. In the D, linear polarizer L and diagonal polarizer C represent two orthogonal quantum states. In the M, rectilinear polarizer R corresponds to L, and diagonal polarizer D corresponds to C. According to the uncertainty principle, R and D polarizers can only measure partial quantum state information. Since the D and M are conjugate states, measurement errors are kept within a controllable range.

Table 1. Prateek et al. [12] conversion example.

Secret Key Material	Values
Binary bit	0	0	1	0	1	1	0	1
Decision sequence	C	L	L	L	C	C	C	L
Quantum bit	↗	→	↑	→	↖	↖	↗	↑
Measurement sequence	D	R	R	D	D	R	R	R
Shared secret key	0	0	1	x	1	x	x	1
Template	1	1	1	0	1	0	0	1
Password	0	0	1	x	1	x	x	1

below shows the correspondence during this scheme’s login and authentication phases.

As shown in Table 1, entities need to exchange the Template and password information during the login and authentication phases. First, the SG entities randomly generate D and M, then compare the two to obtain the Template, where conjugate polarizers correspond to 1, and others to 0. The D encodes the qubits, which generate the Shared Secret Key through partial measurement by the M. Due to measurement errors, failed measurement bits need to be filtered out. The remaining shared key and Template are then XOR to generate the Password exchanged between entities. Through QKD, even if an attacker intercepts the Template and Password, they cannot deduce the original key. This ensures security while enabling safe login and authentication for SM entities.

Prateek et al. [12] proposed the key exchange process: When entity X must enter the SG to provide services, it must first register with the CC. The CC generates an M, D, and a pair of EPR entangled particles for each SG node. When node X receives a unique ID $I_X$ from the CC, it generates its D, M, and IR, then converts the binary ID $I_X$ into a quantum ID $Q{I}_X$. X then sends this information through an authenticated public channel to the CC. The CC selects a quantum string of the same length as $Q{I}_X$ from the EPR pair $|q_{z1}>$ and $|q_{z2}>$ and sends one part to the corresponding node X while retaining the other in its database. The CC measures the retained EPR quantum string, causing the two strings to collapse into the same eigenstate due to the properties of quantum entanglement. Finally, X uses the shared IR to convert the quantum string back into a binary string, obtaining the shared key. The CC also generates a Template and a session password $Passwor{d}_X$ by comparing sequences and stores them in the database for verification.

Prateek et al.’s key exchange scheme [12] has the following two advantages:

• The use of QKD to generate secret keys through quantum strings is innovative and can resist post-quantum attacks.
• By transmitting quantum strings, both communication parties can share the same session key, $Passwor{d}_X$, achieving symmetric encryption, which speeds up the encryption and decryption process.

However, Prateek et al.’s key exchange scheme [12] also has two disadvantages:

• The explanation in the paper regarding the use of D and M to convert quantum strings is inconsistent with its assumptions. According to their IR, the results mentioned in the original text cannot be derived.
• The paper initially transmits the D, M, and IR to the other entity to carry out the key agreement. Still, it does not specify whether the transmission process uses a secure channel or other methods. If an attacker intercepts and successfully deciphers these three sequences, they could share the same key with the receiving entity without being detected.

Security and privacy are essential for the secure smart grid. If the privacy and security of these data cannot be ensured, consumers’ habits will be exposed, and unnecessary waste may occur. Since the above methods cannot satisfy all security requirements, we propose a key distribution process based on QKD. This process enables entities within the SG to encrypt and authenticate each other’s data, ensuring the security and privacy of communication channels and transmitted data.

3. System Model

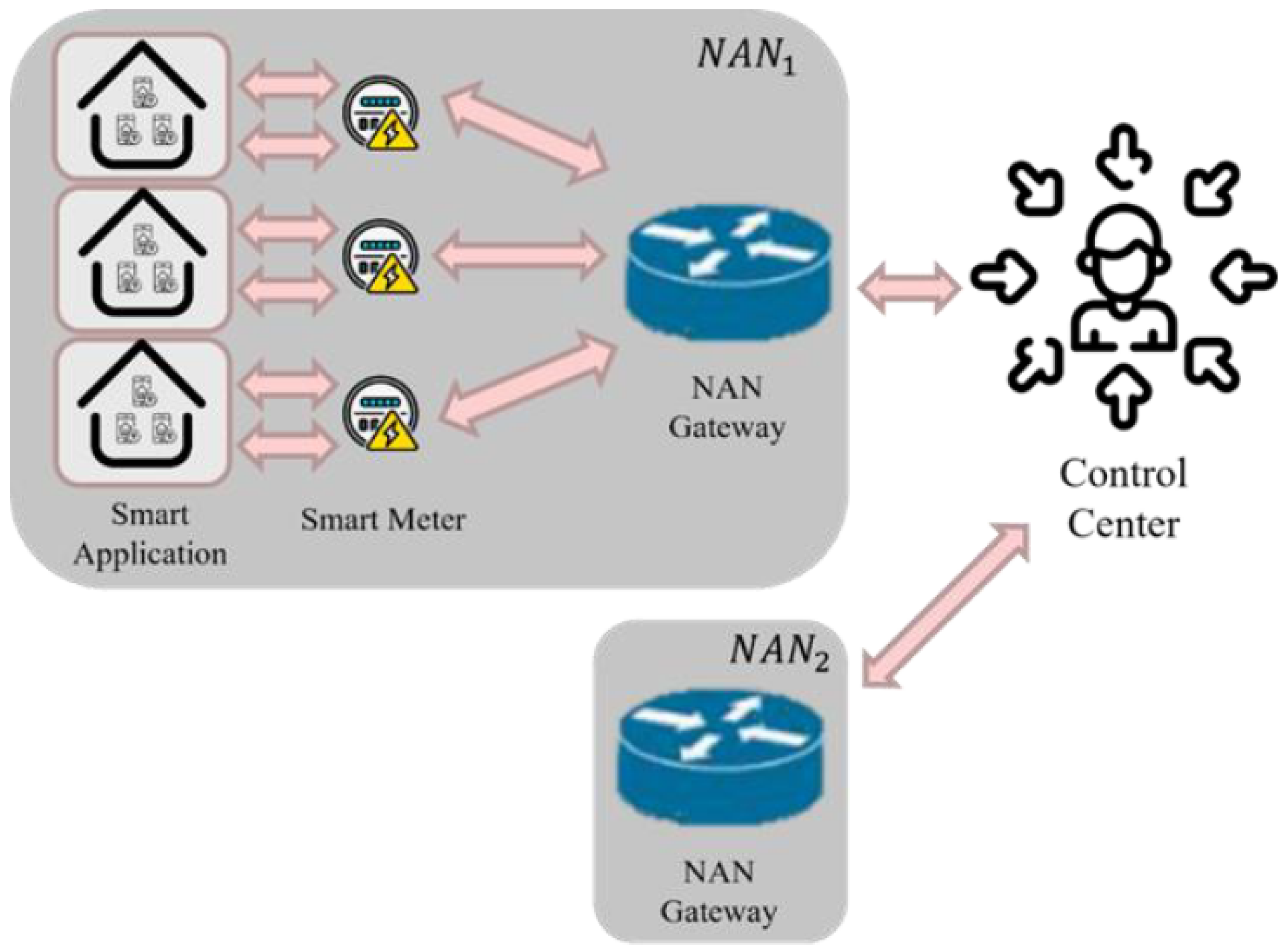
The SG environment includes SAs, SMs, NAN Gateway (GW), and the CC. Figure 3. illustrates the SG environment. The CC is an entity used by the energy supplier to manage the SG and monitor electricity usage, and is responsible for registering and authenticating other entities in the SG and monitoring real-time electricity information. The GW connects the communication between SMs and the CC, enabling the CC to control each NAN within the SG better. The SM, installed at consumer sites such as homes or factories, measures and records users’ electricity consumption and exchanges data with the power company through two-way communication. The SA are devices using electricity at consumer sites, such as refrigerators and televisions, which connect to the SM and serve as terminal devices of the SG.

This article will guide each entity in the SG through the proposed five-phase process, enabling them to authenticate each other and encrypt communications, thus ensuring the integrity, confidentiality, and authenticity of messages during transmission.

In this article, we propose a security scheme based on QKD. The scheme references the key exchange protocol by Prateek et al. [12]. In Prateek et al.’s protocol, the decision sequence D, measurement sequence M, and ID are transmitted once to the receiver to perform the key exchange agreement. Although this approach significantly reduces the number of transmissions, the method of transmission is not specified in the paper. Even if a secure channel is used for transmission, if the encrypted transmission is compromised, an attacker could synchronize the key information with the receiver without either party noticing. This would render the entire key exchange protocol extremely insecure. Therefore, this article improves upon this issue by incorporating the BBM92 QKD protocol [13]. The following is the quantum key exchange process proposed in this article.

This article proposes a QKD protocol based on the BBM92 [13] method and the key exchange process referenced by Prateek et al. [12]. Figure 4 illustrates the proposed QKD protocol, where the blue lines represent quantum channels and the red lines represent classical channels. First, let us explain the key materials used in this article. The inter-conversion rule IR serves as the rule for converting between binary strings and quantum strings. For example, the quantum bits $|\uparrow >$ and $|\nearrow >$ are defined as binary bit 0, and $|\to >$ and $|\nwarrow >$ are defined as binary bit 1. The transmitting parties convert bits according to this rule. The D is a sequence of filters used to measure quantum objects. The sender uses D to determine the polarization state of photons. There are two types of filters: Cross (C) and Diagonal (D). The polarization state of the photons is determined by measuring quantum objects with one of these filters chosen at random. The M is a sequence of filters the receiver uses to measure quantum objects. By measuring quantum objects with one of these filters chosen at random, the receiver observes the bit value carried by the photons. Below is a detailed explanation of the key exchange protocol process.

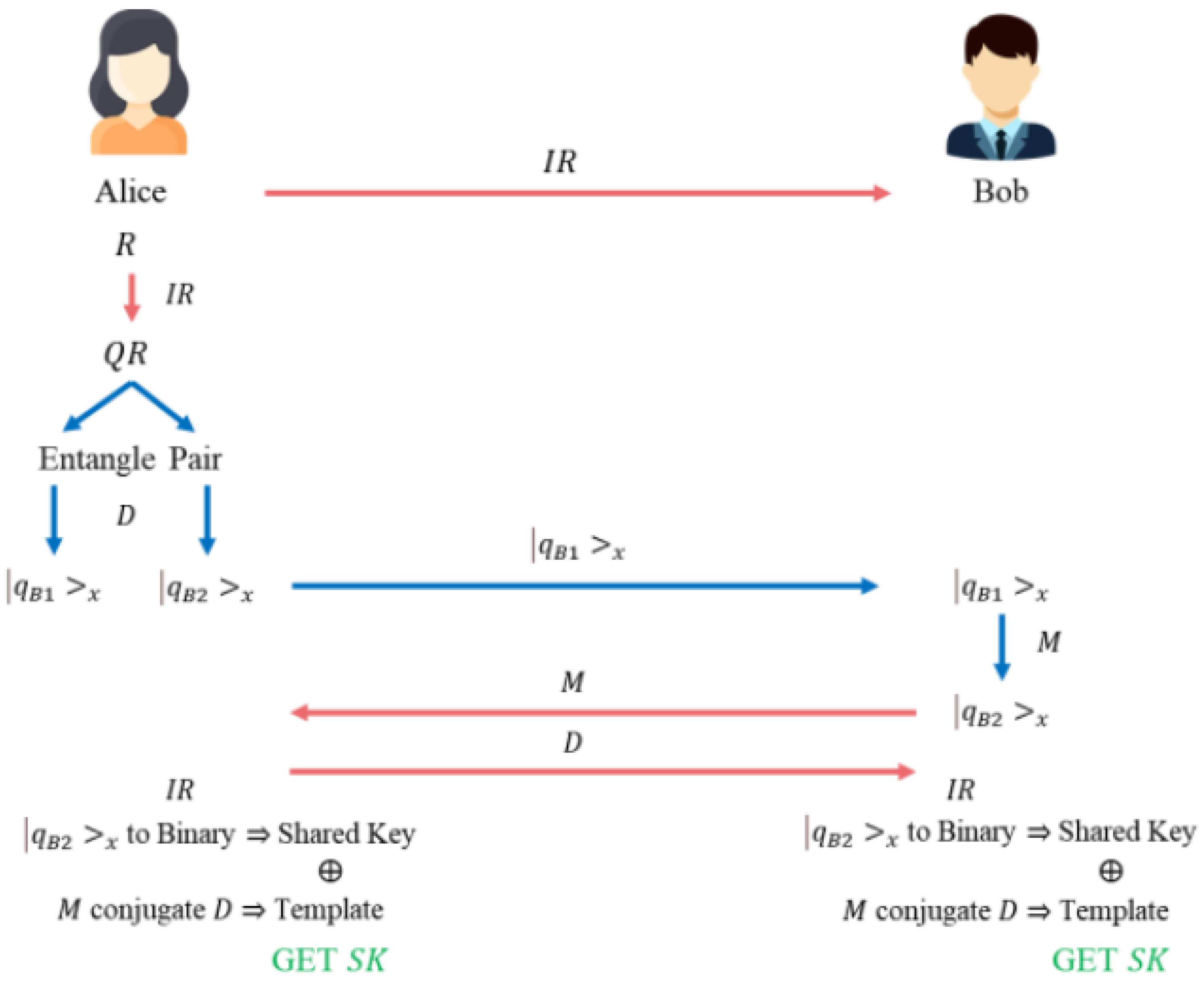
Assume that two entities, A and B, want to perform a key exchange protocol, as shown in Figure 5. Alice is the sender, and Bob is the receiver. First, A defines a set of inter-conversion rules IR and sends IR to Bob. Then, Alice generates a set of random numbers R as key materials and uses IR to convert R into a quantum string QR. Alice also produces an EPR entangled pair $|q_{B1}>$ and $|q_{B2}>$ related to QR. Using the D, Alice measures one of the EPR entangled pairs, resulting in $|q_{B1}{>}_x$ and $|q_{B2}{>}_x$. Alice sends $|q_{B1}{>}_x$ to Bob and retains $|q_{B2}{>}_x$ in its database. Upon receiving $|q_{B1}{>}_x$, Bob uses the M to measure it. Due to quantum entanglement, $|q_{B1}{>}_x$ collapses into the same eigenstate as $|q_{B2}{>}_x$. Bob then sends its used M to Alice. Alice sends its used D to measure the EPR entangled pair to Bob. Both parties use IR to convert $|q_{B2}{>}_x$ into a binary string, which becomes the shared key. They also determine whether D and M have a conjugate relationship to form the Template (0 for conjugate, 1 for not conjugate). Finally, the shared key and Template are XOR to produce SK.

4. The Proposed Scheme

This article proposes a security protection scheme utilizing QKD and various verification mechanisms. Referencing the works of Akgün et al. [11] and Prateek et al. [12], this scheme aims to ensure the transmission security and endpoint protection of SMI.

The scheme involves four entities: the consumer, SM, NAN GW, and the CC. These entities successfully exchange keys and use the key for encryption and identity authentication through the following stages, ensuring secure transmission between entities. The scheme consists of five stages: (1) Consumer registration of the SM; (2) Gateway registration; (3) Identity authentication between the SM and the Gateway; (4) Consumer registration of SA; (5) Consumer transmission of metering data to the Control Center.

Table 2. Symbols used in the proposed method.

Symbols	Description
PN	Consumer’s Phone Number
VT	Consumer’s Verify Text
OTP	One Time Password from CC
$P{K}_{CC}$	CC’s Public Key
$I{D}_x$	Identity of X
$NI{D}_x$	New Identity for X
$R_x$	Random Number for X
$I{R}_x$	Inter-conversion Rule from X
$D_x$	Decision Sequence by X
$M_x$	Measurement Sequence by X
$q_{x1}>$ & $|q_{x2}>$	ERP Entangled Pair
$q_{x1}{>}_x$ & $|q_{x2}{>}_x$	ERP Entangled Pair Measured by $D_x$
$S{K}_x$	Secret Key for X
$T_x$	X’s Timestamp
$Ene(·)$	Enciphering Function
$C_x$	Ciphertext of X
$M{D}_x$	Metering Data of X
$C{D}_x$	Consumption Data of X

provides a list of symbols used in the proposed scheme and briefly explains each symbol’s function.

• Phase 1. Consumer registration of the SM

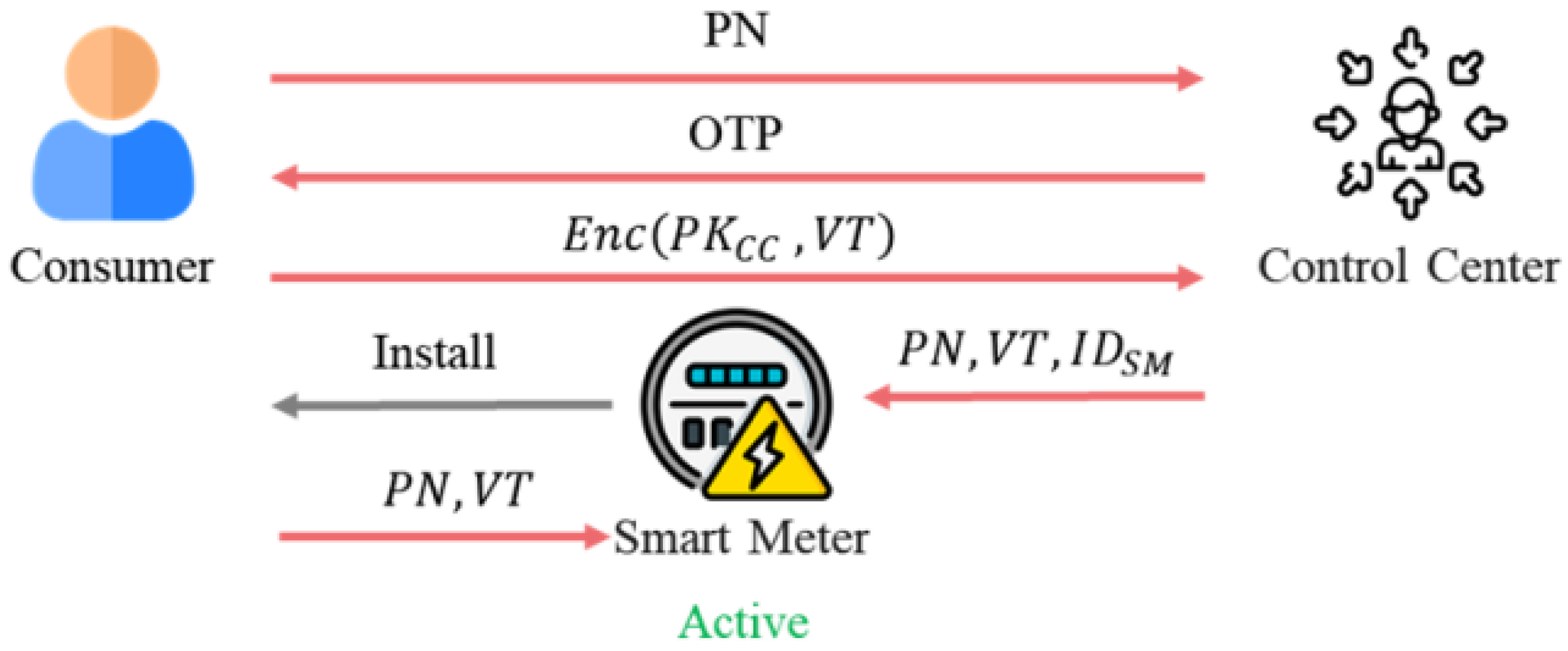
The process of registering an SM is illustrated in Figure 6. Before a consumer can join the SG, they must register with the CC to obtain an SM and its corresponding $I{D}_{SM}$. The consumer starts the registration process by sending their phone number, PN, to the CC. The CC uses a one-time password OTP to verify the user’s PN. Upon successful OTP verification, the consumer inputs Verify Text VT as a password and encrypts it using the CC’s public key $P{K}_{CC}$. The encrypted message $Enc(P{K}_{CC},VT)$ is sent to the CC, which then decrypts it to obtain VT. After entering PN and VT into the SM, the CC records the SM’s $I{D}_{SM}$ and the corresponding user information in the database. The CC installs the SM on the consumer’s premises, such as at home or in a building. The consumer activates the SM using their PN and VT. If the PN and VT are correct, the SM starts operating.

• Phase 2. Gateway registration

Figure 7 shows the registration process for the Gateway (GW). Each NAN GW must register with the CC to enable encrypted communication. The CC sends the inter-conversion rule $I{R}_{GW}$ to the GW through a secure channel. The CC generates a random number $R_{GW}$ of the same length as the ID and uses $I{R}_{GW}$ to convert it into a quantum string $Q{R}_{GW}$. The CC also produces an EPR entangled pair $|q_{GW1}>$ and $|q_{GW2}>$ of the same length as $Q{R}_{GW}$. Using the $D_{GW}$, the CC measures the EPR entangled pair, resulting in $|q_{GW1}{>}_x$ and $|q_{GW2}{>}_x$. The former is sent to the GW, while the latter is stored in the CC’s database.

Upon receiving $|q_{GW1}{>}_x$, the GW uses the $M_{GW}$ to measure it. Due to the properties of quantum entanglement, the measurement of $|q_{GW1}{>}_x$ will collapse into the same eigenstate as $|q_{GW2}{>}_x$. The GW then sends the $M_{GW}$ used to measure $|q_{GW1}{>}_x$ to the CC. Upon receiving this, the CC sends its $D_{GW}$ to the GW. The CC and the GW perform the following operations to generate the final secret key: use $I{R}_{GW}$ to convert $|q_{GW1}{>}_x$ into a binary string for the shared key. The sequences $M_{GW}$ and $D_{GW}$ generate the Template based on conjugate states. The shared key and Template are XOR to produce $S{K}_{GW}$. The CC generates a new $NI{D}_{GW}$ and encrypts it with $S{K}_{GW}$, sending it to the GW for future identification. The GW receives $Enc(S{K}_{GW},I{D}_{GW}|\left|T_{CC}\right)$ and verifies the validity of $S{K}_{GW}$ and $T_{CC}$. Upon successful verification, $NI{D}_{GW}$ replaces its $I{D}_{GW}$.

• Phase 3. Identity authentication between the SM and the Gateway

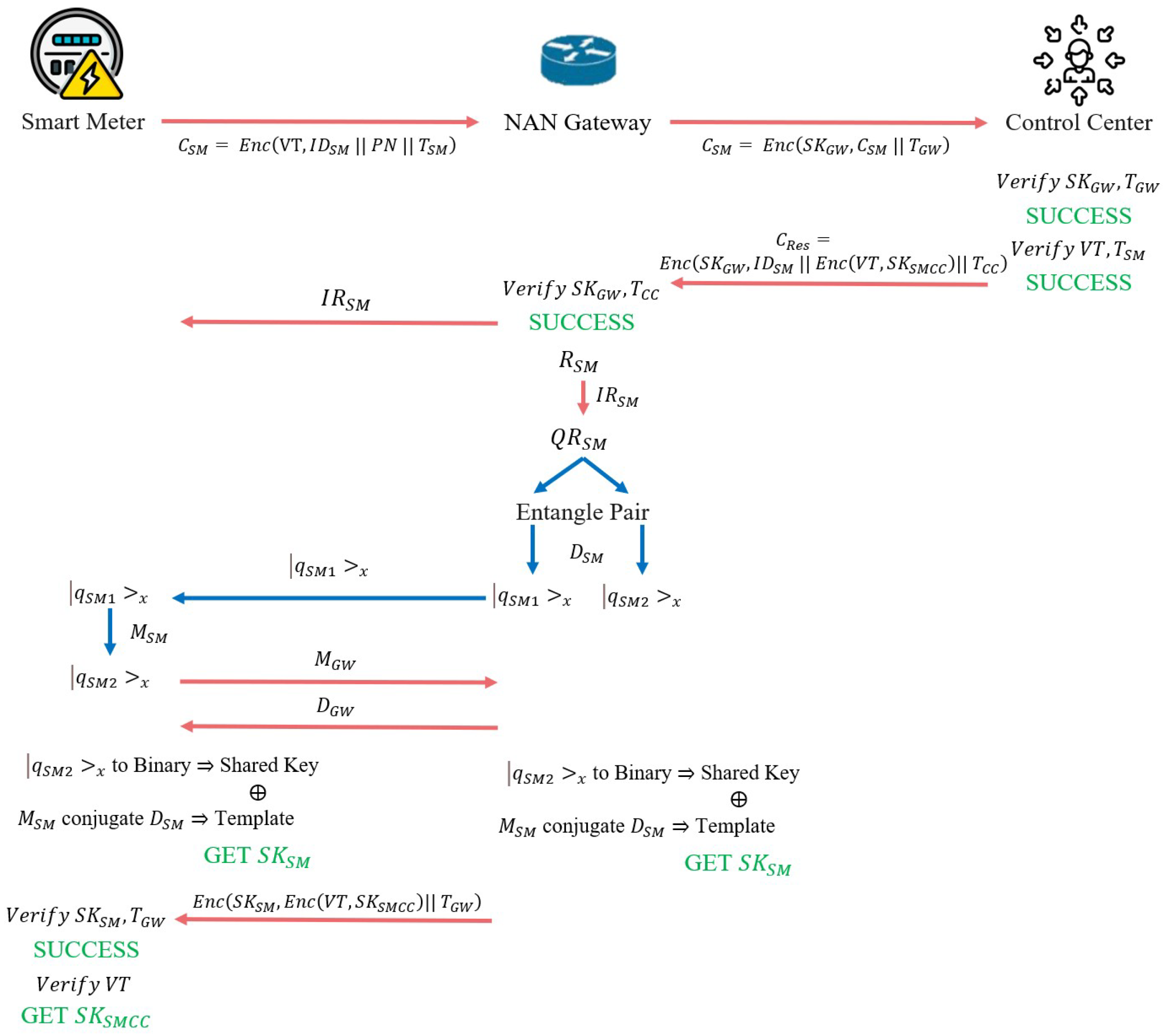
Once the NAN GW and the SM have registered with the CC, they know each other’s identities and keys. The NAN Gateway must know which SMs are under its NAN for future verification and electricity data transmission. The SM must synchronize the relevant information with the NAN Gateway to achieve this. The synchronization process is illustrated in Figure 8.

The SM encrypts its $I{D}_{SM}$, PN, and $T_{SM}$ using the Verify Text VT to generate ciphertext $C_{SM}$, which is then sent to the Gateway. The Gateway encrypts $C_{SM}$ and $T_{GW}$ using $S{K}_{GW}$ to generate ciphertext $C_{GW}$, which is sent to the CC. Upon receiving $C_{GW}$, the CC first verifies the validity of $S{K}_{GW}$ and $T_{GW}$. If the verification is successful, the CC decrypts $C_{GW}$ to extract $C_{GW}$ and then verifies the validity of VT and $T_{SM}$. Upon successful verification, the CC generates a key $S{K}_{SMCC}$ to be used as a verification key for future transmissions of total electricity consumption from the SM to the CC. The CC then encrypts $I{D}_{SM}$, Enc(VT, $S{K}_{SMCC}$), and $T_{CC}$ to generate ciphertext $C_{Res}$, which is transmitted to the GW. The GW verifies the validity of $S{K}_{GW}$ and $T_{CC}$. If the verification is successful, it confirms that the SM is a legitimate entity and that the $I{D}_{SM}$ belongs to the members of this NAN.

Next, the SM and GW begin the key agreement process. The GW sends $I{R}_{SM}$ to the SM through a secure channel. The GW generates a random number $R_{GW}$ and uses $I{R}_{SM}$ to convert it into a quantum string $Q{R}_{SM}$. The GW also produces an EPR entangled pair $|q_{SM1}>$ and $|q_{SM2}>$ of the same length as $Q{R}_{SM}$. Using its $D_{SM}$, the GW measures the EPR entangled pair to obtain $|q_{SM1}{>}_x$ and $|q_{SM2}{>}_x$. The former is sent to the SM, while the latter is stored in the GW’s database.

Upon receiving $|q_{SM1}{>}_x$, the SM uses its $M_{SM}$ to measure it. Due to the properties of quantum entanglement, the measurement of $|q_{SM1}{>}_x$ will collapse into the same eigenstate as $|q_{SM2}{>}_x$. The SM then sends the $M_{SM}$ used to measure $|q_{SM1}{>}_x$ to the GW. Upon receiving this, the GW sends its $D_{SM}$ to the SM. BotThe and the GW perform the following operations to generate the final secret key: use $I{R}_{SM}$ to convert $|q_{SM1}{>}_x$ into a binary string for the shared key. The sequences $M_{SM}$ and $D_{SM}$ generate the Template based on conjugate states. The shared key and Template are XOR to produce $S{K}_{SM}$.

Finally, the GW encrypts the previously received Enc(VT, $S{K}_{SMCC}$) and $T_{GW}$ with $S{K}_{SM}$ and sends it to the SM. The SM verifies the validity of $S{K}_{SM}$ and $T_{GW}$. Upon successful verification, the SM extracts Enc(VT, $S{K}_{SMCC}$) and uses VT to decrypt it, obtaining $S{K}_{SM}$ CC.

After Phases 1 to 3 are completed, secure communication between the SM and the CC can be established, and mutual identity authentication can be performed between them.

• Phase 4. Consumer registration of SA

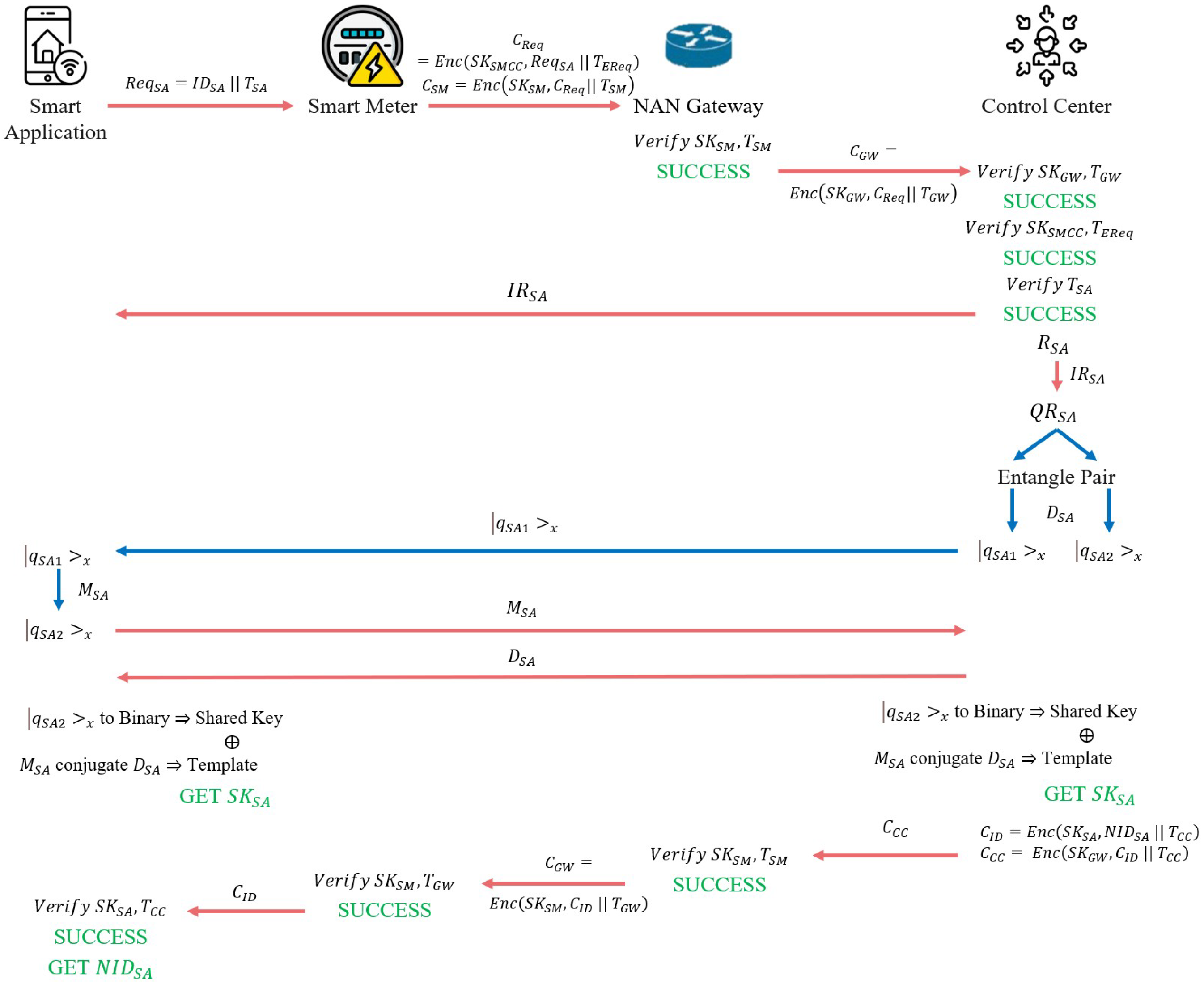
Once the entities in the SG have completed the key agreement and can communicate securely, the user’s SAs also need to register with the CC to become part of the SG, ensuring endpoint protection. The registration process is illustrated in Figure 9.

The SA first sends a key agreement request to the CC. The SA generates $Re{q}_{SA}$ by concatenating $I{D}_{SA}$ and $T_{SA}$, then sends it to the SM through a secure channel. The SM encrypts $Re{q}_{SA}$ and $T_{EReq}$ with $S{K}_{SMCC}$ to produce the ciphertext $C_{Req}$. The SM then encrypts $C_{Req}$ and $T_{SM}$ with $S{K}_{SM}$ to produce the ciphertext $C_{SM}$ sent to the GW. The GW first verifies the validity of $S{K}_{SM}$ and $T_{SM}$. If the verification is successful, the GW decrypts $C_{SM}$ to extract $C_{Req}$. The GW then encrypts $C_{Req}$ and $T_{GW}$ with $S{K}_{GW}$ to produce the ciphertext $C_{GW}$ sent to the CC.

The CC performs three verifications. First, it verifies the validity of $S{K}_{GW}$ and $T_{GW}$. If successful, the CC decrypts $C_{GW}$ to extract $C_{Req}$. Next, it verifies the validity of $S{K}_{SMCC}$ and $T_{EReq}$ in $C_{Req}$. If successful, the CC decrypts $C_{Req}$ to extract $Re{q}_{SA}$. Finally, the CC verifies the validity of $T_{SA}$. If all verifications are successful, the CC records the $I{D}_{SA}$ as belonging to the SM’s $I{D}_{SM}$.

Next, the SA and CC begin the key agreement process. The CC sends $I{R}_{SA}$ to the SA through a secure channel. The CC generates a random number $R_{SA}$ and uses $I{R}_{SA}$ to convert it into a quantum string $Q{R}_{SA}$. The CC also produces an EPR entangled pair $|q_{SA1}>$ and $|q_{SA2}>$ of the same length as $Q{R}_{SA}$. Using its $D_{SA}$, the CC measures the EPR entangled pair to obtain $|q_{SA1}{>}_x$ and $|q_{SA2}{>}_x$. The former is sent to the SA, while the latter is stored in the CC’s database.

Upon receiving $|q_{SA1}{>}_x$, the SA uses its $M_{SA}$ to measure it. Due to the properties of quantum entanglement, the measurement of $|q_{SA1}{>}_x$ will collapse into the same eigenstate as $|q_{SA2}{>}_x$. The SA then sends the $M_{SA}$ used to measure $|q_{SA1}{>}_x$ to the CC. Upon receiving this, the CC sends its $D_{SA}$ to the SA. The SA and the CC perform the following operations to generate the final secret key: use $I{R}_{SA}$ to convert $|q_{SA1}{>}_x$ into a binary string for the shared key. The sequences $M_{SA}$ and $D_{SA}$ generate the Template based on conjugate states. The shared key and Template are XOR to produce $S{K}_{SA}$.

The CC generates a new $NI{D}_{SA}$ to serve as the new identity for future recognition. The CC encrypts $NI{D}_{SA}$ and $T_{CC}$ using $S{K}_{SA}$ to produce the ciphertext $C_{ID}$. Following the previous procedure, $C_{ID}$ is sent to the SA. Upon receiving $C_{ID}$, the SA verifies the validity of $S{K}_{SA}$ and $T_{CC}$. If the verification is successful, the SA replaces its $I{D}_{SA}$ with $NI{D}_{SA}$. All SAs in the consumer’s domain must complete this registration phase to join the SG.

After Phases 1 to 4 are completed, the entire SG can establish encrypted communication, and mutual identity authentication can be performed between all entities.

• Phase 5. Consumer transmission of metering data to the Control Center

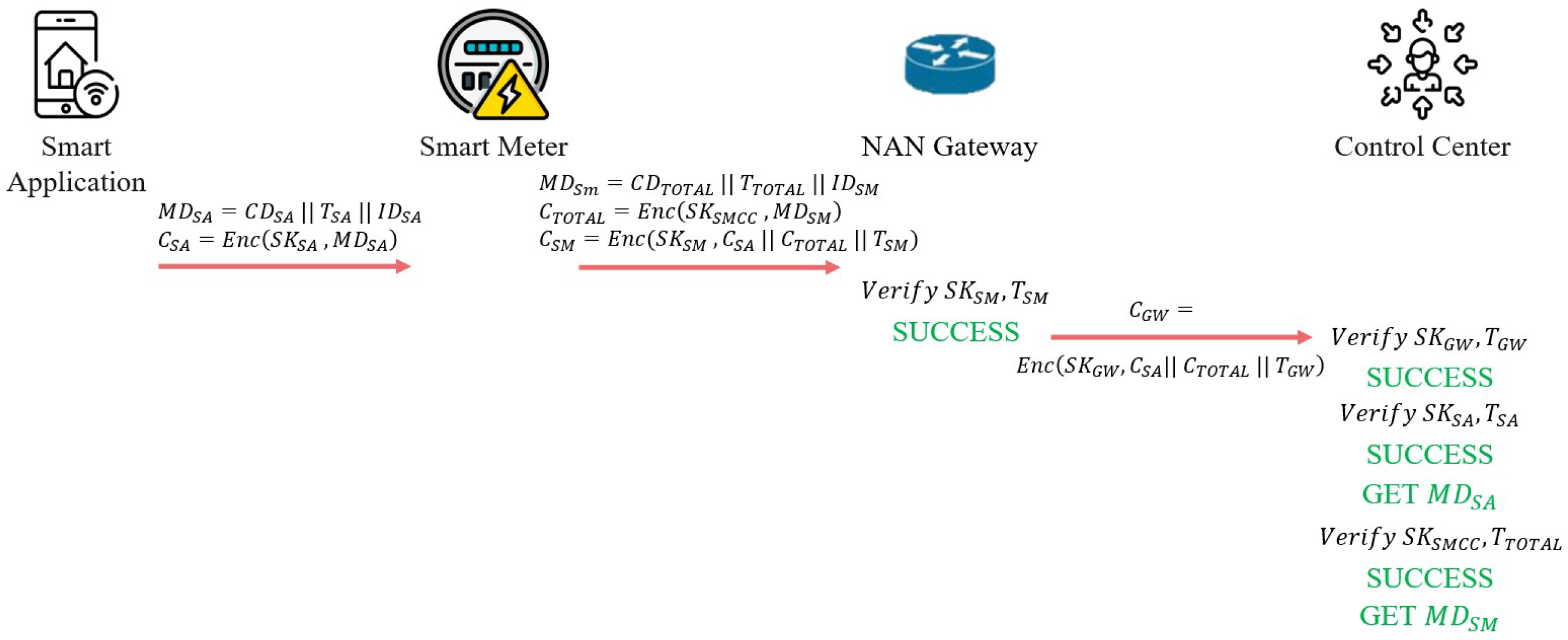
Once all entities in the SG have completed registration and can establish encrypted communication, the next step is to transmit electricity usage data to the CC based on the scheduled time t set within the SG environment. Figure 10 illustrates the process of transmitting electricity usage data.

The SA first encrypts its metering data $M{D}_{SA}$ using $S{K}_{SA}$ to produce the ciphertext $C_{SA}$, which is then sent to the SM. The $M{D}_{SA}$ comprises $C{D}_{SA}$, $T_{SA}$, and $I{D}_{SA}$. Upon receiving $C_{SA}$, the SM encrypts its collected total consumption data $M{D}_{SM}$ using $S{K}_{SMCC}$ to produce the ciphertext $C_{TOTAL}$. The $M{D}_{SM}$ comprises $C{D}_{TOTAL}$, $T_{TOTAL}$, and $I{D}_{SM}$. The SM then encrypts $C_{SA}$, $C_{TOTAL}$, and $T_{SM}$ using $S{K}_{SM}$ to produce the ciphertext $C_{SM}$ sent to the GW. Upon receiving $C_{SM}$, the GW first verifies the validity of $S{K}_{SM}$ and $T_{SM}$. If the verification is successful, the GW encrypts $C_{SA}$, $C_{TOTAL}$, and $T_{GW}$ using $S{K}_{GW}$ to produce the ciphertext $C_{GW}$ sent to the CC. Upon receiving $C_{GW}$, the CC performs three rounds of verification. First, it verifies the validity of $S{K}_{GW}$ and $T_{GW}$. If successful, the CC decrypts $C_{GW}$ and extracts $C_{SA}$ and $C_{TOTAL}$. Next, the CC verifies the validity of $S{K}_{SA}$ and $T_{SA}$ in $C_{SA}$. If successful, the CC decrypts $C_{SA}$ and extracts $M{D}_{SA}$. Then, the CC verifies the validity of $S{K}_{SM}$ and $T_{TOTAL}$ in $C_{TOTAL}$. If successful, the CC decrypts $C_{TOTAL}$ and extracts $M{D}_{SM}$. After these steps, the CC can obtain the energy consumption report for the SG at the scheduled time t.

Transmitting the total consumption data to the CC ensures that the energy consumption recorded by the consumer’s SA matches the total energy consumption recorded by the SM.

5. Security Evaluation

This section will conduct a security analysis of the proposed protocol and support its security through the following theorem.

Theorem 1. 

Comprehensive Security of Quantum Key Distribution System.

The proposed method can defend against attacks and supports secure and private communication. It ensures that the SG can resist quantum attacks while protecting user privacy, thereby guaranteeing the integrity and confidentiality of SMI electricity usage data. The proof will use the following lemma.

Lemma 1. 

Adversary A cannot obtain the electricity usage data.

Proof. 

Assume adversary Acan eavesdrops on all packets in the general communication channel. To obtain the electricity usage data, adversary A would need to decrypt the encrypted messages $C_{SA}=Enc(S{K}_{SA},M{D}_{SA})$ and $C_{TOTAL}=Enc(S{K}_{SMCC},M{D}_{SM})$, where $M{D}_{SA}=C{D}_{SA}\left|\right|T_{SA}\left|\right|I{D}_{SA}$ and $M{D}_{SM}=C{D}_{TOTAL}\left|\right|C{D}_{TOTAL}\left|\right|T_{SM}\left|\right|I{D}_{SM}$.

The consumption data $C{D}_{SA}$ are encrypted using $S{K}_{SA}$. A cannot obtain $S{K}_{SA}$, which is exchanged using the QKD protocol. Although the key $S{K}_{SMCC}$ used for $C{D}_{TOTAL}$ is not agreed upon using the QKD protocol, its transmission is encrypted with $S{K}_S$. When generated by the CC, it is encrypted using the consumer’s Verify Text VT. Therefore, A cannot decrypt the consumption data.

Adversary A might try to obtain the encryption key by tampering with the SA, as the SA might lack hardware tamper-resistance features. However, the SA is located in the consumer’s field, such as their home, which is considered private. Thus, attacks on these devices are not feasible. This article assumes that the consumer’s home, where the SA is located, is a secure environment and that the adversary cannot physically access or tamper with these devices. □

Lemma 2. 

Adversary A cannot impersonate a legitimate entity

Proof. 

For adversary A to successfully impersonate an SA or SM, they would need to obtain $S{K}_{SA}$ or $S{K}_{SM}$. To do this, they would need the Shared Key and Template. However, the Shared Key and Template can only be generated using the D and M, which are produced through random selection. Based on past information, Adversary A cannot deduce the relationship between the Shared Key, Template, and the two sequences.

Even if adversary A knows the D and M, they still cannot obtain $S{K}_{SA}$ or $S{K}_{SM}$. This is because having the D and M only allows one to determine the Template. The Shared Key requires measuring the quantum objects in the quantum channel using the M to know the bit values they carry. The receiver only releases the M after the photon transmission is complete. Therefore, the probability of A guessing the M is $1/2^{(}{M}_{Length})$. □

Lemma 3. 

Adversary A cannot act as a man-in-the-middle (MITM) and resend previously encrypted consumption data

Proof. 

For an adversary to become an MITM, they would need to impersonate a legitimate SA or SM. However, as proven in Lemma 2, adversary A cannot obtain $S{K}_{SA}$ or $S{K}_{SM}$ and thus cannot masquerade as a legitimate entity. If adversary A measures the quantum objects in the quantum channel, it will cause their polarization state to change, which will be detected due to the no-cloning theorem of quantum physics that makes each quantum object unique. A cannot make one measurement and continues transmitting the other.

As mentioned in Lemma 2, the probability of A guessing the M is extremely low if the M is sufficiently long. Each encrypted data packet includes a timestamp, and after verifying the identity, each entity checks whether the timestamp is correct. If it exceeds the acceptable delay range, the packet is discarded. A cannot alter the timestamp because A does not have $S{K}_{SA}$ or $S{K}_{SM}$ a; therefore, re cannot correctly encrypt the data. □

Lemma 4. 

Adversary A cannot eavesdrop on the transmitted data.

Proof. 

For adversary A to eavesdrop on the quantum objects transmitted in the quantum channel, they must measure them. However, as mentioned in Lemma 3, any measurement by A would cause detectable anomalies, revealing their presence. If adversary A attempts to eavesdrop on packets in the general communication channel, they still cannot obtain the actual information because the message is encrypted from the SA and can only be fully decrypted upon reaching the CC. During the transmission process, adversary A cannot decrypt the information since they do not have any of the $S{K}_{SA}$, $S{K}_{SM}$, or $S{K}_{GW}$ keys. □

Lemma 5. 

Adversary A cannot tamper with the electricity usage data.

Proof. 

For adversary A to tamper with the electricity usage data $M{D}_{SM}$ and $M{D}_{SA}$, they would first need to obtain $S{K}_{SM}$ and $S{K}_{SA}$. Lemma 1 demonstrates that A would need to decrypt the encrypted $M{D}_{SM}$ and $M{D}_{SA}$ to access the usage data $C{D}_{SA}$ and $C{D}_{TOTAL}$. However, adversary A cannot obtain or derive the $S{K}_{SA}$ exchanged using the QKD protocol or the $S{K}_{SMCC}$ encrypted with $S{K}_{SM}$. Lemma 2 demonstrates that A cannot forge their legitimate identity to re-encrypt and transmit new CD data because A does not possess the SK. A might attempt to tamper with the usage data by interfering with the SA. Still, the SA is located in the consumer’s private field, making it impractical for an ordinary person to launch such an attack against these devices. □

Lemma 6. 

Adversary A cannot obtain the keys of each entity in the key exchange protocol.

Proof. 

$S{K}_{GW}$ is generated based on $R_{GW}$ as a quantum string. GW receives the quantum string from CC and measures it using $M_{GW}$, then negotiates $S{K}_{GW}$ according to $D_{GW}$. Adversary A needs to measure the quantum string to know the transmitted bit values, but Lemma 4. has proven this behavior ineffective. A knows $M_{GW}$ and $D_{GW}$ only to obtain a Template, and because it does not know the measurement results of the quantum string through $M_{GW}$, it cannot know the Shared Key and thus cannot generate $S{K}_{GW}$. Similarly, $S{K}_{SA}$ and $S{K}_{SM}$ follow the same process, but the initial steps differ slightly, as explained below.

$I{D}_{SM}$ is initially encrypted using VT, and after CC verifies VT, it responds to GW that SM is an entity under its NAN. Only then do both parties begin negotiating $S{K}_{SM}$. Adversary A cannot know VT because, during consumer registration, VT is encrypted using $P{K}_{CC}$. Since A cannot obtain $S{K}_{GW}$, it also cannot obtain $S{K}_{SM}$. $I{D}_{SA}$ is exchanged only after CC and SA agree on $S{K}_{SA}$, using $S{K}_{SA}$, $S{K}_{SM}$, and $S{K}_{GW}$ for encryption. Lemma 4. has proven that A cannot break the ciphertexts generated by these three keys. Although adversary A can interfere with SA to obtain $S{K}_{SA}$, Lemma 1. mentions that SA is in the private space of the consumer, making such attacks infeasible. CC generates $S{K}_{SMCC}$, encrypted using VT, and further encrypted using $S{K}_{GW}$ and $S{K}_{SM}$ during transmission. A cannot obtain $S{K}_{GW}$ or $S{K}_{SM}$. VT was already encrypted using $P{K}_{CC}$ in Phase 1. Even if A knows the consumer’s VT, it cannot extract $S{K}_{SMCC}$ because it cannot break the ciphertexts generated by $S{K}_{GW}$ and $S{K}_{SM}$. □

Lemma 7. 

This scheme supports mutual authentication between entities.

Proof. 

In the proposed scheme, CC can ensure the successful identity authentication of GW, SM, and SA. When GW and SA register, $I{D}_{GW}$ and $I{D}_{SA}$ are distributed by CC, and through the subsequent QKD process, they obtain $S{K}_{GW}$ and $S{K}_{SA}$, enabling them to complete identity verification with CC. Before SM registers, CC first verifies the legitimacy of SM. Upon successful authentication, CC encrypts $I{D}_{SM}$ and sends it to GW, informing GW that this SM is a member of its NAN, thereby completing the negotiation of $S{K}_{SM}$ and $S{K}_{SMCC}$. Only legitimate entities can generate the corresponding SK to authenticate their identities. □

Lemma 8. 

This scheme supports Forward Secrecy.

Proof. 

In the proposed scheme, an attacker cannot use the current key to generate previous keys. D and M are random during the QKD key negotiation, and the resulting Template and Shared Key are unrelated. Eaentity’sy’s QKD negotiation process is identical, but the information exchanged differs. Therefore, even if an attacker obtains the SK of one entity, they cannot deduce the SK between other entities. □

Lemma 9. 

This scheme supports SM identity privacy.

Proof. 

The proposed scheme ensures that SM’s PN and VT cannot be known by any entity other than CC. CC needs to retain SM’s PN for future identification and billing purposes. VT is used only once to encrypt during the initial key negotiation between SMnd and is not used thereafter. Even if VT is unfortunately leaked, it will not affect subsequent transmissions and security. SM can protect the consumer’s PN from being leaked through tamper-resistant hardware. □

Lemma 10. 

This scheme supports Unconditional Security.

Proof. 

The proposed security scheme leverages quantum entanglement pairs and quantum polarization states to generate an SK. During the SK generation phase, the scheme employs fundamental principles of quantum physics, such as quantum superposition, quantum entanglement, and quantum measurement, to ensure a high level of security. The underlying basis of this scheme’s feasibility and robustness is supported by core theories in quantum physics, including the uncertainty principle and the no-cloning theorem. This quantum-based approach offers unconditional security, unlike traditional cryptographic methods that rely on complex mathematical problems such as discrete logarithms or large prime factorization. □

From the above evaluations, it can be concluded that the security methods designed in this article can resist most known attacks. Additionally, using quantum key exchange protocols enhances the security of the key exchange process, making it ready for the upcoming post-quantum era. This article not only demonstrates the feasibility and effectiveness of applying QKD technology in SG but also provides a higher level of protection for SG’s security.

This article compares the proposed scheme and other schemes presented in the related literature [12,14,15,16,17] as shown in

Table 3. Security attributes comparison.

Attributes	1	2	3	4	5	6	7	8	9	10
[14]	Y	Y	Y	Y	Y	Y	N	Y	N	N
[15]	Y	Y	Y	Y	Y	Y	Y	N	N	N
[16]	Y	Y	Y	Y	Y	Y	Y	N	N	N
[17]	Y	Y	Y	Y	Y	Y	Y	N	N	N
[12]	Y	Y	Y	Y	Y	Y	Y	Y	Y	N
Our Scheme	Y	Y	Y	Y	Y	Y	Y	Y	Y	Y

. The article will evaluate the following 10 security attributes: Protection of electricity usage data, impersonation of legitimate entities, tampering with electricity usage data through MITM attacks, replay attacks, obtaining keys during the key exchange process, mutual authentication between entities, forward secrecy, identity privacy, unconditional security, enhanced detection of malicious users.

The results show that the proposed scheme meets all the security evaluation criteria. The authors of [12] conducted a performance analysis of its proposed method, evaluating its communication cost, computational cost, and energy consumption and comparing it with other similar literature. However, there is an issue with the key generation example in the background work explanation of QKD [12]. According to its description, the quantum bits generated by IR, M, and the corresponding results in the shared key example table do not match. The sender initially transmits IR, M, and D to the receiver through a verified public classical channel in the key agreement protocol. Suppose a malicious user compromises this channel in the subsequent key agreement protocol. In that case, the malicious user can measure the quantum objects without being detected and generate a key identical to the receiver’s. This is because the malicious user knows the receiver’s M and can choose the correct filter for the measurement 100% of the time. Meanwhile, the malicious user can masquerade as a legitimate entity and infiltrate the SG undetected.

6. Discussion and Conclusions

The approach presented in this article does not experience such eavesdropping attacks because the communicating parties initially only transmit IR. After transmitting the quantum objects, they send each other M and D. Even if a malicious user intercepts and reads all the contents of the classical channel, they cannot obtain the SK. Knowing M and D allows the calculation of the template, but the shared key requires the quantum string $|q_{B2}{>}_x$ and IR. The malicious user cannot know the bit values they carry without measuring the quantum objects. The malicious user does not know the receiver’s M, so they can only unthinkingly guess the filter. Their presence will be detected if they choose a filter different from the receiver’s. Therefore, this article possesses the characteristic of enhanced detection of malicious users.

Quantum Key Distribution (QKD) with the BBM92 protocol enhances scalability in key management. QKD ensures long-term security with minimal post-deployment maintenance, which is crucial when managing millions of endpoints (SMs and SAs).

In this article, we have investigated the security authentication issues of SG data. A quantum key exchange mechanism is designed to establish a secure communication channel, utilizing the keys obtained from QKD for encryption to ensure data transmission privacy and enhance the security of data transmission within the grid. The proposed scheme underwent a security evaluation, proving its comprehensive security within the QKD system.