Cryptanalysis of Dual-Stage Permutation Encryption Using Large-Kernel Convolutional Neural Network and Known Plaintext Attack

Abstract

Reversible data-hiding in encrypted images (RDHEI) plays a pivotal role in preserving privacy within images stored on cloud platforms. Recently, Wang et al. introduced a dual-stage permutation encryption scheme, which is highly compatible with RDHEI techniques. In this study, we undertake an exhaustive examination of the characteristics inherent to the dual-stage permutation scheme and propose two cryptanalysis schemes leveraging a large-kernel convolutional neural network (LKCNN) and a known plaintext attack (KPA) scheme, respectively. Our experimental findings demonstrate the effectiveness of our cryptanalysis schemes in breaking the dual-stage permutation encryption scheme. Based on our investigation, we highlight significant security vulnerabilities in the dual-stage permutation encryption scheme, raising concerns about its suitability for secure image storage and privacy protection in cloud environments.

1. Introduction

Recently, cloud services have increasingly become a robust solution for data storage, revolutionizing data management for businesses and individuals. Cloud users can access their data, including images, videos, and text files, from anywhere and at any time via the Internet. This ubiquitous access significantly enhances flexibility and productivity, enabling seamless collaboration and real-time data sharing. However, the widespread adoption of cloud services has raised significant concerns regarding data security. Once data are stolen or misused, it can result in financial and personal consequences, such as identity theft, financial fraud, and the loss of sensitive personal information. These concerns have prompted increased research on protecting cloud data. One promising solution is reversible data-hiding [1] in the encrypted domain, which involves encrypting data before uploading them to the cloud for security. Additionally, it allows the embedding of additional data, facilitating efficient data transmission within limited bandwidth environments.

Due to the extensive use of digital images, numerous techniques for reversible data-hiding in encrypted images (RDHEI) have been developed. In RDHEI, three roles are involved: the image owner, the cloud server provider, and the recipient. Initially, the image owner encrypts the sensitive image and uploads it to the cloud. Subsequently, the cloud server provider embeds additional data into the encrypted image, resulting in a marked image. Finally, the recipient receives the marked image and can access the original image, the additional data, or both, based on their permissions. In general, RDHEI schemes can be classified into two categories: reserving room before encryption (RRBE) [2,3,4,5,6,7,8] and vacating room after encryption (VRAE) [9,10,11,12,13,14,15,16,17,18], based on the order of encrypting images and vacating room for additional data. In 2019, Yi et al. [18] highlighted that RRBE-based schemes offer substantial redundant room for data embedding but require image owners to independently vacate space, posing practical challenges for ordinary users. As a result, many scholars have focused on exploring VRAE-based schemes.

The performance of the VRAE-based scheme is dependent on the encryption scheme. Traditional encryption schemes, such as the data encryption standard (DES) [19], chaotic encryption [20,21,22], and homomorphic encryption [23,24,25,26], are deemed unsuitable due to the disruption of pixel correlation in the encrypted results, leaving no redundant space for data-hiding. Consequently, specialized encryption schemes need to be designed for VRAE-based schemes. A common encryption scheme in VRAE-based schemes combines stream cipher exclusive or operation [10,11,12] with block permutation [16,17], preserving partial pixel correlation within a block while altering image pixel values. However, the stream cipher exclusive or operation is sensitive to pixels. Even similar plaintext pixels may drastically differ after experiencing the same exclusive or operation, resulting in a significant loss of redundant space. Therefore, some researchers have proposed the use of modulation operation as a replacement for the exclusive or operation. This substitution effectively enhances the pixel correlation within each block, thereby enhancing the embedding capacity of the VRAE-based scheme.

Although the aforementioned two encryption schemes are highly compatible with the VRAE-based scheme, the occurrence of pixel value overflow within a block remains an inescapable issue. Consequently, some researchers have opted to employ block permutation for image encryption, a scheme that impeccably preserves the correlation of pixels within a block.

In 2023, Wang et al. [27] introduced an efficient dual-stage permutation encryption scheme for the VRAE-based RDHEI scheme. The scheme begins by partitioning the cover image into non-overlapping blocks. These blocks then undergo coarse-level block scrambling, followed by finer-level pixel scrambling within each block. While this encryption scheme offers substantial embedding capacity for additional data, it also introduces significant risks. Theoretically, an attacker cannot extract any information about the original image from the encrypted version. However, the dual-stage permutation encryption method preserves pixel values from the original image within the encrypted image. This preservation can be exploited by an attacker to potentially reconstruct the original content. By reverse-engineering or exploiting patterns within the encrypted image, the attacker may leverage the preserved pixel values to decrypt the original content.

In this paper, we aim to crack the dual-stage permutation encryption scheme under two hypotheses. First, we assume that the attacker possesses a plaintext image from one of the encrypted collections. With this plaintext image, the attacker can identify the corresponding ciphertext image and use a known-plaintext attack (KPA) to estimate the permutation sequences for coarse-level block scrambling and finer-level pixel scrambling. Second, if the attacker does not have a plaintext image, we assume that the image owner uses a finite secret key space during the encryption process. Since the dual-stage permutation encryption scheme does not alter the mean value of pixels within each block, a correct coarse-level block scrambling sequence must exist that makes the ciphertext image meaningful. Therefore, we employ a large-kernel convolutional neural network (LKCNN) to determine if the recovered image is meaningful, thereby automating the search for the correct block permutation sequence. The main contributions of the proposed scheme are summarized as follows:

• Distinct from the existing cryptanalysis schemes, this paper considers two scenarios: one in which the attacker has access to a known plaintext image, and the other where such access is not granted.
• Block modulation is applied to compare ciphertext and plaintext blocks, thereby facilitating the estimation of the block permutation sequence.
• A large-kernel convolutional neural network is developed to automate the detection of permutation sequences, thereby streamlining the analysis process and reducing time requirements.

The remainder of this paper is organized as follows: Section 2 provides an overview of cryptanalysis.Section 3 introduces and analyzes the dual-stage permutation encryption scheme. Section 4 provides a detailed exposition of the proposed known-plaintext attack. Section 5 presents a cryptanalysis scheme using a large-kernel convolutional neural network. Section 6 presents experimental results and analyses. Finally, Section 7 offers conclusions and future prospects.

2. Related Works

Cryptanalysis, the study of breaking encryption systems, is crucial for developing secure communication schemes. Traditionally, cryptanalysts have used mathematical techniques to find weaknesses in specific encryption algorithms [28]. Recently, deep learning has emerged as a powerful tool in cryptanalysis and broader cybersecurity applications.

In cybersecurity, deep learning has shown promise in detecting advanced threats. For example, Javed et al. [29] developed a graph attention network (GAN) to identify advanced persistent threat (APT) attacks in industrial Internet of Things (I-IoT) systems, achieving high accuracy compared to traditional schemes.

In the field of cryptanalysis, several studies have explored the use of deep learning to analyze encryption algorithms. Chen et al. [30] proposed a deep learning scheme to attack chaos-based image encryption. Their method uses a neural network to reconstruct original images from encrypted ones without manual key analysis, showing how deep learning can automate complex cryptanalytic tasks. Singh et al. [31] provided an overview of deep learning in cryptanalysis, highlighting its ability to process raw encrypted data and find weaknesses in ciphers. Their work shows how neural networks can be trained to identify vulnerabilities in encryption systems. Focusing on specific algorithms, Kim et al. [32] developed a deep learning scheme for analyzing lightweight block ciphers like simplified data encryption standard(S-DES), simplified advanced encryption standard(S-AES), and simplified speck(S-SPECK). They used advanced techniques to improve efficiency and accuracy in key recovery, demonstrating how deep learning can be adapted for different encryption methods.

These studies show the potential of deep learning in cryptanalysis across various encryption types. However, challenges remain in applying these schemes to modern, complex encryption algorithms. While deep learning offers new possibilities for cryptanalysis, it has not yet replaced traditional methods in all areas. In this paper, we employ two schemes to analyze the dual-stage permutation encryption scheme [27]. First, we use a traditional plaintext attack to demonstrate its insecurity, and then we explore the possibility of estimating its key sequence using deep learning techniques under specific assumptions.

3. Preliminary Works

In this section, we present the dual-stage permutation encryption scheme introduced by Wang et al. [27] and analyze its characteristics. This scheme employs a dual-stage encryption process, offering a practical and efficient mechanism to obscure visual content.

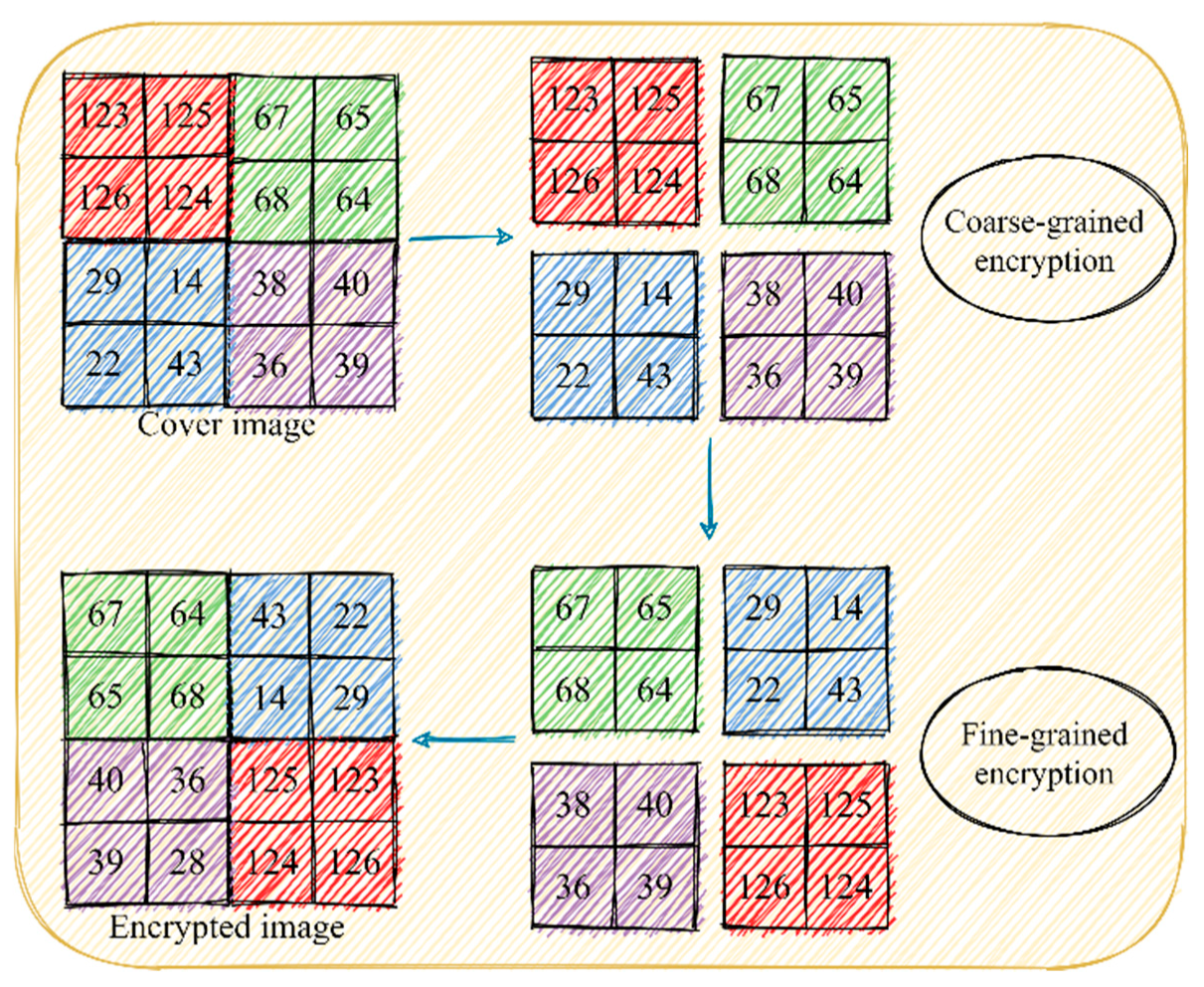
3.1. Dual-Stage Permutation Encryption Scheme

The dual-stage permutation encryption scheme characterized by its ease of operation, which begins by dividing the cover image $I$ into non-overlapping $2\times 2$ blocks. Following this partitioning, these blocks undergo coarse-grained encryption, where the $2\times 2$ blocks are globally scrambled. Finally, we apply fine-grained encryption to permute the pixels within each block. Note that all the scrambling is carried out by generating a random sequence based on an encrypted key $K_e$. For ease of understanding, we provide a schematic of the encryption process in Figure 1.

3.2. Analysis of Dual-Stage Permutation Encryption Scheme

The dual-stage permutation encryption scheme introduced by Wang et al. [27] exhibits several key characteristics, as follows:

• Simplicity and practicality: The dual-stage permutation encryption scheme avoids arithmetic operations, focusing solely on disrupting individual pixel positions. This approach is not only straightforward but also highly suitable for thin-client devices.
• Large encryption space: The dual-stage permutation encryption scheme offers a vast array of potential encryption outcomes. For instance, a $256\times 256$-sized image theoretically yields $\left(128\times 128\right)!\times (128\times 128\times 4!)$ encryption results. This value exceeds $2^{100}$, making it virtually impervious to exhaustive brute force attacks.
• High correlation within block: Despite the encryption result of dual-stage permutation being visually meaningless, the correlation between pixels within each block is losslessly preserved. This unique attribute can be harnessed to generate additional space for reversible data-hiding, thereby enhancing the overall embedding capacity of the encryption scheme.

Nevertheless, the dual-stage permutation encryption scheme encounters notable security challenges, as follows:

• Preservation of pixel value distribution: The dual-stage permutation encryption maintains the pixel value distribution of the plaintext image perfectly, potentially exposing vulnerabilities. Attackers might exploit these statistical patterns to reconstruct the original content.
• Limitations of the random number generator: The inner-block shuffling sequence and block permutation sequence used in the dual-stage permutation encryption scheme are generated by a random number generator requiring a secret key. Due to limitations in hardware, the generator cannot produce all possible permutation sequences. As a result, one can reduce the exhaustive search space and then obtain every feasible permutation from the generator by iterating through all possible secret keys.

In conclusion, while the dual-stage permutation encryption scheme boasts efficient data-hiding capabilities, it is considered insecure due to discernible vulnerabilities and weaknesses.

4. Cryptanalysis with Known-Plaintext Attack Based on Block Modulation

The primary objective of the proposed cryptanalysis is to obtain the plaintext content of the ciphertext image generated by the dual-stage permutation encryption scheme [27]. To achieve this, we first introduce the strategy of inner-block modulation. Subsequently, we propose a KPA scheme for estimating the block permutation sequence ${\displaystyle \widehat{\prod }}$ and inner-block shuffling sequence $\widehat{\mathsf{\Phi }}$, based on the modulated blocks.

Assume that a set of ciphertext images contains $l$ ciphertext images $\mathbb{E}=\{E_1,E_2,\dots ,E_l\}$, according to our hypothesis, if an attacker acquires a plaintext image $I$ corresponding to one of a set of ciphertext images encrypted with the same key, they can use the pixel histogram to identify this ciphertext image $E_{\alpha }$. This is because Wang et al.’s encryption scheme does not alter the distribution of pixel values.

After obtaining the plaintext image $I$ and its corresponding ciphertext image $E_{\alpha }$, the attacker can divide them into blocks and modulate each block in a descending order. Specifically, the $m\times n$-sized plaintext image $I$ can be divided into a set of blocks $I=\{P_1,P_2,\dots ,P_{⌊m/2⌋\times ⌊n/2⌋}\}$; each block can be represented as a set of four pixels $P_i=\{p_i^1,p_i^2,p_i^3,p_i^4\}$. Then, each block is modulated into descending order to obtain $P_i^{\mathrm{\prime }}=\{p_i^{\sigma \left(1\right)},p_i^{\sigma \left(2\right)},p_i^{\sigma \left(3\right)},p_i^{\sigma \left(4\right)}\}$, where $\sigma \left(j\right)$ represents the original index of the $j$-th pixel after sorting. if $p_i^{\sigma \left(j\right)}=p_i^{\sigma \left(k\right)}$ and $j<k$, then $\sigma \left(j\right)<\sigma \left(k\right)$. It is worth mentioning that the original index of four pixels ${\varphi }_i=\{\sigma \left(1\right),\sigma \left(2\right),\sigma \left(3\right),\sigma \left(4\right)\}$ in this block needs to be recorded as an estimated inner-block shuffling sequence to recover the block shuffling. Similarly, the same-sized ciphertext image $E_{\alpha }$ can also be divided into blocks $E_{\alpha }=\{B_1,B_2,\dots ,B_{⌊m/2⌋\times ⌊n/2⌋}\}$ and all blocks can be modulated into descending order.

Finally, the block permutation sequence ${\displaystyle \widehat{\prod }}$ can be estimated by comparing the modulated plaintext images $I\mathrm{\prime }$ and $E_{\alpha }^{\mathrm{\prime }}$. The detailed process of the known-plaintext attack, under the condition that the attacker acquires a plaintext image, is illustrated in Algorithm 1.

Algorithm 1: Estimate block permutation sequence and inner-block shuffling sequence
Input:	Plaintext image $I$ and a set of ciphertext images $\mathbb{E}$.
Output:	Estimated block permutation sequence ${\displaystyle \widehat{\prod }}$ and inner-block shuffling sequence $\widehat{\mathsf{\Phi }}$.
1:	Compare the pixel value histogram of $I$ with all images in $\mathbb{E}$ to find the corresponding ciphertext image $E_{\alpha }$;
2:	Sort each plaintext block $P_i$ in descending order to obtain the modulated plaintext block $P_i^{\mathrm{\prime }}$ and estimated inner-block shuffling sequence ${\varphi }_i$;
3:	${\widehat{\mathsf{\Phi }}}_i^{1:4}={\varphi }_i$;
4:	Sort each ciphertext block $B_i$ in descending order to obtain the modulated ciphertext block $B_i^{\mathrm{\prime }}$.
5:	For $i=1,2,\dots ,⌊m/2⌋\times ⌊n/2⌋$ do
6:	For $j=1,2,\dots ,⌊m/2⌋\times ⌊n/2⌋$ do
7:	If $B_i^{\mathrm{\prime }}$ is equal to $P_i^{\mathrm{\prime }}$ and $j$ has not been recorded
	${\displaystyle \widehat{\prod }}(i)=j$
	Break
	End For
	End For
9:	Return ${\displaystyle \widehat{\prod }}$ and $\widehat{\mathsf{\Phi }}$

Once the estimated block permutation sequence and inner-block shuffling sequence have been obtained, for each block in the ciphertext image, the attacker can recover the inner-block sequence by $\widehat{\mathsf{\Phi }}$ and rearrange these blocks according to ${\displaystyle \widehat{\prod }}$. It is worth mentioning that the correctness of ${\displaystyle \widehat{\prod }}$ and $\widehat{\mathsf{\Phi }}$ can be improved by increasing the number of plaintext images. However, it is also possible to roughly decode the ciphertext image using only one plaintext.

5. Cryptanalysis with Large-Kernel Convolutional Neural Network

When the attacker does not have access to a plaintext image, the above KPA method is ineffective. To address this, we introduce another innovative cryptanalysis network with large-kernel convolution. In this section, we begin by describing our design objectives. Following this, we analyze the feasibility of our scheme. Subsequently, we present the training datasets, network architecture, and training configuration. The details are as follows.

5.1. Design Objectives

The dual-stage permutation encryption scheme encrypts images through block division, coarse-grained permutation, and fine-grained permutation. As previously stated, the resulting encrypted images retain the pixel value information of the original images. Additionally, the mean pixel value of each $2\times 2$ block remains unchanged. Consequently, we can employ the mean value of each block to construct a mean sequence, $\eta$. By iteratively permuting this mean sequence, we can identify a permutation sequence, ${\eta }^{\mathrm{\prime }}$, that corresponds to the mean sequence of the original image. This approach leverages the invariance of the mean values to systematically reverse the permutation process.

5.2. Theoretical Analysis

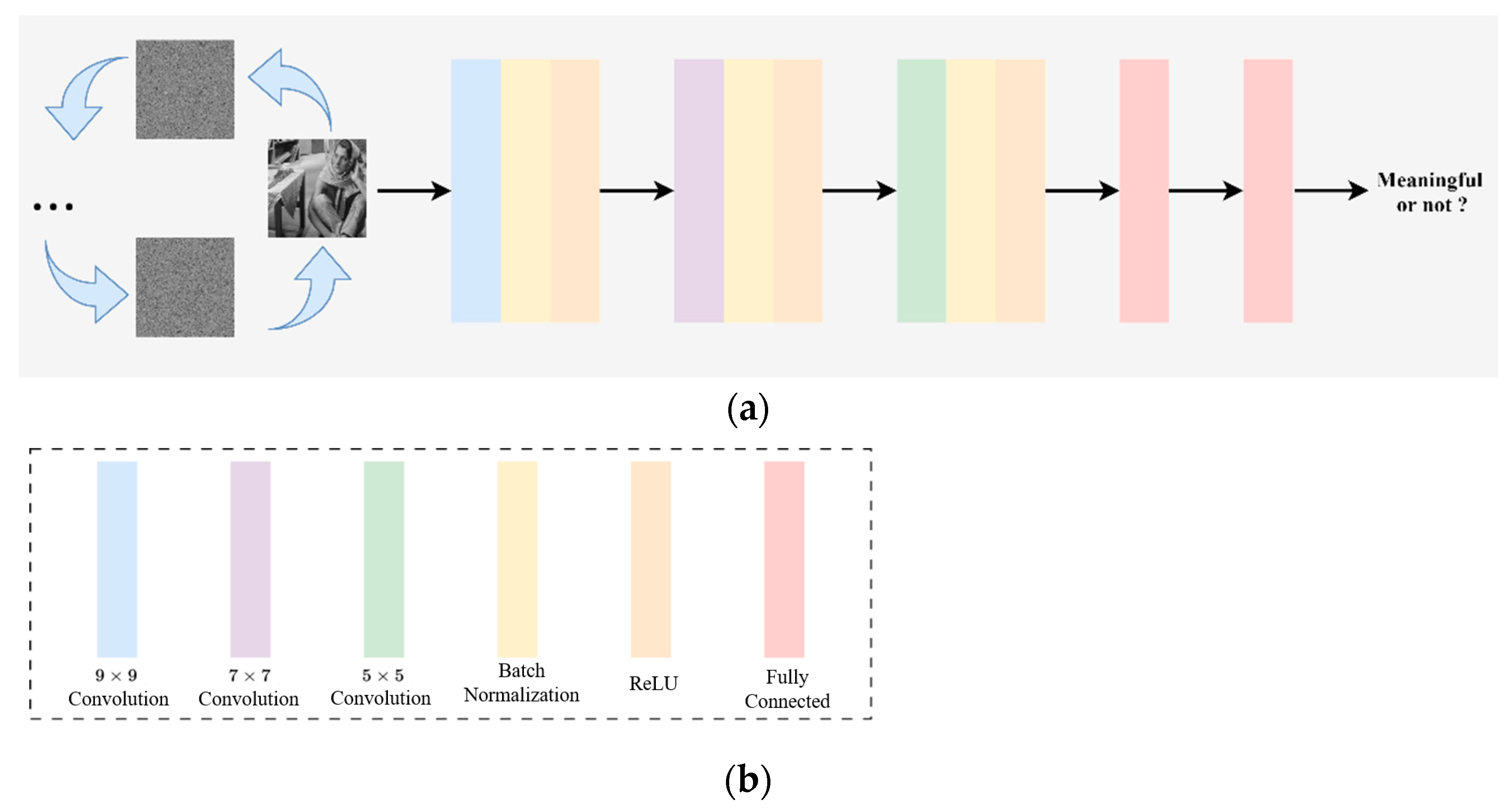
According to our hypothesis, once we obtain an encrypted image generated by dual-stage permutation encryption, we can use a random permutation generator, $\mathcal{G}$, to exhaustively attempt all keys within a finite key space, thereby deriving all possible permutation sequences. It is important to note that current cryptographic software imposes a limit on the length of the secret key. This limitation significantly reduces the time required to exhaust all possible keys, compared to the time it would take to explore all theoretical permutations. As an example, in MATLAB R2022a, the secret key length is capped at $2^{32}=\mathrm{4,294,967,296}$. This constraint necessitates that the secret key be an integer and prevents it from exceeding this specified length. Hence, we can iterate through all possible secret keys to generate $2^{32}$ sequences and identify the most suitable one, rather than searching through the theoretically possible $\left(⌊m/2⌋\times ⌊n/2⌋\right)!$ permutations, where $m$ and $n$ are the width and height of the encrypted image. To facilitate this process, we developed a large-kernel convolutional neural network (LKCNN) to verify the correct permutation sequence that aligns with the original image.

5.3. Dataset

To train the LKCNN, we construct the following positive and negative samples:

Positive samples: Images from the “Bossbase” dataset [33], originally $512\times 512$ pixels, are downscaled to $256\times 256$ pixels. These resized images are divided into $2\times 2$ blocks, and the mean value of each block is calculated to form the positive images.

Negative samples: Images from the “Bossbase” dataset [33], also originally $512\times 512$ pixels, are downscaled to $256\times 256$ pixels. Similarly, these resized images are divided into $2\times 2$ blocks. The blocks underwent a two-stage permutation process to disrupt the original plaintext content. Initially, a coarse-grained permutation shuffled the $2\times 2$ blocks. Subsequently, a fine-grained permutation further shuffled the pixels within each block. The mean value of each block is then calculated to form the negative images.

It is worth noting that we downsample the images in the dataset to $256\times 256$ pixels, resulting in positive and negative samples of size $128\times 128$. However, with sufficient computational resources and time, downsampling can be omitted.

5.4. Network Architecture

In this section, we present the architecture of our LKCNN designed for the cryptanalysis of permutation-encrypted images, as depicted in Figure 2. The LKCNN utilizes a sequence of convolutional layers with large kernels to capture spatial features and discern the accurate permutation sequence effectively. The network begins with a convolutional layer comprising 16 filters with a $9\times 9$ kernel size, a stride of two, and a dilation rate of two, allowing it to capture broad spatial features. This is followed by a second convolutional layer with 32 filters, a $7\times 7$ kernel, a stride of two, and a dilation rate of two, which further refines the extracted features. The third convolutional layer includes 64 filters with a $5\times 5$ kernel, a stride of two, and a dilation rate of two, enabling the detection of finer details within the image. Each convolutional layer is followed by batch normalization and rectified linear unit (ReLU) activation to ensure numerical stability and non-linearity. Following the convolutional layers, the network employs fully connected layers to transform the spatial features into a compact representation. The first fully connected layer consists of 512 neurons, providing an intermediary step between the convolutional outputs and the final decision layer. The output layer is a fully connected layer with two neurons, corresponding to the binary classification task of determining whether the correct permutation sequence has been identified.

5.5. Training Configuration

The LKCNN model is trained for binary classification tasks with the consideration of several key parameters and strategies. Cross-entropy loss was utilized as the objective function, due to its effectiveness in evaluating the alignment between predicted probabilities and actual class labels. The Adam [34] optimizer is chosen for its adaptive learning rate capabilities, enhancing convergence by adjusting learning rates for individual parameters. A learning rate of 0.001 is determined through iterative experimentation, balanced training efficiency and stability. Training batches of 64 samples are used to optimize computational efficiency while maintaining gradient stability. The model is trained over 20 epochs, enabling it to capture intricate patterns in the data without overfitting.

6. Experimental Results and Analysis

In this section, we conduct experiments to evaluate the information leakage of the dual-stage permutation encryption scheme under two hypotheses. Four standard grayscale test images, ‘F16’, ‘Barbara’, ‘Peppers’, and ‘Baboon’, are used, which are resized to $256\times 256$ for testing convenience. Figure 3 shows the test images and ciphertext images generated by the PBE scheme using a $2\times 2$ block size. All programs are implemented using MATLAB R2022a and PyTorch 1.8.

In our experiments, we begin by introducing the experimental setup and evaluation metrics. Subsequently, we present the results of the cryptanalysis under two distinct hypotheses, respectively. The details are as follows.

6.1. Experimental Setting and Evaluation Metrics

To comprehensively evaluate the performance of the proposed scheme, we employ commonly used metrics, peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM), to quantify the visual quality of the estimated plaintext image. The definitions of PSNR and SSIM are as follows:

$$\mathrm{P}\mathrm{S}\mathrm{N}\mathrm{R}=10{\mathit{log}}_{10}\left({\displaystyle \frac{{255}^2\times m\times n}{{\sum }_{m\times n}{\left(p_i-p_i^{\mathrm{\prime }}\right)}^2}}\right)\left(\mathrm{d}\mathrm{B}\right),$$

(1)

where $p_i$ and $p_i^{\mathrm{\prime }}$ represent the corresponding pixel values in the original and estimated plaintext images, respectively, and $m$ and $n$ represent the width and height of the image.

$$\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}(I,\mathrm{}I\mathrm{\prime })={\displaystyle \frac{(2{\mu }_I{\mu }_{I^{\mathrm{\prime }}}+c_1)(2{\sigma }_{I{I}^{\mathrm{\prime }}}+c_2)}{({\mu }_I^2+{\mu }_{I^{\mathrm{\prime }}}^2+c_1)({\sigma }_I^2+{\sigma }_{I^{\mathrm{\prime }}}^2+c_2)}},$$

(2)

$$c_1={\left(k_{1}L\right)}^2,\mathrm{ }\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{ }{k}_1=0.01,$$

(3)

$$c_2={\left(k_{2}L\right)}^2,\mathrm{ }\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{ }{k}_2=0.03,$$

(4)

where ${\mu }_O$ and ${\mu }_S$ represent the average of original plaintext image $I$ and estimated plaintext image $I\mathrm{\prime }$, respectively; ${\sigma }_O^2$ and ${\sigma }_S^2$ are the variances of $I$ and $I\mathrm{\prime }$; and ${\sigma }_{OS}$ is the covariance of $I$ and $I\mathrm{\prime }$.

Except for the visual quality, we also use the correction rates ${\mathcal{A}}_{{\displaystyle \widehat{\prod }}}$ and ${\mathcal{A}}_{\widehat{\mathsf{\Phi }}}$ to evaluate the accuracy of the estimated block permutation sequence and the inner-block shuffling sequence, which are defined as follows:

$${\mathcal{A}}_{{\displaystyle \widehat{\prod }}}={\displaystyle \frac{{\sum }_{i=1}^{⌊m/2⌋\times ⌊n/2⌋}\mathcal{F}(\prod \left(i\right),{\displaystyle \widehat{\prod }}(i\left)\right)}{⌊m/2⌋\times ⌊n/2⌋}},$$

(5)

$${\mathcal{A}}_{\widehat{\mathsf{\Phi }}}={\displaystyle \frac{{\sum }_{i=1}^{⌊m/2⌋\times ⌊n/2⌋}{\sum }_{j=1}^4\mathcal{F}(\prod \left(i\right),{\displaystyle \widehat{\prod }}(i\left)\right)\times \mathcal{F}({\mathsf{\Phi }}_i^j,{\widehat{\mathsf{\Phi }}}_i^j)}{{\sum }_{i=1}^{⌊m/2⌋\times ⌊n/2⌋}\mathcal{F}(\prod \left(i\right),{\displaystyle \widehat{\prod }}(i\left)\right)\times 4}},$$

(6)

$$\mathcal{F}\left(a,\mathrm{}b\right)=\left\{\begin{array}{c}1, if a=b \\ 0, if a\ne b\end{array}\right..$$

(7)

6.2. Cryptanalysis Performance of the Proposed KPA

In this section, we evaluate the effectiveness of the proposed KPA algorithm for cryptanalysis.

6.2.1. Analysis of Estimation Accuracy of ${\displaystyle \widehat{\prod }}$ and $\widehat{\mathsf{\Phi }}$

For the given encryption key, a set of ciphertext images of a set of plaintext images are generated, and the block permutation sequence $\prod$ and inner-block shuffling sequence $\mathsf{\Phi }$ are recorded.

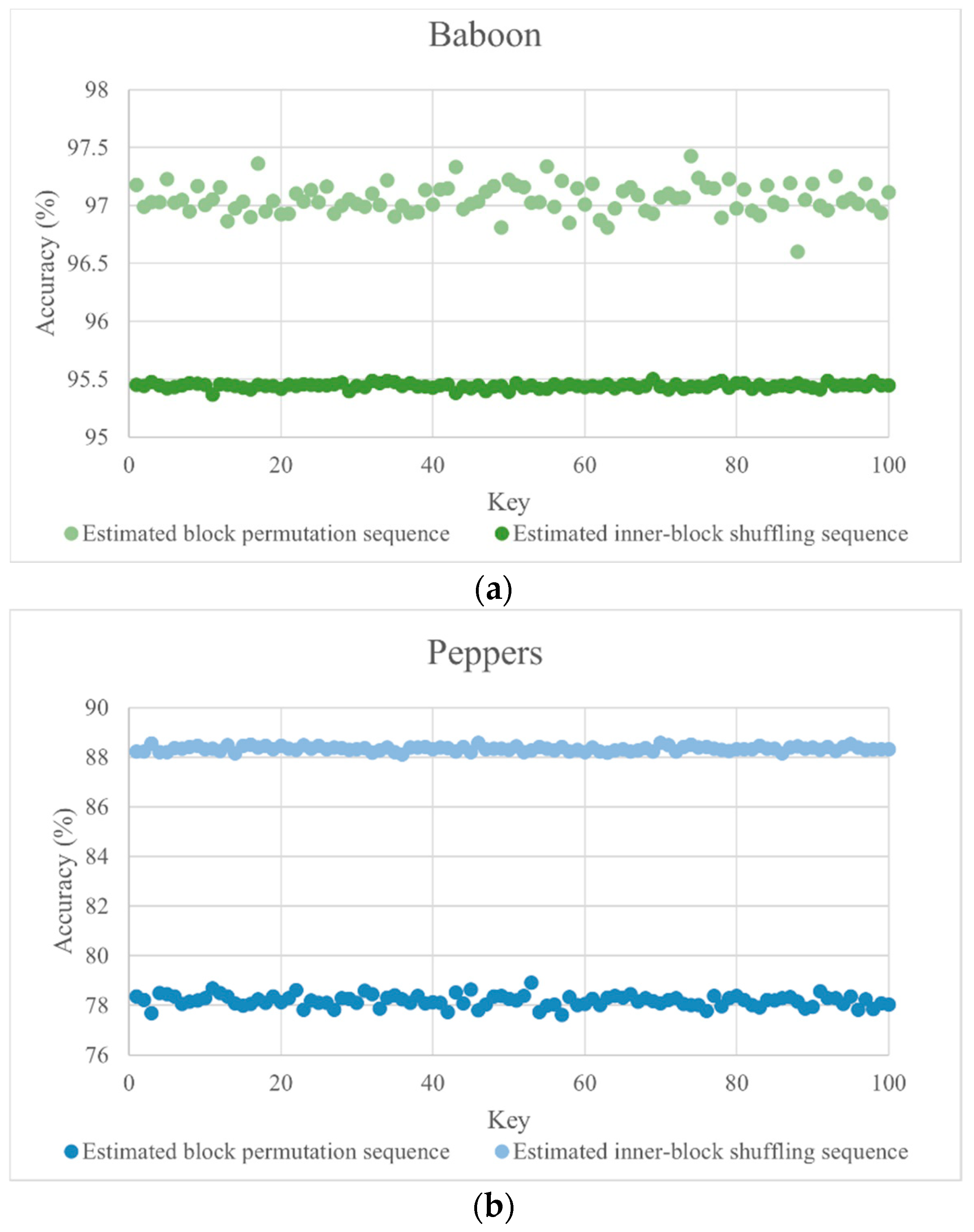
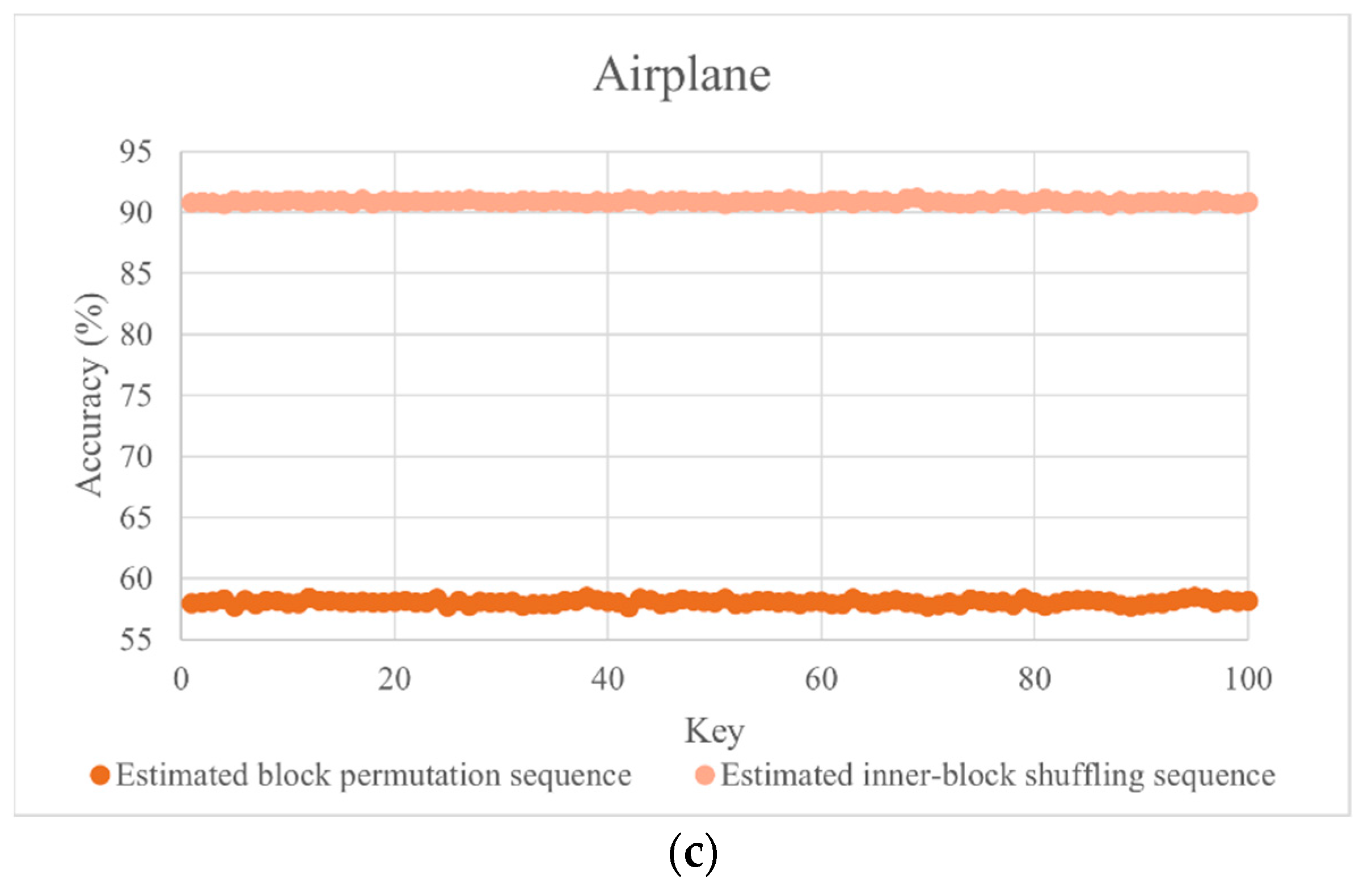
To show the effect of different encryption keys on the accuracy of $\widehat{\prod }$ and $\widehat{\mathsf{\Phi }}$ (${\mathcal{A}}_{{\displaystyle \widehat{\prod }}}$ and ${\mathcal{A}}_{\widehat{\mathsf{\Phi }}}$), 100 different encryption keys are utilized to test the ${\mathcal{A}}_{{\displaystyle \widehat{\prod }}}$ and ${\mathcal{A}}_{\widehat{\mathsf{\Phi }}}$ of “Baboon”, “Airplane”, and “Peppers”. The experimental results are shown in Figure 3a,b.

Figure 4 shows that the ${\mathcal{A}}_{{\displaystyle \widehat{\prod }}}$ of “Baboon”, “Airplane”, and “Peppers” fall within the intervals [96.60, 97.36], [77.69, 78.92], and [57.64, 58.38], with mean values of 97.06, 78.18, and 58.06, respectively. For ${\mathcal{A}}_{\widehat{\mathsf{\Phi }}}$, we only calculate the estimated accuracy of inner-block sequences when the position of the block is correctly recovered. The ${\mathcal{A}}_{\widehat{\mathsf{\Phi }}}$ value lies within the intervals [95.36, 95.50], [88.14, 88.57], and [90.72, 91.20], with mean values of 95.44, 88.34, and 90.89, respectively.

We observe that ${\mathcal{A}}_{{\displaystyle \widehat{\prod }}}$ is higher for complex images due to the intricate texture of the blocks, which results in fewer identical blocks. In contrast, for smooth images, the abundance of identical blocks leads to a significant discrepancy between the estimated sequence and the original sequence. However, as long as the blocks are correctly positioned, the estimation accuracy ${\mathcal{A}}_{\widehat{\mathsf{\Phi }}}$ under KPA remains high for all blocks.

To visually illustrate the correlation between the estimation accuracy of the permutation sequence and the leakage of image content information, the estimated sequences ${\displaystyle \widehat{\prod }}$ and $\widehat{\mathsf{\Phi }}$, with different accuracy (obtained using “Baboon”, “Airplane”, and “Peppers”, respectively) are employed to decrypt the ciphertext image “Barbara”. The resulting approximate decrypted image is presented in Figure 5. It is observed that under the $2\times 2$ block size, the higher the estimation accuracy of ${\displaystyle \widehat{\prod }}$ and the more pronounced the leakage of content information from the ciphertext image is. As depicted in Figure 4c, even when the estimated accuracy of the ${\displaystyle \widehat{\prod }}$ is less than 60%, a portion of the information in the ciphertext image is still leaked (PSNR = 14.93 dB, SSIM = 0.44). The decryption effect deteriorates as the texture complexity of the known plaintext image decreases. For instance, under a $2\times 2$ block size, the visual quality of the decrypted image using “Peppers” (PSNR = 18.36 dB, SSIM = 0.56) is inferior to that of “Baboon” (PSNR = 26.74 dB, SSIM = 0.89) under identical conditions.

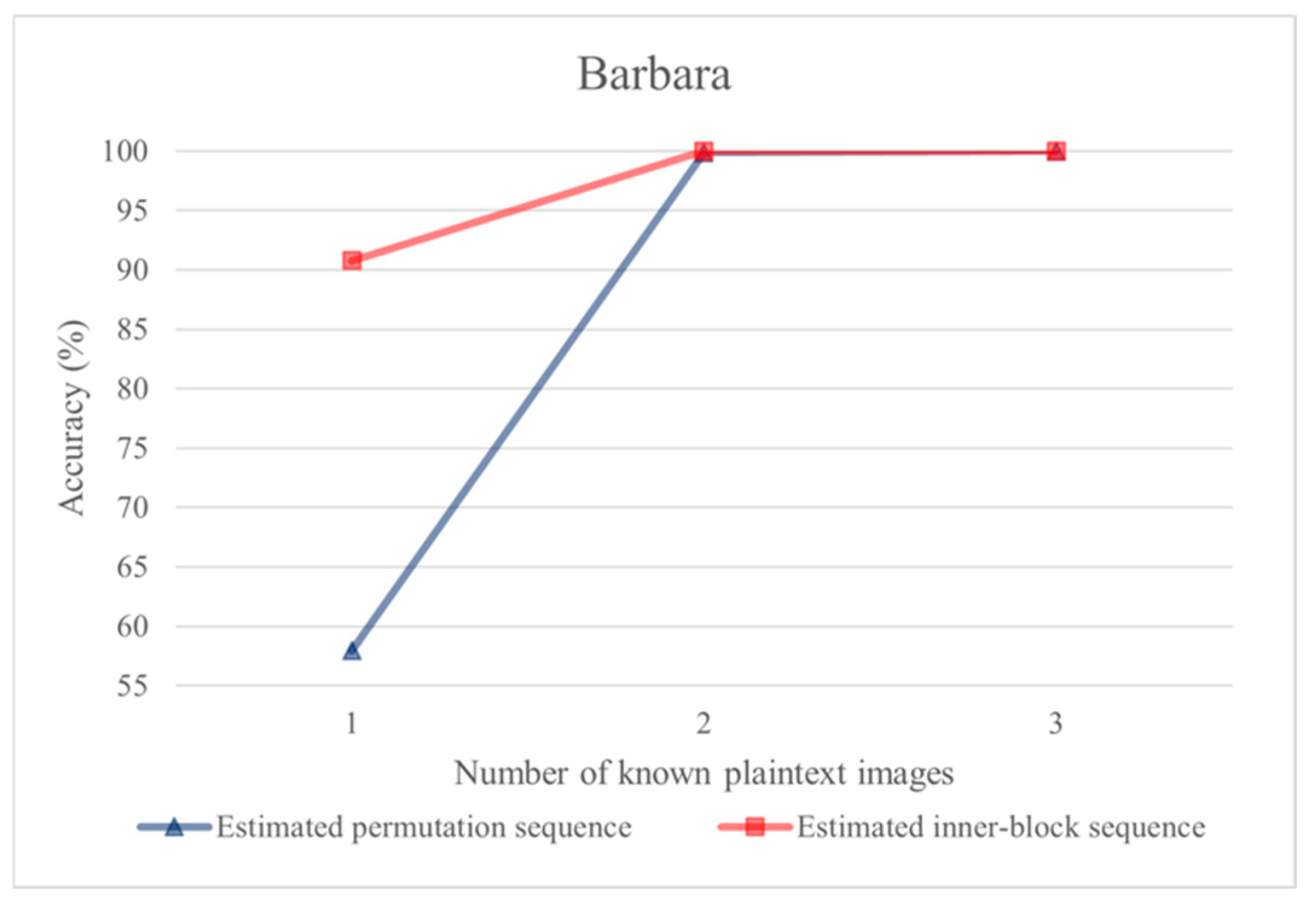
To test the influence of the number of known plaintext images on the estimation accuracy of the estimated sequences ${\displaystyle \widehat{\prod }}$ and ${\displaystyle \widehat{\mathsf{\Phi }}}$, the following three KPAs under different plaintext images are considered: (a) “Airplane”; (b) “Airplane” and “Peppers”; (c) “Airplane”, “Peppers”, and “Baboon”. As shown in Figure 6, when two plaintext images are used, the estimation accuracy of the estimated sequences ${\displaystyle \widehat{\prod }}$ and $\widehat{\mathsf{\Phi }}$ are close to 100%.

6.2.2. Time Complexity Analysis

To evaluate the time complexity of the proposed KPA algorithm, we analyze each step of the KPA in this section. The time complexity of each step is detailed as follows.

Step 1 (comparing histograms): The first step involves comparing the pixel value histogram of the plaintext image $I$ with all images in the set of ciphertext images $\mathbb{E}$ to find the corresponding ciphertext image $E_{\alpha }$. The time complexity of this step depends on the number of images in $\mathbb{E}$. Assuming there are $l$ images in $\mathbb{E}$ and $m\times n$ pixels in $I$, the time complexity of this step is $O(l\times m\times n)$.

Step 2 (sorting plaintext blocks): The second step involves sorting each plaintext block $P_i$ in descending order to obtain the modulated plaintext block $P_i^{\mathrm{\prime }}$ and the estimated inner-block sequence ${\varphi }_i$. The time complexity of this step is $O\left(⌊{\displaystyle \frac{m}{2}}⌋\times ⌊{\displaystyle \frac{n}{2}}⌋log\left(⌊{\displaystyle \frac{m}{2}}⌋\times ⌊{\displaystyle \frac{n}{2}}⌋\right)\right)$, where $⌊{\displaystyle \frac{m}{2}}⌋\times ⌊{\displaystyle \frac{n}{2}}⌋$ is the number of plaintext blocks.

Step 3 (sorting ciphertext blocks): The third step involves sorting each ciphertext block $B_i$ in descending order to obtain the modulated ciphertext block $B_i^{\mathrm{\prime }}$. The time complexity of this step is also $O\left(⌊{\displaystyle \frac{m}{2}}⌋\times ⌊{\displaystyle \frac{n}{2}}⌋log\left(⌊{\displaystyle \frac{m}{2}}⌋\times ⌊{\displaystyle \frac{n}{2}}⌋\right)\right)$.

Step 4 (estimating block permutation sequence): The last step involves an exhaustive search to compare each ciphertext block with plaintext blocks. The time complexity of this step is $O\left({\left(⌊{\displaystyle \frac{m}{2}}⌋\times ⌊{\displaystyle \frac{n}{2}}⌋\right)}^2\right)$.

In the test phase, we implemented the proposed KPA using MATLAB R2022b with an Intel(R) Core(TM) i5 CPU, with a 3.00 GHz processor and 16 GB of installed memory, running under Windows 10. The experimental results in

Table 1. Running time of the proposed KPA under different known plaintext images.

Known Plaintext Image
Baboon	Peppers	Airplane	Average
380.07 s	360.01 s	346.61 s	362.23 s

show that the expected average running time of the proposed KPA is 362.61 s.

6.2.3. User Feedback

To assess the practicality of our cryptanalysis techniques, we conducted a user study with 30 participants who evaluated the decrypted ciphertexts. As shown in

Table 2. User feedback on decrypted ciphertexts.

Participant Feedback	Number of Participants
Effective in identifying plaintext images	25
Generally effective with some limitations	4
Unsatisfactory for accurate identification	1

, the results revealed that 25 participants (83%) found our method effective in identifying the original plaintext images. Four participants (13%) considered the techniques generally effective but noted some limitations, while one participant (3%) found them unsatisfactory. Overall, the feedback indicates that our techniques are effective in practical scenarios, though there is room for improvement.

6.2.4. Comparison

In this sub-section, we present a comparative analysis utilizing a state-of-the-art cryptanalysis scheme [28] based on known-plaintext attack. As illustrated in

Table 3. Comparison of PSNR.

Image	Ciphertext Image	Reconstructed Image
		[28]	Ours
Airplane	11.83	13.26	19.68
Baboon	13.51	15.05	20.35
Barbara	10.76	11.94	18.17

, the ciphertext-plaintext pair image “Peppers” is served as the key to decrypt the ciphertext images “Airplane”, “Baboon”, and “Barbara”. Our analysis reveals that the PSNR value of the ciphertext image hovers around 11 dB. In contrast, the PSNR values of our reconstructed images consistently achieve approximately 20 dB. This level of quality proves sufficient to discern the plaintext content embedded within the ciphertext images.

It is noteworthy that the methodology employed in [28] leverages the differential values of intra-block pixels to estimate the permutation sequence. While innovative, this scheme yields reconstructed images with relatively low PSNR values. Our scheme, in contrast, has been specifically engineered for dual-stage encryption scheme, resulting in superior reconstruction quality.

6.3. Cryptanalyses Performance of the Proposed LKCNN

In this section, we evaluate the effectiveness of the LKCNN model for cryptanalysis. Our evaluation includes assessing the accuracy of the model, analyzing its decryption capabilities, and demonstrating its computational efficiency.

6.3.1. Evaluation of Model Accuracy

To assess the accuracy of our LKCNN model, we constructed a test dataset using the BOW-2 dataset [35], comprising 10,000 positive and 10,000 negative samples, following preprocessing schemes consistent with our training datasets. Figure 7 illustrates some samples from our test dataset, highlighting that positive samples contain rich semantic information, while negative samples exhibit cluttered images with unclear semantic content. During the testing process, we fed 10,000 positive and negative samples each to LKCNN to evaluate its classification accuracy. The results show that the classification accuracies for positive and negative samples are 92.23% and 100%, respectively, indicating that almost all test samples are correctly classified. To delve deeper into the reasons behind misclassifications, we are examining specific instances of misclassified samples. Figure 8 displays some of the misclassified samples. Notably, all misclassifications originate from positive samples with complex details. This highlights the difficulties posed by detailed image features in accurate classification. Nevertheless, our model exhibits robust performance by accurately handling most test samples, showcasing its effectiveness.

6.3.2. Analysis of Estimation Accuracy

Figure 9 depicts the results of four reconstructed images. Visually, these reconstructions closely capture the primary features of the original images. To further evaluate their visual fidelity, we quantify them using PSNR and SSIM metrics, as detailed in

Table 4. The visual quantification results of four test images.

Image	Airplane	Baboon	Barbara	Peppers
PSNR (dB)	28.06	25.71	29.55	31.04
SSIM	0.9236	0.7438	0.8701	0.9465

. The results indicate that our reconstructed images achieve good performance across different test images. Specifically, the PSNR values range from 25.71 to 31.04 dB, with SSIM values ranging from 0.7438 to 0.9465. These metrics suggest that our reconstruction scheme preserves significant details and structural similarities compared to the original images. This highlights the effectiveness of our approach in achieving high-quality reconstructions.

6.3.3. Running Time Estimation

To evaluate the efficiency of the proposed approach, we conducted experiments to measure the time consumption for each phase when processing each encrypted image. As shown in

Table 5. Time consumption of the proposed scheme.

Determine the Block Average	Acquire Permutation Sequence	Evaluate Permutation Sequence
1.8 s	0.8 s	0.008 s

, the time required to calculate the average of blocks for an encrypted image is 1.8 s. Acquiring the permutation sequence takes 0.8 s, while the execution of permutation sequence estimation takes just 0.008 s.

6.3.4. Limitations

While the proposed scheme demonstrates commendable performance, it exhibits inherent limitations. Firstly, we resize images to $256\times 256$ pixels in our scheme. This resizing is a practical necessity due to the constraints of available hardware resources and processing time. However, when sufficient hardware resources and time are available, maintaining the original image sizes would be more optimal. Secondly, although we operate within a limited key space, attempting all possible keys is challenging due to hardware limitations. Lastly, our LKCNN sometimes misclassifies samples, which can affect reliability in critical scenarios. Misclassifications can result in inaccurate interpretations of the images, thereby undermining the overall effectiveness of our cryptanalysis scheme.

7. Conclusions

This paper conducts a comprehensive security analysis of the dual-stage permutation encryption scheme and introduces two cryptanalysis approaches, leveraging a large-kernel convolutional neural network (LKCNN) and a known-plaintext attack (KPA) scheme, respectively. Our experiments demonstrate the effectiveness of both schemes in recovering the contents of encrypted images, reconstructing their key characteristics. While our proposed schemes exhibit certain limitations, our analysis highlights a potential vulnerability within dual-stage permutation encryption. These findings emphasize the critical need to further investigate the security implications of dual-stage permutation encryption in future studies and to develop more resilient techniques to mitigate these identified vulnerabilities.