A Note on the Quasigroup of Lai–Massey Structures

Abstract

In our paper, we explore the consequences of replacing the commutative group operation used in Lai–Massey structures with a quasigroup operation. We introduce four quasigroup versions of the Lai–Massey structure and prove that for quasigroups isotopic with a group $\mathbb{G}$, the complexity of launching a differential attack against these variants of the Lai–Massey structure is equivalent to attacking an alternative structure based on $\mathbb{G}$. Then, we provide the conditions needed for correct decryption and further refine the resulting structure. The emerging structure is both intriguing and novel, and we hope that it will form the basis for future secure block ciphers based on non-commutative groups. In the case of commutative groups, we show that the resulting structure reduces to the classic Lai–Massey structure.

1. Introduction

When developing a block cipher, a key challenge is to design a set of permutations that is both easily implementable and exhibits behavior akin to random permutations. In tackling this challenge, the literature presents three primary approaches [1]. The first approach involves substitution–permutation networks (SPNs), which create a large block random-looking permutation by employing a series of substitution layers (composed of several substitution boxes (s-boxes) with a small block length) and permutation layers iterated over multiple rounds. On the other hand, Feistel and Lai–Massey structures adopt a different strategy. Instead of relying on invertible building blocks, these structures construct permutations using non-invertible components.

Differential cryptanalysis, introduced by Biham and Shamir [2], stands out as one of the most efficient tools for attacking block ciphers [3]. This method exploits how changes in certain plaintext bits propagate to the corresponding ciphertext, aiming to uncover vulnerabilities in the encryption process. In an ideal scenario with truly random permutations, the probability of predicting these changes is precisely $1/2^n$, where n denotes the number of input bits. For instance, if n is set to 128 bits, this probability would be negligible, rendering predictions practically infeasible. However, the challenge lies in the need for practical block ciphers where permutations can be easily described, a criterion not satisfied by ideal permutations.

To overcome this hurdle, designers often resort to theoretical estimates based on assumptions that might not always align with real-world conditions. Consequently, practical block ciphers deviate from the ideal, rendering them susceptible to differential cryptanalysis. Hence, guarding against this type of attack becomes a fundamental design criterion for ensuring the security of symmetric primitives [4].

Latin squares, defined as $\mathsf{\ell }\times \mathsf{\ell }$ matrices containing only ℓ symbols, possess the distinctive property that each symbol appears exactly once in every row and column [5]. When a set is equipped with a multiplication table that forms a Latin square, it establishes a quasigroup, a structure akin to a group but without the requirements of associativity and the presence of an identity element.

Despite quasigroups not being a prevalent choice in constructing cryptographic primitives, the literature showcases various designs based on these structures [6,7,8,9,10,11,12,13,14]. These cryptosystems highlight the versatility of quasigroups as group-like structures, offering an alternative perspective for certain cryptographic applications.

A recent approach, as highlighted in [15,16,17,18], employs commutative regular subgroups within the symmetric group to design SPN structures that exhibit resilience against classical differential cryptanalysis. However, these structures are vulnerable to differential attacks utilizing different group operations. Specifically, the security level of such structures against differential attacks is operation-dependent, indicating a variation in susceptibility based on the chosen operation. This approach is similar to the methodology employed in our paper, where we also explore different operations for constructing differential attacks against the proposed Lai–Massey structures. It is worth noting that the focus of [15,16,17,18] was to illustrate how a designer can embed a trapdoor into a symmetric structure, defined by knowledge of the weakening group operation. In contrast, our investigation aims to explore the potential strengthening of a Lai–Massey structure against differential cryptanalysis by changing the group operation to a quasigroup one.

In [19,20,21], the author proposes a direct extension of the three fundamental symmetric structures (SPNs, Feistel, and Lai–Massey) using quasigroup operations instead of traditional group operations between keys and (intermediary) plaintexts. The study focuses on quasigroup operations isotopic with a group operation, a popular method for constructing quasigroups. We further discuss only the results concerning Lai–Massey structures since this is the focus of our paper. In [20], the author begins by establishing the necessary conditions for correct decryption when employing a quasigroup operation. Unfortunately, the previous conditions limit the generalization of the Lai–Massey structure solely to non-commutative groups. Then, two structure categories are presented, one symmetric and one asymmetric. Subsequently, the author employs several arguments to prove the equivalence of the two categories in terms of differential cryptanalysis.

In this paper, we study the quasigroup Lai–Massey structure from a different perspective. We commence by generalizing the structures outlined in [20], subsequently delving into the security analysis of the derived structures, and ultimately, focusing on the necessary conditions needed for correct decryption. We manage to prove that the symmetric and asymmetric structures are differentially equivalent; thus, we only need to focus on one of them. In the non-commutative group case, we obtain a novel symmetric structure that generalizes the symmetric structure from [20]. To the best of the authors’ knowledge, this particular design has not been previously documented in the existing literature. Consequently, we believe that this structure warrants attention for future research, offering valuable insights from both theoretical and design perspectives.

In the case of commutative groups, the structure coincides with the classic Lai–Massey symmetric structure. Therefore, in this case, we obtain a negative result. Nevertheless, we believe its significance is two-fold.

1.

In the majority of scientific reports and papers, authors often depict their results as if they were achieved seamlessly, without acknowledging the intricacies and challenges encountered during the process. This tendency contributes to a skewed perception of scientific research [22,23,24,25] and fosters the misconception that failure, serendipity, and unexpected outcomes are not integral aspects of scientific endeavors [23,26]. Consequently, our report aims to provide readers with insight into the authentic processes involved in the design phase of a cryptographic primitive.

2.

Negative results and misguided directions are frequently under-reported in the scientific literature [23,27], leading to the risk of repeated errors. By sharing our findings, we aspire to prevent others from traversing similar unproductive paths, thereby contributing to a collective learning process. This approach aligns with the recommendation in [28], where the author advises documenting mistakes to avoid their recurrence in the future.

Structure of the Paper

We introduce notations and definitions in Section 2. A generic Lai–Massey structure in introduced in Section 3 and its security is analyzed. We conclude the paper in Section 4.

2. Preliminaries

2.1. Notations

Throughout the paper, $\left|\mathbb{G}\right|$ will denote the cardinality of set $\mathbb{G}$, and ⊕ will denote the bitwise xor operation. Also, using $x\parallel y$, we understand the concatenation of the strings x and y, and by ${\mathbb{G}}^2$, the set $\{x\parallel y\mid x,y\in \mathbb{G}\}$. When defining a permutation $\pi$, we further use the shorthand $\pi =\{a_0,a_1,\dots ,a_{\mathsf{\ell }}\}$, which translates into $\pi \left(i\right)=a_i$ for all i values. We also define the identity permutation $Id=\{0,\dots ,\mathsf{\ell }\}$. Let • and ⊲ be binary operators. We define the binary operators ${\Delta }_{•}(X,Y)=X•Y$ and ${\Delta }_{•,⊲}(X_0\parallel X_1,Y_0\parallel Y_1)=(X_0•Y_0,X_1⊲Y_1)$. Let $X\in {\mathbb{G}}^2$. Using $X_l$ and $X_r$, we understand the left and right half of X, respectively.

2.2. Quasigroups

In this section, we introduce a few basic notions about quasigroups. We base our exposition on [29].

Definition 1.

A quasigroup $(\mathbb{G},\otimes )$ is a set $\mathbb{G}$ equipped with a binary operation of multiplication $\otimes :\mathbb{G}\times \mathbb{G}\to \mathbb{G}$, in which the specification of any two of the values $x,y,z$ in the equation $x\otimes y=z$ determines the third uniquely.

Definition 2.

For a quasigroup $(\mathbb{G},\otimes )$, we define the left division $x⦸z=y$ as the unique solution y to $x\otimes y=z$. Similarly, we define the right division $z\oslash y=x$ as the unique solution x to $x\otimes y=z$.

Lemma 1.

The following identities hold:

$$\begin{array}{cccc}\hfill y⦸(y\otimes x)& =x,\hfill & \hfill (x\otimes y)\oslash y& =x,\hfill \\ \hfill y\otimes (y⦸x)& =x,\hfill & \hfill (x\oslash y)\otimes y& =x.\hfill \end{array}$$

Lemma 2.

If $(\mathbb{G},\otimes )$ is a group, $x⦸z=x^{-1}\otimes z$ and $z\oslash y=z\otimes y^{-1}$.

One common approach to constructing quasigroups [7,8,11,30] involves the following procedure. A group $(\mathbb{G},★)$, such as $({\mathbb{Z}}_{2^n},\oplus )$ or $({\mathbb{Z}}_{2^n},+)$, and three random permutations $\pi ,\rho ,\omega :\mathbb{G}\to \mathbb{G}$ are chosen. Subsequently, we define the quasigroup operation as $x\otimes y={\omega }^{-1}(\pi \left(x\right)★\rho \left(y\right))$. To understand why this leads to a quasigroup, observe that the mappings of x, y, and z to $\pi \left(x\right)$, $\rho \left(y\right)$, and $\omega \left(z\right)$ are unique. Consequently, any equation of the form $\pi \left(x\right)★\rho \left(y\right)=\omega \left(z\right)$ is uniquely resolved in the base group $\mathbb{G}$ when provided with $\pi \left(x\right)$, $\rho \left(y\right)$, or $\omega \left(z\right)$.

Definition 3.

Let $(\mathbb{G},\otimes )$, $(\mathbb{H},★)$ be two quasigroups. An ordered triple of bijections π, ρ, ω of a set $\mathbb{G}$ onto the set $\mathbb{H}$ is called an isotopy of $(\mathbb{G},\otimes )$ to $(\mathbb{H},★)$ if for any $x,y\in \mathbb{G}$ $\pi \left(x\right)★\rho \left(y\right)=\omega (x\otimes y)$. If such an isotopism exists, then $(\mathbb{G},\otimes )$, $(\mathbb{H},★)$ are called isotopic.

Example 1.

Let $(\mathbb{G},★)=({\mathbb{Z}}_4,\oplus )$, ${\omega }^{-1}=\{2,1,0,3\}$, $\pi =\{2,1,3,0\}$ and $\rho =\{2,0,3,1\}$. The corresponding quasigroup operations for $({\mathbb{Z}}_4,\otimes )$ can be found in Table 1 [19].

Table 1. Quasigroup operations.

⊗	0	1	2	3	$⦸$	0	1	2	3	$⦸$	0	1	2	3
0	2	0	1	3	0	1	2	0	3	0	3	0	1	2
1	3	1	0	2	1	2	1	3	0	1	2	1	0	3
2	1	3	2	0	2	3	0	2	1	2	0	3	2	1
3	0	2	3	1	3	0	3	1	2	3	1	2	3	0

Example 2.

Let $(\mathbb{G},★)=({\mathbb{Z}}_n,-)$. Then, $\mathbb{G}$ is isotopic with $({\mathbb{Z}}_n,+)$, where $\omega ,\pi =Id$ and $\rho \left(i\right)=n-imodn$ [30].

To gain a deeper understanding of the concept of isotopy, it is helpful to note that its three permutations correspond to the permutation of rows, columns, and symbols within a Latin square. These permutations naturally lead to the creation of another Latin square. Notably, being isotopic establishes an equivalence relation among quasigroups but not among groups, as isotopisms do not generally preserve associativity. It is important to recall that every group is an associative quasigroup.

Note that counting the number of distinct Latin squares is challenging. More precisely, the exact number, together with that of their isotopism classes, is known only for Latin squares of order smaller or equal to 11 [31,32,33].

2.3. Group Differential Cryptanalysis

Differential cryptanalysis was introduced by Biham and Shamir in [2] to analyze the Data Encryption Standard; as such, it was formulated exclusively for the group $({\mathbb{Z}}_{2^n},\oplus )$. Subsequently, the concept was generalized to commutative groups [34], non-commutative groups [19], and quasigroups [19,20,21]. Let $(\mathbb{G},★)$ be a group. We further present the notions of left and right differential probabilities for a permutation. Remark that these notions can also be defined for functions.

Definition 4.

Let ${\Delta }_{★}(X,X^{\prime })=X★X^{\prime }$, where $X,X^{\prime }\in (\mathbb{G},★)$. We define the group differential probabilities as follows:

$$\begin{array}{cc}\hfill LD{P}_{★}(\sigma ,\alpha ,\beta )& ={\displaystyle \frac{1}{\left|\mathbb{G}\right|}}\sum _{\stackrel{X,X^{\prime }\in \mathbb{G}}{{\Delta }_{★}(X^{-1},X^{\prime })=\alpha }}[{\Delta }_{★}(\sigma {\left(X\right)}^{-1},\sigma \left(X^{\prime }\right))=\beta ],\hfill \\ \hfill RD{P}_{★}(\sigma ,\alpha ,\beta )& ={\displaystyle \frac{1}{\left|\mathbb{G}\right|}}\sum _{\stackrel{X,X^{\prime }\in \mathbb{G}}{{\Delta }_{★}(X,X^{\prime -1})=\alpha }}[{\Delta }_{★}(\sigma \left(X\right),\sigma {\left(X^{\prime }\right)}^{-1})=\beta ],\hfill \end{array}$$

where $\sigma :\mathbb{G}\to \mathbb{G}$ is a permutation and $\alpha ,\beta \in \mathbb{G}$. When $(G,★)$ is commutative, we simply refer to $LDP$ and $RDP$ as $DP$.

Remark 1.

Let σ be randomly chosen. When $(\mathbb{G},★)=({\mathbb{Z}}_{2^n},★)$, the distribution of $DP$ values is studied in [35,36] and when $(\mathbb{G},★)$ is a generic abelian group in [37]. When σ is static (i.e., fixed and public for all symmetric structure’s implementations), the distribution of $DP$s for $({\mathbb{Z}}_{2^n},\oplus )$ is studied, for example, in [38,39,40].

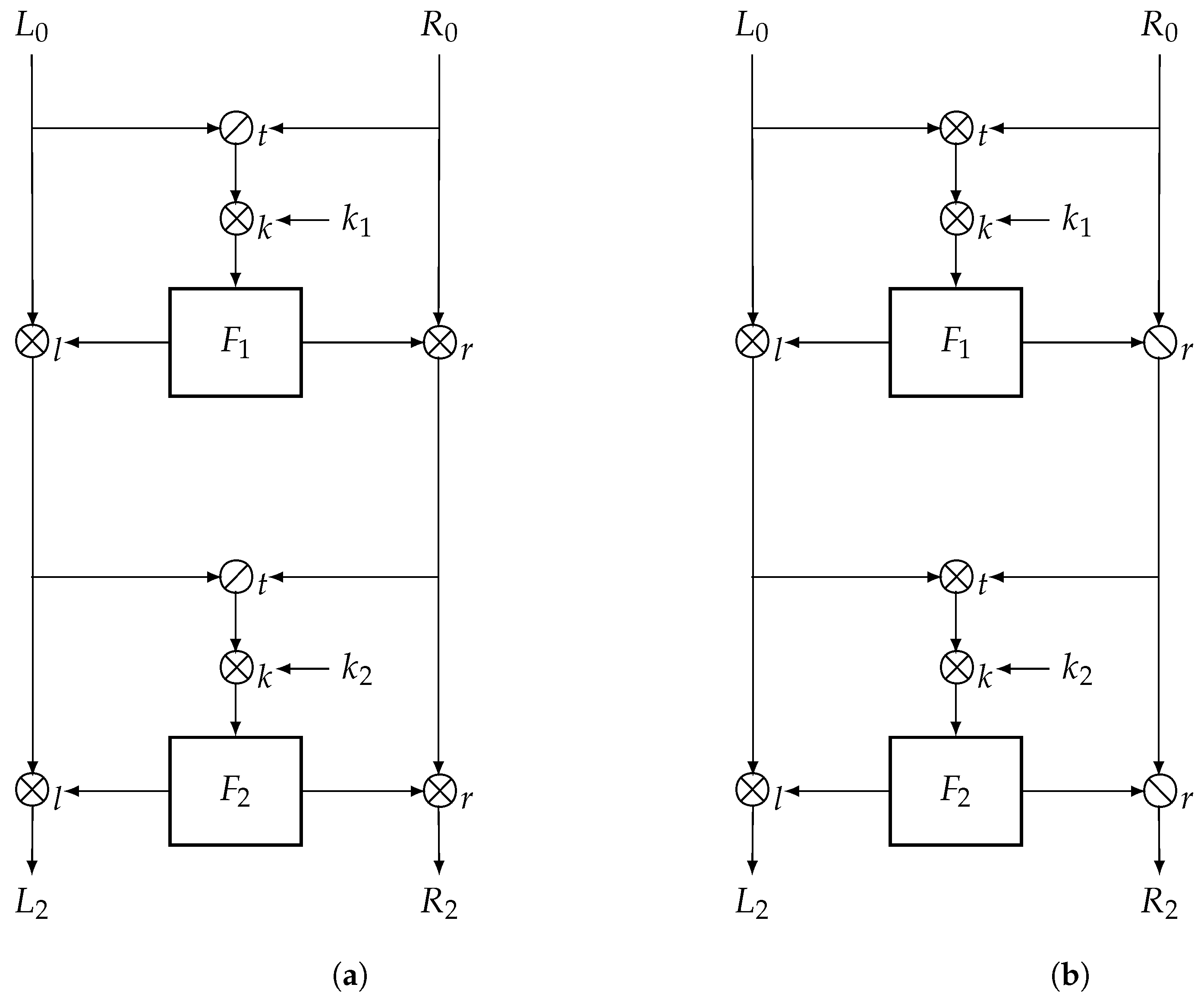
3. Lai–Massey Structure

3.1. Description

We further present two non-commutative versions of the Lai–Massey structure: a symmetric construction Figure 1a and an asymmetric one, Figure 1b. Note that, as mentioned in Section 1, we currently do not focus on their invertibility.

Figure 1. Quasigroup Lai–Massey structures. (a) Symmetric version; (b) Asymmetric version.

In both constructions, the first step is to parse the plaintext into two halves, $L_0$ and $R_0$. Note that for all versions, we make use of four quasigroup operations defined on $\mathbb{G}$ indexed by t: top, l: left, r: right, and k: key, which are not necessarily distinct. In the symmetric case, for r rounds we compute the following:

$$\begin{array}{c}\hfill L_i=L_{i-1}{\otimes }_l{F}_i(k_i,L_{i-1}{\oslash }_t{R}_{i-1})\mathrm{and}{R}_i=R_{i-1}{\otimes }_r{F}_i(k_i,L_{i-1}{\oslash }_t{R}_{i-1}),\end{array}$$

where $F_i(k_i,x)$ is defined as $F_i\left(k_i{\otimes }_{k}x\right)$ or $F_i\left(x{\otimes }_k{k}_i\right)$. We further call these versions the left symmetric Lai–Massey structures. We can also define the right symmetric Lai–Massey structures as follows:

$$\begin{array}{c}\hfill L_i=F_i(k_i,L_{i-1}{⦸}_t{R}_{i-1}){\otimes }_l{L}_{i-1}\mathrm{and}{R}_i=F_i(k_i,L_{i-1}{⦸}_t{R}_{i-1}){\otimes }_r{R}_{i-1}.\end{array}$$

In the asymmetric case, we define the outer versions as

$$\begin{array}{c}\hfill L_i=L_{i-1}{\otimes }_l{F}_i(k_i,L_{i-1}{\otimes }_t{R}_{i-1})\mathrm{and}{R}_i=F_i(k_i,L_{i-1}{\otimes }_t{R}_{i-1}){⦸}_r{R}_{i-1},\end{array}$$

and the inner versions as

$$\begin{array}{c}\hfill L_i=F_i(k_i,L_{i-1}{\otimes }_t{R}_{i-1}){\otimes }_l{L}_{i-1}\mathrm{and}{R}_i=R_{i-1}{\oslash }_r{F}_i(k_i,L_{i-1}{\otimes }_t{R}_{i-1}).\end{array}$$

Remark 2.

When $\otimes =★$, and we define ${\otimes }_t=⦸$, ${\otimes }_k={\otimes }_r=\otimes$, and ${\otimes }_l=\rho (x\otimes y)$; the result is the symmetric non-commutative group Lai–Massey structure detailed in [21]. For the asymmetric version, as outlined in [21], we need to set ${\otimes }_r=⦸$, ${\otimes }_k={\otimes }_t=\otimes$ in our asymmetric structure.

3.2. Symmetric Structure Analysis

In this subsection, we extend the differential probabilities introduced in [21] for non-commutative group symmetric Lai–Massey structures to our quasigroup version.

Definition 5.

Let K be a key, $X^i,Y^i\in {\mathbb{G}}^2$, for $i\in \{0,1\}$ and $j\in \{l,r\}$. We define the symmetric Lai–Massey quasigroup differential probabilities as follows:

1. 

Let $Z^i=X_l^i{\oslash }_t{X}_r^i$ and $Y_j^i=X_j^i{\otimes }_{j}F\left(K{\otimes }_k{Z}^i\right)$. Then,

$$\begin{array}{c}\hfill LL{M}_{⦸,{⦸}_k}(F,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\stackrel{X^0,X^1\in {\mathbb{G}}^2}{\stackrel{{\Delta }_{{⦸}_l,{⦸}_r}(X^0,X^1)=\alpha }{{\Delta }_{{⦸}_k}(Z^0,Z^1)=\gamma }}}[{\Delta }_{{⦸}_l,{⦸}_r}(Y^0,Y^1)=\beta ];\end{array}$$

2. 

Let $Z^i=X_l^i{\oslash }_t{X}_r^i$ and $Y_j^i=X_j^i{\otimes }_{j}F\left(Z^i{\otimes }_{k}K\right)$. Then,

$$\begin{array}{c}\hfill LL{M}_{⦸,{\oslash }_k}(F,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\stackrel{X^0,X^1\in {\mathbb{G}}^2}{\stackrel{{\Delta }_{{⦸}_l,{⦸}_r}(X^0,X^1)=\alpha }{{\Delta }_{{\oslash }_k}(Z^0,Z^1)=\gamma }}}[{\Delta }_{{⦸}_l,{⦸}_r}(Y^0,Y^1)=\beta ];\end{array}$$

3. 

Let $Z^i=X_r^i{⦸}_t{X}_l^i$ and $Y_j^i=F\left(K{\otimes }_k{Z}^i\right){\otimes }_j{X}_j^i$. Then,

$$\begin{array}{c}\hfill RL{M}_{\oslash ,{⦸}_k}(F,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\stackrel{X^0,X^1\in {\mathbb{G}}^2}{\stackrel{{\Delta }_{{\oslash }_l,{\oslash }_r}(X^0,X^1)=\alpha }{{\Delta }_{{⦸}_k}(Z^0,Z^1)=\gamma }}}[{\Delta }_{{\oslash }_l,{\oslash }_r}(Y^0,Y^1)=\beta ];\end{array}$$

4. 

Let $Z^i=X_r^i{⦸}_t{X}_l^i$ and $Y_j^i=F\left(Z^i{\otimes }_{k}K\right){\otimes }_j{X}_j^i$. Then,

$$\begin{array}{c}\hfill RL{M}_{\oslash ,{\oslash }_k}(F,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\stackrel{X^0,X^1\in {\mathbb{G}}^2}{\stackrel{{\Delta }_{{\oslash }_l,{\oslash }_r}(X^0,X^1)=\alpha }{{\Delta }_{{\oslash }_k}(Z^0,Z^1)=\gamma }}}[{\Delta }_{{\oslash }_l,{\oslash }_r}(Y^0,Y^1)=\beta ];\end{array}$$

where $F:\mathbb{G}\to \mathbb{G}$ is a function, $\alpha ,\beta \in {\mathbb{G}}^2$, and $\gamma \in \mathbb{G}$.

Remark 3.

Let $F_l,F_r:\mathbb{G}\to \mathbb{G}$ be two functions. When $Y_j^i=X_j^i{\otimes }_j{F}_j\left(K{\otimes }_k{Z}^i\right)$, we denote the differential probability with $LL{M}_{⦸,{⦸}_k}(F_l,F_r,\alpha ,\beta ,\gamma ,K)$. We also use the same convention for the rest of the Lai–Massey differential probabilities.

Let $x{\otimes }_{i}y={\omega }_i^{-1}({\pi }_i\left(x\right)★{\rho }_i\left(y\right))$, where $i\in \{k,l,r,t\}$. We further study the impact of the ${\omega }_i$s, ${\pi }_i$s, and ${\rho }_i$s on the symmetric Lai–Massey structures.

Lemma 3.

Let $i\in \{l,r\}$, ${\pi }_i^{\prime }={\pi }_i\circ {\omega }_i^{-1}$, ${\rho }_i^{\prime }={\rho }_i\circ {\omega }_i^{-1}$, and $F_i={\omega }_i\circ F\circ {\pi }_t^{-1}$. Also, let ${\rho }_t^{\prime }={\rho }_t\circ {\omega }_r^{-1}$, ${\omega }_t^{\prime }={\omega }_t\circ {\omega }_l^{-1}$, ${\pi }_k^{\prime }={\pi }_k\circ {\pi }_t^{-1}$, ${\rho }_k^{\prime }={\rho }_k\circ {\pi }_t^{-1}$, and ${\omega }_k^{\prime }={\omega }_k\circ {\pi }_t^{-1}$. We define ${x\ast }_{i}y={\pi }_i^{\prime }\left(x\right)★{\rho }_i^{\prime }\left(y\right)$, $x{\ast }_{t}y={{\omega }_t^{\prime }}^{-1}(x★{\rho }_t^{\prime }\left(y\right))$, $x{\ast }_{k}y={{\omega }_k^{\prime }}^{-1}({\pi }_k^{\prime }\left(x\right)★{\rho }_k^{\prime }\left(y\right))$, and ${\setminus }_j$, ${/}_j$ as the associated left and right divisions, where $j\in \{l,r,t,k\}$. Then, the following identities hold:

$$\begin{array}{cc}\hfill LL{M}_{⦸,{⦸}_k}(F,\alpha ,\beta ,\gamma ,K)& =LL{M}_{{\setminus ,\setminus }_k}(F_l,F_r,A,B,{\pi }_t\left(\gamma \right),{\pi }_t\left(K\right)),\hfill \\ \hfill LL{M}_{⦸,{\oslash }_k}(F,\alpha ,\beta ,\gamma ,K)& =LL{M}_{\setminus ,{/}_k}(F_l,F_r,A,B,{\pi }_t\left(\gamma \right),{\pi }_t\left(K\right)),\hfill \end{array}$$

where $A={\omega }_l\left({\alpha }_l\right)\parallel {\omega }_r\left({\alpha }_r\right)$ and $B={\omega }_l\left({\beta }_l\right)\parallel {\omega }_r\left({\beta }_r\right)$.

Proof. 

Let $i\in \{0,1\}$ and $j\in \{l,r\}$. First, we rewrite $LL{M}_{⦸,{⦸}_k}$ as follows:

$$\begin{array}{c}\hfill LL{M}_{⦸,{⦸}_k}(F,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\stackrel{X^0,X^1\in {\mathbb{G}}^2}{\stackrel{{\Delta }_{{\otimes }_l,{\otimes }_r}(X^0,\alpha )=X^1}{{\Delta }_{{\otimes }_k}(Z^0,\gamma )=Z^1}}}[{\Delta }_{{\otimes }_l,{\otimes }_r}(Y^0,\beta )=Y^1].\end{array}$$

Let ${\omega }_j\left(X_j^i\right)=S_j^i$. Then,

$$\begin{array}{cc}\hfill X_j^0{\otimes }_j{\alpha }_j=X_j^1& ⟺{\pi }_j\left(X_j^0\right)★{\rho }_j\left({\alpha }_j\right)={\omega }_j\left(X_j^1\right)\hfill \\ \hfill & ⟺{\pi }_j^{\prime }\left({\omega }_j\left(X_j^0\right)\right)★{\rho }_j^{\prime }\left({\omega }_j\left({\alpha }_j\right)\right)={\omega }_j\left(X_j^1\right)\hfill \\ \hfill & ⟺{\pi }_j^{\prime }\left(S_j^0\right)★{\rho }_j^{\prime }\left(A_j\right)=S_j^1\hfill \\ \hfill & ⟺S_j^0{\ast }_j{A}_j=S_j^1\hfill \end{array}$$

(1)

and

$$\begin{array}{cc}\hfill Z^j=X_l^j{\oslash }_t{X}_r^j& ⟺Z^j{\otimes }_t{X}_r^j=X_l^j\hfill \\ \hfill & ⟺{\pi }_t\left(Z^j\right)★{\rho }_t\left(X_r^j\right)={\omega }_t\left(X_l^j\right)\hfill \\ \hfill & ⟺{\pi }_t\left(Z^j\right)={\omega }_t\left(X_l^j\right)★{\rho }_t{\left(X_r^j\right)}^{-1}\hfill \\ \hfill & ⟺{\pi }_t\left(Z^j\right)={\omega }_t^{\prime }\left({\omega }_l\left(X_l^j\right)\right)★{\rho }_t^{\prime }{\left({\omega }_r\left(X_r^j\right)\right)}^{-1}\hfill \\ \hfill & ⟺Z^j={\pi }_t^{-1}({\omega }_t^{\prime }\left(S_l^j\right)★{\rho }_t^{\prime }{\left(S_r^j\right)}^{-1})\hfill \\ \hfill & ⟺Z^j={\pi }_t^{-1}\left(S_l^{j}t{S}_r^j\right).\hfill \end{array}$$

(2)

Let $T^j=S_l^j{/}_t{S}_r^j$, ${\pi }_t\left(\gamma \right)=\Gamma$ and ${\pi }_t\left(K\right)=K^{\prime }$. Then, using Equation (2), we obtain

$$\begin{array}{cc}\hfill Z_{⦸k}^0{Z}^1=\gamma & ⟺{\pi }_k\left({\pi }_t^{-1}\left(T^0\right)\right)★{\rho }_k\left(\gamma \right)={\omega }_k\left({\pi }_t^{-1}\left(T^1\right)\right)\hfill \\ \hfill & ⟺{\pi }_k^{\prime }\left(T^0\right)★{\rho }_k^{\prime }\left({\pi }_t\left(\gamma \right)\right)={\omega }_k^{\prime }\left(T^1\right)\hfill \\ \hfill & ⟺T^0{\ast }_k\Gamma =T^1\hfill \\ \hfill & ⟺T^0{\setminus }_k{T}^1=\Gamma \hfill \end{array}$$

(3)

and

$$\begin{array}{cc}\hfill F\left(K{\otimes }_k{Z}^j\right)& =F\left({\omega }_k^{-1}({\pi }_k\left(K\right)★{\rho }_k\left(Z^j\right))\right)\hfill \\ \hfill & =F({\pi }_t^{-1}\left({{\omega }_k^{\prime }}^{-1}({\pi }_k^{\prime }\left({\pi }_t\left(K\right)\right)★{\rho }_k^{\prime }\left({\pi }_t\left(Z^j\right)\right))\right)\hfill \\ \hfill & =F\left({\pi }_t^{-1}\left(K^{\prime }{\ast }_k{T}^j\right)\right).\hfill \end{array}$$

(4)

Let $W_j^i=S_j^i{\ast }_j{F}_j\left(K^{\prime }{\ast }_k{T}^i\right)$. From Equation (4), we derive

$$\begin{array}{cc}\hfill Y_j^i=X_j^i{\otimes }_{j}F\left(K{\otimes }_k{Z}^i\right)& ⟺{\omega }_j\left(Y_j^i\right)={\pi }_j\left(X_j^i\right)★{\rho }_j\left(F\left(K{\otimes }_k{Z}^i\right)\right)\hfill \\ \hfill & ⟺{\omega }_j\left(Y_j^i\right)={\pi }_j^{\prime }\left({\omega }_j\left(X_j^i\right)\right)★{\rho }_j^{\prime }\left({\omega }_j\left(F\left({\pi }_t^{-1}\left(K^{\prime }{\ast }_k{T}^i\right)\right)\right)\right)\hfill \\ \hfill & ⟺{\omega }_j\left(Y_j^i\right)={\pi }_j^{\prime }\left(S_j^i\right)★{\rho }_j^{\prime }\left(F_j\left(K^{\prime }{\ast }_k{T}^i\right)\right)\hfill \\ \hfill & ⟺{\omega }_j\left(Y_j^i\right)=S_j^i{\ast }_j{F}_j\left(K^{\prime }{\ast }_k{T}^i\right)\hfill \\ \hfill & ⟺{\omega }_j\left(Y_j^i\right)=W_j^i,\hfill \end{array}$$

which leads to

$$\begin{array}{cc}\hfill Y_j^0{\otimes }_j{\beta }_j=Y_j^1& ⟺{\pi }_j\left(Y_j^0\right)★{\rho }_j\left({\beta }_j\right)={\omega }_j\left(Y_j^1\right)\hfill \\ \hfill & ⟺{\pi }_j^{\prime }\left(W_j^0\right)★{\rho }_j^{\prime }\left({\omega }_j\left({\beta }_j\right)\right)=W_j^1\hfill \\ \hfill & ⟺W_j^0{\ast }_j{B}_j=W_j^1.\hfill \end{array}$$

(5)

Using Equations (1), (3) and (5), we obtain

$$\begin{array}{cc}\hfill LL{M}_{⦸,{⦸}_r}(F,\alpha ,\beta ,\gamma ,K)& ={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\stackrel{S^0,S^1\in {\mathbb{G}}^2}{\stackrel{{\Delta }_{{\ast }_l,{\ast }_r}(S^0,A)=S^1}{{\Delta }_{{\ast }_k}(T^0,\Gamma )=T^1}}}[{\Delta }_{{\ast }_l,{\ast }_r}(W^0,B)=W^1]\hfill \\ \hfill & =LL{M}_{{\setminus ,\setminus }_k}(F_l,F_r,A,B,\Gamma ,K^{\prime }).\hfill \end{array}$$

The remaining equality is proven using similar techniques. □

The proof of Lemma 4 follows a similar rationale to the proof of Lemma 3; thus, it is omitted.

Lemma 4.

Let $i\in \{l,r\}$, ${\pi }_i^{\prime }={\pi }_i\circ {\omega }_i^{-1}$, ${\rho }_i^{\prime }={\rho }_i\circ {\omega }_i^{-1}$, $F_i={\omega }_i\circ F\circ {\pi }_t^{-1}$. Also, let ${\pi }_t^{\prime }={\pi }_t\circ {\omega }_r^{-1}$, ${\omega }_t^{\prime }={\omega }_t\circ {\omega }_l^{-1}$, ${\pi }_k^{\prime }={\pi }_k\circ {\rho }_t^{-1}$, ${\rho }_k^{\prime }={\rho }_k\circ {\rho }_t^{-1}$, and ${\omega }_k^{\prime }={\omega }_k\circ {\rho }_t^{-1}$. We define $x{\ast }_{i}y={\pi }_i^{\prime }\left(x\right)★{\rho }_i^{\prime }\left(y\right)$, $x{\ast }_{t}y={{\omega }_t^{\prime }}^{-1}({\pi }_t^{\prime }\left(x\right)★y)$, $x{\ast }_{k}y={{\omega }_k^{\prime }}^{-1}({\pi }_k^{\prime }\left(x\right)★{\rho }_k^{\prime }\left(y\right))$, and ${\setminus }_j$, ${/}_j$ as the associated left and right divisions, where $j\in \{l,r,t,k\}$. Then, the following identities hold:

$$\begin{array}{cc}\hfill RL{M}_{\oslash ,{⦸}_k}(F,\alpha ,\beta ,\gamma ,K)& =RL{M}_{/,\setminus k}(F_l,F_r,A,B,{\rho }_t\left(\gamma \right),{\rho }_t\left(K\right)),\hfill \\ \hfill RL{M}_{\oslash ,{\oslash }_k}(F,\alpha ,\beta ,\gamma ,K)& =RL{M}_{/,/k}(F_l,F_r,A,B,{\rho }_t\left(\gamma \right),{\rho }_t\left(K\right)),\hfill \end{array}$$

where $A={\omega }_l\left({\alpha }_l\right)\parallel {\omega }_r\left({\alpha }_r\right)$ and $B={\omega }_l\left({\beta }_l\right)\parallel {\omega }_r\left({\beta }_r\right)$.

Lemmas 3 and 4 tell us that it is irrelevant from a differential point of view (e.g., we obtain the same differential probabilities $LLM$ and $RLM$) if we define the quasigroup operation with ${\omega }_i\ne Id$ or ${\omega }_i=Id$, where $i\in \{l,r\}$. The same is true for ${\pi }_t$ (left case) or ${\rho }_t$ (right case). Thus, we further restrict our study (without loss of generality) to the quasigroup operations $x{\otimes }_{i}y={\pi }_i\left(x\right)★{\rho }_i\left(y\right)$ and $x{\otimes }_{tl}y={\omega }_t^{-1}(x★{\rho }_t\left(y\right))$ (left case) or $x{\otimes }_{tr}y={\omega }_t^{-1}({\pi }_t\left(x\right)★y)$ (right side). Now, considering the non-linear layer F, we observe, according to Lemmas 3 and 4, that it would be simpler to study $F_l$ and $F_r$ instead of F.

Lemma 5.

Let ${\pi }_l^{\prime }={\pi }_l\circ {\omega }_t^{-1}$, ${\pi }_r^{\prime }={\pi }_r\circ {\rho }_t^{-1}$, $F_i^{\prime }={\rho }_i\circ F_i$, where $i\in \{l,r\}$. We define $x{\ast }_{l}y={\omega }_t({\pi }_l^{\prime }\left(x\right)★y)$, $x{\ast }_{r}y={\rho }_t({\pi }_r^{\prime }\left(x\right)★y)$, and ${/}_i$, ${\setminus }_i$ as the associated left and right divisions, where $i\in \{l,r\}$. Then, the following identities hold:

$$\begin{array}{cc}\hfill LL{M}_{⦸,{⦸}_k}(F_l,F_r,\alpha ,\beta ,\gamma ,K)& =LL{M}_{\setminus ,{⦸}_k}(F_l^{\prime },F_r^{\prime },A,B,\gamma ,K),\hfill \\ \hfill LL{M}_{⦸,{\oslash }_k}(F_l,F_r,\alpha ,\beta ,\gamma ,K)& =LL{M}_{\setminus ,{\oslash }_k}((F_l^{\prime },F_r^{\prime },A,B,\gamma ,K),\hfill \end{array}$$

where $A={\rho }_l\left({\alpha }_l\right)\parallel {\rho }_r\left({\alpha }_r\right)$ and $B={\rho }_l\left({\beta }_l\right)\parallel {\rho }_r\left({\beta }_r\right)$.

Proof. 

As before, let $i\in \{0,1\}$ and $j\in \{l,r\}$. Also, let ${\omega }_t\left(X_l^i\right)=S_l^i$ and ${\rho }_t\left(X_r^i\right)=S_r^i$. Then,

$$\begin{array}{cc}\hfill X_l^0{\otimes }_l{\alpha }_l=X_l^1& ⟺{\pi }_l\left(X_l^0\right)★{\rho }_l\left({\alpha }_l\right)=X_l^1\hfill \\ \hfill & ⟺{\omega }_t({\pi }_l^{\prime }\left({\omega }_t\left(X_l^0\right)\right)★A_l)={\omega }_t\left(X_l^1\right)\hfill \\ \hfill & ⟺{\omega }_t({\pi }_l^{\prime }\left(S_l^0\right)★A_l)=S_l^1\hfill \\ \hfill & ⟺S_l^0{\ast }_l{A}_l=S_l^1,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill X_r^0{\otimes }_r{\alpha }_r=X_r^1& ⟺{\rho }_t({\pi }_r^{\prime }\left(S_r^0\right)★A_r)=S_r^1\hfill \\ \hfill & ⟺S_r^0{\ast }_r{A}_r=S_r^1,\hfill \end{array}$$

(7)

and

$$\begin{array}{cc}\hfill Z^j=X_l^j{\oslash }_{tl}{X}_r^j& ⟺Z^j={\omega }_t\left(X_l^j\right)★{\rho }_t{\left(X_r^j\right)}^{-1}\hfill \\ \hfill & ⟺Z^j=S_l^j★{\left(S_r^j\right)}^{-1}.\hfill \end{array}$$

(8)

Let $W_l^i=S_l^i{\ast }_l{F}_l^{\prime }\left(K{\otimes }_k{Z}^i\right)$ and $W_r^i=S_r^i{\ast }_r{F}_r^{\prime }\left(K{\otimes }_k{Z}^i\right)$. Then, we derive

$$\begin{array}{cc}\hfill Y_l^i& =X_l^i{\otimes }_l{F}_l\left(K{\otimes }_k{Z}^i\right)={\pi }_l\left(X_l^i\right)★{\rho }_l\left(F_l\left(K{\otimes }_k{Z}^i\right)\right)\hfill \\ \hfill & ={\pi }_l^{\prime }\left({\omega }_t\left(X_l^i\right)\right)★F_l^{\prime }\left(K{\otimes }_k{Z}^i\right)={\omega }_t^{-1}\left(S_l^i{\ast }_l{F}_l^{\prime }\left(K{\otimes }_k{Z}^i\right)\right),\hfill \\ \hfill \\ \hfill Y_r^i& ={\pi }_r^{\prime }\left(S_r^i\right)★F_r^{\prime }\left(K{\otimes }_k{Z}^i\right)={\rho }_t^{-1}\left(S_r^i{\ast }_r{F}_r^{\prime }\left(K{\otimes }_k{Z}^i\right)\right),\hfill \end{array}$$

which leads to

$$\begin{array}{cc}\hfill Y_l^0{\otimes }_l{\beta }_l=Y_l^1& ⟺{\pi }_l\left(Y_l^0\right)★{\rho }_l\left({\beta }_l\right)=Y_l^1\hfill \\ \hfill & ⟺{\pi }_l^{\prime }\left(W_l^0\right)★B_l={\omega }_t^{-1}\left(W_l^1\right)\hfill \\ \hfill & ⟺W_l^0{\ast }_l{B}_l=W_l^1,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill Y_r^0{\otimes }_r{\beta }_r=Y_r^1& ⟺{\pi }_r^{\prime }\left(W_r^0\right)★B_r={\omega }_t^{-1}\left(W_r^1\right)\hfill \\ \hfill & ⟺W_r^0{\ast }_r{B}_r=W_r^1.\hfill \end{array}$$

(10)

Using Equations (6)–(10), we obtain

$$\begin{array}{cc}\hfill LL{M}_{⦸,{⦸}_k}(F_l,F_r,\alpha ,\beta ,\gamma ,K)& ={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\stackrel{S^0,S^1\in {\mathbb{G}}^2}{\stackrel{{\Delta }_{{\ast }_l,{\ast }_r}(S^0,A)=S^1}{{\Delta }_{{\otimes }_k}(Z^0,\gamma )=Z^1}}}[{\Delta }_{{\ast }_l,{\ast }_r}(W^0,B)=W^1]\hfill \\ \hfill & =LL{M}_{\setminus ,{⦸}_k}(F_l^{\prime },F_r^{\prime },A,B,\gamma ,K).\hfill \end{array}$$

The second equality is proven using similar techniques. □

The proof of Lemma 6 follows a similar rationale to the proof of Lemma 5; thus, it is omitted.

Lemma 6.

Let ${\rho }_l^{\prime }={\rho }_l\circ {\pi }_t^{-1}$, ${\rho }_r^{\prime }={\rho }_r\circ {\omega }_t^{-1}$, and $F_i^{\prime }={\pi }_i\circ F_i$, where $i\in \{l,r\}$. We define $x{\ast }_{l}y={\pi }_t(x★{\rho }_l^{\prime }\left(y\right))$, $x{\ast }_{r}y={\omega }_t(x★{\rho }_r^{\prime }\left(y\right))$, and ${\setminus }_i$, ${/}_i$ as the associated left and right divisions, where $i\in \{l,r\}$. Then, the following identities hold:

$$\begin{array}{cc}\hfill RL{M}_{\oslash ,{⦸}_k}(F_l,F_r,\alpha ,\beta ,\gamma ,K)& =RL{M}_{/,{⦸}_k}(F_l^{\prime },F_r^{\prime },A,B,\gamma ,K),\hfill \\ \hfill RL{M}_{\oslash ,{\oslash }_k}(F_l,F_r,\alpha ,\beta ,\gamma ,K)& =RL{M}_{/,{\oslash }_k}((F_l^{\prime },F_r^{\prime },A,B,\gamma ,K),\hfill \end{array}$$

where $A={\pi }_l\left({\alpha }_l\right)\parallel {\pi }_r\left({\alpha }_r\right)$ and $B={\pi }_l\left({\beta }_l\right)\parallel {\pi }_r\left({\beta }_r\right)$.

Lemmas 5 and 6 indicate that the choice of ${\rho }_i$ (in the left case) and ${\pi }_i$ (in the right case) is irrelevant from a differential perspective. As illustrated in Equation (8), we can restrict our study to ${\otimes }_t=★$. Therefore, we further consider ${\rho }_i=Id$ (in the left case) and ${\pi }_i=Id$ (in the right case) and that $\otimes ={\otimes }_t=★$. Moreover, these lemmas indicate that we can consider $F_l^{\prime }$ and $F_r^{\prime }$ instead of $F_l$ and $F_r$. A closer examination of the non-linear layers reveals that they can be expressed as $F_i^{″}=F_i^{\prime }\circ {\omega }_k^{-1}$. Consequently, it is more convenient to investigate $F_i^{″}$ rather than $F_i^{\prime }$.

Since K and, for example, ${\pi }_k$ are generated as a pair, it suffices from a differential point of view to simply consider $K^{\prime }={\pi }_k\left(K\right)$ as being the key that we want to recover. This is possible since our final scope is to recover the plaintexts and not the initial key used by the symmetric structure. As a consequence, it suffices to restrict our study to $x{\otimes }_{kl}y={\pi }_k\left(x\right)★y$ (left version) and $x{\otimes }_{kr}y=x★{\rho }_k\left(y\right)$ (right version).

Taking into account the previous arguments, we obtain the Lai–Massey structure depicted in Figure 2.

Figure 2. Symmetric non-commutative group Lai–Massey structure (version 1).

A different point of view of studying the version 1 structure is to redefine the differential probabilities as follows:

1.

Let $Z^i=X_l^i\oslash X_r^i$ and $Y_j^i={\rho }_j({\pi }_j\left(X_j^i\right)\otimes F_j(K\otimes {\pi }_k\left(Z^i\right)))$. Then,

$$\begin{array}{c}\hfill LL{M}_{⦸,⦸}(F_l,F_r,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\stackrel{X^0,X^1\in {\mathbb{G}}^2}{\stackrel{{\Delta }_{⦸,⦸}(X^0,X^1)=\alpha }{{\Delta }_{⦸}(Z^0,Z^1)=\gamma }}}[{\Delta }_{⦸,⦸}(Y^0,Y^1)=\beta ];\end{array}$$

2.

Let $Z^i=X_l^i\oslash X_r^i$ and $Y_j^i={\rho }_j({\pi }_j\left(X_j^i\right)\otimes F_j({\pi }_k\left(Z^i\right)\otimes K))$. Then,

$$\begin{array}{c}\hfill LL{M}_{⦸,\oslash }(F_l,F_r,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\stackrel{X^0,X^1\in {\mathbb{G}}^2}{\stackrel{{\Delta }_{⦸,⦸}(X^0,X^1)=\alpha }{{\Delta }_{\oslash }(Z^0,Z^1)=\gamma }}}[{\Delta }_{⦸,⦸}(Y^0,Y^1)=\beta ];\end{array}$$

3.

Let $Z^i=X_r^i⦸X_l^i$ and $Y_j^i={\rho }_j(F_j(K\otimes {\pi }_k\left(Z^i\right))\otimes {\pi }_j\left(X_j^i\right))$. Then,

$$\begin{array}{c}\hfill RL{M}_{\oslash ,⦸}(F_l,F_r,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\stackrel{X^0,X^1\in {\mathbb{G}}^2}{\stackrel{{\Delta }_{\oslash ,\oslash }(X^0,X^1)=\alpha }{{\Delta }_{⦸}(Z^0,Z^1)=\gamma }}}[{\Delta }_{\oslash ,\oslash }(Y^0,Y^1)=\beta ];\end{array}$$

4.

Let $Z^i=X_r^i⦸X_l^i$ and $Y_j^i={\rho }_j(F_j({\pi }_k\left(Z^i\right)\otimes K)\otimes {\pi }_j\left(X_j^i\right))$. Then,

$$\begin{array}{c}\hfill RL{M}_{\oslash ,\oslash }(F_l,F_r,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\stackrel{X^0,X^1\in {\mathbb{G}}^2}{\stackrel{{\Delta }_{\oslash ,\oslash }(X^0,X^1)=\alpha }{{\Delta }_{\oslash }(Z^0,Z^1)=\gamma }}}[{\Delta }_{\oslash ,\oslash }(Y^0,Y^1)=\beta ].\end{array}$$

We further provide the reader with some conditions that guarantee key independence for the differential probabilities associated with the Lai–Massey round functions.

Lemma 7.

If ${\pi }_k$, ${\pi }_l$ and ${\rho }_l$ are morphisms; then, $LL{M}_{⦸,⦸}(F_l,F_r,\alpha ,\beta ,\gamma ,K)$ and $RL{M}_{\oslash ,\oslash }(F_l,F_r,\alpha ,\beta ,\gamma ,K)$ are key independents.

Proof. 

We begin by rewriting $X_l^i={\pi }_k^{-1}\left(K^{-1}\right)\otimes S_l^i$ and $X_r^i=S_r^i$. Then,

$$\begin{array}{c}\hfill {\alpha }_l={\left(X_l^0\right)}^{-1}\otimes X_l^1={\left(S_l^0\right)}^{-1}\otimes {\pi }_k^{-1}(K\otimes K^{-1})\otimes S_l^1={\left(S_l^0\right)}^{-1}\otimes S_l^1\end{array}$$

(11)

and

$$\begin{array}{c}\hfill Z^i=X_l^i\otimes {\left(X_r^i\right)}^{-1}={\pi }_k^{-1}\left(K^{-1}\right)\otimes S_l^i\otimes {\left(S_r^i\right)}^{-1}.\end{array}$$

(12)

Let $T^i=S_l^i\oslash S_r^i$ and $F_j^{\prime }={\pi }_l^{-1}\circ F_j\circ {\pi }_k$. Using Equations (11) and (12), we obtain

$$\begin{array}{cc}\hfill \gamma ={\left(Z^0\right)}^{-1}\otimes Z^1& ={({\pi }_k^{-1}\left(K^{-1}\right)\otimes S_l^0\otimes {\left(S_r^0\right)}^{-1})}^{-1}\otimes ({\pi }_k^{-1}\left(K^{-1}\right)\otimes S_l^1\otimes {\left(S_r^1\right)}^{-1})\hfill \\ \hfill & =S_r^0\otimes {\left(S_l^0\right)}^{-1}\otimes {\pi }_k^{-1}(K\otimes K^{-1})\otimes S_l^1\otimes {\left(S_r^1\right)}^{-1}\hfill \\ \hfill & =S_r^0\otimes {\left(S_l^0\right)}^{-1}\otimes S_l^1\otimes {\left(S_r^1\right)}^{-1}\hfill \\ \hfill & ={\left(T^0\right)}^{-1}\otimes T^1\hfill \end{array}$$

(13)

and

$$\begin{array}{cc}\hfill F_j(K\otimes {\pi }_k\left(Z^i\right))& =F_j(K\otimes K^{-1}\otimes {\pi }_k(S_l^i\otimes {\left(S_r^i\right)}^{-1}))\hfill \\ \hfill & ={\pi }_l\left(F_j^{\prime }(S_l^i\otimes {\left(S_r^i\right)}^{-1})\right)={\pi }_l\left(F_j^{\prime }\left(T^i\right)\right).\hfill \end{array}$$

(14)

Let ${\pi }_r^{\prime }={\pi }_l^{-1}\circ {\pi }_r$, ${\rho }_l^{\prime }={\rho }_l\circ {\pi }_l$ and ${\rho }_r^{\prime }={\rho }_r\circ {\pi }_l$. From Equation (14), we derive

$$\begin{array}{cc}\hfill Y_r^i& ={\rho }_r({\pi }_r\left(X_r^i\right)\otimes F_r(K\otimes {\pi }_k\left(Z^i\right)))\hfill \\ \hfill & ={\rho }_r({\pi }_r\left(X_r^i\right)\otimes {\pi }_l\left(F_r^{\prime }\left(T^i\right)\right))\hfill \\ \hfill & ={\rho }_r\left({\pi }_l({\pi }_r^{\prime }\left(X_r^i\right)\otimes F_r^{\prime }\left(T^i\right))\right)\hfill \\ \hfill & ={\rho }_r^{\prime }({\pi }_r^{\prime }\left(S_r^i\right)\otimes F_r^{\prime }\left(T^i\right))\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill Y_l^i& ={\rho }_l({\pi }_l\left(X_l^i\right)\otimes F_l(K\otimes {\pi }_k\left(Z^i\right)))\hfill \\ \hfill & ={\rho }_l({\pi }_l\left(X_l^i\right)\otimes {\pi }_l\left(F_l^{\prime }\left(T^i\right)\right))\hfill \\ \hfill & ={\rho }_l\left({\pi }_l(X_l^i\otimes F_l^{\prime }\left(T^i\right))\right)\hfill \\ \hfill & ={\rho }_l^{\prime }(X_l^i\otimes F_l^{\prime }\left(T^i\right))\hfill \\ \hfill & ={\rho }_l^{\prime }{\left({\pi }_k^{-1}\left(K\right)\right)}^{-1}\otimes {\rho }_l^{\prime }(S_l^i\otimes F_l^{\prime }\left(T^i\right)).\hfill \end{array}$$

Hence, we have

$$\begin{array}{cc}\hfill Y_l^0⦸Y_l^1& ={\left({\rho }_l^{\prime }(S_l^0\otimes F_l^{\prime }\left(T^0\right))\right)}^{-1}\otimes {\rho }_l^{\prime }(S_l^1\otimes F_l^{\prime }\left(T^1\right)),\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill Y_r^0⦸Y_r^1& ={\left({\rho }_r^{\prime }({\pi }_r^{\prime }\left(S_r^0\right)\otimes F_r^{\prime }\left(T^0\right))\right)}^{-1}\otimes \left({\rho }_r^{\prime }({\pi }_r^{\prime }\left(S_r^1\right)\otimes F_r^{\prime }\left(T^1\right))\right).\hfill \end{array}$$

(16)

Note that Equation (15) is equivalent to

$$\begin{array}{c}\hfill {{\rho }_l^{\prime }}^{-1}\left({\beta }_l\right)={(S_l^0\otimes F_l^{\prime }\left(T^0\right))}^{-1}\otimes S_l^1\otimes F_l^{\prime }\left(T^1\right).\end{array}$$

Using Equations (11), (13), (15) and (16), we obtain the desired equality. The remaining relations are proven similarly. □

Upon closer examination of Lemma 7’s proof, it becomes evident that we can derive the equivalent structure depicted in Figure 3. Its corresponding differential probabilities are

$$\begin{array}{c}\hfill LL{M}_{⦸,⦸}(F_l,F_r,\alpha ,\beta ,\gamma )={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\stackrel{X^0,X^1\in {\mathbb{G}}^2}{\stackrel{{\Delta }_{⦸,⦸}(X^0,X^1)=\alpha }{{\Delta }_{⦸}(Z^0,Z^1)=\gamma }}}[{\Delta }_{⦸,⦸}(Y^0,Y^1)=\beta ],\end{array}$$

where $Y_l^i=X_l^i\otimes F_l\left(Z^i\right)$ and $Y_r^i={\rho }_r({\pi }_r\left(X_r^i\right)\otimes F_r\left(Z^i\right))$, and

$$\begin{array}{c}\hfill RL{M}_{\oslash ,\oslash }(F_l,F_r,\alpha ,\beta ,\gamma )={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\stackrel{X^0,X^1\in {\mathbb{G}}^2}{\stackrel{{\Delta }_{\oslash ,\oslash }(X^0,X^1)=\alpha }{{\Delta }_{\oslash }(Z^0,Z^1)=\gamma }}}[{\Delta }_{\oslash ,\oslash }(Y^0,Y^1)=\beta ],\end{array}$$

where $Y_l^i=F_l\left(Z^i\right)\otimes X_l^i$ and $Y_r^i={\rho }_r(F_r\left(Z^i\right)\otimes {\pi }_r\left(X_r^i\right))$. When $LLM$ and $RLM$ are independent of the key, the security analysis simplifies and we can offer higher security guarantees (in practice, we cannot check the differential probabilities for all the keys). Hence, we restrict our study to ${\rho }_l={\pi }_l={\pi }_k=Id$ for $LL{M}_{⦸,⦸}$ and $RL{M}_{\oslash ,\oslash }$.

Figure 3. Symmetric non-commutative group Lai–Massey structure (version 2).

We further state, without proof, the conditions required for key independence for the remaining differential probabilities.

Lemma 8.

If ${\pi }_k$, ${\pi }_r$ and ${\rho }_r$ are morphisms, then $LL{M}_{⦸,\oslash }(F_l,F_r,\alpha ,\beta ,\gamma ,K)$ and $RL{M}_{\oslash ,⦸}(F_l,F_r,\alpha ,\beta ,\gamma ,K)$ are key independents.

Similarly to the previous case, we can derive an equivalent structure using Lemma 8’s proof. We provide only its corresponding differential probabilities

$$\begin{array}{c}\hfill LL{M}_{⦸,\oslash }(F_l,F_r,\alpha ,\beta ,\gamma )={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\stackrel{X^0,X^1\in {\mathbb{G}}^2}{\stackrel{{\Delta }_{⦸,⦸}(X^0,X^1)=\alpha }{{\Delta }_{\oslash }(Z^0,Z^1)=\gamma }}}[{\Delta }_{⦸,⦸}(Y^0,Y^1)=\beta ],\end{array}$$

where $Y_l^i={\rho }_l({\pi }_l\left(X_l^i\right)\otimes F_l\left(Z^i\right))$ and $Y_r^i=X_r^i\otimes F_r\left(Z^i\right)$, and

$$\begin{array}{c}\hfill RL{M}_{\oslash ,⦸}(F_l,F_r,\alpha ,\beta ,\gamma )={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\stackrel{X^0,X^1\in {\mathbb{G}}^2}{\stackrel{{\Delta }_{\oslash ,\oslash }(X^0,X^1)=\alpha }{{\Delta }_{⦸}(Z^0,Z^1)=\gamma }}}[{\Delta }_{\oslash ,\oslash }(Y^0,Y^1)=\beta ],\end{array}$$

where $Y_l^i={\rho }_l(F_l\left(Z^i\right)\otimes {\pi }_l\left(X_l^i\right))$ and $Y_r^i=F_r\left(Z^i\right)\otimes X_r^i$.

The following corollaries indicate that it is sufficient to focus solely on a version 2 structure from a differential perspective if ${\rho }_r$ is a morphism.

Corollary 1.

Let $\overline{\alpha }={\alpha }_r\parallel {\alpha }_l$ and $\overline{\beta }={\beta }_r\parallel {\beta }_l$. Then,

$$\begin{array}{cc}\hfill LL{M}_{⦸,⦸}(F_l,F_r,\alpha ,\beta ,\gamma )& =LL{M}_{⦸,\oslash }(F_r,F_l,\overline{\alpha },\overline{\beta },{\gamma }^{-1}),\hfill \\ \hfill RL{M}_{\oslash ,\oslash }(F_l,F_r,\alpha ,\beta ,\gamma )& =RL{M}_{\oslash ,⦸}(F_l,F_r,\overline{\alpha },\overline{\beta },{\gamma }^{-1}).\hfill \end{array}$$

Proof. 

We first observe that

$$\begin{array}{c}\hfill \gamma =Z^0⦸Z^1=Z_0^{-1}\otimes Z_1={(Z_1^{-1}\otimes Z_0)}^{-1}={(Z_1\oslash Z_0)}^{-1}.\end{array}$$

So, ${\Delta }_{\oslash }(Z^1,Z^0)={\gamma }^{-1}$. Also,

$$\begin{array}{cc}\hfill {\Delta }_{⦸,⦸}(X_r^0\parallel X_l^0,X_r^1\parallel X_l^1)& =\overline{\alpha }\mathrm{and}{\Delta }_{⦸,⦸}(Y_r^0\parallel Y_l^0,Y_r^1\parallel Y_l^1)=\overline{\beta }.\hfill \end{array}$$

Thus, we obtain the desired result. □

Corollary 2.

We define $G_l\left(x\right)=F_l{\left(x\right)}^{-1}$, $G_r\left(x\right)=F_r{\left(x\right)}^{-1}$ and ${\epsilon }_r\left(x\right)={\pi }_r{\left(x^{-1}\right)}^{-1}$. If ${\rho }_r$ is a morphisms, then

$$\begin{array}{c}\hfill LL{M}_{⦸,⦸}(F_l,F_r,\alpha ,\beta ,\gamma )=RL{M}_{\oslash ,\oslash }(F_l,F_r,\alpha ,\beta ,\gamma ).\end{array}$$

Proof. 

Let $j\in \{l,r\}$ and $S_j^i={\left(X_j^i\right)}^{-1}$. We observe that

$$\begin{array}{cc}\hfill {\alpha }_j& =X_j^0⦸X_j^1={\left(X_j^0\right)}^{-1}\otimes X_j^1=S_j^0\otimes {\left(S_j^1\right)}^{-1}=S_j^0\oslash S_j^1\hfill \\ \hfill Z^i& =X_l^i\oslash X_r^i=X_l^i\otimes {\left(X_r^i\right)}^{-1}={\left(S_l^i\right)}^{-1}\otimes S_r^i=S_l^i⦸S_r^i\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill Y_l^0⦸Y_l^1& =F_l{\left(Z^0\right)}^{-1}\otimes {\left(X_l^0\right)}^{-1}\otimes X_l^1\otimes F_l\left(Z^1\right)\hfill \\ \hfill & =G_l\left(Z^0\right)\otimes S_j^0\otimes {\left(S_j^1\right)}^{-1}\otimes G_l{\left(Z^1\right)}^{-1}\hfill \\ \hfill & ={\Delta }_{\oslash }(G_l\left(Z^0\right)\otimes S_l^0,G_l\left(Z^1\right)\otimes S_l^1)\hfill \\ \\ \hfill Y_r^0⦸Y_r^1& ={\rho }_r{({\pi }_r\left(X_r^0\right)\otimes F_r\left(Z^0\right))}^{-1}\otimes {\rho }_r({\pi }_r\left(X_r^1\right)\otimes F_r\left(Z^1\right))\hfill \\ \hfill & ={\rho }_r(F_r{\left(Z^0\right)}^{-1}\otimes {\pi }_r{\left(X_r^0\right)}^{-1}\otimes {\pi }_r\left(X_r^1\right)\otimes F_r\left(Z^1\right)\hfill \\ \hfill & ={\rho }_r(G_r\left(Z^0\right)\otimes {\epsilon }_r{\left(S_r^0\right)}^{-1}\otimes {\epsilon }_r{\left(S_r^1\right)}^{-1}\otimes G_r{\left(Z^1\right)}^{-1}\hfill \\ \hfill & ={\rho }_r(G_r\left(Z^0\right)\otimes {\epsilon }_r{\left(S_r^0\right)}^{-1})\otimes {\rho }_r{(G_r\left(Z^1\right)\otimes {\epsilon }_r\left(S_r^1\right))}^{-1}\hfill \\ \hfill & ={\Delta }_{\oslash }({\rho }_r(G_r\left(Z^0\right)\otimes {\epsilon }_r{\left(S_r^0\right)}^{-1}),{\rho }_r(G_r\left(Z^1\right)\otimes {\epsilon }_r\left(S_r^1\right))).\hfill \end{array}$$

Thus, we obtain the desired equality. □

We further delve into the conditions required for correct decryption. We can observe that this requirement translates into

$$\begin{array}{c}\hfill X_l\oslash X_r=(X_l\otimes F_l\left(Z\right))\oslash ({\pi }_r\left(X_r\right)\otimes F_r\left(Z\right)),\end{array}$$

(17)

where $Z=X_l\oslash X_r$. We remark that Equation (17) is equivalent to

$$\begin{array}{cc}\hfill X_l\otimes X_r^{-1}& =(X_l\otimes F_l\left(Z\right))\otimes {({\pi }_r\left(X_r\right)\otimes F_r\left(Z\right))}^{-1}\hfill \\ \hfill & =X_l\otimes F_l\left(Z\right)\otimes F_r{\left(Z\right)}^{-1}\otimes {\pi }_r{\left(X_r\right)}^{-1},\hfill \end{array}$$

which leads to

$$\begin{array}{cc}\hfill {\pi }_r\left(X_r\right)\otimes X_r^{-1}& =F_l\left(Z\right)\otimes F_r{\left(Z\right)}^{-1}.\hfill \end{array}$$

(18)

Lemma 9.

Let $\eta \in \mathbb{G}$. We can decrypt it if and only if ${\pi }_r\left(x\right)=\eta \otimes x$ and $F_l\left(x\right)=\eta \otimes F_r\left(x\right)$.

Proof. 

First, note that Equation (18) holds for any $X_r$ and $X_l$. Therefore, we can fix an arbitrary $X_r$ and denote it by $\eta ={\pi }_r\left(X_r\right)\otimes X_r^{-1}$. Thus, we obtain that $F_l\left(Z\right)=\eta \otimes F_r\left(Z\right)$ for any $X_l$. This leads to $F_l\left(x\right)=\eta \otimes F_r\left(x\right)$ for any x since Z is simply a translation of any $X_l$ with a fixed point. Consequently, from Equation (18), we obtain that ${\pi }_r\left(x\right)=\eta \otimes x$ for any x. We leave the converse as an exercise. □

Taking into account the previous arguments, we obtain the Lai–Massey structure depicted in Figure 4.

Figure 4. Symmetric non-commutative group Lai–Massey structure (version 3).

The following corollary tells us that, in the case of commutative groups, the only meaningful (from a differential perspective) structure is the one with ${\pi }_r=Id$ and $F_l=F_r$ (equivalently, the one with $\eta ={\mathbb{1}}_{\mathbb{G}}$, where ${\mathbb{1}}_{\mathbb{G}}$ is the identity element of $\mathbb{G}$).

Corollary 3.

If $(\mathbb{G},\otimes )$ is Abelian and ${\rho }_r$ is a morphism, then

$$\begin{array}{c}\hfill LL{M}_{⦸,⦸}(F_l,F_r,\alpha ,\beta ,\gamma )=LL{M}_{⦸,⦸}(F_r,F_r,{\alpha }_{,}\beta ,\gamma ).\end{array}$$

Proof. 

Let $j\in \{l,r\}$ and $S_j^i=X_j^i\otimes \eta$. We observe that

$$\begin{array}{cc}\hfill {\alpha }_j& =X_j^0⦸X_j^1={\left(X_j^0\right)}^{-1}\otimes X_j^1={\left(X_j^0\right)}^{-1}\otimes {\eta }^{-1}\otimes \eta \otimes X_j^1=S_j^0⦸S_j^1\hfill \\ \hfill Z^i& =X_l^i\oslash X_r^i=X_l^i\otimes {\left(X_r^i\right)}^{-1}=X_l^i\otimes \eta \otimes {\eta }^{-1}\otimes {\left(X_r^i\right)}^{-1}=S_l^i\oslash S_r^i\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill Y_l^0⦸Y_l^1& =F_l{\left(Z^0\right)}^{-1}\otimes {\left(X_l^0\right)}^{-1}\otimes X_l^1\otimes F_l\left(Z^1\right)\hfill \\ \hfill & =F_r{\left(Z^0\right)}^{-1}\otimes {\eta }^{-1}\otimes {\left(X_l^0\right)}^{-1}\otimes X_l^1\otimes \eta \otimes F_r\left(Z^1\right)\hfill \\ \hfill & =F_r{\left(Z^0\right)}^{-1}\otimes {\left(S_l^0\right)}^{-1}\otimes S_l^1\otimes F_r\left(Z^1\right)\hfill \\ \hfill & ={\Delta }_{⦸}(S_l^0\otimes F_r\left(Z^0\right),S_l^1\otimes F_r\left(Z^1\right))\hfill \\ \\ \hfill Y_r^0⦸Y_r^1& ={\rho }_r{({\pi }_r\left(X_r^0\right)\otimes F_r\left(Z^0\right))}^{-1}\otimes {\rho }_r({\pi }_r\left(X_r^1\right)\otimes F_r\left(Z^1\right))\hfill \\ \hfill & ={\rho }_r{(\eta \otimes X_r^0\otimes F_r\left(Z^0\right))}^{-1}\otimes {\rho }_r(\eta \otimes X_r^1\otimes F_r\left(Z^1\right))\hfill \\ \hfill & ={\rho }_r{(S_r^0\otimes F_r\left(Z^0\right))}^{-1}\otimes {\rho }_r(S_r^1\otimes F_r\left(Z^1\right))\hfill \\ \hfill & ={\Delta }_{⦸}({\rho }_r(S_r^0\otimes F_r\left(Z^0\right)),{\rho }_r(S_r^1\otimes F_r\left(Z^1\right))).\hfill \end{array}$$

Thus, we obtain the desired equality. □

When $\rho =Id$, the version 3 structure can be easily distinguished from a random permutation by simply checking if, for example, $L_2\oslash R_2=L_0\oslash R_0$. We further introduce a definition from [20], which will prove useful for removing this vulnerability.

Definition 6.

A permutation φ is a right orthomorphism if ${\phi }^{\prime }\left(x\right)=\phi \left(x\right)\oslash x$ is a permutation. If ${\phi }^{\prime }\left(x\right)=x⦸\phi \left(x\right)$ is a permutation, then φ is called a left orthomorphism.

Lemma 10.

Let $Z=K\otimes (X_l\oslash X_r)$ and $t=F_r(K,Z)$. The following property holds:

$$\begin{array}{cc}\hfill Y_l\oslash Y_r& =(X_l\otimes \eta )\oslash (\eta \otimes X_r)\otimes (\eta \otimes X_r\otimes t)\oslash {\rho }_r(\eta \otimes X_r\otimes t).\hfill \end{array}$$

Proof. 

We observe that

$$\begin{array}{cc}\hfill Y_l\oslash Y_r& =X_l\otimes F_l\left(Z\right)\otimes {\rho }_r{({\pi }_r\left(X_r\right)\otimes F_r\left(Z\right))}^{-1}\hfill \\ \hfill & =X_l\otimes \eta \otimes t\otimes {\rho }_r{(\eta \otimes X_r\otimes t)}^{-1}.\hfill \end{array}$$

If we denote $A=\eta \otimes X_r\otimes t$, we obtain

$$\begin{array}{cc}\hfill Y_l\oslash Y_r& =X_l\otimes \eta \otimes t\otimes {\rho }_r{\left(A\right)}^{-1}\hfill \\ \hfill & =X_l\otimes \eta \otimes {(\eta \otimes X_r)}^{-1}\otimes \eta \otimes X_r\otimes t\otimes {\rho }_r{\left(A\right)}^{-1}\hfill \\ \hfill & =(X_l\otimes \eta )\oslash (\eta \otimes X_r)\otimes A\oslash {\rho }_r\left(A\right),\hfill \end{array}$$

and thus, we obtain the desired property. □

Corollary 4.

If ${\rho }_r$ is a right orthomorphism, then $Y_l\oslash Y_r$ is a random element.

Proof. 

Let ${\rho }_r^{\prime }\left(x\right)={\rho }_r\left(x\right)\oslash x$. According to Lemma 10, we obtain that

$$\begin{array}{cc}\hfill Y_l\oslash Y_r& =(X_l\otimes \eta )\oslash (\eta \otimes X_r)\otimes {\rho }_r^{\prime }{\left(A\right)}^{-1}.\hfill \end{array}$$

Since $F(K,·)$ is random function, A is randomly distributed. Since ${\rho }_r$ is a right orthomorphism, ${\rho }_r^{\prime }\left(A\right)$ is also random. Therefore, we obtain that $Y_l\oslash Y_r$ is uniformly distributed. □

To summarize all the lemmas and observations we provide the reader with Proposition 1.

Proposition 1.

A symmetric quasigroup Lai–Massey structure derived from a symmetric non-commutative group Lai–Massey structure using an isotopy has the same differential security as version 3 (see Figure 4) if ρ is a morphism and we require correct decryption. If the group is commutative, we obtain that symmetric group Lai–Massey structure and version 3 are equivalent.

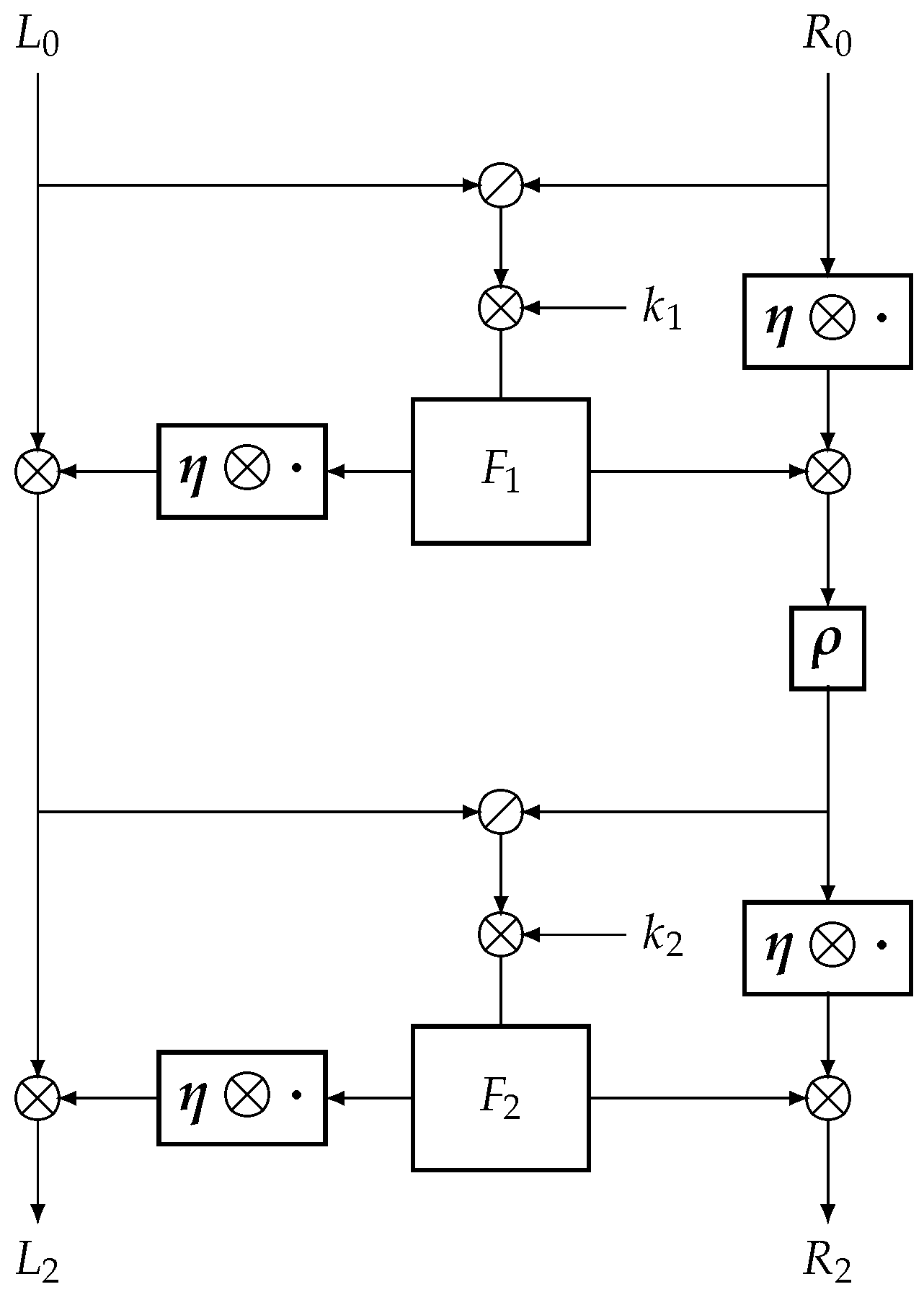
3.3. Asymmetric Structure Analysis

In this section, we extend the notion of differential cryptanalysis to asymmetric Lai–Massey structures. Then, as in the symmetric case, we show that the structure can be defined using only group operations. Finally, we show that the resulting structure is equivalent to the version 1 symmetric structure.

Definition 7.

Let K be a key and $X^i,Y^i\in {\mathbb{G}}^2$ for $i\in \{0,1\}$. We define the asymmetric Lai–Massey quasigroup differential probabilities as follows:

1. 

Let $Z^i=X_l^i{\otimes }_t{X}_r^i$, $Y_l^i=X_l^i{\otimes }_{l}F(K\otimes Z^i))$ and $Y_r^i=F(K\otimes Z^i){⦸}_r{X}_r^i$. Then,

$$\begin{array}{c}\hfill OL{M}_{⦸,{⦸}_k}(F,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\begin{array}{c}{X}^0,X^1\in {\mathbb{G}}^2\\ {\Delta }_{{⦸}_l,{\oslash }_r}(X^0,X^1)=\alpha \\ {\Delta }_{{⦸}_k}(Z^0,Z^1)=\gamma \end{array}}[{\Delta }_{{⦸}_l,{\oslash }_r}(Y^0,Y^1)=\beta ];\end{array}$$

2. 

Let $Z^i=X_l^i{\otimes }_t{X}_r^i$, $Y_l^i=X_l^i{\otimes }_{l}F(Z^i\otimes K)$ and $Y_r^i=F(Z^i\otimes K){⦸}_r{X}_r^i$. Then,

$$\begin{array}{c}\hfill OL{M}_{⦸,{\oslash }_k}(F,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\begin{array}{c}{X}^0,X^1\in {\mathbb{G}}^2\\ {\Delta }_{{⦸}_l,{\oslash }_r}(X^0,X^1)=\alpha \\ {\Delta }_{{\oslash }_k}(Z^0,Z^1)=\gamma \end{array}}[{\Delta }_{{⦸}_l,{\oslash }_r}(Y^0,Y^1)=\beta ];\end{array}$$

3. 

Let $Z^i=X_r^i{\otimes }_t{X}_l^i$, $Y_l^i=F(K\otimes Z^i){\otimes }_l{X}_l^i$ and $Y_r^i=X_r^i{\oslash }_{r}F(K\otimes Z^i)$. Then,

$$\begin{array}{c}\hfill IL{M}_{\oslash ,{⦸}_k}(F,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\begin{array}{c}{X}^0,X^1\in {\mathbb{G}}^2\\ {\Delta }_{{\oslash }_l{⦸}_r}(X^0,X^1)=\alpha \\ {\Delta }_{{⦸}_k}(Z^0,Z^1)=\gamma \end{array}}[{\Delta }_{{\oslash }_l,{⦸}_r}(Y^0,Y^1)=\beta ];\end{array}$$

4. 

Let $Z^i=X_r^i{\otimes }_t{X}_l^i$, $Y_l^i=F(Z^i\otimes K){\otimes }_l{X}_l^i$ and $Y_r^i=X_r^i{\oslash }_{r}F(Z^i\otimes K)$. Then,

$$\begin{array}{c}\hfill IL{M}_{\oslash ,{\oslash }_k}(F,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\begin{array}{c}{X}^0,X^1\in {\mathbb{G}}^2\\ {\Delta }_{{\oslash }_l,{⦸}_r}(X^0,X^1)=\alpha \\ {\Delta }_{{\oslash }_k}(Z^0,Z^1)=\gamma \end{array}}[{\Delta }_{{\oslash }_l,{⦸}_r}(Y^0,Y^1)=\beta ];\end{array}$$

where $F:\mathbb{G}\to \mathbb{G}$ is a function, and $\alpha ,\beta \in {\mathbb{G}}^2$, and $\gamma \in \mathbb{G}$.

The next lemmas enable us to restrict our study to the case where ${\omega }_l={\omega }_r={\omega }_t=Id$ due to the differential equivalency. Note that the Lemmas 11 and 12 are proven similarly to Lemma 3; hence, we omit their proof.

Lemma 11.

Let $i\in \{l,r\}$, ${\pi }_i^{\prime }={\pi }_i\circ {\omega }_i^{-1}$, ${\rho }_i^{\prime }={\rho }_i\circ {\omega }_i^{-1}$, $F_i={\omega }_i\circ F\circ {\omega }_t^{-1}$. Also, let ${\rho }_t^{\prime }={\rho }_t\circ {\omega }_r^{-1}$, ${\pi }_t^{\prime }={\pi }_t\circ {\omega }_l^{-1}$, ${\pi }_k^{\prime }={\pi }_k\circ {\omega }_t^{-1}$, ${\rho }_k^{\prime }={\rho }_k\circ {\omega }_t^{-1}$, and ${\omega }_k^{\prime }={\omega }_k\circ {\omega }_t^{-1}$. We define $x{\ast }_{i}y={\pi }_i^{\prime }\left(x\right)★{\rho }_i^{\prime }\left(y\right)$, $x{\ast }_{t}y={\pi }_t^{\prime }\left(x\right)★{\rho }_t^{\prime }\left(y\right)$, $x{\ast }_{k}y={{\omega }_k^{\prime }}^{-1}({\pi }_k^{\prime }\left(x\right)★{\rho }_k^{\prime }\left(y\right))$, and ${\setminus }_j$, ${/}_j$ as the associated left and right divisions, where $j\in \{l,r,t,k\}$. Then, the following identities hold:

$$\begin{array}{cc}\hfill OL{M}_{⦸,{⦸}_k}(F,\alpha ,\beta ,\gamma ,K)& =OL{M}_{{\setminus ,\setminus }_k}(F_l,F_r,A,B,{\omega }_t\left(\gamma \right),{\omega }_t\left(K\right)),\hfill \\ \hfill OL{M}_{⦸,{\oslash }_k}(F,\alpha ,\beta ,\gamma ,K)& =OL{M}_{\setminus ,{/}_k}(F_l,F_r,A,B,{\omega }_t\left(\gamma \right),{\omega }_t\left(K\right)),\hfill \end{array}$$

where $A={\omega }_l\left({\alpha }_l\right)\parallel {\omega }_l\left({\alpha }_l\right)$ and $B={\omega }_l\left({\beta }_l\right)\parallel {\omega }_l\left({\beta }_l\right)$.

Lemma 12.

Let $i\in \{l,r\}$, ${\pi }_i^{\prime }={\pi }_i\circ {\omega }_i^{-1}$, ${\rho }_i^{\prime }={\rho }_i\circ {\omega }_i^{-1}$, $F_i={\omega }_i\circ F\circ {\omega }_t^{-1}$. Also, let ${\rho }_t^{\prime }={\rho }_t\circ {\omega }_l^{-1}$, ${\pi }_t^{\prime }={\pi }_t\circ {\omega }_r^{-1}$, ${\pi }_k^{\prime }={\pi }_k\circ {\omega }_t^{-1}$, ${\rho }_k^{\prime }={\rho }_k\circ {\omega }_t^{-1}$, and ${\omega }_k^{\prime }={\omega }_k\circ {\omega }_t^{-1}$. We define $x{\ast }_{i}y={\pi }_i^{\prime }\left(x\right)★{\rho }_i^{\prime }\left(y\right)$, $x{\ast }_{t}y={\pi }_t^{\prime }\left(x\right)★{\rho }_t^{\prime }\left(y\right)$, $x{\ast }_{k}y={{\omega }_k^{\prime }}^{-1}({\pi }_k^{\prime }\left(x\right)★{\rho }_k^{\prime }\left(y\right))$, and ${\setminus }_j$, ${/}_j$ as the associated left and right divisions, where $j\in \{l,r,t,k\}$. Then, the following identities hold:

$$\begin{array}{cc}\hfill IL{M}_{\oslash ,{⦸}_k}(F,\alpha ,\beta ,\gamma ,K)& =IL{M}_{/,{\setminus }_k}(F_l,F_r,A,B,{\omega }_t\left(\gamma \right),{\omega }_t\left(K\right)),\hfill \\ \hfill IL{M}_{\oslash ,{\oslash }_k}(F,\alpha ,\beta ,\gamma ,K)& =IL{M}_{/,{/}_k}(F_l,F_r,A,B,{\omega }_t\left(\gamma \right),{\omega }_t\left(K\right)),\hfill \end{array}$$

where $A={\omega }_l\left({\alpha }_l\right)\parallel {\omega }_l\left({\alpha }_l\right)$ and $B={\omega }_l\left({\beta }_l\right)\parallel {\omega }_l\left({\beta }_l\right)$.

The following lemmas are the asymmetric equivalents of Lemmas 5 and 6; thus, we state them without proof.

Lemma 13.

Let ${\pi }_l^{\prime }={\pi }_l\circ {\pi }_t^{-1}$, ${\rho }_r^{\prime }={\rho }_r\circ {\rho }_t^{-1}$, $F_l^{\prime }={\rho }_l\circ F_l$, $F_r^{\prime }={\pi }_r\circ F_r$. We define $x{\ast }_{l}y={\pi }_t({\pi }_l^{\prime }\left(x\right)★y)$, $x{\ast }_{r}y={\rho }_t(x★{\rho }_r^{\prime }\left(y\right))$, and ${\setminus }_i$, ${/}_i$ as the associated left and right divisions, where $i\in \{l,r\}$. Then, the following identities hold:

$$\begin{array}{cc}\hfill OL{M}_{⦸,{⦸}_k}(F_l,F_r,\alpha ,\beta ,\gamma ,K)& =OL{M}_{\setminus ,{⦸}_k}(F_l^{\prime },F_r^{\prime },A,B,\gamma ,K),\hfill \\ \hfill OL{M}_{⦸,{\oslash }_k}(F_l,F_r,\alpha ,\beta ,\gamma ,K)& =OL{M}_{\setminus ,{\oslash }_k}(F_l^{\prime },F_r^{\prime },A,B,\gamma ,K),\hfill \end{array}$$

where $A={\rho }_l\left({\alpha }_l\right)\parallel {\pi }_r\left({\alpha }_l\right)$ and $B={\rho }_l\left({\beta }_l\right)\parallel {\pi }_r\left({\beta }_l\right)$.

Lemma 14.

Let ${\rho }_l^{\prime }={\rho }_l\circ {\rho }_t^{-1}$, ${\pi }_r^{\prime }={\pi }_r\circ {\pi }_t^{-1}$, $F_l^{\prime }={\pi }_l\circ F_l$, $F_r^{\prime }={\rho }_r\circ F_r$. We define $x{\ast }_{l}y={\rho }_t(x★{\rho }_l^{\prime }\left(y\right))$, $x{\ast }_{r}y={\pi }_t({\pi }_r^{\prime }\left(x\right)★y)$, and ${\setminus }_i$, ${/}_i$ as the associated left and right divisions, where $i\in \{l,r\}$. Then, the following identities hold:

$$\begin{array}{cc}\hfill IL{M}_{\oslash ,{⦸}_k}(F_l,F_r,\alpha ,\beta ,\gamma ,K)& =IL{M}_{/,{⦸}_k}(F_l^{\prime },F_r^{\prime },A,B,\gamma ,K),\hfill \\ \hfill IL{M}_{\oslash ,{\oslash }_k}(F_l,F_r,\alpha ,\beta ,\gamma ,K)& =IL{M}_{/,{\oslash }_k}(F_l^{\prime },F_r^{\prime },A,B,\gamma ,K),\hfill \end{array}$$

where $A={\pi }_l\left({\alpha }_l\right)\parallel {\rho }_r\left({\alpha }_l\right)$ and $B={\pi }_l\left({\beta }_l\right)\parallel {\rho }_r\left({\beta }_l\right)$.

Let $\otimes =★$. Before presenting the resulting asymmetric structure, we would like to point out that

$$\begin{array}{cc}\hfill Y_r^i=F\left(t\right){⦸}_r{X}_r^i& \iff F\left(t\right){\otimes }_r{Y}_r^i=X_r^i\iff {\rho }_t(F\left(t\right)★{\rho }_r^{\prime }\left(Y_r^i\right))=X_r^i\hfill \\ \hfill & \iff Y_r^i={\rho }_r^{\prime -1}(F{\left(t\right)}^{-1}★{\rho }_t^{-1}\left(X_r^i\right))\hfill \\ \hfill & \iff Y_r^i={\rho }_r^{\prime -1}(F\left(t\right)⦸{\rho }_t^{-1}\left(X_r^i\right))\hfill \\ \\ \hfill Y_r^i=X_r^i{\oslash }_{r}F\left(t\right)& \iff Y_r^i{\otimes }_{r}F\left(t\right)=X_r^i\iff {\pi }_t({\pi }_r^{\prime }\left(Y_r^i\right)★F\left(t\right))=X_r^i\hfill \\ \hfill & \iff Y_r^i={\pi }_r^{\prime -1}({\pi }_t^{-1}\left(X_r^i\right)★F{\left(t\right)}^{-1})\hfill \\ \hfill & \iff Y_r^i={\pi }_r^{\prime -1}({\pi }_t^{-1}\left(X_r^i\right)\oslash F\left(t\right)),\hfill \end{array}$$

where, for the last equalities, we used Lemma 2.

Considering the aforementioned remark and employing arguments akin to the symmetric counterpart, we obtain a Lai–Massey structure similar (the top and right operations are changed to ⊗ and $⦸$ (OLM) or ⊘ (ILM)) to the one depicted in Figure 2. The associated differential properties are as follows:

1.

Let $Z^i=X_l^i\otimes X_r^i$, $Y_l^i={\rho }_l({\pi }_l\left(X_l^i\right)\otimes F(K\otimes {\pi }_k\left(Z^i\right)))$, and $Y_r^i={\rho }_r(F(K\otimes {\pi }_k\left(Z^i\right))⦸{\pi }_r\left(X_r^i\right))$. Then,

$$\begin{array}{c}\hfill OL{M}_{⦸,⦸}(F,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\begin{array}{c}{X}^0,X^1\in {\mathbb{G}}^2\\ {\Delta }_{⦸,\oslash }(X^0,X^1)=\alpha \\ {\Delta }_{⦸}(Z^0,Z^1)=\gamma \end{array}}[{\Delta }_{⦸,\oslash }(Y^0,Y^1)=\beta ];\end{array}$$

2.

Let $Z^i=X_l^i\otimes X_r^i$, $Y_l^i={\rho }_l({\pi }_l\left(X_l^i\right)\otimes F({\pi }_k\left(Z^i\right)\otimes K))$, and $Y_r^i={\rho }_r(F({\pi }_k\left(Z^i\right)\otimes K)⦸{\pi }_r\left(X_r^i\right))$. Then,

$$\begin{array}{c}\hfill OL{M}_{⦸,\oslash }(F,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\begin{array}{c}{X}^0,X^1\in {\mathbb{G}}^2\\ {\Delta }_{⦸,\oslash }(X^0,X^1)=\alpha \\ {\Delta }_{\oslash }(Z^0,Z^1)=\gamma \end{array}}[{\Delta }_{⦸,\oslash }(Y^0,Y^1)=\beta ];\end{array}$$

3.

Let $Z^i=X_r^i\otimes X_l^i$, $Y_l^i={\rho }_l(F(K\otimes {\pi }_k\left(Z^i\right))\otimes {\pi }_l\left(X_l^i\right))$, and $Y_r^i={\rho }_r({\pi }_r\left(X_r^i\right)\oslash F(K\otimes {\pi }_k\left(Z^i\right)))$. Then,

$$\begin{array}{c}\hfill IL{M}_{\oslash ,⦸}(F,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\begin{array}{c}{X}^0,X^1\in {\mathbb{G}}^2\\ {\Delta }_{\oslash ,⦸}(X^0,X^1)=\alpha \\ {\Delta }_{⦸}(Z^0,Z^1)=\gamma \end{array}}[{\Delta }_{\oslash ,⦸}(Y^0,Y^1)=\beta ];\end{array}$$

4.

Let $Z^i=X_r^i\otimes X_l^i$, $Y_l^i={\rho }_l(F({\pi }_k\left(Z^i\right)\otimes K)\otimes {\pi }_l\left(X_l^i\right))$, and $Y_r^i={\rho }_r({\pi }_r\left(X_r^i\right)\oslash F({\pi }_k\left(Z^i\right)\otimes K))$. Then,

$$\begin{array}{c}\hfill IL{M}_{\oslash ,\oslash }(F,\alpha ,\beta ,\gamma ,K)={\displaystyle \frac{1}{{\left|\mathbb{G}\right|}^2}}\sum _{\begin{array}{c}{X}^0,X^1\in {\mathbb{G}}^2\\ {\Delta }_{\oslash ,⦸}(X^0,X^1)=\alpha \\ {\Delta }_{\oslash }(Z^0,Z^1)=\gamma \end{array}}[{\Delta }_{\oslash ,⦸}(Y^0,Y^1)=\beta ].\end{array}$$

The following lemma shows that the asymmetric and the symmetric structures are differentially equivalent. Therefore, we can directly apply the results from Section 3.2.

Lemma 15.

Let ${\pi }_r^{\prime }\left(x\right)={\pi }_r{\left(x^{-1}\right)}^{-1}$, ${\rho }_r^{\prime }\left(x\right)={\rho }_r\left(x^{-1}\right)$. Then, the following identities hold:

$$\begin{array}{cc}\hfill OL{M}_{⦸,⦸}(F_l,F_r,\alpha ,\beta ,\gamma ,K)& =LL{M}_{⦸,⦸}(F_l,F_r,A,B,\gamma ,K),\hfill \\ \hfill OL{M}_{⦸,\oslash }(F_l,F_r,\alpha ,\beta ,\gamma ,K)& =LL{M}_{⦸,\oslash }(F_l,F_r,A,B,\gamma ,K),\hfill \\ \hfill IL{M}_{⦸,⦸}(F_l,F_r,\alpha ,\beta ,\gamma ,K)& =RL{M}_{⦸,⦸}(F_l,F_r,A,B,\gamma ,K),\hfill \\ \hfill IL{M}_{⦸,\oslash }(F_l,F_r,\alpha ,\beta ,\gamma ,K)& =RL{M}_{⦸,\oslash }(F_l,F_r,A,B,\gamma ,K).\hfill \end{array}$$

Proof. 

Let $S_l^i=X_l^i$ and $S_r^i={\left(X_r^i\right)}^{-1}$. We observe that

$$\begin{array}{cc}\hfill {\alpha }_r& =X_r^0\oslash X_r^1=X_r^0\otimes {\left(X_r^1\right)}^{-1}={\left(S_r^0\right)}^{-1}\otimes S_r^1=S_r^0⦸S_r^1\hfill \\ \hfill Z^i& =X_l^i\otimes X_r^i=S_l^i\otimes {\left(S_r^i\right)}^{-1}=S_l^i\oslash S_r^i\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill Y_r^i& ={\rho }_r(F(K\otimes {\pi }_k\left(Z^i\right))⦸{\pi }_r\left(X_r^i\right))\hfill \\ \hfill & ={\rho }_r(F{(K\otimes {\pi }_k\left(Z^i\right))}^{-1}\otimes {\pi }_r\left(X_r^i\right))\hfill \\ \hfill & ={\rho }_r(F{(K\otimes {\pi }_k\left(Z^i\right))}^{-1}\otimes {\pi }_r^{\prime }{\left(S_r^i\right)}^{-1})\hfill \\ \hfill & ={\rho }_r\left({({\pi }_r^{\prime }\left(S_r^i\right)\otimes F(K\otimes {\pi }_k\left(Z^i\right)))}^{-1}\right)\hfill \\ \hfill & ={\rho }_r^{\prime }({\pi }_r^{\prime }\left(S_r^i\right)\otimes F(K\otimes {\pi }_k\left(Z^i\right))).\hfill \end{array}$$

The remaining equalities are proven similarly. □

To summarize all the lemmas and observations, we refer the reader to Proposition 2.

Proposition 2.

An asymmetric quasigroup Lai–Massey structure has the same differential security a symmetric quasigroup Lai–Massey structure.

4. Conclusions

In this paper, we studied the effect of isotropic quasigroups concerning groups in the design of cryptographic symmetric structures. More precisely, for quasigroup extensions of the Lai–Massey structure, we investigated the security implications and unveiled interesting equivalences with other symmetric structures based on the underlying group. Furthermore, we highlighted the necessary conditions for having correct decryption and we established that mounting a differential attack against the symmetric version is equivalent to attacking an alternative asymmetric structure.

Future Work

It would be intriguing to investigate the effect of using quasigroups that do not exhibit isotopy to groups. Additionally, exploring the influence of other symmetries, such as parastrophisms [41] or paratopisms [42], could provide valuable insights. Another interesting area of research is to compare the performance and security of the proposed non-commutative structure with other block cipher architectures, such as SPNs or Feistel networks.