Securing Data Exchange with Elliptic Curve Cryptography: A Novel Hash-Based Method for Message Mapping and Integrity Assurance
Abstract
1. Introduction
2. Background and Literature Review
2.1. Elliptic Curve over Prime Fields
2.2. Elliptic Curve Diffie–Hellman Protocol
| Algorithm 1 Elliptic curve Diffie–Hellman algorithm |
|
2.3. Elliptic Curve Analogue of ElGamal Encryption
- Generate a random ephemeral key .
- Compute and .
- Transmit the encrypted ciphertext pairs to the receiver.
2.4. Ground Rules of a Valid Message Mapping
- ∘
- Ensuring the operationality: The sender can map a block, m, of the message to a point , and the receiver can reverse the message mapping process to retrieve .
- ∘
- Key dependency: Incorporates shared secret keys into the mapping process to make it key-dependent. This enhances security and prevents unauthorized parties from mapping plaintexts to curve points.
- ∘
- Randomization: Introduce an element of randomness into the mapping process to prevent attackers from predicting the mapping for specific plaintexts, namely, systems with small plaintext spaces. This can be achieved by using a random value or salt in the mapping.
- ∘
- Resistance to attacks: The mapping process should be designed to resist cryptographic attacks, such as chosen-plaintext attacks (CPA) and chosen-ciphertext attacks (CCAs), and should not mount a weakness that could be exploited by the statistical attack against ciphertext.
- ∘
- Bandwidth usage: Well-designed message mapping must depress the bandwidth utilization. For example, if each character of a message is mapped separately to a point on the curve, then the encryption will produce a large amount of data when compared with another mapping scheme that embeds a block of the message.
- ∘
- Complexity: Sometimes, there may be trade-offs between complexity and efficiency. More complex mapping processes may provide stronger security but require more computational resources, and, therefore, more power consumption.
2.5. Related Work
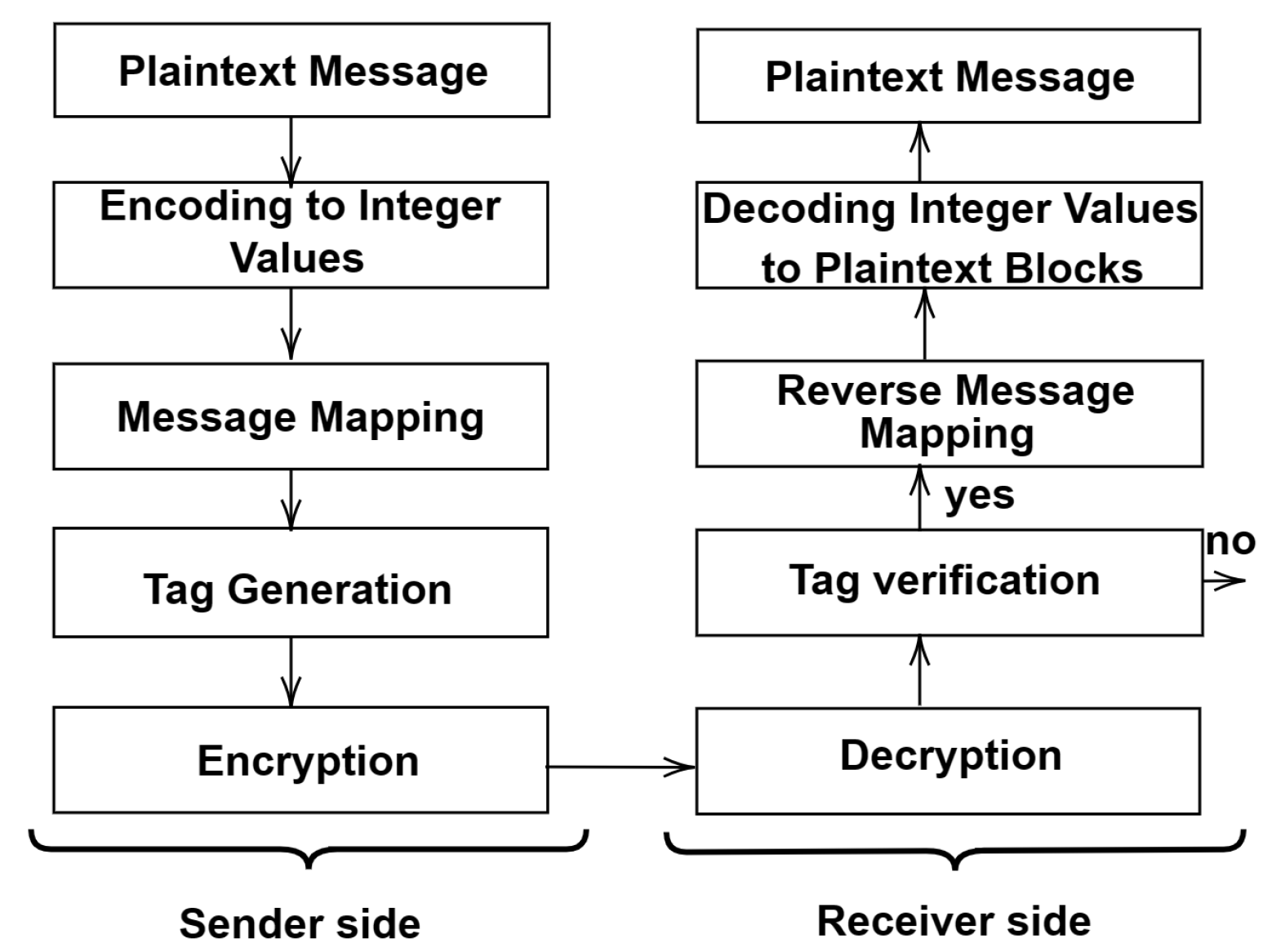
3. The Proposed Scheme
3.1. Key Generation
| Algorithm 2 Key Generation |
|
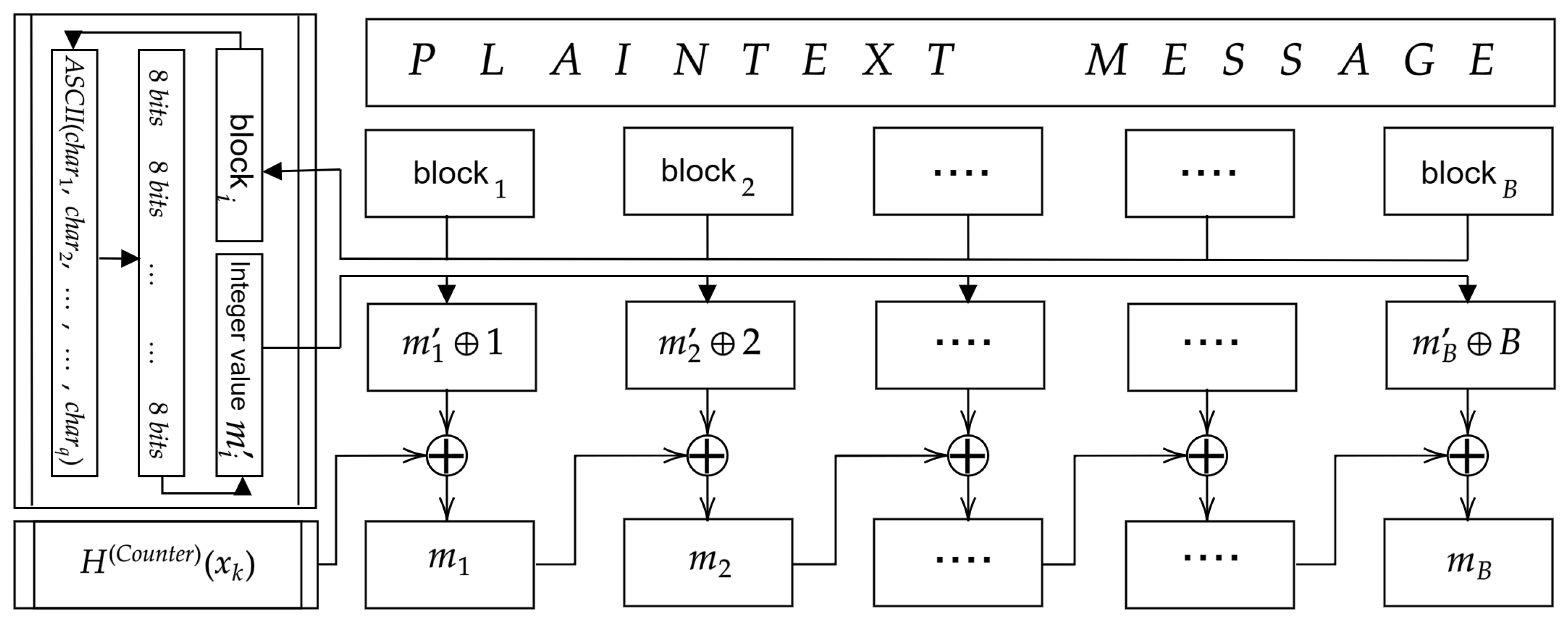
3.2. Message Encoding
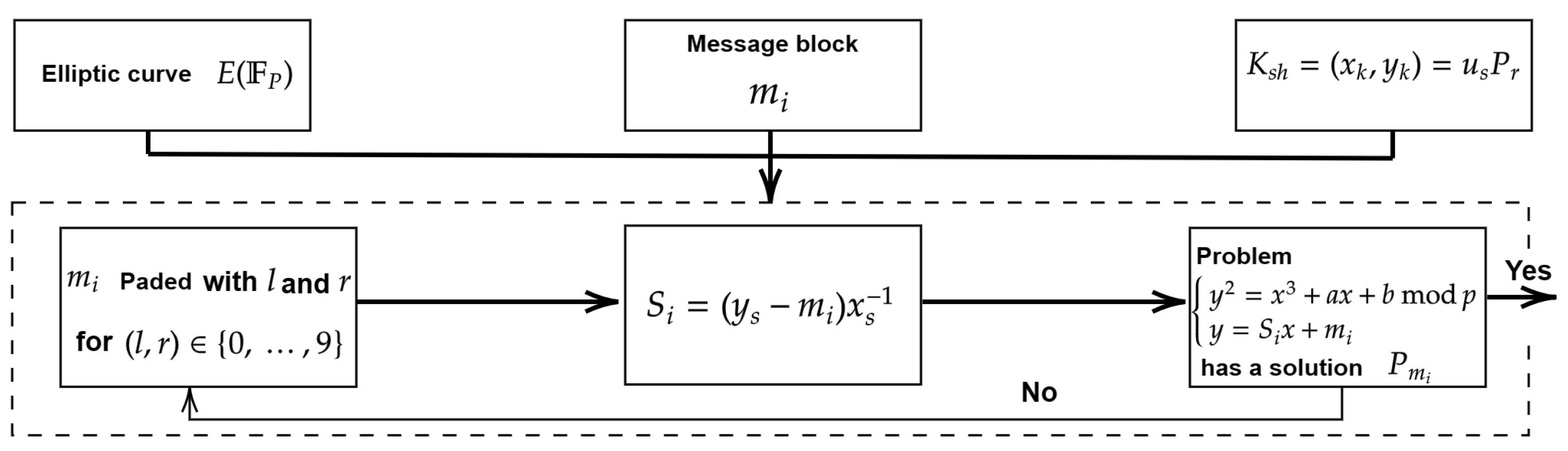
3.3. Message Mapping
| Algorithm 3 Message mapping algorithm |
|
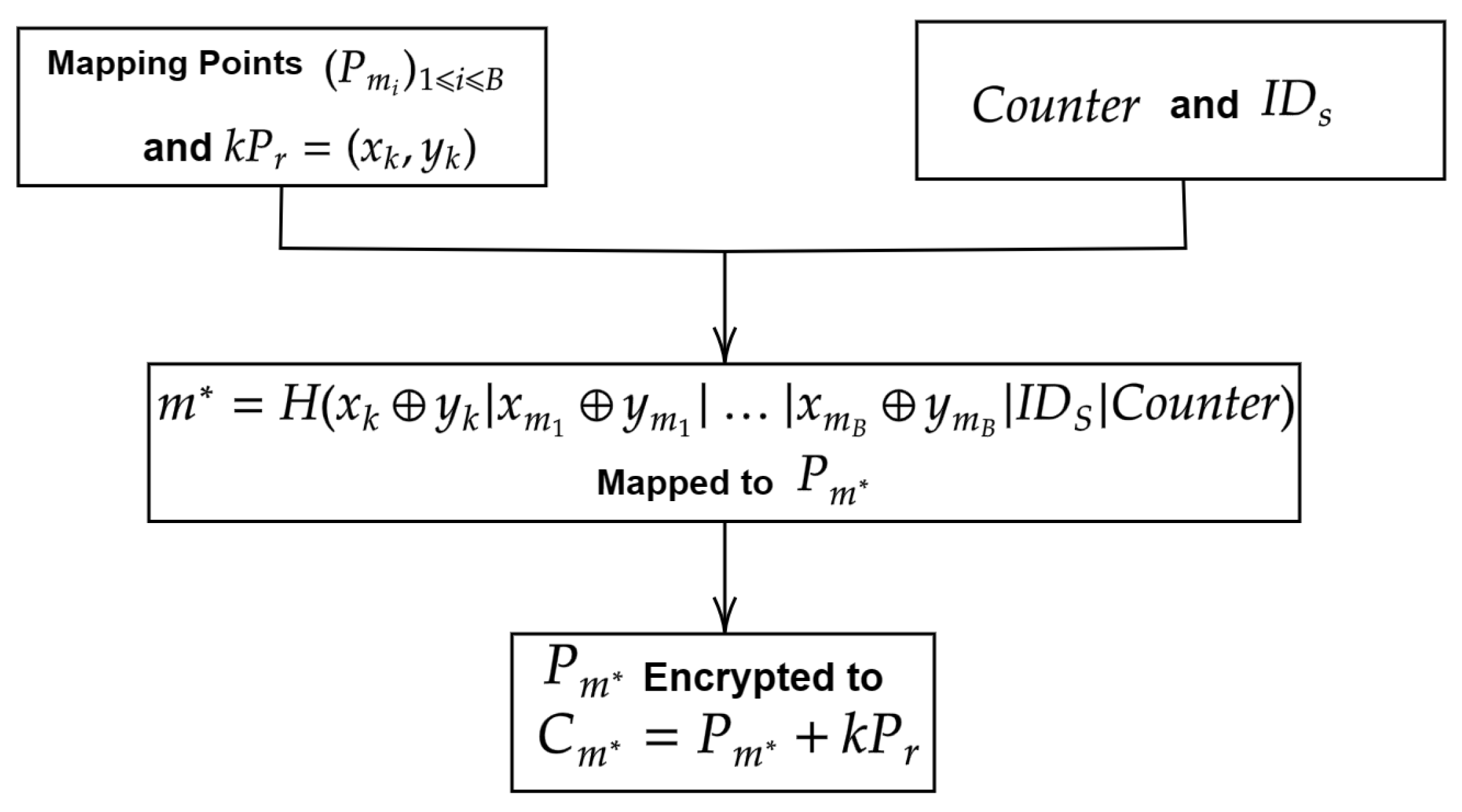
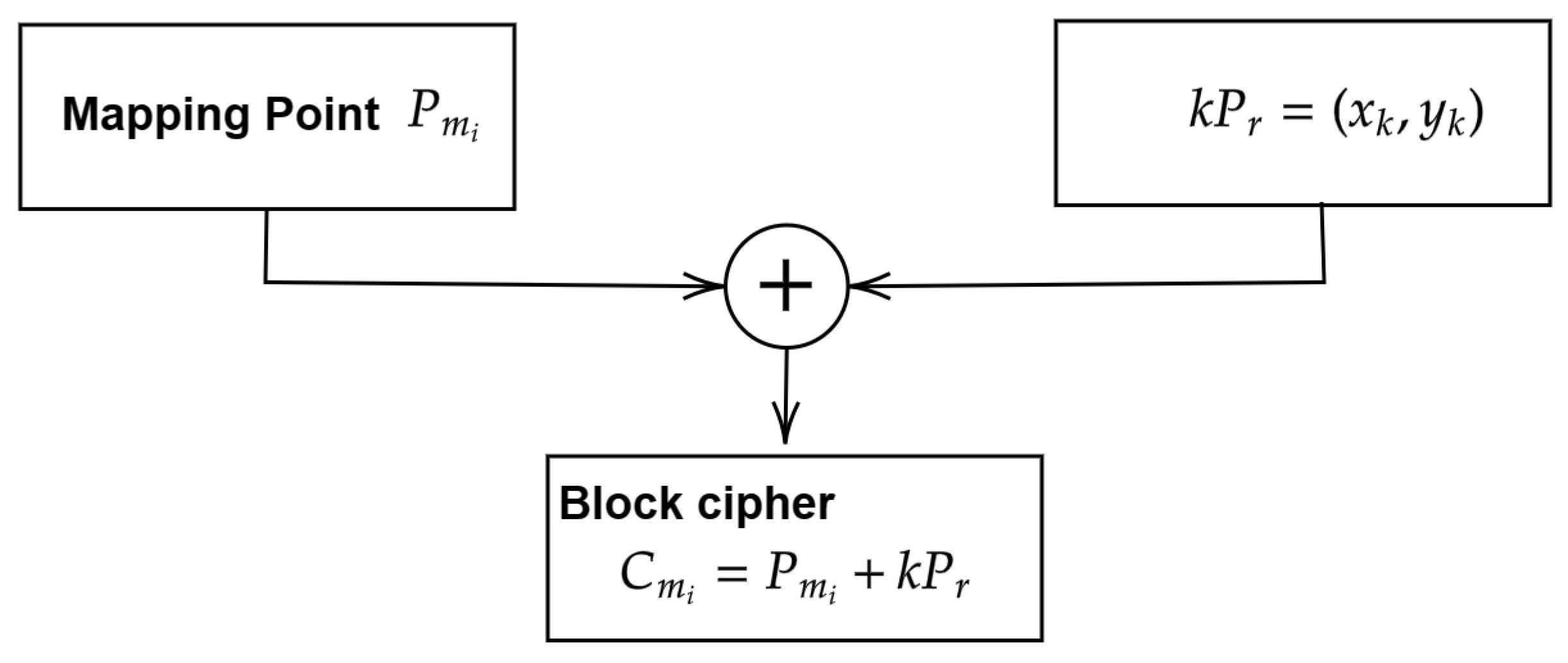
3.4. Encryption
| Algorithm 4 Proposed encryption scheme |
|
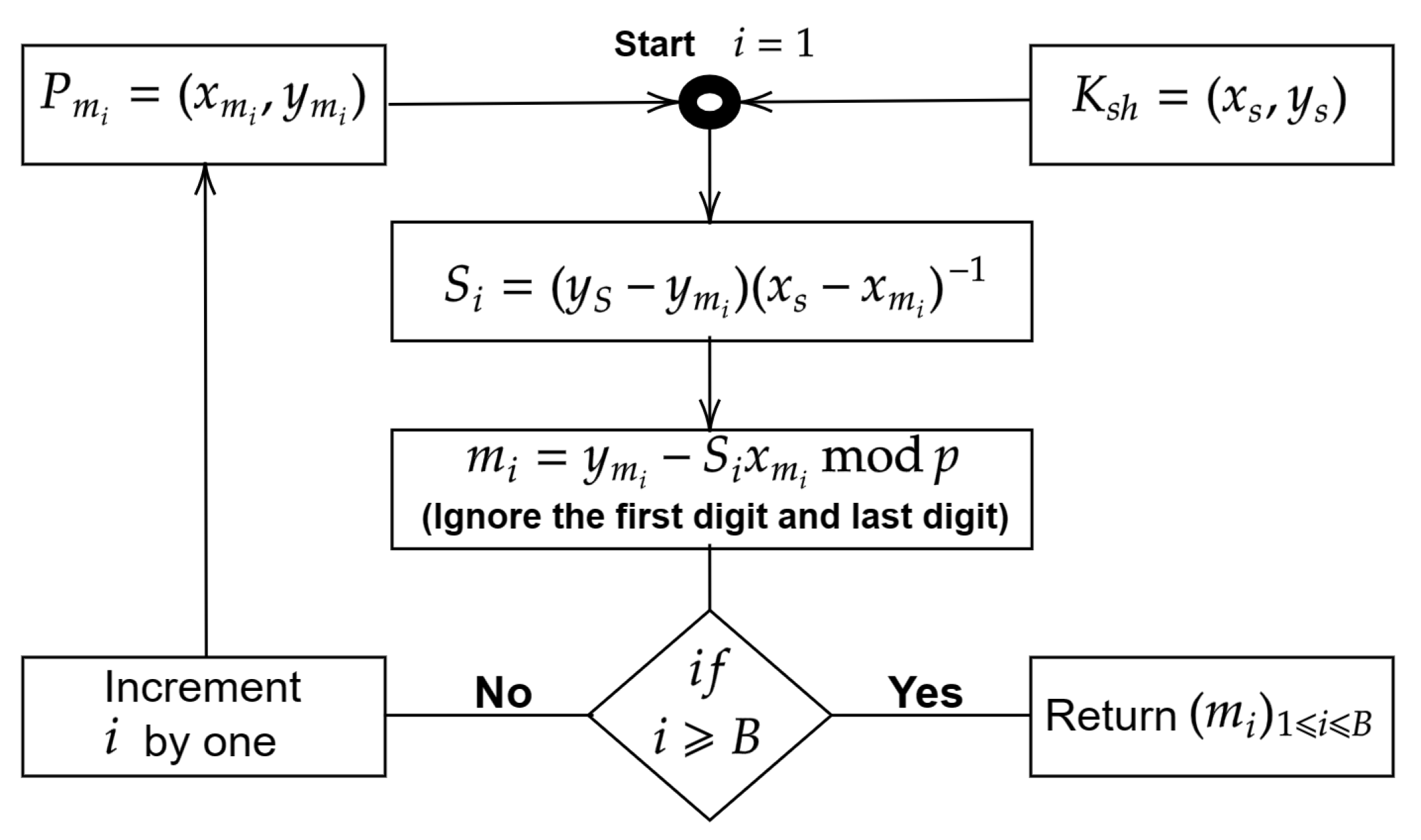
3.5. Decryption
3.6. Reverse Mapping and Decoding Process
| Algorithm 5 Decryption algorithm |
|
| Algorithm 6 Reverse mapping and decoding |
|
4. Performance Evaluation
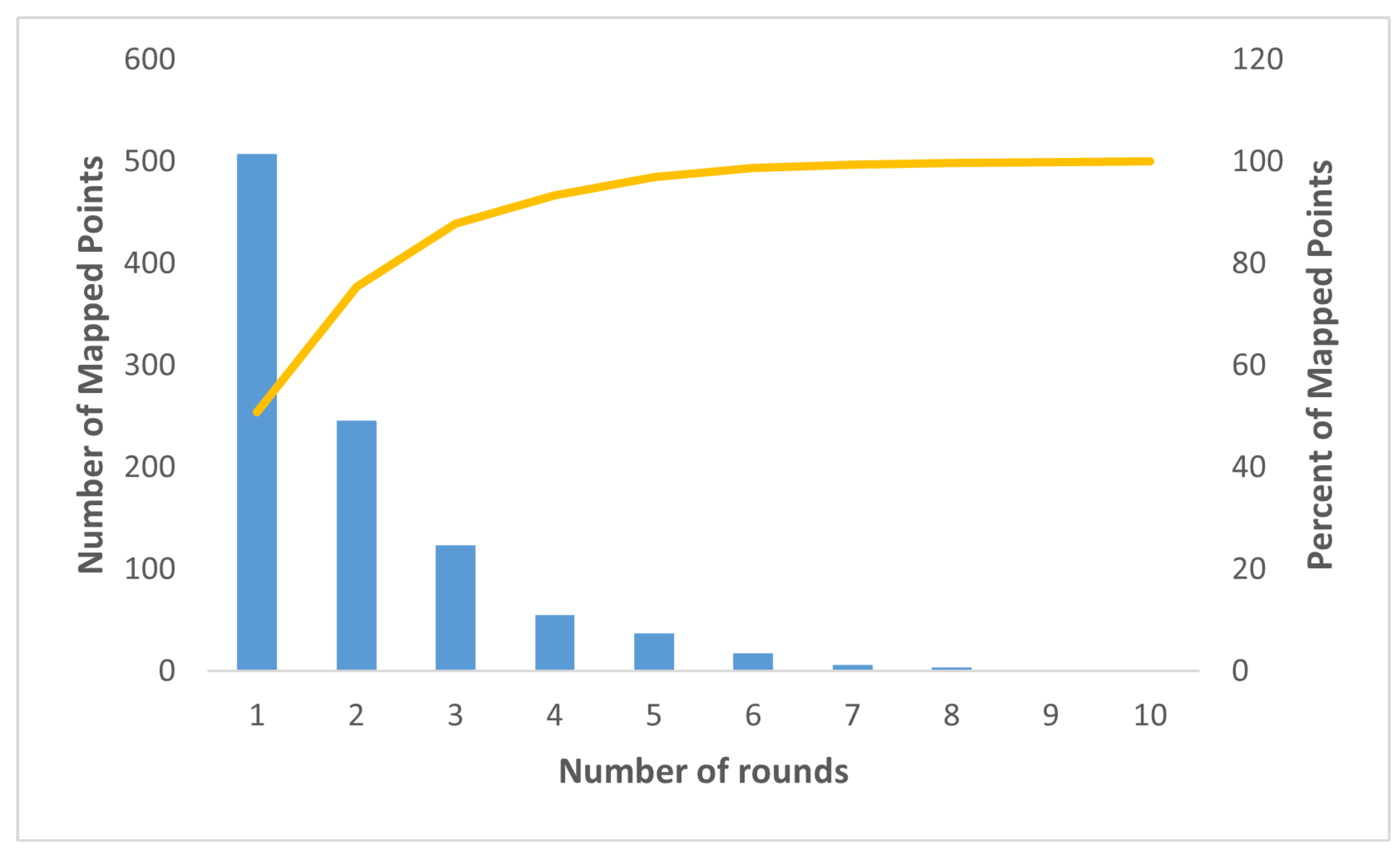
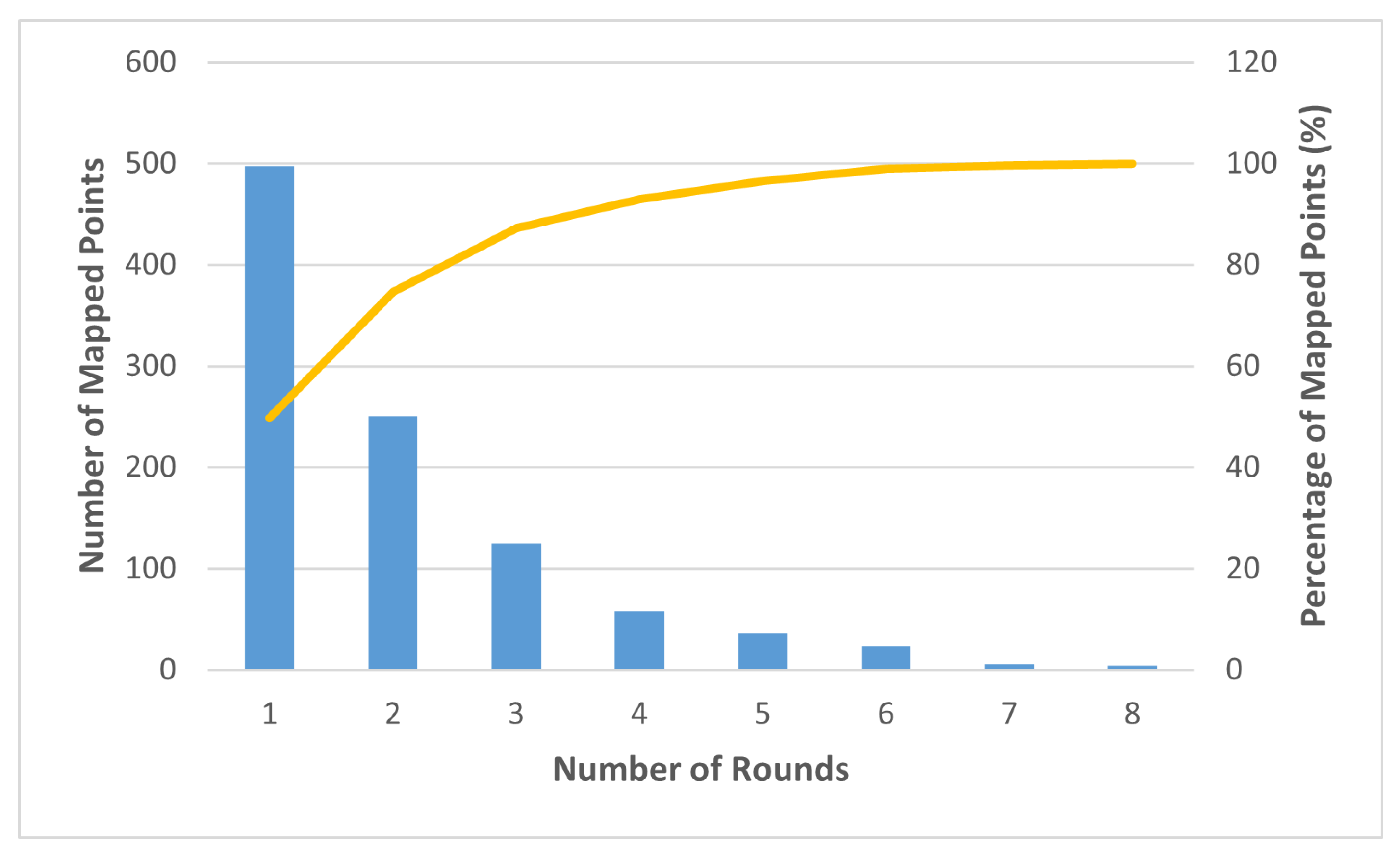
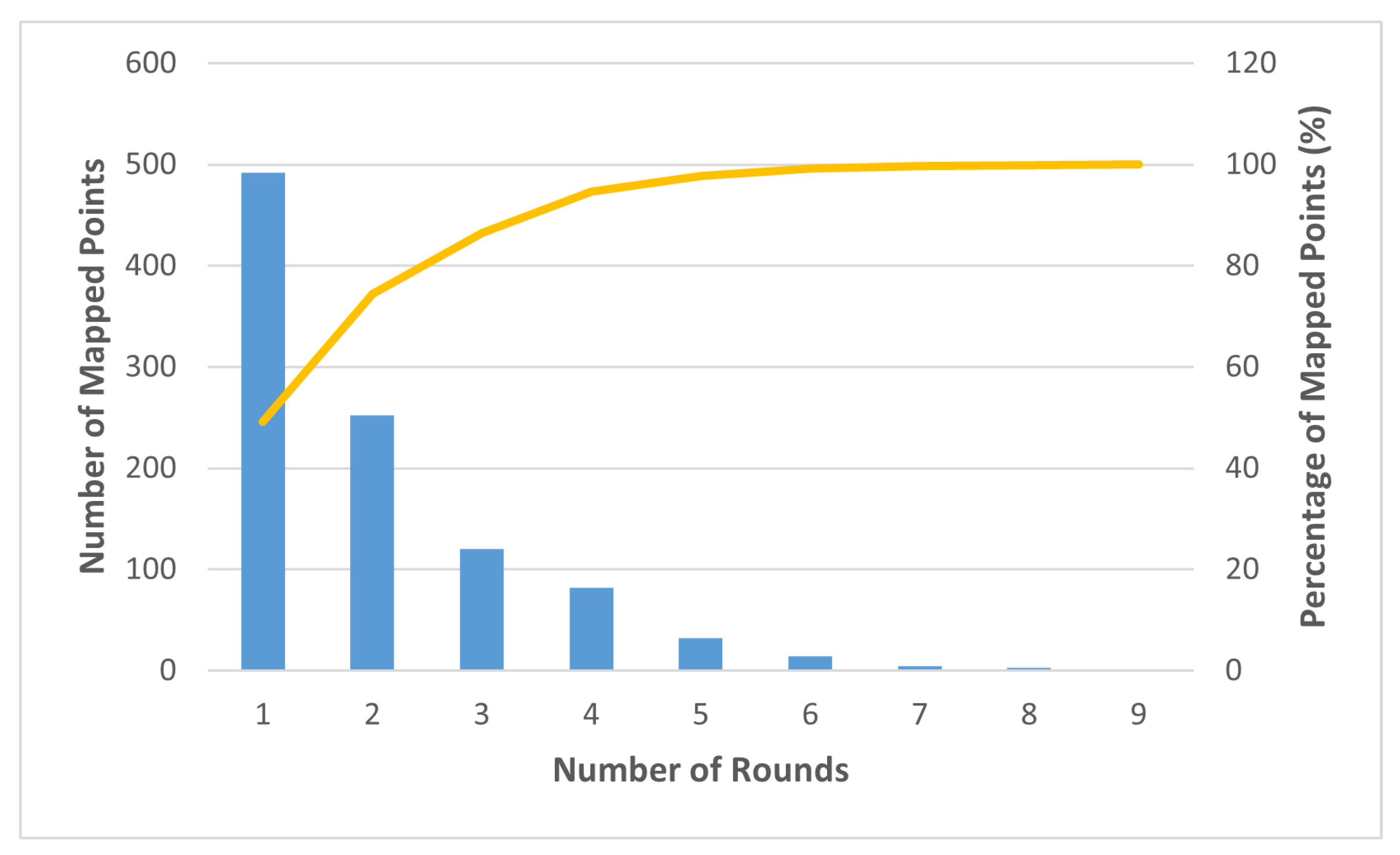
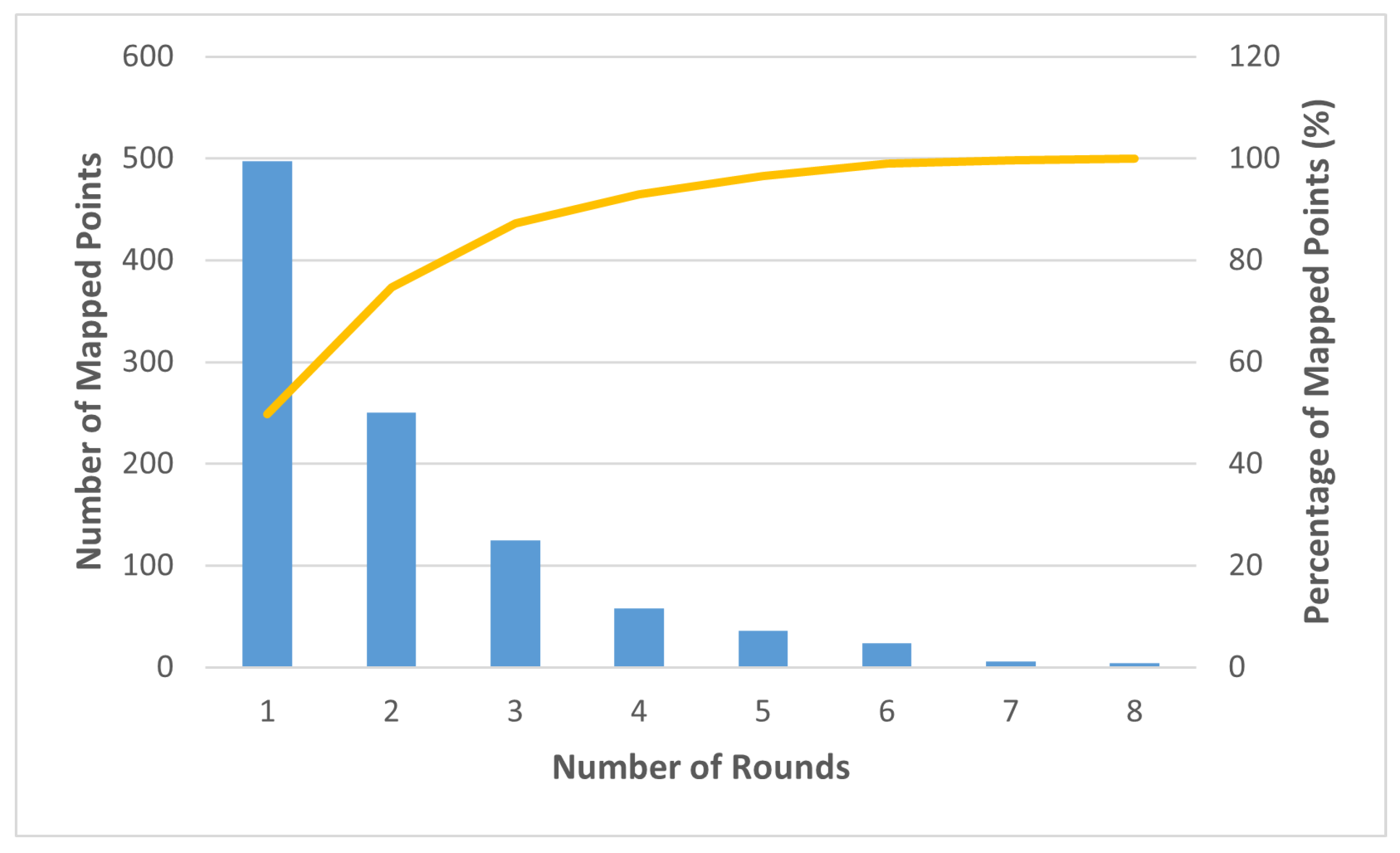
4.1. Overlapping Problem
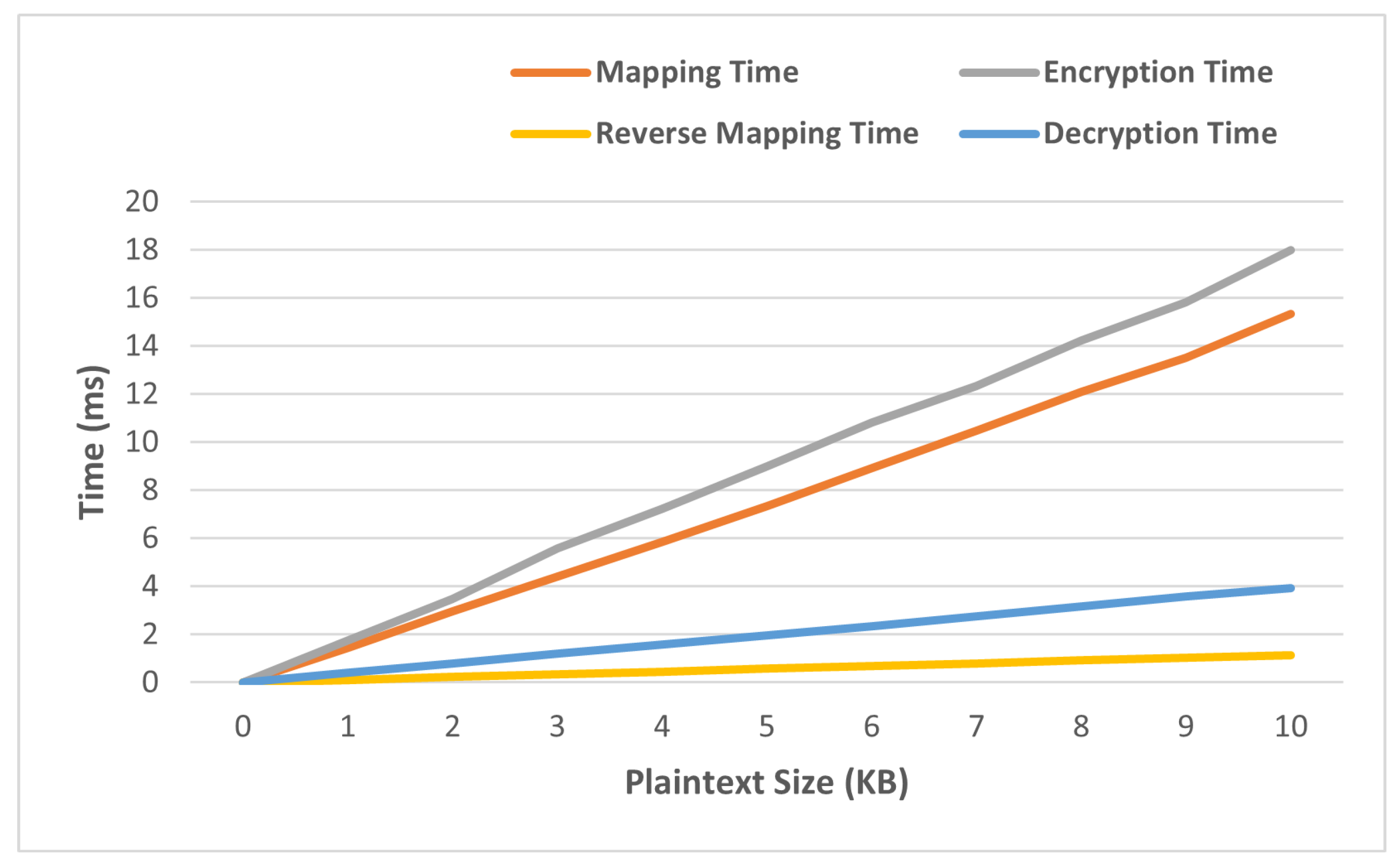
4.2. Complexity Analysis
5. Sensitivity Assessment and Security Analysis
5.1. Sensitivity Assessment
5.1.1. Key Sensitivity Analysis
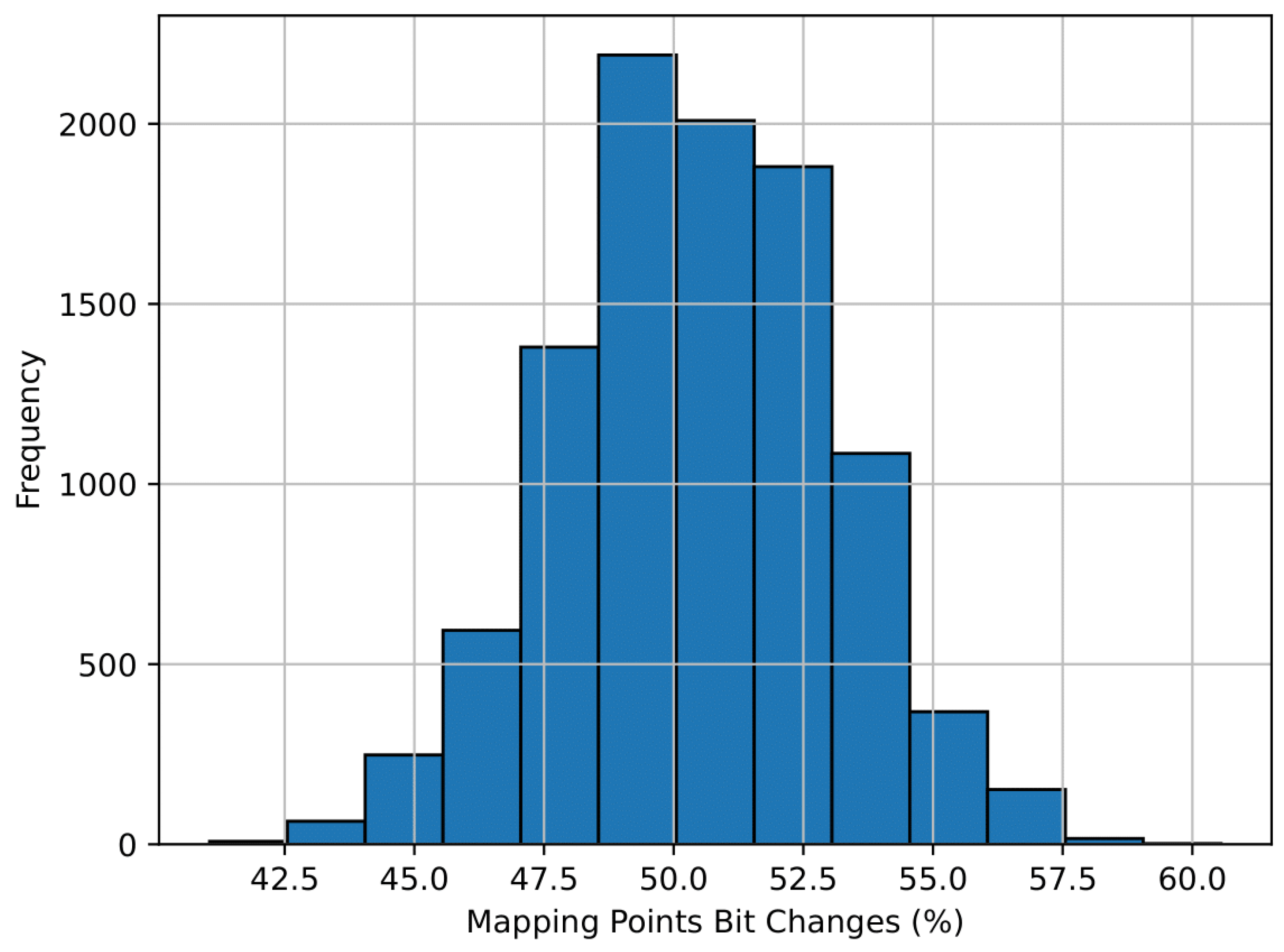
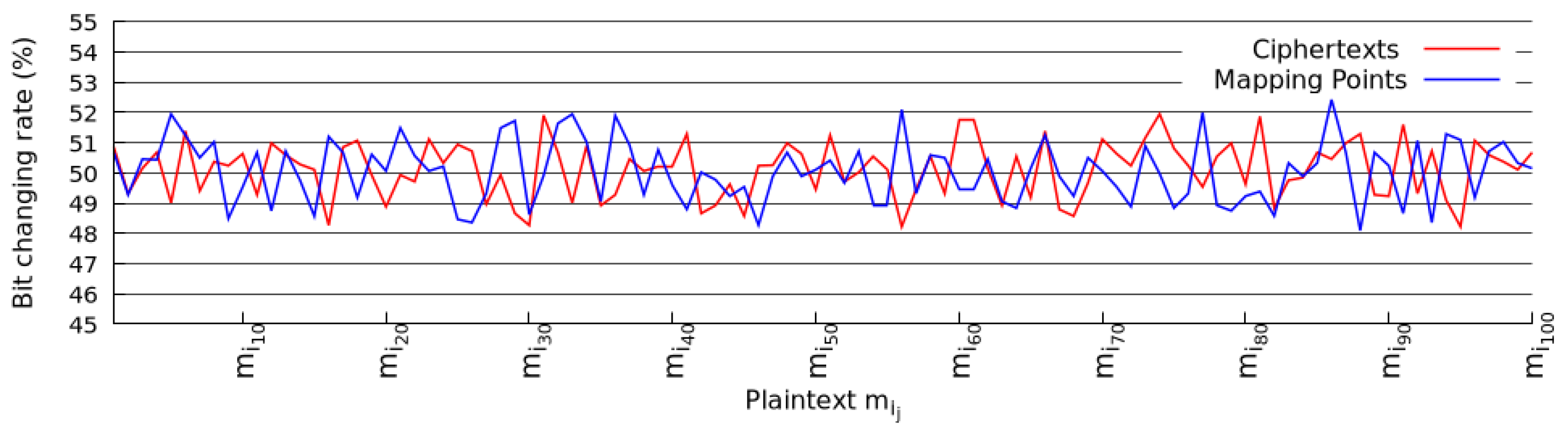
5.1.2. Plaintext Sensitivity Analysis
5.1.3. Statistical Analysis
5.2. Security Analysis
5.2.1. Key Spacing Analysis and Brute Force
5.2.2. Known Plaintext Attack (KPA)
5.2.3. Ciphertext-Only Attack (COA)
5.2.4. Chosen-Plaintext Attack (CPA)
- The challenger generates a key pair with a security parameter k, shares the public key with the adversary, and keeps the private key .
- The adversary requests ciphertexts for a polynomially bounded number of chosen plaintexts and/or performs other operations.
- The adversary submits two distinct chosen plaintexts, and , with the same size.
- The challenger selects a bit randomly, and sends the ciphertext back to the adversary.
- The adversary can conduct any desired number of additional computations or encryptions.
- In the end, the adversary outputs a conjecture for the value of b.
5.2.5. Malleability
5.2.6. Replay Attack (RA)
5.2.7. Chosen-Ciphertext Attack (CCA)
- The challenger generates a key pair with a security parameter k, shares the public key with the adversary, and keeps the private key .
- The adversary requests ciphertexts for a polynomially bounded number of chosen plaintexts and/or performs other operations.
- The adversary requests the decryption of a polynomially bounded number of chosen ciphertexts and/or performs other operations.
- The adversary submits two distinct chosen ciphertexts, and .
- The challenger selects a bit randomly, and sends the decryption back to the adversary.
- The adversary can conduct any desired number of additional computations or encryptions.
- In the end, the adversary outputs a conjecture for the value of b.
5.2.8. Side-Channel Attacks
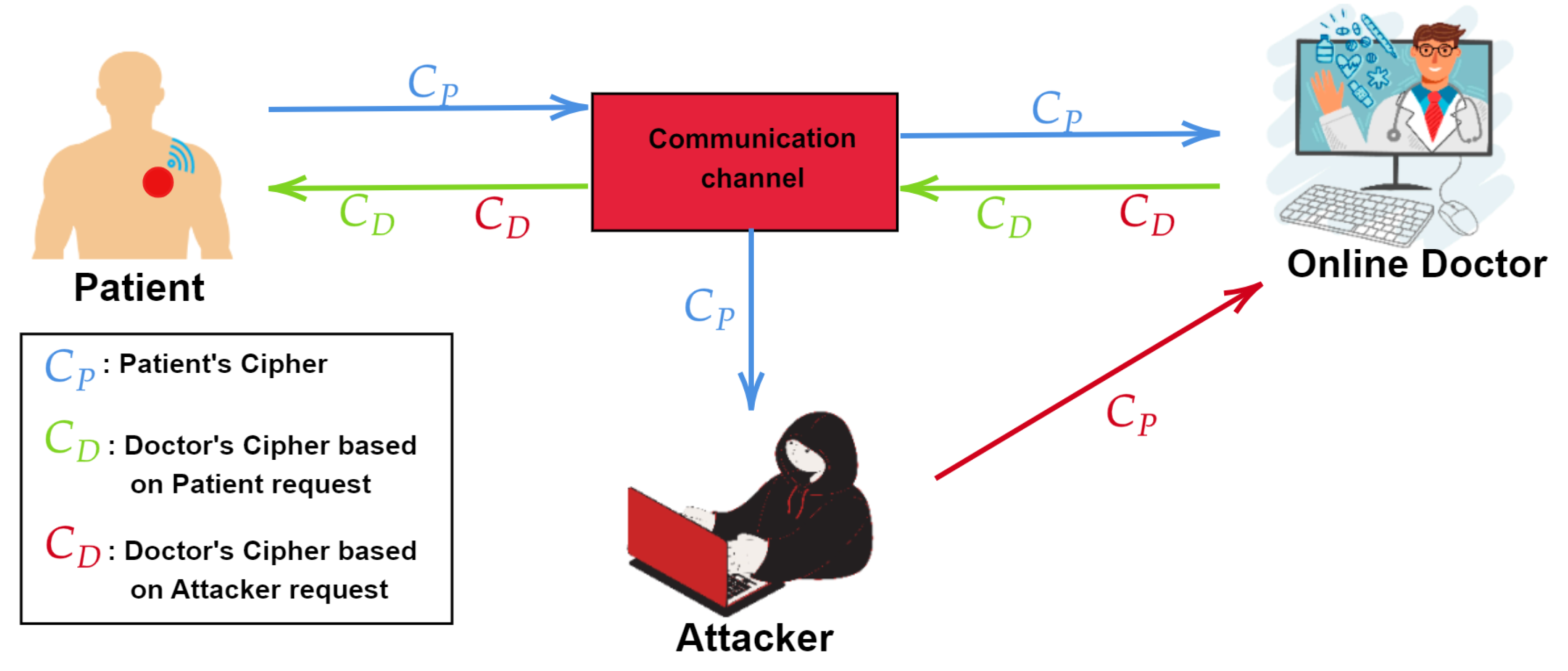
5.2.9. Man-in-the-Middle Attack (MitM)
6. Implementation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| ECC | elliptic curve cryptography |
| EC | elliptic curve |
| NIST | National Institute of Standards and Technology |
| ECDHP | elliptic curve Diffie–Hellman protocol |
| ECDSA | elliptic curve digital signature algorithm |
| ECIES | elliptic curve integrated encryption scheme |
| CPA | chosen-plaintext attack |
| CCA | chosen-ciphertext attack |
| RA | replay attack |
| ECDLP | elliptic discrete logarithm problem |
| AES | advanced encryption standard |
| IND-CPA | indistinguishability under chosen-plaintext attack |
| IND-CCA | indistinguishability under chosen-ciphertext attack |
| MitM | man-in-the-middle |
| STS | station to station |
| KPA | known-plaintext attack |
| COA | ciphertext-only attack |
References
- Mid-Year Update to the 2023 SonicWall Cyber Threat Report | Threat Intelligence. Available online: https://www.sonicwall.com/2023-mid-year-cyber-threat-report/ (accessed on 1 May 2024).
- IBM. Cost of a Data Breach 2023. Available online: https://www.ibm.com/reports/data-breach (accessed on 1 May 2024).
- Gura, N.; Patel, A.; Wander, A.; Eberle, H.; Shantz, S.C. Comparing elliptic curve cryptography and RSA on 8-Bit CPUs. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2004; Volume 3156, pp. 119–132. [Google Scholar] [CrossRef]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- 1363-2000; IEEE Standard Specifications for Public-Key Cryptography. IEEE: Piscataway, NJ, USA, 2000.
- King, B. Mapping an Arbitrary Message to an Elliptic Curve when Defined over GF (2n). Int. J. Netw. Secur. 2009, 8, 169–176. [Google Scholar]
- Gayoso, V.; Hernandez, L.; Sanchez, C. A survey of the elliptic curve integrated encryption scheme. J. Comput. Sci. Eng. 2010, 2, 7–13. [Google Scholar]
- Almajed, H.; Almogren, A. A secure and efficient ECC-based scheme for edge computing and internet of things. Sensors 2020, 20, 6158. [Google Scholar] [CrossRef]
- Barker, E.; Chen, L.; Keller, S.; Roginsky, A.; Vassilev, A.; Davis, R. Recommendation for Pair-Wise Key-Establishment Schemes Using Discrete Logarithm Cryptography; Technical Report; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2017.
- Ullah, S.; Zheng, J.; Din, N.; Hussain, M.T.; Ullah, F.; Yousaf, M. Elliptic Curve Cryptography; Applications, challenges, recent advances, and future trends: A comprehensive survey. Comput. Sci. Rev. 2023, 47, 100530. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Miles, S.; Barker, E.; Leigh, S.; Levenson, M.; Vangel, M.; Banks, D.; Heckert, A.; et al. SP800-22: A statistical test suite for random and pseudorandom number generators for cryptographic applications. In National Institute of Standards and Technology; National Institute of Standards and Technology: Gaithersburg, MA, USA, 2010; Volume 800, Issue April. [Google Scholar] [CrossRef]
- Hankerson, D.; Menezes, A.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer Professional Computing; Springer: New York, NY, USA, 2006. [Google Scholar]
- Sengupta, A.; Ray, U.K. Message mapping and reverse mapping in elliptic curve cryptosystem. Secur. Commun. Netw. 2016, 9, 5363–5375. [Google Scholar] [CrossRef]
- Padma, B.; Chandravathi, D.; Roja, P.P. Encoding And Decoding of a Message in the Implementation of Elliptic Curve Cryptography using Koblitz’s Method. (IJCSE) Int. J. Comput. Sci. Eng. 2010, 2, 1904–1907. [Google Scholar]
- Srinath, M.S.; Chandrasekaran, V. Elliptic Curve Cryptography using Mirrored Elliptic Curves over Prime Fields. In Proceedings of the International Conference on Information and Knowledge Engineering, Las Vegas, NV, USA, 12–15 July 2010; pp. 271–277. [Google Scholar]
- Koblitz, N. A Course in Number Theory and Cryptography; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1994; Volume 114. [Google Scholar]
- Boneh, D.; Franklin, M. Identity-based encryption from the weil pairing. SIAM J. Comput. 2003, 32, 2003. [Google Scholar] [CrossRef]
- Icart, T. How to Hash into Elliptic Curves. In Advances in Cryptology, Proceedings of the CRYPTO 2009, 29th Annual International Cryptology Conference, Santa Barbara, CA, USA, 16–20 August 2009; Proceedings; Halevi, S., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5677, pp. 303–316. [Google Scholar] [CrossRef]
- Vigila, S.M.C.; Muneeswaran, K. Implementation of text based cryptosystem using elliptic curve cryptography. In Proceedings of the 2009 First International Conference on Advanced Computing, Chennai, India, 13–15 December 2009. [Google Scholar] [CrossRef]
- Kumar, D.S. Encryption of Data Using Elliptic Curve over Finite Fields. Int. J. Distrib. Parallel Syst. 2012, 3, 301–308. [Google Scholar] [CrossRef]
- Reyad, O. Text Message Encoding Based on Elliptic Curve Cryptography and a Mapping Methodology. Inf. Sci. Lett. 2018, 7, 7–11. [Google Scholar] [CrossRef]
- Amounas, F.; El Kinani, E. Fast mapping method based on matrix approach for elliptic curve cryptography. Int. J. Inf. Netw. Secur. (IJINS) 2012, 1, 54–59. [Google Scholar]
- Kamalakannan, V.; Tamilselvan, S. Security Enhancement of Text Message Based on Matrix Approach Using Elliptical Curve Cryptosystem. Procedia Mater. Sci. 2015, 10, 489–496. [Google Scholar] [CrossRef]
- Almajed, H.N.; Almogren, A.S. SE-Enc: A Secure and Efficient Encoding Scheme Using Elliptic Curve Cryptography. IEEE Access 2019, 7, 175865–175878. [Google Scholar] [CrossRef]
- Reegan, A.S.; Kabila, V. Highly Secured Cluster Based WSN Using Novel FCM and Enhanced ECC-ElGamal Encryption in IoT. Wirel. Pers. Commun. 2021, 118, 1313–1329. [Google Scholar] [CrossRef]
- Moosavi, S.R.; Izadifar, A. End-to-End Security Scheme for E-Health Systems Using DNA-Based ECC. In Silicon Valley Cybersecurity Conference; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar] [CrossRef]
- Tiwari, H.D.; Kim, J.H. Novel Method for DNA-Based Elliptic Curve Cryptography for IoT Devices. ETRI J. 2018, 40, 396–409. [Google Scholar] [CrossRef]
- Das, S.; Namasudra, S. A Novel Hybrid Encryption Method to Secure Healthcare Data in IoT-enabled Healthcare Infrastructure. Comput. Electr. Eng. 2022, 101, 107991. [Google Scholar] [CrossRef]
- Lahraoui, Y.; Amal, Y.; Lazaar, S. Definition and Implementation of an Elliptic Curve Cryptosystem using a New Message Mapping Scheme. In Proceedings of the 3rd International Conference on Networking, Information Systems & Security, San Jose, CA, USA, 9–12 March 2020. [Google Scholar] [CrossRef]
- Brier, E.; Coron, J.S.; Icart, T.; Madore, D.; Randriam, H.; Tibouchi, M. Efficient indifferentiable hashing into ordinary elliptic curves. In Advances in Cryptology—CRYPTO 2010: 30th Annual Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 237–254. [Google Scholar]
- Berlekamp, E.R. Algebraic Coding Theory. In Negacyclic Codes; World Scientific: Singapore, 1968; pp. 207–217. [Google Scholar]
- Burgess, D.A. The distribution of quadratic residues and non-residues. Mathematika 1957, 4, 106–112. [Google Scholar] [CrossRef]
- Webster, A.F.; Tavares, S.E. On the Design of S-Boxes. In Advances in Cryptology—CRYPTO’85 Proceedings; Springer: Berlin/Heidelberg, Germany, 1986; Volume 218. [Google Scholar] [CrossRef]
- Seyedzadeh, S.M.; Norouzi, B.; Mosavi, M.R.; Mirzakuchaki, S. A novel color image encryption algorithm based on spatial permutation and quantum chaotic map. Nonlinear Dyn. 2015, 81, 511–529. [Google Scholar] [CrossRef]
- Barker, E.; Barker, W.C. Recommendation for Key Management: Part 2—Best Practices for Key Management Organizations; National Institute of Standards and Technology NIST: Gaithersburg, MA, USA, 2019. Available online: https://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.800-57pt2r1.pdf (accessed on 1 May 2024).
- Chen, L.; Moody, D.; Regenscheid, A.; Robinson, A.; Randall, K. Recommendations for Discrete Logarithm-Based Cryptography. 2023. Available online: https://csrc.nist.gov/pubs/sp/800/186/final (accessed on 1 May 2024).
- Dolev, D.; Dwork, C.; Naor, M. Non-malleable cryptography. In Proceedings of the Twenty-Third Annual ACM Symposium on Theory of Computing, New Orleans, LA, USA, 6–8 May 1991; pp. 542–552. [Google Scholar]
- Halperin, D.; Clark, S.S.; Fu, K.; Heydt-Benjamin, T.S.; Defend, B.; Kohno, T.; Ransford, B.; Morgan, W.; Maisel, W.H. Pacemakers and implantable cardiac defibrillators: Software radio attacks and zero-power defenses. In Proceedings of the 2008 IEEE Symposium on Security and Privacy, Oakland, CA, USA, 18–22 May 2008. [Google Scholar] [CrossRef]
- Zhou, Y.; Feng, D. Side-Channel Attacks: Ten Years after Its Publication and the Impacts on Cryptographic Module Security Testing; IACR Eprint Archive: Lyon, France, 2005; Available online: http://eprint.iacr.org/2005/388 (accessed on 1 May 2024).
- Socha, P.; Miškovský, V.; Novotný, M. A Comprehensive Survey on the Non-Invasive Passive Side-Channel Analysis. Sensors 2022, 22, 8096. [Google Scholar] [CrossRef]
- Vanhoef, M.; Ronen, E. Dragonblood: Analyzing the Dragonfly Handshake of WPA3 and EAP-pwd. Cryptology ePrint Archive, Paper 2019/383; IACR Eprint Archive: Lyon, France, 2019; Available online: https://eprint.iacr.org/2019/383 (accessed on 1 May 2024).
- Gabsi, S.; Kortli, Y.; Beroulle, V.; Kieffer, Y.; Hamdi, B. Proposal of a lightweight differential power analysis countermeasure method on elliptic curves for low-cost devices. Multimed. Tools Appl. 2024. [Google Scholar] [CrossRef]
- Pavithran, D.; Shaalan, K. Towards Creating Public Key Authentication for IoT Blockchain. In Proceedings of the ITT 2019—Information Technology Trends: Emerging Technologies Blockchain and IoT, Ras Al Khaimah, United Arab Emirates, 20–21 November 2019. [Google Scholar] [CrossRef]
- Kumagai, K.; Kakei, S.; Shiraishi, Y.; Saito, S. Distributed Public Key Certificate-Issuing Infrastructure for Consortium Certificate Authority Using Distributed Ledger Technology. Secur. Commun. Netw. 2023. [Google Scholar] [CrossRef]
- Wendlandt, D.; Andersen, D.G.; Perrig, A. Perspectives: Improving SSH-Style Host Authentication with Multi-Path Probing. In Proceedings of the 2008 USENIX Annual Technical Conference, USENIX 2008, San Diego, CA, USA, 14–19 June 2009; USENIX: Boston, MA, USA, 2008. Available online: https://www.usenix.org/legacy/event/usenix08/tech/full_papers/wendlandt/wendlandt_html/ (accessed on 1 May 2024).
- Gultekin, E.; Aktas, M.S. Real-Time Anomaly Detection Business Process for Industrial Equipment Using Internet of Things and Unsupervised Machine Learning Algorithms. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 14108 LNCS; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar] [CrossRef]
- Khudri, W. Sutanto, Implementation of Elgamal Elliptic Curve Cryptography Using Matlab. In Proceedings of the Conference on Instrumentation, Communication and Information Technology (ICICI), Bandung, Indonesia, 3–5 August 2005; Available online: https://wan.khudri.com/my_files/icici2005/paper_ICICI_2005.pdf (accessed on 1 May 2024).








| ElGamal-v1 | ElGamal-v2 | |
|---|---|---|
| Number of Point Additions | B | B |
| Number of Point Multiplications | 2 | |
| Throughput | High (considering B) | Lower (compared to B) |
| Symbol | Description |
|---|---|
| p | Big prime number. |
| Prime field . | |
| Elliptic curve defined over . | |
| G | Base point on the elliptic curve. |
| Private key of user k. | |
| Public key of user u. | |
| Secret key shared between sender (s) and receiver (r). | |
| M | The plaintext message. |
| Length of the object o (number of digits or number of characters). | |
| Hash value of x converted to an integer with digits. | |
| the n-th nested composition of the hash function H applied to the input x. | |
| B | Number of message blocks. |
| The message block number i as an integer. | |
| x, after discarding its n least significant digits. | |
| + | Employed to represent the addition of points and the addition of numbers. |
| Aligning binary values of x and y by left-padding with ‘0’s to ensure equal size, | |
| then applying bitwise XOR. |
| Elliptic Curve | Algorithm | Random Plaintext | ||
|---|---|---|---|---|
| Num. of Blocks | Num. of Mapping Rounds | Average of Mapping Rounds | ||
| secp192r1 | Ref. [16] | 435 | 858 | 1.972 |
| Ref. [24] | 435 | 891 | 2.048 | |
| This paper | 435 | 878 | 2.018 | |
| secp256r1 | Ref. [16] | 323 | 652 | 2.018 |
| Ref. [24] | 323 | 658 | 2.037 | |
| This paper | 323 | 643 | 1.990 | |
| secp384r1 | Ref. [16] | 213 | 430 | 2.018 |
| Ref. [24] | 213 | 421 | 1.976 | |
| This paper | 213 | 428 | 2.009 | |
| secp521r1 | Ref. [16] | 157 | 314 | 2 |
| Ref. [24] | 157 | 317 | 2.019 | |
| This paper | 157 | 315 | 2.006 | |
| Change Rate of | Number of Tests | ||
|---|---|---|---|
| Mapping scheme | 10000 | 50.10% | 2.57% |
| Encryption scheme | 10000 | 50.02% | 2.81% |
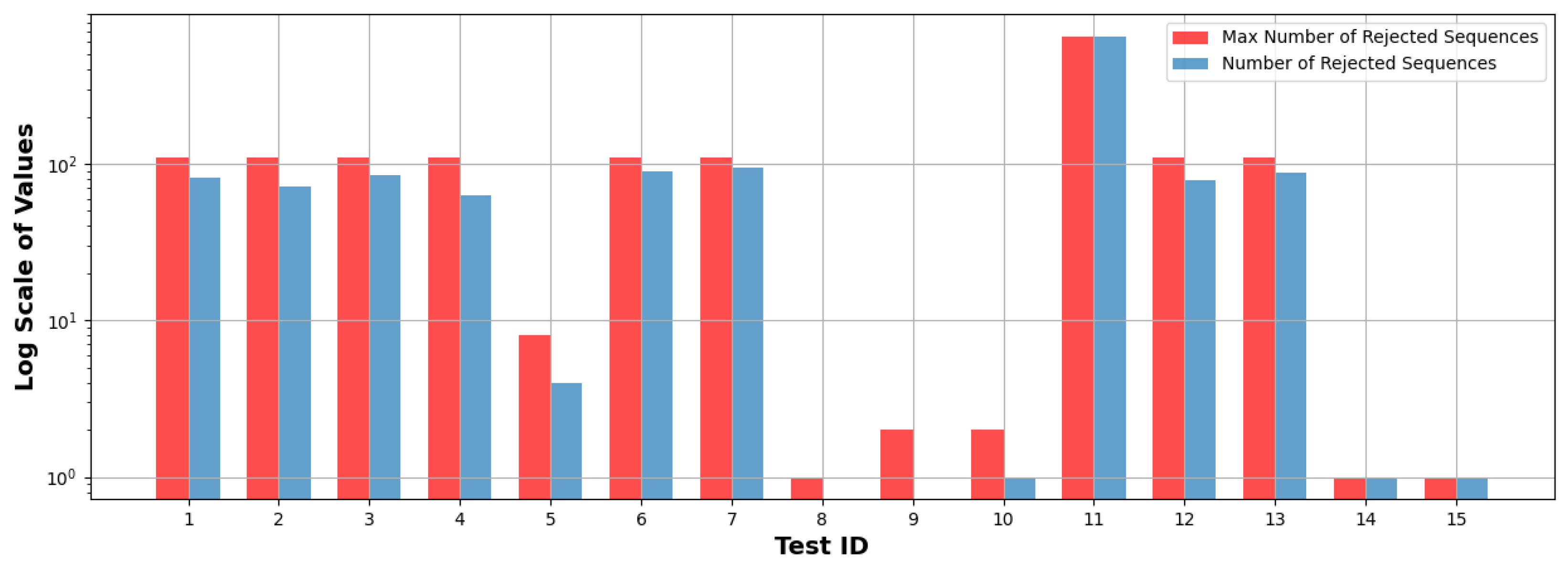
| ID | Test | Number of Sequences | Length of Sequences (bits) | Assessment |
|---|---|---|---|---|
| 01 | Monobit Test | 8198 | 2000 | Pass |
| 02 | Frequency Within Block Test | 8198 | 2000 | Pass |
| 03 | Runs Test | 8198 | 2000 | Pass |
| 04 | Longest Run of Ones in a Block Test | 8198 | 2000 | Pass |
| 05 | Binary Matrix Rank Test | 279 | 77841 | Pass |
| 06 | DFT Test | 8198 | 2000 | Pass |
| 07 | Non-Overlapping Template Matching Test | 8198 | 2000 | Pass |
| 08 | Overlapping Template Matching Test | 10 | 2056039 | Pass |
| 09 | Maurer’s Universal Test | 28 | 775698 | Pass |
| 10 | Linear Complexity Test | 21 | 1000033 | Pass |
| 11 | Serial Test | 57392 | 384 | Fail |
| 12 | Approximate Entropy Test | 8198 | 2000 | Pass |
| 13 | Cumulative Sums Test | 8198 | 2000 | Pass |
| 14 | Random Excursion Test | 10 | 2000072 | Pass |
| 15 | Random Excursion Variant Test | 10 | 2000072 | Pass |
| Scheme | Security | |||||
|---|---|---|---|---|---|---|
| KPA | COA | CPA | Malleability | Replay Attack | CCA | |
| Refs. [20,21] | ✓ | ✓ | ✓ | × | × | × |
| Refs. [13,22] | ✓ | ✓ | × | × | × | × |
| Ref. [24] | ✓ | ✓ | × | ✓ | × | × |
| This paper | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Section | Parameter | Value |
|---|---|---|
| EC Parameters | Equation’s Coefficient a | 537680305 |
| Equation’s Coefficient b | 1059676324 | |
| Prime Number p | 3946183951 | |
| Generator Point G | (1152222263, 3133703258) | |
| Generator Point Order | 3946206427 | |
| Elliptic Curve Equation: | ||
| Sender (s) Parameters | Private Key | 2441052953 |
| Random Parameter k | 655846922069 | |
| Public Key | (2365961577, 2642871165) | |
| Point | (2634041647, 2827619405) | |
| Point | (1135983708, 381375075) | |
| Shared Secret Point | (3400454298, 1533875807) | |
| Exchange | Send | Send |
| Receiver (r) Parameters | Private Key | 1429753181 |
| Public Key | (2830164285, 942020493) | |
| Shared Secret Point | (3400454298, 1533875807) | |
| Point | (1135983708, 381375075) | |
| Block | Decimal Value | Encoded Value | Mapping Point |
|---|---|---|---|
| 4420217 | 6419119 | (1851134498, 2848058768) | |
| 7369839 | 1148610 | (3450323358, 1700398742) | |
| 6779489 | 7795872 | (1240965444, 3560781816) | |
| 7366777 | 433373 | (2171276352, 3891369897) |
| Block | Decimal Value | Encoded Value | Mapping Point |
|---|---|---|---|
| 4420217 | 4346998 | (2024477685, 3189489356) | |
| 7369839 | 3285019 | (2313133495, 3782223150) | |
| 6779489 | 5591673 | (1363974206, 480205177) | |
| 7366777 | 2439684 | (3918942662, 300263470) |
| Round | Equation (9) Has a Solution | ||
|---|---|---|---|
| 1 | 143469980 | 2389772309 | No, |
| 2 | 143469981 | 1029763873 | Yes, |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lahraoui, Y.; Lazaar, S.; Amal, Y.; Nitaj, A. Securing Data Exchange with Elliptic Curve Cryptography: A Novel Hash-Based Method for Message Mapping and Integrity Assurance. Cryptography 2024, 8, 23. https://doi.org/10.3390/cryptography8020023
Lahraoui Y, Lazaar S, Amal Y, Nitaj A. Securing Data Exchange with Elliptic Curve Cryptography: A Novel Hash-Based Method for Message Mapping and Integrity Assurance. Cryptography. 2024; 8(2):23. https://doi.org/10.3390/cryptography8020023
Chicago/Turabian StyleLahraoui, Younes, Saiida Lazaar, Youssef Amal, and Abderrahmane Nitaj. 2024. "Securing Data Exchange with Elliptic Curve Cryptography: A Novel Hash-Based Method for Message Mapping and Integrity Assurance" Cryptography 8, no. 2: 23. https://doi.org/10.3390/cryptography8020023
APA StyleLahraoui, Y., Lazaar, S., Amal, Y., & Nitaj, A. (2024). Securing Data Exchange with Elliptic Curve Cryptography: A Novel Hash-Based Method for Message Mapping and Integrity Assurance. Cryptography, 8(2), 23. https://doi.org/10.3390/cryptography8020023







