Faster Spiral: Low-Communication, High-Rate Private Information Retrieval

Abstract

Private information retrieval (PIR) enables a client to retrieve a specific element from a server’s database without disclosing the index that was queried. This work introduces three improvements to the efficient single-server PIR protocol Spiral. We found that performing a modulus switching towards expanded ciphertexts can improve the server throughput. Secondly, we apply two techniques called the composite $\mathsf{NTT}$ algorithm and approximate decomposition to Spiral to further improve it. We conduct comprehensive experiments to evaluate the concrete performance of our protocol, and the results confirm an approximately 1.7 times faster overall throughput than Spiral.

1. Introduction

The private information retrieval (PIR) protocol [1] involves a server holding a database $\mathsf{DB}$ and a client wishing to retrieve a record from the $\mathsf{DB}$ without revealing which record they are querying. PIR protocols are widely applied in various domains, including but not limited to anonymous messaging [2,3], private contact tracing [4], safe browsing [5,6], and more [7].

Chor et al. [1] introduced the concept of PIR and in recent years, homomorphic encryption (HE)-based PIR protocols have become highly efficient. Homomorphic encryption enables the hiding of the query message but performs meaningful computations. Specifically, the server holds a database $\mathsf{DB}$ and the client encrypts an index to query the database homomorphically, ensuring that the response is encrypted for the client to decrypt locally.

Kushilevitz and Ostrovsky [8] proposed the first construction of single-server PIR. Their construction applies a linearly homomorphic encryption scheme to fetch records. The database of N records is structured as a v-dimension hypercube. The communication of this construction is roughly $N^{1/v}{F}^{v-1}$ where F is the expansion factor of the encryption scheme. The server has to perform roughly $N·F^{v-1}$ homomorphic operations to answer each query from the client.

To instantiate Kushilevitz–Ostrovsky construction, PIR protocols in recent years have applied a well-known, highly efficient and post-quantum safe scheme called Ring Learning with Errors ($\mathsf{RLWE}$) encryption. For example, XPIR [9] instantiates $v=2$ to achieve a balance between communication and computation costs. However, in this case, the communication reaches tens of MB per online query for a database of hundreds of MB, for the client has to upload $2\sqrt{N}$ $\mathsf{RLWE}$ ciphertexts. Large comunication limits the practical deployment of PIR.

This issue was not solved until Chen et al. [3] introduced an $\mathsf{RLWE}$ expansion algorithm. They found that automorphism can eliminate some interval coefficients of the message polynomial in $\mathsf{RLWE}$ ciphertext. The coefficients of the polynomial can also be rotated by i positions if this $\mathsf{RLWE}$ ciphertext is multiplied by a monomial $x^{-i}$. By iteratively running the automorphism algorithm and rotation (on coefficients), the server obtains many $\mathsf{RLWE}$ ciphertexts that encrypt each coefficient of the input message polynomial. The $\mathsf{RLWE}$ expansion algorithm greatly reduces the online query size to around tens of KB, which is roughly one thousand times smaller than prior construction. As a trade-off, the server needs to store some client-dependent key-switching keys for these automorphisms.

Subsequently, MulPIR [10], OnionPIR [11], and Spiral [12] additionally use fully homomorphic encryption [13] to further reduce the communication cost by a factor of F, and improve the server throughput, i.e., database size divided by server response time. For example, the query size of Spiral is only around 14 KB, and the server throughput reaches more than 300 MB/s. Spiral leverages a series of works, including the $\mathsf{RLWE}$ expansion algorithm [3], Kushilevitz–Ostrovsky’s dimension folding [8] as well as the Gentry–Halevi blueprint [14], and $\mathsf{RGSW}$ multiplication [15], and thus outperforms previous solutions, e.g., SealPIR [3], MulPIR [10], and OnionPIR [11]. The workflow in Spiral primarily includes a query expansion algorithm and two folding algorithms. Specifically, the server expands the query to a sequence of $\mathsf{RLWE}$ ciphertexts and a sequence of $\mathsf{RGSW}$ ciphertexts. The $\mathsf{RLWE}$ ciphertexts are used for multiplying the database $\mathsf{DB}$, which is inherent. The $\mathsf{RGSW}$ multiplication is for subsequent folding and ultimately returns a smaller response.

Spiral is applicable to a wide range of scenarios, e.g., small and large records, and small and large databases. It also has significant small communication and client computation, and the highest rate, where rate refers to plaintext size divided by response ciphertext size. This allows it to be deployed in most application scenarios where private information retrieval is required. Recently, Li et al. [16] proposed HintlessPIR and Menon and Wu [17] proposed YPIR. These two PIR protocols eliminate the need to store a hint in the client side as in Simple/Double PIR [6], and they outperform Spiral in terms of server throughput. Moreover, Luo et al. [18] proposed a novel $\mathsf{RLWE}$-based PIR protocol called KsPIR that also outperform Spiral in terms of server throughput. However, HintlessPIR [16], YPIR [17] and KsPIR [16] do not outperform Spiral in all aspects, especially in terms of communication. We believe that Spiral still offers its unique advantages for applications when the client is resource constrained, or the communication is very expensive.

Our Contribution

The start point of our work is Spiral. Following the design of Spiral [12], we propose three optimizations that can accelerate the server’s computation.

• First, we found that the noise introduced by query expansion would impact the subsequent plaintext–plaintext multiplications and ciphertext–ciphertext multiplications. Therefore, we add a modulus switching towards those expanded $\mathsf{RLWE}$ ciphertexts and $\mathsf{RGSW}$ ciphertexts. In this way, we propose a Residue Number System (RNS) variant of Spiral.
• Secondly, we apply two existing techniques called the composite $\mathsf{NTT}$ algorithm [19] and approximate decomposition [15]. The former is used to execute the $\mathsf{NTT}$ algorithm on a composite modulus of two $\mathsf{NTT}$-friendly moduli. The latter is first proposed for the torus variant of $\mathsf{LWE}$ and $\mathsf{RLWE}$ samples in TFHE [15] and it works well in our protocol.
• We implement our scheme in C++ with library [20] to evaluate the concrete performances. Particularly, our protocol confirms an approximately $1.7\times$ faster online runtime than that of Spiral. This demonstrates the practicality of our work, and more details are presented in Section 5.

Those three optimizations are easy to understanding and highly efficient. Our work improve Spiral’s server throughput while retaining its advantages, i.e., its significant small communication and client computation, and its high rate, which demonstrates its unique advantages even when compared with other recent state-of-the-art PIR protocols such as HintlessPIR [16], YPIR [17], and KsPIR [18].

2. Preliminary

2.1. Notations

We use $\mathbb{N}$, $\mathbb{Z}$, and $\mathbb{R}$ to denote the set of natural numbers, integers and real numbers, respectively. log refers to the base-2 logarithm. For a positive $k\in \mathbb{Z}$, let $\left[k\right]$ be the set of integers $\{0,\dots ,k-1\}$ and let $[a,b]$ be the set $[a,b]\cap \mathbb{Z}$ for any integers $a\le b$. For $x\in \mathbb{R}$, $\lfloor x\rfloor$ and $\lfloor x\rceil$ denote the rounding to the lower and closest integer, respectively.

In this paper, a vector is always a column vector by default and is denoted by a bold lower-case letter, e.g., $\mathit{x}$. We use $\mathit{x}\left[i\right]$ to denote the i-th element of $\mathit{x}$. For a vector $\mathit{x}$ with k entries, we start the index from 0, i.e., $\mathit{x}\left[0\right]$, and the last element is $\mathit{x}[k-1]$. For convenience, we let $\mathit{x}\left[k\right]=\mathit{x}\left[0\right]$. For a v-dimensional hypercube ($v_0\times v_1\times \cdots \times v_{v-1}$) $\mathbf{X}$, $\mathbf{X}[i_0,i_1,\cdots ,i_{v-1}]$ indexes the ${\left(i_j\right)}_{j\in \left[v\right]}$-th position, where $i_j$ starts from 0.

We use ${\parallel \mathit{x}\parallel }_{\infty }$ to denote the $l_{\infty }$-norm of $\mathit{x}$, i.e., ${\parallel \mathit{x}\parallel }_{\infty }=\underset{i}{max}\{\parallel \mathit{x}[i]\parallel \}$. For a matrix $\mathbf{X}$, ${\mathit{x}}_i$ denotes its i-th column vector without extra instructions, ${\mathbf{X}}^{\top }$ denotes the transpose of $\mathbf{X}$, ${\parallel \mathbf{X}\parallel }_{\infty }:={max}_i\{\parallel {\mathit{x}}_i{\parallel }_{\infty }\}$. Given some set S, $S^{m\times n}$ denotes the set of all $m\times n$ matrices with entries in S.

For a set A and a probability distribution $\mathcal{P}$, we use $a\leftarrow A$ to denote that a is uniformly chosen from A and $a\leftarrow \mathcal{P}$ to denote that a is chosen according to the distribution $\mathcal{P}$.

2.2. Lattice-Based Encryptions

Regev introduced the Learning with Errors ($\mathsf{LWE}$) problem [21], whose hardness can be based on some lattice problems. Consider the distribution $A_{\mathit{s},\chi }$, where $\chi$ is a distribution over $\mathbb{Z}$ and $\mathit{s}\in {\mathbb{Z}}_q^d$ for modulus $q\in \mathbb{N}$. A sample from the distribution $A_{\mathit{s},\chi }$ is of the form $(b,\mathit{a})\in {\mathbb{Z}}_q\times {\mathbb{Z}}_q^d$, where $\mathit{a}\leftarrow {\mathbb{Z}}_q^d$, $e\leftarrow \chi$ and $b=\langle \mathit{a},\mathit{s}\rangle +e\mathrm{mod}q$.

Definition 1

($\mathsf{LWE}$). Let $\chi$ be a distribution over $\mathbb{Z}$, and let $q\ge 2$ be an integer modulus. The decision version of $\mathsf{LWE}$ is given m samples with the form of $(b^{\prime },{\mathit{a}}^{\prime })\in {\mathbb{Z}}_q\times {\mathbb{Z}}_q^n$ and decides whether these pairs are from the uniform distribution or $A_{\mathit{s},\chi }$.

Another important variant is $\mathsf{LWE}$ in the ring setting, known as the Ring Learning with Errors ($\mathsf{RLWE}$) problem [22]. In this work, we only focus on the polynomial ring $\mathcal{R}=\mathbb{Z}\left[X\right]/(X^d+1)$, where d is a power of 2, also known as the $2d$-th cyclotomic ring.

For the $\mathsf{RLWE}$ problem, now we present the distribution $A_{s,\chi }$. Let $\chi$ be a distribution over $\mathcal{R}$ and $s\in {\mathcal{R}}_q=\mathcal{R}/q\mathcal{R}$, and a sample from $A_{s,\chi }$ is of the form $(b,a)\in {\mathcal{R}}_q\times {\mathcal{R}}_q,$ where $a\leftarrow {\mathcal{R}}_q$, $e\leftarrow \chi$ and $b=s·a+e\mathrm{mod}q$. Then, the problem $\mathsf{RLWE}$ is presented as:

Definition 2

($\mathsf{RLWE}$). For security parameter $\lambda$, let $q=q\left(\lambda \right)\ge 2$ be an integer modulus and $\chi =\chi \left(\lambda \right)$ be a distribution over $\mathcal{R}$. The task of decision $\mathsf{RLWE}$ is given m pairs of $(b^{\prime },a^{\prime })\in {\mathcal{R}}_q\times {\mathcal{R}}_q$, and decides whether these pairs are from the uniform distribution or $A_{s,\chi }$.

The hardness of the above two problems have been extensively studied in the NIST’s post-quantum standardization process in recent years. There are a number of plausible encryption schemes based on $\mathsf{LWE}$ or $\mathsf{RLWE}$ [23,24].

In the following, we use two basic encryption schemes based on the $\mathsf{RLWE}$— (1) $\mathsf{RLWE}$ and (2) $\mathsf{RGSW}$. For convenience, we denote $\mathsf{RLWE}\left(\mu \right)$ as a message hidden by an $\mathsf{RLWE}$ sample, and sometimes the secret s is specified by ${\mathsf{RLWE}}_s\left(\mu \right)$. The similar notation $\mathsf{RGSW}\left(\mu \right)$ is applied to $\mathsf{RGSW}$ encryption. Further, we denote $\mathsf{Err}\left((b,a)\right)$ as the noise of ciphertext $(b,a)$, and the same is true for $\mathsf{Err}\left(\mathsf{RGSW}\right(\mu \left)\right)$. Clearly, the security of these schemes can be based on the hard problems of (Ring) Learning with Errors. These schemes have been widely used in the lattice-based cryptography [23,24] and FHE [15,25,26,27], which imply various homomorphic operations.

2.3. Useful Algorithms

Here, we present some useful notations and algorithms for our PIR protocol. Let $\mathcal{R}=\mathbb{Z}\left[X\right]/(X^d+1)$ where d is a power of two.

2.3.1. Plaintext–Ciphertext Multiplication

Given a plaintext ${\mu }_1\in {\mathcal{R}}_p$, and an $\mathsf{RLWE}$ ciphertext $\mathsf{RLWE}(\Delta {\mu }_2)$ where ${\mu }_2\in {\mathcal{R}}_p$ and $\Delta =\lfloor q/p\rfloor$, the plaintext–ciphertext multiplication is defined as ${\mu }_1·\mathsf{RLWE}(\Delta {\mu }_2)$. The output is an $\mathsf{RLWE}$ ciphertext $\mathsf{RLWE}(\Delta {\mu }_1{\mu }_2)$ with a noise growth.

2.3.2. Ciphertext–Ciphertext Multiplication

Given an $\mathsf{RGSW}$ ciphertext $\mathsf{RGSW}\left({\mu }_1\right)\in {\mathcal{R}}_q^{2\times 2\ell }$ and an $\mathsf{RLWE}$ ciphertext $\mathsf{RLWE}(\Delta {\mu }_2)\in {\mathcal{R}}_q^2$ where ${\mu }_1,{\mu }_2\in {\mathcal{R}}_p$ and $\Delta =\lfloor q/p\rfloor$, the external product of ciphertext–ciphertext multiplication [15] is defined as $\mathsf{RGSW}\left({\mu }_1\right)⊠\mathsf{RLWE}(\Delta {\mu }_2):=\mathsf{RGSW}\left({\mu }_1\right)·{\mathit{g}}^{-1}\left(\mathsf{RLWE}(\Delta {\mu }_2)\right)$. The output is an $\mathsf{RLWE}$ ciphertext $\mathsf{RLWE}(\Delta {\mu }_1{\mu }_2)$ with a noise growth.

Here, we recall several useful algorithms for Spiral [12] and our design: (1) key-switching, (2) $\mathsf{RLWE}$ sxpansion, and (3) Conversion from $\mathsf{RLWE}$(s) to $\mathsf{RGSW}$.

2.3.3. Key-Switching

The procedure is denoted as $\mathsf{KS}$ (Key-switching) with the following algorithms:

• $\mathsf{KS}$($\mathsf{KSkey},(b,a)$). Given an $\mathsf{RLWE}$ ciphertext $(b,a)\in {\mathsf{RLWE}}_s\left(\mu \right)$ and key-switching key $\mathsf{KSkey}$ as input, the algorithm outputs an $\mathsf{RLWE}$ ciphertext $(b^{\prime },a^{\prime })\in {\mathsf{RLWE}}_{s^{\prime }}\left(\mu \right)$ by computing

  $${(b^{\prime },a^{\prime })}^{\top }={(b,0)}^{\top }-\mathsf{KSkey}·{\mathit{g}}^{-1}\left(a\right)$$

  and outputting $(b^{\prime },a^{\prime })$ accordingly.

This idea was proposed by [28] and was later used widely in the research of FHE [15,25,26,27].

2.3.4. $\mathsf{RLWE}$ Expansion

Given an $\mathsf{RLWE}$ ciphertext $(b,a)\in {\mathsf{RLWE}}_s\left(\mu \right)$, there is an algorithm that expands it to an r$\mathsf{RLWE}$ ciphertext ${\left((b_i,a_i)\in {\mathsf{RLWE}}_{\mathit{s}}\left({\mu }_i\right)\right)}_{i\in \left[r\right]}$, where $\mu ={\mu }_0+{\mu }_1{x}^t+\cdots +{\mu }_{r-1}{x}^{(r-1)t}$ and $t=d/r$. Through the $\mathsf{RLWE}$ expansion algorithm, the server obtains many $\mathsf{RLWE}$ ciphertexts that encrypt each coefficient of the input message polynomial $\mu$. We use $expand\left(\right(b,a),autoKey,t)$ to denote this expansion process, where $\mathsf{pk}.autoKey$ is a proper key-switching key for these automorphisms.

2.3.5. Conversion from $\mathsf{RLWE}$(s) to $\mathsf{RGSW}$

According to [12], there is an algorithm that given ℓ $\mathsf{RLWE}$ ciphertexts, namely $(b_0,a_0)\in {\mathsf{RLWE}}_s\left(\mu \right),\cdots ,(b_{\ell -1},a_{\ell -1})\in {\mathsf{RLWE}}_s({\mathcal{B}}_{\ell }^{\ell -1}·\mu )$ and a proper key-switching key, outputs an $\mathsf{RGSW}$ ciphertext $({\mathit{b}}^{\top };{\mathit{a}}^{\top })\in {\mathsf{RGSW}}_s\left(\mu \right)$, where ${\mathcal{B}}_{\ell }$ is the decomposition base. We simply call this algorithm $\mathsf{RLWE}$s-to-$\mathsf{RGSW}$.

2.4. Private Information Retrieval

Here, we describe the syntax of private information retrieval (PIR). PIR is a protocol between two stateful machines, namely the server and the client with the following structure. The server holds a database $\mathsf{DB}$ of size $N\in \mathbb{N}$, i.e., the number of entries, while the client would like to retrieve $\mathsf{DB}\left[\mathsf{index}\right]$ for some private $\mathsf{index}\in \left[N\right]$. Implicitly, the security parameter $1^{\lambda }$ is taken in all procedures below.

• Setup ($\mathsf{DB}$): This phase is run one time per database. Particularly, the client receives nothing and the server receives a database $\mathsf{DB}$ of size $N\in \mathbb{N}$. The server can preprocess to generate some public things, e.g., preprocess the database $\mathsf{DB}$ to a preprocessed $\mathsf{hint}$, thus it can accelerate the online computation.
• Keygen: The client generates a public and secret key pair $(\mathsf{pk},\mathsf{sk})$. Next, the client sends the public key $\mathsf{pk}$ to the server while privately storing the corresponding secret key $\mathsf{sk}$. Generally speaking, the $\mathsf{pk}$ usually consists of some key-switching keys and the $\mathsf{sk}$ is used for encryption and decryption.
• Query ($\mathsf{sk},\mathsf{index}$): Once given an indice $\mathsf{index}\in \left[N\right]$, the client computes an online query $\mathsf{qu}$ and sends the query to the server.
• Response $(\mathsf{qu},\mathsf{pk},\mathsf{hint})$: Input, an online query $\mathsf{qu}$ and the public key $\mathsf{pk}$ from the client, and preprocessed $\mathsf{hint}$, the server computes a response $\mathsf{r}$ and sends it back to the client.
• Recover $(\mathsf{ans},\mathsf{sk})$: Input an answer $\mathsf{ans}$ and the secret key $\mathsf{sk}$, the client outputs the desired record d.

In general, the Setup phase is run one time per database for all clients, i.e., $\mathsf{hint}$ is generated based on the database $\mathsf{DB}$, which is not relevant with client’s $\mathsf{pk}$. A PIR protocol formed by the above algorithms should satisfy the following two basic properties: correctness and security.

2.4.1. Correctness

The correctness is satisfied if the client always recovers the desired record, i.e., regardless of the database and indices, and only a negligible probability of decryption failure is allowed. The formal definition of correctness is as follows.

For all configurable $\lambda \in \mathbb{N}$, and database size $N=N\left(\lambda \right)$, for all databases $\mathsf{DB}=\{d_0,\cdots ,d_{N-1}\}$ and all indices $\mathsf{index}\in \left[N\right]$, we say that the PIR protocol is correct if and only if it satisfies

$$\mathsf{Prob}[\mathbf{Recover}(\mathsf{ans},\mathsf{sk})\ne d_{\mathsf{index}}]\le negl\left(\lambda \right),$$

where $\mathsf{ans}\leftarrow$Response$(\mathsf{qu},\mathsf{pk},\mathsf{hint})$, $\mathsf{qu}\leftarrow$Query($\mathsf{sk},\mathsf{index}\in \left[N\right]$), $(\mathsf{pk},\mathsf{sk})\leftarrow$Keygen and $\mathsf{hint}\leftarrow$Setup($\mathsf{DB}$).

2.4.2. Security

We define that a single-server PIR scheme satisfies security if and only if for any probabilistic polynomial-time (PPT) adversary $\mathcal{A}$ (such as the server), for any $\mathsf{DB}$ of size $N\in \mathbb{N}$, the adversary’s view is computationally indistinguishable for the following experiments: If the query $\mathsf{qu}$ is the encryption of $\mathsf{index}\in \left[N\right]$, the adversary outputs 1, otherwise it outputs 0. Given a correct plaintext–ciphertext pair or an unmatched pair, the adversary’s advantage is negligible. Next, we can give the formal definition of security, as follows.

For all integer $N=N\left(\lambda \right)$ and all adversaries $\mathcal{A}$, there exists a negligible function $negl(·)$ such that for all configurable $\lambda \in \mathbb{N}$ and all index $i,j\in \left[N\right]$, we say that the PIR protocol is safe if and only if the advantage of the adversary satisfies

$$\left|\mathsf{Prob}\right[\mathcal{A}\left(1^{\lambda },N,\mathsf{DB},\mathsf{pk},i,\mathbf{Query}(\mathsf{sk},i\in \left[N\right])\right)=1]-$$

$$\mathsf{Prob}[\mathcal{A}\left(1^{\lambda },N,\mathsf{DB},\mathsf{pk},i,\mathbf{Query}(\mathsf{sk},j\in \left[N\right])\right)=1]|\le negl\left(\lambda \right),$$

where $\mathsf{sk}$ and other materials are generated as above.

2.5. Spiral Protocol

The single-server PIR scheme Spiral [12] follows the Gentry–Halevi [14] blueprint. They rely on two basic encryption schemes: the $\mathsf{RLWE}$ encryption scheme and the $\mathsf{RGSW}$ encryption scheme. After a query expansion phase, the server performs plaintext–ciphertext multiplications in the first dimension folding. Then, the server uses an external product to perform ciphertext–ciphertext multiplications, which is also called the subsequent dimensions folding. Thanks to the expansion algorithm and the low noise growth of the external product, Spiral as well as its family outperforms prior PIR protocols, e.g., SealPIR [3], FastPIR [29], MulPIR [10], and OnionPIR [11].

Spiral structured its database of $N=2^{v_1\times v_2}$ records as a $2^{v_1}\times 2\times \cdots \times 2$ hypercube. Each record is a ring element in ${\mathcal{R}}_p^{n\times n}$, where p is the plaintext modulus, and n is the dimension of the matrix. In the following, we only let $n=1$ for simplicity. In the following, we give a brief description about how Spiral works, as in Figure 1.

2.5.1. Setup and Keygen Phase

In these two phases, the server preprocesses database $\mathsf{DB}$ and the client prepares $\mathsf{sk}$ and $\mathsf{pk}$, and then sends $\mathsf{pk}$ to the server.

2.5.2. Query Generation Phase

In this phase, the client would like to retrieve $\mathsf{DB}\left[\mathsf{index}\right]$ for some private $\mathsf{index}\in \left[N\right]$. The client parses $\mathsf{index}$ into $\pi \left(\mathsf{index}\right)=(u,{\mathit{w}}^{\top })\in \left[2^{v_1}\right]\times {\{0,1\}}^{v_2}$ such that $\mathsf{index}=u+2^{v_1}·{\mathit{w}}^{\top }\mathit{b}$, where $\mathit{b}={[1,2,4,\cdots ,2^{v_2-1}]}^{\top }$. The client encodes indicator vector $\Delta \mathit{u}$ where the u-th element is 1 and the others are 0, and $\mathit{w}\otimes \mathit{g}$. Then, the client encrypts it to an $\mathsf{RLWE}$ ciphertext and sends it to the server.

2.5.3. Response Phase

In this phase, the server would like to process the query and response. The server only receives an $\mathsf{RLWE}$ ciphertext so that it sees nothing about $\mathsf{index}$. This phase can be divided into three sub-stages as follow:

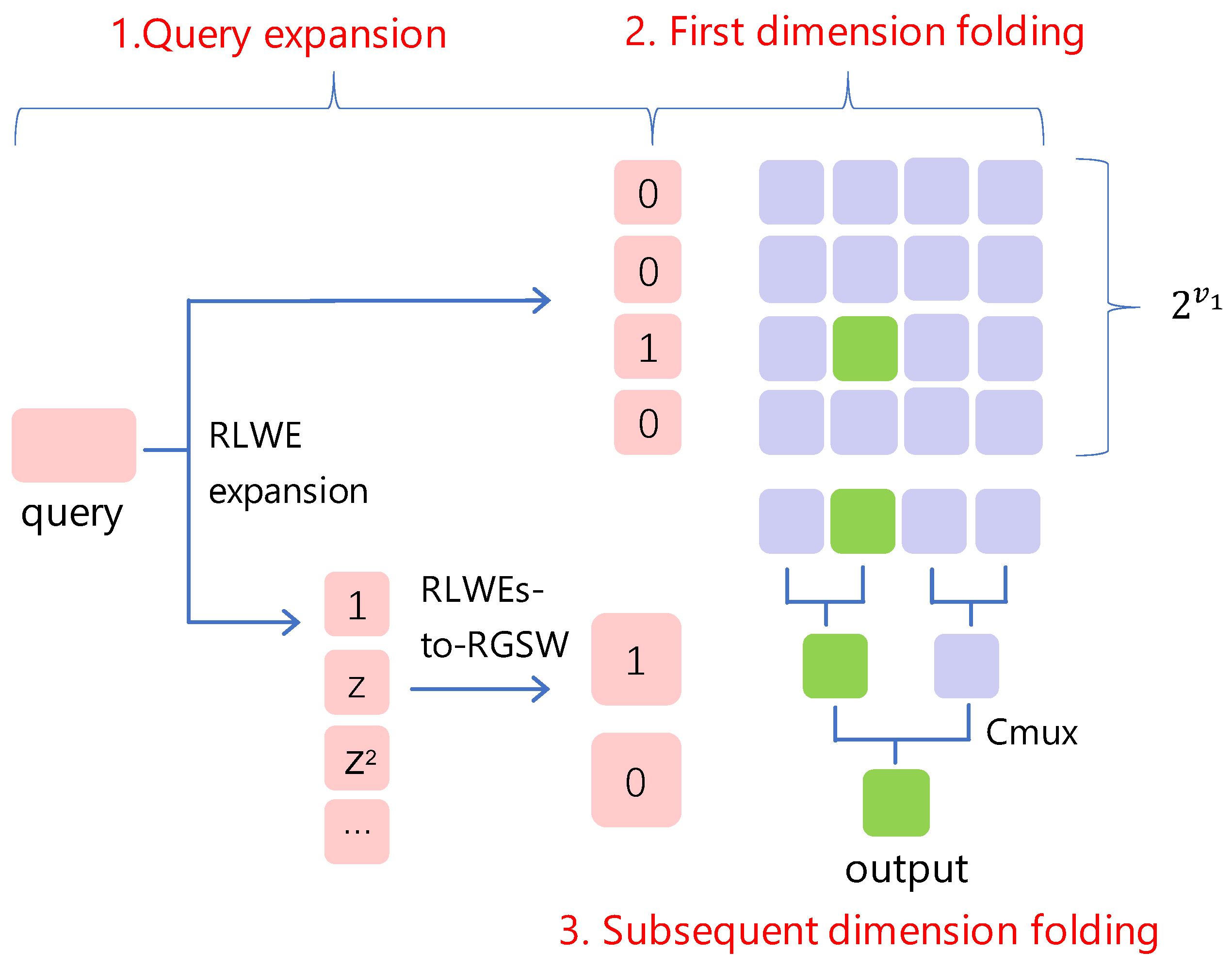
• (Query expansion). Once it receives the online query $\mathsf{qu}$, the server expands it to a series of $\mathsf{RLWE}$ ciphertexts that can be divided into two groups. The first group consists of $2^{v_1}$ $\mathsf{RLWE}$ ciphertexts that only the u-th ciphertext encrypts as 1 and the remaining encrypt as 0. The second group consists of $v_2\times \ell$ $\mathsf{RLWE}$ ciphertexts, which are the input of the $\mathsf{RLWE}$s-to-$\mathsf{RGSW}$ algorithm. The sever converts these ciphertexts belonging to the second group to $v_2$ $\mathsf{RGSW}$ cipertexts that encrypt $\mathit{w}$.
• (First dimension folding). Once given $2^{v_1}$ $\mathsf{RLWE}$ ciphertexts, that only one of them encrypts as 1 and the others encrypt as 0, the server can do plaintext–ciphertext multiplications and ciphertext–ciphertext additions for each column in the database. For each column, the server obtains one $\mathsf{RLWE}$ ciphertext. Consequently, the output $2^{v_2}$ $\mathsf{RLWE}$ ciphertexts encrypt the u-th row of the database.
• (Subsequent dimension folding). Once given $2^{v_2}$ $\mathsf{RLWE}$ ciphertexts (generated in the first dimension-folding phase) and $v_2$ $\mathsf{RGSW}$ ciphertexts (generated in the query expansion phase), the server evaluates many homomorphic $Cmux$ functions, i.e., $m_i=Cmux(i,m_0,m_1)$ for $i\in \{0,1\}$. Consequently, the server outputs one $\mathsf{RLWE}$ ciphertext that encrypts the desired record, and relays it to the client.

2.5.4. Recover Phase

In this phase, the client would like to decrypt the answer $\mathsf{ans}$ to recover the desired message $\mathsf{DB}\left[\mathsf{index}\right]$.

Remark 1. 

The concept of a simpler database structure is a $2^{v_1}\times 2^{v_2}$ two-dimension matrix. In other words, the server generates $2^{v_1}$ $\mathsf{RLWE}$ ciphertexts and $2^{v_2}$ $\mathsf{RGSW}$ ciphertexts so that the subsequent dimension folding is performed like the first dimension folding, but in a ciphertext–ciphertext manner. Compared with homomorphic $Cmux$ function, this way is simpler in concept and faster to computate. However, this setting enables the server to reduce the computation of a subsequent dimension folding from $2^{v_2+1}$ external product operations to $2^{v_2}$, but it increases the number of expansion $\mathsf{RGSW}$ from $v_2$ to $2^{v_2}$, thus increasing query expansion cost.

3. Our Improvement

Following the design of Spiral [12], we propose three optimizations that can accelerate the server’s computation. We found that performing a modulus switching before the first dimension folding will improve the server’s throughput, so we propose a Residue Number System (RNS) variant of Spiral. Then, we apply two existing techniques called the composite $\mathsf{NTT}$ algorithm and approximate decomposition to further improve it. These two techniques are independent of PIR protocols, but are compatible with Spiral and work well. We suggest to use them in any application where they can be used.

3.1. RNS Variant of Spiral

The server of the Spiral protocol performs the $\mathsf{RLWE}$ expansion algorithm and the $\mathsf{RLWE}$s-to-$\mathsf{RGSW}$ algorithm to obtain a series of $\mathsf{RLWE}$ and $\mathsf{RGSW}$ ciphertexts. Through the select large decomposition dimension ℓ, Spiral protocol controls the noise growth of the query expansion phase. However, the noise growth introduced by the query expansion phase would consume some space, thereby influencing the subsequent computation, i.e., the first dimension folding and the subsequent dimension folding. The database is multiplied by not only the valid message but also the growth noise introduced by the query expansion phase, which seems to not be worthwhile.

We propose an RNS variant of Spiral, with the core goal to construct nearly fresh expanded ciphertexts. The core technique we used is modulus switching [26]. Given an $\mathsf{RLWE}$ ciphertext $(b,a)\in {\mathcal{R}}_Q^2$, modulus switching is defined as

$$(\overline{b},\overline{a})=⌊{\displaystyle \frac{q·(b,a)}{Q}}⌉\mathrm{mod}q,$$

where q is a smaller modulus than Q. The noise growth is $\mathsf{Err}\left((\overline{b},\overline{a})\right)=q·\mathsf{Err}\left((b,a)\right)/Q+e$ where e is a very small noise introduced by modulus switching. The squared sub-Gaussian parameter of $\mathsf{Err}\left((\overline{b},\overline{a})\right)$ is $s_o^2=q^2{s}_i^2/Q^2+2\pi (h+1)/4$, where h is the Hamming weight of the secret, and $s_i$ is the sub-Gaussian parameter of $\mathsf{Err}(b,a)$.

The origin of Spiral works on ring ${\mathcal{R}}_q$ where q is around 56 bits. We select a big modulus $Q=q·\tilde{q}$ as the parameter of the initial work ring ${\mathcal{R}}_Q={\mathbb{Z}}_Q\left[x\right]/(x^d+1)$ where d is a power of two. At a later appropriate time, the server can perform a modulus switching operation to reduce the noise of the ciphertexts. Specifically, the server performs the modulus switching algorithm towards those expanded ciphertexts before the first dimension-folding phase, so that the growth noise introduced by query expansion does not influence the subsequent computation. This method can improve the server’s throughput.

The security level of $\mathsf{RLWE}$ cryptography mainly depends on the ring dimension d and the modulus Q, and a bigger ring dimension and a smaller modulus lead to higher security [30]. We have to double the ring dimension to retain the same level of security if we use a bigger modulus Q. Our experiments show that this leads to a slightly bigger query size, but no reduction to the server throughput. For more details about parameter selection and concrete performance, the reader can refer to Secition Section 5.

At the same time, Q is more than 64 bits, so we split it into two smaller rings, ${\mathcal{R}}_q$ and ${\mathcal{R}}_{\tilde{q}}$, to align with computations on uint64_t that are used in most computer systems. The additions and multiplications on ${\mathcal{R}}_Q$ can be performed by additions and multiplications on two smaller rings, ${\mathcal{R}}_q$ and ${\mathcal{R}}_{\tilde{q}}$, respectively. The modulus switching is performed in its RNS variant [31]. To be precise, it is performed as $\left((b_0-b_1)·{\tilde{q}}^{-1}\mathrm{mod}q,(a_0-a_1)·{\tilde{q}}^{-1}\mathrm{mod}q\right)\in {\mathcal{R}}_q^2$, where $\left((b_0,a_0),(b_1,a_1)\right)\in {\mathcal{R}}_q^2\times {\mathcal{R}}_{\tilde{q}}^2$ is the input ciphertext. The output ciphertext is in ring ${\mathcal{R}}_q^2$ and it is a nearly fresh ciphertext, i.e., with a very small amount of noise. In our construction, the server performs RNS modulus switching towards those expanded ciphertexts to improve server throughput. The readers can refer to the full protocol in Section 4 and the concise performance in Section 5.

3.2. Improvement by Composite $\mathsf{NTT}$ Algorithm

In the Spiral protocol, the work ring ${\mathcal{R}}_q$ is divided into two smaller rings, ${\mathcal{R}}_{q_1}$ and ${\mathcal{R}}_{q_2}$, where $q=q_1{q}_2$. This strategy contributes to plaintext–ciphertext multiplications and ciphertext–ciphertext additions in the first dimension-folding phase. When we perform a large number of plaintext–ciphertext multiplications and then add them up, the server does not have to always have module q. Instead, the server adds the multiplied numbers first and then module q. Modular reduction is a heavier operation compared with addition and multiplication, so reducing the amount of modular reduction can be seen as a more efficient strategy. Specifically, the modulus $q_1$ and $q_2$ are around 28 bits in Spiral so that the multiplication of two elements in ${\mathbb{Z}}_{q_1}$ (resp. ${\mathbb{Z}}_{q_2}$) will never be beyond 56 bits. Spiral adds many multiplied numbers and then module $q_1$ (resp. $q_2$), ensuring that they will not reach $2^{64}$.

Spiral performs standard $\mathsf{NTT}$s in ${\mathcal{R}}_{q_1}$ and ${\mathcal{R}}_{q_2}$, respectively. The computation is twice that of a single one. We apply a technique called the composite $\mathsf{NTT}$ algorithm [19] to reduce the computation without any other cost. In the following, we recall the standard $\mathsf{NTT}$ algorithm first and show how to apply the composite $\mathsf{NTT}$ algorithm to Spiral.

The standard $\mathsf{NTT}$ algorithm works on cyclotomic ring ${\mathcal{R}}_q$ only when the $2d$-th primitive root exists. There is a well-known fact [32] that, when $q\equiv 1\left(\mathrm{mod}2d\right)$ and q is a prime, the $2d$-th primitive root $\zeta \in {\mathbb{Z}}_q$ exists. At this time, cyclotomic polynomial $(x^d+1)$ can be divided into a series of monomials $(x^d+1)=(x-\zeta )(x-{\zeta }^3)\cdots (x-{\zeta }^{2d-1})$. Then, we have

$${\mathcal{R}}_q={\mathbb{Z}}_q\left[x\right]/(x^d+1)\cong {\displaystyle \frac{{\mathbb{Z}}_q\left[x\right]}{(x-\zeta )}}\times {\displaystyle \frac{{\mathbb{Z}}_q\left[x\right]}{(x-{\zeta }^3)}}\times \cdots \times {\displaystyle \frac{{\mathbb{Z}}_q\left[x\right]}{(x-{\zeta }^{2d-1})}}.$$

The standard $\mathsf{NTT}$ algorithm [32] coverts the element $a\in {\mathcal{R}}_q$ to its $\mathsf{NTT}$ form $\widehat{a}\in {\mathbb{Z}}_q^d$, and the inv-$\mathsf{NTT}$ algorithm coverts it back. The input of $\mathsf{NTT}$ and the inv-$\mathsf{NTT}$ algorithm include $a\in {\mathcal{R}}_q$ and $\widehat{a}\in {\mathbb{Z}}_q^d$, respectively, as well as a $2d$-th primitive root $\zeta$.

The composite $\mathsf{NTT}$ algorithm [19] reduces the condition of q which is a prime, i.e., in fact, it is not a necessary condition to implement an $\mathsf{NTT}$ algorithm. Supposing that $q=q_1{q}_2$ where $q_1$ and $q_2$ are primes, and $q_1\equiv 1\left(\mathrm{mod}2d\right)$, $q_2\equiv 1\left(\mathrm{mod}2d\right)$, we know that the $2d$-th primitive root ${\zeta }_1\in {\mathbb{Z}}_{q_1}$ and ${\zeta }_2\in {\mathbb{Z}}_{q_2}$ exist. In fact, there is a $\zeta \in {\mathbb{Z}}_q$ that exists such that ${\zeta }_1\equiv \zeta \mathrm{mod}{q}_1$ and ${\zeta }_2\equiv \zeta \mathrm{mod}{q}_2$. The value $\zeta$ can by solved by the Chinese Remainder Theorem (CRT) algorithm, i.e., $\zeta ={\mathit{CRT}}^{-1}({\zeta }_1,{\zeta }_2)$. At this time, we know that $\zeta$ is the $2d$-th primitive root in ${\mathbb{Z}}_{q=q_1{q}_2}$. Therefore,

$${\mathcal{R}}_q\cong {\mathcal{R}}_{q_1}\times {\mathcal{R}}_{q_2}\cong {\left({\mathbb{Z}}_{q_1}\right)}^d\times {\left({\mathbb{Z}}_{q_2}\right)}^d\cong {\mathbb{Z}}_q^d.$$

We can implement a standard $\mathsf{NTT}$ algorithm over ${\mathcal{R}}_q$, where $q_1$ and $q_2$ are two $\mathsf{NTT}$-friendly moduli, by inputing a composite $2d$-th primitive root $\zeta ={\mathit{CRT}}^{-1}({\zeta }_1,{\zeta }_2)$. Whether the input primitive root is composite or not does not affect the computation cost. Therefore, the composite $\mathsf{NTT}$ algorithm is a completely lossless improvement and will never bring other extra costs to the server and the client.

3.3. Improvement by Approximate Decomposition

We recall the following lemma which states an algorithm ${\mathit{g}}^{-1}$ that is heavily used in homomorphic operations over ciphertexts, especially in key-switching-type operations including automorphic transformation and an external product.

Lemma 1

(Adapted from [15,33,34]).  For a given integer q and a base integer ${\mathcal{B}}_{\ell }$, let $\ell =⌈{\log }_{{\mathcal{B}}_{\ell }}q⌉$ and $\mathit{g}={(1,{\mathcal{B}}_{\ell },..,{\mathcal{B}}_{\ell }^{\ell -1})}^{\top }$. Then, there is a randomized, efficiently computable algorithm denoted as ${\mathit{g}}^{-1}$: ${\mathbb{Z}}_q\to {\mathbb{Z}}^{\ell }$ such that the output of the algorithm, $\mathit{x}\leftarrow {\mathit{g}}^{-1}\left(a\right)$, is a sub-Gaussian with parameter $O\left({\mathcal{B}}_{\ell }\right)$, satisfying $\langle \mathit{g},\mathit{x}\rangle =a\mathrm{mod}q$.

We use another variant of algorithm ${\mathit{g}}^{-1}$ in our implementation. The high-level insight is that ${\mathit{g}}^{-1}$ need not always be exact. $\langle \mathit{g},{\mathit{g}}^{-1}\left(a\right)\rangle$ can be approximately equal to $a\mathrm{mod}q$ and the difference $a-\langle \mathit{g},{\mathit{g}}^{-1}\left(a\right)\rangle \mathrm{mod}q$ is counted into noise growth. For distinguishing this, we denote the approximate variant as ${\tilde{\mathit{g}}}^{-1}$ in the following.

Given a modulus q and $\ell :=\lceil {\log }_{{\mathcal{B}}_{\ell }}q/{\mathcal{B}}_e\rceil$, we denote the gadget vector as $\tilde{\mathit{g}}={\mathcal{B}}_e·{(1,{\mathcal{B}}_{\ell },\dots ,{\mathcal{B}}_{\ell }^{\ell -1})}^{\top }$ for some base ${\mathcal{B}}_{\ell },{\mathcal{B}}_e\in \mathbb{N}$. Then, we use the algorithm ${\tilde{\mathit{g}}}^{-1}$: ${\mathbb{Z}}_q\to {\mathbb{Z}}^{\ell }$, such that the output of the algorithm $\mathit{x}\leftarrow {\tilde{\mathit{g}}}^{-1}\left(a\right)$ satisfies $\langle \tilde{\mathit{g}},\mathit{x}\rangle \approx a\mathrm{mod}q$. The approximate gadget decomposition is first used for the torus variant of $\mathsf{LWE}$ and $\mathsf{RLWE}$ samples in TFHE [15]. It also works well in our protocol. In the following, we call ℓ, ${\mathcal{B}}_{\ell }$ and ${\mathcal{B}}_e$ a decomposition dimension, a decomposition base and an approximate base, respectively.

The advantage of approximate decomposition is a smaller decomposition dimension compared with its standard counterpart. A smaller decomposition dimension ℓ leads to a smaller number of $\mathsf{NTT}$, therefore accelerating the key-switching-type operations, e.g., automorphic transformation and the external product. The growth noise introduced by an approximate is added to the origin noise, which will never lead to a high compact when parameters are reasonably set.

For example, when inputing an $\mathsf{RLWE}$ ciphertext $(b,a)\in {\mathcal{R}}_q^2$ and a key-switching key $\mathsf{KSkey}$$\in {\mathcal{R}}_q^{2\ell }$, the key-switching operation is performed as

$${(\overline{b},\overline{a})}^{\top }={(b,0)}^{\top }-\mathsf{KSkey}·{\mathit{g}}^{-1}\left(a\right).$$

The decomposed vector ${\mathit{g}}^{-1}\left(a\right)$ and b should be converted to the $\mathsf{NTT}$ form, and finally, two inv-$\mathsf{NTT}$ are required after some Hadmard multiplications and additions in the $\mathsf{NTT}$ form. Therefore, these are total $(3+\ell )$ $\mathsf{NTT}$/inv-$\mathsf{NTT}$ transformations. The noise growth of $(\overline{b},\overline{a})$ is $\mathsf{Err}\left((\overline{b},\overline{a})\right)=\mathsf{Err}\left((b,a)\right)+{\mathit{g}}^{-1}\left(a\right)·\mathit{e}$ where $\mathit{e}$ is the initial error of key-switching key $\mathsf{KSkey}$. The squared sub-Gaussian parameter is $s_o^2=s_i^2+d\ell {\mathcal{B}}_{\ell }^2{s}_{\sigma }^2/4$, where $s_i$, $s_o$ and $s_{\sigma }$ are the sub-Gaussian parameters of $\mathsf{Err}(b,a)$, $\mathsf{Err}(\overline{b},\overline{a})$ and $\mathsf{Err}\left(\mathit{e}\right)$, respectively.

When origin decomposition is substituted by approximate decomposition, a key-switching operation consumes $(3+\tilde{\ell })$ $\mathsf{NTT}$/inv-$\mathsf{NTT}$ transformations where commonly $\tilde{\ell }$ is smaller than ℓ. The noise growth is $\mathsf{Err}\left((\overline{b},\overline{a})\right)=\mathsf{Err}\left((b,a)\right)+{\tilde{\mathit{g}}}^{-1}\left(a\right)·\mathit{e}+(a-\langle \tilde{\mathit{g}},{\tilde{\mathit{g}}}^{-1}\left(a\right)\rangle )$. The squared sub-Gaussian parameter is $s_o^2=s_i^2+d\tilde{\ell }{\mathcal{B}}_{\tilde{\ell }}^2{s}_{\sigma }^2/4+2\pi (h+1){\mathcal{B}}_e^2/4$.

In the Spiral protocol, we can apply approximate decomposition in the $\mathsf{RLWE}$ expansion algorithm, the $\mathsf{RLWE}$s-to-$\mathsf{RGSW}$ algorithm, and the external product, thus improving server throughput.

4. The Full Protocol

In this section, we detail the construction of the full protocol. The basic structure and design principle are the same as those for Spiral, other than the three improvements described in Section 3. For readers who are familiar with Spiral [12], we recommend reading Remarks 2 and 3 below to get the differences between our construction and Spiral’s without getting bogged down in details.

4.1. The Description of Full Protocol

Spiral structures its database of $N=2^{v_1\times v_2}$ records as a $2^{v_1}\times 2\times \cdots \times 2$ hypercube. Each record is a ring element in ${\mathcal{R}}_p^{n\times n}$, where p is the plaintext modulus, and n is the dimension of the plaintext matrix. For simplicity and better server throughput, we only let $n=1$ and treat each record as a ring element in ${\mathcal{R}}_p$.

Let $Q=q·\tilde{q}$ and $q=q_1{q}_2$ be a multiplied modulus of two $\mathsf{NTT}$-friendly moduli, $q_1$ and $q_2$. The initial work ring is ${\mathcal{R}}_Q={\mathbb{Z}}_Q\left[x\right]/(x^d+1)$ where d is a power of two. Let p be a plaintext modulus, and $\Delta =\lfloor q/p\rfloor$ be the encode factor.

4.1.1. Setup Phase

In this phase, the server inputs security parameter $\left(1^{\lambda }\right)$ and database $\mathsf{DB}\in {\mathcal{R}}_p^N$, and outputs the structure form $\widetilde{\mathsf{DB}}\in {\mathcal{R}}_p^{2^{v_1}\times 2\times 2\times \cdots \times 2}$. The $\mathsf{index}\in \left[N\right]$ is parsed into $\pi \left(\mathsf{index}\right)=(u,{\mathit{w}}^{\top })\in \left[2^{v_1}\right]\times {\{0,1\}}^{v_2}$ such that $\mathsf{index}=u+2^{v_1}·{\mathit{w}}^{\top }\mathit{b}$, where $\mathit{b}={[1,2,4,\cdots ,2^{v_2-1}]}^{\top }$. Therefore, the record $\mathsf{DB}\left[\mathsf{index}\right]$ is equal to $\widetilde{\mathsf{DB}}[u,{\mathit{w}}^{\top }]$. Next, the server preprocesses them to $\mathsf{NTT}$ forms and stores them as $\mathsf{hint}\in {\mathcal{R}}_q^{2^{v_1}\times 2\times 2\times \cdots \times 2}$, i.e., preprocess each record $d_i\in {\mathcal{R}}_p$ to its $\mathsf{NTT}$ form ${\tilde{d}}_i\in {\mathcal{R}}_q$.

4.1.2. Keygen Phase

In this phase, the client inputs security parameter $\left(1^{\lambda }\right)$, and outputs $s\leftarrow$$\mathsf{RLWE}$$.KeyGen\left(1^{\lambda }\right)$. The client then generates the key-switching keys $autoKey$, $r2gKey$ and $packKey$, which will be used in the $\mathsf{RLWE}$ expansion algorithm, the $\mathsf{RLWE}$s-to-$\mathsf{RGSW}$ algorithm, and packing the $\mathsf{RLWE}$s to the matrix Regev algorithm [12], respectively.

4.1.3. Query Generation Phase

In this phase, the client would like to retrieve $\mathsf{DB}\left[\mathsf{index}\right]$ for some private $\mathsf{index}\in \left[N\right]$. The client parses $\mathsf{index}$ into $\pi \left(\mathsf{index}\right)=(u,{\mathit{w}}^{\top })\in \left[2^{v_1}\right]\times {\{0,1\}}^{v_2}$ such that $\mathsf{index}=u+2^{v_1}·{\mathit{w}}^{\top }\mathit{b}$, where $\mathit{b}={[1,2,4,\cdots ,2^{v_2-1}]}^{\top }$. The client encodes indicator vector $\Delta \mathit{u}$ and $\tilde{\mathit{w}}=\mathit{w}\otimes \tilde{\mathit{g}}$, where the u-th element of $\mathit{u}$ is 1 and others are zeros, and $\tilde{\mathit{g}}$ is the approximate gadget vector.

The client encodes the indicator vector $\Delta \mathit{u}$ (that will be used in the first dimension folding) as polynomial $m_1\left(x\right)$ and $\mathit{w}\otimes \tilde{\mathit{g}}$ (that will be used in the subsequent dimension folding) as polynomial $m_2\left(x\right)$, as

$$m_1\left(x\right)=\Delta \tilde{q}·\left(\sum _{i=0}^{2^{v_1}-1}\mathit{u}\left[i\right]x^{i{t}_1}\right),$$

$$m_2\left(x\right)=\tilde{q}·\sum _{i=0}^{v_2\ell -1}\tilde{\mathit{w}}\left[i\right]x^{i{t}_2},$$

where $t_1=d/2^{v_1+1}$, $t_2=d/\left(2\rho \right)$, and $\rho =max(2^{\lceil {\log }_2\left(v_2\ell \right)\rceil },v_2\ell )$ is the smallest power of two that is bigger than or equal to $v_2\ell$. We assume that $2^{v_1}+\rho \le d$ so that only one query ciphertext is required.

Then, the client encodes the packing polynomial

$$m\left(x\right)=2^{-(v_1+1)}·m_1\left(x\right)+{\left(2\rho \right)}^{-1}·m_2\left(x\right)·x^{min(t_1,t_2)/2}.$$

The client encrypts $m\left(x\right)$ to $\mathsf{qu}=\mathsf{RLWE}\left(m\right)\in {\mathcal{R}}_Q^2$ and sends it to the server.

4.1.4. Response Phase

In this phase, the server would like to process the query and response. The server only receives an $\mathsf{RLWE}$ ciphertext so that it sees nothing about $\mathsf{index}$. This phase can be divided into three sub-stages as follows:

• (Query expansion). Upon receiving the online query $\mathsf{qu}$, the server first expands it to two $\mathsf{RLWE}$ ciphertexts

  $$(c{t}_1,c{t}_2)=\mathit{expand}\left(\mathsf{qu},\mathsf{pk}.autoKey,min(t_1,t_2)/2\right).$$
  For the property of the $\mathsf{RLWE}$ expansion algorithm, we know that $(c{t}_1,c{t}_2)=(\mathsf{RLWE}\left(m_1\right),$ $\mathsf{RLWE}\left(m_2\right))$.
  Then, the server continues to expand them to

  $${\mathsf{qu}}_{rlwe}=\mathit{expand}(c{t}_1,\mathsf{pk}.autoKey,t_1),$$

  $${\mathsf{qu}}_1=\mathit{expand}(c{t}_2,\mathsf{pk}.autoKey,t_2).$$
  We further know that ${\mathsf{qu}}_{rlwe}={\left(\mathsf{RLWE}(\Delta \tilde{q}·\mathit{u}\left[i\right])\right)}_{i\in \left[2^{v_1}\right]}\in {\left({\mathcal{R}}_Q^2\right)}^{2^{v_1}}$ and ${\mathsf{qu}}_1={\left(\mathsf{RLWE}(\tilde{q}·\tilde{\mathit{w}}\left[i\right])\right)}_{i\in \left[v_2\ell \right]}\in {\left({\mathcal{R}}_Q^2\right)}^{v_2\ell }$.
  For each $i\in \left[v_2\right]$, compute

  $${\mathsf{qu}}_{rgsw}\left[i\right]=\mathsf{RLWE}\mathrm{s}\text{-}\mathrm{to}\text{-}\mathsf{RGSW}\left({\mathsf{qu}}_1[i\ell :(i+1)\ell ),\mathsf{pk}.r2gKey\right),$$

  where ${\mathsf{qu}}_1[i\ell :(i+1)\ell )$ is an $\mathsf{RLWE}$ ciphertexts vector.
  For the property of the $\mathsf{RLWE}$s-to-$\mathsf{RGSW}$ algorithm, we know that ${{\mathsf{qu}}_{rgsw}=\left(\mathsf{RGSW}\left(\mathit{w}\right[i\left]\right)\right)}_{i\in \left[v_2\right]}\in {\left({\mathcal{R}}_Q^{2\times 2\ell }\right)}^{v_2}$.
  The server performs modulus-switching operations for all expanded $\mathsf{RLWE}$ ciphertexts ${\mathsf{qu}}_{rlwe}\in {\left({\mathcal{R}}_Q^2\right)}^{2^{v_1}}$ and $\mathsf{RGSW}$ ciphertexts ${\mathsf{qu}}_{rgsw}\in {\left({\mathcal{R}}_Q^{2\times 2\ell }\right)}^{v_2}$, as

  $${\mathsf{qu}}_{rlwe}=⌊{\displaystyle \frac{q·{\mathsf{qu}}_{rlwe}}{Q}}⌉\mathrm{mod}q\in {\left({\mathcal{R}}_q^2\right)}^{2^{v_1}},$$

  $${\mathsf{qu}}_{rgsw}=⌊{\displaystyle \frac{q·{\mathsf{qu}}_{rgsw}}{Q}}⌉\mathrm{mod}q\in {\left({\mathcal{R}}_q^{2\times 2\ell }\right)}^{v_2}.$$
  Consequently, ${\mathsf{qu}}_{rlwe}$ consists of $2^{v_1}$ $\mathsf{RLWE}$ ciphertexts that only the u-th ciphertext encrypts as 1 and the remaining encrypt as 0, while ${\mathsf{qu}}_{rgsw}$ consists of $v_2$ $\mathsf{RGSW}$ cipertexts that encrypt $\mathit{w}$.
  Remark 2. 

  There are two main differences from the original Spiral in the query generation and query expansion phases. The first one is that we work on a bigger ring ${\mathcal{R}}_{Q=q\tilde{q}}$ instead of ring ${\mathcal{R}}_q$, and we implement the modulus switching algorithm towards those expanded ciphertexts before the first dimension-folding phase. The other is that we use the composite $\mathsf{NTT}$ algorithm and approximate decomposition, instead of the standard $\mathsf{NTT}$ algorithm and exact decomposition in the original Spiral.
• (First dimension folding). Once given $2^{v_1}$ $\mathsf{RLWE}$ ciphertexts that only one of them encrypts as 1 and the others encrypt as 0, the server can do plaintext–ciphertext multiplications and ciphertext–ciphertext additions for each column of database. For each column, the server obtains one $\mathsf{RLWE}$ ciphertext, and the output $2^{v_2}$ $\mathsf{RLWE}$ ciphertexts encrypt the u-th row of the database.
  For each $j\in \left[2^{v_2}\right]$, the server computes

  $$c{t}_j=\sum _{i=0}^{2^{v_1}-1}{\mathsf{qu}}_{rlwe}\left[i\right]·\mathsf{hint}[i,{\mathit{j}}^{\top }],$$

  where $\mathit{j}$ is the bit decomposition of j, i.e., $\mathit{j}={\mathit{b}}^{-1}\left(j\right)\in {\{0,1\}}^{v_2}$.
  In total, there are $N=2^{v_1}\times 2^{v_2}$ plaintext–ciphertext multiplications and $(2^{v_1}-1)\times 2^{v_2}$ ciphertext–ciphertext additions.
• (Subsequent dimension folding). Once given $v_2$ $\mathsf{RGSW}$ ciphertexts and $2^{v_1}$ $\mathsf{RLWE}$ ciphertexts generated in the first dimension-folding phase, the server can do a ciphertext–ciphertext $Cmux$ function, i.e., $m_i=Cmux(i,m_0,m_1)$ for $i\in \{0,1\}$. Specifically, inputing two $\mathsf{RLWE}$ ciphertexts $c{t}_1=\mathsf{RLWE}\left(m_1\right)$, $c{t}_2=\mathsf{RLWE}\left(m_2\right)$, and an $\mathsf{RGSW}$ ciphertext $C=\mathsf{RGSW}\left(i\right)$ where $i\in \{0,1\}$, the $Cmux$ is defined as

  $$Cmux(C,c{t}_0,c{t}_1):=(\tilde{\mathit{g}}\otimes {\mathbf{I}}_2-C)⊠c{t}_0+C⊠c{t}_1.$$
  For each $i\in \left[v_2\right]$, let $interval=2^i$;
  For each $j\in [0,2\times interval,4\times interval,\cdots ,2^{v_2}-2\times interval]$, the server computes

  $$c{t}_j=Cmux({\mathsf{qu}}_{rgsw}\left[i\right],c{t}_j,c{t}_{j+interval}).$$
  Finally, let $\mathsf{ans}=(\mathsf{ans}.b,\mathsf{ans}.a)=c{t}_0\in {\mathcal{R}}_q^2$. In order to reduce the communication, the server computes a modulus switching

  $$\mathsf{ans}=\left(⌊{\displaystyle \frac{q_{mod1}·\mathsf{ans}.b}{q}}⌉\mathrm{mod}{q}_{mod1},⌊{\displaystyle \frac{q_{mod2}·\mathsf{ans}.a}{q}}⌉\mathrm{mod}{q}_{mod2}\right)\in {\mathcal{R}}_{q_{mod1}}\times {\mathcal{R}}_{q_{mod2}},$$

  where $q_{mod1}$ and $q_{mod2}$ are two smaller moduli compared with q. Using two unequal moduli contributes to a smaller ciphertext size compared with the original modulus switching which uses one modulus. Finally, the server relays it to the client.
  Remark 3. 

  There is no difference in the first dimension-folding phase compared with Spiral. In the subsequent dimension-folding phase, we use the composite $\mathsf{NTT}$ algorithm and approximate decomposition.

4.1.5. Recover Phase

In this phase, the client would like to decrypt the answer $\mathsf{ans}$ to an element ${\mathcal{R}}_p$. The server computes $r=\mathsf{RLWE}.Dec\left(\mathsf{ans}\right)$.

4.2. Additional Analysis

We present the noise growth, correctness and security analysis in Appendix A.

4.3. Pack and Stream Variant

Menon and Wu [12] also introduce three variants of Spiral, including SpiralPack, SpiralStream and SpiralPackStream. SpiralPack does not apply a matrix Regev ciphertext in the query expansion phase, the first dimension-folding phase and the second dimension-folding phases, i.e., set $n=1$. The server in SpiralPack performs multiple first-dimension foldings and second-dimension foldings using the same expanded ciphertexts, and obtains multiple $\mathsf{RLWE}$ ciphertexts. Finally, the server converts them to a matrix Regev ciphertext. SpiralStream directly uploads $\mathsf{RLWE}$ ciphertexts and $\mathsf{RGSW}$ ciphertexts, instead of applying the query expansion algorithm. Therefore, the throughput of SpiralStream is much better than tat of Spiral and SpiralPack, but the query size is much worse. SpiralPackStream is similar to SpiralStream, except that it incorporates the insight of SpiralPack.

All three improvements are compatible with SpiralPack. Due to the fact that SpiralStream and SpiralPackStream do not apply the query expansion algorithm, we do not apply the RNS variant to SpiralStream and SpiralPackStream. Certainly, we use the remaining improvements including the composite $\mathsf{NTT}$ algorithm and approximate decomposition to improve SpiralStream and SpiralPackStream.

5. Implementation and Evaluation

We implement our protocols in C++ to evaluate their concrete efficiency. Our implementations do not use any existing FHE libraries but adopt the Intel HEXL library (v1.2.5) [35] to implement the $\mathsf{NTT}$s. The source code is available at [20].

5.1. Parameter Selection

In this section, we present how we select parameters for our protocol.

5.1.1. Lattice Parameters

Our protocol always works over a power-of-two cyclotomic ring. In order to ensure 128 bits of classical security and take the noise growth into account, we set ring dimension $d=4096$, which is twice that of Spiral. Each secret is sampled as a uniform ternary secret, and all the initial noise is sampled from a discrete Gaussian distribution with standard deviation $\sigma =3.19$. We set the bigger modulus $Q=q\tilde{q}$, where $\tilde{q}\approx 2^{24}$ and $q\approx 2^{56}$, $q=q_1{q}_2$ is a multiplied modulus of two close $\mathsf{NTT}$-friendly primes $q_1$ and $q_2$, as in Spiral.

5.1.2. Parameters Compared with Spiral

We add three improvements to Spiral [12]. Therefore, our parameter set is different from that of Spiral. All the notations are taken from the full protocol in Section 4. p is the plaintext modulus. Q and q are the ciphertext moduli. $(v_1,v_2)$ refer to the numbers of the first dimension and the subsequent dimension of database $\mathsf{DB}$, respectively. Roughly speaking, our plaintext modulus is much bigger while the decomposition dimension is smaller, i.e., this implies the reason why our server throughput is better than Spiral. Taking the $2^{20}\times 256$ B (256 MB) database as an example, we can achieve around a $1.7\times$ better overall throughput, as shown in

Table 1. Parameter sets for $2^{20}\times 256$ B (256 MB) database. $({\ell }_{expr}$, ${\mathcal{B}}_{{\ell }_{expr}}$, ${\mathcal{B}}_{expr})$ stand for the decomposition dimension, decomposition base and approximate base used in the $\mathsf{RLWE}$ expansion algorithm, respectively. $({\ell }_{expr}$, ${\mathcal{B}}_{{\ell }_{expr}}$, ${\mathcal{B}}_{expr})$ stand for that of the $\mathsf{RLWE}$s-to-$\mathsf{RGSW}$ algorithm while $({\ell }_{expr}$, ${\mathcal{B}}_{{\ell }_{expr}}$, ${\mathcal{B}}_{expr})$ stand for that of the external product. $p_f$ stands for the probability of decryption failure. “Server Time” refers to the server response time.

Protocols	$\log \mathit{p}$	$(\log \mathit{Q},\log \mathit{q})$	d	$({\mathit{v}}_1,{\mathit{v}}_2)$	n	(${\mathit{\ell }}_{\mathbf{expr}}$, ${\mathcal{B}}_{{\mathit{\ell }}_{\mathbf{expr}}}$, ${\mathcal{B}}_{\mathbf{expr}}$)	(${\mathit{\ell }}_{\mathit{r}2\mathit{g}}$, ${\mathcal{B}}_{{\mathit{\ell }}_{\mathit{r}2\mathit{g}}}$, ${\mathcal{B}}_{\mathit{r}2\mathit{g}}$)	(${\mathit{\ell }}_{\mathbf{eP}}$, ${\mathcal{B}}_{{\mathit{\ell }}_{\mathbf{eP}}}$, ${\mathcal{B}}_{\mathbf{eP}}$)	${\mathit{p}}_{\mathit{f}}$	Server Time
Spiral	8	$(-,56)$	2048	$(8,7)$	2	$(8,2^7,-)$	$(4,2^{16},-)$	$(8,2^7,-)$	<$2^{-100}$	1883 ms
Ours	18	$(80,56)$	4096	$(7,8)$	1	$(6,2^{15},-)$	$(7,2^{10},2^{10})$	$(4,2^{14},-)$	<$2^{-145}$	1222 ms

and

Table 2. Compared with other PIR protocols. “Server preproc.” stands for the server preprocessing time. “Server resp.” stands for the server response time. “Client comp.” stands for the sum of query generation time and recovery time. “Through.” stands for the server throughput, i.e., the database size/server response time. “Ours-Stream” stands for the stream variant of our protocol.

Database 1	Metric	FastPIR [29]	Spiral [12]	SpiralPack [12]	SpiralPack Stream [12]	KsPIR [18]	Ours	Ours-Stream
$2^{20}\times$ 256B (256 MB)	Server storage	-	13.3 MB	13.5 MB	-	8.8 MB	6.7 MB	-
	Server prepro.	2.1 s	9.8 s	8.2 s	8.2 s	4.5 s	2.6 s	2.6 s
	Server resp.	1832 ms	1883 ms	1339 ms	602 ms	246 ms	1222 ms	427 ms
	Query size	1 MB	14 KB	14 KB	8.3 MB	140 KB	40 KB	4.8 MB
	Response size	64 KB	20 KB	20 KB	20 KB	26 KB	26 KB	30 KB
	Through.	140 MB/s	136 MB/s	191 MB/s	425 MB/s	1041 MB/s	236 MB/s	749 MB/s
	Client comp.	12 ms	11 ms	1 ms	378 ms	7.7 ms	2.2 ms	53 ms
$2^{18}\times$ 8 KB (2 GB)	Server storage	-	13.8 MB	14 MB	-	9.1 MB	6.7 MB	-
	Server prepro.	16.3 s	101 s	89 s	90 s	37.1 s	29.6 s	31.6 s
	Server resp.	8932 ms	6013 ms	4998 ms	3332 ms	1641 ms	3645 ms	2223 ms
	Query size	8 MB	14 KB	14 KB	15.8 MB	140 KB	40 KB	8.6 MB
	Response size	64 KB	20 KB	20 KB	20 KB	26 KB	26 KB	30 KB
	Through.	229 MB/s	341 MB/s	410 MB/s	615 MB/s	1248 MB/s	632 MB/s	1152 MB/s
	Client comp.	68 ms	43 ms	1 ms	717 ms	7.8 ms	2.2 ms	160 ms
$2^{20}\times$ 8 KB (8 GB)	Server storage	-	15.5 MB	15.4 MB	-	9.3 MB	6.7 MB	-
	Server prepro.	68.9 s	535 s	410 s	492 s	186 s	166 s	119 s
	Server resp.	35.6 s	24.9 s	13.9 s	11.6 s	6.9 s	14.2 s	5.4 s
	Query size	32 MB	14 KB	14 KB	30 MB	140 KB	40 KB	14.7 MB
	Response size	64 KB	20 KB	20 KB	20 KB	26 KB	26 KB	90 KB
	Through.	230 MB/s	329 MB/s	589 MB/s	706 MB/s	1187 MB/s	649 MB/s	1896 MB/s
	Client comp.	286 ms	91 ms	1 ms	1.5 s	8.2 ms	2.2 ms	158 ms

¹ The databases are 288 MB, 2.25 GB and 9 GB, respectively, for our protocol, and are 320 MB, 2.5 GB and 10 GB, respectively, for the stream variant of our protocol.

.

5.2. Concrete Performances for Our PIR Protocol

In this section, we report the concrete performances of our protocol. Our computing environment is a server with Intel(R) Xeon(R) Gold 6230R CPU @ 2.10 GHz and 256 GB RAM, running Ubuntu 22.04.1. The compiler we used is clang++ 14.0.0.

5.2.1. Compared with Spiral and Prior Works

For a fair comparison with Spiral, we use their C++ implementation [36], which adapts procedure from the SEAL library [37] and the HEXL library [35] to implement $\mathsf{NTT}$s. Moreover, we selected a pre-Spiral PIR protocol, FastPIR [29], as another comparison object. The comparison results are given in Table 2. Taking the performance of the 256 MB database as an example, our server’s overall throughput is around $1.7\times$ faster than that of Spiral. Our online computations are 1.7–2.8× better than those of FastPIR [29] and our online communications are much better. We also found that our three optimizations slightly increase the query and response size, but the increase is acceptable. This allows our protocol to perform well even for resource-constrained clients.

5.2.2. Compared with KsPIR

Recently, Luo et al. [18] proposed a novel PIR protocol called KsPIR. Instead of applying the $\mathsf{RLWE}$ expansion algorithm like most $\mathsf{RLWE}$-based PIR protocols, they use a BSGS (baby-step giant-step) algorithm to perform multiple homomorphic matrix vector multiplications, and finally they pack these $\mathsf{RLWE}$ ciphertexts through an $\mathsf{RLWE}$ packing algorithm. The server throughput of KsPIR is faster than that of Spiral; therefore, it seems to have better application prospects. However, the query of KsPIR consists of an $\mathsf{RLWE}$ ciphertext and an $\mathsf{RGSW}$ ciphertext, so the query size is at least $2\times$ bigger than that of Spiral as well as ours. Taking the performance of the 256 MB database as an example, our server’s overall throughput is worse than that of KsPIR [18], but our communication is $2.5\times$ better than that of KsPIR. Moreover, our server storage is around $1.3\times$ better than that of KsPIR.

6. Recent Works

6.1. $\mathsf{LWE}$-Based PIR Protocols

Henzinger et al. [6] proposed two efficient $\mathsf{LWE}$-based PIR protocols called Simple PIR and Double PIR. They can achieve high throughput while the drawback of them is that the client must download and store an around 124 MB (Simple PIR) and 16 MB (Double PIR) hint, respectively. Recently, Li et al. [16] proposed HintlessPIR and Menon and Wu [17] proposed YPIR. These two PIR protocols eliminate the need to store a hint on the client side, and they outperform Spiral in terms of server throughput. However, their communications, client computations and rate are much worse than those of Spiral. For example, when the database reaches 1 GB, the query and response sizes of Spiral are $14+20$ KB (40 + 22 KB for ours) while those of HintlessPIR are $443+3008$ KB and those of YPIR are $846+12$ KB. Therefore, Spiral is still the state-of-the-art low-communication, high-rate PIR solution at present, which makes it still have important application value when the client resources are limited. As PIR is an essential privacy-preserving technology, it is critical to have various options available for users to determine the best tradeoff based on their specific scenarios.

6.2. Efficient Sublinear PIR Protocols

Two-server PIR protocols [5] have received widespread attention for they can achieve a sublinear server computation cost. However, two-server PIR protocols require the two servers to store two copies of the same database, which brings difficulties to real-world deployment. Recently, there has been a breakthrough in how to convert a two-server PIR into a single-server PIR [38]. Piano [38] utilizes lightweight cryptography such as PRFs to achieve sublinear server computation. However, their current solution is not optimal. In the preprocessing phase, the communication size is the same as the size of the entire database, although the client does not need to store it. In addition, the client needs to do more than hundreds of seconds of preprocessing. This would not be suitable for clients who are computing-resource constrained.

6.3. Keyword PIR Protocols

Sometimes index PIR cannot meet the requirements of some applications, and keyword PIR is more general. Fortunately, there are some methods to convert an index PIR into a keyword PIR. Refs. [10,39,40] are all using some probabilistic data structure to encode the database; specifically, they are using cuckoo hashing, a random band matrix and a binary fuse filter, respectively. The cuckoo hashing approach is more generic, ref. [39] is suitable for some $\mathsf{RLWE}$-based protocols, and ref. [40] is suitable for some $\mathsf{LWE}$-based protocols. Additionally, these are also other methods that are not based on an index PIR, e.g., ref. [41] is based on an equality operator.